Energy–Logistics Cooperative Optimization for a Port-Integrated Energy System
Abstract
:1. Introduction
2. Related Works
2.1. Logistics System Scheduling Model
2.2. Logistics System Load Model
2.3. Energy System Model
2.4. Literature Analysis and Motivations
- Motivation: To overcome this drawback and achieve optimal operating costs for the port, we construct a collaborative optimization model for logistics and energy systems and conduct relevant research and a sensitivity analysis using a port in Shanghai as an example. The results verify the effectiveness of the proposed optimization method in port energy conservation and emission reductions.
- Motivation: To address this challenge, efforts should be made to promote the development of ports in a green and low-carbon direction. In this model, we introduce a renewable energy consumption system, and the intermittency of renewable energy leads to its low direct utilization rate. The introduction of P2H technology, MR, and hydrogen storage (HS) tanks absorbed some of the remaining renewable energy, thereby maximizing the consumption of renewable energy.
- Motivation: To overcome the problems of a slow model solving speed and a low solving accuracy, in this study, we construct a hybrid system modeling method that decouples and finely describes coupling constraints by increasing the number of variables, ultimately achieving fast and high-precision model solving. Compared with traditional modeling methods, this method leads to significant improvements in running speed and accuracy.
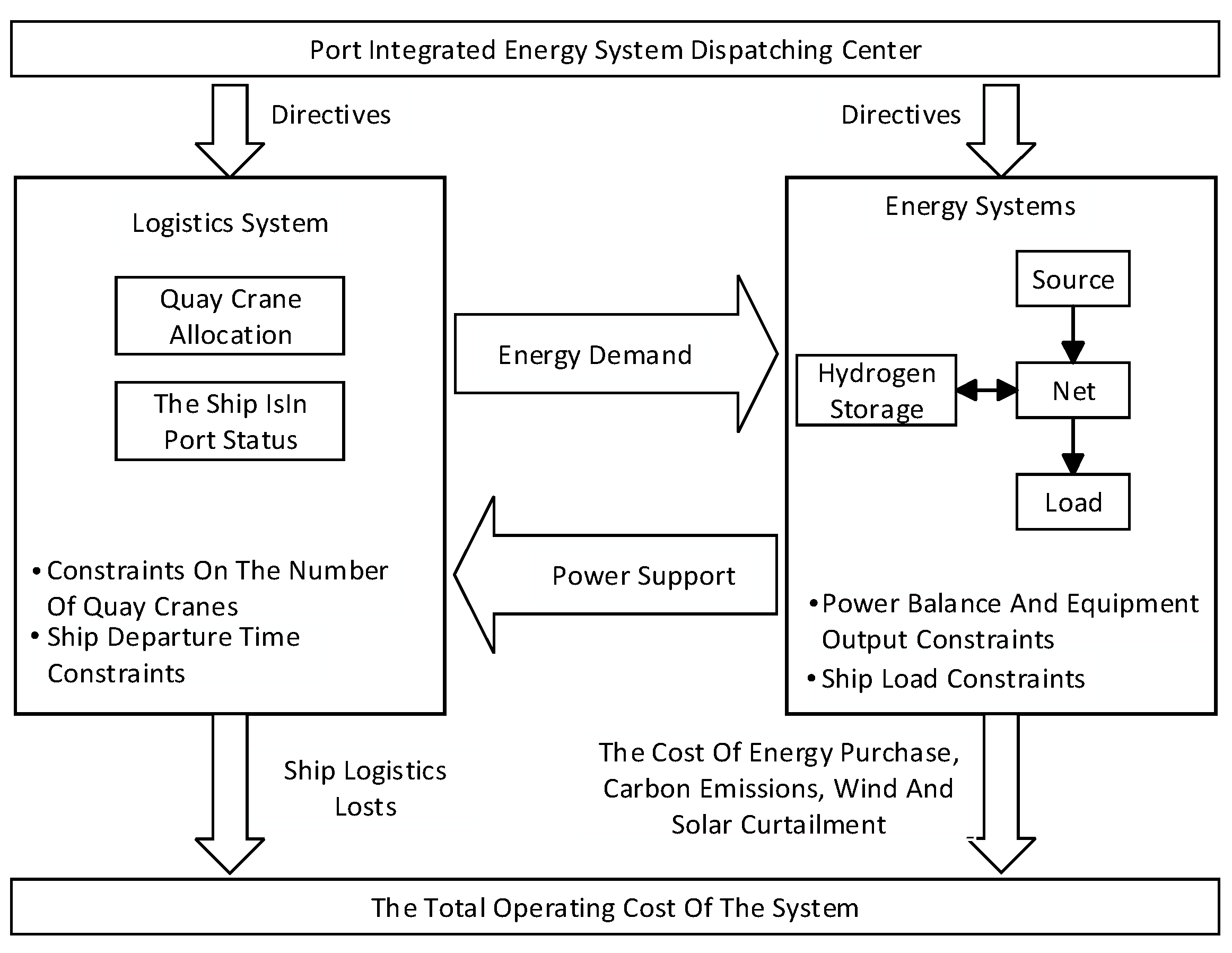
3. System Description
3.1. Description of the Port-Integrated Energy System
3.2. Description of the Modeling Method
4. Energy–Logistics Integrated Systems Modeling
4.1. Logistics System Scheduling Model
4.1.1. Ship Berthing Time Model
4.1.2. Ship-in-Port State Model
4.1.3. Port Logistics Constraint Mode
4.2. Logistics System Load Model
4.2.1. Quay Crane Load Model
4.2.2. Ship Load Model
4.3. Energy System Model
4.3.1. Combined Cooling, Heating and Power
4.3.2. Gas Turbine
4.3.3. Fuel Cell
4.3.4. Photovoltaics and Wind Turbine
4.3.5. Power to Hydrogen
4.3.6. Hydrogen Storage
4.3.7. Methanation Device
5. Energy–Logistics Optimization
5.1. Objective Functions
5.2. Balance Model
5.3. Model Solving
6. Case Verification
6.1. Results and Discussion
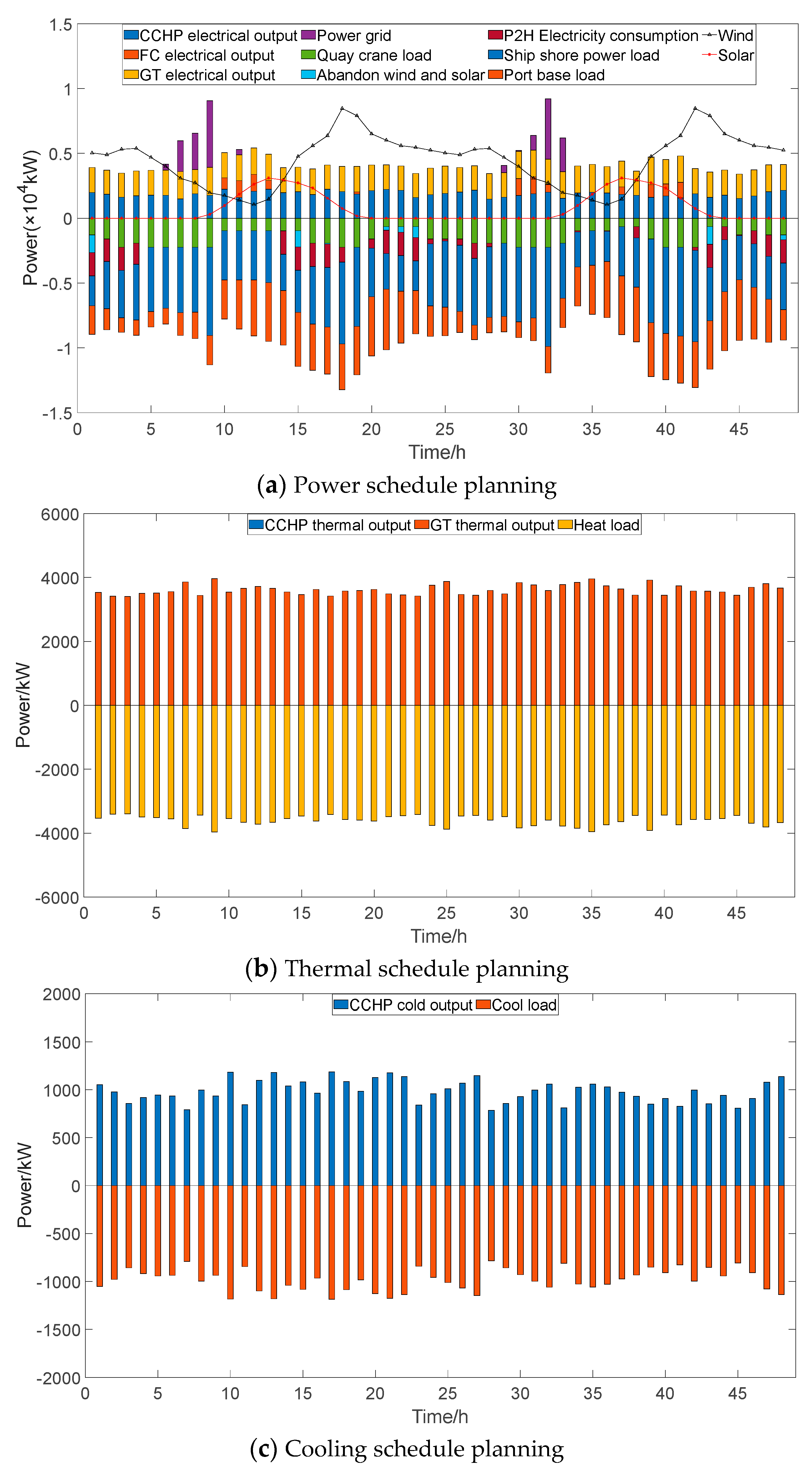
6.1.1. Energy–Logistics System Collaborative Optimization Analysis
- (1)
- Case A: Separate optimization of logistics and energy systems;
- (2)
- Case B: Collaborative optimization of logistics and energy systems.
6.1.2. Scheduling Analysis of Ships Waiting for Berth
6.2. Sensitivity Analysis
- (a)
- Through a data comparison, it is found that when the upper limit of P2H power increases, the consumption rate of renewable energy improves, indirectly reducing the purchasing power of the port, thereby reducing the operating costs of the port.
- (b)
- When only renewable energy generation is increased, this will cause excessive waste, and the operating costs of ports will not significantly increase; when the upper limit of P2H power and the amount of renewable energy generation increase synchronously, the operating costs of the port will be further reduced. Therefore, when expanding, it is possible to consider binding the two together.
- (c)
- When a fixed electricity price is used in ports instead of time-of-use electricity prices, the flexibility of berth scheduling is independent of electricity prices, which further reduces the performance of port collaborative optimization scheduling. Therefore, time-of-use electricity prices are an indispensable part of port collaborative optimization scheduling.
- (d)
- When doubling the carbon emission price of the port, the carbon emission cost of the port also doubles and the operating cost increases significantly. Thus, it can be seen that carbon emission prices have a significant impact on port operating costs.
7. Managerial Implications
- (a)
- We should advocate for the coordinated optimization of port logistics and energy systems, which can reduce the operating costs of a port overall. This can promote the collaborative optimization of ports by implementing practical reward and punishment mechanisms for port operators and relevant stakeholders.
- (b)
- Policy-makers can encourage port operators to install more PV and WTs, emphasizing the importance of renewable energy for green and low-carbon ports. This can not only promote energy conservation and emission reductions in ports, but also reduce dependence on fossil fuel power generation, thereby protecting the environment.
- (c)
- Governments should encourage port operators to adopt P2H technology and related hydrogen equipment to reduce carbon dioxide emissions. This may include providing subsidies to ports that purchase equipment that helps reduce carbon dioxide emissions.
- (d)
- Policy-makers should encourage learning and exchange between different countries and ports to share knowledge and learn about port operation strategies and carbon reduction methods. This can promote a global approach to reducing port operating costs and promoting the consumption of renewable energy.
8. Conclusions, Limitation and Future Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Acronyms | |
| PIES | Port-Integrated Energy System. |
| CCHP | Combined Cooling, Heating, and Power. |
| GT | Gas turbine. |
| AC | Refrigeration machine. |
| P2H | Power to hydrogen. |
| PV | Photovoltaics. |
| WT | Wind turbine. |
| HS | Hydrogen storage. |
| EH | Energy hub. |
| MR | Methanation device. |
| FC | Fuel cell. |
| Indices | |
| n/j | Set/index of ships. |
| T,t | Set/index of operation periods. |
| m/i | Set/index of variable power equipment. |
| Parameters | |
| t0/ | Estimated arrival/departure time of a ship. |
| Nj | Number of loading or unloading containers. |
| η | Loading and unloading efficiency of quay cranes. |
| / | Maximum and minimum number of quay cranes. |
| Power consumption of a single quay crane. | |
| Δt | Unit scheduling period. |
| Cmax | Total amount of quay crane resources. |
| Wvar,i | Rated workload of the intermittent equipment. |
| / | Upper/lower limits of the intermittent equipment. |
| Electrical efficiency of GT. | |
| Heat loss rate of GT. | |
| Flue gas recovery rate of GT. | |
| Recovery rate of waste heat of GT. | |
| Refrigeration coefficient of AC. | |
| Electrical efficiency of GT. | |
| Thermal efficiency of GT. | |
| COPFC | Electrical efficiency of FC. |
| COPP2H | Electrolytic efficiency of P2H. |
| Charging efficiency of HS. | |
| Discharging efficiency of HS. | |
| COPMR | Conversion efficiency of MR. |
| Hload | Constant heat load of the port. |
| Lload | Constant cooling load of the port |
| α/β | Carbon emission coefficient of power/gas. |
| Pgas | Natural gas price. |
| Pco2 | Carbon emission price. |
| Maximum carbon emissions of ports. | |
| Pabandon | Abandoned wind and solar punishment cost. |
| a1 | Valley price. |
| a2 | Ordinary price. |
| a3 | Peak price. |
| Variables | |
| t1/tleave | Berthing time/departure time of ship. |
| Cj | Allocation quantity of quay cranes. |
| / | Earliest/latest departure time of ship. |
| / | Maximum and minimum number of quay cranes. |
| Xj(t) | Ship in port state. |
| Pcrane(t) | Power consumption of all quay cranes. |
| Lship(t) | Total load power of the ship. |
| Lcons(t) | Constant power load of the ship. |
| Lvar(t) | Variable power load of the ship. |
| Lvar,i(t) | Size of variable power. |
| si(t) | Status of intermittent working equipment. |
| Pship(t) | Sum of the shore power of all ships. |
| QCCHP | Gas consumption of CCHP. |
| Power generation of GT. | |
| Recyclable heat power of GT exhaust gas. | |
| Total thermal produced by CCHP. | |
| Cold power output by CCHP. | |
| Heat supplied to the port outputting by CCHP. | |
| Power generation of GT. | |
| Heat generation of GT. | |
| QGT | Gas consumption of GT. |
| MFC | Hydrogen consumption of FC. |
| PFC | Power generated by FC. |
| PP2H | Electrical power consumed by P2H. |
| MP2H | Hydrogen production of P2H. |
| MHS,t | Energy storage state value of HS. |
| / | Charging/discharging hydrogen power of HS. |
| MMR | Hydrogen consumption of the MR. |
| QMR | Power of methane production of the MR. |
References
- Ezeh, C.I.; Richter, U.H.; Seufert, J.H.; Peng, C. Operational-Based Decarbonization of Container Ports: The Case of Ningbo-Zhoushan Port. Int. J. Sustain. Transp. 2024, 18, 34–45. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhou, H. The Emission Reduction Technology Decision of the Port Supply Chain. Mathematics 2024, 12, 848. [Google Scholar] [CrossRef]
- Daniel, H.; Trovão, J.P.F.; Williams, D.; Boulon, L. Unlocking Shore Power in St. Lawrence and Great Lakes for Cargo Ships. Transp. Res. Part D Transp. Environ. 2024, 131, 104230. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, H.; Zhen, L. Berth and Quay Cranes Allocation Problem with On-Shore Power Supply Assignment in Container Terminals. Comput. Ind. Eng. 2024, 188, 109910. [Google Scholar] [CrossRef]
- Karimi, S.; Zadeh, M.; Suul, J.A. Operation-Based Reliability Assessment of Shore-to-Ship Charging Systems Including On-Shore Batteries. IEEE Trans. Ind. Appl. 2023, 59, 4752–4763. [Google Scholar] [CrossRef]
- Qi, P.; Gao, W. Study on Load Forecasting of Combined Cooling, Heat and Power System with Deep Learning Algorithm Based on Attention Mechanism. In Proceedings of the 2023 5th International Academic Exchange Conference on Science and Technology Innovation (IAECST), Guangzhou, China, 8–10 December 2023; pp. 1353–1358. [Google Scholar]
- Holder, D.; Percy, S.D.; Yavari, A. A Review of Port Decarbonisation Options: Identified Opportunities for Deploying Hydrogen Technologies. Sustainability 2024, 16, 3299. [Google Scholar] [CrossRef]
- Giri, B.K.; Roy, S.K.; Deveci, M. Fuzzy Robust Flexible Programming with Me Measure for Electric Sustainable Supply Chain. Appl. Soft Comput. 2023, 145, 110614. [Google Scholar] [CrossRef]
- Giri, B.K.; Roy, S.K. Fuzzy-Random Robust Flexible Programming on Sustainable Closed-Loop Renewable Energy Supply Chain. Appl. Energy 2024, 363, 123044. [Google Scholar] [CrossRef]
- Lei, J.; Zhang, H.; Pan, J.; Zhuo, Y.; Chen, A.; Chen, W.; Yang, Z.; Feng, K.; Li, L.; Wang, B.; et al. Techno-Economic Assessment of a Full-Chain Hydrogen Production by Offshore Wind Power. Energies 2024, 17, 2447. [Google Scholar] [CrossRef]
- Chavan, H.R.; Knollmeyer, J.; Khan, S. A Study on the Potential of Hydrogen Fuel Cells for Maritime Transportation Applications. In Proceedings of the SoutheastCon 2023, Orlando, FL, USA, 1–16 April 2023; pp. 498–503. [Google Scholar]
- Kelmalis, A.; Dimou, A.; Lekkas, D.F.; Vakalis, S. Cold Ironing and the Study of RES Utilization for Maritime Electrification on Lesvos Island Port. Environments 2024, 11, 84. [Google Scholar] [CrossRef]
- Zhang, L.; Zeng, Q.; Wang, L. How to Achieve Comprehensive Carbon Emission Reduction in Ports? A Systematic Review. J. Mar. Sci. Eng. 2024, 12, 715. [Google Scholar] [CrossRef]
- Sun, P.; Wang, L.; Yuan, T.; Ma, D.; Ma, L.; Li, L.; Guo, J.; Dong, X.; Gao, K. A Comprehensive Study on Electric Field Coupling Effects of Medium-Voltage SiC Power Module and Optimization Design. In Proceedings of the 2024 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 25–29 February 2024; pp. 2556–2561. [Google Scholar]
- He, W.; Feng, Y.; Wu, S.; Wang, W. Mechanical–Thermal–Electrical Coupling Modeling and Temperature Rise Characteristic of a Parallel Groove Clamp with Improved Representation of Contact Interactions. IEEE Trans. Compon. Packag. Manuf. Technol. 2023, 13, 356–364. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, C.; Sun, B.; Liu, S. The Electric-Thermal Coupling Simulation and State Estimation of Lithium-Ion Battery. J. Energy Storage 2023, 58, 106431. [Google Scholar] [CrossRef]
- Fu, L.; Li, H.; Deng, Y.; Tang, C. The Influence of Small Molecule Products on Natural Ester Impregnated Cellulose Insulation Paper under Electric-Thermal Coupling Field. Colloids Surf. A Physicochem. Eng. Asp. 2024, 697, 134426. [Google Scholar] [CrossRef]
- Song, R.; Hamacher, T.; Terzija, V.; Perić, V.S. Potentials of Using Electric-Thermal Sector Coupling for Frequency Control: A Review. Int. J. Electr. Power Energy Syst. 2023, 151, 109194. [Google Scholar] [CrossRef]
- Liu, W.; Teh, J.; Alharbi, B.; Yang, G.; Wang, B.; Meng, D.; Shi, J.; AlKassem, A.; Aljabr, A.; Alshammari, N. An Electric-Thermal Coupling Modeling Method for Lithium-Ion Battery Using the State of Charge Normalization Calculation Method. J. Energy Storage 2023, 72, 108724. [Google Scholar] [CrossRef]
- Skowron, Ł.; Chygryn, O.; Gąsior, M.; Koibichuk, V.; Lyeonov, S.; Drozd, S.; Dluhopolskyi, O. Interconnection between the Dynamic of Growing Renewable Energy Production and the Level of CO2 Emissions: A Multistage Approach for Modeling. Sustainability 2023, 15, 9473. [Google Scholar] [CrossRef]
- Putranto, L.M.; Budi, R.F.S.; Novitasari, D. Generation Expansion Planning with a Renewable Energy Target and Interconnection Option: A Case Study of the Sulawesi Region, Indonesia. Renew. Sustain. Energy Rev. 2023, 183, 113489. [Google Scholar] [CrossRef]
- Ren, Y. Research of AGV Scheduling in Container Terminal. Master’s Thesis, Jimei University, Xiamen, China, 2014. [Google Scholar]
- Borelli, D.; Devia, F.; Schenone, C.; Silenzi, F.; Tagliafico, L.A. Dynamic Modelling of LNG Powered Combined Energy Systems in Port Areas. Energies 2021, 14, 3640. [Google Scholar] [CrossRef]
- Aljuaid, A.M.; Koubâa, M.; Ammar, M.H.; Kammoun, K.; Hachicha, W. Mathematical Programming Formulations for the Berth Allocation Problems in Container Seaport Terminals. Logistics 2024, 8, 50. [Google Scholar] [CrossRef]
- Song, T.; Li, Y.; Zhang, X.-P.; Wu, C.; Li, J.; Guo, Y.; Gu, H. Integrated Port Energy System Considering Integrated Demand Response and Energy Interconnection. Int. J. Electr. Power Energy Syst. 2020, 117, 105654. [Google Scholar] [CrossRef]
- Kovač, M.; Tadić, S.; Krstić, M.; Roso, V. Modelling Dry Port Systems in the Framework of Inland Waterway Container Terminals. Comput. Model. Eng. Sci. 2023, 137, 1019–1046. [Google Scholar] [CrossRef]
- Xu, X.; Li, Z.; Jiang, X.; Huang, X.; Lu, Y.; Li, L. Port Berth Allocation and Microgrid Cluster Joint Optimization Scheduling Based on Master-Slave Game. J. Clean. Prod. 2024, 452, 142220. [Google Scholar] [CrossRef]
- Zhao, W.; Ma, K.; Yang, J.; Guo, S. A Risk-Averse Logistics-Energy Coordination Optimization Strategy for Port Energy System Considering Demand Response Program. Electr. Power Syst. Res. 2024, 231, 110297. [Google Scholar] [CrossRef]
- Shi, Z.; Fan, F.; Tai, N.; Qing, C.; Meng, Y.; Guo, R. An Optimal Operation Strategy for Integrated Energy-Logistics System in Green Port. In Proceedings of the 2022 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Shanghai, China, 8–11 July 2022; pp. 1592–1597. [Google Scholar]
- Lassoued, R.; Elloumi, A. A Bi-Level Optimization Model for Solving the Berth and Quay Cranes Allocation Problems in Port Terminal. In Proceedings of the 2021 International Conference on Decision Aid Sciences and Application (DASA), Sakheer, Bahrain, 7–8 December 2021; pp. 981–985. [Google Scholar]
- Lassoued, R.; Elloumi, A. Hierarchical Optimization for Solving the Integrated Berth and Quay Crane Assignment Problem in Port Terminal. In Proceedings of the 2022 8th International Conference on Control, Decision and Information Technologies (CoDIT), Istanbul, Turkey, 17–20 May 2022; Volume 1, pp. 1479–1483. [Google Scholar]
- Chang, S.-C.; Lin, M.-H.; Tsai, J.-F. An Optimization Approach to Berth Allocation Problems. Mathematics 2024, 12, 753. [Google Scholar] [CrossRef]
- Ji, B.; Huang, H.; Yu, S.S. An Enhanced NSGA-II for Solving Berth Allocation and Quay Crane Assignment Problem with Stochastic Arrival Times. IEEE Trans. Intell. Transp. Syst. 2023, 24, 459–473. [Google Scholar] [CrossRef]
- Wang, Z. Optimization of Port Ship Collaborative Scheduling Based on Differential NSGA-II Algorithm. China Water Transp. 2023, 23, 19–21. [Google Scholar]
- Pu, Y.; Liu, H.; Wang, J.; Hou, Y. Collaborative Scheduling of Port Integrated Energy and Container Logistics Considering Electric and Hydrogen-Powered Transport. IEEE Trans. Smart Grid 2023, 14, 4345–4359. [Google Scholar] [CrossRef]
- Jiang, M.; Ma, F.; Zhang, Y.; Lv, S.; Pei, Z.; Wu, G. Collaborative Scheduling Optimization of Container Port Berths and Cranes under Low-Carbon Environment. Sustainability 2024, 16, 2985. [Google Scholar] [CrossRef]
- Yu, M.; Lv, Y.; Li, W. Multi objective optimization of low-carbon global scheduling for field bridges. Logist. Technol. 2020, 39, 41–47. [Google Scholar]
- Mao, A.; Yu, T.; Ding, Z.; Fang, S.; Guo, J.; Sheng, Q. Optimal Scheduling for Seaport Integrated Energy System Considering Flexible Berth Allocation. Appl. Energy 2022, 308, 118386. [Google Scholar] [CrossRef]
- Yang, J.; Wang, J.; Ma, K.; Liu, H.; Dai, Y.; Li, C. A Multi-Energy Pricing Strategy for Port Integrated Energy System Based on Bayesian Stackelberg Game. Sustain. Energy Grids Netw. 2024, 38, 101264. [Google Scholar] [CrossRef]
- Zhen, L.; Yang, Z.; Wang, S.; Hu, H.; Chew, E.P.; Fan, T. Integrated Planning Model for Two-Story Container Ports. Transp. Res. Part C Emerg. Technol. 2024, 160, 104535. [Google Scholar] [CrossRef]
- Bemporad, A.; Morari, M. Control of Systems Integrating Logic, Dynamics, and Constraints. Automatica 1999, 35, 407–427. [Google Scholar] [CrossRef]
- Heemels, W.P.M.H.; Schutter, B.D.; Bemporad, A. Equivalence of Hybrid Dynamical Models. Automatica 2001, 37, 1085–1091. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, T.; Gao, Y.; Lv, L.; Song, X. A MATLAB GUI Toolbox for Surrogate-Based Design and Optimization. In Proceedings of the 2019 IEEE 9th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Suzhou, China, 29 July–2 August 2019; pp. 103–106. [Google Scholar]
- Xu, L.; Xu, X.; Tang, Y.; Ren, X.; Guo, Y. A Matlab Toolbox for Modelling Viscoelastic Constitutive Equation and Parameter Optimization. In Proceedings of the 2017 3rd IEEE International Conference on Computer and Communications (ICCC), Chengdu, China, 13–16 December 2017; pp. 2884–2888. [Google Scholar]
- Huang, Y.; Huang, W.; Wei, W.; Tai, N.; Li, R. Logistics-energy Collaborative Optimization Scheduling Method for Large Seaport Integrated Energy System. Chin. J. Electr. Eng. 2022, 42, 6184–6196. [Google Scholar] [CrossRef]






| Study | DN | SO | RE | P2H | FP | SM |
|---|---|---|---|---|---|---|
| Lassoued and Elloumi [30] | M | LSO | bi-level programming model | |||
| Zhao et al. [28] | M | COLE | √ | √ | risk-aware stochastic method | |
| Ji et al. [33] | S | LSO | √ | enhanced non-dominated sorting genetic algorithm II | ||
| Shi et al. [29] | M | COLE | √ | √ | mixed-integer linear programming | |
| Chang et al. [32] | M | LSO | genetic algorithm optimization approach | |||
| Wang et al. [4] | M | LSO | √ | adaptive immune clone selection algorithm | ||
| Pu et al. [35] | M | COLE | √ | √ | distributed algorithm based on Benders decomposition | |
| Jiang et al. [36] | M | LSO | √ | nonlinear mixed-integer programming formulation | ||
| Lassoued and Elloumi [31] | M | LSO | bi-level programming model | |||
| Song et al. [25] | M | ESO | √ | mixed-integer linear programming | ||
| Aljuaid et al. [24] | M | LSO | multi-objective optimization model based on goal programming | |||
| Kovač et al. [26] | S | LSO | hybrid metaheuristic model | |||
| Mao et al. [38] | M | COLE | Mixed-integer linear programming | |||
| Xu et al. [27] | M | LSO | a multi-objective berth allocation model | |||
| Proposed study | M | COLE | √ | √ | √ | hybrid system modeling method |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| η (TEU/H) | 35 | 0.3 | β (kg/kWh) | 2.262 | |
| Cmax | 7 | 0.55 | Pgas (USD/kWh) | 0.0422 | |
| (kW) | 320 | COPFC | 0.65 | Pco2 (USD/kg) | 0.0068 |
| 0.3 | COPP2H | 0.6 | (kg/h) | 35,000 | |
| 0.15 | 0.98 | Pabbandon (USD/kWh) | 0.0138 | ||
| 0.3 | 0.98 | a1 (USD/kWh) | 0.0651 | ||
| 0.8 | COPMR | 0.5 | a2 (USD/kWh) | 0.1211 | |
| 1.2 | α (kg/kWh) | 0.7129 | a3 (USD/kWh) | 0.1514 |
| Ship Number | Time of Arrival/h | Latest Departure Time/h | Loading And Unloading /Box | Largest Quay Crane Demand/Unit | Minimal Quay Crane Demand/Unit |
|---|---|---|---|---|---|
| 1 | 1 | 14 | 450 | 4 | 2 |
| 2 | 2 | 14 | 600 | 3 | 1 |
| 3 | 5 | 25 | 800 | 5 | 2 |
| 4 | 8 | 27 | 500 | 3 | 2 |
| 5 | 11 | 30 | 550 | 3 | 2 |
| 6 | 15 | 25 | 500 | 3 | 1 |
| 7 | 18 | 34 | 600 | 2 | 1 |
| 8 | 23 | 42 | 500 | 3 | 2 |
| 9 | 27 | 39 | 650 | 3 | 1 |
| 10 | 29 | 42 | 550 | 4 | 2 |
| 11 | 31 | 46 | 450 | 3 | 1 |
| 12 | 34 | 47 | 550 | 2 | 1 |
| 13 | 38 | 48 | 600 | 5 | 2 |
| 14 | 40 | 48 | 500 | 4 | 2 |
| Parameter | Case A | Case B |
|---|---|---|
| Cbuy/USD | 30,094.7 | 27,199 |
| Cco2/USD | 8896.5 | 9511.1 |
| Closs/USD | 362.4 | 83.1 |
| Abandoned wind and solar rate/% | 10.32 | 2.37 |
| Cship/USD | 10,926.7 | 11,894.9 |
| Total cost/USD | 50,280.3 | 48,688.1 |
| Compare with case B | +3.27% | - |
| Parameter | Case B | Case C |
|---|---|---|
| Cbuy/USD | 27,199 | 31,653.8 |
| Cco2/USD | 9511.1 | 9690 |
| Closs/USD | 83.1 | 412.2 |
| Abandon wind and solar rate/% | 2.37 | 11.73 |
| Cship/USD | 11,894.9 | 11,203.3 |
| Total cost/USD | 48,688.1 | 52,959.3 |
| Compare with case B | - | +8.77% |
| Parameter | Case B | P2H*2 | Re*2 | (P2H+Re)*2 | Fixed Electricity Price | CO2*2 |
|---|---|---|---|---|---|---|
| Cbuy/USD | 27,119 | 27,072.7 | 24,992.9 | 24,340.4 | 27,690.3 | 26,968.7 |
| Cco2/USD | 9511.1 | 9503.4 | 9413.9 | 9418 | 9486.1 | 18,987.7 |
| Closs/USD | 83.1 | 0 | 2568.5 | 1749.9 | 53 | 65.7 |
| Abandon rate/% | 2.37 | 0 | 36.56 | 24.91 | 1.51 | 1.87 |
| Cship/USD | 11,894.9 | 11,894.9 | 11,203.3 | 11,065 | 12,309.8 | 12,171.5 |
| Total cost/USD | 48,688.1 | 48,471 | 48,178.6 | 46,573.3 | 49,539.2 | 58,193.6 |
| Compared with case B | - | −0.45 | −1.05 | −4.34 | +1.75 | +19.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mo, A.; Zhang, Y.; Xiong, Y.; Ma, F.; Sun, L. Energy–Logistics Cooperative Optimization for a Port-Integrated Energy System. Mathematics 2024, 12, 1917. https://doi.org/10.3390/math12121917
Mo A, Zhang Y, Xiong Y, Ma F, Sun L. Energy–Logistics Cooperative Optimization for a Port-Integrated Energy System. Mathematics. 2024; 12(12):1917. https://doi.org/10.3390/math12121917
Chicago/Turabian StyleMo, Aiming, Yan Zhang, Yiyong Xiong, Fan Ma, and Lin Sun. 2024. "Energy–Logistics Cooperative Optimization for a Port-Integrated Energy System" Mathematics 12, no. 12: 1917. https://doi.org/10.3390/math12121917
APA StyleMo, A., Zhang, Y., Xiong, Y., Ma, F., & Sun, L. (2024). Energy–Logistics Cooperative Optimization for a Port-Integrated Energy System. Mathematics, 12(12), 1917. https://doi.org/10.3390/math12121917






