Sliding Mode Control of a Class of Hybrid-Switched Systems with Disturbances

Abstract

This paper investigates the problem of sliding mode control for a class of hybrid switched systems with matching disturbances. Firstly, a sliding mode surface is designed, and the corresponding sliding mode equation for the switched system is derived. Then, we analyzed the stability of the sliding mode equation using the Lyapunov function and average dwell time. Moreover, a sliding mode control law is designed with the approach law method to drive the system state to a bounded sliding mode region and then maintain it there subsequently. Finally, an illustrative example is given to demonstrate the efficiency of the approach.

1. Introduction

With the continuous expansion of modern control system application field, switched systems become more and more important in practical application. Switched systems are composed of continuous or discrete-time subsystems, ang switching regulations coordinating the transitions between them. Switched system can simplify the mathematical model of the system, minimize the computational complexity and enhance the real-time efficiency of the system. It has been widely used in different fields, such as PI control of vehicle transmission [1], flight control system [2], power electronics system [3,4], network control system [5,6,7], and has attracted great attention from researchers. In the switched system, the switching signal indicates how each subsystem operates, and it is the core factor that determines the stable operation of the system. Because of the uncertainty and non-linearity in the switched process, it has become an important research focus to design effective control strategies to ensure the stability and performance. Using the event-triggered mechanism, Fei et al. [8] studied the dynamic output feedback control for switched systems with asynchronous switching. On the basis of the common Lyapunov function search method, Zhang et al. [9] proposed an integral sliding mode surface with good robustness to uncertainty, which is suitable for uncertain switched systems under arbitrary time-varying switched rules. Lian et al. [10] proposed a dynamic quantization strategy with known perturbation bounds for a class of switched linear systems with uncertain non-linearity.

As a robust control strategy, sliding mode control (SMC) is favored for its simple structure and rapid response. Sliding mode control technology regulates the dynamic characteristics of the system by predefined sliding mode surfaces, thereby guiding the system state to converge onto and subsequently slide along these surfaces. The design concept of SMC aims to ensure optimal performance and stability of the system, even in the presence of uncertainties such as external disturbances and inaccuracies in modeling. Due to these advantages of SMC, it has been an extensive application in diverse and intricate systems [11,12,13,14]. In recent years, the SMC technology has seen a wide range of application and has made some key progress. It has been applied to Markov jump systems, switched systems, stochastic systems and fuzzy systems [15,16,17,18,19,20,21]. Fei et al. [22] proposed a scheme combining fractional-order SMC and fuzzy neural network, which can effectively reduce the nonlinear influence caused by the combination of environmental fluctuations and unknown uncertainties, and this scheme has strong robustness. Meng et al. [23] researched the event-triggered SMC problem of switched systems with fractional order less than 1 based on the observer and constructed trigger rules to limit the updating of control signals. Zhao et al. [24] proposed an event-triggered observer SMC strategy for a class of Markov jump systems with time-varying delays. Huynh et al. [25] proposed a highly robust second-order sliding mode control method for a class of multi-region steam-hydropower dynamics systems, which improves the reliability of MASHPS LFC and power systems.

Inspired by the above discussion, the aim of this paper is to provide an efficient SMC design method for discrete-time switched systems with matching perturbations, which differs from existing works [26,27]. In this paper, considering the particularity of the system, a reduced-order sliding mode dynamical system of the switched system is constructed by state transformation and provides the sufficient conditions for the exponential stability of the related sliding mode dynamic systems. A new sliding mode controller design scheme based on the system model is proposed by using Lyapunov function method. This paper makes the following contributions:

(1)

We address the SMC problem for a category of switched systems with matching disturbances. By using a state transformation and proposing a sliding mode surface function, we construct the sliding mode equation for the switched system.

(2)

We present sufficient conditions for the exponential stability of switched sliding mode equation using Lyapunov function theory and ADT method.

(3)

Based on the characteristics of sliding mode control for switched systems, we devised a sliding mode controller for guaranteeing the convergence of the closed-loop system to the sliding mode region. Using an example, this conclusion is demonstrated to be valid.

The following is the structure of the rest of this article. In Section 2, the problem description is given, and the sliding mode surface function is designed. In Section 3, we analyze the exponential stability of the switching sliding mode dynamic equation is analyzed. In Section 4, we design an appropriate sliding mode controller to ensure the accessibility of the quasi-sliding modes. In Section 5, we provide a numerical example that verifies the effectiveness of the method proposed. In Section 6, we summarize our research work.

Notations: $\mathbb{R}$ and ${\mathbb{N}}^{+}$ denote real numbers and positive integers, respectively; ${\mathbb{R}}^n$ signals the real n-dimensional space; ${\mathbb{R}}^{m\times n}$ signals the real $m\times n$ dimensional matrix space. $X^T$ signals the transpose of matrix X. The notion $P>0$ means that P is the positive definite symmetric matrix. I is used to represent an identity matrix of appropriate dimensions. ‘∗’ represents an ellipsis of the symmetrically induced term. $rank\left(·\right)$ represents the rank of the matrix, ${\lambda }_{max}\left(·\right)$ and ${\lambda }_{min}\left(·\right)$ represent the maximum and minimum eigenvalue of a symmetric matrix, respectively.

2. System Description and Problem Statement

Consider the following systems:

$$\begin{array}{c}\hfill x(k+1)=A\left(\sigma \left(k\right)\right)x\left(k\right)+D\left[u\left(k\right)+F\left(\sigma \left(k\right)\right)f(x,k)\right],\end{array}$$

(1)

where $x\left(k\right)\in R^n$ represent the state variables of the system, and $u\left(k\right)\in R^m$ is the control input. $\left\{A\left(\sigma \left(k\right)\right),F\left(\sigma \left(k\right)\right):\sigma \in \mathcal{N}\right\}$ represent a family of known matrices depending on the index set $\mathcal{N}=\left\{1,2,\cdots ,N\right\}$. $\sigma \left(k\right):{\mathbb{N}}^{+}\to \mathcal{N}$ specifies the index of the active subsystem at the instant k. Suppose that the sequence of sub-modes of the switching signal $\sigma \left(k\right)$ is unknown beforehand, but its instantaneous value is available in real-time.

For $\sigma \left(k\right)=i$, we denote the system associated with the i th subsystem by $A\left(\sigma \left(k\right)\right)\triangleq A\left(i\right)$, $F\left(\sigma \left(k\right)\right)\triangleq F\left(i\right)$. In this paper, $f(x,k)$ represents a disturbance function satisfying $∥F\left(i\right)f(x,k)∥⩽\eta \left(i\right)$, where $\eta \left(i\right)>0$ is a known scalar. Therefore, system (1) can be expressed as

$$\begin{array}{c}\hfill x(k+1)=A\left(i\right)x\left(k\right)+D\left[u\left(k\right)+F\left(i\right)f(x,k)\right].\end{array}$$

(2)

Assumption 1.

$\left(A\left(i\right),D\right)$ is controllable for $i\in \mathcal{N}$, and the matrix D is column full rank.

Based on the Assumption 1, there is an invertible matrix E that satisfies $ED=\left[\begin{array}{c}{0}_{\left(n-m\right)\times m}\\ D_1\end{array}\right]$, in which $D_1\in R^{m\times m}$ is invertible. By state transformation $y\left(k\right)=Ex\left(k\right)$, the system in (1) can be transformed into

$$\begin{array}{c}\hfill y(k+1)=\overline{A}\left(i\right)y\left(k\right)+\left[\begin{array}{c}{0}_{\left(n-m\right)\times m}\\ D_1\end{array}\right]\times \left[u\left(k\right)+F\left(i\right)f(x,k)\right],\end{array}$$

(3)

where $\overline{A}\left(i\right)=EA\left(i\right)E^{-1}$, $i\in \mathcal{N}$.

Define $y\left(k\right)\triangleq \left[\begin{array}{c}{y}_1\left(k\right)\\ y_2\left(k\right)\end{array}\right]$,

where $y_1\left(k\right)\in R^{n-m}$, $y_2\left(k\right)\in R^m$ and $\overline{A}\left(i\right)\triangleq \left[\begin{array}{cc}{\overline{A}}_{11}\left(i\right)& {\overline{A}}_{12}\left(i\right)\\ {\overline{A}}_{21}\left(i\right)& {\overline{A}}_{22}\left(i\right)\end{array}\right]$.

Then, system (3) can be represented as

$$\left[\begin{array}{c}{y}_1(k+1)\\ y_2(k+1)\end{array}\right]\triangleq \left[\begin{array}{cc}{\overline{A}}_{11}\left(i\right)& {\overline{A}}_{12}\left(i\right)\\ {\overline{A}}_{21}\left(i\right)& {\overline{A}}_{22}\left(i\right)\end{array}\right]\left[\begin{array}{c}{y}_1\left(k\right)\\ y_2\left(k\right)\end{array}\right]+\left[\begin{array}{c}{0}_{\left(n-m\right)\times m}\\ D_1\end{array}\right]\left[u\left(k\right)+F\left(i\right)f(x,k)\right].$$

(4)

In this paper, we first analyze the stability of sliding mode dynamics and then design an SMC strategy to ensure that the system reaches the predetermined sliding mode surface in finite time. For system (4), we design the sliding mode surface function as follows:

$$\begin{array}{c}\hfill s\left(k\right)=\mathbb{M}\left(i\right)y\left(k\right)=M\left(i\right)y_1\left(k\right)+y_2\left(k\right),i\in \mathcal{N},\end{array}$$

(5)

where $\mathbb{M}\left(i\right)=\left[\begin{array}{cc}M\left(i\right)& I\end{array}\right]$ and $M\left(i\right)$ are matrices to be designed later.

When the switched system states reaches the sliding mode surface (5), the sliding mode surface function satisfies $s\left(k\right)=0$. Meanwhile, we have

$$\begin{array}{c}\hfill y_2\left(k\right)=-M\left(i\right)y_1\left(k\right),\sigma \in \mathcal{N}.\end{array}$$

(6)

By substituting (6) into (4), we obtain

$$\begin{array}{c}\hfill y_1(k+1)=\overline{\mathbb{A}}\left(i\right)y_1\left(k\right),\end{array}$$

(7)

where $\overline{\mathbb{A}}\left(i\right)=\overline{A_{11}}\left(i\right)-\overline{A_{12}}\left(i\right)M\left(i\right)$, $\sigma \in \mathcal{N}$.

Definition 1

([28]). The sliding trajectory of switched system (2) can be driven into a quasi-sliding mode band (QSMB) in finite time and if there are parameters $\delta >0$ and $\widehat{k}>0$ that satisfy $∥s\left(k\right)∥⩽\delta$. In this case, the constant δ is called a QSMB.

Definition 2

([13]). For any $k_2>k_1>0$, let $N_{\sigma \left(k\right)}(k_1,k_2)$ denote the number of the switched signals of $\sigma \left(k\right)$ over $(k_1,k_2)$. If $N_{\sigma \left(k\right)}(k_1,k_2)⩽N_0+\frac{k_2-k_1}{T_{\sigma }}$ holds for $T_{\sigma }>0$ and $N_0⩾0$, then, $T_{\sigma }$ is called the ADT. As commonly used in the literature, we choose $N_0=0$.

Definition 3

([1]). The switched system (1) is said to be exponential stability under the switching signal $\sigma \left(k\right)$, if there are scalars $\rho >0$, $0<\beta <1$ such that $x\left(k\right)$ satisfies $∥x\left(k\right)∥⩽\rho {\beta }^{k-k_0}∥x\left(k_0\right)∥$, $\forall k⩾k_0$.

3. Controller Design and Stability Analysis

Theorem 1.

Consider the systems (1) satisfying the Assumption 1. For given $\mu ⩾1$, $0<\beta <1$, if there exist matrices $p\left(i\right)>0$ and $M\left(i\right)$, satisfying the following inequalities ( for $\forall i,j\in \mathcal{N}$, $i\ne j$ )

$$\begin{array}{c}\hfill \left[\begin{array}{cc}-p^{-1}\left(i\right)& \overline{\mathbb{A}}\left(i\right)\\ {\overline{\mathbb{A}}}^T\left(i\right)& -\beta p\left(i\right)\end{array}\right]<0,\end{array}$$

(8)

$$\begin{array}{c}\hfill p\left(i\right)-\mu p\left(j\right)\le 0,\end{array}$$

(9)

where $\overline{\mathbb{A}}\left(i\right)=\overline{A_{11}}\left(i\right)-\overline{A_{12}}\left(i\right)M\left(i\right)$, and the ADT $T_{\sigma }$ satisfying

$$\begin{array}{c}\hfill T_{\sigma }\ge {T_{\sigma }}^{*}>-\frac{ln\mu }{ln\beta }.\end{array}$$

(10)

Then, the switched system (7) is exponentially stable, which is determined by

$$\begin{array}{c}\hfill ∥y_1\left(k\right)∥\le \gamma {\rho }^{k-k_0}∥y_1\left(k_0\right)∥,\end{array}$$

(11)

with the parameters

$$\begin{array}{c}\hfill a\stackrel{\Delta }{=}\underset{i\in \mathcal{N}}{min}{\lambda }_{min}\left(p\left(i\right)\right),b\stackrel{\Delta }{=}\underset{i\in \mathcal{N}}{max}{\lambda }_{max}\left(p\left(i\right)\right),\rho =\sqrt{\beta {\mu }^{\frac{1}{T_a}}},\gamma =\sqrt{\frac{b}{a}}\ge 1.\end{array}$$

(12)

Proof. 

For the switched system (7), construct the following Lyapunov function:

$$\begin{array}{c}\hfill V_i\left(k\right)=y_1^T\left(k\right)p\left(i\right)y_1\left(k\right),i\in \mathcal{N}.\end{array}$$

(13)

Thus, from (7) and (13), we have

$$\begin{array}{cc}\hfill \Delta V_i\left(k\right)=& V_i\left(k+1\right)-V_i\left(k\right)\hfill \\ \hfill =& y_1^T\left(k\right){\overline{\mathbb{A}}}^T\left(i\right)p\left(i\right)\overline{\mathbb{A}}\left(i\right)y_1\left(k\right)-y_1^T\left(k\right)p\left(i\right)y_1\left(k\right)\hfill \\ \hfill =& y_1^T\left(k\right)\left[{\overline{\mathbb{A}}}^T\left(i\right)p\left(i\right)\overline{\mathbb{A}}\left(i\right)-p\left(i\right)\right]y_1\left(k\right).\hfill \end{array}$$

(14)

Then,

$$\begin{array}{cc}\hfill & \Delta V_i\left(k\right)+\left(1-\beta \right)V_i\left(k\right)\hfill \\ \hfill =& y_1^T\left(k\right)\left[{\overline{\mathbb{A}}}^T\left(i\right)p\left(i\right)\overline{\mathbb{A}}\left(i\right)-\beta p\left(i\right)\right]y_1\left(k\right)\hfill \\ \hfill =& y_1^T\left(k\right)\Pi \left(i\right)y_1\left(k\right),\hfill \end{array}$$

(15)

where $\Pi \left(i\right)={\overline{\mathbb{A}}}^T\left(i\right)p\left(i\right)\overline{\mathbb{A}}\left(i\right)-\beta p\left(i\right)$. In view of Schur’s complement, we can easily obtain

$$\begin{array}{c}\hfill \Delta V_i\left(k\right)+\left(1-\beta \right)V_i\left(k\right)<0.\end{array}$$

(16)

We only have to obtain $\Pi \left(i\right)<0$. It can be obtained by Equation (8). For any $y_1\left(k\right)\ne 0$, we can figure out

$$\begin{array}{c}\hfill \Delta V_i\left(k\right)+V_i\left(k\right)<\beta V_i\left(k\right).\end{array}$$

(17)

Therefore,

$$\begin{array}{c}\hfill V_i\left(k+1\right)<\beta V_i\left(k\right).\end{array}$$

(18)

Then, for $k\in \left[k_l,k_{l+1}\right]$, it can be derived from (16) that

$$\begin{array}{c}\hfill V_{\sigma \left(k\right)}\left(k\right)\le {\beta }^{k-k_l}{V}_{\sigma \left(k_l\right)}\left(k_l\right).\end{array}$$

(19)

From (9) and (13), we have

$$\begin{array}{c}\hfill V_{\sigma \left(k_l\right)}\left(k_l\right)\le \mu V_{\sigma \left(k_{l-1}\right)}\left(k_l\right).\end{array}$$

(20)

According to (19), (20) and the relationship $\tau \triangleq N_{\sigma }\left(k_0,k\right)\le \frac{k-k_0}{T_a}$, it holds that

$$\begin{array}{cc}\hfill & V_{\sigma \left(k\right)}\left(k\right)\hfill \\ & \le {\beta }^{k-k_l}{V}_{\sigma \left(k_l\right)}\left(k_l\right)\hfill \\ & \le {\beta }^{k-k_l}\mu V_{\sigma \left(k_{l-1}\right)}\left(k_l\right)\hfill \\ & \le {\beta }^{k-k_{l-1}}{\mu }^2{V}_{\sigma \left(k_{l-2}\right)}\left(k_{l-1}\right)\hfill \\ \hfill & \le \cdots \hfill \\ & \le {\beta }^{k-k_0}{\mu }^{\tau }{V}_{\sigma \left(k_0\right)}\left(k_0\right)\hfill \\ & \le {\left(\beta {\mu }^{\frac{1}{T_a}}\right)}^{\left(k-k_0\right)}{V}_{\sigma \left(k_0\right)}\left(k_0\right).\hfill \end{array}$$

(21)

Considering (12), one has

$$\begin{array}{c}\hfill \left\{\begin{array}{c}a{∥y_1\left(k\right)∥}^2\le V_{\sigma \left(k\right)}\left(k\right),\\ V_{\sigma \left(k_0\right)}\left(k_0\right)\le b{∥y_1\left(k_0\right)∥}^2.\end{array}\right.\end{array}$$

(22)

Combining (21) and (22), we have

$$\begin{array}{c}\hfill {∥y_1\left(k\right)∥}^2\le \frac{1}{a}{V}_{\sigma \left(k\right)}\left(k\right)\le \frac{1}{a}{\left(\beta {\mu }^{\frac{1}{T_a}}\right)}^{\left(k-k_0\right)}{V}_{\sigma \left(k_0\right)}\left(k_0\right)\le \frac{b}{a}{\left(\beta {\mu }^{\frac{1}{T_a}}\right)}^{\left(k-k_0\right)}{∥y_1\left(k_0\right)∥}^2.\end{array}$$

(23)

Therefore, the sliding mode (7) is exponentially stable, the proof is completed. □

4. Sliding Mode Controller Design

In this section, we design a sliding mode controller to ensure that quasi-sliding modes are accessible. To accomplish control, an approach law method is applied:

$$\begin{array}{c}\hfill s(k+1)-s\left(k\right)=-\varpi Tsgn\left(s\left(k\right)\right)-qTs\left(k\right),\end{array}$$

(24)

where T is sample time, $\varpi$ and q are scalars that satisfying $0<\varpi <1$, $1-qT>0$. From (4), (5) and (24), we have

$$\begin{array}{cc}\hfill & s(k+1)-s\left(k\right)\hfill \\ \hfill =& M\left(i\right)y_1(k+1)+y_2(k+1)-\left[M\left(i\right)y_1\left(k\right)+y_2\left(k\right)\right]\hfill \\ \hfill =& M\left(i\right)\left[{\overline{A}}_{11}\left(i\right)y_1\left(k\right)+{\overline{A}}_{12}\left(i\right)y_2\left(k\right)\right]+\left[{\overline{A}}_{21}\left(i\right)y_1\left(k\right)+{\overline{A}}_{22}\left(i\right)y_2\left(k\right)\right]\hfill \\ \hfill & +D_1\left[u\left(k\right)+F\left(i\right)f(x,k)\right]-M\left(i\right)y_1\left(k\right)-y_2\left(k\right)\hfill \\ \hfill =& \mathbb{M}\left[\overline{A}\left(i\right)-I\right]y\left(k\right)+D_1\left[u\left(k\right)+F\left(i\right)f(x,k)\right]\hfill \\ \hfill =& -\varpi Tsgn\left(s\left(k\right)\right)-qTs\left(k\right).\hfill \end{array}$$

(25)

From (25), the SMC law can be proposed as follows:

$$\begin{array}{c}\hfill u\left(k\right)=-D_1^{-1}\left\{\mathbb{M}\left(i\right)\left[\overline{A}\left(i\right)-I\right]y\left(k\right)+qT\mathbb{M}\left(i\right)y\left(k\right)\right\}-D_1^{-1}\varpi Tsgn\left(s\left(k\right)\right)-{\mathbb{F}}_i\left(k\right),\end{array}$$

(26)

where ${\mathbb{F}}_i\left(k\right)=F\left(i\right)f(x,k)$.

Since the presence of the uncertain term ${\mathbb{F}}_i\left(k\right)$ in the control system (26), it is impractical for application. Therefore, the SMC law is constructed as follows:

$$\begin{array}{c}\hfill u\left(k\right)=-D_1^{-1}\left\{\left(\mathbb{M}\left(i\right)\overline{A}\left(i\right)-\left(1-qT\right)\mathbb{M}\left(i\right)\right)y\left(k\right)\right\}-D_1^{-1}\varpi Tsgn\left(s\left(k\right)\right)-{\tilde{u}}_i\left(k\right),\end{array}$$

(27)

where

$$\begin{array}{c}\hfill {\tilde{u}}_i\left(k\right)=\left\{\begin{array}{cc}\eta \left(i\right)\frac{s\left(k\right)}{∥s\left(k\right)∥},& ∥s\left(k\right)∥\ne 0,\\ 0,& ∥s\left(k\right)∥=0.\end{array}\right.\end{array}$$

(28)

In the following part, the following theorem is given to guarantee the reachability of the QSM.

Theorem 2.

Consider the system (4) and the sliding surface function (5). If the SMC law is designed as (27), the system state trajectory can reach the quasi-sliding mode domain

$$\begin{array}{c}\hfill \mathrm{{\rm Y}}=\left\{∥s\left(k\right)∥<\xi \left|\xi =\underset{i\in \mathcal{N}}{min}\left\{\frac{{\left(\varpi T\right)}^2+\eta \left(i\right)∥D_1∥\left(2\varpi T+\eta \left(i\right)∥D_1∥\right)}{2\varpi T\left(1-qT\right)+2\eta \left(i\right)\left(1-qT\right)∥D_1∥}\right\}\right.\right\}\end{array}$$

(29)

in a finite time. Moreover, once the system’s state trajectory enters this region, it will not escape from the domain.

Proof. 

According to the system (4) and the sliding mode surface function (5), we have

$$\begin{array}{cc}\hfill & s\left(k+1\right)\hfill \\ \hfill =& \mathbb{M}\left(i\right)y\left(k+1\right)\hfill \\ \hfill =& M\left(i\right)y_1(k+1)+y_2(k+1)\hfill \\ \hfill =& M\left(i\right)\left[{\overline{A}}_{11}\left(i\right)y_1\left(k\right)+{\overline{A}}_{12}\left(i\right)y_2\left(k\right)\right]+\left[{\overline{A}}_{21}\left(i\right)y_1\left(k\right)+{\overline{A}}_{22}\left(i\right)y_2\left(k\right)\right]\hfill \\ \hfill & +D_1\left[u\left(k\right)+F\left(i\right)f(x,k)\right]\hfill \\ \hfill =& \mathbb{M}\left(i\right)\overline{A}\left(i\right)y\left(k\right)+D_1\left[u\left(k\right)+F\left(i\right)f(x,k)\right]\hfill \\ \hfill =& \mathbb{M}\left(i\right)\overline{A}\left(i\right)y\left(k\right)+D_1\left(-D_1^{-1}\left\{\mathbb{M}\left(i\right)\left[\overline{A}\left(i\right)-I\right]y\left(k\right)+qT\mathbb{M}\left(i\right)y\left(k\right)\right\}\right)\hfill \\ \hfill & -\varpi Tsgn\left(s\left(k\right)\right)+D_1\left(F\left(i\right)f(x,k)-{\tilde{u}}_i\left(k\right)\right)\hfill \\ \hfill =& \mathbb{M}\left(i\right)\overline{A}\left(i\right)y\left(k\right)-\mathbb{M}\left(i\right)\left[\overline{A}\left(i\right)-I\right]y\left(k\right)-qT\mathbb{M}\left(i\right)y\left(k\right)-\varpi Tsgn\left(s\left(k\right)\right)\hfill \\ \hfill & +D_1\left({\mathbb{F}}_i\left(k\right)-{\tilde{u}}_i\left(k\right)\right)\hfill \\ \hfill =& \mathbb{M}\left(i\right)y\left(k\right)-qT\mathbb{M}\left(i\right)y\left(k\right)-\varpi Tsgn\left(s\left(k\right)\right)+D_1\left({\mathbb{F}}_i\left(k\right)-{\tilde{u}}_i\left(k\right)\right)\hfill \\ \hfill =& \left(1-qT\right)\mathbb{M}\left(i\right)y\left(k\right)-\varpi Tsgn\left(s\left(k\right)\right)+D_1\left({\mathbb{F}}_i\left(k\right)-{\tilde{u}}_i\left(k\right)\right)\hfill \\ \hfill =& \left(1-qT\right)s\left(k\right)-\varpi Tsgn\left(s\left(k\right)\right)+D_1\left({\mathbb{F}}_i\left(k\right)-{\tilde{u}}_i\left(k\right)\right).\hfill \end{array}$$

(30)

Next, construct the following Lyapunov function

$$\begin{array}{c}\hfill V\left(k\right)=s^T\left(k\right)s\left(k\right).\end{array}$$

(31)

It follows that

$$\begin{array}{cc}\hfill & \Delta V\left(k\right)\hfill \\ \hfill =& V\left(k+1\right)-V\left(k\right)\hfill \\ \hfill =& s^T\left(k+1\right)s\left(k+1\right)-s^T\left(k\right)s\left(k\right)\hfill \\ \hfill =& {\left[\left(1-qT\right)s\left(k\right)-\varpi Tsgn\left(s\left(k\right)\right)+D_1\left({\mathbb{F}}_i\left(k\right)-{\tilde{u}}_i\left(k\right)\right)\right]}^T\times \hfill \\ \hfill & \left[\left(1-qT\right)s\left(k\right)-\varpi Tsgn\left(s\left(k\right)\right)+D_1\left({\mathbb{F}}_i\left(k\right)-{\tilde{u}}_i\left(k\right)\right)\right]-s^T\left(k\right)s\left(k\right)\hfill \\ \hfill =& {\left[\left(1-qT\right)s\left(k\right)-\varpi Tsgn\left(s\left(k\right)\right)\right]}^T\times \left[\left(1-qT\right)s\left(k\right)-\varpi Tsgn\left(s\left(k\right)\right)\right]\hfill \\ \hfill & +2\left(1-qT\right)\times {\left[D_1\left({\mathbb{F}}_i\left(k\right)-{\tilde{u}}_i\left(k\right)\right)\right]}^{T}s\left(k\right)-2\varpi Tsgn\left(s\left(k\right)\right)D_1\left({\mathbb{F}}_i\left(k\right)-{\tilde{u}}_i\left(k\right)\right)\hfill \\ \hfill & +{\left[D_1\left({\mathbb{F}}_i\left(k\right)-{\tilde{u}}_i\left(k\right)\right)\right]}^T\left[D_1\left({\mathbb{F}}_i\left(k\right)-{\tilde{u}}_i\left(k\right)\right)\right]-s^T\left(k\right)s\left(k\right).\hfill \end{array}$$

(32)

In view of (28), we have

$$\begin{array}{c}\hfill 2\left(1-qT\right){\left[D_1\left({\mathbb{F}}_i\left(k\right)-{\tilde{u}}_i\left(k\right)\right)\right]}^{T}s\left(k\right)⩽-2\eta \left(i\right)\left(1-qT\right)∥D_1∥∥s\left(k\right)∥,\end{array}$$

(33)

$$\begin{array}{cc}\hfill & -2\varpi Tsgn\left(s\left(k\right)\right)D_1\left({\mathbb{F}}_i\left(k\right)-{\tilde{u}}_i\left(k\right)\right)+{\left[D_1\left({\mathbb{F}}_i\left(k\right)-{\tilde{u}}_i\left(k\right)\right)\right]}^T\left[D_1\left({\mathbb{F}}_i\left(k\right)-{\tilde{u}}_i\left(k\right)\right)\right]\hfill \\ \hfill ⩽& 2\varpi T∥D_1∥\eta \left(i\right)+∥D_1∥\eta \left(i\right)\times ∥D_1∥\eta \left(i\right)\hfill \\ \hfill =& \eta \left(i\right)∥D_1∥\left(2\varpi T+\eta \left(i\right)∥D_1∥\right).\hfill \end{array}$$

(34)

Combining (32)–(34), we have

$$\begin{array}{cc}\hfill & \Delta V\left(k\right)\hfill \\ \hfill =& {\left(1-qT\right)}^2{s}^T\left(k\right)s\left(k\right)-2\varpi T\left(1-qT\right)∥s\left(k\right)∥+{\left(\varpi T\right)}^2-s^T\left(k\right)s\left(k\right)\hfill \\ \hfill & -2{\eta }_i\left(1-qT\right)∥D_1∥∥s\left(k\right)∥+\eta \left(i\right)∥D_1∥\left(2\varpi T+\eta \left(i\right)∥D_1∥\right)\hfill \\ \hfill =& \left({\left(1-qT\right)}^2-1\right)s^T\left(k\right)s\left(k\right)-\left[2\varpi T\left(1-qT\right)+2\eta \left(i\right)\left(1-qT\right)∥D_1∥\right]∥s\left(k\right)∥\hfill \\ \hfill & +{\left(\varpi T\right)}^2+\eta \left(i\right)∥D_1∥\left(2\varpi T+\eta \left(i\right)∥D_1∥\right).\hfill \end{array}$$

(35)

According to (29) and (35), there holds $\Delta V\left(k\right)⩽0$ when $∥s\left(k\right)∥>\xi$. Consequently, it is established that the system state trajectory can attain the quasi-sliding mode domain within a finite time. Once reached, the trajectory will persistently remain within the quasi-sliding mode domain without any deviation. Thus, the proof is concluded. □

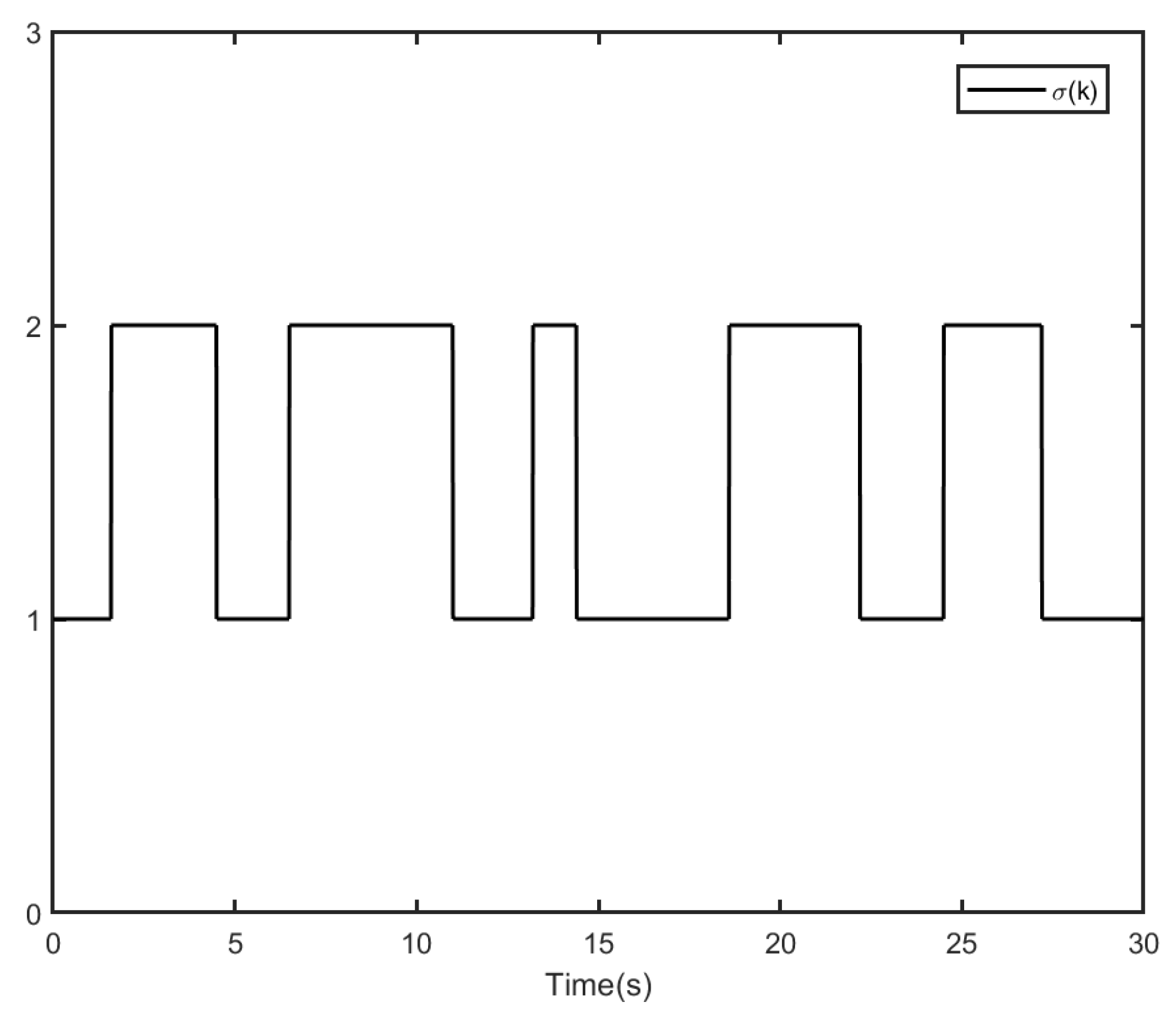
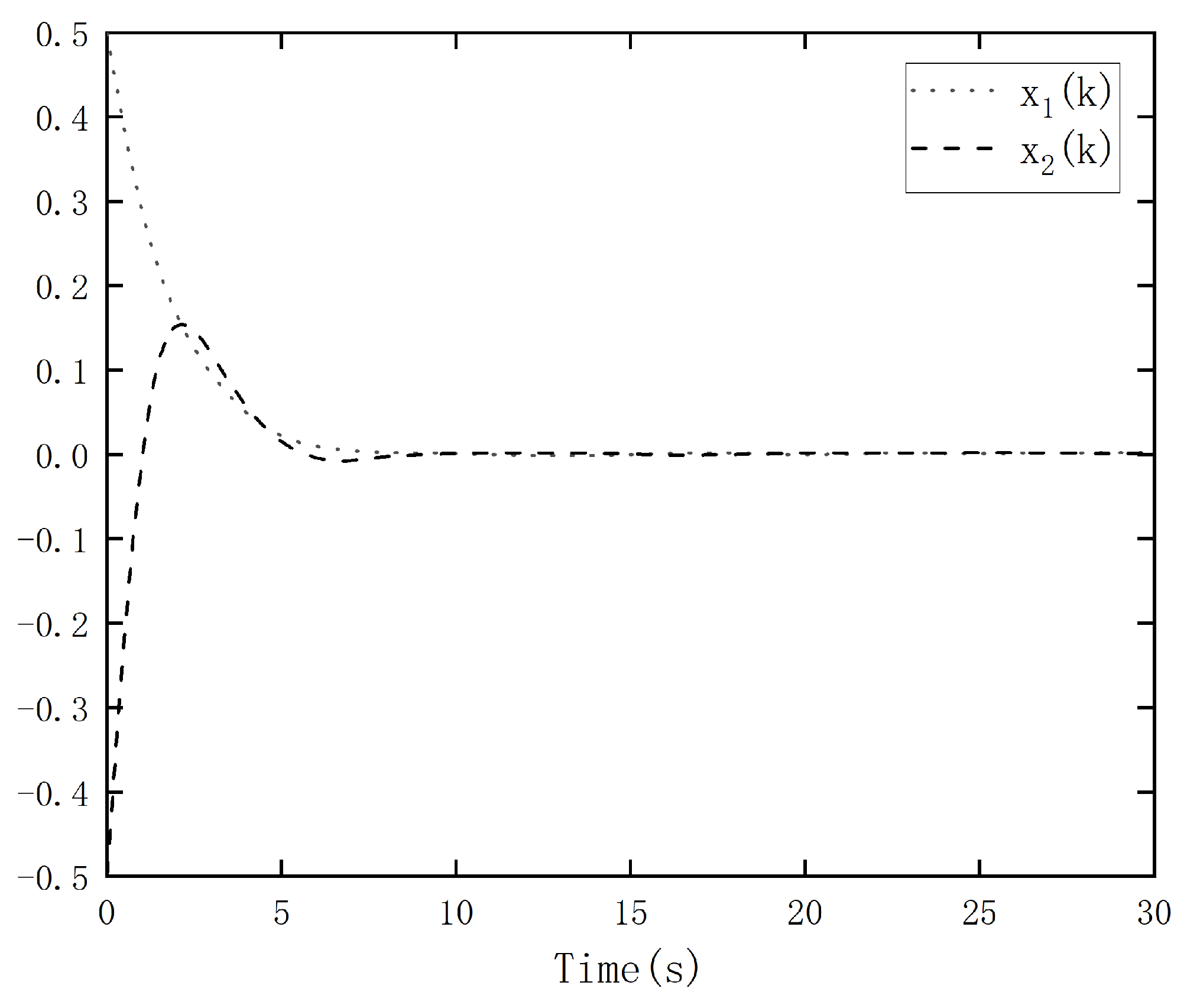
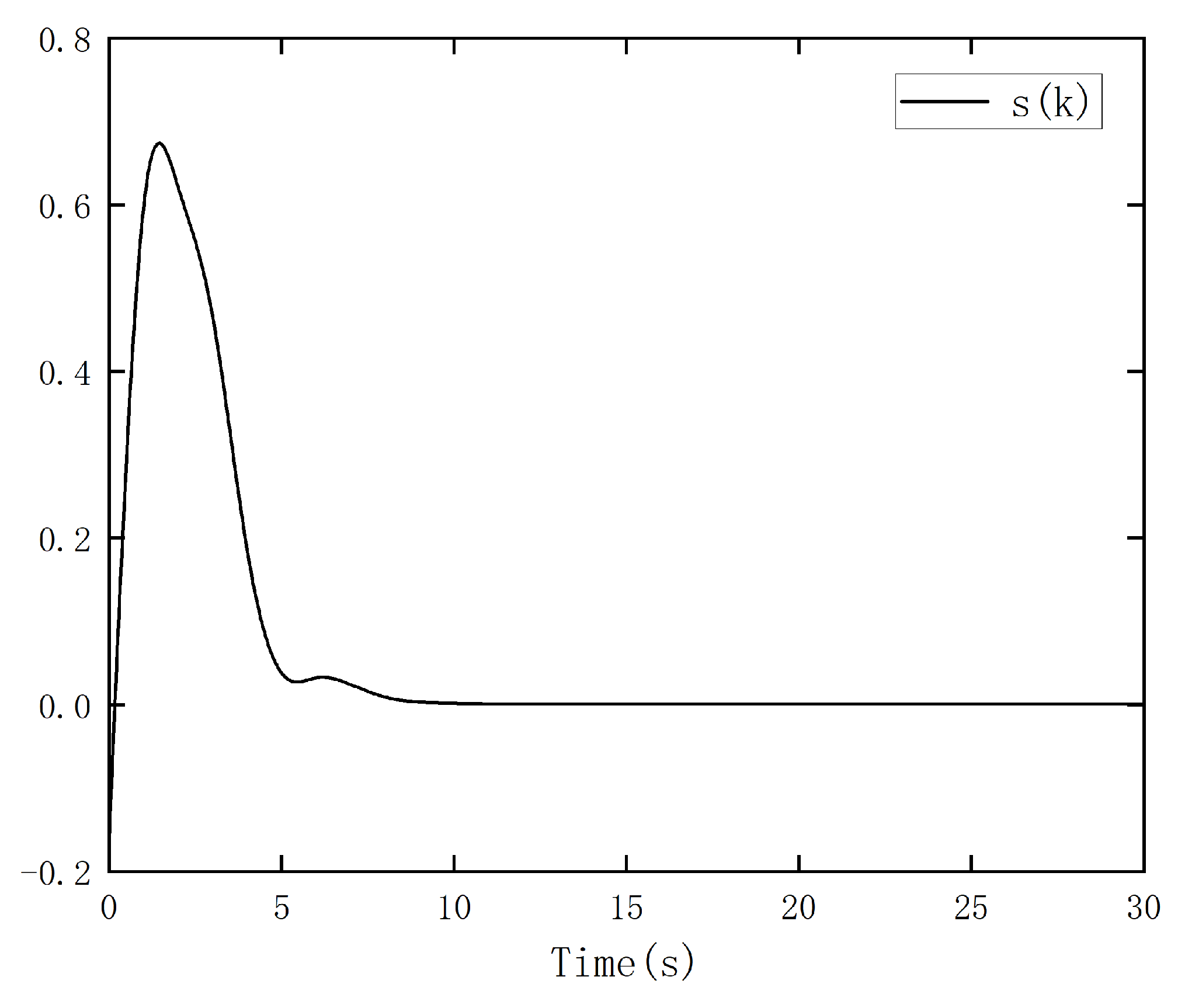
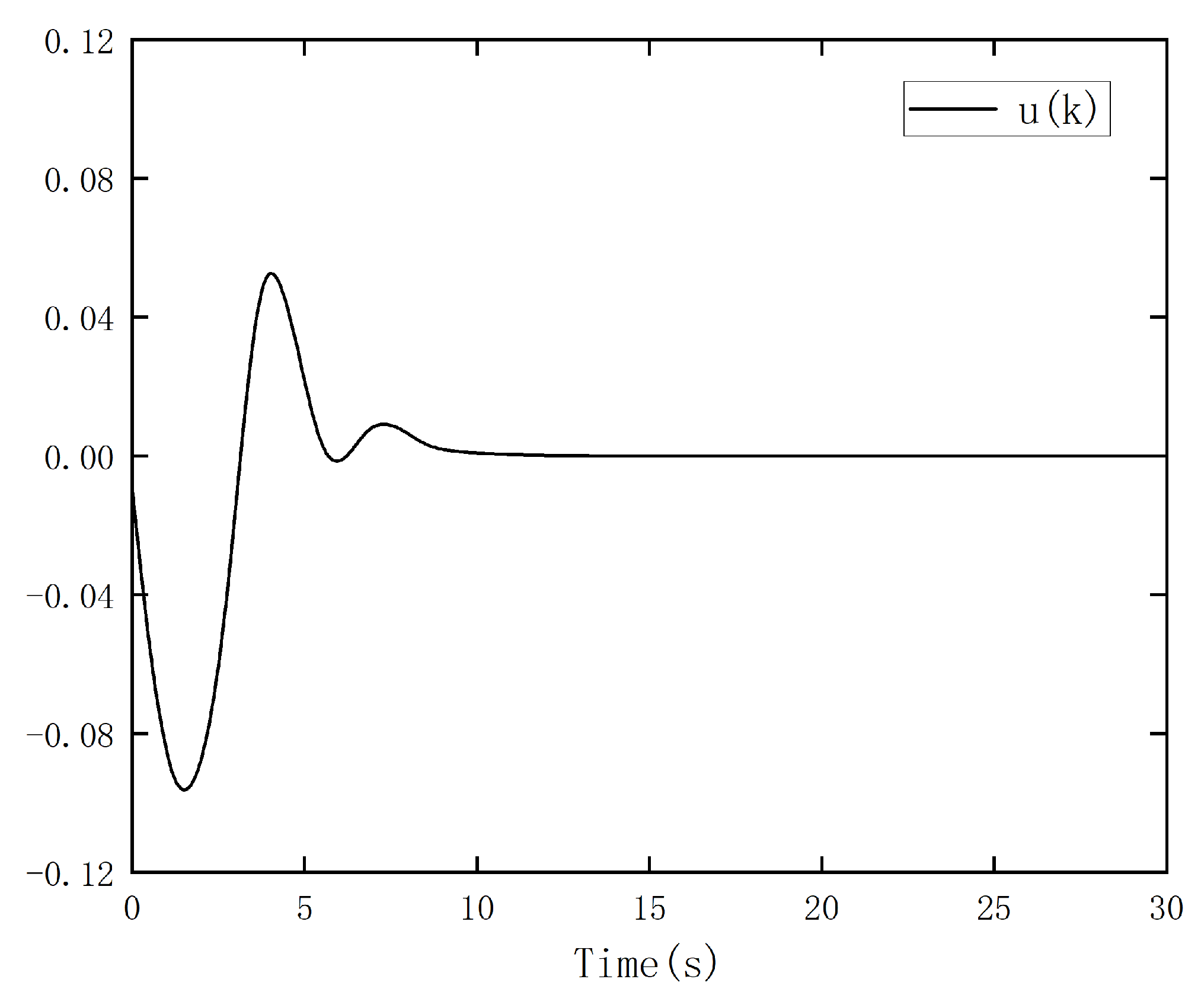
5. Simulation Examples

For the system (1) with ($N=2$), the parameter matrices are as follows:

$A\left(1\right)=\left[\begin{array}{cc}-0.29& 2.01\\ 0.62& 0.49\end{array}\right]$, $A\left(2\right)=\left[\begin{array}{cc}1.30& -0.45\\ -0.56& 0.52\end{array}\right]$, $D=\left[\begin{array}{c}0\\ 2.0\end{array}\right]$, $F\left(1\right)=1.6$, $F\left(2\right)=2.0$, choose $f\left(x\left(k\right),k\right)=0.5exp\left(-k\right)sin\sqrt{x_1^2\left(k\right)+x_2^2\left(k\right)}$. For system (1), set $\mu =1.2$, $\beta =0.8$ and select $T_{\sigma }^{*}=1$. Suppose that the initial condition is $x\left(0\right)={\left[\begin{array}{cc}0.5& -0.5\end{array}\right]}^T$. Our objective is to formulate the SMC law so that the sliding mode dynamics exponentially stable. First, we solve Equation (8) in Theorem 2 to obtain the sliding mode surface parameter of Equation (5) as follows

$$\begin{array}{c}\hfill M\left(1\right)=-0.7174,M\left(2\right)=-0.7222.\end{array}$$

(36)

Therefore, the sliding mode surface equation can be obtained as

$$\begin{array}{c}\hfill s\left(k\right)=\left\{\begin{array}{cc}\left[\begin{array}{cc}-0.7174& 1.0000\end{array}\right]y\left(k\right),& i=1,\\ \left[\begin{array}{cc}-0.7222& 1.0000\end{array}\right]y\left(k\right),& i=2.\end{array}\right.\end{array}$$

(37)

Suppose sampling time $T=0.1$, select parameters $\varpi =0.5$ and $q=2$, according to (27) and (28), the SMC law can be designed as

$$\begin{array}{c}\hfill u\left(k\right)=\left\{\begin{array}{c}\left[\begin{array}{cc}-0.7010& 0.8760\end{array}\right]y\left(k\right)-0.025sgn\left(s\left(k\right)\right),i=1and∥s\left(k\right)∥=0,\hfill \\ \left[\begin{array}{cc}-0.7010& 0.8760\end{array}\right]y\left(k\right)-0.025sgn\left(s\left(k\right)\right)-\eta \left(1\right)\frac{s\left(k\right)}{∥s\left(k\right)∥},i=1and∥s\left(k\right)∥\ne 0,\hfill \\ \left[\begin{array}{cc}0.4593& -0.0214\end{array}\right]y\left(k\right)-0.025sgn\left(s\left(k\right)\right),i=2and∥s\left(k\right)∥=0,\hfill \\ \left[\begin{array}{cc}0.4593& -0.0214\end{array}\right]y\left(k\right)-0.025sgn\left(s\left(k\right)\right)-\eta \left(2\right)\frac{s\left(k\right)}{∥s\left(k\right)∥},i=2and∥s\left(k\right)∥\ne 0.\hfill \end{array}\right.\end{array}$$

(38)

For the initial state of $x\left(0\right)={\left[\begin{array}{cc}3& -1\end{array}\right]}^T$, selecting parameters $\eta \left(1\right)=0.8$ and $\eta \left(2\right)=1$, the simulation outcomes are depicted in Figure 1, Figure 2, Figure 3 and Figure 4. Among them, Figure 1 illustrates the switched signal. Analysis of Figure 2 and Figure 3 reveals that the system’s state trajectory asymptotically converges to the quasi-sliding mode region within a finite duration, demonstrating the efficacy of the proposed control approach. Figure 4 displays the SMC law.

Recently, the event-triggered control problem of discrete-time switching systems was studied in [7]. In the case of ignoring disturbances, our system model corresponds to a special case in [7], that is, the uncertainty $\Delta A_i=0$ in [7], and the matrix is $B_i$ consistent. However, when disturbances are present, it is possible to try to solve the problem using the method proposed in this paper. However, it could not be solved by the method in [7]. In control systems, disturbances are generally considered as external uncertainties, which may adversely affect the stability and performance of the system. Therefore, developing effective control strategies to counteract these disturbances is very important.

To increase the readability of the simulation, our experimental background is provided here. This article is implemented under the Win10 system, with the help of Matlab R2021b (MathWorks Inc., Natick, MA, USA).

6. Conclusions

This paper has studied the issue of sliding mode control for switched systems in the presence of disturbances. Considering the particularity of the system, a reduced-order sliding mode dynamic system for the switched system has been constructed through state transformation, and sufficient conditions for the exponential stability of the related sliding mode dynamic systems have been proposed. A novel design scheme for sliding mode controllers based on the system model is presented using the Lyapunov function method. Finally, the effectiveness of this method has been demonstrated through a simulation example. Future research will be dedicated to extend this approach to switched systems with asynchronous switching.