An Output Cooperative Controller for a Hydraulic Support Multi-Cylinder System Based on Neural Network Compensation

Abstract

The straightness control of a fully mechanized working face is the key technology used in intelligent coal mining, so the position control of a hydraulic support multi-cylinder moving system is of great significance. However, due to the harsh environment of coal mines, complex friction, external disturbances, and the coupling relationship between adjacent cylinders, the accuracy of position control is restricted. Therefore, an output cooperative controller is proposed in this paper for a multi-cylinder system. A high-order sliding mode observer is utilized to estimate the system states with the only available output position signal. A neural network disturbance observer is applied to estimate the lump disturbance of the strict-feedback model, including the system uncertainty, disturbance force and the coupling force between adjacent cylinders. Then, continuous motion position tracking simulation is conducted and the estimation performance of the state observer and neural network is analyzed. Furthermore, a multi-cylinder collaborative control test rig is designed, and experiments based on the actual actions of the hydraulic support are conducted. The results show that the proposed output cooperative controller has an excellent position control performance compared with the traditional proportional–integral controller.

1. Introduction

With the development of automation and intelligence in coal mines, electro-hydraulic control technology has attracted more and more attention [1]. Compared with mechanical transmission and electrical transmission, hydraulic transmission has a higher power-to-weight ratio, which has been widely used in the mining field, such as in coal shearers and hydraulic supports [2,3]. However, the electro-hydraulic system is hard to control because of the strong nonlinearities, parameter uncertainties, modelling errors and external disturbances that are present [4]. To realize unmanned underground mining, the straightness of the fully mechanized mining face must be guaranteed, and this is directly controlled by the position accuracy of the hydraulic support moving cylinder. Due to the fixed connection between the adjacent moving cylinders of the hydraulic support group, the coupling relationship during the movement of multiple cylinders increases the difficulty of position control. Therefore, it is essential to find a suitable control method to improve the control performance of the hydraulic support moving cylinder under coal mine conditions [5,6].

Each single hydraulic support moving cylinder system is a typical valve-controlled single-rod hydraulic cylinder system, and many advanced methods have been proposed to improve their control performance [7,8]. Sliding mode control (SMC) was designed to suppress disturbances and unmodeled dynamics through robust terms, and it has been widely applied in many control systems due to its simple structure. To improve the chattering problem of sliding mode control, many advanced methods have been introduced into the traditional sliding mode design, such as terminal, super-twisting and online learning methods [9,10]. Adaptive robust control (ARC) combined the advantages of adaptive control and robust control to achieve good performance by adjusting the model parameters online and suppressing uncertain disturbances [11]. Due to its excellent control performance, it has prompted many scholars to optimize the design of its control structure [12,13,14]. Additionally, disturbance observer (DO) was also used as an effective means to solve the problem of system uncertainty; it considered the internal parameter uncertainty as a lumped interference, and then observed and compensated it to improve the anti-interference ability of the system [15,16]. The high-gain disturbance observer (HGDO), extended disturbance observer (EDO) and unknown dynamics estimator (UDE) were proposed to estimate the lumped disturbances, including the friction, the load force, and the parameter uncertainty of electro-hydraulic systems, which helped improve the anti-interference ability of the electro-hydraulic system [17,18,19].

Although the aforementioned advanced approaches have been proven effective in improving the control performance of electro-hydraulic systems, the traditional proportional–integral–differential control (PID) is still the most widely used controller in industrial production [20]. This is mainly because PID only needs to measure the output of the control system, while other advanced controllers often need to measure more system information, such as the speed and pressure, which increases the configuration cost of the controller. Therefore, output feedback control has received more and more attention in recent years [21]. A proportional–integral observer (PIO) was proposed to ensure suitable tracking performance and to increase robustness against unknown inputs for a nonlinear hydraulic differential cylinder system [22]. A high-order sliding mode observer (HSMO) for hydraulic actuators was presented; this considered different sets of available measurements, parametric uncertainties and model nonlinearities, which effectively improved the position tracking accuracy of the hydraulic actuation system [23]. A high-gain observer (HGO) was designed for a single-rod electro-hydraulic actuator to realize position tracking [24,25]. Extended state observer (ESO) was originally proposed in relation to the active disturbance rejection control method (ADRC); then, it was combined with other advanced control strategies such as the sliding mode method and the adaptive robust method [20,26,27,28]. Differentiators are also an efficient method of state estimation and have generally been used in systems with a strict-feedback form [29,30]. An extended differentiator based on the backstepping method was presented in a hydraulic motor system for position tracking [31]. Levant’s differentiator was proposed and used in an output feedback control system, which had fast convergence properties for control error and a low sensitivity to measurement noise [32]. Compared with state feedback, output feedback only needs to measure the control quantity, which saves system configuration costs and enables the replacement of the PID controller in industrial applications [33,34].

The ground conditions of the hydraulic support moving system are complex, and the force is constantly changing during the moving process [35]. In addition, the adjacent moving cylinders are rigidly connected by scraper conveyors, and an excessive displacement difference will not only generate additional disturbance force and reduce the life of components, but also directly affect the straightness of the fully mechanized mining face [36]. Therefore, a new output controller based on a neural network for the hydraulic support multi-cylinder system is proposed to improve the position control accuracy of the moving cylinder. Compared with the existing related literature, the contribution of the new control method can be summarized in the following aspects:

(1) A standard Brunovsky model of the hydraulic support multi-cylinder moving system is established in the sliding processes, which takes the synergistic relationship between adjacent multi-cylinders into account.

(2) The mathematical free model of hydraulic support multi-cylinders without relying on a strict model is firstly established in this article, and this only consists of three parts: the order of the system, the gain of the control input, and the lumped unknown function.

(3) A higher-order sliding mode observer (HOSMO) is designed to estimate unavailable system states with the only available output position signal of the moving cylinder.

(4) A neural-network-based disturbance observer (NNDO) is proposed to approximate the unknown nonlinear functions of the model-free system, which includes system uncertainty and external disturbances.

(5) An output cooperative controller is presented in the position tracking control of the multi-cylinder system, whose feedback error includes the error of tracking the desired trajectory and the error of tracking the previous cylinder.

The remainder of this paper is organized as follows. In Section 2, the mathematical model of the hydraulic support multi-cylinder system is presented. The design process of the proposed observer and controller is discussed in Section 3. The simulation results and experimental results of the proposed controller for the multi-cylinder system are obtained to show its applicability in Section 4. The conclusion is found in Section 5.

2. System Modeling and Problem Formulation

2.1. System Description

Figure 1 depicts the multi-cylinder system of a hydraulic support in the coal mining face. The fully mechanized mining face is generally composed of dozens or hundreds of hydraulic supports, and the straightness of the scraper conveyor ensures the normal advancement of the coal mining face, which is directly determined by the position of the hydraulic support moving cylinder [37]. The load force of the moving cylinder during the action process is constantly changing due to the complex environment of the coal mining face. In addition, the scraper conveyor is connected by dumbbell pins. During the cooperative pushing action of multiple cylinders, the adjacent moving cylinders have a coupling force due to the scraper conveyor. A single hydraulic support moving cylinder system is a typical valve-controlled single-rod cylinder system, where only the position signal can be measured by the magnetostrictive sensor. Therefore, it is important to improve the straightness of the mining face by designing an output feedback controller that meets the downhole conditions and realizes the position control of the hydraulic support moving cylinder under disturbance conditions.

2.2. Dynamic Model

Taking one of the hydraulic support moving cylinders as an example, the load dynamics model of the cylinder can be expressed as follows [38]:

$$m\ddot{y}=(A_1{P}_1-A_2{P}_2)-b\dot{y}+F_d-f_c$$

(1)

where $m$ is the total mass of the middle trough and falling coal, $A_1$ and $A_2$ are the areas of the rodless chamber and the rod chamber, $P_1$ and $P_2$ are the pressures of the rodless chamber and the rod chamber, $b$ is the viscous damping coefficient, $y$ is the displacement of the rod, $F_d$ is the additional disturbance force that mainly includes various friction forces and parameter uncertainty, and $f_c$ is the coupling force of the moving cylinder, which will appear when the displacement difference between the adjacent cylinders exceeds the threshold.

The flows into the two chambers of the moving cylinder can be written as follows:

$$\begin{array}{l}{Q}_1=k_q{x}_v\sqrt{\frac{P_s}{2}+sign(x_v)\left(\frac{P_s}{2}-P_1\right)}\\ Q_2=k_q{x}_v\sqrt{\frac{P_s}{2}+sign(x_v)\left(P_2-\frac{P_s}{2}\right)}\end{array}$$

(2)

where $Q_1$ is the flow rate supplied to the forward chamber and $Q_2$ is the return flow rate of the return chamber. $k_q$ is the servo valve flow gain coefficient, $x_v$ is the servo valve spool displacement, and $P_s$ and $P_r$ are the pump supply pressure and tank pressure of the system. The function $sign(\ast )$ is the symbolic function.

Since the hydraulic support moving system is typically a heavy duty system, the hydraulic valve responds much faster than the whole system; then, an approximation between $x_v$ and the control input voltage $u$ is described as $x_v=k_v·u$.

The pressure dynamic equation of the asymmetric cylinder when only the internal leakage is considered can be written as follows:

$$\begin{array}{l}{\dot{P}}_1=\frac{{\beta }_e}{V_{01}+A_{1}y}[Q_1-A_1\dot{y}-C_t(P_1-P_2)]+{\Delta }_1\\ {\dot{P}}_2=\frac{{\beta }_e}{V_{02}-A_{2}y}[-Q_2+A_2\dot{y}+C_t(P_1-P_2)]+{\Delta }_2\end{array}$$

(3)

where ${\beta }_e$ is the effective hydraulic fluid bulk modulus, $V_{01}$ and $V_{02}$ are the initial control volumes of the two actuator chambers, $C_t$ is the total internal leakage coefficient, and ${∆}_1$ and ${∆}_2$ are the modeling errors.

When the states are defined as ${[x_1, x_2, x_3]}^T={\left[y_1, {\dot{y}}_1, {(A}_1{P}_1-A_2{P}_2\right)/m]}^T$, then the following state space equation holds:

$$\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=x_3-B{x}_2+d_1\\ {\dot{x}}_3=g_{1}u-g_2{x}_2-g_3(P_1-P_2)+d_2\end{array}$$

(4)

The coefficient of (4) can be expressed as follows:

$$\left\{\begin{array}{l}B=\frac{b}{m}, d_1=\frac{-F_d+f_c}{m}, d_2=\frac{A_1{\Delta }_1-A_2{\Delta }_2}{m}\hfill \\ g_1=\frac{k_t{\beta }_e}{m}\left(\frac{A_1{R}_1}{V_1+A_{1}y}+\frac{A_2{R}_2}{V_2-A_{2}y}\right)\hfill \\ g_2=\frac{{\beta }_e}{m}\left(\frac{A_1{ }^2}{V_1+A_{1}y}+\frac{A_2{ }^2}{V_2-A_{2}y}\right)\hfill \\ g_3=\frac{{\beta }_e{C}_t}{m}\left(\frac{A_1}{V_1+A_{1}y}+\frac{A_2}{V_2-A_{2}y}\right)\hfill \\ R_1=\sqrt{\frac{P_s}{2}+sign(u)\left(\frac{P_s}{2}-P_1\right)}\hfill \\ R_2=\sqrt{\frac{P_s}{2}+sign(u)\left(P_2-\frac{P_s}{2}\right)}\hfill \end{array}\right.$$

(5)

2.3. Dynamic Model

Since only the position signal of the hydraulic support moving cylinder can be measured, the new system state variables are defined as $z_1=x_1, z_2={\dot{z}}_1, z_3={\dot{z}}_2$. Taking the adjacent three moving cylinders i, j and k as examples, the new model of the No. j cylinder is simplified into the following form:

$$\begin{array}{l}{\dot{z}}_{1j}=z_{2j}\\ {\dot{z}}_{2j}=z_{3j}\\ {\dot{z}}_{3j}=g_{1j}{u}_j+{\mathrm{\Phi }}_j\end{array}$$

(6)

In fact, $\mathrm{\Phi }$ can be more specifically written as the following formula according to the system model:

$$\mathrm{\Phi }=-\left(g_2+g_3\frac{(1+n^2)b}{(1+n^3)A_1}\right)x_2-\left(g_3\frac{(1+n^2)m}{(1+n^3)A_1}+\frac{b}{m}\right)x_3-\frac{(n-1)g_3{P}_s}{2(1+n^3)}\left((n^2+1)+sign(u)(n^2-1)\right)-g_3\frac{(1+n^2)m}{(1+n^3)A_1}{d}_1-{\dot{d}}_1+d_2$$

(7)

Remark 1. 

It is obvious that the unknown nonlinear function $\Phi$ is a very complex function affected by the system state $x_2$, $x_3$ and unknown disturbances $d_1$, $d_2$. Therefore, the unknown nonlinear function is regarded as a lumped disturbance, and the system model is described in Brunovsky form, which only needs the system order and the control input coefficient.

Assumption 1. 

The fixed physical parameters of each moving cylinder of the hydraulic support are the same, but the load and disturbance of different hydraulic cylinders are variable. Additionally, $P_1$ and $P_2$ are bounded by $P_s$ and $P_r$, where $0\le {P_r<P}_1,P_2<P_s$.

Assumption 2. 

The force disturbance $d_1$ satisfies conditions $d_{1min}\le d_1\le d_{1max}$, and ${\dot{d}}_{1min}\le {\dot{d}}_1\le {\dot{d}}_{1max}$, where $d_{1min}$ and $d_{1max}$ are the known lower and upper bounds of $d_1$. In addition, ${\dot{d}}_{1min}$ and ${\dot{d}}_{1max}$ are the known lower and upper bounds of ${\dot{d}}_1$. Similarly, the pressure flow disturbance $d_2$ is also bounded by $d_{2min}\le d_2\le d_{2max}$. As a result, the unknown nonlinear function $\Phi$ is bounded.

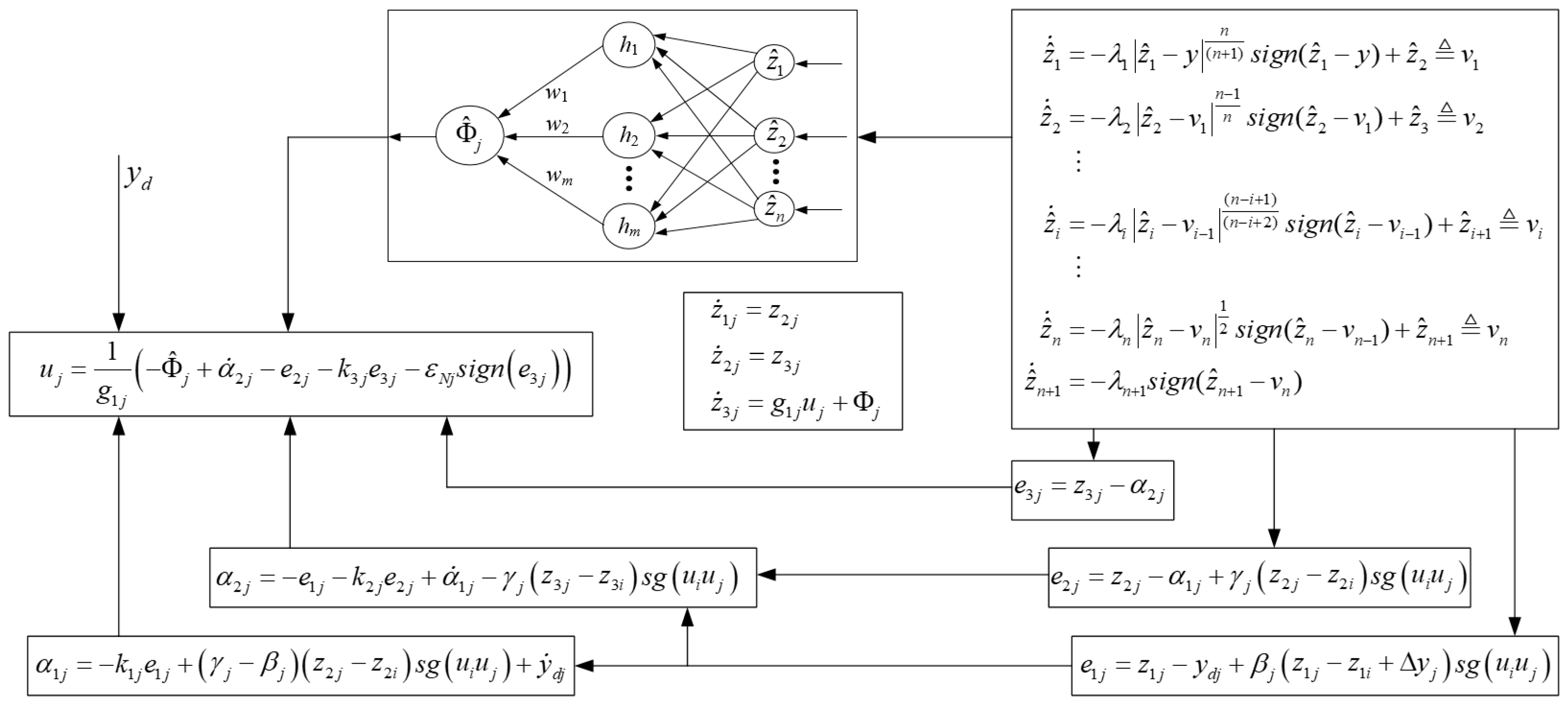
3. Design and Stability Analysis of the Controller

In this section, an output cooperative controller based on neural network compensation is designed for the hydraulic support multi-cylinder system. The block diagram of the proposed controller is demonstrated in Figure 2.

3.1. State Observer Design

In this section, a high-order sliding mode observer (HOSMO) is proposed to estimate the immeasurable states of each moving cylinder. For the standard system model, if the n-order derivative of the system state has a Lipschitz constant, HOSMO can be used to estimate the unmeasurable state in the system. Hence, the structure of the designed observer can be expressed as follows:

$$\begin{array}{c}\hspace{1em}{\dot{\widehat{z}}}_1=-{\lambda }_1{\left|{\widehat{z}}_1-y\right|}^{\frac{n}{(n+1)}}sign({\widehat{z}}_1-y)+{\widehat{z}}_2\triangleq v_1\hfill \\ \hspace{1em}{\dot{\widehat{z}}}_2=-{\lambda }_2{\left|{\widehat{z}}_2-v_1\right|}^{\frac{n-1}{n}}sign({\widehat{z}}_2-v_1)+{\widehat{z}}_3\triangleq v_2\hfill \\ \hspace{1em}\hspace{1em}⋮\hfill \\ \hspace{1em}{\dot{\widehat{z}}}_i=-{\lambda }_i{\left|{\widehat{z}}_i-v_{i-1}\right|}^{\frac{(n-i+1)}{(n-i+2)}}sign({\widehat{z}}_i-v_{i-1})+{\widehat{z}}_{i+1}\triangleq v_i\hfill \\ \hspace{1em}\hspace{1em}⋮\hfill \\ \hspace{1em}{\dot{\widehat{z}}}_n=-{\lambda }_n{\left|{\widehat{z}}_n-v_n\right|}^{\frac{1}{2}}sign({\widehat{z}}_n-v_{n-1})+{\widehat{z}}_{n+1}\triangleq v_n\hfill \\ {\dot{\widehat{z}}}_{n+1}=-{\lambda }_{n+1}sign({\widehat{z}}_{n+1}-v_n)\hfill \end{array}$$

(8)

where ${\lambda }_1, \cdots {\lambda }_i, \cdots {\lambda }_n, {\lambda }_{n+1}$ are the positive gains of the HOSMO, ${\widehat{z}}_1, \cdots {\widehat{z}}_i, \cdots {\widehat{z}}_n, {\widehat{z}}_{n+1}$ are the estimation of the system states, and $v_1, \cdots v_i, \cdots v_n$ are auxiliary variables.

Assumption 3. 

The noise of the measured displacement signal $z_1$ is bounded as $|z_1-y|\le \epsilon$, where $\epsilon$ is the maximal magnitude of the measurement noise.

Therefore, the following inequalities are established in finite time.

$$\begin{array}{c}\left|z_i-{\widehat{z}}_i\right|\le {\mu }_i{\epsilon }^{(n-i+2)/(n+1)},i=1,2,\cdot \cdot \cdot n\\ \left|z_{i+1}-v_i\right|\le {\rho }_i{\epsilon }^{(n-i+1)/(n+1)},i=1,2,\cdot \cdot \cdot n-1\end{array}$$

(9)

where ${\mu }_i$ and ${\rho }_i$ are positive constants that depend on the designed parameters of HOSMO. In other words, the estimation errors of HOSMO will converge to a small set within a finite time in practice [32,39,40].

Remark 2. 

Due to the fast convergence of HOSMO, the state observer basically realizes the separation principle, which means that the controller and the observer can be designed separately so that the designed output feedback controller retains the main characteristics of the full state. Moreover, the estimation errors of the HOSMO are defined as ${\tilde{z}}_i=z_i-{\widehat{z}}_i, i=\mathrm{1,2},\cdots n$, and there exists a positive constant $\sigma$ and a certain time $t_c$; for $t>t_c$, the observation errors are bounded by $\left|{\tilde{z}}_i\right|\le \sigma$, which is determined by the control parameters ${\mu }_i$ and the maximal magnitude of the measurement noise $\epsilon$.

3.2. Disturbance Observer Design

To estimate and compensate for the unknown nonlinear function $\mathrm{\Phi }$ of the moving system in time, a radial basis function neural-network-based disturbance observer is designed (NNDO). Accordingly, the output of the radial basis function neural network for the j-th moving cylinder can be expressed as follows:

$$\begin{array}{l}{h}_j=\exp \left(-\frac{{‖\lambda -c_j‖}^2}{b_j{ }^2}\right)\\ \widehat{\mathrm{\Phi }}={\widehat{W}}^{T}H(\lambda )\end{array}$$

(10)

where $h_j$ is the j-th output of the hidden layer calculated by the Gaussian function, $j$ is the number of nodes, $c_j$ and $b_j$ are the center coordinates and width of the Gaussian function, respectively, $\mathit{\lambda }={[z_1,z_2,\cdots z_i,\cdots z_n]}^T$ is the input layer of the neural network, $\widehat{W}={[{\widehat{w}}_1, {\widehat{w}}_2, \cdots {\widehat{w}}_j]}^T$ is the estimation weight, and $H={[h_1, h_2, \cdots h_j]}^T$ is the final output of the whole hidden layer.

Indeed, the unknown nonlinear function can be shown as

$$\mathrm{\Phi }=W^{\ast }{ }^{T}H(\lambda )+\delta$$

(11)

where $W^{\ast }={[{w_1}^{\ast }, {w_2}^{\ast }\cdots {w_n}^{\ast }]}^T$ is the ideal weight vector, and $\delta$ is the approximation error of the neural network disturbance observer.

Remark 3. 

Generally, the neural network can approximate any nonlinear function through a proper combination of a set of linear Gaussian. The optimal weight in the approximation is chosen properly to ensure that the approximation error $\delta$ is as small as possible, and the approximation error of neural network is bounded by $\left|\delta \right|\le {\delta }_{max}$. Additionally, the estimation error for the unknown nonlinear function can be shown as $\tilde{\Phi }=\Phi -\widehat{\Phi }={\tilde{W}}^T+\delta$, where $\tilde{W}=W-\widehat{W}$.

3.3. Controller Design

Take an adjacent moving cylinder like the i-th, j-th and k-th cylinder as an example. The multi-cylinder system moves sequentially, but the speed synchronization needs to be ensured during the movement, so as to avoid coupling force due to the large displacement difference. Therefore, the controller is designed as follows:

Step 1: define the position error as

$$e_{1j}=z_{1j}-y_{dj}+{\beta }_j\left(z_{1j}-z_{1i}+\Delta y_j\right)sg\left(u_i{u}_j\right)$$

(12)

It can be seen from (12) that the position tracking error of the multi-cylinder sequential moving system includes not only the error of tracking the desired trajectory, but also the error between following the previous hydraulic cylinder.

where $∆y_j$ is the initial displacement difference between two adjacent hydraulic cylinders, ${\beta }_j$ is the feedback weight of the set displacement difference, and $u_i$ and $u_j$ are the control voltages of two adjacent cylinders, respectively. $sg(\ast )$ is a self-defined function to ensure that there will be additional feedback of displacement difference only when two adjacent hydraulic cylinders move at the same time, which can be expressed as

$$sg\left(\ast \right)=\left\{\begin{array}{c}0, \ast =0\\ 1, \ast \ne 0\end{array}\right.$$

(13)

By defining a Lyapunov function $V_{1j}$ as $V_{1j}={e_{1j}}^2/2$, then taking the time derivative of $V_{1j}$, we can obtain

$${\dot{V}}_{1j}=e_{1j}\left(z_{2j}-{\dot{y}}_{dj}+{\beta }_j\left(z_{2j}-z_{2i}\right)sg\left(u_i{u}_j\right)\right)$$

(14)

To make ${\dot{V}}_{1j}\le 0$, the virtual control of $z_{2j}$ is chosen as follows:

$${\alpha }_{1j}=-k_{1j}{e}_{1j}+\left({\gamma }_j-{\beta }_j\right)\left(z_{2j}-z_{2i}\right)sg\left(u_i{u}_j\right)+{\dot{y}}_{dj}$$

(15)

where $k_{1j}$ is a positive feedback gain and ${\gamma }_j$ is the weight of the set speed difference.

Step 2: By defining the error between $z_{2j}$ and its virtual input ${\alpha }_{1j}$ as

$$e_{2j}=z_{2j}-{\alpha }_{1j}+{\gamma }_j\left(z_{2j}-z_{2i}\right)sg\left(u_i{u}_j\right)$$

(16)

The derivative of $e_{2j}$ is written as

$${\dot{e}}_{2j}=z_{3j}-{\dot{\alpha }}_{1j}+{\gamma }_j\left(z_{3j}-z_{3i}\right)sg\left(u_i{u}_j\right)$$

(17)

By defining the Lyapunov function for Step 2 as $V_{2j}=V_{1j}+{e_{2j}}^2/2$, the time derivative of $V_{2j}$ can be shown as

$${\dot{V}}_{2j}={\dot{V}}_{1j}+e_{2j}\left(z_{3j}-{\dot{\alpha }}_{1j}+{\gamma }_j\left(z_{3j}-z_{3i}\right)sg\left(u_i{u}_j\right)\right)$$

(18)

Similar to Step 1, the virtual control input of $z_{3j}$ is designed as ${\alpha }_{2j}$. To ensure ${\dot{V}}_{2j}\le 0$, the virtual control input can be expressed as

$${\alpha }_{2j}=-e_{1j}-k_{2j}{e}_{2j}+{\dot{\alpha }}_{1j}-{\gamma }_j\left(z_{3j}-z_{3i}\right)sg\left(u_i{u}_j\right)$$

(19)

where $k_{2j}$ is a positive feedback gain.

Step 3: By defining the error between $z_{3j}$ and its virtual input ${\alpha }_{2j}$ as

$$e_{3j}=z_{3j}-{\alpha }_{2j}$$

(20)

and taking the time derivative of (20), we obtain

$${\dot{e}}_{3j}=g_{1j}{u}_j+{\mathrm{\Phi }}_j-{\dot{\alpha }}_{2j}$$

(21)

By defining the Lyapunov function for Step 3 as $V_{3j}=V_{3j}+{e_{3j}}^2/2$, the time derivative of $V_{3j}$ can be shown as

$${\dot{V}}_{3j}={\dot{V}}_{2j}+e_{3j}\left(g_{1j}{u}_j+{\mathrm{\Phi }}_j-{\dot{\alpha }}_{2j}\right)$$

(22)

The actual input of the j-th actuator of the multi-actuator system is designed as

$$u_j=\frac{1}{g_{1j}}\left(-{\widehat{\mathrm{\Phi }}}_j+{\dot{\alpha }}_{2j}-e_{2j}-k_{3j}{e}_{3j}-{\epsilon }_{Nj}sign\left(e_{3j}\right)\right)$$

(23)

where $k_{j3}$ is a positive feedback gain, and $\tau$ is a time constant.

3.4. Stability Analysis

To test the stability of the whole system, the Lyapunov function of the whole system can be defined as

$$V_j=V_{3j}+\frac{1}{2{\kappa }_j}{\tilde{W}}_j{ }^2$$

(24)

where ${\kappa }_j$ is the adaptation law coefficient and is a positive constant.

The dynamic of $V_j$ can be expressed as

$${\dot{V}}_j=-k_{1j}{e}_{1j}{ }^2-k_{2j}{e}_{2j}{ }^2-k_{3j}{e}_{3j}{ }^2+{\tilde{W}}_j{ }^T\left(e_{3j}{H}_j(\lambda )-\frac{1}{{\kappa }_j}{\dot{\widehat{W}}}_j\right)+e_{3j}{\epsilon }_j-{\epsilon }_{Nj}\left|e_{3j}\right|$$

(25)

Moreover, the on-line adaptive law of the neural network is selected as follows:

$${\dot{\widehat{W}}}_j={\kappa }_j{e}_{3j}{H}_j(\lambda )$$

(26)

In addition, we have

$$e_{3j}{\epsilon }_j-{\epsilon }_{Nj}\left|e_{3j}\right|\le 0$$

(27)

By combining (25), (26) and (27), we obtain

$${\dot{V}}_j\le -k_{1j}{e}_{1j}{ }^2-k_{2j}{e}_{2j}{ }^2-k_{3j}{e}_{3j}{ }^2\le 0$$

(28)

Remark 4. 

According to (28), the Lyapunov function of this system is negative definite, which proves that the whole system is stable. The new controller combining HOSMO and NNDO solves the coupling problem between the state estimation and disturbance estimation and obtains excellent control performance with the only available position signal. The controller takes into account not only its own position tracking, but also the velocity relationship with adjacent cylinders, which helps to improve the synergy in multi-cylinder systems.

4. Simulation and Experimental Results

In this section, a simulation is conducted to prove the effectiveness of the designed NNDO and HOSMO through MATLAB/Simulink 2017a. Furthermore, the proposed neural-network-based output feedback controller (NNOC) is compared with the proportional integral controller (PI) to verify the position control advantages of the presented method for a hydraulic support multi-cylinder moving system.

4.1. Simulation Results

Simulation analysis is conducted to verify the performance of the proposed controller in this section, and the parameters of the moving cylinder are shown in

Table 1. Physical parameters of the moving cylinder system.

Parameters	Values	Parameters	Values
$A_1\left({\mathrm{m}}^2\right)$	1.9625 × 10−3	$m\left(\mathrm{k}\mathrm{g}\right)$	50
$A_2\left({\mathrm{m}}^2\right)$	1.000875 × 10−3	$b(\mathrm{N}·\mathrm{m})$	4500
$P_s\left(\mathrm{P}\mathrm{a}\right)$	5 × 106	${\beta }_e\left(\mathrm{P}\mathrm{a}\right)$	7 × 108
$P_r\left(\mathrm{P}\mathrm{a}\right)$	0	$C_t({\mathrm{m}}^3/\mathrm{s}/\mathrm{P}\mathrm{a})$	4 × 10−13
$V_{01}\left({\mathrm{m}}^3\right)$	3 × 10−3	$k_t({\mathrm{m}}^3/\mathrm{s}/\mathrm{V}/\sqrt{\mathrm{P}\mathrm{a}})$	8.43 × 10−8
$V_{02}\left({\mathrm{m}}^3\right)$	3 × 10−3

. The desired trajectory is set as $y_d=0.2\sin \left(0.125\pi t\right)(1-\mathrm{e}\mathrm{x}\mathrm{p}(0.01t^2\left)\right)$. The load force of the moving cylinder is unknown and variable, the integrated force is defined as $F_d=1000\times \sin \left(0.2\mathrm{\pi }\mathrm{t}\right)$, and the modeling uncertainty of the system is defined as $∆1=∆2=100\times \sin \left(\mathrm{t}\right)$ in the simulation experiment. The control parameters of HOSMO are ${\lambda }_1=8$, ${\lambda }_2=5$, and ${\lambda }_3=2$, ${\lambda }_4=1$. The input of NNDO is chosen as ${[z_1, z_2,z_3, e_1, e_2, e_3]}^T$. The basic coordinate vector of the Gaussian function is selected as $c_j={[-1,-0.5, 0, 0.5, 1]}^T$, and the width is chosen as $b_j=100$. The adaptation law coefficient is $\kappa =500$. Additionally, the control parameters of PI are chosen as $k_p=800$ and $k_i=20$. The control parameters of NNOC are chosen as $k_1=180$, $k_2=80$ and $k_3=80$.

In addition, three tracking error indicators (average, maximum, and mean square error of absolute tracking error) are defined as follows:

1. The average absolute tracking error is defined as

$$A_e=\frac{1}{N}{\displaystyle \sum _{i=1}^N\left|e_1(i)\right|}$$

(29)

where $N$ denotes the number of recorded digital signals.

2. The maximum absolute tracking error is defined as

$$M_e=\underset{i=1,\dots ,N}{\max }\left\{\left|e_1(i)\right|\right\}$$

(30)

3. The mean square error of the absolute tracking error is defined as

$$S_e=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N{\left[\left|e_1(i)\right|-A_e\right]}^2}}$$

(31)

Taking a single moving cylinder as an example, the performance of the proposed controller is analyzed. The trajectory tracking performance and tracking error are shown in Figure 3. The average absolute tracking error of the PI controller is 0.89 mm, while the error of the NNOC controller is only 0.1 mm. The maximum tracking error of the PI controller is 1.76 mm, while the error of the NNOC controller is only 0.46 mm. The mean square error of the absolute tracking error of the PI controller is 0.54 mm, while the error of the NNOC controller is only 0.09 mm. Therefore, the designed output cooperative controller has the potential to replace the PI controller.

Figure 4 shows the estimation performance of HOSMO. It can be seen from the figure that the estimation of the moving cylinder position is very accurate, and that it basically coincides with the actual value. The estimated velocity value of the moving cylinder is consistent with the actual value in the overall trend, and the average absolute estimation error is 8.84 mm/s. There is a significant fluctuation in the acceleration signal of the moving cylinder, especially during the moment of reversing. The average absolute estimation error of the acceleration is 2.35 m/s², and the estimated acceleration fluctuation is smaller, which is more conducive to application in controller design.

The estimated effect of the NNDO is shown in Figure 5. The estimated value is a smooth curve, and it is generally consistent with the actual unknown function, which proves the excellent estimation ability of NNDO. The average absolute estimation error is 371.92 N, so the tracking error of NNDO for the entire unknown function is only 3.13%, which could greatly simplify the design process of the controller. The maximum estimation error is 1399.26 N and the mean square error of the absolute estimation error is 316.04 N, which means that the estimation effect of NNDO is relatively stable. It can be seen that the designed NNDO in this paper has a strong ability to estimate unknown functions, which can effectively simplify controller design and improve system robustness. Therefore, the proposed output cooperative controller has a simple structure and good control performance, with the potential to replace the PI controller in the multi-cylinder system of a hydraulic support.

4.2. Experimental Results

To further verify the performance of the designed controller, a multi-cylinder control system test bench is built, as shown in Figure 6. The test rig of the multi-cylinder system includes three asymmetric cylinders, a pump station, three servo valves and three displacement sensors. The displacement of the single cylinder movement is 100 mm, and the action interval is 1 s between the three cylinders, which is mainly to ensure the safety of the roof.

Figure 7 shows the trajectory tracking of the adjacent moving cylinders. Cylinder 1 is taken as an example for analysis. The maximum tracking errors of the PI and NNOC controllers in the early stage of movement are 4.31 mm and 3.95 mm, respectively. The moving cylinder has a maximum tracking error at the moment of startup, and the maximum error of the new controller is 8.35% higher than that of the PI controller. The average absolute tracking error of the PI controller is 2.87 mm, while the error of the NNOC controller is only 0.51 mm, which indicates that the proposed controller has been improved significantly. In addition, the mean square error of the absolute tracking error of the PI controller is 0.59 mm, but the error of the NNOC controller is 0.74 mm. The reason for this result may be that the tracking process of the PI controller is always lagging, while the proposed controller fluctuates around the zero value. The tracking error indexes of other cylinders are further described in

Table 2. Tracking error indexes of three cylinders.

Indexes	Cylinder 1			Cylinder 2			Cylinder 3
	${\mathit{A}}_{\mathit{e}}$	${\mathit{M}}_{\mathit{e}}$	${\mathit{S}}_{\mathit{e}}$	${\mathit{A}}_{\mathit{e}}$	${\mathit{M}}_{\mathit{e}}$	${\mathit{S}}_{\mathit{e}}$	${\mathit{A}}_{\mathit{e}}$	${\mathit{M}}_{\mathit{e}}$	${\mathit{S}}_{\mathit{e}}$
PI	2.87	4.31	0.59	2.87	4.1	0.6	2.64	3.99	0.57
NNOC	0.51	3.95	0.74	0.55	4.44	0.89	0.44	2.31	0.42

. Compared with the traditional PI controller, the designed NNOC has a smaller termination error, which helps to improve the straightness of the fully mechanized mining face.

Figure 8, Figure 9 and Figure 10 show the observation results of the designed HOSMO for different moving cylinders. It can be seen from the figures that the estimation of the position state of each moving cylinder is very accurate, and basically coincides with the actual value. The velocity value of each moving cylinder fluctuates greatly in the initial stage of motion, and shows a smooth curve after smooth motion. The acceleration signal fluctuates more than the velocity signal, which is mainly because the differentiation of the signal tends to amplify the negative influence of the noise. But on the whole, the designed HOSMO is stable in the estimation of the system states within a certain range and shows no shock phenomenon, which proves that HOSMO is effective. The integrated disturbance estimation plot for each moving cylinder is presented in Figure 11. The designed NNDO has a gentle estimation curve for the integrated disturbance of each moving cylinder, which enables the controller to compensate for it, and helps to improve the anti-disturbance capabilities and control accuracy of the hydraulic support multi-cylinder system.

5. Conclusions

In this paper, a neural-network-based output cooperative controller is proposed for the multi-cylinder system of a hydraulic support, which improves the multi-cylinder’s capacity for synergy under the conditions of the coal mine environment. The multi-cylinder system is represented as a standard feedback model with lump disturbances, including parameter uncertainties and external disturbances. HOSMO is designed to estimate the system states with the only available output signal, which can be applied directly in controller design due to the finite-time convergence property. NNDO is presented to approximate the unknown nonlinear function of the model-free system, and the tracking error for the entire unknown function is only 3.13%. Furthermore, simulations and experiments are carried out to demonstrate the effectiveness of the proposed controller. The experimental results show that the maximum error of the proposed controller is 8.35% higher than that of the PI controller. The proposed controller has an average absolute tracking error of 0.51 mm, and the mean square error of the absolute tracking error is 0.74 mm. Therefore, the proposed output cooperative controller has the potential to replace the PI controller in the multi-cylinder system of a hydraulic support.