Deep Bidirectional Learning Based Enhanced Outage Probability for Aerial Reconfigurable Intelligent Surface Assisted Communication Systems

Abstract

The reconfiguration of wireless channels with reconfigurable reflecting surface (RIS) technology offers new design options for future wireless networks. Due to its high altitude and increased probability of establishing line-of-sight linkages with ground source/destination nodes, aerial RIS (ARIS) has greater deployment flexibility than traditional terrestrial RIS. It also provides a wider-view signal reflection. To leverage the advantages of ARIS-enabled systems, this paper defines air-to-ground linkages via Nakagami-m small-scale fading and inverse-Gamma large-scale shadowing, considering realistic composite fading channels. To construct a tight approximate closed-form formula for the outage probability (OP), a new mathematical framework is proposed. Additionally, a deep-learning-based system called the BiLSTM model is deployed to evaluate OP performance in the 3D spatial movement of the ARIS system. In the offline phase, the proposed model is trained with real-value channel state estimation sets and enhances OP performance in the online phase by learning channel information in a bidirectional manner. Simulation results demonstrate that the proposed BiLSTM model outperforms all other models in analyzing OP for the ARIS system.

1. Introduction

As the fifth-generation (5G) wireless communication network unfolds globally, the exploration of the sixth-generation (6G) wireless network is now underway. 6G aims to establish pervasive connectivity with data rates surpassing 100 to 1000 times those of 5G, reaching an impressive 1 Terabyte per second [1,2]. For this purpose, prominent wireless transmission technologies like Terahertz communication and ultra-massive multiple-input multiple-output have become focal points of extensive research attention [3]. Flexible and mobile wireless smart communication environments are encountering challenges in sustaining direct line-of-sight connections between mobile devices or IoT devices and base stations, particularly in obstructed or densely populated urban settings. A potential solution to overcome these obstacles is the utilization of reconfigurable intelligent surfaces (RIS) [4]. RIS operates by manipulating the propagation of wireless signals and enhancing or suppressing them through reflective or refractive mechanisms. The recent advancements in smart radio systems, which enable the control of wireless signal operations, have paved the way for exploring novel applications of RIS in advanced wireless communication networks beyond the realms of 5G and into the domain of 6G. Various strategies have initially employed stationary RIS installed on buildings and utilized unmanned aerial vehicles (UAVs) as relays to enhance different communication metrics, including transmission rate, throughput, age of information, energy efficiency, sum secrecy rate, and signal-to-interference-plus-noise ratio, primarily in non-adversarial scenarios [5,6,7,8].

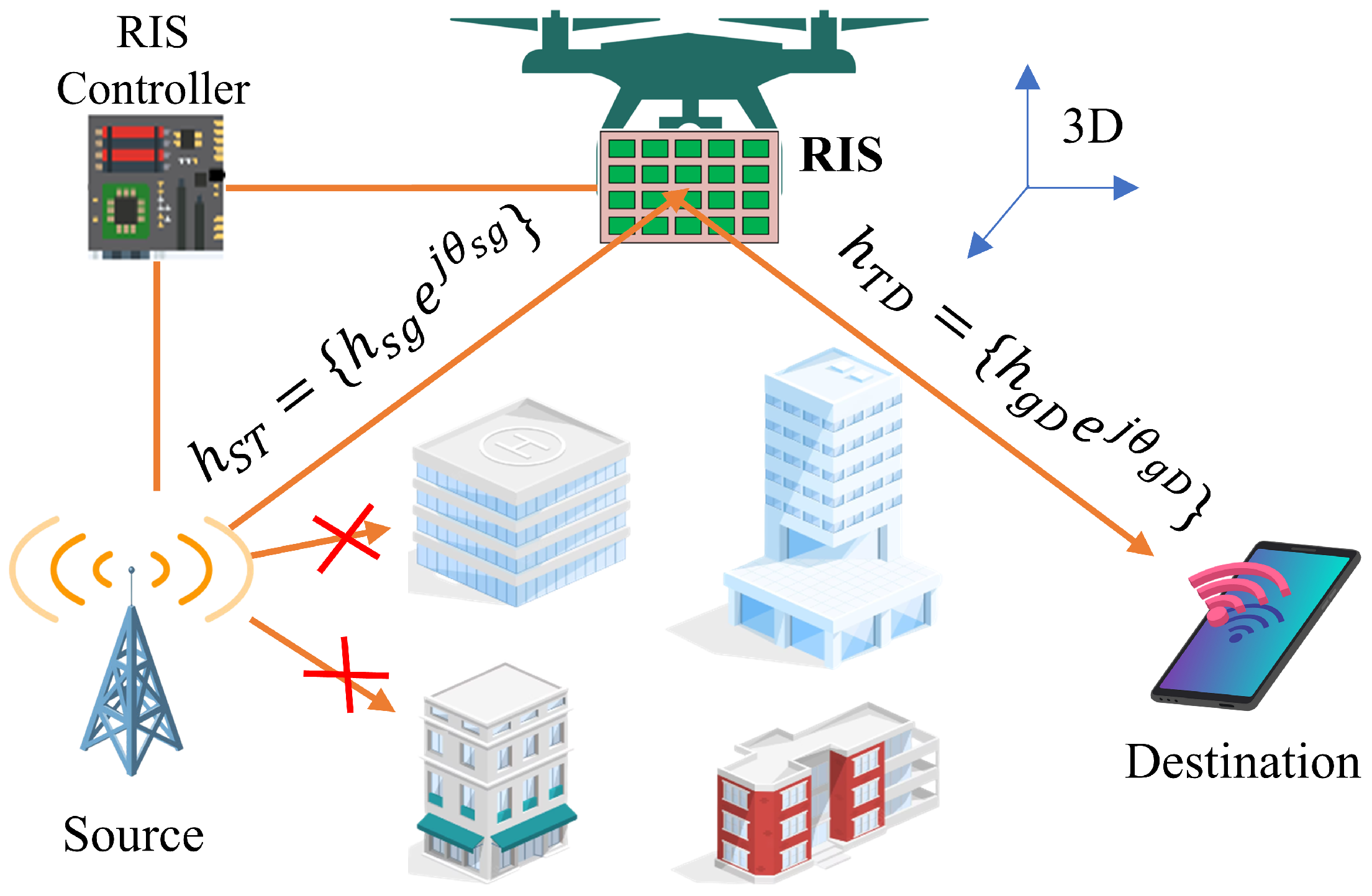
The research focus has shifted towards terrestrial RIS-assisted communication, primarily used within interior walls, ceilings, or building facades. However, this architecture presents several fundamental challenges. Firstly, determining optimal RIS installation locations can be complex due to factors like site rent, urban environment effects, and property-owner permissions. Comprehensive RIS placement: Using the strategy depicted in Figure 1, it can be identified by a set of all potential spots in the layout that are organized in a grid, denoted as $G_R$, with a predefined distance, $d_R$, separating each position. The orientation of the RIS panels is equally distributed within the range [0, $2\pi$] at every position in $G_R$. It is crucial to note that RIS grid coordinates lying inside any prohibited regions are not considered when placing the RIS, as the line of sight (LOS) for the base station (BS)-RIS link would be obstructed. After determining the placement of RIS within each blocked region, the shortest distance is calculated between each identified RIS position and the boundaries of the corresponding blocked region [9].

Site rent: It is assumed that a telecom operator wishes to improve signal coverage in a highly populated metropolitan region by implementing RIS technology. When installing RIS panels on utility poles or buildings, they must contend with the expense of site leasing. Deploying RIS in other regions may not be as feasible due to high site leasing expenses. To reduce these expenses, companies could have to bargain with property owners or look into different deployment techniques. Effects of the urban environment: RIS technology is being implemented in a busy city center characterized by tall buildings and winding streets. The urban setting adds complications such as restricted line-of-sight chances, multipath propagation, and signal interference from nearby structures. These surrounding conditions may have an impact on how well RIS deployment works. To determine the best places for RIS installations to reduce the impacts of urban morphology on signal transmission, sophisticated modeling approaches like ray-tracing simulations could be required. 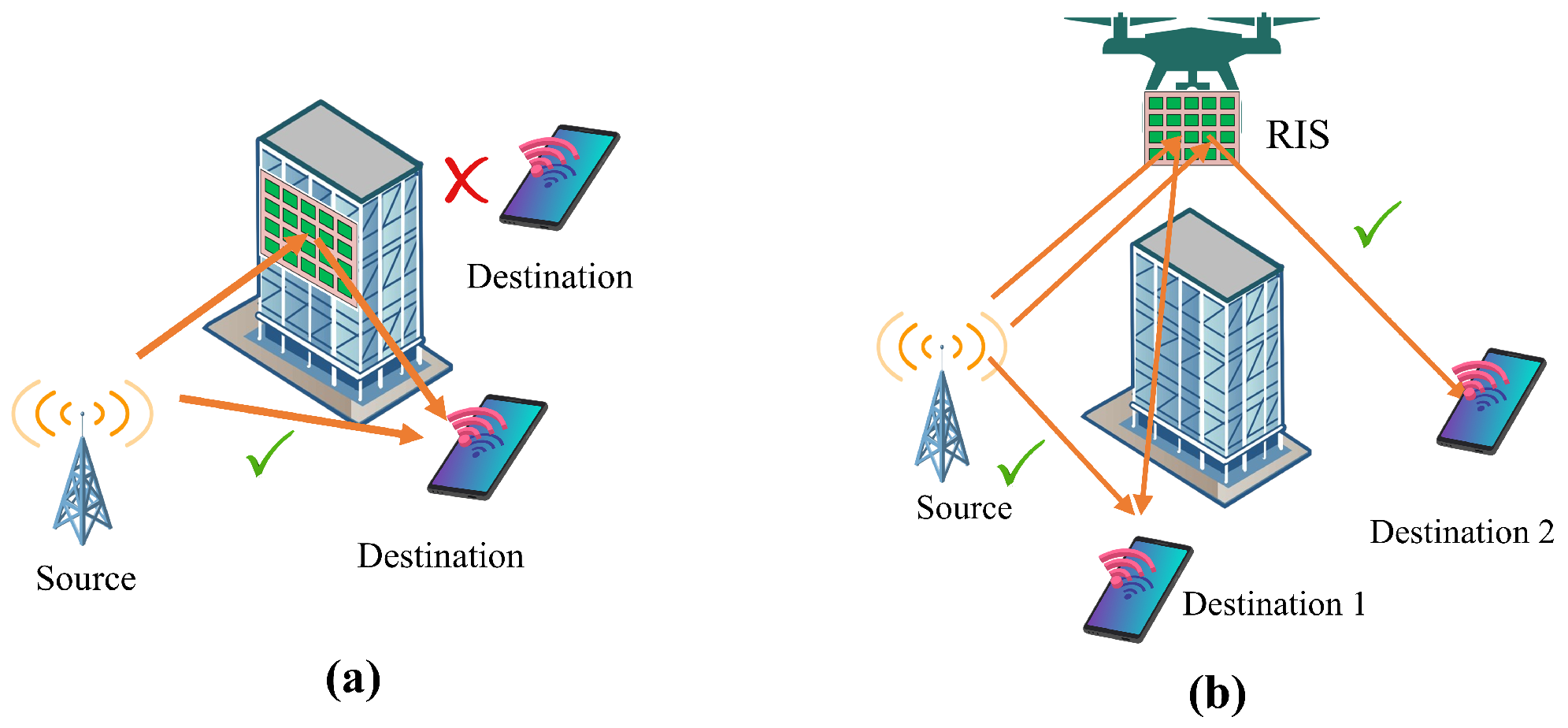Permissions from property owners: It is assumed that a telecom company wants to enhance network coverage by installing RIS panels on private properties. However, it becomes logistically difficult to obtain property owners’ consent to put the panels on their buildings or other structures. Some property owners can be worried about liability, possible structural damage, or aesthetics. Deployment plans can be postponed or stopped completely in the absence of sufficient authorization. RIS installation approvals may need to be obtained through revenue-sharing or incentive agreements, property-owner negotiations, and resolving their concerns. Secondly, the RIS positioned on building walls or facades only serves terminals on one side, limiting coverage as shown in Figure 2a. Thirdly, radio signals undergo multiple reflections in urban environments, leading to signal scattering and attenuation even with RIS passive beamforming which is shown in Figure 3a. To address these issues, this paper proposes a novel three-dimensional (3D) wireless network enabled by aerial RIS (ARIS), where RIS is deployed on aerial platforms such as balloons or UAVs for intelligent reflection from the sky. ARIS offers several advantages over traditional terrestrial RIS. Firstly, it establishes line-of-sight (LoS) communication with ground nodes more effectively due to its elevated position [10], enhancing channel strength and enabling flexible optimization of aerial platform location or trajectory. Secondly, ARIS enables panoramic/full-angle reflection, allowing it to theoretically assist in reflecting signals between any pair of ground-based nodes shown in Figure 2b, unlike terrestrial RIS limited to half of the available space. Lastly, ARIS with its high probability of LoS linkages typically achieves required signal modification by a single reflection even in complex urban environments (see Figure 3b), significantly reducing signal power loss compared to terrestrial RIS. For example, the advantages of ARIS over traditional terrestrial RIS are an important factor in enabling future wireless communication non-orthogonal multiple access (NOMA) systems. The authors in [11] showed, through a comparison of ARIS-NOMA with the outcomes of terrestrial RIS-NOMA and ADF-NOMA deployment, that the energy efficiency curves versus transmit power for various reflecting element counts and their corresponding ARIS-NOMA, terrestrial RIS-NOMA, and ADF-NOMA schemes are depicted in Figure 4. It is evident that ARIS-NOMA systems may achieve higher levels of energy efficiency compared to conventional terrestrial RIS deployment. The analysis indicates that greater performance benefits can be obtained with less transmit power by investigating aerial mobility than with traditional terrestrial RIS-NOMA.

In recent years, deep learning (DL)-based techniques have gained attention in the ARIS-assisted system due to the prominent benefits of performance increment [12,13,14,15,16,17]. In ref. [12], the authors suggested the utilization of the deep deterministic policy gradient as a model-free off-policy reinforcement learning (RL) method to maximize the MU-MISO system’s sum rate. This is achieved by the cooperative optimization of the phase shifters of the passive reflecting components at the ARIS and the active beamforming matrix at the ground base station. In the context of a UAV eavesdropper, an efficient ARIS-assisted PLS technique in [13] maximizes the average downlink secrecy rate of several terrestrial ground terminals using a DDPG. The authors in [14] maximized the average secrecy rate by jointly investigating the reflection of RISs and the flying trajectory of the ARIS by deploying an RL model.

In the progression towards 6G technology, non-terrestrial communication methods are acknowledged as dependable tools for establishing connections in remote and challenging terrains. However, the dynamic nature of spatial movements necessitates the development of novel fading models that can accurately depict both the downlink and uplink channels in air-to-ground (A2G) communication scenarios. Research on A2G communication, particularly focusing on UAV-aided dual-hop relaying and outage probability (OP) analysis, has gained significant attention due to its potential applications in various fields like surveillance, disaster management, and communication in remote areas. A2G channel modeling for UAV-assisted communication was discussed in [18,19,20,21,22]. The authors in [18] presented the ideal height of the UAV in terms of communication coverage in the A2G channel, as well as the ideal height and location of UAVs while acting as relays. The authors of [19] examined how the interfering node affects dependable UAV communications. They calculated the OP in closed form for all feasible situations (A2G, G2A, G2G, A2A) of main and interference connections after describing the channel model impacted by the communication link’s elevation angle. The study in [20] developed a LOS probability expression for A2G channels using urban scenario statistics and geometry. Their simplified parametric model expedites predictions and aids in channel modeling. Leveraging this analytical model, they trained a back-propagation neural network for parameter generation. Simulation results confirmed its versatility across altitudes and agreement with Monte Carlo data. In a densely populated urban setting, the authors in [21] calculated the likelihood of a loss of service for A2G connection based on the drone’s height and the typical building height. Additionally, the study [22] discussed UAV-based relaying in urban contexts in conjunction with energy harvesting. They considered A2G channels which are classified as either shadowing Rayleigh fading or shadowed Rician fading. The authors created a closed-form expression for OP and a cooperative channel model for a space-to-ground network. A 3D UAV stochastic mixed mobility (MM) model mechanism allows a UAV to move either vertically by adhering to the random waypoint mobility (RWPM) model or experiencing a spatial digression determined by the random movement model for raw walk [23,24]. The following mechanisms, such as trajectory control and altitude control, define the 3D UAV movement process. The analytically tractable MM model may be used to evaluate ARIS network performance. However, UAVs are more likely to travel in a uniform spatial manner. As a result, developing an efficient 3D mobility model for UAV movement that accounts for both of the aforementioned mechanisms remains very challenging. Furthermore, the 3D mobility model’s steady-state distribution of UAV positions must be tractable enough to allow for UE performance monitoring inside the network [24]. Therefore, this study presents a mixed mobility model for the 3D UAV movement process, with the RWPM models characterizing the vertical and spatial motions. Next, the coverage probability of the interference received at a reference ground destination under inverse-Gamma shadowing and Nakagami-m fading is assessed based on the suggested 3D mixed mobility model. In the study [25], the OP of UAV-aided dual-hop relaying was investigated, taking into account 3D spatial movements. Another recent work [26] utilized empirical data from A2G trials to model A2G channels, employing Nakagami-m multipath fading and inverse-Gamma shadowing. Deep neural networks (DNNs) have shown promising effectiveness in predicting the secrecy performance of A2G communications and OP in ARIS-assisted wireless communication networks. By leveraging their ability to learn complex patterns from data, DNNs can capture the intricate relationships between various parameters affecting secrecy and OP. DNN represents the connection between system characteristics and the associated secure OP, which can accurately forecast the secure OP’s performance for a range of interesting real-world scenarios [15]. This enables more accurate predictions, aiding network optimization and resource allocation. In a different approach [15], DNN were employed to predict the secrecy performance of A2G communications. Furthermore, considering the ARIS’s 3D spatial mobility, the authors in [27] constructed a DNN that can precisely anticipate the OP. In order to obtain consistent performance and a notable improvement in secure performance, in [16], authors suggested a DNN-based method that additionally takes use of ARIS in the non-orthogonal multiple access assisted wireless system. In ref. [17], the authors suggested the use of ARIS in a relaying system to preserve the accuracy of data on distant Internet of Things wireless networks using the RL model. The goal is to reduce the predicted cumulative age of information by optimizing the RIS components’ phase-shift matrix, communication schedule, and UAV elevation.

In a feed-forward neural network execution, RNN is capable of processing input sequences of different durations across time. RNNs remember past occurrences and use knowledge to predict future results. To regulate access to memory cells, an RNN variation called LSTM is created using certain gating approaches [28]. Sequencing problems are often solved using RNNs such as LSTM. Unlike the hidden unit in a typical RNN design, the LSTM has a gate architecture that allows it to identify and store important information while rejecting irrelevant information. The BiLSTM network is better at sequence classification than LSTM as it allows for bidirectional data flow. By using information from both previous (backward) and subsequent (forward) events concurrently, BiLSTM outperforms LSTM in terms of accuracy. This architecture improves the flow of data in the BiLSTM network, which improves learning performance by capturing more characteristics in the input data [29]. For RIS-enabled multi-user multiple-input single-output downlink orthogonal frequency division multiplexing systems, in ref. [30], authors suggested a BiLSTM-model-based channel estimation and signal detection. By capturing more characteristics from the input data, this architecture improves learning performance as the data flow inside the BiLSTM network is optimized [31]. According to the study [32], the experiment’s results show that BiLSTM extracts features more effectively than LSTM. A stacked BiLSTM architecture for RIS-assisted unmanned aerial vehicle communication systems was previously reported by [33]. The authors in [34] proposed a BiLSTM-based massive MIMO system for channel estimation, where the proposed model effectively reduces the pilot overhead. BiLSTM has difficulties with hyperparameter tweaking, data reliance, and complexity. However, BiLSTM networks provide benefits for OP analysis by capturing bidirectional information flow and sequential context. Furthermore, the BiLSTM is promising for OP estimation problems due to its automated feature representation and context awareness.

Motivated by the above research work and the effective advantages of the BiLSTM model in wireless systems, in this paper, we suggest an effective ARIS-assisted wireless communication network that is susceptible to a combined fading channel model, in which the large-scale shadowing is distributed according to an inverse-Gamma distribution, and the small-scale fading is governed by a Nakagami-m distribution. We examine the ARIS-assisted method’s outage efficiency in such a realistic fading channel scenario. In order to provide a tight approximated closed-form formulation for the OP, we put forth a novel mathematical framework. Next, we examine a mobile setting in which the RWMM is used to simulate the 3D spatial movement of ARIS. Because the locations of the ARIS are represented as random variables in such a mobile framework, the outage investigation becomes intractable. Therefore, in the offline phase, a BiLSTM is employed, and trained by pre-collected OP data as well as related channel state information (CSI) to forecast the OP. The BiLSTM model effectively trains the channel data in the forward and backward directions and enhances the learning efficiency of the model. The Adam optimization algorithm is utilized to effectively lessen the loss. In the online phase, the trained model is deployed for testing using the test data and it is found that during testing the proposed model effectively performs the OP analysis. The OP performance of the proposed model outperforms the other models which are shown in the simulation results.

2. Methods

2.1. System Model

In this study, we employ a low-complexity system assuming a source/transmitter and a destination/receiver equipped with a single antenna. In addition, it is considered that the direction channel of source to destination is not applicable in this system due to the ground obstacles. Alternatively, the source-to-destination channel is connected by ARIS, T, and can work passively to reflect signals from source to destination. The designed system is illustrated in Figure 5. Consider that the ARIS consists of N reflective elements and the complex channel coefficient vectors between the source and ARIS and ARIS and destination is ${\mathbf{h}}_{\mathbf{ST}}\in {\mathbb{C}}^{N\times 1}$ and ${\mathbf{h}}_{\mathbf{TD}}\in {\mathbb{C}}^{N\times 1}$, respectively. Through phase-shift matrix $\mathsf{\Psi }=\kappa$diag$(e^{j{\varphi }_1},\dots ,e^{j{\varphi }_N})$, the properties of ARIS are defined where ${\varphi }_t\in [0,2\pi ]$, $t=1,\dots ,N,$ is the phase-shift angle in the ARIS elements of t, and the reflection coefficient is $\kappa \in [0,1]$ [35]. The transmit signal from source to destination is defined as $\mathbb{E}\left[\right|s{|}^2]=1$. Therefore, the received signal at the destination can be formulated as follows:

$$y=\sqrt{P}\sum _{t=1}^N{\left[{\mathbf{h}}_{\mathrm{ST}}\right]}_t\kappa e^{j{\varphi }_t}{\left[{\mathbf{h}}_{\mathrm{TD}}\right]}_{t}s+w,$$

(1)

where the transmission signal power of the source is P and the additive white Gaussian noise (AWGN) at the destination is $\mathbf{w}\sim \mathcal{CN}(0,{\sigma }^2)$ with zero mean and ${\sigma }^2$ variance.

2.2. Channel Model

For the channel model, it is assumed that ${\left[{\mathbf{h}}_{\mathbf{ST}}\right]}_t\triangleq {\tilde{\mathbf{h}}}_{St}$ and ${\left[{\mathbf{h}}_{\mathbf{TD}}\right]}_t\triangleq {\tilde{\mathbf{h}}}_{tD}$. The expression of polar complex channel coefficient ${\tilde{h}}_{ccc}$ is as ${\tilde{h}}_{ccc}=h_{ccc}{e}^{j{\theta }_{ccc}}$, with $ccc\in \{St,tD\}$ where $h_{ccc}=\left|{\tilde{h}}_{ccc}\right|$ and ${\theta }_{ccc}\in [0,2\pi ]$. In a real-world composite fading channel, the small-scale fading, denoted by $G_{ccc}$, is represented by a Nakagami-m random variable, while the large-scale shadowing effects, denoted by $L_{ccc}$, follow an inverse-Gamma random variable. The composite fading channel, $h_{ccc}$, is then expressed as the product of these two components: $h_{ccc}=L_{ccc}{G}_{ccc}$. In more detail, $G_{ccc}$’s Nakagami-m probability density function (PDF) is provided as follows [27,36]:

$$f_{G_{ccc}}(x;m,\sigma )=2{\left(\frac{m}{\sigma }\right)}^m\frac{1}{\xi \left(m\right)}{x}^{(2m-1)}{e}^{\frac{-m}{\sigma }{x}^2},x>0,$$

(2)

where the parameter of $m>0$ is the shape parameter, indicating the severity of fading, and $\sigma >0$ is the spread parameter of the distribution. However, if the $L_{ccc}$ is given, the inverse-Gamma PDF is formulated as follows [27]:

$$f_{L_{ccc}}(x;\zeta ,\delta )=\frac{{\delta }^{\zeta }}{\xi \left(\zeta \right)}{x}^{(-\zeta -1)}{e}^{\frac{-\delta }{x}},x>0,$$

(3)

where $\zeta >1$ is the shaping parameter of the distribution, related to the severity of the shadowing, i.e., lower values of $\zeta$ result in lighter shadowing conditions, $\delta$ denotes the scaling parameter.

However, from (1), the proposed system’s achievable capacity can be expressed as follows:

$$A_c=\underset{{\varphi }_1,\dots ,{\varphi }_N}{max}{log}_2\left(1+\frac{P_{\mathrm{S}}}{{\tau }^2}{\left|\kappa \sum _{t=1}^N{\left[{\mathbf{h}}_{\mathrm{ST}}\right]}_t{e}^{j{\varphi }_t}{\left[{\mathbf{h}}_{\mathrm{TD}}\right]}_t\right|}^2\right).$$

(4)

2.3. Analysis of Outage Performance

This section examines the OP of the suggested communication system because it is typical practice to assess a communication system’s performance and dependability using this measurement. A possibility that the system’s instant mutual information would fall short of a predetermined goal spectral efficiency $A_{cth}$, [b/s/Hz], is known as the Op of the system. This can be stated mathematically as follows:

$$\begin{array}{c}{\mathrm{P}}_{\mathrm{out}}=Pr\left(A_c<A_{\mathrm{cth}}\right)=Pr\left(\eta <{\eta }_{\mathrm{th}}\right),\end{array}$$

(5)

where ${\eta }_{\mathrm{th}}\triangleq 2^{A_{\mathrm{cth}}}-1$ and at the destination, and $\eta$ represents the end-to-end received signal-to-noise ratio (SNR), which can be formulated as follows:

$$\eta =\underset{{\varphi }_1,\dots ,{\varphi }_N}{max}\overline{\eta }{\left|\kappa \sum _{t=1}^N{L}_{\mathrm{S}t}{G}_{\mathrm{S}t}{e}^{j\left({\varphi }_t+{\theta }_{\mathrm{s}t}+{\theta }_{t\mathrm{D}}\right)}{G}_{t\mathrm{D}}{L}_{t\mathrm{D}}\right|}^2,$$

(6)

where $\kappa$ is the fixed amplitude reflection coefficient of ARIS, $L_t=L_{St},L_{tD}$ is expressed as the end-to-end fading with respect to the one RIS element and $G_t=G_{St},G_{tD}$ is expressed as the end-to-end shadowing with respect to the one RIS element, and the average transmit SNR [dB] is shown by $\overline{\eta }=P/{\tau }^2$. To solve (5), we first build up the phase-shift matrix, or ${\mathsf{\Psi }}^{*}$, in the best possible way so that (6) maximizes the end-to-end SNR. For each reflective element of ARIS, following the works [35,37,38], we configured the ${\varphi }_t^{*}=-({\theta }_{\mathrm{s}t}+{\theta }_{t\mathrm{D}}){\forall }_t$. As a result, the OP in (5) can be rewritten as follows:

$$P_{\mathrm{out}}=\mathrm{Pr}\left(\overline{\eta }{\kappa }^2{\left|\sum _{t=1}^N{L}_{St}{G}_{St}{G}_{tD}{L}_{tD}\right|}^2<{\eta }_{\mathrm{th}}\right).$$

(7)

In (7), derived the expression OP $P_{\mathrm{out}}$, which is the probability that the received SNR falls below a certain threshold ${\eta }_{\mathrm{th}}$ in a wireless communication system. This expression is derived by analyzing the statistical properties of the received SNR, path loss, shadowing, and fading, resulting in an approximate closed-form expression for the OP $P_{\mathrm{out}}$ analysis. It is assumed that $W_t\triangleq L_{St}{G}_{St}{G}_{tD}{L}_{tD},G_t\triangleq G_{St}{G}_{tD},L_t\triangleq L_{St}{L}_{tD},$ and ${\tilde{L}}_t\triangleq \frac{1}{\sqrt{L_t}}$ and a [Gamma/(Gamma2)] distribution can be matched to the distribution of $W_t$, whose theoretical details are provided in Theorem 1. To achieve this, we first suggest a distribution matching for $G_t$ and ${\tilde{L}}_t$, which is shown in Lemma 1. Assumed X is a Gamma random variable, and the PDF is provided as follows:

$$f_X(x;\mu ,\varsigma )=\frac{1}{{\varsigma }^{\mu }\xi \left(\mu \right)}{x}^{(\mu -1)}{e}^{\frac{-x}{\varsigma }},x>0,$$

(8)

where it is indicated that $X\sim \mathrm{Gamma}(\mu ,\varsigma )$, where $\mu$ and $\varsigma$ stand for the shape and scale parameters, respectively.

However, Lemma 1 is given for the $G_t$ and ${\tilde{L}}_t$ distributions, which are roughly matched to a Gamma distribution in the manner described as follows:

$$\begin{array}{cc}& G_t\stackrel{\mathrm{approx}.}{\sim }Gamma\left(m_G,{\sigma }_G/m_G\right),\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & {\tilde{L}}_t\stackrel{\mathrm{approx}.}{\sim }Gamma\left(m_L,{\sigma }_L/m_L\right),\hfill \end{array}$$

(10)

where ${\sigma }_G\triangleq \frac{\xi (m_s+1/2)\xi (m_d+1/2)}{\xi \left(m_s\right)\xi \left(m_d\right)}{\mathsf{{\rm Y}}}_G^{-1/2},$ ${\mathsf{{\rm Y}}}_G\triangleq \frac{m_s{m}_d}{{\sigma }_s{\sigma }_d},$ $m_G\triangleq \frac{{\sigma }_G^2}{{\sigma }_s{\sigma }_d-{\sigma }_G^2},$ ${\sigma }_L\triangleq \frac{\xi ({\zeta }_s+1/2)\xi ({\zeta }_d+1/2)}{\sqrt{{\delta }_s{\delta }_d}\xi \left({\zeta }_s\right)\xi \left({\zeta }_d\right)},$ $m_L\triangleq \frac{{\sigma }_L^2}{\left(\frac{{\zeta }_s{\zeta }_d}{{\delta }_s{\delta }_d}\right)-{\sigma }_L^2}$. The proof of Lemma 1 is described in [27].

$$\begin{array}{cc}\hfill F_{|Z{|}^2}\left(z\right)\approx & \frac{1}{\xi \left(N{m}_G+1\right)}{z}^{\frac{N{m}_G}{2}}\sum _{{\mathsf{\Xi }}_{\tau },\forall \tau }\left(\genfrac{}{}{0pt}{}{N}{{\tau }_1,\dots ,{\tau }_K}\right)\hfill \\ & \left[\prod _{k=1}^K{\aleph }_k^{v_k}\right]{\mathsf{\Phi }}_2^{\left(K\right)}\left(m_G{\tau }_1,\dots ,m_G{\tau }_K;1+N{m}_G;-\frac{\sqrt{z}}{{\varsigma }_1},\dots ,-\frac{\sqrt{z}}{{\varsigma }_K}\right),\hfill \end{array}$$

(11)

The closed-form formulas for the OPs, which are solely dependent on fading coefficients, are provided by Theorem 1. To determine the OP of the proposed ARIS-aided system, we offer a technological framework. Specifically, we employ the moment-matching approach to fit the distribution of the product of four separate random variables to that of a [Gamma/(Gamma2)] random variable, thus avoiding the emergence of parabolic cylinder functions. Gaussian–Laguerre quadrature is used to restructure the random variable and then convert it into a mixed Gamma random variable once more. The distribution of the sum of many converted mixed Gamma random variables is then obtained using the Laplace transform. We derive a tight approximate closed-form equation for the system OP with the help of our suggested technical framework [27].

Theorem 1.

Let consider $Z\triangleq {\displaystyle \sum _{t=1}^N}{W}_t={\displaystyle \sum _{t=1}^N}{L}_{St}{G}_{St}{G}_{tD}{L}_{tD}$, for the cumulative distribution function (PDF) of ${\left|Z\right|}^2$, an approximate closed-form formula may be obtained, as in (11), top of the next page, where $\left(\genfrac{}{}{0pt}{}{N}{{\tau }_1,\dots ,{\tau }_K}\right)$$\triangleq \frac{N!}{{\tau }_1!\dots {\tau }_K!},{\mathsf{\Xi }}_{\tau }\triangleq {({\tau }_1,\dots ,{\tau }_K)}^{\left(\tau \right)}$ signifies a potential pairing of ${\tau }_1,\dots ,{\tau }_K$, in which ${\tau }_K$$\in {\tau }_1,\dots ,{\tau }_K$ are positive integers that meet ${\displaystyle \sum _{k=1}^K}{\tau }_k=N$.

The proof of the theorem is provided as follows:

Proof. 

Consider ${\mathsf{\Lambda }}_G\triangleq {\sigma }_G/m_G$ and ${\mathsf{\Lambda }}_L\triangleq {\sigma }_L/m_L$, and relying on Lemma 1 to determine the approximate PDF of the [Gamma/(Gamma2)] random variables of $W_t=G_t/{\tilde{L}}_t$ can be expressed as follows:    □

$$f_{W_t}\left(y\right)\approx \frac{{\mathsf{\Lambda }}_L^{-m_L}}{\xi \left(m_L\right)}{\int }_0^{\infty }{x}^{m_L+1}{f}_{G_t}\left(y{x}^2\right)e^{-\frac{x}{{\mathsf{\Lambda }}_L}}dx.$$

(12)

We utilize the Gaussian–Laguerre (G-L) quadrature [39] to provide a tractable equation for the integral in (12) which is expressed as follows:

$$f_{W_t}\left(y\right)\approx \sum _{k=1}^K{\psi }_k\frac{y^{m_G-1}}{\xi \left(m_G\right)}{e}^{-\frac{y}{{\varsigma }_k}},y>0.$$

(13)

After normalization, the PDF of $W_t$ may be obtained in approximate closed form as follows:

$$f_{W_r}\left(y\right)\approx \sum _{k=1}^K{\aleph }_k\frac{y^{m_G-1}}{\xi \left(m_G\right)}{e}^{-\frac{y}{{\varsigma }_k}},$$

(14)

Therefore, the Laplace transform of $W_t$ can be expressed as follows:

$${\mathcal{LP}}_{W_r}\left(v\right)={\int }_0^{\infty }{e}^{-vy}{f}_{W_t}\left(y\right)dy=\sum _{k=1}^K{\aleph }_k{\left(\frac{1}{{\varsigma }_k}+v\right)}^{-m_G}.$$

(15)

The CDF of Z may be stated as follows after a few derivation steps using the Laplace transform for Z.

$$F_Z\left(z\right)={\mathcal{LP}}^{-1}\left\{\frac{1}{v}{\left[\sum _{k=1}^K{\aleph }_k{\left(\frac{1}{{\varsigma }_k}+v\right)}^{-m_G}\right]}^N;v,z\right\},$$

(16)

The inverse Laplace transform of $H\left(v\right)$ from the v-domain to the z-domain is shown by the notation ${\mathcal{LP}}^{1}H\left(v\right),v,z$. (16) is reformulated using the multinominal theorem as follows:

$$\begin{array}{c}{F}_Z\left(z\right)={\displaystyle \sum _{{\mathsf{\Xi }}_{\tau },\forall \tau }}\left(\genfrac{}{}{0pt}{}{N}{{\tau }_1,\dots ,{\tau }_K}\right)\left[{\displaystyle \prod _{k=1}^K}{\aleph }_k^{{\tau }_k}\right]\\ \times {\mathcal{LP}}^{-1}\left\{\frac{1}{v}{\displaystyle \prod _{k=1}^K}{\left(\frac{1}{{\varsigma }_k}+v\right)}^{-{\tau }_k{m}_G};v,z\right\}.\end{array}$$

(17)

Considering the Laplace transform’s linearity feature, we obtain as follows:

$$\begin{array}{c}{\mathcal{LP}}^{-1}\left\{\frac{1}{v}{\displaystyle \prod _{k=1}^K}{\left(\frac{1}{{\varsigma }_k}+v\right)}^{-{\tau }_k{m}_G};v,z\right\}=\frac{1}{\xi \left(N{m}_G+1\right)}\\ \times {\mathcal{LP}}^{-1}\left\{\frac{\xi \left(N{m}_G+1\right)}{v^{N{m}_G+1}}{\displaystyle \prod _{k=1}^K}{\left(\frac{1}{{\varsigma }_{k}v}+1\right)}^{-{\tau }_k{m}_G};v,z\right\},\end{array}$$

(18)

In addition, using [40], Equation (10) and following some minor mathematical adjustments or simplifications, the CDF of Z may be roughly expressed in closed form as follows:

$$\begin{array}{c}{F}_Z\left(z\right)\approx \frac{z^{N{m}_G}}{\xi \left(N{m}_G+1\right)}{\displaystyle \sum _{{\aleph }_{\tau },\forall \tau }}\left(\genfrac{}{}{0pt}{}{N}{{\tau }_1,\dots ,{\tau }_K}\right)\left[{\displaystyle \prod _{k=1}^K}{\xi }_k^{{\tau }_k}\right]\\ \times {\mathsf{\Phi }}_2^{\left(K\right)}\left(m_G{\tau }_1,\dots ,m_G{\tau }_K;N{m}_G+1;-\frac{z}{{\varsigma }_1},\dots ,-\frac{z}{{\varsigma }_K}\right).\end{array}$$

(19)

The CDF of ${\left|Z\right|}^2$ may be obtained as in (11) since $F\left(X^2\right)=F(X-\sqrt{X})$, $X>0$ and with this, Theorem 1 is completely proved.

Corollary 1.

By using Theorem 1, one may obtain a closed-form formula approximating the system OP as follows:

$$P_{\mathit{out}}\approx F_{|Z{|}^2}\left({\eta }_{\mathrm{th}}/\left(\overline{\eta }{\kappa }^2\right)\right).$$

(20)

3. Proposed Deep Learning Model

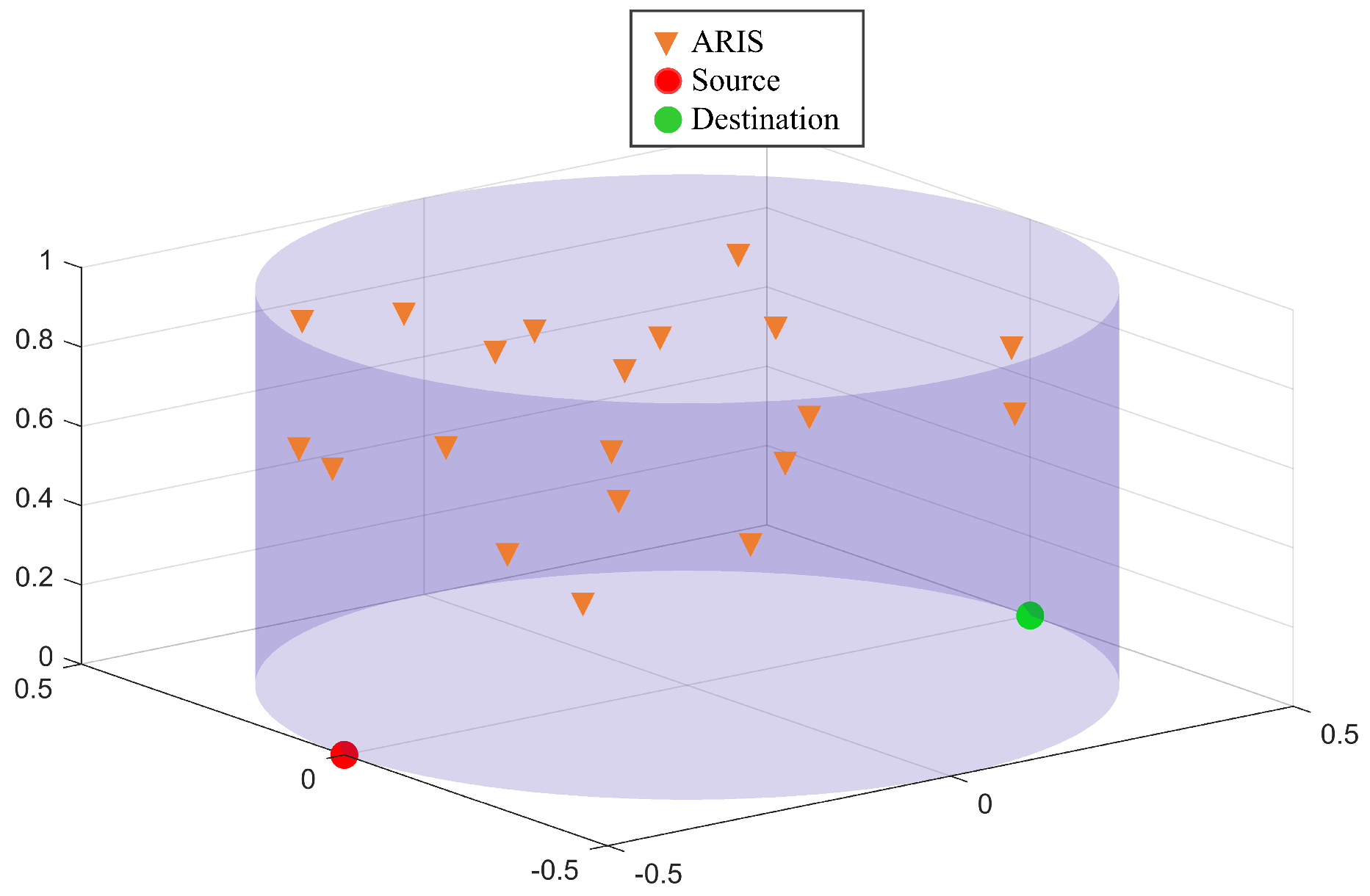
In this study, it is assumed that the ARIS’s 3D spatial movement is characterized by the RWMM [41]. Samples of its positions may be obtained from a homogeneous 3D Poisson process and the system model discussed in the preceding sections. For the purpose of explanation, we additionally assume that the ARIS moves spatially in a 3D cylinder, as shown in Figure 6. As a result, every element of the cylindrical coordinate of T can be produced from a uniform distribution which are as follows [27]: $\overline{\eta }$[dB] $=[5-{ϵ}_{\eta },5+{ϵ}_{\eta }]$, ${\omega }_T\sim \varkappa (0,2\pi )$, $m_c=[2-{ϵ}_m,2+{ϵ}_m]$, ${\zeta }_c=[2.5-{ϵ}_{\zeta },2.5+{ϵ}_{\zeta }]$, $N=[15/20/30-{ϵ}_N,15/20/30+{ϵ}_N]$, $\upsilon =[2.7-{ϵ}_{\upsilon },2.7+{ϵ}_{\upsilon }]$, $r_T\sim 0.5\sqrt{\varkappa (0,1)}$, $h_T\sim \varkappa (0,1)$, ${\delta }_c=[1-{ϵ}_{\delta },1+{ϵ}_{\delta }]$, and $A_{\mathrm{cth}}=[5-{ϵ}_{A_c},5+{ϵ}_{A_c}]$, respectively. It should be observed that distances among nodes in the suggested framework are now RVs due to the incorporation of 3D movement. This makes it impossible to derive the system OP specified in (7), mostly due to the multivariate confluent hypergeometric function. To get over this obstacle, we approach the task of locating the system OP in supervised learning. Specifically, we produce a data set that thoroughly describes the system under consideration. This dataset is used to train the generated BiLSTM model, enabling it to estimate the OP with high accuracy in different system configurations.

3.1. 3D Modeling of Spatial Movement and Datasets Preparation

It is assumed that the azimuth, radial distance, and height of the cylindrical coordinate of T are represented by the symbols ${\phi }_T$, $r_T$, and $q_T$, respectively. We take into consideration a unit normalization cylinder, that is, ${\phi }_T\in [0,2\pi ]$, $r_T\in [0,0.5]$, and $q_T\in [0,1]$, without losing generality. This results in the conversion of R’s 3D Cartesian coordinates, ($x_T$, $y_T$, $z_T$), to $x_T=r_{T}sin{\phi }_T$, $y_T=r_{T}cos{\phi }_T$, and $z_T=q_T$. Given the 3D Cartesian coordinates of the source and destination as (−0.5, 0, 0) and (0.5, 0, 0), respectively, one can compute the distance between two nodes using the following formula: $d_{ab}=\sqrt{{(x_a-x_b)}^2+{(y_a-y_b)}^2+{(z_a-z_b)}^2}$ where $\{a,b\}\in \{\mathrm{source},\mathrm{destination},\mathrm{T}\}$.

In this study, the preparation of datasets, $\chi$, is involved in the proposed ARIS system. Specifically, in the datasets, $\chi$ includes samples $d_s$ of the information gathered from the AIRS system where the input–output connection could be $Data[d_s]=[\mathbf{F}[d_s]$, $P_{d_j}^{d_s}]$, where $\mathbf{F}\left[d_s\right]$ represents the feature vector involving with all inputs characterized as shown in

Table 1. Inputs for the BiLSTM training and testing.

Parameters	Input Value
$\overline{\eta }\left[dB\right]$	$-10\sim 20$
${\phi }_T$	1
$r_T$	1
$q_T$	1
$m_{St}$	$2.5$
$m_{tD}$	$2.5$
${\zeta }_c$	$2.5$
N	$15,20,30$
$\upsilon$	1
$h_T$	1
${\delta }_{St}$	1
${\delta }_{tD}$	1
${\zeta }_{St}$	3
${\zeta }_{tD}$	3
$A_{\mathrm{cth}}$	5

. However, this work has enough simulation samples to produce highly accurate outage performance estimates. After generating real-value CSI sets for each feature vector $\mathbf{F}\left[d_s\right]$, the simulation runs a Monte Carlo. To build the data set, we generate ${20}^3$ samples in total, i.e., $Data\left[d_s\right]$, $d_s$$=1,...,$ ${20}^3$, for utilizing the proposed model. After that, it splits the data set with ratios of $80\%$, $10\%$, and $10\%$ for the training set $T{r}_{\chi }$, validation set $V{a}_{\chi }$, and test set $T{e}_{\chi }$. Through the mean-squared error (MSE), the accuracy of such a forecast may be assessed using (25).

3.2. Proposed BiLSTM Model Structure and Mathematical Formulation

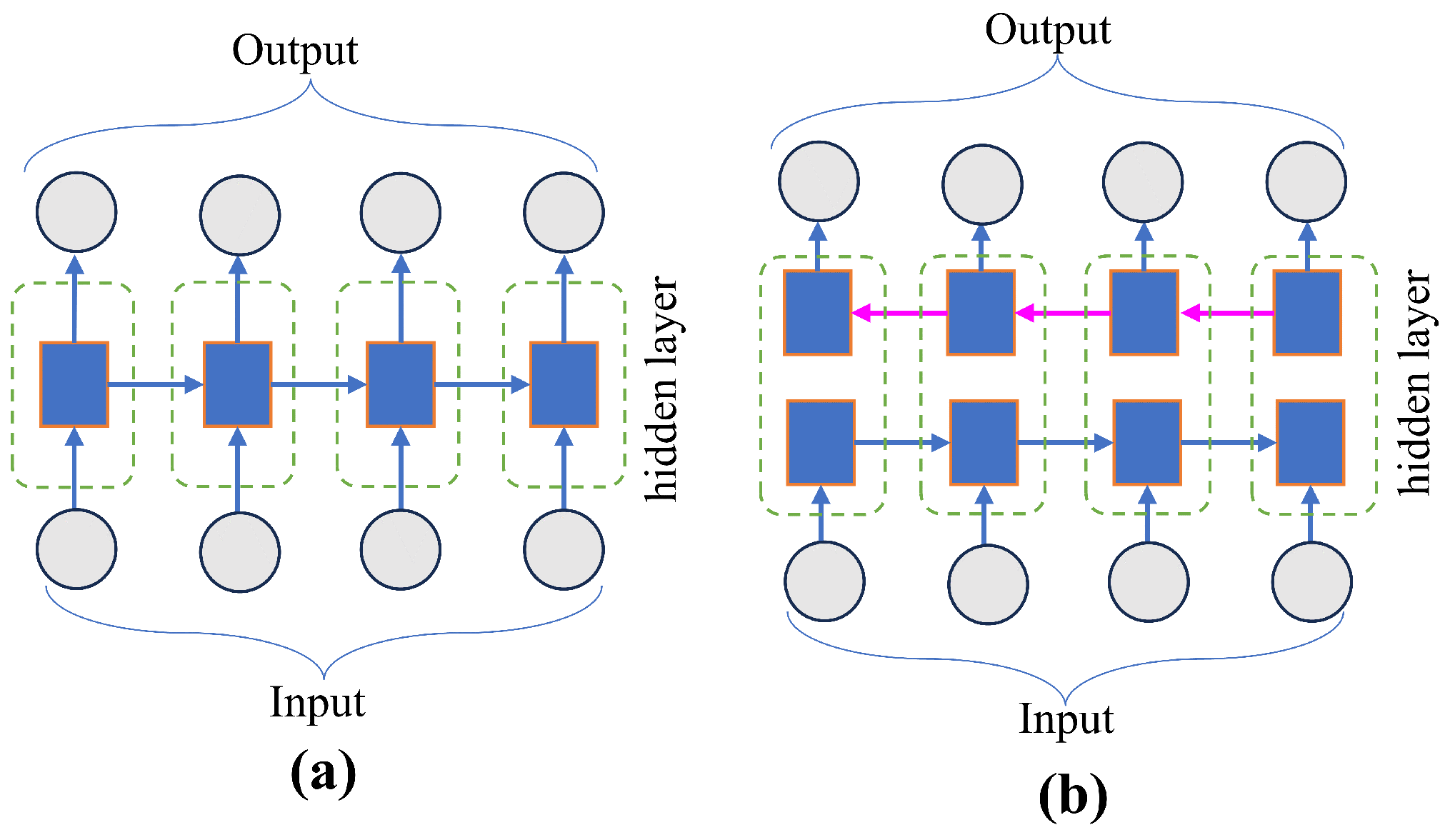
The BiLSTM network is proposed for the following objectives. Unidirectional LSTM networks execute sequences in the past without taking the future into account. This is because, since it only accepts input from the past, unidirectional LSTM only stores data from previous time steps [42]. Conversely, the BiLSTM consists of the unidirectional LSTM’s forward (one from past to future) and backward (one from future to past) perspectives. As the input is bidirectional, it may leverage both sides of the data, providing more opportunities to extract training features and enhancing prediction accuracy. A schematic illustration of the internal cell architecture of the unidirectional LSTM and the BiLSTM is shown in Figure 7a,b, respectively. The proposed BiLSTM model consists of the input layer, BiLSTM layer, fully connected layer, dense layer, and output layer, respectively. The proposed model structure with different layers is shown in Figure 8. The mathematical formulation and operation of each of the layers are as follows:

Input Layer: The sequence of data with accompanying labels makes up the BiLSTM model input. The input sequence of features $\mathbf{F}=[s_1,s_2,s_3,...,s_n]$ that contained the CSI is assumed. The dimension of $13\times 1$ considers the size of the input features. The created dataset, which has the same number of features in the input data as the input size, is fed with the numerical values of sequence features together with their labels into the input layer of the BiLSTM.

BiLSTM Layer: The several gates such as input, output, and forget gates create the LSTM cell. In the proposed model, we have built up three BiLTM layers for obtaining the optimal training by the flow of the information in both directions. The BiLSTM layers in both directions flow can be calculated for an input signal of s at the current time step t as follows:

$$\overrightarrow{h_f}=\mathsf{\Theta }({\mathcal{W}}_f{s}_t+{\mathcal{W}}_f{h}_{t-1}+b_f),$$

(21)

$$\overleftarrow{h_r}=\mathsf{\Theta }({\mathcal{W}}_r{s}_t+{\mathcal{W}}_r{h}_{t+1}+b_r),$$

(22)

where the direction in both forward and reverse $h_f$ and $h_r$ is the corresponding output of the LSTM network, and $\mathsf{\Theta }$ indicates the activation function. The future state is represented by $h_{t+1}$, and the past state is represented by $h_{t-1}$, respectively. The time steps of forward and backward are denoted by $t-1$ and $t+1$, and finally, for both directions, the weight and learnable bias are ${\mathcal{W}}_f$, ${\mathcal{W}}_r$ and $b_f$, $b_r$, respectively. As a result, the BiLSTM’s output $s_1$ may be expressed as follows:

$$\begin{array}{cc}\hfill s_1& =\mathsf{\Theta }({\mathcal{W}}_{s_1}\overrightarrow{h_f}\oplus {\mathcal{W}}_{s_1}\overleftarrow{h_r}+b_{s_1})\hfill \\ & =\mathsf{\Theta }({\mathcal{W}}_{s_1}{\tilde{h}}_t+b_{s_1}),\hfill \end{array}$$

(23)

where the concentration of the hidden state in both directions of the BiLSTM is ${\tilde{h}}_t$, the learnable component of the BiLSTM output bias is $b_{s_1}$, and the output weights of the BiLSTM network are ${\mathcal{W}}_{s_1}$.

Fully Connected Layer: The fully connected layer is crucial because it performs OP tasks. In particular, the fully connected layer does the final distinction, and it processes the output of the BiLSTM layers. In the BiLSTM network, the fully linked layer operates independently on each time step. To get the optimal OP, a linear activation is explicitly specified for the dense output layer. Therefore, the predicted OP $\left(\hat{Y}\right)$ can be expressed as follows:

$$\left(\hat{Y}\right)\left(d_s\right)=f(L=l_{d_s}|S_1;(\mathcal{W},b)),$$

(24)

where $\mathcal{W}$ and b stand for the weight and bias values, respectively; $l_{d_s}$ is the computation result of the $d_s$-th samples of the input data; and finally, the linear activation function is $f(·)$. However, the mean-squared error (MSE) of $\mathsf{\Pi }$ for the overall network is expressed as follows:

$$\mathsf{\Pi }=\frac{1}{d_s}\sum _{q=1}^{d_s}{(Y_q-{\hat{Y}}_q)}^2,$$

(25)

where the predicted and target output OP of the q-th samples are ${\hat{Y}}_q$ and $Y_q$, respectively. The Adam optimization approach is used to lessen the loss [43].

3.3. Training and Testing of the Proposed Model

After the preparation of sufficient datasets and the design of the proposed BiLSTM model, we perform the training procedure in the offline phase. The algorithmic procedure of the training is described in the Algorithm 1. The sequence input train $T{r}_{\chi }$ and validation data $V{a}_{\chi }$ are fed into the input layer and corresponding label as supervised training. The BiLSTM layers feed the input data with labels as a dimension of $13\times 1$, and they train in a bidirectional manner. During training the model, a total of 50 epochs are performed, and the model achieves optimal knowledge, and we stop the training of the model. In addition, the learning rate of $0.01$, minibatch of 32, and a hidden layer of 200 are set up for sufficient training of the model. In the testing phase, the trained model is loaded for inference by utilizing the test datasets $T{e}_{\chi }$ and calculating the MSE according to the testing samples. The testing procedure of the proposed BiLSTM model algorithm is shown in Algorithm 2.

Algorithm 1 BiLSTM Training Algorithm

Initialize estimation function $\mathsf{\Theta }$, epochs E, training set $T{r}_{\chi }$. Load training dataset, $T{r}_{\chi }$ Initialize the weights and biases of forward and backward as (${\mathcal{W}}_f$, ${\mathcal{W}}_r$) and ($b_f$, $b_r$) Compute loss $\mathsf{\Pi }\left(\mathcal{L}\right)$ Optimization operation: ${\mathcal{L}}_{t+1}={\mathcal{L}}_t-\frac{{\mathcal{E}}_t}{\sqrt{{\hat{v}}_t}+\mathcal{Z}}·{\hat{m}}_t$ where $m_t$ and $v_t$ are first and second moment estimates of gradients $\left({\mathcal{L}}_t\right)$ and $\mathcal{Z}$ is a small value to avoid division by zero. for $e=1:E$ do    for $q\in (1,\dots ,T{r}_{\chi })$ do      Perform OP: ${\hat{Y}}_q=\mathsf{\Theta }[\overrightarrow{h_f}\left(s\right);\overleftarrow{h_r}\left(s\right)]$      Calculate loss by (25)      Gradient descent: ${\nabla }_{{\mathcal{L}}_t}\mathsf{\Pi }=\frac{\partial \mathsf{\Pi }}{\partial {\mathcal{L}}_t}$      Update parameters: ${\mathcal{L}}_t\leftarrow {\mathcal{L}}_t-{\mathcal{E}}_t{\nabla }_{{\mathcal{L}}_t}\mathsf{\Pi }$    end for end for Save the model as BiLSTM.h5

Algorithm 2 BiLSTM Testing Algorithm

Load the model as BiLSTM.h5 Input: Test dataset $T{e}_{\chi }$ Output: Estimated outputs ${\left\{{\widehat{{\mathbf{Y}}_{\mathbf{q}}}}_{\mathrm{test}}\right\}}_{q=1}^{T{s}_{\chi }}$ Initialize RMSE = 0 for $q\in (1,\dots ,T{s}_{\chi })$ do    for $w:-10$ to SNR do      Perform estimation:      ${\hat{Y}}_{q\mathrm{test}}=\mathsf{\Theta }[\overrightarrow{h_f}\left(s_{q\mathrm{test}}\right);\overleftarrow{h_r}\left(s_{q\mathrm{test}}\right)]$      Compute MSE for q th samples:      ${\mathsf{\Pi }}_q=\mathsf{\Pi }=\frac{1}{d_s}{\sum }_{q=1}^{d_s}{(Y_q-{\hat{Y}}_q)}^2,$      Compute RMSE $=\sqrt{\mathsf{\Pi }}$    end for end for

3.4. Simulation Results

In this work, the simulation analysis is conducted in the Windows 11 operating system with the graphics processing unit. The program is written in the Keras-TensorFlow environment. An NVIDIA graphics card improves training performance. For the training of the model, we have considered (0–20) dB SNR during the generation of datasets. The Nakagami-m fading method considers the large-scale fading effect, represented as ${\sigma }_{ccc}=d_{ccc}^{\upsilon }$ for $ccc\in \{St,tD\}$, where $\upsilon$ represents the path-loss exponent, and the shape parameter m determines the fading severity. In IG shadowing, $\delta$ is normalized in relation to $\overline{\eta }$, and $\zeta$ denotes the intensity of shadowing. During the online testing phase, we consider (−10:2:20) dB SNR and obtain the optimal testing OP for the proposed system. The simulation is conducted in this study to evaluate the OP analysis against previous research and the suggested DL model. The DNN [27] and LSTM models are used to compare the efficacy of the suggested BiLSTM model. Acquiring knowledge about the channel parameter and other parameter adjustments enhances the efficacy of the proposed model.

To validate the proposed DL algorithm effectively, we analyze the MSE calculation for the suggested network, as seen in Figure 9, with different DL models such as LSTM and DNN. In this analysis, the training and validation of MSE BiLSTM, LSTM, and DNN models are calculated corresponding with different epoch numbers. It is seen from the figure that the proposed network has gained lower MSE with training and validation compared to the other models. For the case of the DNN model, the training and validation MSE with different epochs is gained with ${10}^{-4}$, and the convergence is conducted very fast. In addition, the LSTM model shows almost the same MSE with DNN up to the epoch of 10, and after that, it outperforms the DNN model and gains ${10}^{-5}$ MSE. In contrast, the MSE of the proposed BiLSTM model outperforms the other models in terms of training and validation datasets. In the beginning, the curve for the BiLSTM model is not stable, and after the eigth epoch, it becomes stable. Furthermore, the convergence of the BILSTM model is slower than the other models and gains the MSE of ${10}^{-6}$, which demonstrates the model’s effectiveness in training.

During the training performance evaluation, we observed the iteration speeds for the proposed BiLSTM model compared to other models (DNN and LSTM). The iteration speed of the proposed BiLSTM model is 12 milliseconds (ms) per step, whereas the LSTM and DNN models showed 11 ms and 4 ms, respectively. Although the iteration speed of the proposed model is slower than the other models, it demonstrated a significant improvement in performance compared to the others. Additionally, it can be seen from Figure 7 that the convergence speed of the proposed model starts after the 25th epoch, which is almost the same as for the DNN and LSTM models. Furthermore, we have analyzed the computational complexity of the proposed model compared to other models, as shown in

Table 2. Computation complexity analysis.

Models	Learnable Parameters	RMSE Computation Time
BiLSTM	2,266,001	8 ms
LSTM	329,857	6 ms
DNN	67,969	2 ms

. From Table 2, it can be seen that the RMSE computation time is not significantly different from that of the other two models, as the proposed model has a large number of learnable parameters. Although the suggested HyDNN model has many parameters, the complexity can be reduced by leveraging GPU parallelization [44,45] during the real-time process. The suggested model has a higher complexity requirement than the others, but it performs better in estimation, and GPU parallel computing can shorten the calculation time.

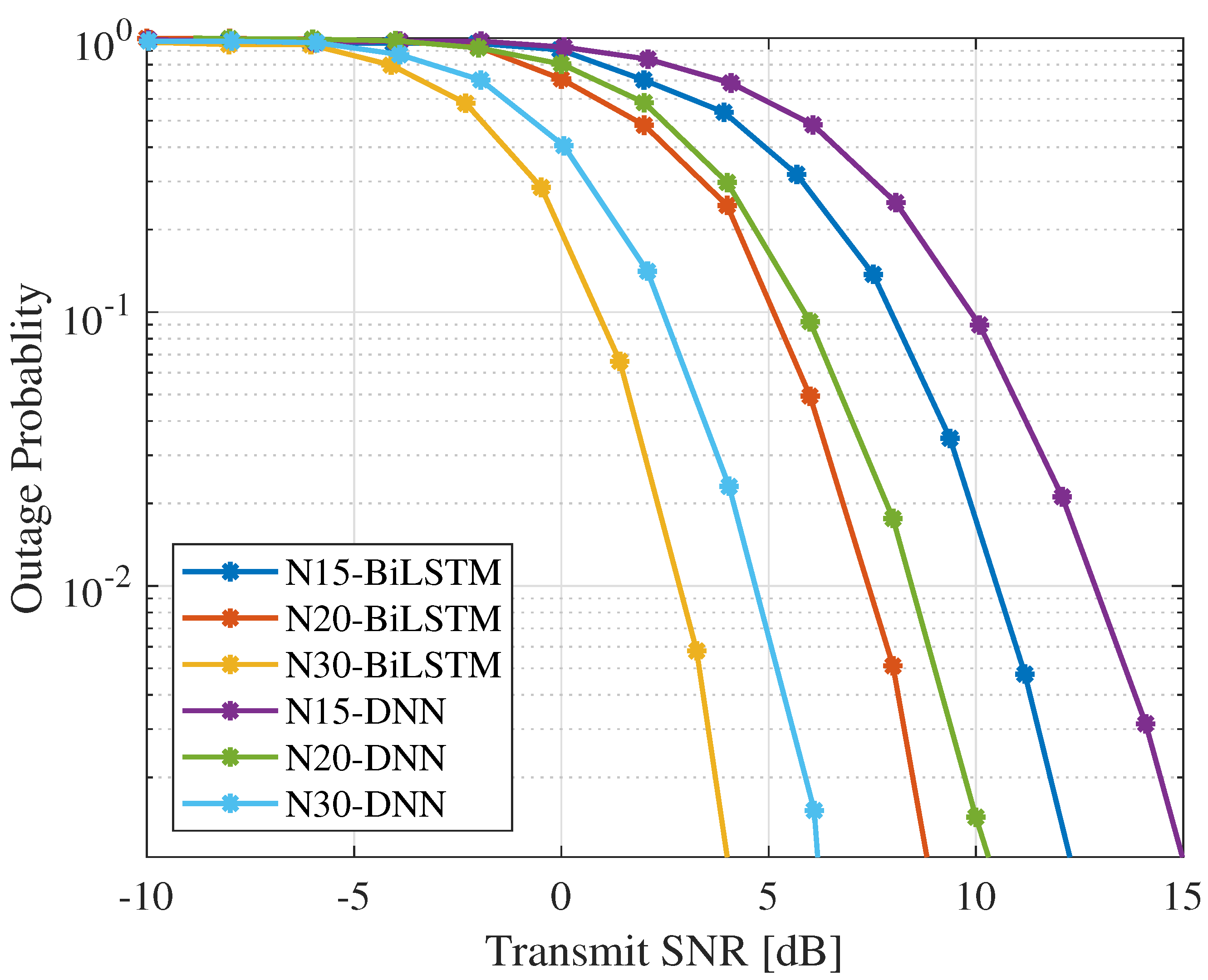
Figure 10, we have analyzed the OP versus transmit SNR in dB for the proposed system and compared it with the DNN model for different numbers of reflecting elements of $N=15,20$, and 30. It is evident from the figure that the increment of reflecting elements significantly reduces the power budget requirement for achieving the maximal OP performance. Compared to the DNN model, for $N=15$, the proposed model gains almost $2.5$ dB SNR; for $N=20$, it gains almost $1.5$ dB SNR; and finally, for $N=20$, it gains almost $2.4$ dB SNR. In summary, the OP of the ARIS system is increased with different reflecting N for the proposed BiLSTM model compared with others.

The proposed BiLSTM OP performance is compared to the DNN model and the LSTM model based on the OP versus various SNR values in Figure 11. The proposed BILSTM-based system outperforms all other approaches, as the graph demonstrates. It appears that the suggested model works much better than other systems for SNRs between $-2$ and 12 dB SNR and OP up to ${10}^{-5}$. On the other hand, the LSTM model has OP of around ${10}^{-3}$ and SNR ranges of $-2$ to 12 dB. Furthermore, the DNN model has OP of about ${10}^{-4}$ and SNR ranges between $-2$ to 12. The suggested BilSTM model has a significantly improved OP accuracy compared to the DNN and LSTM models. However, the LSTM model performs similarly to DNN models up to 6 dB SNR because of the lower SNR; at greater SNR, it performs a similar trend with the suggested model. The aforementioned simulation results demonstrate how the BilSTM outperforms the other schemes in terms of performance. The aforementioned simulation results provide a summary: the suggested model may be a useful way to improve the OP for ARIS-based systems.

4. Conclusions

In this paper, a DL network called the BiLSTM model is proposed to improve the OP in the 3D spatial excursion of the ARIS-assisted wireless communication system. The proposed model is configured with a BiLSTM layer that is capable of learning the ARIS system channel data in a bidirectional manner. Thus, the OP of the ARIS-based wireless system is enhanced with different SNR ranges and different reflecting elements. In the offline phase, the proposed model is trained using simulated data over the channel network assisted by ARIS. The effectiveness of the suggested model is next tested by retrieving the original data from the target terminal using the learned model, which is then implemented in the online phase. Thus, the sent data may be extracted to evaluate the OP performance. The well-known Adam optimization approach is used in order to evaluate the proposed model’s error performance. The simulation results show that the suggested strategy outperforms other schemes in terms of MSE performance. Furthermore, in comparison to previous benchmarking models, the suggested BiLSTM model obtains an OP of ${10}^{-5}$ in 12 dB SNR. The simulation results clearly demonstrate that the suggested framework outperforms the DNN and LSTM models in terms of OP analysis. By training on long input sequence data utilizing a bidirectional framework, the proposed BiLSTM improves OP performance. The system’s OP increases, and its training capacity is strengthened by adding bidirectional (forward and backward) tasks to the BiLSTM’s hidden layers. A potential solution to improve the 6G communication system might be found in the suggested system. Further developments of the suggested paradigm might be used in more complex, sophisticated ARIS-assisted wireless communication systems. The limitation of the proposed system is that we did not consider the multiple antenna system for diverse wireless communication to analyze the OP. However, observing the effectiveness of the suggested approach could be the subject of further research. Furthermore, the proposed technology may be promising for AIRS-NOMA-OFDM systems and could be deployed in a hybrid DL model to improve system performance. Accurate channel estimation and feedback present issues in dynamic aerial situations. To improve RIS settings in real-time communication environments, several challenges must be addressed, and this can be a potential research direction [46].