Wasserstein Dissimilarity for Copula-Based Clustering of Time Series with Spatial Information

Abstract

The clustering of time series with geo-referenced data requires a suitable dissimilarity matrix interpreting the comovements of the time series and taking into account the spatial constraints. In this paper, we propose a new way to compute the dissimilarity matrix, merging both types of information, which leverages on the Wasserstein distance. We then make a quasi-Gaussian assumption that yields more convenient formulas in terms of the joint correlation matrix. The method is illustrated in a case study involving climatological data.

1. Introduction

Time-series cluster analysis collects various unsupervised learning techniques for organizing data points collected over time into groups based on their similarity. The general objective is to maximize data similarity within clusters and minimize it across clusters (see, for instance, [1,2]).

Usually, such methods depend on the different ways of defining the similarity among time series, which can be based on (a) the observed time series values or suitable transformations thereof; (b) specific features extracted from the time series, such as autocorrelation, periodograms, etc.; or (c) the data-generating stochastic process (see [3]).

Copula-based clustering methods for time series tend to group time series according to the degree of cross-sectional dependence among different patterns (see [4] and references therein). Typical choices include rank-correlation measures [5], tail dependence coefficients [6,7,8], and copula distances and/or divergences [9,10,11,12,13]. As their specific feature, the obtained cluster composition is invariant under a monotone transformation of the original time series, hence it is usually more robust against the presence of outliers. Copula-based algorithms, hence, focus on the joint comovements among time series and, as such, are particularly used in risk analysis due to their ability to detect extreme scenarios that occur when both time series tend to fall/rise at the same time) [6,7,14,15,16].

When time series are collected at different geographic locations, i.e., geo-referenced data are considered where a variable is observed over time at a static spatial location, copula-based algorithms may, hence, detect the impacts of extreme events across space [17]. In such cases, it may be of interest to obtain clusters that show geographical proximity in order to enhance their interpretability. See, for instance, [18,19]. These situations occur not only in environmental science, but also in the financial context. In this latter case, the attributes may describe the economic distance between the markets and can provide deeper insights into the dependence structure of stock returns (see, e.g., [20,21,22]).

The goal of this paper is to consider clustering of time series for geo-referenced data. In particular, we focus on the construction of a novel pairwise dissimilarity among time series that takes into account the spatial information.

To fix ideas, consider $n\ge 2$ real-valued time series ${\mathbf{x}}_i=(x_{i1},\dots ,x_{iT})$ of length T, where $x_{it}$ represents the observed value of the i-th time series $(i=1,\dots ,n)$ at the t-th period $(t=1,\dots ,T)$. Each time series is equipped with additional information on the phenomenon under consideration, represented by a p-dimensional vector of attributes, ${\mathbf{s}}_i=(s_{i1},\dots ,s_{ip})\in {\mathbb{R}}^p$, where $s_{ik}$ represents the value of the i-th unit $(i=1,\dots ,n)$ at the k-th attribute $(k=1,\dots ,p)$. The additional attributes are typically geographic coordinates of the location at which the i-th time series is observed (thus, $p=2$ and latitude and longitude are collected). For this reason, we will refer to these vectors as the spatial information.

The classical strategy in spatio-temporal clustering (see, e.g., [23]) is to start with a $(n\times n)$ matrix of pairwise dissimilarities among ${\mathbf{x}}_1,\dots ,{\mathbf{x}}_n$. This latter matrix is, hence, modified by a nonlinear function of the separating distances among ${\mathbf{s}}_1,\dots ,{\mathbf{s}}_n$. Finally, the modified dissimilarity matrix is used as the input to obtain the clustering partition via algorithms such as (agglomerative) hierarchical clustering, PAM, and fuzzy C-means (see, e.g., [24,25,26]). In the copula-based framework, such an approach has been adopted, for instance, in [27,28], which considers the temporal matrix induced by the (pairwise) copula parameters. In [29], instead, the correlation-based dissimilarity matrix is transformed by means of the spatial information, taking into account the intrinsic geometry of the space of correlation matrices. According to [30], all these methods have the tendency to produce a smooth dissimilarity matrix without, however, reinforcing the spatial contiguity between the resulting clusters.

In [11] (see also [31]), a different strategy has been proposed. It consists of associating with the spatial information (usually contained in the Euclidean space) a suitable copula (the spatial copula). Such a latter object is, hence, combined with the temporal copula to obtain an element of the copula space that merges temporal and spatial information, and is used for the calculation of the associated dissimilarity.

The present work exploits tools from optimal transport and the Wasserstein metric (see, e.g., [32,33]) to modify the framework of [11] by introducing the following main novelties: (a) the dissimilarity measure is constructed by equipping the space of bivariate copulas $\mathcal{C}$ with the Wasserstein metric $d_{{\mathcal{W}}_2}$; (b) the temporal and spatial information is merged (at the level of pairwise association) via geodetic curves [34] (also known as weighted barycenters [35]) in $(\mathcal{C},d_{{\mathcal{W}}_2})$. Such an approach has the following advantages:

• The Wasserstein distance allows for a meaningful comparison between distributions also without density. This property is not shared by the most common distances and divergences, such as the total variation distance, the Hellinger distance, or the Kullback–Leibler divergence (see, e.g., [36]).
• The Wasserstein metric seems to be more appropriate to measure distance between copulas since it does not lead to counter-intuitive clusters (see, e.g., [37]).

As possible limitations, however, the calculations cannot always be explicitly made. For this reason, we rely on a quasi-Gaussian approach of the presented framework, as in [38].

The paper is organized as follows. In Section 2, we consider some tools from optimal transport theory that will be used in the manuscript. In Section 3, we present the methodology underlying the computation of a dissimilarity matrix. In Section 4, we present a quasi-Gaussian approximation of the dissimilarity matrix extraction. Section 5 illustrates the effect of the spatial dependence to the whole procedure. Finally, Section 6 presents an empirical application. Section 7 concludes the paper.

2. Background on Optimal Transport, Wasserstein Distance, and Copulas

In order to extract the spatial information and to merge the temporal and spatial dependencies, we will leverage on the 2-Wasserstein distance between probability measures [39,40] and on optimal transport theory [32,33]. To this end, we recall some basic facts that will be used in this paper (see, e.g., [32,33,39]).

Given a domain $\mathsf{\Omega }\subseteq {\mathbb{R}}^d$ (that we take to be compact and convex for simplicity), we define the space ${\mathcal{W}}_2\left(\mathsf{\Omega }\right)$ as the space of probability measures on $\mathsf{\Omega }$ with finite moments of order 2 endowed with the distance $d_{{\mathcal{W}}_2}$, defined through

$$d_{{\mathcal{W}}_2}({\mu }_X,{\mu }_Y)={\left(\underset{\gamma \in \mathsf{\Gamma }({\mu }_X,{\mu }_Y)}{\inf }{\int }_{\mathsf{\Omega }\times \mathsf{\Omega }}{|x-y|}^{2}d\gamma (x,y)\right)}^{1/2},$$

(1)

where $\mathsf{\Gamma }({\mu }_X,{\mu }_Y)$ denotes the collection of all joint measures on $\mathsf{\Omega }\times \mathsf{\Omega }$ whose marginals are ${\mu }_X$ and ${\mu }_Y$, respectively.

It is possible to prove that the above minimization problem has a solution, which is unique (and it is concentrated on the graph of a map $f^{OT}:\mathsf{\Omega }\to \mathsf{\Omega }$, called the optimal transport map) if ${\mu }_X$ is absolutely continuous with respect to the Lebesgue measure (actually, it is enough that ${\mu }_X$ vanishes on small sets [32]). Moreover, $d_{{\mathcal{W}}_2}$ is a distance in ${\mathcal{W}}_2\left(\mathsf{\Omega }\right)$.

The space ${\mathcal{W}}_2\left(\mathsf{\Omega }\right)$ is a geodesic space where, for two measures ${\mu }_X$ and ${\mu }_Y$, the unique geodesic curve connecting them is obtained through

$${\mu }^{\left(\alpha \right)}={((1-\alpha )id+\alpha f^{\mathrm{OT}})}_{\#}{\mu }_X,$$

(2)

where $f^{\mathrm{OT}}$ is the optimal transport map from ${\mu }_X$ to ${\mu }_Y$, $id$ is the identity mapping on ${\mathbb{R}}^d$, and $\alpha \in [0,1]$. Here, $T_{\#}\mu$ denotes the push-forward of the measure $\mu$ under the mapping T. Such a curve is also known as the displacement interpolation [34]. This provides a useful interpolation between ${\mu }_X$ and ${\mu }_Y$ which is, in general, different from the convex combination of the two measures. As a matter of fact, ${\mu }^{\left(\alpha \right)}$ coincides with the weighted barycenter [35] of $({\mu }_X,1-\alpha )$ and $({\mu }_Y,\alpha )$, i.e., it solves the minimization problem

$${\mu }^{\left(\alpha \right)}=\underset{\mu }{\mathrm{arg\; min}}\left((1-\alpha )d_{{\mathcal{W}}_2}^2({\mu }_X,\mu )+\alpha d_{{\mathcal{W}}_2}^2({\mu }_Y,\mu )\right)$$

(3)

over all possible probability measures $\mu$ (see also [41,42]). Wasserstein barycenters have found various applications in machine learning, especially in dealing with image recognition (see, for instance, [39]).

The actual computation related to the Wasserstein distances is largely simplified when we deal with Gaussian measures. In fact, the Wasserstein distance between centered Gaussian distributions is well known and it is given by the so-called Bures–Wasserstein distance between their covariance matrices. Specifically, let $\mathbf{X}\sim N(\mathbf{0},{{\displaystyle \sum }}_1)$ and $\mathbf{Y}\sim N(\mathbf{0},{{\displaystyle \sum }}_2)$ be two Gaussian random vectors with positive semi-definite covariance matrices ${{\displaystyle \sum }}_1$ and ${{\displaystyle \sum }}_2$, respectively. Then, the following holds (see, e.g., Theorem 2.2 in [43]):

$$d_{{\mathcal{W}}_2}^2(\mathbf{X},\mathbf{Y})=d_{{\mathcal{W}}_2}^2({{\displaystyle \sum }}_1,{{\displaystyle \sum }}_2)=tr\left({{\displaystyle \sum }}_1\right)+tr\left({{\displaystyle \sum }}_2\right)-2tr\left({\left({{\displaystyle \sum }}_1^{1/2}{{\displaystyle \sum }}_2{{\displaystyle \sum }}_1^{1/2}\right)}^{1/2}\right).$$

(4)

Such a formula also extends to the case when ${{\displaystyle \sum }}_1$ and ${{\displaystyle \sum }}_2$ are singular (see [44], p. 239). In the particular case that $\mathbf{X}$ and $\mathbf{Y}$ are also two-dimensional, the Wasserstein distance has the following expression (see [44], p. 239):

$$d_{{\mathcal{W}}_2}^2(\mathbf{X},\mathbf{Y})=tr\left({{\displaystyle \sum }}_1\right)+tr\left({{\displaystyle \sum }}_2\right)-2{\left(tr\left({{\displaystyle \sum }}_1{{\displaystyle \sum }}_2\right)+2\sqrt{det\left({{\displaystyle \sum }}_1{{\displaystyle \sum }}_2\right)}\right)}^{1/2}.$$

(5)

The (weighted) barycenter among the Gaussian vectors $\mathbf{X}$ and $\mathbf{Y}$ is a Gaussian vector whose covariance matrix is of the form (see, e.g., Lemma 2.3 in [43])

$${{\displaystyle \sum }}^{\left(\alpha \right)}={{\displaystyle \sum }}_1{\#}_{\alpha }{{\displaystyle \sum }}_2={{\displaystyle \sum }}_1^{-1/2}\left((1-\alpha ){{\displaystyle \sum }}_1+\alpha {\left({{\displaystyle \sum }}_1^{1/2}{{\displaystyle \sum }}_2{{\displaystyle \sum }}_1^{1/2}\right)}^{1/2}\right){{\displaystyle \sum }}_1^{-1/2}.$$

(6)

Standard references for the study of the Wasserstein distance for Gaussian measures include [44,45,46,47].

Beyond the Gaussian cases, explicit expressions for the Wasserstein distance and/or the optimal couplings for multivariate measures are rare. However, the involved probability measures can be approximated by taking consistent empirical versions of the input measures. See, for instance, [39,40].

In the following, we will mainly consider doubly stochastic measures [48], i.e., probability measures on ${[0,1]}^2$ whose margins coincide with the Lebesgue measure on $[0,1]$. These measures are better known as copulas. The space $\mathcal{C}$ of a bivariate copula can be ordered with respect to pointwise order among functions. It contains the Fréchet–Hoeffding upper-bound copula $M(u,v)=\min (u,v)$, which interprets the maximal degree of similarity (comonotonicity) between two random variables. Moreover, the Fréchet–Hoeffding lower bound is given by the copula $W(u,v)=\max (u+v-1,0)$, which interprets the counter-monotonic behavior of two variables. Another notable copula is $\mathsf{\Pi }(u,v)=uv$, which represents the independence of random variables.

The set $\mathcal{C}$, considered as a compact subset of ${\mathcal{W}}_2\left({[0,1]}^2\right)$ with respect to weak convergence, will be equipped with the metric $d_{{\mathcal{W}}_2}$. In general, the use of the Wasserstein metric for capturing dependence aspects has been recently employed in [38,49,50], among others. Typically, copula-based dependence measurements are expressed as a discrepancy of the estimated copula from the independent case. Here, instead, we will consider the Wasserstein distance between a copula and the comonotonicity copula M. This perspective has been also recently considered in [36] in a Bayesian setting.

Copulas have been recently adopted in the construction of various dissimilarity measures that are used as input to clustering algorithms (see, for instance, [51] and references therein). The use of a dissimilarity based on the Wasserstein distance between copulas appeared, for instance, in [37] in order to measure the distances among different Gaussian copulas for clustering purposes (see also [52]). Here, we extend the range of applications to the case of time series with geo-referenced information.

3. The Methodology

Our aim is to cluster $n\ge 2$ time series, each of them equipped with a (static) p-dimensional vector of attributes associated with each unit, which are typically geographic coordinates of the location at which the time series are observed.

Given the input time series and the (static) attributes, and a fixed weighting parameter $\alpha \in [0,1]$, we aim at finding an $(n\times n)$ dissimilarity matrix ${\mathbf{\Delta }}^{\left(\alpha \right)}$ that merges all the previous information. The ($i,j)$-entry ${\Delta }_{ij}^{\left(\alpha \right)}$ of ${\mathbf{\Delta }}^{\left(\alpha \right)}$ interprets the temporal dependence between units i and j by taking into account the similarity between ${\mathbf{s}}_i$ and ${\mathbf{s}}_j$. The relative importance of each of the two criteria is summarized by the parameter $\alpha$, i.e., $\alpha =0$ corresponds to no influence of the spatial component.

For every pair $(i,j)$ with $i\ne j$, ${\Delta }_{ij}^{\left(\alpha \right)}$ is constructed in the following way:

• Determine the copula $C_{ij}^{\mathrm{ts}}$ that describes the temporal dependence between the i-th and j-th time series.
• Determine the copula $C_{ij}^{\mathrm{sp}}$ that interprets the spatial proximity between the attribute vectors ${\mathbf{s}}_i$ and ${\mathbf{s}}_j$ associated with the i-th and j-th time series.
• Merge $C_{ij}^{\mathrm{ts}}$ and $C_{ij}^{\mathrm{sp}}$ into one single copula $C_{ij}^{\left(\alpha \right)}$ that represents their weighted barycenter. This copula depends on the tuning parameter $\alpha$. Then, define

  $${\Delta }_{ij}^{\left(\alpha \right)}=d_{{\mathcal{W}}_2}(M,C_{ij}^{\left(\alpha \right)}),$$

  i.e., the distance of $C_{ij}^{\left(\alpha \right)}$ from the comonotonicity copula M, which represents maximal concordance.

Once the dissimilarity matrix is obtained, it can be used as an input of various algorithms like hierarchical agglomerative methods, medoids-based procedures, etc.

The previously described procedure is illustrated in detail below.

3.1. Extract the Temporal Dependence

In order to capture the dependence among the time series, it is usual in the context of copula-based clustering (see, for instance, [4]) to proceed in two steps. First, we filter serial dependence using univariate time-series models, like the ARMA-GARCH family, and hence, we model the cross-sectional dependence using a copula for the residuals (see, for instance, [53,54,55,56]).

To fix ideas, we assume that the multivariate time series follows the model ${\mathbf{X}}_t=(X_{1t},\dots ,X_{nt})$, where

$${\mathbf{X}}_t={\mathit{\mu }}_t\left(\theta \right)+{\mathit{\sigma }}_t\left(\theta \right){\mathit{\epsilon }}_t,(t=1,\dots ,T)$$

(7)

where the innovations ${\mathit{\epsilon }}_t=({\epsilon }_{1t},\dots ,{\epsilon }_{nt})$ are independent and identically distributed, with $\mathbb{E}\left({\epsilon }_{it}\right)=0$ and $\mathbb{V}\left({\epsilon }_{it}\right)=1$ for $i=1,\dots ,n$, with the continuous joint distribution function H. Moreover, ${\mathit{\mu }}_t$ and ${\mathit{\sigma }}_t$ are the (time-varying) conditional mean and standard deviation, respectively, and they are both ${\mathcal{F}}_{t-1}$-measurable and independent of ${\mathit{\epsilon }}_t$. Here, ${\mathcal{F}}_{t-1}$ contains information from the past and possibly information from exogenous variables as well (see, e.g., [55]). Since the distribution function H is continuous, there exists a unique copula C so that for all $\mathbf{x}\in {\mathbb{R}}^n$,

$$H\left(\mathbf{x}\right)=C(F_1\left(x_1\right),\dots ,F_n\left(x_n\right)),$$

where $F_i$ is the distribution function of ${\epsilon }_{it}$ for every t. Defining ${\mathbf{U}}_t=(F_1\left({\epsilon }_{1t}\right),\dots ,F_n\left({\epsilon }_{nt}\right))$, one obtains that ${\mathbf{U}}_1,\dots ,{\mathbf{U}}_T$ are independent and identically distributed with distribution function C. Since the marginal distributions are unknown, ${\mathbf{U}}_t$ is not observable. However, given an estimator $\hat{\theta }$ of $\theta$, we can compute the residuals

$${\mathbf{e}}_t={\displaystyle \frac{{\mathbf{x}}_t-{\mathit{\mu }}_t\left(\hat{\theta }\right)}{\mathit{\sigma }\left(\hat{\theta }\right)}}$$

(8)

for $t=1,\dots ,n$. The ranks associated with the residuals contain the information about the copula among the time series for any fixed t and, as such, they can be used to capture the cross-sectional dependence (see, e.g., [56]). Specifically, for any $t=1,\dots ,T$, let $r_{it}$ be the rank of $e_{it}$ among the residuals $e_{i1},\dots ,e_{iT}$ of the i-th time series. The multivariate scaled ranks

$${\mathbf{u}}_t=\left({\displaystyle \frac{r_{1t}}{T+1}},\dots ,{\displaystyle \frac{r_{nt}}{T+1}}\right)$$

(9)

are the so-called pseudo-observations.

Now, for every pair $(i,j)$, $i\ne j$, the copula $C_{ij}^{\mathrm{ts}}$ that describes the cross-sectional dependence between the i-th and j-th time series can be obtained from the associated pseudo-observations ${(u_{it},u_{jt})}_{t=1,\dots ,T}$. Here, one can adopt:

• a parametric approach, i.e., one assumes that $C_{ij}^{\mathrm{ts}}$ belongs to the same specific family of copulas, whose parameter can be fitted via, e.g, maximum likelihood techniques. See, e.g., [57].
• a non-parametric approach, which assumes that $C_{ij}^{\mathrm{ts}}$ coincides with one smoothed version of the empirical copula associated with the pseudo-observations, such as the empirical checkerboard copula [58,59] or the empirical beta copula [60].

In the following, if not otherwise stated, we assume that every $C_{ij}^{\mathrm{ts}}$ is absolutely continuous (with respect to the Lebesgue measure).

3.2. Extract the Spatial Dependence

In order to describe the geographical proximity, we preliminarily select a specific family of copulas that can be parameterized as ${\left(C_{\theta }\right)}_{\mathsf{\Theta }}$, with $\mathsf{\Theta }=[{\theta }_{\min },{\theta }_{\max }]\subset \mathbb{R}$. In particular, we assume that $M\in \{C_{{\theta }_{\min }},C_{{\theta }_{\max }}\}$, i.e., the family includes the Fréchet–Hoeffding upper bound as a limiting case. Moreover, the following technical condition is assumed

$$\theta \mapsto d_{{\mathcal{W}}_2}(M,C_{\theta })\mathrm{is\; continuous\; and\; strictly\; monotone\; in} \theta .$$

(10)

The continuity should be interpreted in the sense of topology of uniform convergence, which is equivalent to pointwise convergence (see, e.g., [48]). Roughly speaking, condition (10) implies a one-to-one correspondence between the copula parameter and the Wasserstein distance between M and any member of the given parametric family.

Now, for every pair $(i,j)$, $i\ne j$, we assume that the copula $C_{ij}^{\mathrm{sp}}$ that describes the proximity among the attributes ${\mathbf{s}}_i$ and ${\mathbf{s}}_j$ belongs to ${\left(C_{\theta }\right)}_{\mathsf{\Theta }}$, i.e., $C_{ij}^{\mathrm{sp}}=C_{{\theta }_{ij}}$. Moreover, we assume that ${\theta }_{ij}$ only depend on the (normalized) distance $d_{ij}$ between ${\mathbf{s}}_i$ and ${\mathbf{s}}_j$.

Furthermore, we want to ensure that $C_{{\theta }_{ij}}$ approaches M, i.e., it is close to the comonotonic case, when the normalized geographic distance is close to zero. To this end, we propose to select, for every pair $(i,j)$, ${\theta }_{ij}$ as the unique value satisfying the equality:

$${\displaystyle \frac{d_{{\mathcal{W}}_2}(M,C_{\theta })}{{\max }_{{\theta }^{\prime }\in \mathsf{\Theta }}{d}_{{\mathcal{W}}_2}(M,C_{{\theta }^{\prime }})}}={\displaystyle \frac{dist({\mathbf{s}}_i,{\mathbf{s}}_j)}{{\max }_{i^{\prime },j^{\prime }}dist({\mathbf{s}}_{i^{\prime }},{\mathbf{s}}_{j^{\prime }})}}(=d_{ij}).$$

(11)

The existence and uniqueness of such a parameter is guaranteed by (10).

Various copula families satisfy the conditions stated above.

Example 1.

Consider the parametric family of copulas of type

$$\begin{array}{c}\hfill C_{\theta }^{\mathrm{Fre}}(u,v)=(1-\theta )M(u,v)+\theta W(u,v)\end{array}$$

(12)

where $\theta \in [0,1]$, M and W are the Fréchet–Hoeffding upper- and lower-bound copulas, respectively. Copulas of type (12) belong to the so-called Fréchet class, which was suggested as a possible model for spatial dependence in [11]. For such copulas, we have (see Appendix A)

$$d_{{\mathcal{W}}_2}(M,C_{\theta }^{\mathrm{Fre}})=\sqrt{{\displaystyle \frac{\theta }{3}}}.$$

Moreover, the family is continuous in θ with respect to uniform convergence.

Now, according to Equation (11), if such a family is used to model spatial dependence, then the parameter is chosen so that

$${\displaystyle \frac{\sqrt{{\theta }_{ij}/3}}{\sqrt{1/3}}}={\displaystyle \frac{dist({\mathbf{s}}_i,{\mathbf{s}}_j)}{{\max }_{i^{\prime },j^{\prime }}dist({\mathbf{s}}_{i^{\prime }},{\mathbf{s}}_{j^{\prime }})}}=d_{ij},$$

which gives ${\theta }_{ij}=d_{ij}^2$.

3.3. Create the Dissimilarity Measure

In order to merge the temporal and spatial information, for a fixed $\alpha \in [0,1]$, we associate to each pair of units $(i,j)$, $i\ne j$, the copula $C_{ij}^{\left(\alpha \right)}$ associated with the displacement interpolation of (2). Namely, $C_{ij}^{\left(\alpha \right)}$ is the copula associated with the probability measures ${\mu }^{\left(\alpha \right)}$ that solves the minimization problem

$${\mu }^{\left(\alpha \right)}=\underset{\mu \in {\mathcal{W}}_2\left({[0,1]}^2\right)}{\mathrm{arg\; min}}\left((1-\alpha )d_{{\mathcal{W}}_2}^2({\mu }_{C_{ij}^{\mathrm{ts}}},\mu )+\alpha d_{{\mathcal{W}}_2}^2({\mu }_{C_{ij}^{\mathrm{sp}}},\mu )\right),$$

(13)

where ${\mu }_{C_{ij}^{\mathrm{ts}}}$ and ${\mu }_{C_{ij}^{\mathrm{sp}}}$ are the measures associated with the copulas $C^{\mathrm{ts}}$ and $C^{\mathrm{sp}}$, respectively. The existence of such a copula is guaranteed under the assumption that $C_{ij}^{\mathrm{ts}}$ is absolutely continuous. Moreover, in such a case, ${\mu }^{\left(\alpha \right)}$ is also absolutely continuous and it admits a unique copula in view of Sklar’s theorem [48].

Remark 1.

Generally, given two copulas $C_1$ and $C_2$, the copula of their weighted barycenter, given by (2), does not coincide with the convex combination of the two copulas. This fact follows from, e.g., [34], and it is illustrated in Figure 1.

Finally, according to a general way of calculating dissimilarity as a distance from the comonotonic case [51], we define the dissimilarity between the time series i and j as

$${\Delta }_{ij}^{\left(\alpha \right)}=d_{{\mathcal{W}}_2}(M,C_{ij}^{\left(\alpha \right)}).$$

(14)

4. The Quasi-Gaussian Approach

Although theoretically appealing, the actual computation related to the dissimilarity in (14) is involved. In fact, generally, ${\mu }^{\left(\alpha \right)}$ (and, hence, $C^{\left(\alpha \right)}$) cannot be calculated in a closed form. Therefore, following seminal ideas in [38], we use a a quasi-Gaussian approach based on correlation matrices in order to define a modified dissimilarity. The main idea is to replace the copula space with the space of all bivariate Gaussian distributions with standard marginals. Such distributions are called G-copulas in [38] and their space will be denoted by $\mathcal{G}$. In fact, in this latter case, the calculations can be obtained only in terms of the corresponding correlation matrices, as recalled in Section 2.

We recall that each G-copula is characterized by a Gaussian vector with mean $(0,0)$ and correlation matrix

$${\displaystyle \sum }\left(\theta \right)=\left(\begin{array}{cc}1& \theta \\ \theta & 1\end{array}\right).$$

Then, for every pair $(i,j)$, $i\ne j$, we proceed as follows.

• The copula $C_{ij}^{\mathrm{ts}}$ from Section 3.1 is replaced with the G-copula with correlation matrix ${\displaystyle \sum }({\hat{\theta }}_{ij}^{\mathrm{ts}})$, where ${\hat{\theta }}_{ij}^{\mathrm{ts}}$ equals the estimation of the normal score correlation among the involved observations (as suggested in [38]).
• The copula $C_{ij}^{\mathrm{sp}}$ from Section 3.2 is replaced with the G-copula with correlation matrix ${\displaystyle \sum }({\hat{\theta }}_{ij}^{\mathrm{sp}})$, where ${\hat{\theta }}_{ij}^{\mathrm{sp}}$ is the unique value $\theta$ that solves

  $${\displaystyle \frac{d_{{\mathcal{W}}_2}({\displaystyle \sum }\left(1\right),{\displaystyle \sum }\left(\theta \right))}{{\max }_{{\theta }^{\prime }\in [0,1]}{d}_{{\mathcal{W}}_2}({\displaystyle \sum }\left(1\right),{\displaystyle \sum }\left({\theta }^{\prime }\right))}}=d_{ij},$$

  where $d_{ij}$ is the normalized distance between ${\mathbf{s}}_i$ and ${\mathbf{s}}_j$. Notice that ${\displaystyle \sum }\left(1\right)$ is the (singular) correlation matrix showing maximal dependence (comonotonic case). For the existence and uniqueness of ${\hat{\theta }}_{ij}^{\mathrm{sp}}$ see Remark 2. In particular, we notice that since ${\theta }^{\prime }\in [0,1]$, the maximal spatial distance is interpreted by the vector of independent components.
• For a fixed $\alpha \in ]0,1[$, the copula $C_{ij}^{\left(\alpha \right)}$ from Section 3.3 is replaced with the G-copula having the correlation matrix

  $${{\displaystyle \sum }}^{\left(\alpha \right)}=D^{-1/2}{{\displaystyle \sum }}^{\prime }{D}^{-1/2},$$

  (15)

  where ${{\displaystyle \sum }}^{\prime }={\displaystyle \sum }({\hat{\theta }}_{ij}^{\mathrm{ts}}){\#}_{\alpha }{\displaystyle \sum }({\hat{\theta }}_{ij}^{\mathrm{sp}})$ is the weighted barycenter of ${\displaystyle \sum }({\hat{\theta }}_{ij}^{\mathrm{ts}})$ and ${\displaystyle \sum }({\hat{\theta }}_{ij}^{\mathrm{sp}})$ given by (6) and D is the diagonal matrix associated with ${{\displaystyle \sum }}^{\prime }$. In other words, we transform the covariance matrix of the weighted barycenter into a correlation matrix with the natural projection.

Summarizing, in the quasi-Gaussian approach, we define the modified dissimilarity between the time series i and j as

$${\tilde{\Delta }}_{ij}^{\left(\alpha \right)}=d_{{\mathcal{W}}_2}({\displaystyle \sum }\left(1\right),{{\displaystyle \sum }}^{\left(\alpha \right)}),$$

(16)

i.e., in terms of the Wasserstein distance between two correlation matrices associated with elements of $\mathcal{G}$. This is analogous to Equation (14) since both matrices ${\displaystyle \sum }\left(1\right)$ and M represent the comonotonic case, while $C_{ij}^{\left(\alpha \right)}$ and ${{\displaystyle \sum }}^{\left(\alpha \right)}$ correspond to the weighted barycenters in their respective spaces.

Remark 2.

In the bivariate case, the Wasserstein distance among two Gaussian distributions is obtained via Formula (5). In particular, if we consider the singular correlation matrix ${\displaystyle \sum }\left(1\right)$, we obtain that

$$d_{{\mathcal{W}}_2}^2({\displaystyle \sum }\left(1\right),{\displaystyle \sum }\left(\theta \right))=4-2\sqrt{2+2\theta }.$$

The plot of $\theta \mapsto d_{{\mathcal{W}}_2}({\displaystyle \sum }\left(1\right),{\displaystyle \sum }\left(\theta \right))$ is visualized in Figure 2.

5. An Illustration with a Fuzzy-PAM Algorithm

Given an $(n\times n)$ dissimilarity matrix among time series, various algorithms can be exploited to provide a suitable clustering. Here, we will apply a (fuzzy) partitioning-around-medoid (PAM) clustering method for time series whose output expresses the membership degree of each time series to a cluster (see [11]). As known, the main advantage of PAM is that the prototypes (i.e., medoids) of each cluster are time series actually observed and not average time series, which is often very appealing for the interpretation of the selected clusters (see, e.g., [61]). For a fixed number K of clusters, the fuzzy PAM algorithm can be formalized as follows:

$$\begin{array}{cc}\hfill \underset{u_{ij}}{\min }& {\displaystyle \sum }_{i=1}^n{\displaystyle \sum }_{k=1}^K{u}_{ik}^p{\Delta }_{ik}\hfill \\ \hfill & s.t.{\displaystyle \sum }_{k=1}^K{u}_{ik}=1,u_{ik}\ge 0,\hfill \end{array}$$

where $u_{ik}$ indicates the membership degree of the i-th unit to the k-th cluster ($k=1,\dots ,K$); and $p>1$ is a weighting exponent that controls the fuzziness of the obtained partition (hereinafter, $p=1.5$). Here, ${\Delta }_{ik}$ is a suitable dissimilarity between the time series of the i-th unit and the time series of the k-th medoid.

To illustrate the proposed algorithm, we consider the fuzzy PAM algorithm applied to the dissimilarity given in (16). We consider a scenario similar to the one in Section 3.1 of [11]. Specifically, we consider $n=48$ time series of innovations of length $T=100$. We assume that for each $i=1,\dots ,48$, the i-th time series has been observed with a vector of attributes ${\mathbf{s}}_i$ so that $dist({\mathbf{s}}_i,{\mathbf{s}}_j)=dist({\mathbf{s}}_j,{\mathbf{s}}_i)=1$ if $1\le i\le 12$ and $13\le j\le 48$; otherwise, $dist({\mathbf{s}}_i,{\mathbf{s}}_j)=0$. Roughly speaking, the time series can be either contiguous (distance equal to 0) or not (distance equal to 1).

Moreover, the time series have a temporal dependence given by the following copula model:

$$C(u_1,\dots ,u_{48})=C_1(u_1,\dots ,u_{24})·C_2(u_{25},\dots ,u_{48}),$$

(17)

where $C_1$ and $C_2$ are copulas belonging to the Frank family (see, e.g., [48]), with a pairwise Kendall’s $\tau \in \{0.25,0.50,0.75\}$.

Figure 3 reports the membership degree of unit 1 to the same cluster of unit 13 at different levels of $\alpha$ (which is the weight assigned to the spatial component). Clearly, when $\alpha =0$ (i.e., no spatial information) units 1 and 13 tend to belong to the same cluster, since they are positively associated via the copula $C_1$. However, when $\alpha$ increases, the spatial component plays a major role and, roughly speaking, it moves unit 13 far from unit 1, i.e., into a different cluster.

It is important to highlight the effects of different choices of the spatial component. When we assume that the maximal spatial distance between two units corresponds to a zero correlation in the Gaussian model (Figure 3, on the left), the membership degree of unit 1 to its natural temporal cluster tends to decline sharply only for $\alpha$ close to $0.5$. Instead, the decline comes earlier when the maximal spatial distance between two units corresponds to a correlation equal to $-1$ in the Gaussian model (Figure 3, on the right). We notice that this latter choice was also adopted in [11] when the Fréchet family of copulas was used.

6. An Empirical Application

In this section, we apply the fuzzy-PAM clustering algorithm on time series representing the summer temperature maxima of Italy from 1971 to 2023. The data have been downloaded from the Climate Data Store (https://cds.climate.copernicus.eu/, accessed on 1 September 2023) which collects global climate and weather data of the past eight decades. Specifically, we focus on JJA (June–July–August) maxima of daily maximum temperatures over a grid of the Italian land. The considered data are $n=527$ grid points. Similarly to [62], we detrend the observed temperatures from the long-term warming trend, following a two-step procedure. First, we remove the multi-year climatological average from the daily temperature maxima within the dataset. Then, from these temperature residuals, we remove the 92-day running average. After this detrending process, we consider the maximum value of each season for each grid point, leading to a collection of time series of length $T=53$. Given the set of detrended time series and the geographical locations, we compute the temporal and the spatial dependencies, as described in Section 4. Specifically, for every pair of $(i,j)$, $i\ne j$, we use the estimation of the normal score correlation to compute the temporal correlation matrix ${\displaystyle \sum }({\hat{\theta }}_{ij}^{\mathrm{ts}})$ as in step 1, and we use the normalized distances $d_{ij}$ to compute the spatial correlation matrix ${\displaystyle \sum }({\hat{\theta }}_{ij}^{\mathrm{sp}})$ according to step 2. Initially, we consider the fuzzy-PAM algorithm applied to the dissimilarity given in (16) for $\alpha =0$ representing the pure temporal case. We select the number of clusters via the fuzzy silhouette (FS) index [63], a suitable measure for the fuzzy clustering algorithm that is computed as the weighted average of the individual silhouettes. The better the units are assigned to the clusters, at the same time as minimizing intra-cluster distance and maximizing inter-cluster distance, the higher the value of FS. We represent the obtained clusters in the pure temporal case ($\alpha =0$) in Figure 4. From the maximization of the FS we have that the optimal number of clusters is $K=3$.

In the pure temporal case, time series belonging to the same cluster may be not contiguous. This aspect can be reduced by combining the two dissimilarities via Equation (16) for some $\alpha \in [0,1]$. As an illustration, we show the cluster composition when $\alpha =0.30$ (clearly, other values are possible, although a range of 0.05–0.30 seems generally reasonable, as suggested in [30]).

In order to choose the optimal number of clusters for $\alpha =0.30$, we proceed with the fuzzy silhouette index maximization.

Table 1. Fuzzy silhouette index for $\alpha =0.30$ and $K\in \{2,\dots ,10\}$.

$\mathit{k}=2$	$\mathit{k}=3$	$\mathit{k}=4$	$\mathit{k}=5$	$\mathit{k}=6$	$\mathit{k}=7$	$\mathit{k}=8$	$\mathit{k}=9$	$\mathit{k}=10$
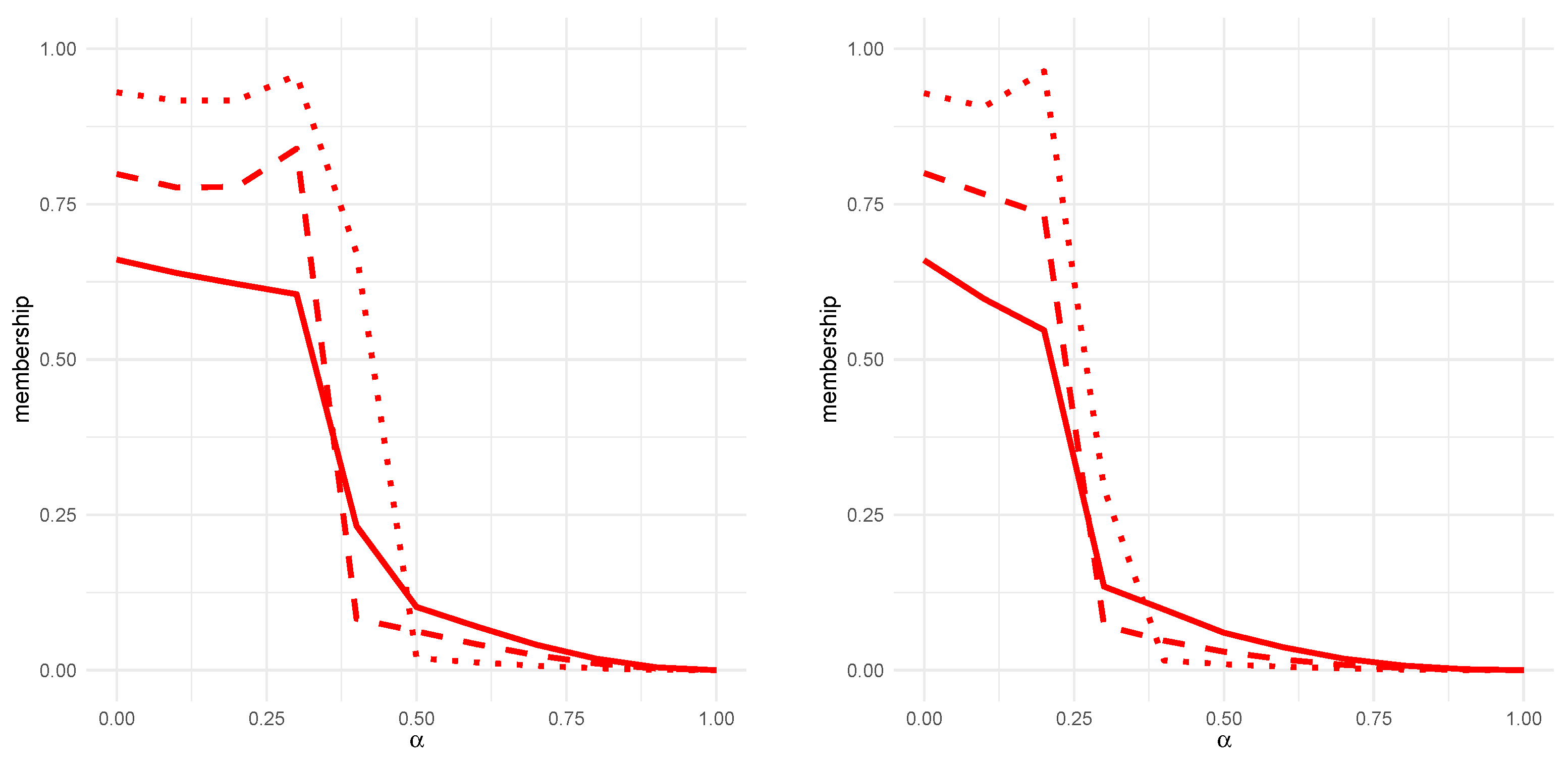
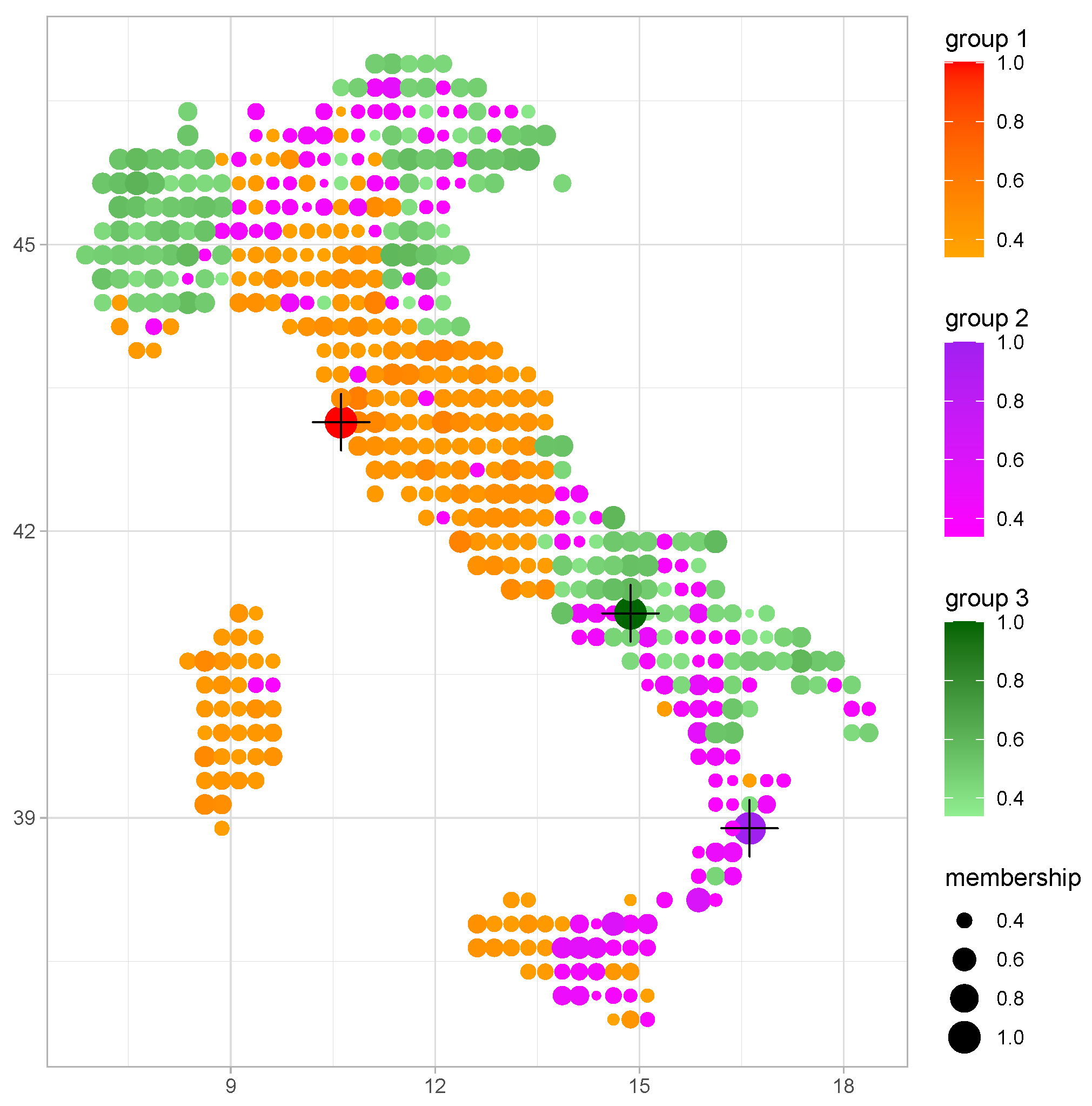
0.176	0.208	0.194	0.163	0.120	0.154	0.118	0.105	0.102

shows the evolution of the fuzzy silhouette index for different values of $K\in \{2,\dots ,10\}$. Thus, $K=3$ is selected.

The corresponding clustering configuration is shown in Figure 5.

We note that when $\alpha$ increases, the cluster composition increases the spatial contiguity among its elements. Clearly, however, some time series still exhibit a behavior that is not driven by geographic proximity. Such time series are particularly of interest in order to detect spatial anomalies in some geographic area, and their behavior should be the object of in-depth investigations.

7. Conclusions

In this paper, we proposed a way to define a suitable dissimilarity matrix interpreting the comovements of time series subjected to spatial constraints. The ultimate goal was the clustering of time series with geo-referenced information. The proposed extraction of the dissimilarity matrix leverages on the 2-Wasserstein distance between probability measures and on optimal transport theory. Moreover, as the computational aspects of such an extraction are involved in practical applications, we proposed a quasi-Gaussian approximation of the correlation matrices in order to define a modified dissimilarity and reduce the complexity and the computational burden of the procedure. In the second part of the paper, we presented an illustration with a fuzzy-PAM algorithm to show the effect of the spatial dependence on the whole procedure. Lastly, we proposed a case study showing the effects of the proposed method on real data involving climatic time series.