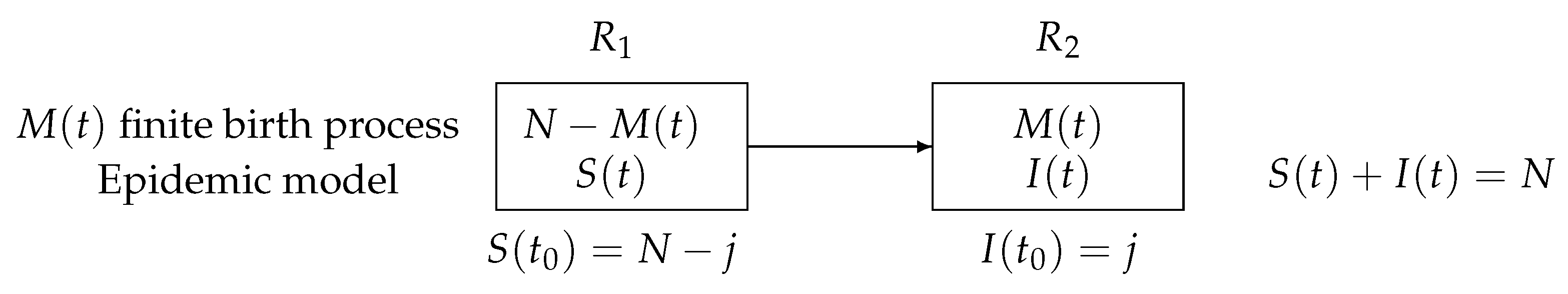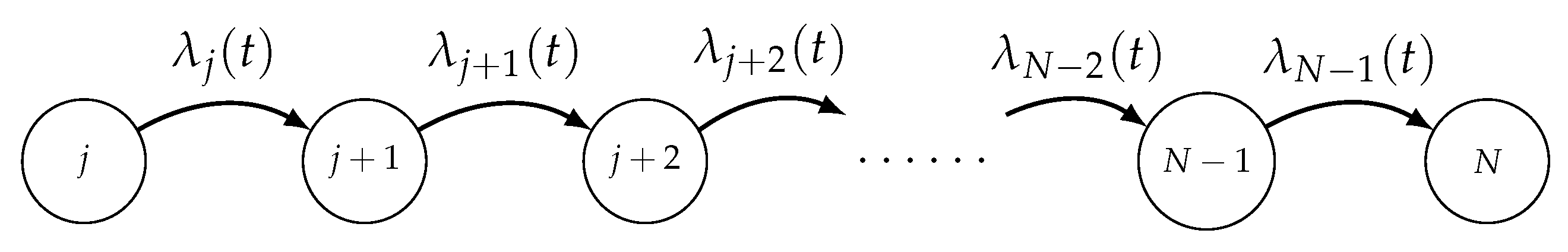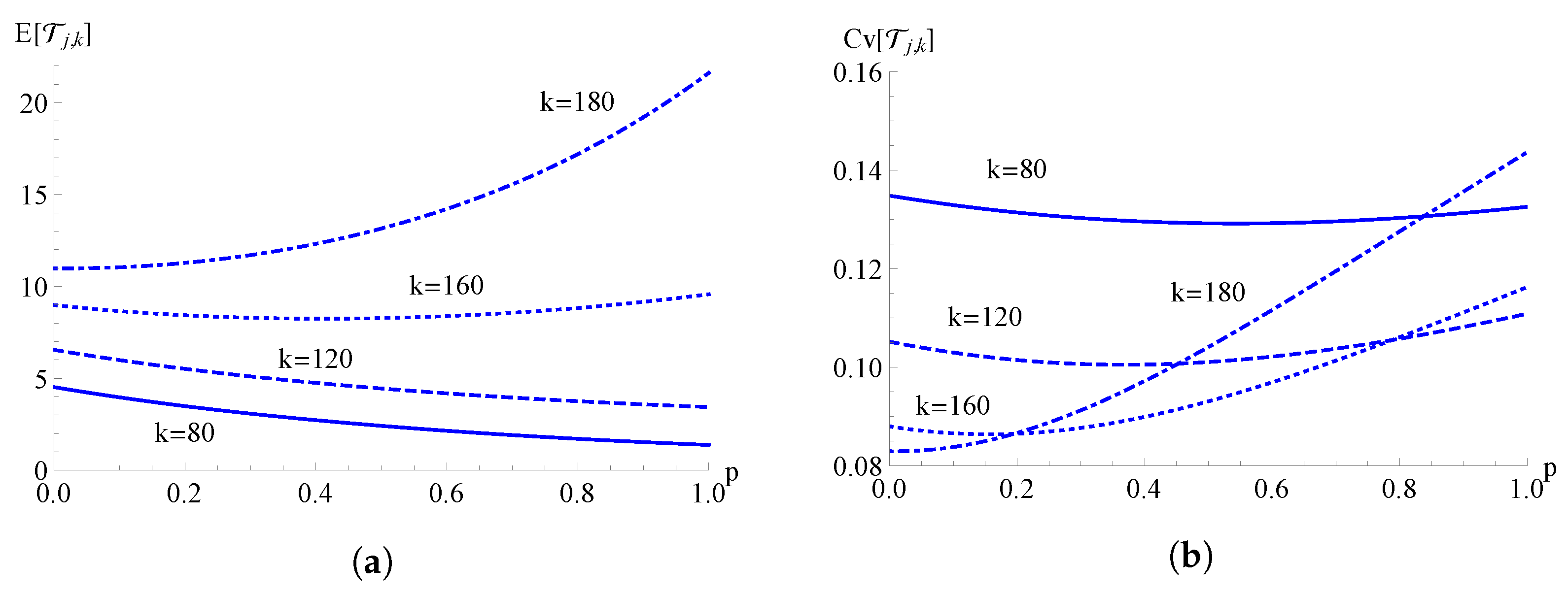Figure 1.
A schematic compartmental representation with two states: susceptible and infectious.
Figure 1.
A schematic compartmental representation with two states: susceptible and infectious.
Figure 2.
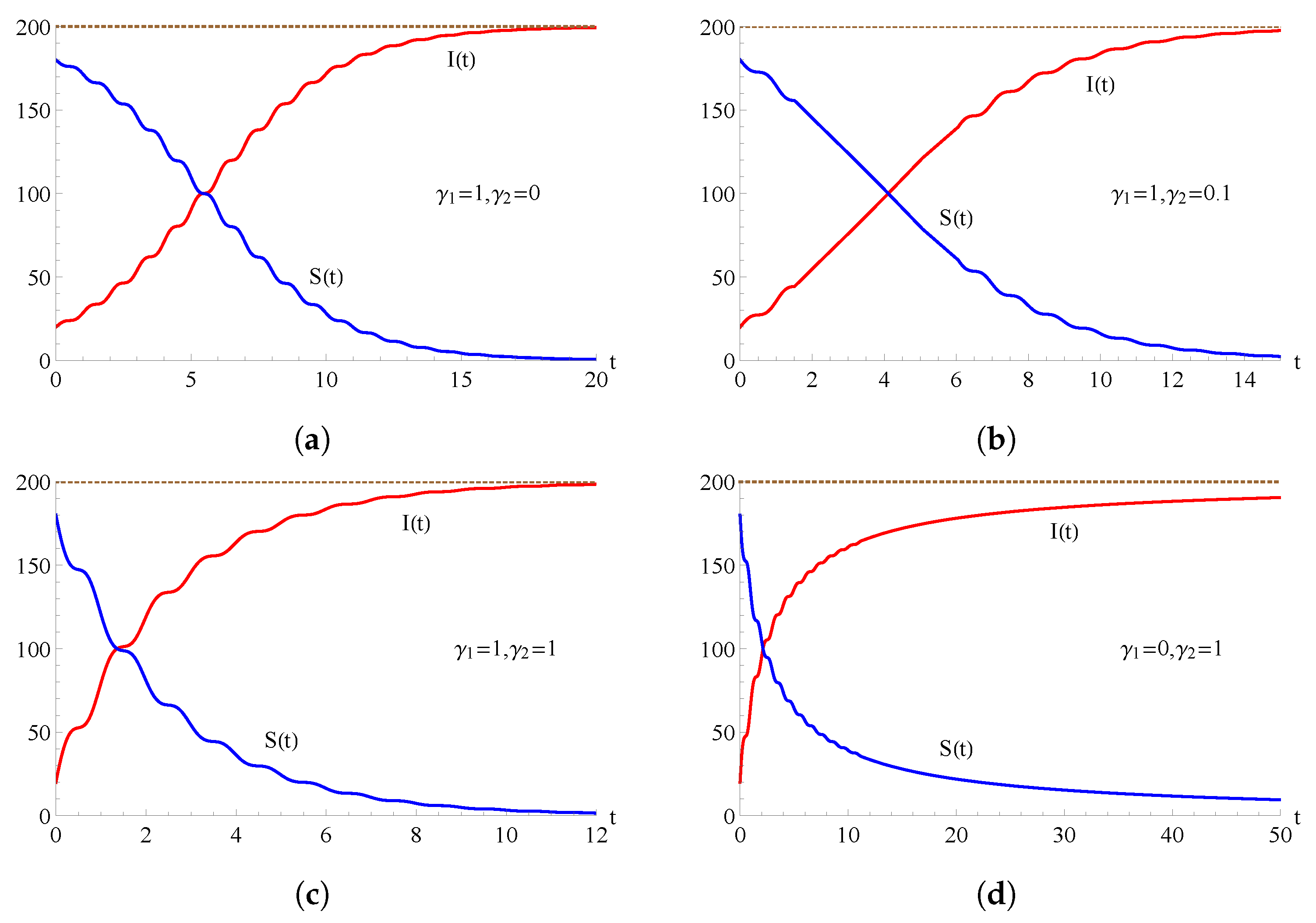
For the flexible model with , the population of the infected (red curve) and of the susceptible (blue curve) are plotted as functions of t for , , , and for some choices of the parameters and . In (a) , in (b) , in (c) and in (d) .
Figure 2.
For the flexible model with , the population of the infected (red curve) and of the susceptible (blue curve) are plotted as functions of t for , , , and for some choices of the parameters and . In (a) , in (b) , in (c) and in (d) .
Figure 3.
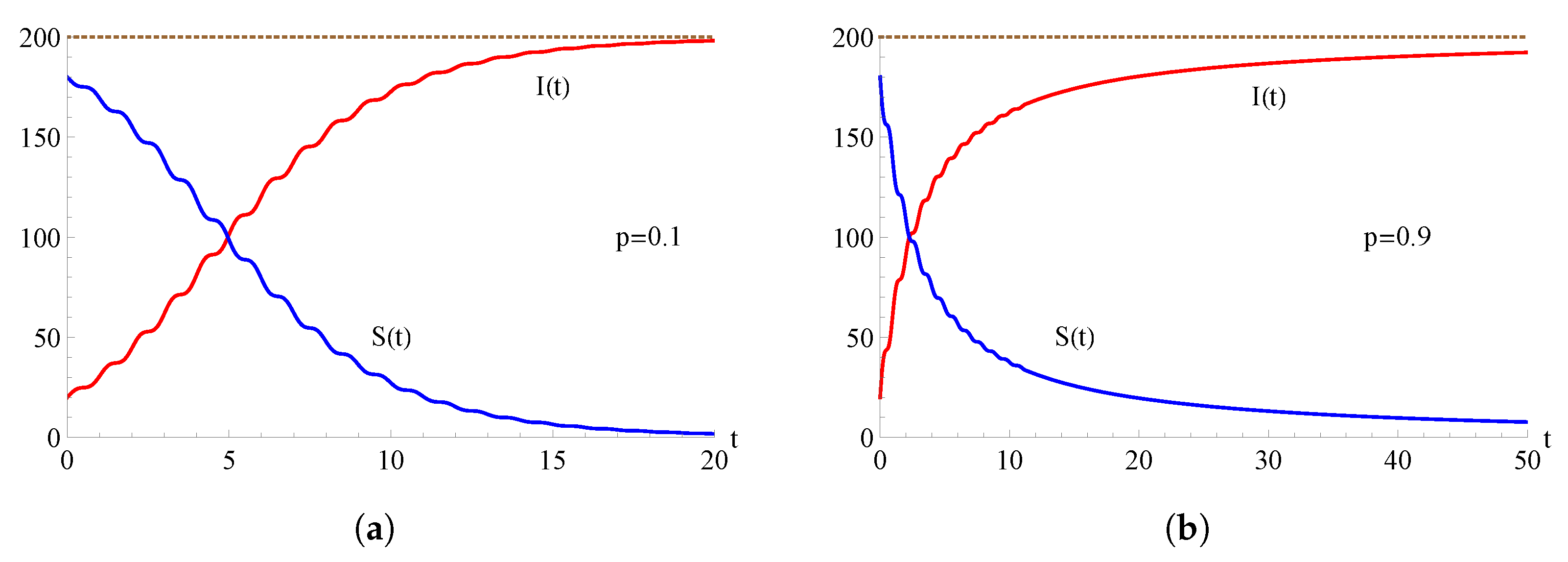
For the hyper-logistic model with , the population of the infected (red curve) and of the susceptible (blue curve) are plotted as functions of t for , , , and for some choices of the parameter p. In (a) and in (b) .
Figure 3.
For the hyper-logistic model with , the population of the infected (red curve) and of the susceptible (blue curve) are plotted as functions of t for , , , and for some choices of the parameter p. In (a) and in (b) .
Figure 4.
The state diagram of the TNH finite birth process .
Figure 4.
The state diagram of the TNH finite birth process .
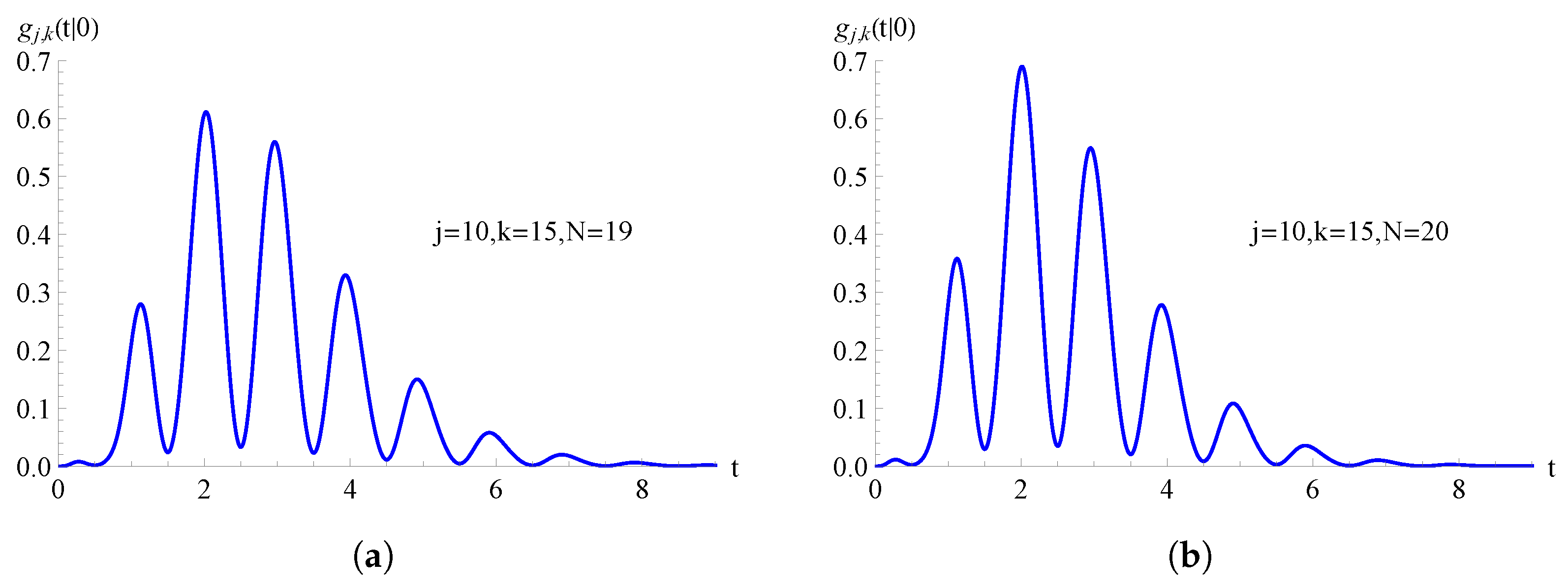
Figure 5.
For the TNH-binomial birth process with , the FPT pdf is plotted as a function of t for and . In (a) and in (b) .
Figure 5.
For the TNH-binomial birth process with , the FPT pdf is plotted as a function of t for and . In (a) and in (b) .
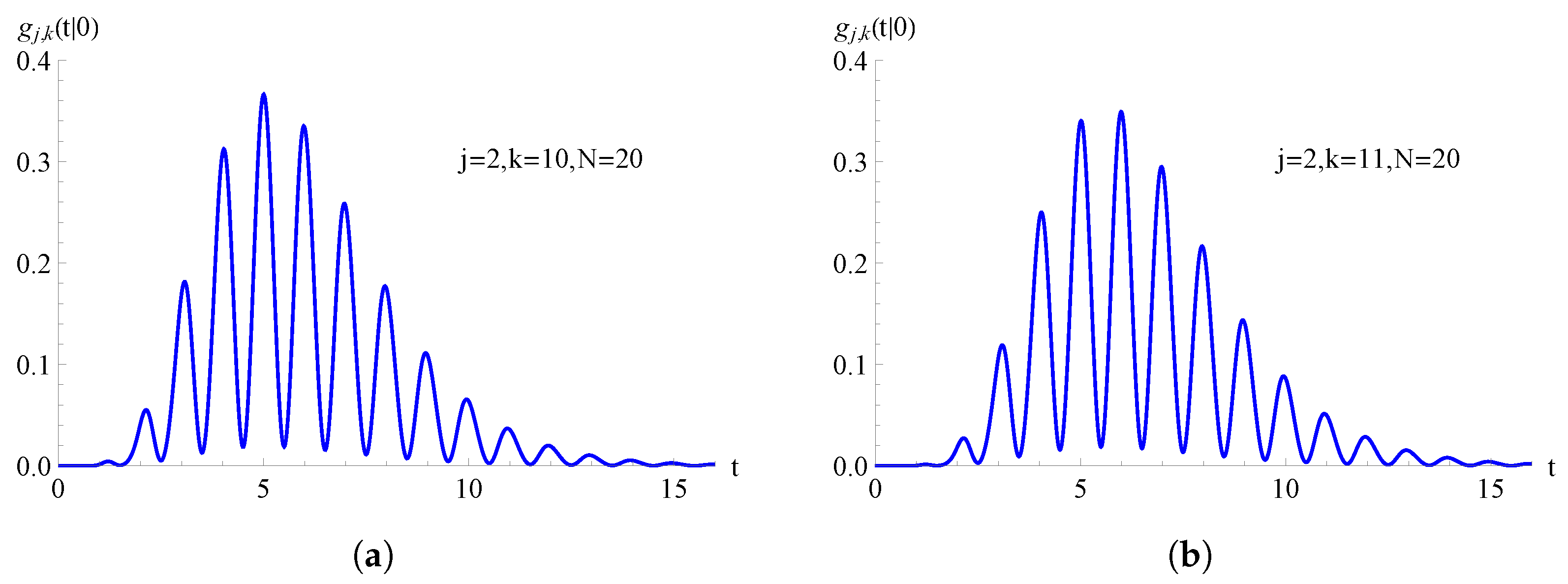
Figure 6.
For the TNH-quadratic birth process with , with , the FPT pdf is plotted as function of t for and . In (a) and in (b) .
Figure 6.
For the TNH-quadratic birth process with , with , the FPT pdf is plotted as function of t for and . In (a) and in (b) .
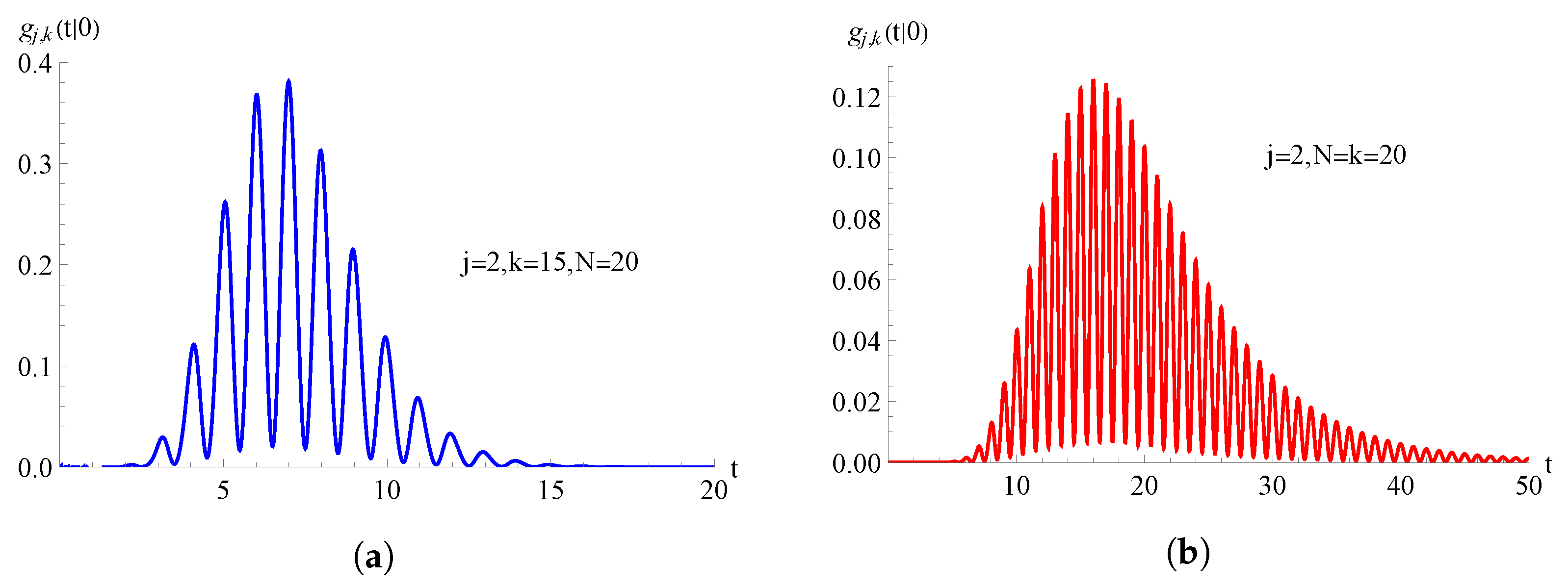
Figure 7.
For the TNH-SI birth process with , the FPT pdf is plotted as a function of t for and . In (a) and in (b) .
Figure 7.
For the TNH-SI birth process with , the FPT pdf is plotted as a function of t for and . In (a) and in (b) .
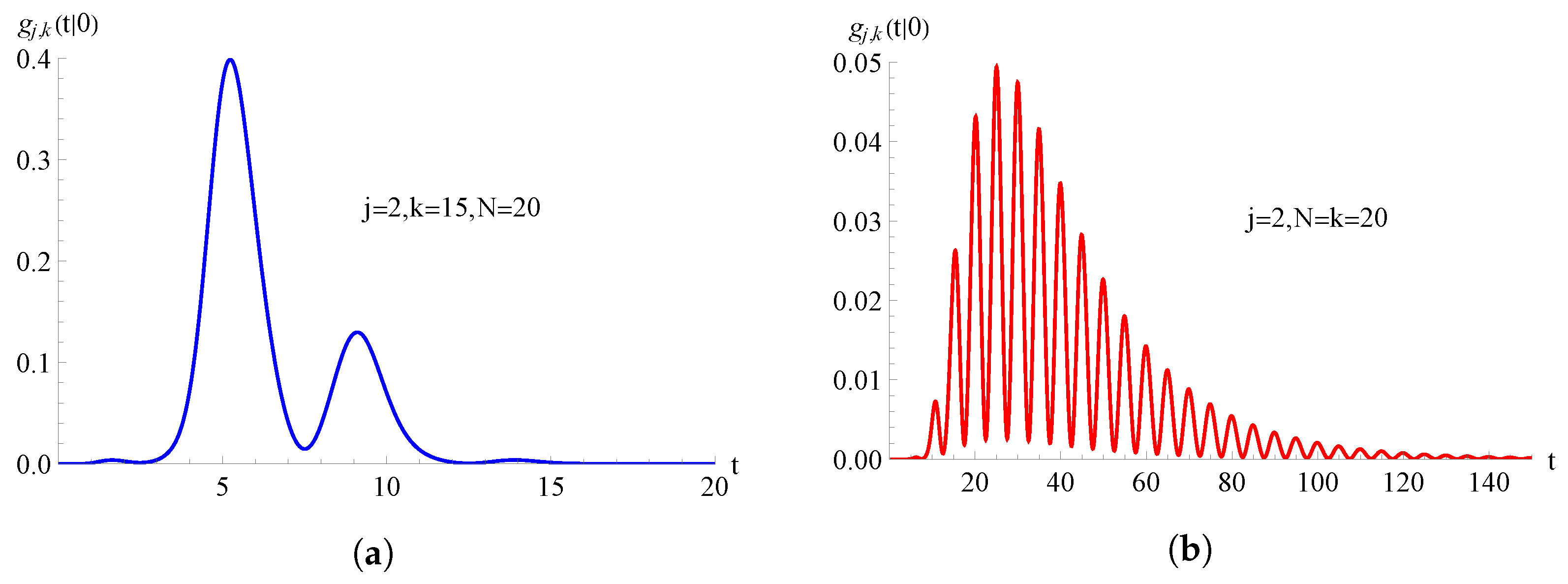
Figure 8.
For the TNH-SI birth process with , the FPT pdf is plotted as function of t for and . In (a) and in (b) .
Figure 8.
For the TNH-SI birth process with , the FPT pdf is plotted as function of t for and . In (a) and in (b) .
Figure 9.
For the TNH-SI birth process with , the FPT pdf is plotted as function of t for and . In (a) and in (b) .
Figure 9.
For the TNH-SI birth process with , the FPT pdf is plotted as function of t for and . In (a) and in (b) .
Figure 10.
For the TNH-hyper-logistic birth process with and , the FPT pdf is plotted as function of t for and . In (a) and in (b) .
Figure 10.
For the TNH-hyper-logistic birth process with and , the FPT pdf is plotted as function of t for and . In (a) and in (b) .
Figure 11.
For the TNH-hyper-logistic birth process with , , with , the FPT pdf is plotted as function of t for and . In (a) and in (b) .
Figure 11.
For the TNH-hyper-logistic birth process with , , with , the FPT pdf is plotted as function of t for and . In (a) and in (b) .
Figure 12.
For the TH-hyper-logistic birth process, the mean in (a) and the coefficient of variation in (b) of the FPT are plotted as functions of for , , , and for different values of k.
Figure 12.
For the TH-hyper-logistic birth process, the mean in (a) and the coefficient of variation in (b) of the FPT are plotted as functions of for , , , and for different values of k.
Table 1.
The duration
, given in (
5), is indicated for
,
,
, and various choices of
.
Table 1.
The duration
, given in (
5), is indicated for
,
,
, and various choices of
.
| Binomial Model | SI Model | Quadratic Model |
|---|
| 0.4 | 12.9824 | 18.7263 | 497.222 |
| 0.8 | 6.49120 | 9.36316 | 248.611 |
| 1.2 | 4.32746 | 6.24211 | 165.741 |
| 1.6 | 3.24560 | 4.68158 | 124.306 |
| 2.0 | 2.59648 | 3.74526 | 99.4444 |
Table 2.
For the hyper-logistic model, the duration is listed for , , , and various choices of and p.
Table 2.
For the hyper-logistic model, the duration is listed for , , , and various choices of and p.
| p | | | | | |
|---|
| 0.1 | 22.3763 | 11.1882 | 7.45878 | 5.59409 | 4.47527 |
| 0.5 | 68.8670 | 34.4335 | 22.9557 | 17.2168 | 13.7734 |
| 0.9 | 325.201 | 162.601 | 108.400 | 81.3003 | 65.0402 |
Table 3.
Special cases of TNH-flexible finite birth processes .
Table 3.
Special cases of TNH-flexible finite birth processes .
| TNH-Flexible Birth Processes | Birth Intensity Functions | Birth Rates | Parameters |
|---|
| Binomial birth process | | | |
| Quadratic birth process | | | |
| SI birth process | | | |
Table 4.
For the TH-binomial birth process, with , the mean, the variance, and the coefficient of variation of the FPT are listed for , , , and for different values of k.
Table 4.
For the TH-binomial birth process, with , the mean, the variance, and the coefficient of variation of the FPT are listed for , , , and for different values of k.
| k | | | |
|---|
| 40 | 0.293591 | 0.00431473 | 0.223735 |
| 60 | 0.626306 | 0.00985785 | 0.158527 |
| 80 | 1.01020 | 0.0172410 | 0.129979 |
| 100 | 1.46393 | 0.0275626 | 0.113407 |
| 120 | 2.01867 | 0.0430128 | 0.102739 |
| 140 | 2.73269 | 0.0686775 | 0.0958995 |
| 160 | 3.73601 | 0.119687 | 0.0926010 |
| 180 | 5.43802 | 0.270192 | 0.0955862 |
| 200 | 14.4324 | 10.2462 | 0.221791 |
Table 5.
For the TH-binomial birth process, with
, the deterministic time
, given in (
5) with
, the mean of
, the mean and the variance of
, and their asymptotic behaviors are listed for
,
, and for different values of
N.
Table 5.
For the TH-binomial birth process, with
, the deterministic time
, given in (
5) with
, the mean of
, the mean and the variance of
, and their asymptotic behaviors are listed for
,
, and for different values of
N.
| N | | | | | | |
|---|
| 50 | 8.50299 | 7.48747 | 9.98747 | 9.94603 | 10.0759 | 10.2808 |
| 100 | 10.9551 | 9.91370 | 12.4137 | 12.3981 | 10.2032 | 10.2808 |
| 200 | 12.9824 | 11.9324 | 14.4324 | 14.4254 | 10.2462 | 10.2808 |
| 300 | 14.0870 | 13.0345 | 15.5345 | 15.5300 | 10.2586 | 10.2808 |
| 400 | 14.8504 | 13.7968 | 16.2968 | 16.2935 | 10.2644 | 10.2808 |
| 500 | 15.4345 | 14.3801 | 16.8801 | 16.8775 | 10.2678 | 10.2808 |
| 1000 | 17.2189 | 16.1632 | 18.6632 | 18.6619 | 10.2745 | 10.2808 |
| 10000 | 23.0208 | 21.9640 | 24.4640 | 24.4639 | 10.2802 | 10.2808 |
Table 6.
For the TH-quadratic birth process, with , the mean, the variance, and the coefficient of variation of the FPT are listed for , , , and for different values of k.
Table 6.
For the TH-quadratic birth process, with , the mean, the variance, and the coefficient of variation of the FPT are listed for , , , and for different values of k.
| k | | | |
|---|
| 40 | 0.345179 | 0.00598477 | 0.224119 |
| 60 | 0.788628 | 0.0158751 | 0.159767 |
| 80 | 1.37928 | 0.0334555 | 0.132612 |
| 100 | 2.20501 | 0.0679213 | 0.118193 |
| 120 | 3.44102 | 0.145564 | 0.110876 |
| 140 | 5.49420 | 0.362094 | 0.109523 |
| 160 | 9.57498 | 1.23990 | 0.116293 |
| 180 | 21.6153 | 9.64726 | 0.143694 |
| 200 | 819.697 | 270581 | 0.634593 |
Table 7.
For the TH-quadratic birth process, with
, the deterministic time
, given in (
5) with
and
, the mean of
, the mean and the variance of
, and their asymptotic behaviors are listed for
,
. and for different values of
N.
Table 7.
For the TH-quadratic birth process, with
, the deterministic time
, given in (
5) with
and
, the mean of
, the mean and the variance of
, and their asymptotic behaviors are listed for
,
. and for different values of
N.
| N | | | | | | |
|---|
| 50 | 120.833 | 76.5188 | 201.519 | 205.617 | 16,911.1 | 16,911.3 |
| 100 | 246.875 | 158.128 | 408.128 | 411.234 | 67,645.2 | 67,645.2 |
| 200 | 497.222 | 319.697 | 819.697 | 822.467 | 270,581 | 270,581 |
| 300 | 747.321 | 481.027 | 1231.03 | 1233.70 | 608,807 | 608,807 |
| 400 | 997.368 | 642.306 | 1642.31 | 1644.93 | 1,082,323 | 1,082,323 |
| 500 | 1247.40 | 803.566 | 2053.57 | 2056.17 | 1,691,130 | 1,691,130 |
| 1000 | 2497.45 | 1609.79 | 4109.79 | 4112.34 | 6,764,520 | 6,764,520 |
| 10,000 | 24,997.5 | 16,120.8 | 41,120.8 | 41,123.4 | 676,452,021 | 676,452,021 |
Table 8.
For the TH-SI birth process, with , the mean, the variance, and the coefficient of variation of the FPT are listed for , , , and for different values of k.
Table 8.
For the TH-SI birth process, with , the mean, the variance, and the coefficient of variation of the FPT are listed for , , , and for different values of k.
| k | | | |
|---|
| 40 | 2.05810 | 0.217990 | 0.226857 |
| 60 | 3.41497 | 0.310635 | 0.163207 |
| 80 | 4.52330 | 0.372151 | 0.134867 |
| 100 | 5.53802 | 0.423642 | 0.117529 |
| 120 | 6.55066 | 0.474921 | 0.105202 |
| 140 | 7.65155 | 0.535606 | 0.0956474 |
| 160 | 8.98982 | 0.625690 | 0.0879891 |
| 180 | 10.9872 | 0.830494 | 0.0829437 |
| 200 | 20.2456 | 11.04150 | 0.164128 |
Table 9.
For the TH-SI birth process, with
, the deterministic time
, given in (
5) with
and
, the mean of
, the mean and the variance of
, and their asymptotic behaviors are listed for
,
, and for different values of
N.
Table 9.
For the TH-SI birth process, with
, the deterministic time
, given in (
5) with
and
, the mean of
, the mean and the variance of
, and their asymptotic behaviors are listed for
,
, and for different values of
N.
| N | | | | | | |
|---|
| 50 | 10.7432 | 9.76511 | 12.3161 | 12.2493 | 11.5017 | 11.8262 |
| 100 | 14.9535 | 13.9625 | 16.4878 | 16.4596 | 11.2852 | 11.4243 |
| 200 | 18.7263 | 17.7330 | 20.2456 | 20.2324 | 11.0415 | 11.1071 |
| 300 | 20.8488 | 19.8551 | 22.3635 | 22.3548 | 10.9309 | 10.9739 |
| 400 | 22.3335 | 21.3397 | 23.8460 | 23.8396 | 10.8673 | 10.8993 |
| 500 | 23.4766 | 22.4828 | 24.9878 | 24.9827 | 10.8256 | 10.8511 |
| 1000 | 26.9964 | 26.0025 | 28.5050 | 28.5025 | 10.7312 | 10.7438 |
| 10000 | 38.5571 | 37.5632 | 40.0634 | 40.0632 | 10.6201 | 10.6213 |
Table 10.
For the TH-hyper-logistic birth process, with the mean, the variance, and the coefficient of variation of the FPT are listed for , , , and for different values of p and k.
Table 10.
For the TH-hyper-logistic birth process, with the mean, the variance, and the coefficient of variation of the FPT are listed for , , , and for different values of p and k.
| | | |
|---|
| | | | | | |
|---|
| 40 | 1.19754 | 0.0724041 | 0.224693 | 0.586319 | 0.0171893 | 0.223612 |
| 60 | 2.16519 | 0.119272 | 0.159505 | 1.20496 | 0.0363428 | 0.158211 |
| 80 | 3.08125 | 0.161231 | 0.130316 | 1.91714 | 0.0617673 | 0.129636 |
| 100 | 4.03376 | 0.206619 | 0.112687 | 2.79428 | 0.100423 | 0.113409 |
| 120 | 5.10727 | 0.264364 | 0.100673 | 3.95689 | 0.168593 | 0.103768 |
| 140 | 6.43227 | 0.352653 | 0.092323 | 5.65705 | 0.315452 | 0.0992835 |
| 160 | 8.29745 | 0.529273 | 0.087679 | 8.57046 | 0.754576 | 0.101356 |
| 180 | 11.7024 | 1.14076 | 0.091269 | 15.5559 | 3.45829 | 0.119546 |
| 200 | 43.8655 | 198.557 | 0.321233 | 208.389 | 11893.5 | 0.523335 |
Table 11.
For the TH-hyper-logistic birth process, the deterministic time
, given in (
16), the mean of
and of
are listed for
,
, and for different values of
p and
N.
Table 11.
For the TH-hyper-logistic birth process, the deterministic time
, given in (
16), the mean of
and of
are listed for
,
, and for different values of
p and
N.
| | | |
|---|
| | | | | | |
|---|
| 50 | 19.4052 | 16.1976 | 24.3968 | 51.7587 | 37.2634 | 76.1546 |
| 100 | 27.5778 | 23.6011 | 33.6241 | 87.7280 | 64.1692 | 127.156 |
| 200 | 36.4719 | 31.5692 | 43.8655 | 144.457 | 106.221 | 208.389 |
| 300 | 42.3053 | 36.7659 | 50.6364 | 192.550 | 141.787 | 277.418 |
| 400 | 46.802 | 40.7617 | 55.8736 | 235.878 | 173.803 | 339.651 |
| 500 | 50.5221 | 44.0623 | 60.2148 | 275.998 | 203.439 | 397.296 |
| 1000 | 63.5814 | 55.624 | 75.4961 | 449.067 | 331.231 | 646.057 |
| 10,000 | 130.778 | 114.883 | 154.508 | 2253.22 | 1662.80 | 3240.24 |