Optimal Control Strategy of a Mathematical Model for the Fifth Wave of COVID-19 Outbreak (Omicron) in Thailand
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mathematical Model

| Variables | Description |
|---|---|
| Susceptible population. | |
| Exposed population. | |
| Symptomatic, infected population with the ω variant. | |
| Asymptomatic, infected population with the other variant. | |
| Quarantined population. | |
| Recovered population. | |
| Number of total populations. |
| Parameters | Description |
|---|---|
| The recruitment number of population. | |
| The infection rate of symptomatic population with the ω variant. | |
| The infection rate of asymptomatic population with the other variant. | |
| Incubation period. | |
| The rate of exposed moving to symptomatic. | |
| Quarantine rate of the symptomatic, infected population. | |
| Rate at which quarantine to be recovered. | |
| Rate at which asymptomatic, infected population to be recovered. | |
| Mortality rate of COVID-19. | |
| Mortality rate of natural causes. |
2.2. Stability Analysis
2.2.1. Equilibrium Point and Basic Reproduction Number
2.2.2. Global Stability of Equilibrium Points
3. Numerical Analysis Result
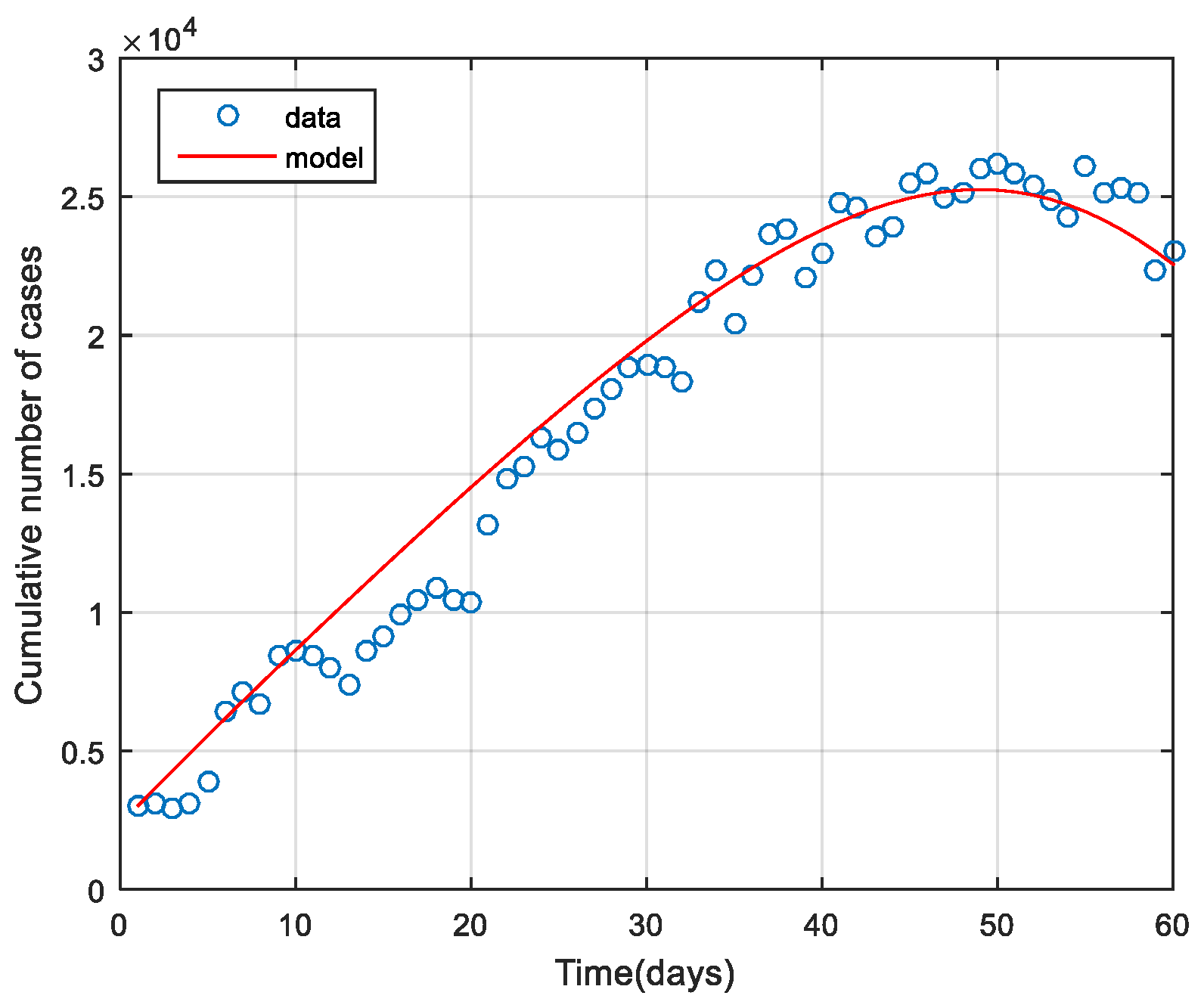
3.1. Model Fitting
3.2. Numerical Simulations
3.2.1. Part 1: The Analysis of Parameter Values Suitable for the Actual Epidemic Data
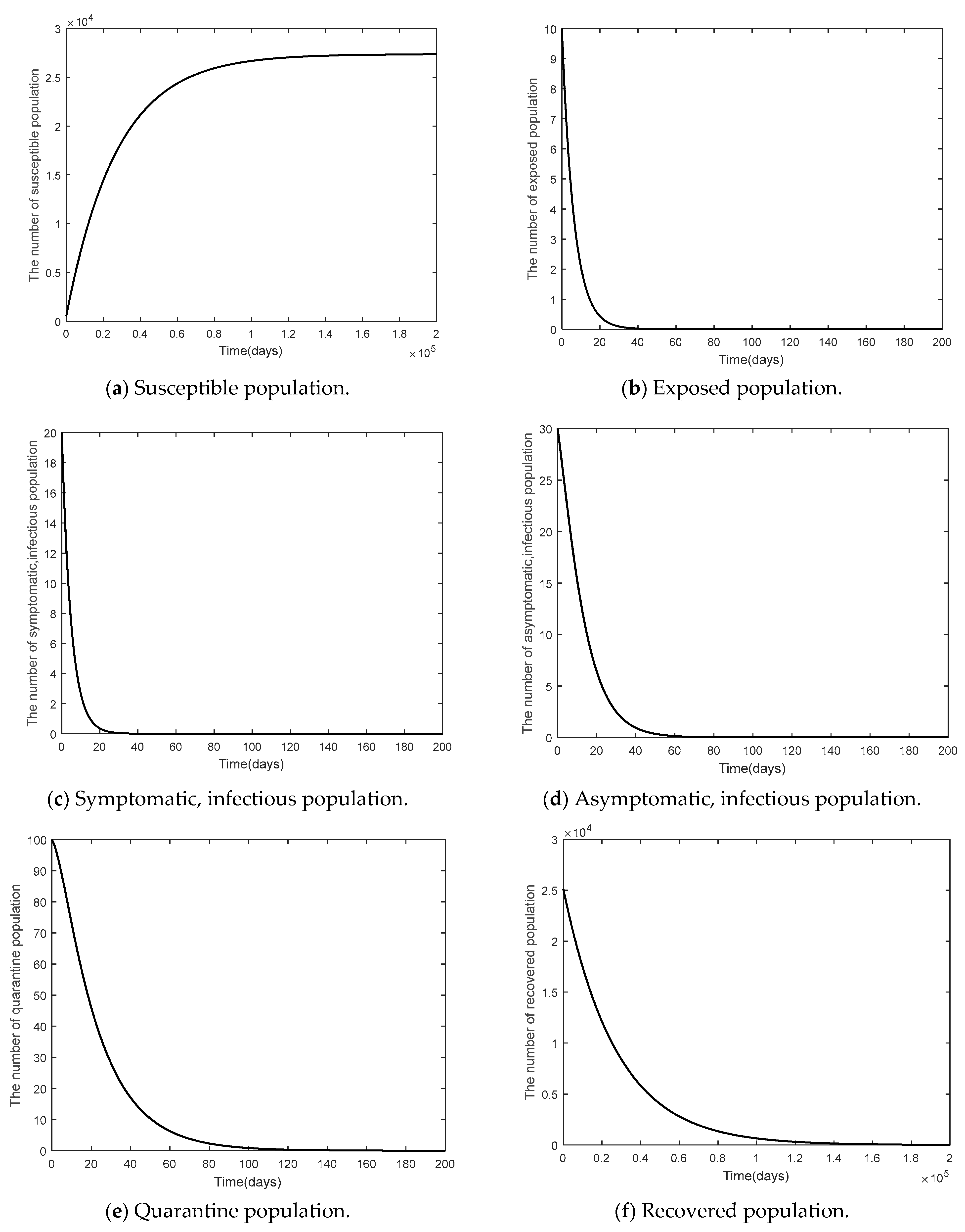
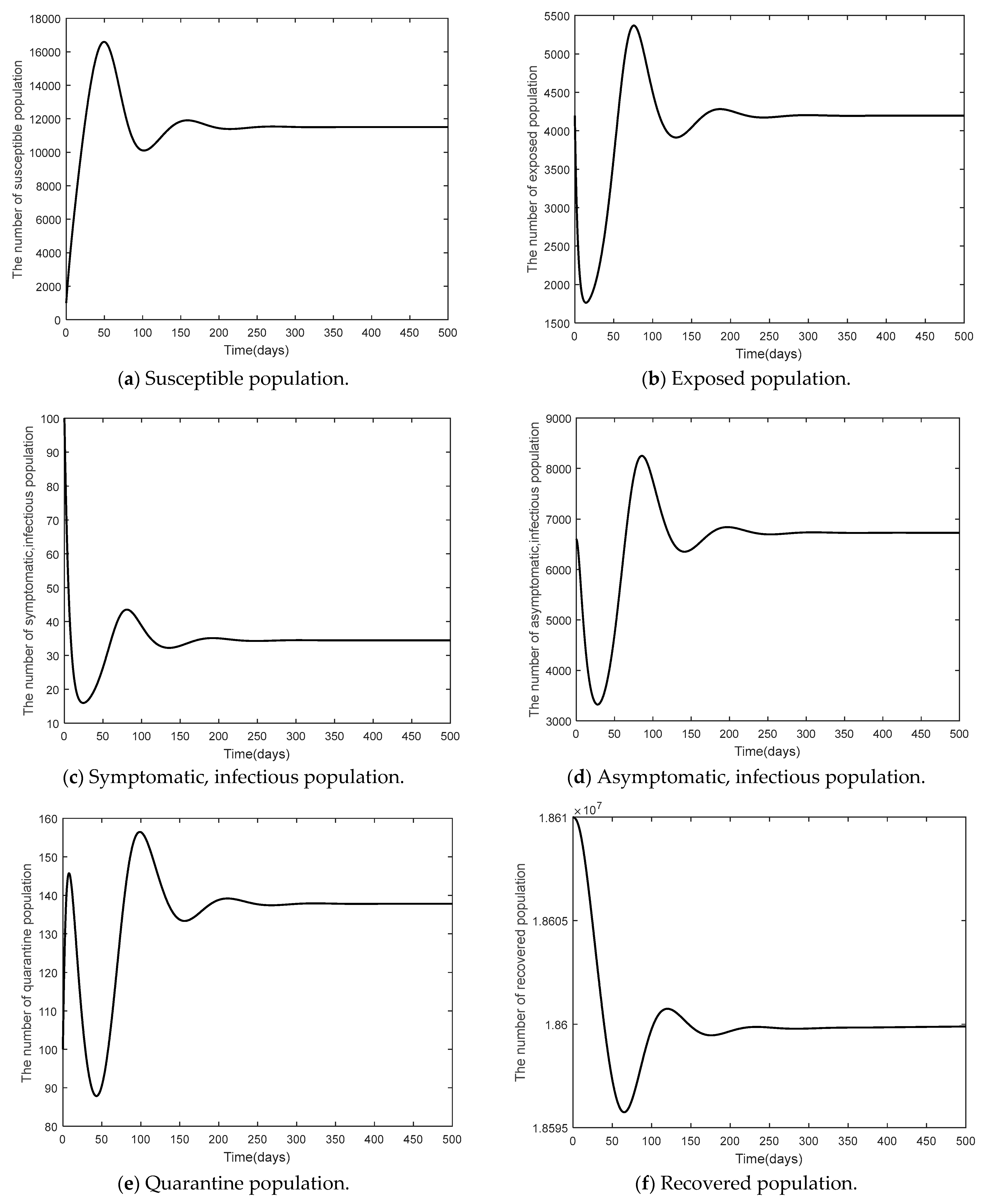
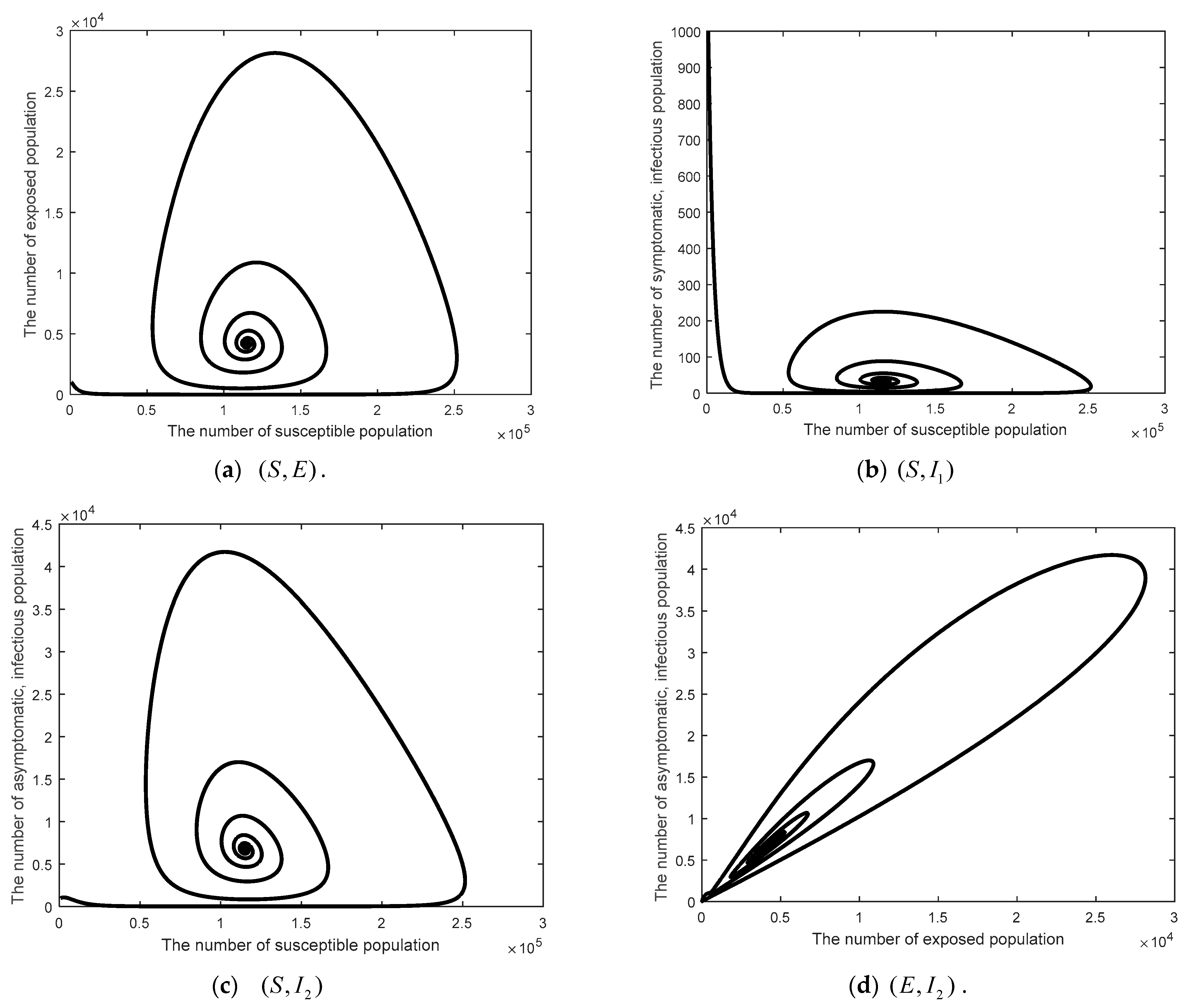
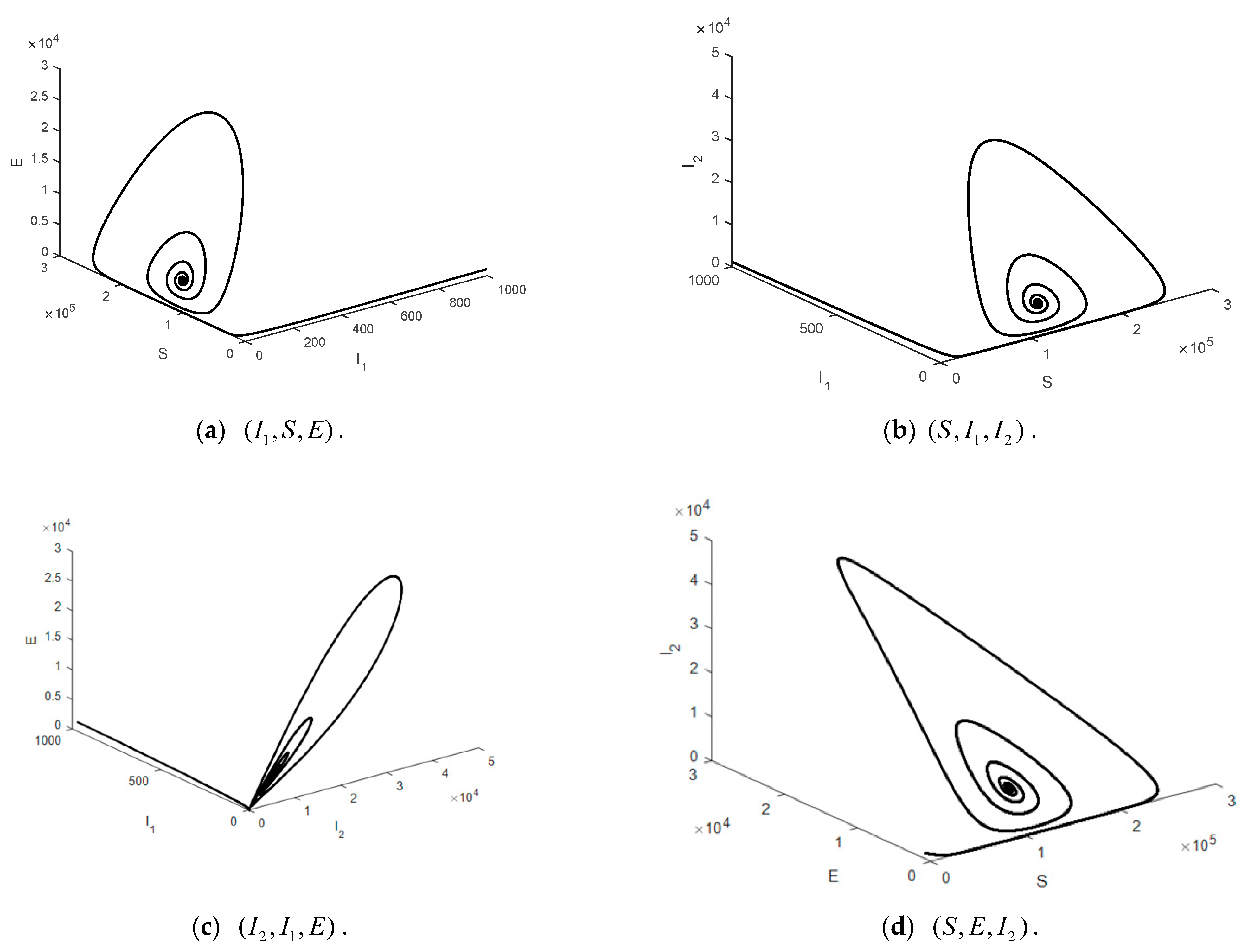
3.2.2. Part 2: Stability Analysis of the Model (1)
3.2.3. Part 3: Comparison of Parameters
| Parameters | Disease-Free | Endemic | Reference |
|---|---|---|---|
| 1 | 700 | Assume | |
| 0.0000075 | 0.0000075 | Fitting | |
| 0.0000009 | 0.0000009 | Fitting | |
| 1/6 | 1/6 | [36,47] | |
| 0.01 | 0.01 | Fitting | |
| 0.2 | 0.2 | [47] | |
| 0.05 | 0.05 | [47] | |
| 1/10 | 1/10 | [47] | |
| 0.00286 | 0.00286 | [47] | |
| 0.000036529 | 0.000036529 | [47,48] |
| Parameter | Sensitivity |
|---|---|
| 1 | |
| 0.000425 | |
| 0.995749 | |
| 0.000219 | |
| −0.005807 | |
| −0.004190 | |
| −0.967719 | |
| −0.027737 | |
| 1.000570 |
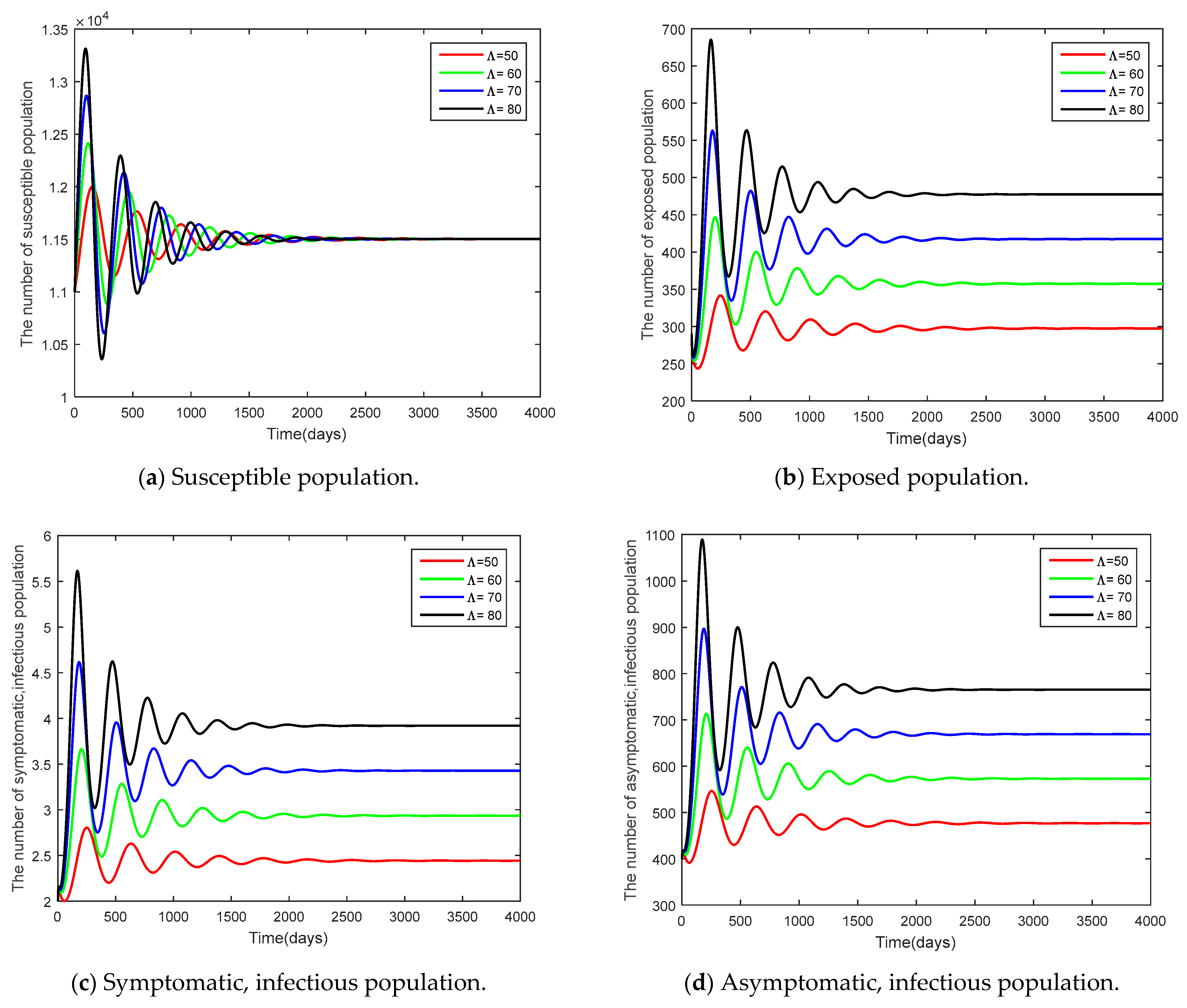
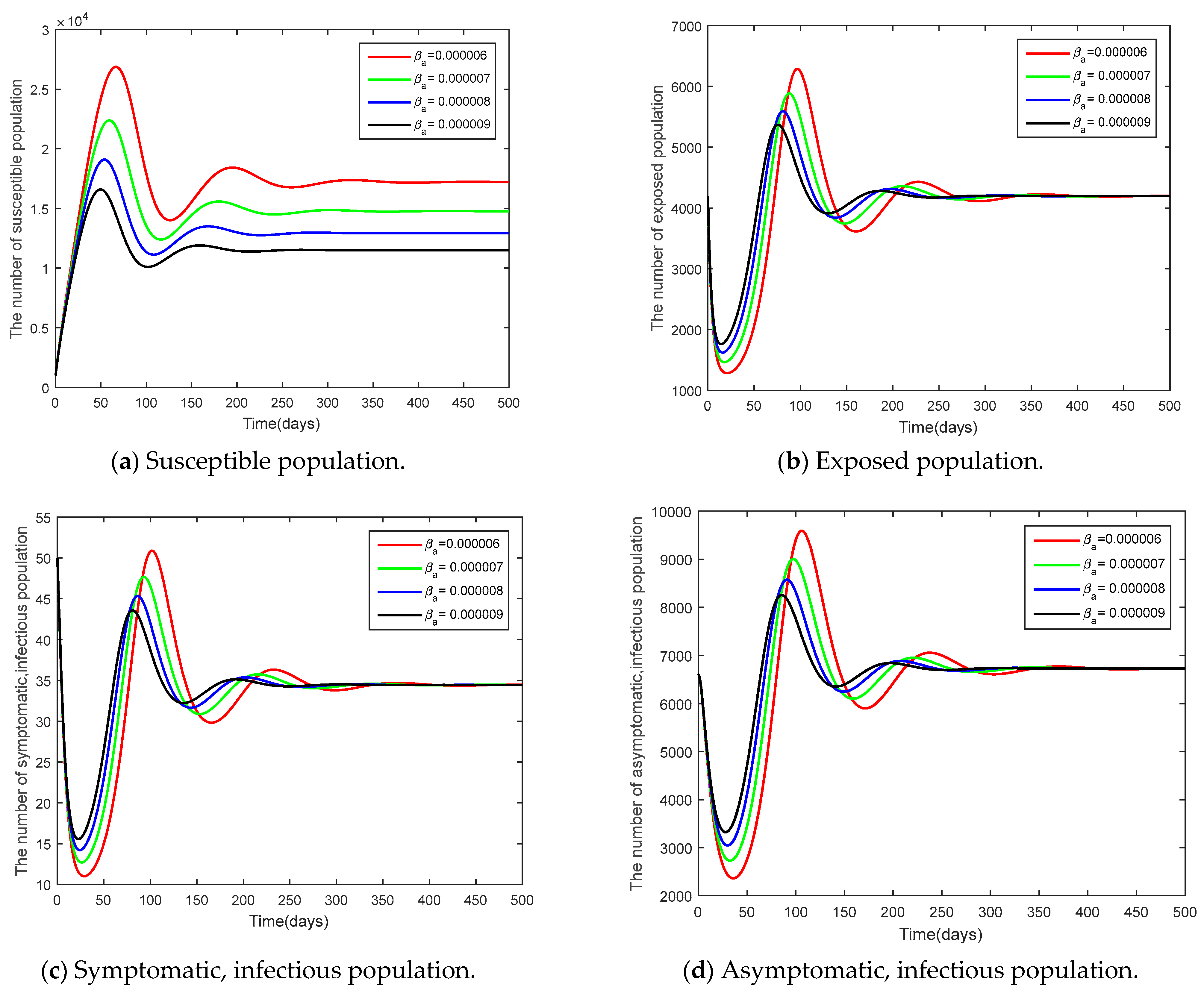
3.3. Sensitivity Analysis of Parameters
4. Optimal Control Problem
5. Numerical Results for Optimal Control Problem
- Case 1:
- and
- Case 2:
- and
- Case 3:
- and

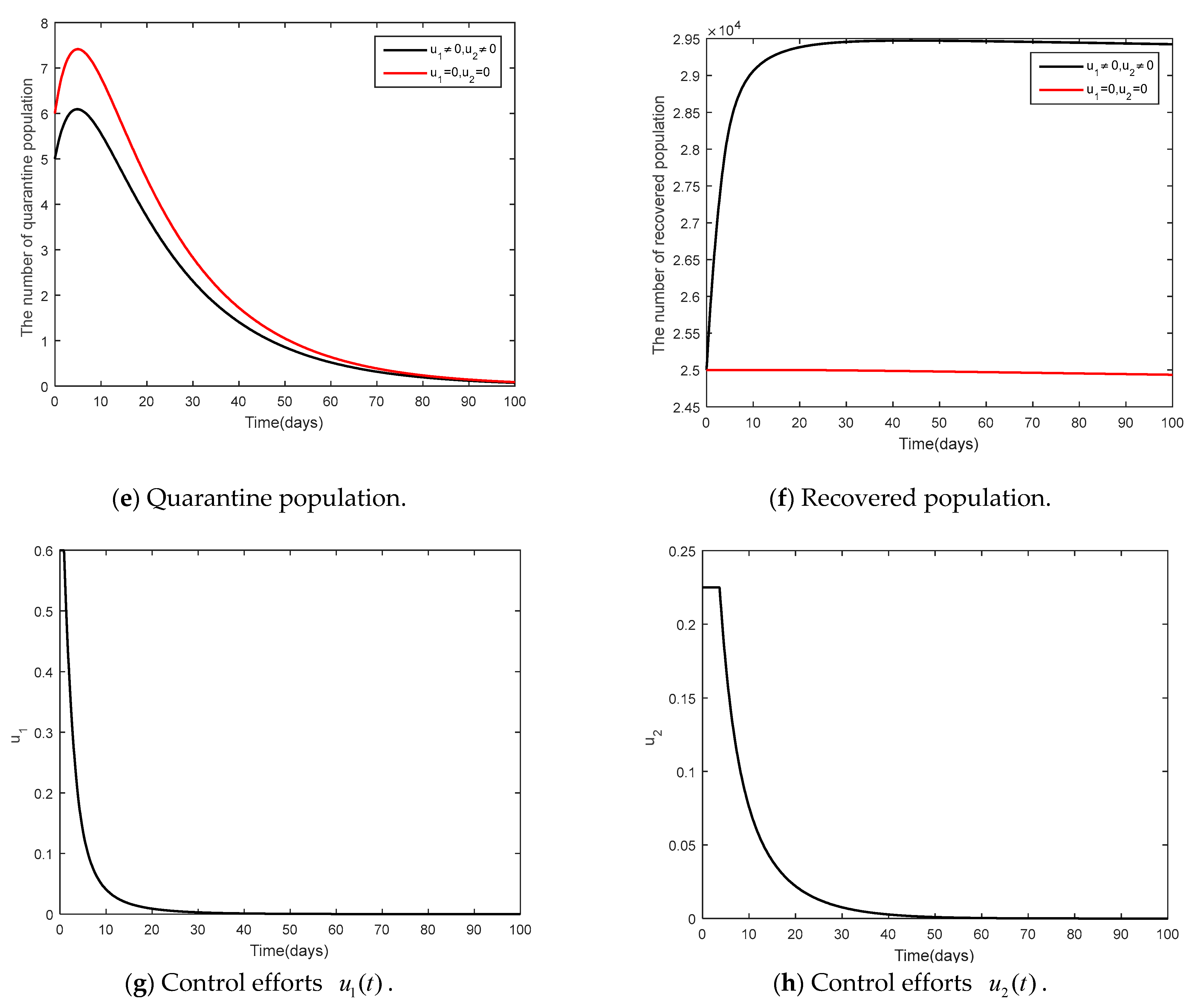
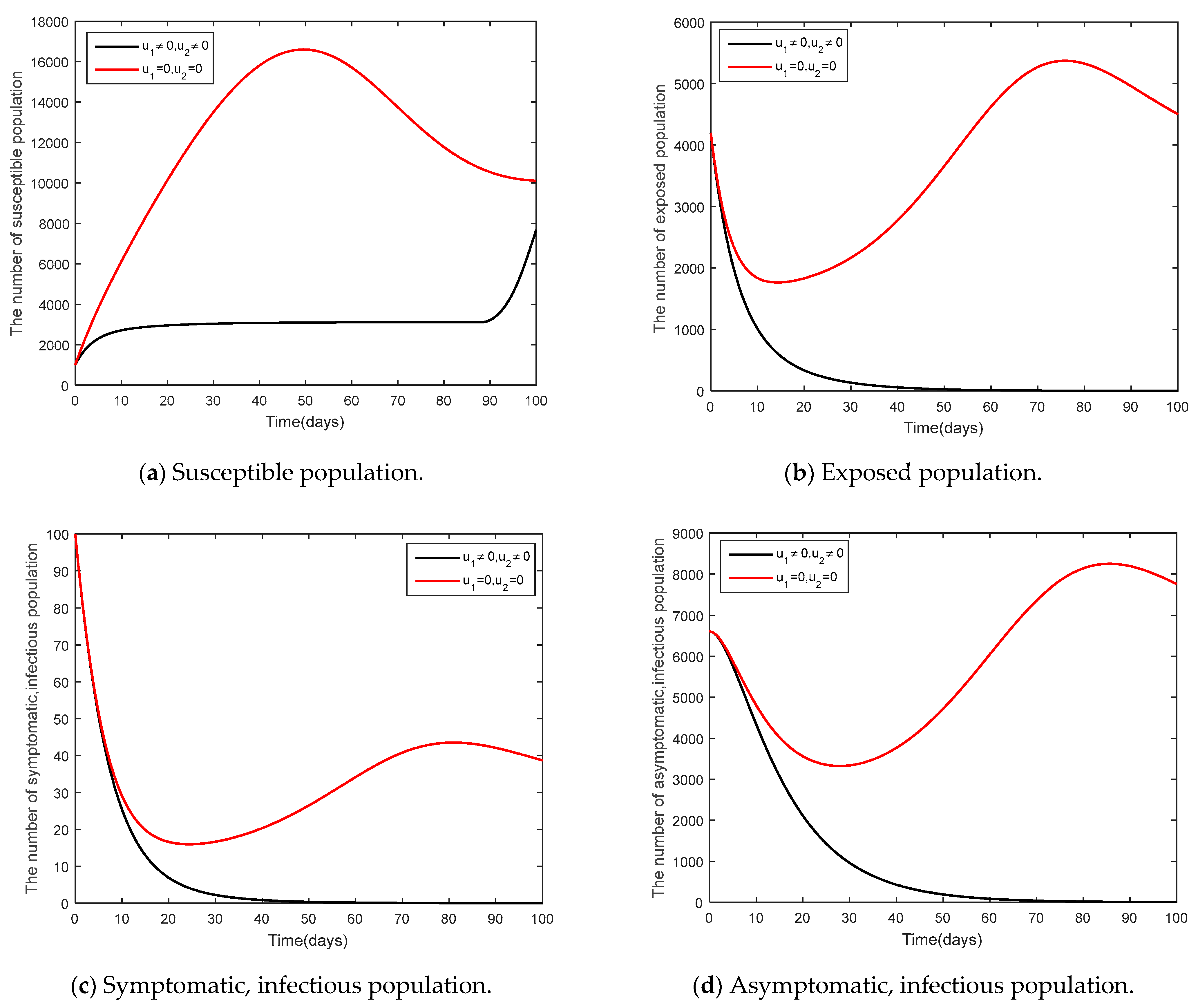
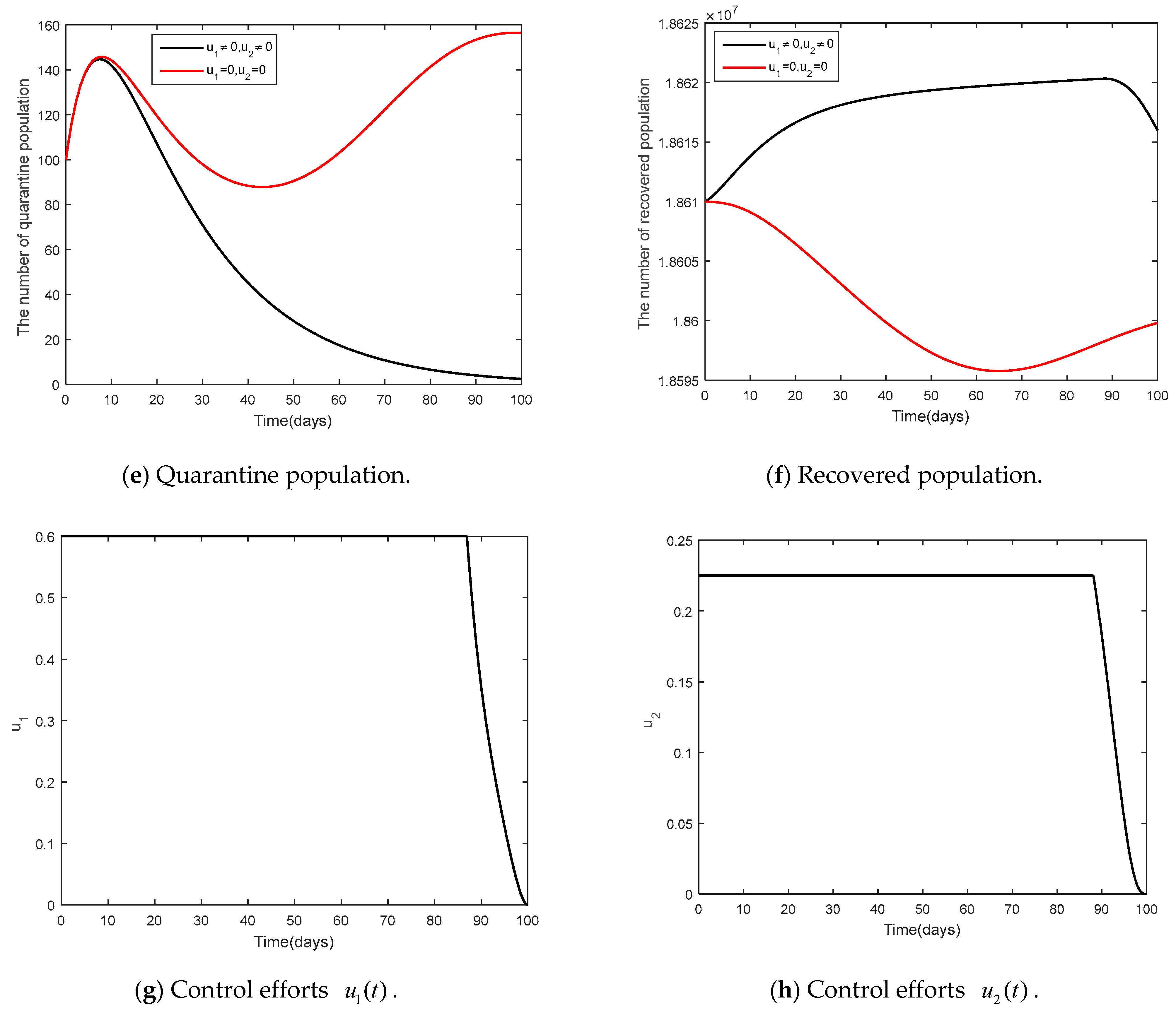

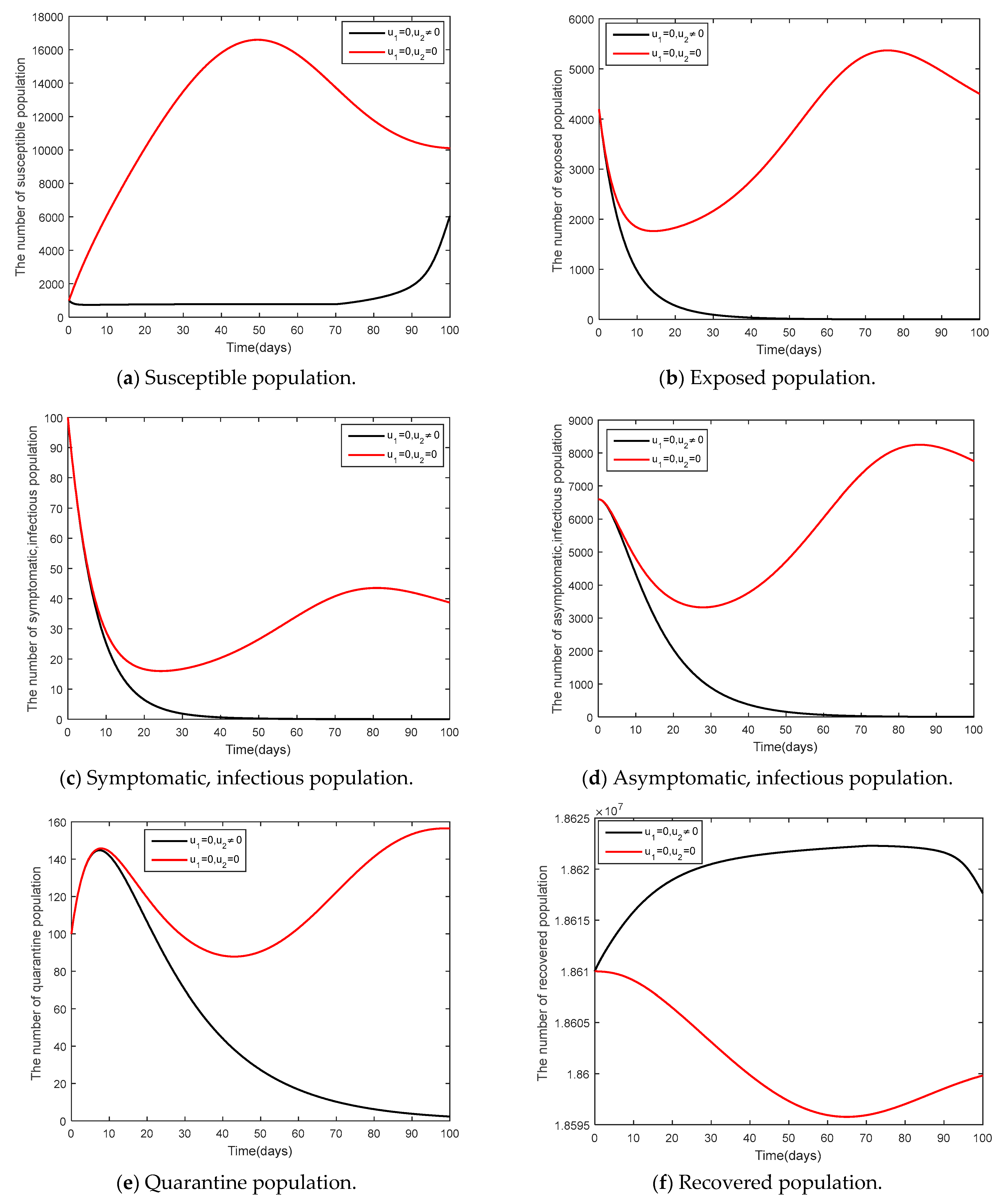
6. Discussion and Conclusions
- 1.
- Analysis of equilibrium point and the basic reproduction number of model (1). Disease-free equilibrium point , equilibrium point of endemic steady state and the basic reproduction number were calculated using the next-generation matrix method.
- 2.
- Stability analysis of model (1). The Lyapunov function was used to measure stability. It was found that in there was stability in the equilibrium point under the disease-free steady state when , and under the endemic steady state there was stability in the equilibrium point when .
- 3.
- fmincon Algorithm in MATLAB was used to be a technique for adjusting parameter values to ensure the model was suitable for the actual data of COVID-19 spread in Thailand and to estimate any spread than may come after. The parameters adjusted to be suitable for the model are the infection rate of symptomatic population , the infection rate of asymptomatic population , and the rate of exposed moving to symptomatic , making the data analysis more precise.
- 4.
- Based on the model (1), numerical data analysis was presented to verify and support theoretical conditions. The comparison of parameters found that an increase in recruitment number of people and the infection rate of asymptomatic population with the other variant had an effect on a faster control of the epidemic.
- 5.
- Parameter sensitivity analysis showed the relationship between parameter values and the basic reproduction number , indicating the importance of each parameter value affecting the epidemic. The analysis results of the model (1) are shown in Table 4. From Table 4, it can be described that positive parameter sensitivity and increased parameters affect an increase in the basic reproduction numbers, leading to an increasing epidemic. Similarly, negative parameter sensitivity and increased parameters shall affect a decrease in the basic reproduction numbers. Based on the analysis, it was found that the most sensitive parameter was the initial number of the population .
- 6.
- In this study, there were two control strategies, namely, social distancing strategy ( in conjunction with mask wearing strategy) and (vaccination control strategy). Pontryagin’s maximum principle was used to analyze the needs of conditions. The analysis was divided into three cases. Case 1 is social distancing strategy in conjunction with mask wearing strategy and vaccination control strategy, Case 2 is social distancing strategy together with mask wearing, and Case 3 is vaccination control strategy.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thirthar, A.A.; Abboubakar, H.; Khan, A.; Abdeljawad, T. Mathematical modeling of the COVID-19 epidemic with fear impact. AIMS Math. 2023, 8, 6447–6465. [Google Scholar] [CrossRef]
- Khan, M.A.; Atangana, A. Mathematical modeling and analysis of COVID-19: A study of new variant Omicron. Phys. A 2022, 599, 127452. [Google Scholar] [CrossRef]
- Zhang, Z.; Zeb, A.; Hussain, S.; Alzahrani, E. Dynamics of COVID-19 mathematical model with stochastic perturbation. Adv. Differ. Equ. 2020, 2020, 451. [Google Scholar] [CrossRef]
- Babaei, A.; Ahmadi, M.; Jafari, H.; Liya, A. A mathematical model to examine the effect of quarantine on the spread of coronavirus. Chaos Solitons Fractals 2021, 142, 110418. [Google Scholar] [CrossRef] [PubMed]
- Mendoza, V.M.P.; Mendoza, R.; Lee, J.; Jung, E. Managing bed capacity and timing of interventions: A COVID-19 model considering behavior and underreporting. AIMS Math. 2023, 8, 2201–2225. [Google Scholar] [CrossRef]
- Ghiasi Hafezi, S.; Seif, N.; Bahari, H.; Mohammadi, M.; Ghasemabadi, A.; Ferns, G.A.; Farkhani, E.M.; Ghayour-mobarhan, M. The association between macronutrient intakes and coronavirus disease 2019 (COVID-19) in an Iranian population: Applying a dynamical system model. J. Health Popul. Nutr. 2023, 42, 114. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.H.; Chu, Y.M.; Khan, M.A.; Al-Hartomy, O.A.; Higazy, M. Mathematical modeling and optimal control of the COVID-19 dynamics. Results Phys. 2021, 31, 105028. [Google Scholar] [CrossRef]
- Ghazizadeh, H.; Shakour, N.; Ghofchi, S.; Mansoori, A.; Saberi-Karimiam, M.; Rashidmayvan, M.; Ferns, G.; Esmaily, H.; Ghayour-Mobarhan, M. Use of data mining approaches to explore the association between type 2 diabetes mellitus with SARS-CoV-2. BMC Pulm. Med. 2023, 23, 203. [Google Scholar] [CrossRef]
- Sepulveda, G.; Arenas, A.J.; González-Parra, G. Mathematical Modeling of COVID-19 Dynamics under Two Vaccination Doses and Delay Effects. Mathematics 2023, 11, 369. [Google Scholar] [CrossRef]
- Khan, A.A.; Ullaha, S.; Amin, R. Optimal control analysis of COVID-19 vaccine epidemic model: A case study. Eur. Phys. J. Plus 2022, 137, 156. [Google Scholar] [CrossRef]
- Philip, N.A.A.; Seidu, B.; Bornaa, C.S. Mathematical Analysis of COVID-19 Transmission Dynamics Model in Ghana with Double-Dose Vaccination and Quarantine. Comput. Math. Methods Med. 2022, 2022, 7493087. [Google Scholar]
- Jankhonkhan, J.; Sawangtong, W. Model Predictive Control of COVID-19 pandemic With Social Isolation and Vaccination Policies in Thailand. Axioms 2021, 10, 274. [Google Scholar] [CrossRef]
- Wickramaarachchi, W.P.T.M.; Perera, S.S.N. An SIER model to estimate optimal transmission rate and initial parameters of COVD-19 dynamic in Sri Lanka. Alex. Eng. J. 2021, 60, 1557–1563. [Google Scholar] [CrossRef]
- Daniel, D.O. Mathematical Model for the Transmission of COVID-19 with Nonlinear Forces of Infection and the Need for Prevention Measure in Nigeria. J. Infect. Dis. Epidemiol. 2020, 6, 158. [Google Scholar]
- Veera Krishna, M.; Prakas, J. Mathematical modelling on phase based transmissibility of Coronavirus. Infect. Dis. Model. 2020, 5, 375–385. [Google Scholar] [CrossRef] [PubMed]
- Mishraa, A.M.; Purohit, S.D.; Owolabi, K.M.; Sharma, Y.D. A nonlinear epidemiological model considering asymptotic and quarantine classes for SARS CoV-2 virus. Chaos Solitons Fractals 2020, 138, 109953. [Google Scholar] [CrossRef]
- Satar, H.A.; Naji, R.K. A Mathematical Study for the Transmission of Coronavirus Disease. Mathematics 2023, 11, 2330. [Google Scholar] [CrossRef]
- Zamir, M.; Abdeljawad, T.; Nadeem, F.; Yousef, A. An optimal control analysis of a COVID-19 model. Alex. Eng. J. 2021, 60, 2875–2884. [Google Scholar] [CrossRef]
- Baba, I.A.; Nasidi, B.A.; Baleanu, D.; Saadi, S.H. A mathematical model to optimize the available control measures of COVID–19. Ecol. Complex. 2021, 46, 100930. [Google Scholar] [CrossRef]
- World Health Organization. SARS-CoV-2 Variant Tracking. Available online: https://www.who.int/fr/activities/tracking-SARS-CoV-2-variants (accessed on 31 May 2022).
- Minka, S.; Minka, F. A tabulated summary of the evidence on humoral and cellular responses to the SARS-CoV-2 Omicron VOC, as well as vaccine efficacy against this variant. Immunol. Lett. 2022, 243, 38–43. [Google Scholar] [CrossRef]
- González-Parra, G.; Arenas, A.J. Mathematical Modeling of SARS-CoV-2 Omicron Wave under Vaccination Effects. Computation 2023, 11, 36. [Google Scholar] [CrossRef]
- Martin, D.P.; Lytras, S.; Lucaci, A.G.; Maier, W.; Gruning, B.; Shank, S.D.; Weaver, S.; MacLean, O.A.; Orton, R.J.; Lemey, P.; et al. Selection Analysis Identifies Significant Mutational Changes in Omicron That Are Likely to Influence Both Antibody Neutralization and Spike Function (Part 1 of 2). Virological. Org. 2021, 5, pp. 1–2. Available online: https://virological.org/t/selection-analysis-identifies-significant-mutational-changes-in-omicron-that-are-likely-to-influence-both-antibody-neutralization-and-spike-function-part-1-of-2/771 (accessed on 10 June 2023).
- World Health Organization. WHO Coronavirus (COVID-19) Dashboard. 2023. Available online: https://covid19.who.int/ (accessed on 31 May 2022).
- World Health Organization. WHO Coronavirus (COVID-19) Dashboard. 2023. Available online: https://covid19.who.int/region/searo/country/th (accessed on 31 May 2022).
- Sun, T.-C.; DarAssi, M.H.; Alfwzan, W.F.; Khan, M.A.; Alshahrani, A.S.; Alqahtani, S.S.; Muhammad, T. Mathematical Modeling of COVID-19 with Vaccination Using Fractional Derivative: A Case Study. Fractal Fract. 2023, 7, 234. [Google Scholar] [CrossRef]
- Gumu, O.A.; Selvam, A.G.M.; Janagaraj, R.; Selvam, G.M.; Janagaraj, R. Dynamics of the Mathematical Model Related to COVID-19 Pandemic with Treatment. Thai J. Math. 2022, 20, 957–970. [Google Scholar]
- Chhetri, B.; Bhagat, V.M.; Muthusamy, S.; Ananth, V.S.; Vamsi, D.K.K.; Sanjeevi, C.B. Time Optimal Control Studies on COVID-19 Incorporating Adverse Events of the Antiviral Drugs. Comput. Math. Biophys. 2021, 9, 214–241. [Google Scholar] [CrossRef]
- Nabi, K.N.; Kumar, P.; Erturk, V.S. Projections and fractional dynamics of COVID-19 with optimal control strategies. Chaos Solitons Fractals 2021, 145, 110689. [Google Scholar] [CrossRef] [PubMed]
- Lamwong, J.; Tang, I.-M.; Pongsumpun, P. Mers Model of Thai and South Korean Population. Curr. Appl. Sci. Technol. 2018, 18, 45–57. [Google Scholar]
- Sardar, T.; Ghosh, I.; Rodo, X.; Chattopadhyay, J. A realistic two-strain model for MERS-CoV infection uncovers the high risk for epidemic propagation. PLoS Negl. Trop. Dis. 2020, 14, e0008065. [Google Scholar] [CrossRef]
- Mwalili, S.; Kimathi, M.; Ojiambo, V.; Gathungu, D.; Mbogo, R. SEIR model for COVID-19 dynamics incorporating the environment and social distancing. BMC. Res. Notes 2020, 13, 352. [Google Scholar] [CrossRef]
- Mahardika, Y.D. Dynamical Modeling of COVID-19 and Use of Optimal Control to Reduce the Infected Population and Minimize the Cost of Vaccination and Treatment. ComTech Comput. Math. Eng. Appl. 2021, 12, 65–73. [Google Scholar] [CrossRef]
- Omame, A.; Rwezaura, H.; Diagne, M.L.; Inyama, S.C.; Tchuenche, J.M. COVID-19 and dengue co-infection in Brazil: Optimal control and cost-effectiveness analysis. Eur. Phys. J. Plus 2021, 136, 1090. [Google Scholar] [CrossRef]
- Nainggolan, J.; Ansori, M.F. Stability and Sensitivity Analysis of the COVID-19 Spread with Comorbid Diseases. Symmetry 2022, 14, 2269. [Google Scholar] [CrossRef]
- Carcione, J.M.; Santos, J.E.; Bagaini, C.; Ba, J. A Simulation of a COVID-19 Epidemic Based on a Deterministic SEIR Model. Front. Public Health 2020, 8, 230. [Google Scholar] [CrossRef] [PubMed]
- Bhadauria, A.S.; Devi, S.; Nivedita, G. Modelling and analysis of a SEIQR model on COVID-19 pandemic with delay. Model. Earth Syst. Environ. 2022, 8, 3201–3214. [Google Scholar] [CrossRef] [PubMed]
- Youssef, H.; Alghamdi, N.; Ezzat, M.A.; El-Bary, A.A.; Shawky, A.M. Study on the SEIQR model and applying the epidemiological rates of COVID-19 epidemic spread in Saudi Arabia. Infect. Dis. Model. 2021, 6, 678–692. [Google Scholar] [CrossRef] [PubMed]
- Hussain, T.; Ozair, M.; Ali, F.; Rehman, S.; Assiri, T.A.; Mahmoud, E.E. Sensitivity analysis and optimal control of COVID-19 dynamics based on SEIQR model. Results Phys. 2021, 22, 103956. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.; Zarin, R.; Hussain, G.; Ahmad, N.A.; Mohd, M.H.; Yusuf, A. Stability analysis and optimal control of COVID-19 with convex incidence rate in Khyber Pakhtunkhawa (Pakistan). Results. Phys. 2021, 20, 103703. [Google Scholar] [CrossRef] [PubMed]
- Li, M.-T.; Sun, G.-Q.; Zhang, J.; Zhao, Y.; Pei, X.; Li, L.; Wang, Y.; Zhang, W.-Y.; Zhang, Z.-K.; Jin, Z. Analysis of COVID-19 transmission in Shanxi Province with discrete time imported cases. Math. Biosci. Eng. 2020, 17, 3710–3720. [Google Scholar] [CrossRef]
- Abioye, A.I.; Peter, O.J.; Ogunseye, H.A.; Oguntolu, F.A.; Oshinubi, K.; Ibrahim, A.A.; Khan, I. Mathematical model of COVID-19 in Nigeria with optimal control. Results Phys. 2021, 28, 104598. [Google Scholar] [CrossRef]
- van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Perkins, T.A.; España, G. Optimal Control of the COVID-19 Pandemic with Non-pharmaceutical Interventions. Bull. Math. Biol. 2020, 82, 118. [Google Scholar] [CrossRef]
- Lamwong, J.; Pongsumpun, P.; Tang, I.-M.; Wongvanich, N. Vaccination’s Role in Combating the Omicron Variant Outbreak in Thailand: An Optimal Control Approach. Mathematics 2022, 10, 3899. [Google Scholar] [CrossRef]
- World Health Organization. COVID-19—WHO Thailand Situation Reports. Available online: https://www.who.int/thailand/emergencies/novel-coronavirus-2019/situation-reports (accessed on 25 January 2023).
- Riyapan, P.; Shuaib, S.E.; Intarasit, A. A Mathematical Model of COVID-19 Pandemic: A Case Study of Bangkok, Thailand. Comput. Math. Methods Med. 2021, 2021, 6664483. [Google Scholar] [CrossRef] [PubMed]
- Alshammari, F.S. A Mathematical Model to Investigate the Transmission of COVID19 in the Kingdom of Saudi Arabia. Comput. Math. Methods Med. 2020, 2020, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Bandekara, S.R.; Ghosh, M. Mathematical modeling of COVID-19 in India and Nepal with optimal control and sensitivity analysis. Eur. Phys. J. Plus 2021, 136, 1058. [Google Scholar] [CrossRef] [PubMed]
- Kamien, M.I.; Schwartz, N.L. Dynamic Optimization: The Calculus of Variations and Optimal Control in Economics and Management; Elsevier: Amsterdam, The Netherlands, 1991. [Google Scholar]
- Guo, T.; Li, Y. Modeling and optimal control of mutated COVID-19 (Delta strain) with imperfect vaccination. Chaos Solitons Fractals 2022, 156, 111825. [Google Scholar]
- Adepoju, O.A.; Samson Olaniyi, S. Stability and optimal control of a disease model with vertical transmission and saturated incidence. Sci. Afr. 2021, 12, e00800. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lamwong, J.; Wongvanich, N.; Tang, I.-M.; Pongsumpun, P. Optimal Control Strategy of a Mathematical Model for the Fifth Wave of COVID-19 Outbreak (Omicron) in Thailand. Mathematics 2024, 12, 14. https://doi.org/10.3390/math12010014
Lamwong J, Wongvanich N, Tang I-M, Pongsumpun P. Optimal Control Strategy of a Mathematical Model for the Fifth Wave of COVID-19 Outbreak (Omicron) in Thailand. Mathematics. 2024; 12(1):14. https://doi.org/10.3390/math12010014
Chicago/Turabian StyleLamwong, Jiraporn, Napasool Wongvanich, I-Ming Tang, and Puntani Pongsumpun. 2024. "Optimal Control Strategy of a Mathematical Model for the Fifth Wave of COVID-19 Outbreak (Omicron) in Thailand" Mathematics 12, no. 1: 14. https://doi.org/10.3390/math12010014
APA StyleLamwong, J., Wongvanich, N., Tang, I.-M., & Pongsumpun, P. (2024). Optimal Control Strategy of a Mathematical Model for the Fifth Wave of COVID-19 Outbreak (Omicron) in Thailand. Mathematics, 12(1), 14. https://doi.org/10.3390/math12010014






