Abstract
A set of one-dimensional (as well as one two-dimensional) Fredholm integral equations (IEs) of the first kind of convolution type is solved. The task for solving these equations is ill-posed (first of all, unstable); therefore, the Wiener parametric filtering method (WPFM) and the Tikhonov regularization method (TRM) are used to solve them. The variant is considered when a kernel of the integral equation (IE) is unknown or known inaccurately, which generates a significant error in the solution of IE. The so-called “spectral method” is being developed to determine the kernel of an integral equation based on the Fourier spectrum, which leads to a decrease of the error in solving the IE and image improvement. Moreover, the authors also propose a method for diffusing the solution edges to suppress the possible Gibbs effect (ringing-type distortions). As applications, the problems for processing distorted (smeared, defocused, noisy, and with the Gibbs effect) images are considered. Numerical examples are given to illustrate the use of the “spectral method” to enhance the accuracy and stability of processing distorted images through their mathematical and computer processing.
Keywords:
integral equation; “spectral method”; determining the distortion type; the equation kernel; elimination of image distortions MSC:
45B05; 45Q05; 45E10; 68U10; 94A08
1. Introduction
Problem formulation. When solving various integral equations numerically, the kernel of the integral equation (IE) is often unknown or inaccurately known.
For example, in applied optics, an important task is to obtain clear images in the form of photographs of various objects, such as nature, animals, people, airplanes, the surface of the Earth, and others. These images can be obtained using various optical devices and image recording devices (IRDs); namely, photo and film cameras, microscopes, telescopes, and others. Such images give rich information about various objects and processes. IRDs can be installed both permanently on a stationary base and moving objects, such as cars, airplanes, unmanned aerial vehicles, and satellites, and allow the viewing of various environments (see, for example, [1] (pp. 12–19)). However, the images often have resections (damages, distortions); namely, smearing (diffusing) due to the object shifting during an exposure, defocusing (out of focus) because of setting the focus incorrectly, noise caused by external (atmospheric) or internal (instrumental) factors, the Gibbs effect, and others.
These distortions can be eliminated by mathematical and computer image processing (cf. [2,3,4]). For this purpose, various authors have developed a number of image processing methods, in particular, using integral equations [2,5,6,7] for image restoration by solving them using regular (stable) methods, as well as using the elimination (removal) of noise from images using filtering and other methods [1,5,8,9,10,11]. In most publications by other authors (except for the rather complex method of “blind” deconvolution [12]), it is assumed that the kernel of the IE (or PSF, AF) is known. In our article, we consider the case of an unknown kernel of the IE (PSF, AF) and, thereby, make an addition to the existing methods for solving the IEs and image processing.
Simultaneously, the type of distortion (smear or defocus) and the kernel of the integral equation can be known with errors, even insignificant, which generates a significant error in the IE solution. This work develops a so-called “spectral method” for determining the type and parameters of image distortions, after which the determined parameters are used to eliminate image distortions by solving the IEs (see below).
However, the following issues related to the restoration of distorted images have not been sufficiently developed: determining the type and parameters of distortion; the presence of smearing, defocusing, noise, and the Gibbs effect in the image at the same time; non-uniform smearing; and others. This paper is intended to demonstrate a number of techniques for eliminating some damage to images via mathematical processing.
The research is mostly focused on the “spectral method” of determining the IE kernel, which allows us to solve the IE effectively. This is a contribution to mathematical methods for solving IEs. For applications, the “spectral method” is used in the task of restoring distorted images, and the point spread function (PSF) or hardware function (HF) plays a role in the IE kernel.
Thus, the following problem is formulated: determine the kernel of an integral equation mathematically, which allows solving an integral equation. This problem generates the “spectral method”.
2. Formation of the Shift Problem and Restoration of the Integrand Function
Let us consider a problem in which, instead of the function w, a function g is given and averaged due to a uniform linear shift (smear) of the function w.
We direct the x-axis along the shift at an angle θ to the horizontal and the y-axis perpendicular to the shift.
Lemma 1.
The direct problem of distortion (smear, shift) is described by the expression:
where is the original function, is the distorted (smeared, averaged) function at each value of y, and is the parameter (the smear magnitude).
Proof.
The smear is assumed to be continuous; thus, an integral, meaning continuous summation (integration) of values over the interval is used. Another factor is added, meaning that when (in the absence of smear) on the right side of (1), an uncertainty of type is obtained, which, according to L’Hopital’s rule, is transformed into the (correct) expression: wy(x). If the factor is not added, then, when is on the right side of (1), we will obtain zero, which is incorrect. □
Lemma 2.
By swapping the left and right sides of expression (1), we obtain the inverse problem, in which is the desired solution to be restored by solving a set of one-dimensional Volterra integral equations (IEs) of the first kind for each value of y [8,9,13,14]:
where is the right side of the IE (measured, smeared function), is the desired function, and is a parameter (the smear magnitude).
Proof.
The integral Equation (2) is a non-standard IE (it has no kernel, and both integration limits are variable). To obtain a standard IE, we write (2) in the form of the Fredholm IE of the first kind of convolution type (a rare result when the Volterra IE goes to the Fredholm IE):
where, in relation to the problem of smearing, the kernel h is equal to:
or
For a stable solution of the IE (3), we use the Wiener parametric filtering (WPF) method [1,15]:
where H(ω) and Gy(ω) are one-dimensional Fourier transform (FT) of the functions h(x) and gy(x), respectively, and K ≥ 0 is the filtering parameter. The zero-order Tikhonov regularization method was also used [6,10,16,17,18,19,20,21,22], where the solution is the same as (6), and only the regularization parameter α ≥ 0 is used instead of K.
However, to solve IE (3), it is necessary to know the kernel h, namely, its parameters Δ and θ, which are not always known (see below).
Thus, we described both the direct problem for image smearing using relation (1), as well as the inverse problem for restoring a smeared image by solving the Volterra IE of the first kind (2) or the Fredholm IE of the first kind of convolution type (3). To solve the IE (3), the Wiener parametric filtering method (6) is proposed. □
3. Elimination (Removal) of Defocusing and Restoration of the Integrand Function
In this case, we solve the two-dimensional Fredholm IE of the first kind of convolution type:
where is the right side of the IE (the damaged measured image), is the desired solution (the restored image), and h is the kernel of the IE, or the point spread function (PSF). To solve the IE (7), we should know the kernel of IE h. Let us consider the case when each point in the region turns into a diffused disk (spot).
Lemma 3.
If the kernel of IE (7) is generated by a homogeneous disk with a radius of ρ ≥ 0, then the kernel is equal to:
Proof.
Let us select a homogeneous circle of radius ρ on the xy region with a center at some point A(x,y), as well as a number of other circles with centers at points . Let the radii of all circles be the same and equal to ρ, and then the areas of the circles be equal to . The intensity at a point is equal to the sum (integral) of all those circles that cover the point . The condition for covering a point by a circle with a center at the point and radius ρ is:
As a result, the intensity at the point will be equal in the direct problem:
and in the inverse problem:
Relationship (10) is a two-dimensional integral equation of the first kind with respect to . However, it has a non-standard form; namely, instead of the limits of integration, inequality (9) is used; in addition, there is no explicit kernel (more precisely, it is equal to the constant ). The non-standard nature of Equation (10) creates difficulties in solving it. Let us convert it to standard form. We write (10) in the form (7) and (8). See below for the method of determining ρ. Lemma 3 on the form of the kernel (8) is proven. □
Lemma 4.
If the kernel of the IE (7) is Gaussian, then the kernel is equal to:
where parameter is the standard deviation (SD).
Lemmas 3 and 4 define two variants of the kernel or point spread function. In the first variant, the kernel (8) is typical for a thin homogeneous disk of radius ρ > 0, which corresponds to a spatially invariant PSF, and in the second variant, the kernel (11) of the IE (or PSF) is Gaussian. See below for the method of determining .
Lemma 5.
The inverse problem of restoring the desired solution (defocus elimination problem) is reduced by solving the two-dimensional Fredholm integral equation (IE) of the first kind (7) using the stable method of parametric Wiener filtering (PWF) [5,8,9,10,11,15,23] (cf. (6)):
where and are two-dimensional FTs of the functions h(x,y) and g(x,y) and K ≥ 0 is the filtering parameter. The Tikhonov zero-order regularization method (RT) was also used [21,22]:
Proof.
Solutions (12) and (13) are well-known. However, the kernel of the IE h and its parameters Δ, θ, ρ, , K, and α are often unknown or known approximately. In this case, many authors determine h(x,y) using known w and g(x,y); however, usually w is unknown or is specified only in model examples or is estimated by the “blind” deconvolution method [12,24,25,26,27]—a rather cumbersome method. In this work, a simpler but also effective “spectral method” is developed (see below).
The authors described the problem of eliminating the image defocusing by solving the two-dimensional Fredholm IE of the first kind of convolution type (7). The cases are considered when the kernel of the IE (7) is a homogeneous disk or Gaussian. They are proposed to solve the IE (7) using the Wiener parametric filtering method according to (12) or the Tikhonov regularization method according to (13).
It has been proven Lemma 5 on integral equations has unknown parameters Δ, θ, ρ, , K, and α. □
4. “Spectral Method” for Estimating the Kernel Type of the IE
Let us denote by g(x,y) as the measured distorted intensity in several variants (smear and defocus). In this case, we will determine the axes direction: x, horizontally, and y, vertically downwards.
We use the two-dimensional Fourier transform (FT) of the smeared and defocused function g(x,y):
where and are Fourier frequencies (directed as x and y). We assume that the FT (Fourier spectrum) (14) is calculated in the form of DFT/FFT in the system MatLab 7.11 (R2010) and MatLab 8 [16,28,29]; for example, through the m-function fftshift.m (FFT with centering). A complex Fourier spectrum will be obtained, which for further convenience is deduced as the modulus of the spectrum . Figure 1 demonstrates the modules of the Fourier spectra for three functions g(x,y).
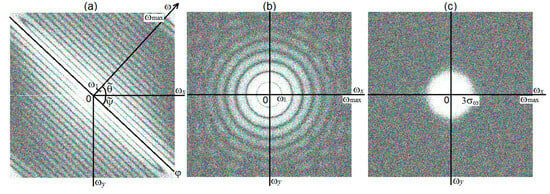
Figure 1.
Modules of spectra and for three different and unknown functions g(x,y).
Theorem 1.
Proof.
In practice, continuous FT (14) is calculated through discrete FT. In this case, the discretization step in x and y is s = 1 px (pixel). The maximum discretization frequencies for ω and for ϕ are also the same and equal to (the Kotelnikov–Nyquist frequency).
Due to smearing, the high Fourier frequencies ω are smoothed. As a result, the intensities of high frequencies along the ω–axis (along the smear) decrease faster than along the ϕ–axis (perpendicular to the smear), and the spectrum G(ω,ϕ) is deformed in the direction ω, namely, the spectrum lines experience compression along ω (see Figure 1a). We can obtain an expression of from the first zero of the transfer function [9]:
where is half of the smear along x in px. However, considering discretization:
As a result, the ratio of the semi-axes of the internal line in Figure 1a will equal to . Let us divide by according to (18), and we obtain at :
In Formula (19), the ratio can be found in the spectrogram (Figure 1a). Then, the desired smear Δ is equal to:
Let us also estimate the smear angle θ. According to the smear in Figure 1a, we can estimate the angle between the horizontal and the smear axis, as well as the angle . However, estimates of and usually do not coincide with the true values of ψ and θ. This is due to the fact that the image and its spectrum (in Figure 1a) are rectangular in size .
In [8], the method for estimating the true ψ and θ was proposed.
Let us take into account that is equal to the slope coefficient of the direct line, and when stretching or compressing the image, i.e., when r changes, the slope coefficient changes by r times: , whence the true angle ψ is equal:
Thus, as a result of region smearing, its spectrum changes; namely, the spectrum is compressed in the direction of the smear, and the spectrum does not experience compression in the direction perpendicular to the smear (Figure 1a). As shown, according to the spectrum, it is possible to estimate the smear size Δ and the smear angle θ and restore the area; for example, using the Wiener parametric filtering method or the Tikhonov regularization (see (12), (13)).
We may conclude that the “spectral method” is explained for determining the type of distortion (smear, defocus – two variants, noise), as well as smear parameters. The |DFT| of the image is executed, and it is demonstrated that the |DFT| of the smeared image is a set of almost parallel lines (see Figure 1a). The formulas for the smear parameters Δ and angle θ are derived. □
5. Estimates of the Image Defocusing Parameter (Two Variants)
Let us estimate the defocusing parameters of an image (see Figure 1b,c) using the “spectral method” [8,9,30].
Theorem 2 (Variant 1).
Estimation of the defocus parameter in the case when the PSF is a homogeneous disk (Figure 1b). The parameter ρ (disk radius) is equal to:
where are the Fourier frequencies that correspond to the zeros of the Bessel function of the first kind of the first order.
Proof.
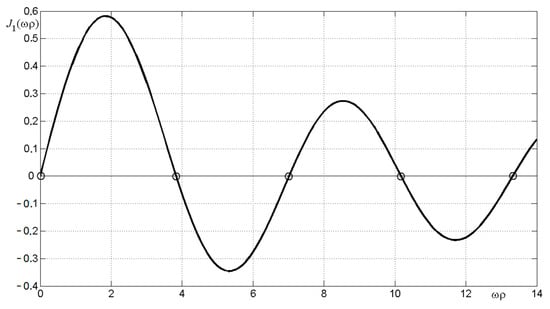
First, let us consider the simplest variant, when each point on the object turns into a homogeneous circle (disk) of radius ρ density 1/πρ2 [16] (p. 158). We consider one such circle. The two-dimensional Fourier transform of a homogeneous circle of radius ρ (its transfer function) is expressed through the one-dimensional Hankel transform [31,32]:
where D is the area of the circle and is the Bessel function of the first kind of the zero order. The last integral in (23) is equal to [32]:
where is the Bessel function of the first kind of the first order. Taking (24) into account, we obtain (cf. [9] (p. 100)):

Figure 2.
The Bessel function J1(ωρ) of the first kind of the first order.
These zeros correspond to the elliptical contours in Figure 1b.
In order to determine ρ based on the zeros (26), it is necessary to estimate the values of the frequencies ω corresponding to each zero. First, we estimate the value of corresponding to zero (ωρ)1 = 3.84. Let the object and its spectrum (Figure 1b) have dimensions (in px) M × N. Consider the horizontal (minor) semi-axis of the internal (first) ellipse in Figure 1b. Let us denote the dimensionless ratio in Figure 1b through . Then, the frequency itself will be equal to . Hence, ρ = 3.84/ω1.
The same operation can be performed in relation to other zeros (26), and we obtain a set of close values ρ according to (22). The theorem is proven. □
Theorem 3 (Variant 2).
Estimation of the defocus parameter in the case when the PSF is Gaussian (Figure 1c). The parameter (SD) using the “three-sigma” rule is equal to:
where and are the value of ω at which the spectrum F(ω) = F(3σω) ≈ 0.
Proof.
Let each point on an object turn into a Gaussian axisymmetric spot on its image. In this case, the kernel of IE is two-dimensional axisymmetric Gaussian (cf. (11)) [9] (p. 101) [33]:
where . Consider one such spot. The two-dimensional Fourier transform (FT) of the Gaussian (28) (transfer function) is expressed by the following formula, which is more general than Formula (23) [31] (p. 69) [32] (p. 249):
or [9] (p. 102):
where k is a certain coefficient (which has no effect on further results).
However, Formulas (29) and (30), unlike Formulas (23)–(26), do not allow us to estimate as effectively as ρ is estimated. This is due to the fact that in the case when the kernel is a homogeneous circle, we have clear landmarks—the zeros of the Bessel function (26) and the corresponding ellipses of the function F(ω1,ω2) (Figure 1b). Meanwhile, in the case when the kernel is Gaussian (28), there are no such clear guidelines since F(ω), according to (30), is a smooth monotonically decreasing function ω.
The following method is proposed for estimating the parameter based on the “three sigma” rule [16] (p. 161). Let us consider it using the example shown in Figure 1c. Let us draw an ellipse along the region where F(ω) = F(3σω) ≈ 0. Evaluating 3σω and considering that , we find:
It has been revealed that the |DFT| of a defocus image is a set of ellipses (see Figure 1b) in the case when the PSF is a homogeneous disk of radius ρ or Gaussian when the PSF is also Gaussian with standard deviation (see Figure 1c). The formulas for the parameters ρ and are derived.
Thus, we have obtained the estimates for (15), (16), (22), and (27) of parameters Δ, θ, ρ, and for integral kernels in Equations (3) and (7), which allows performing solutions (6), (12), and (13).
It is possible to estimate the optimality of the parameters, for example, by solving model examples and estimating the error according to (37). We can say that the “spectral method” is a quasi-optimal one. □
6. Applied Problem: Restoration of Distorted (Smeared, Defocused, Noisy) Images
Let us illustrate the “spectral method” described above with an applied image processing problem.
In applied optics, an important task is to obtain clear images in the form of photographs of various objects such as nature, animals, people, airplanes, and the surface of the Earth. These images can be obtained using various optical systems and image recording devices (IRDs); namely, photo and film cameras, microscopes, telescopes, and others. Such images provide rich information about objects and various processes. IRDs can be installed both permanently on a stationary base and moving objects, such as cars, airplanes, unmanned aerial vehicles, and satellites, and allow for the viewing of various environments (see, for example, [1] (pp. 12–19)). However, the images often have resections (damage, distortion); namely, smearing (diffusing) due to the object shifting during the exposure; defocusing because of setting the focus of the IRD incorrectly; noise caused by external (atmospheric) and internal (instrumental) noise; and others.
These distortions can be eliminated by mathematical and computer image processing (cf. [3,6]). For this purpose, various authors have developed a number of processing methods, in particular, using integral equations for image restoration by solving them using regular (stable) methods, as well as using the elimination (removal) of noise from images using filtering methods, etc. [1,5,8,9,10,11].
However, the following questions related to the restoration of distorted images have not been sufficiently developed: determining the type and parameters of distortion; the presence of smear, defocus, and noise in the image at the same time; non-uniform smearing; and other issues. This paper is intended to demonstrate a number of techniques for eliminating these image damages through mathematical processing.
This work develops the so-called “spectral method” for determining the type and parameters of image distortions, and then certain parameters are used to eliminate image distortions by solving the IE (see below). Figure 3 demonstrates three photographs (images) of 512 × 511 × 3 px of the galaxy M100 (NGC 4321) with different point spread functions (PSFs).

Figure 3.
(a–c) Distorted (smeared, outoffocus, noisy) images of the M100 galaxy; the relative error in mean δrel ≈ 0.1 = 10%; (d) undistorted training image of the M51 galaxy.
The galaxy image was obtained by the Hubble Space Telescope [9] (p. 105) [34,35], and the image is unclear due to the residual spherical aberration of the telescope mirror. Image unclearness is quite similar to defocus. To obtain a clear image, the so-called wavefront deformation modeling method with a selection of the point spread function was developed [35].
We have also processed a distorted image of the M100 galaxy. Figure 3 shows three distorted (smeared and defocused) images; however, the types of distortions (smeared or defocused) are not indicated and will be further defined by the “spectral method”. The image error is estimated approximately. Next, it will be refined through the m-function rmsd.m using a training image of another galaxy; namely, M51.
We believe that we do not know the exact image of the M100 galaxy, but only its distorted images are known (Figure 3a–c). To further process these images, we include a learning image of the galaxy M51 with a known accurate image and with parameters near the M100 image (cf. [36]). Using a training image of the galaxy M51 will allow us to refine the M100 parameters; namely, the error , filtering parameter K, regularization parameter α, and others (a similar example is considered in [23] (three images of the Black Sea) without specifying the types of distortions).
According to the images in Figure 3a–c, it is almost impossible to visually determine the type of damage (which image is smeared and which is outoffocus) and determine the presence and the type of noise (impulse, Gaussian, etc.), as well as evaluate the processing error. An important task is also to identify the damage parameters: the magnitude ∆ and angle θ of the smear in the case of image smearing, the size of the smear spot ρ or in the case of image defocusing, and noise parameters. A program has been developed in the form of an m-function Gal_M100.m, as well as Gal_M51.m in MatLab.
Types and parameters of image distortions in Figure 1a–c will be further defined by the “spectral method”. The errors will also be determined according to the following Formula (37) (see below).
7. “Spectral Method” for Estimating the Type of the Image Damage
Let us denote g(x,y) as the intensity of a damaged (spoiled, distorted) image; for example, a photograph, and determine the direction of the axes: x—horizontally and y—vertically downwards. We use the two-dimensional Fourier transform (FT) of the damaged image g(x,y):
where and are the Fourier frequencies. We assume that the FT (Fourier spectrum) (32) of the image is calculated in the form of DFT/FFT in the MatLab system [16,28,29]; for example, through the m-function fftshift.m (FFT with centering). A complex Fourier spectrum is obtained, which we derive as the modulus of the spectrum for further convenience. Figure 1 demonstrates the modules of the Fourier spectra of three images g(x,y) shown in Figure 3a–c.
The view of the spectra in Figure 1 is very different, which will help to estimate the types and parameters of the image damage in Figure 3a–c. The above-mentioned theory of spectral processing for distorted (smeared and defocused) images using FT demonstrates the following:
- The Fourier spectrum of a smeared image has the form of almost parallel lines with a slope angle (see Figure 1a), which, generally speaking, does not coincide with the true smear angle θ.
Therefore, according to the appearance of the spectra in Figure 1, we can determine that Figure 3a shows a smear image, Figure 3b demonstrates a defocused image when the PSF is a homogeneous disk, and Figure 3c shows a defocused image when the PSF is Gaussian.
Let us estimate the damage parameters using the “spectral method”.
8. Determining the Image Smear Parameters
According to the discrete spectrum of the smeared image (Figure 3a) shown in Figure 1a, we determine the smearing angle θ using Formula (16).
Then, we measure the value of the angle and obtain an average from several measurements: and (see Figure 1a). According to Formula (16), we calculate the average of and , which are close to the exact value of the smear angle . The error is (0.6/47)·100% ≈ 1.3%.
To determine the parameter Δ (the smear magnitude), we mark the frequency and the Nyquist frequency , the first and last zeros of the function , on the ω-axis in Figure 1a. According to (15), the parameter Δ will be equal to:
Formula (33) has a positive property, and the ratio is dimensionless.
Based on several measurements of the ratio , we obtain from Formula (33) an average , which is quite comparable with the exact value of the smear value px.
We can see that the “spectral method” allowed us to fairly accurately estimate the parameters θ and Δ of the image smear. The information on image restoration using the found parameters θ and Δ is presented below.
9. Estimates of the Image Defocus Parameter (Two Variants)
According to the type of spectra in Figure 1b,c, we conclude that Figure 3b,c show defocused images. Let us estimate the parameters of the defocused image by the “spectral method” [8,9,30].
Variant 1. The view of the Fourier spectrum (Figure 1b) in the form of ellipses/circles indicates that a defocused image is shown in Figure 3b. Moreover, the point spread function (PSF) is a uniform disk of some radius ρ. In optics, Variant 1 corresponds to the passage of light through a thin lens with a circular aperture [9] (p. 100).
As shown above (see (22)–(26)), each such disk is described by a two-dimensional FT, as well as an optical transfer function, a one-dimensional Hankel transform, and a Bessel function of the first kind of the first order. The Bessel function is shown in Figure 2.
According to Figure 1b, we find the dimensionless ratio to be equal to . Here, is the Kotelnikov–Nyquist frequency. Since the discretization steps are equal to , then . As a result, . We calculate the defocus parameter ρ using the formula ρ = 3.84/ω1 (or ρ = 7.02/ω2, etc.) and finally obtain ρ = 8.15 ± 0.3, which is close to the exact value ρ = 8 px. The error of ρ is (0.3/8.185)·100% ≈ 3.6%.
See below for image restoration using the found parameter ρ.
Variant 2. Let each point of the object in the damaged image be two-dimensional Gaussian, which occurs, for example, when radiation passes from the object through the atmosphere [1] (p. 258). Then, the PSF will also be Gaussian [9,33]:
where is the standard deviation (SD) of PSF Gaussian. The Fourier spectrum H for such PSF and the spectrum of a defocused image will also be Gaussians [23,33]:
Spectrum G appeared to be real in the form of a spot with a monotonic decrease in intensity from the center (Figure 1c). Note that in Variant 1 (Figure 1b), there are zeros in the spectrum G and this helped to estimate the parameter ρ, but in Variant 2 (Figure 1c), there are no such zeros. However, the Gaussian (35) decreases quickly and practically becomes zero at ; thus, the “three sigma” method is proposed. As follows from (34) and (35), = 1/σω and, according to the “three sigma” method:
Let us consider that and estimate the Figure 1c value 3σω ≈ 1–1.2. Then, using (36), we obtain on average over several measurements = 2.85 ± 0.35, which is close to the exact value = 3 px. In this variant, due to the fuzziness of the boundary (where G ≈ 0), the relative error in estimating appeared to be quite large; namely, (0.35/2.85)·100% ≈ 12.2%. Nevertheless, using multiple measurements of brought the average closer to the exact value.
We can see that the “spectral method” allowed us to estimate the parameter ρ with an acceptable error and the defocusing image parameter with a greater error. These parameters will be needed later when restoring images.
10. Elimination (Removal) of Image Smearing and Defocusing
After estimating the spectral method of the type and parameters of damage (resection, distortion, breakage) of images, we solve the problem of stable elimination (removal) by mathematical and programmatic means of image damage and their restoration (reconstruction, renewal). Wherein, to refine the image parameters of the M100 galaxy, we use the results for training images of the M51 galaxy.
The restoration of distorted (smeared, defocused, noisy) images of the M100 galaxy was performed via solving integral Equations (3), (6), (7), (12), and (13) by the Wiener parametric filtering (WPF) method and the Tikhonov regularization method (TRM). In this case, the found parameters Δ, θ, ρ, and of kernels h of the integral equations were used. The equations were solved using the m-functions deconvwnr.m (solution by the WPF method), deconvreg.m (solution by TRM), and refocusing.m in MatLab.
The value of the parameter K in the WPF method was selected according to the condition in and specified by selection in relation to the training images of the M51 galaxy, in which the exact image is known and the error or can be calculated according to Formula (37) for the relative error (see below).
Figure 4 presents the result of eliminating smear and defocus from three photographs (image, defocus).

Elimination (filtration) of noise. Detailed analysis in Figure 4 shows the presence of noise in image 4abc. Figure 5 shows the result of impulse noise filtering.

Figure 5.
Results of eliminating (removing) the bipolar impulse noise by the median filter. The relative errors of are 0.0482 in (a), 0.0534 in (b), and 0.0431 in (c).
Noise filtering is performed using the Tukey [1] median filter (as shown in [10]; impulse noise is best filtered by median filters). We also used the Gonzalez adaptive median filter [1], the Naranyanan iterative filter [37], and our modified median filter [8], which gave results similar to the Tukey median filter when applied to the M100. The m-function medfilt2c.m has been developed to filter a noisy color image using the median filter.
Figure 5 demonstrates a satisfactory final result; namely, the types and parameters of image damages were determined using a spectral method (see Figure 1 and Figure 3), which allowed restoring the damaged images with reduced error by solving integral Equations (3) and (7).
Estimation of error. Image processing errors were indicated above. We propose the following formula for the relative error of image processing [10,23]:
where is the calculated image and is the exact image. Formula (37), as applied to images, is more convenient and intuitive than the well-known formula for the PSNR error [7], which is widely used in radio engineering, acoustics, and other fields of knowledge. The formula for PSNR uses the logarithm of the intensities and is effective when the range of intensities is large. If the range of intensities is small, as in images, then it is advisable to use the intensities directly, as in Formula (37). Indeed, if, for example, the error according to (37) is equal to δrel = 0.0482 (see caption to Figure 5), then this means that the relative error of image reconstruction is equal to 4.82%, and this value does not depend on the system of units w.
To implement Formula (37), the m-function rmsd.m was developed. Note that Formula (37) can only be applied in the case when it is known, for example, for the galaxy M51.
11. Suppression of the Gibbs Effect in Images
In the inverse problem of restoring damaged images, the Gibbs effect (“ringing-type” effect), may also occur (see Figure 6b).

Figure 6.
The result of processing a smeared image of runners. (a) Image g 123 × 400 px with strong smear; (b) reconstructed image w 123 × 380 using inverse filtering with the Gibbs effect.
Figure 6a shows a horizontally smeared image of runners (file Bearings.m on MatLab) with an image size of 123 × 400 and a smear value of Δ = 20 px. Figure 6b reveals the result of inverse filtering (cf. [28] (p. 172)). We see not only a fuzzy (unstable) image due to the incorrectness of the problem but also strong edge and internal Gibbs effects.
The Gibbs effect is due to the fact that in the case where the function gy(x) (example in Figure 6a) has discontinuities at the edges and inside the image, such as the Heaviside function (step function, square wave, or gate function). Thus, this leads to the appearance of fluctuations, like the sinc function, under the use of DFT (see Figure 6b).
To suppress these spurious fluctuations, the function edgetaper.m in the MatLab system can be used [28] (p. 172), which diffuses and smooths the image edges. However, as modeling has shown, this function diffuses and smooths the edges insufficiently, and the following scheme with the introduction of diffused edges of the image gives a more effective result [16] (p. 84):
where j is the row number, i is the horizontal point number in the jth row and
The diffused edges of the smeared image 6a are shown in Figure 7a in accordance with Formulas (38) and (39). We see that the intensities beyond the image edges decreased smoothly to zero, which is necessary to suppress the Gibbs effect. Figure 7b demonstrates the result of image restoration by the PFW method using relations (7) and (12) at K = 10–5. In this case, the amount of smear Δ is determined by the “spectral method”. We can see that the image was restored without the Gibbs effect.

Figure 7.
The result of processing smeared images with diffusion. (a) Image g 123 × 420 with smear and diffusion of edges; (b) reconstructed image w 123 × 400 without the Gibbs effect.
12. Conclusions
1. The task of eliminating the resection (damage, distortion, breakage) of images (smearing, defocusing, noising) by mathematical methods as examples of image galaxies and runners is solved. The types and parameters of damage were estimated using the original “spectral method”. After their evaluation, a restoration of damaged images was performed by solving integral equations by the stable methods of parametric Wiener filtering (PWF) or Tikhonov regularization (TR).
2. To refine the image parameters of galaxy M100 (filtering parameters K and regularization α, error δrel, etc.), a training image of the galaxy M51 with a known exact image and parameters close to M100 is taken (see Figure 1d).
3. The impulse noise in the image is eliminated by the Tukey median filter, which distorts the image itself, as well as by the more accurate Gonzalez adaptive filter and by our even more accurate, image-free modified filter.
4. To suppress the Gibbs effect in an image, a method for diffusing the image edges is proposed, as opposed to the edgetaper.m function in the MatLab system, which weakly diffuses the image edges.
5. The results of this paper can be used to improve the quality of image restoration when they contain smear, defocus, and/or noise. This will increase the resolution of optical image recording devices (film cameras, tracking systems, cameras, microscopes, and others).
6. The “spectral method” has been tested on a large number of examples; namely, images of people, cars, airplanes, and planets. The results have been published in J. Opt. Tech. [8], Computers, CEUR [23], and books [10,16], and presented at scientific conferences.
Author Contributions
Conceptualization, V.S. and N.R.; Writing—original draft, V.S. and N.R. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by a grant from the Mega-Faculty of Computer Technologies and Control (MFCTC), ITMO, project No. 620164—Methods of artificial intelligence of cyber-physical systems.
Data Availability Statement
The data presented in this study are openly available.
Conflicts of Interest
The authors declare that there are no conflicts of interest.
References
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing; Prentice Hall: Saddle River, NJ, USA, 2002; 793p. [Google Scholar]
- Sidorov, D. Integral Dynamical Models: Singularities, Signals and Control; World Sci. Series: Singapore; London, UK, 2014; 343p. [Google Scholar]
- Boikov, I.B.; Kravchenko, M.V.; Kryuchko, V.I. The approximate method for reconstructing the potential fields. Izvestiya. Phys. Solid Earth 2010, 46, 339–349. [Google Scholar] [CrossRef]
- Yushikov, V.S. Blind Deconvolution—Automatic Restoration of Blurred Images. Available online: https://habr.com/ru/post/175717/ (accessed on 1 October 2023).
- Donatelli, M.; Estatico, C.; Martinelli, A.; Serra-Capizzano, S. Improved image deblurring with antireflective boundary conditions and re-blurring. Inverse Probl. 2006, 22, 2035–2053. [Google Scholar] [CrossRef]
- Kabanikhin, S.I. Inverse and Ill-Posed Problems: Theory and Applications; Walter de Gruyter: Berlin, Germany, 2011; 459p. [Google Scholar]
- Hansen, P.C.; Nagy, J.G.; O’Leary, D.P. Deblurring Images: Matrices, Spectra, and Filtering; SIAM: Philadelphia, PA, USA, 2006; 130p. [Google Scholar]
- Sizikov, V.S. Spectral method for estimating the point-spread function in the task of eliminating image distortions. J. Optical Technol. 2017, 84, 95–101. [Google Scholar] [CrossRef]
- Gruzman, I.S.; Kirichuk, V.S.; Kosykh, V.P.; Peretyagin, G.I.; Spektor, A.A. Digital Image Processing in Information Systems; Novosibirsk NGTU-Verlag: Novosibirsk, Russia, 2002; 352p. (In Russian) [Google Scholar]
- Sizikov, V.S. Direct and Inverse Problems of Image Reconstruction, Spectroscopy and Tomography with MatLab; Lan’: St. Petersburg, Russia, 2017; 412p. (In Russian) [Google Scholar]
- Kumar, S.; Kumar, P.; Gupta, M.; Nagawat, A.K. Performance comparison of median and wiener filter in image de-noising. Intern. J. Comp. Appl. 2010, 12, 27–31. [Google Scholar] [CrossRef]
- Yan, L.; Liu, H.; Zhong, S.; Fang, H. Semi-blind spectral deconvolution with adaptive Tikhonov regularization. Appl. Spectrosc. 2012, 66, 1334–1346. [Google Scholar] [CrossRef] [PubMed]
- Solodusha, S.V. Numerical solution of a class of systems of Volterra polynomial equations of the first kind. Numer. Analysis Appl. 2018, 11, 89–97. [Google Scholar] [CrossRef]
- Solodusha, S.V. Methods for Constructing Integral Models of Dynamic Systems. Ph.D. Thesis, ISEM SS RAS, Irkutsk, Russia, 2019; 44p. (In Russian). [Google Scholar]
- Egoshkin, N.A.; Eremeev, V.V. Correction smear images in the space surveillance system Earth. Digit. Signal Process. 2010, 4, 28–32. (In Russian) [Google Scholar]
- Sizikov, V.S. Inverse Applied Problems and MatLab; Lan’: St. Petersburg, Russia, 2011; 256p. (In Russian) [Google Scholar]
- Petrov, Y.P.; Sizikov, V.S. Well-Posed, Ill-Posed, and Intermediate Problems with Applications; VSP: Leiden, The Netherlands; Boston, MA, USA, 2005; 234p. [Google Scholar]
- Protasov, K.T.; Belov, V.V.; Molchunov, N.V. Image reconstruction with pre-estimation of the point-spread function. Opt. Atmos. Ocean 2000, 13, 139–145. [Google Scholar]
- Voskoboinikov, Y.E. A combined nonlinear contrast image reconstruction algorithm under inexact point-spread function. Optoel. Instrum. Data Proces. 2007, 43, 489–499. [Google Scholar] [CrossRef]
- Antonova, T.V. Methods of identifying a parameter in the kernel of the first kind equation of the convolution type on the class of functions with discontinuities. Sib. Zh. Vychisl. Mat. 2015, 18, 107–120. [Google Scholar] [CrossRef]
- Bahmanpour, M.; Kajani, M.T.; Maleki, M. Solving Fredholm integral equations of the first kind using Müntz wavelets. Appl. Numer. Math. 2019, 143, 159–171. [Google Scholar] [CrossRef]
- Wazwaz, A. The regularization method for Fredholm integral equations of the first kind. Comp. Mathem. Appl. 2011, 61, 2981–2986. [Google Scholar] [CrossRef]
- Sizikov, V.; Loseva, P.; Medvedev, E.; Sharifullin, D.; Dovgan, A.; Rushchenko, N. Removal of complex image distortions via solving integral equations using the “spectral method”. CEUR Workshop Proc. 2020, 2893, 11. [Google Scholar]
- Fergus, R.; Singh, B.; Hertzmann, A.; Roweis, S.T.; Freeman, W.T. Removing camera shake from a single photograph. ACM Trans. Graph. 2006, 25, 787–794. [Google Scholar] [CrossRef]
- Cho, S.; Lee, S. Fast motion deblurring. ACM Trans. Graph. 2009, 28, 145. [Google Scholar] [CrossRef]
- Voskoboinikov, Y.E.; Litasov, V.A. A stable image reconstruction algorithm for inexact point-spread function. Avtometriya (Optoel. Instrum. Data Proces) 2006, 42, 3–15. [Google Scholar]
- Bishop, T.E.; Babacan, S.D.; Amizic, B.; Katsaggelos, A.K.; Chan, T.; Molina, R. Blind image deconvolution: Problem formulation and existing approaches. In Blind Image Deconvolution: Theory and Applications; Campisi, P., Egiazarian, K., Eds.; CRC Press: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2007; pp. 1–41. [Google Scholar]
- Gonsales, R.C.; Woods, R.E.; Eddins, S.L. Digital Image Processing Using MATLAB; Prentice Hall: Saddle River, NJ, USA, 2004; 609p. [Google Scholar]
- Hansen, P.C. Discrete Inverse Problems: Insight and Algorithms; SIAM: Philadelphia, PA, USA, 2010; 213p. [Google Scholar]
- Jähne, B. Digital Image Processing; Springer: Berlin, Germany, 2005; 584p. [Google Scholar]
- Bracewell, R.N. The Hartley Transform; Oxford University Press: New York, NY, USA, 1986; 168p. [Google Scholar]
- Korn, G.A.; Korn, T.M. Mathematical Handbook for Scientists and Engineers, 2nd revision ed.; Dover Publications: London, UK, 2000; 1152p. [Google Scholar]
- Arefieva, M.V.; Sysoev, A.F. Fast regularizing algorithms for digital image restoration. Calculate. Methods Program. 1983, 39, 40–55. (In Russian) [Google Scholar]
- Chaisson, E.J. Early results from the Hubble space telescope. Sci. Am. 1992, 266, 44–53. [Google Scholar] [CrossRef]
- Saïsse, M.; Rousselet, K.; Lazarides, E. Modeling technique for the Hubble space telescope wave-front deformation. Appl. Opt. 1995, 34, 2278–2283. [Google Scholar] [CrossRef] [PubMed]
- Pronina, V.S. Image Recovery Using Trained Optimization-Neural Network Algorithms. Ph.D. Thesis, Skolkogo Institute, Moscow, Russia, 2023; 36p. (In Russian). [Google Scholar]
- Narayanan, S.A.; Arumugam, G.; Bijlani, K. Trimmed median filters for salt and pepper noise removal. Intern. J. Emerging Trends Technol. Comp. Sci. 2013, 2, 35–40. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).