A New 3D Chaotic Attractor in Gene Regulatory Network

Abstract

This paper introduces a new 3D chaotic attractor in a gene regulatory network. The proposed model has eighteen parameters. Formulas for characteristic numbers of critical points for three-dimensional systems were considered. We show that the three equilibrium points of the new chaotic 3D system are unstable and deduce that the three-dimensional system exhibits chaotic behavior. The possible outcomes of this 3D model were compared with the results of the Chua circuit. The bifurcation structures of the proposed 3D system are investigated numerically, showing periodic solutions and chaotic solutions. Lyapunov exponents and Kaplan-Yorke dimension are calculated. For calculations, the Wolfram Mathematica is used.

1. Introduction

Deterministic chaos of nonlinear dynamic systems is not chaos, usually understood as complete disorganization and randomness of events; modern ideas about chaos are to some extent closer to the original ancient Greek ones: “chaos” like a boundless disordered mass from which everything that exists arose.

Chaos theory is a branch of science that deals with complex systems and their behavior. Meteorologist Edward Lorenz made a major contribution to chaos theory [1]. During the 1960s, Lorenz developed a computer program that simulated the motion of air masses within the Earth’s atmosphere [2]. The Lorenz model demonstrated a susceptibility to initial conditions [3]. Tiny variations in input data resulted in significant discrepancies in outcomes over time. This reliance on the starting conditions was termed chaos. Lorenz coined a famous feature of chaos called the “butterfly effect”, the notion that a butterfly stirring the air in Hong Kong today can transform storm systems in New York next month [4]. After Lorenz’s studies, many chaotic systems have been presented to the literature Rossler system [5], Chen system [6], LU system [7], Sprott system [8] and others. For a long time, chaos theory was considered a kind of mathematical abstraction that had no confirmation in real conditions. Now it has applications in various scientific disciplines, including physics [9], biology (in the study of uneven heart rate and an uneven number of diseases) [10], meteorology, economics [11], finance [12], geology [13], computer science, engineering, algorithmic trading, politics [14], population dynamics [15], robotics [16], philosophy [17] and mathematics.

Chaos is a complex phenomenon defying easy classification or identification. Although there exists no universally accepted definition for chaos, the solutions of chaotic systems typically exhibit the characteristics [18].

Characteristics of chaos:

• chaotic behavior is characterized by the presence of an attractor to which all nearby solutions tend to converge over time, provided there is ample time for the process [19];
• a common feature of chaotic solutions lies in the geometric structure of their attractors. These attractors often exhibit intricate and unconventional shapes, characterized by a twisted and “strange” appearance. This strangeness is indicative of a fractional (fractal) dimension, although it’s important to note that this isn’t always the case [19];
• sensitivity to initial conditions [18].

Nonlinear ordinary differential equations are the most widespread formalism for modeling genetic regulatory networks [20]. The main contributions of the present study are summarized as follows:

• formulas for characteristic numbers of critical points for three-dimensional systems were considered;
• the new chaotic attractor is obtained;
• the three-dimensional system (7) can have attractors of various kinds;
• the irregular behavior of solutions near the chaotic attractor is conceivable and may manifest within a narrow parameter range.

2. Materials and Methods

2.1. Chua Circuit

Leon O. Chua is a renowned electrical engineer and computer scientist who has made significant contributions to the fields of electronics, circuits, and nonlinear science. He was born on 28 June 1936, in Manila, Philippines. He is a professor in the Electrical Engineering and Computer Sciences department at the University of California, Berkeley. The professor’s scientific projects are related to cellular neural network technologies, bifurcation theory, nonlinear dynamics, and chaos theory. Leon Chua aimed to show that it was possible to create chaos. For this purpose, in 1983 he assembled an electrical circuit [21]. It is a simple oscillatory circuit demonstrating a series of bifurcations and a transition to chaos. In the simple case, Chua’s equations can be written in the following form:

$$\left\{\begin{array}{c}{\displaystyle \frac{dx}{d\tau }=\alpha (y-x-f\left(x\right)),}\hfill \\ \\ {\displaystyle \frac{dy}{d\tau }=x-y+z,}\hfill \\ \\ {\displaystyle \frac{dz}{d\tau }=-\beta y,}\hfill \end{array}\right.$$

(1)

$$f\left(x\right)=\left\{\begin{array}{c}{\displaystyle bx+a-b,x\ge 1,}\hfill \\ {\displaystyle ax,\left|x\right|\le 1,}\hfill \\ {\displaystyle bx-a+b,x\le -1,}\hfill \end{array}\right.$$

(2)

where $x,y,z$-phase variables, $\alpha ,\beta ,a,b$-parameters $(\alpha >0,\beta >0,a<0,b<0)$. Consider

$$a=-\frac{8}{7};b=-\frac{5}{7},\alpha =9,\beta =14.$$

(3)

We will replace the piecewise linear function with a cubic polynomial [22].

$$f\left(x\right)=\frac{1}{16}{x}^3-\frac{7}{6}x.$$

(4)

The initial conditions are

$$x\left(0\right)=0.1;y\left(0\right)=0.2;z\left(0\right)=1.$$

(5)

The nullclines are depicted in Figure 1.

The system possesses precisely three critical points, determined and illustrated as the intersection points of the nullclines in Figure 1. There are three critical points at $(1.633,0,-1.633)$, $(0,0,0)$ and $(-1.633,0,1.633)$. Linearization around these points provides us with the characteristic numbers $\lambda$. The characteristic numbers are considered in

Table 1. Characteristic numbers.

The Critical Point	${\mathit{\lambda }}_1$	${\mathit{\lambda }}_2$	${\mathit{\lambda }}_3$
$(1.633,0,-1.633)$	−4.3563	0.1782 − 3.1315 i	0.1782 + 3.1315 i
$(0,0,0)$	2.4730	−0.9865 − 2.7734 i	−0.9865 − 2.7734 i
$(-1.633,0,1.633)$	−4.3563	0.1782 − 3.1315 i	0.1782 + 3.1315 i

.

The type of two critical points is a saddle-focus with one-dimensional stable and two-dimensional unstable manifolds. The type of critical point $(0,0,0)$ is a saddle-focus with two-dimensional stable and one-dimensional unstable manifolds. The chaotic attractor is depicted in Figure 2 and the graph of solutions is depicted in Figure 3.

In the equilibrium state at the origin, one root is real and positive, indicating the direction in which the initial disturbance will grow. A pair of complex conjugate roots with a negative real part signifies the presence of rotational motion and twisting of the trajectory towards a singular critical point in the plane of rotation. For each of the other two equilibrium states, the motion is unstable in the plane of rotation (the real parts of the complex conjugate pair are greater than zero). At the same time, there exists a direction in which the phase trajectory approaches the critical point.

Lyapunov exponents after 5000 steps were $L_1=0.3329$, $L_2=-0.0012$, and $L_3=-2.9923$. The largest Lyapunov exponent was greater than 0 as shown in Figure 4.

The Lyapunov exponents characterize the exponential expansion or contraction of phase-space entities, such as one-dimensional lengths, two-dimensional areas, and three-dimensional volumes. The largest Lyapunov exponent denoted as $L{E}_1$ characterizes the average rate of divergence over time between two adjacent trajectories separated by a specific distance $\delta$. The sum of the first n Lyapunov exponents describes the divergence or convergence rate of an n-dimensional phase-space volume [23]. The paper [24] states that the presence of at least one positive Lyapunov exponent leads to the divergence of neighboring trajectories, classifying the phase-space motion as “chaotic”, but the positivity of the calculated senior Lyapunov’s exponent is not the criteria of occurrence in the system of chaotic dynamics [25,26]. The computation of the full Lyapunov exponent spectrum is a rather mathematically complicated issue. Computations are performed using Wolfram Mathematica. For Lyapunov exponents calculation the package “lce.m for Mathematica” was used [27].

Meanwhile, according to the Kaplan–Yorke formula,

$$D_{KY}=j+\frac{1}{|L_{j+1}|}\sum _{i=1}^j{L}_i=2+\frac{L_1+L_2}{|L_3|}=2.1109$$

(6)

the fractal dimension also further verifies that the new system has a chaotic behavior [28]. For a dissipative dynamical system, the sum of all Lyapunov exponents should equate to a negative value [29]. Only dissipative dynamical systems have attractors [30].

2.2. 3D Gene Regulatory System

Consider the system

$$\left\{\begin{array}{c}\hfill {\displaystyle \frac{dx}{dt}=\frac{1}{1+e^{-{\mu }_1(w_{11}x+w_{12}y+w_{13}z-{\theta }_1)}}-v_{1}x,}\hfill \\ \\ \hfill {\displaystyle \frac{dy}{dt}=\frac{1}{1+e^{-{\mu }_2(w_{21}x+w_{22}y+w_{23}z-{\theta }_2)}}-v_{2}y,}\hfill \\ \\ \hfill {\displaystyle \frac{dz}{dt}=\frac{1}{1+e^{-{\mu }_3(w_{31}x+w_{32}y+w_{33}z-{\theta }_3)}}-v_{3}z,}\hfill \end{array}\right.$$

(7)

where ${\mu }_i$, ${\theta }_i$ and $v_i$ are the parameters, $w_{ij}$ are the coefficients of the so-called regulatory matrix

$$W=\left(\begin{array}{ccc}{w}_{11}& w_{12}& w_{13}\\ w_{21}& w_{22}& w_{23}\\ w_{31}& w_{32}& w_{33}\end{array}\right).$$

(8)

The parameters of the GRN have the following biological interpretations:

• $v_i$—degradation of the i-th gene expression product;
• $w_{ij}$—the connection weight or strength of control of gene j on gene i. Positive values of $w_{ij}$ signify activating influences, whereas negative values denote repressing influences;
• ${\theta }_i$—The impact of external stimuli on gene i is reflected in its ability to modulate the gene’s responsiveness to activating or repressing factors [31].

The nullclines and the critical points for the system are defined by the relations

$$\left\{\begin{array}{c}\hfill {\displaystyle x=\frac{1}{v_1}\frac{1}{1+e^{-{\mu }_1(w_{11}x+w_{12}y+w_{13}z-{\theta }_1)}},}\hfill \\ \\ \hfill {\displaystyle y=\frac{1}{v_2}\frac{1}{1+e^{-{\mu }_2(w_{21}x-w_{22}y+w_{23}z-{\theta }_2)}},}\hfill \\ \\ \hfill {\displaystyle z=\frac{1}{v_3}\frac{1}{1+e^{-{\mu }_2(w_{21}x+w_{22}y+w_{33}z-{\theta }_3)}}.}\hfill \end{array}\right.$$

The sigmoidal function $f\left(t\right)=\frac{1}{1+e^{-\mu }}$ is used in (7). Sigmoidal functions exhibit a continuous increase from zero to one and possess a solitary inflection point. While various sigmoidal functions exist, the one mentioned above is particularly suitable for analysis and visualization [32]. Such systems were considered in [20,33,34,35].

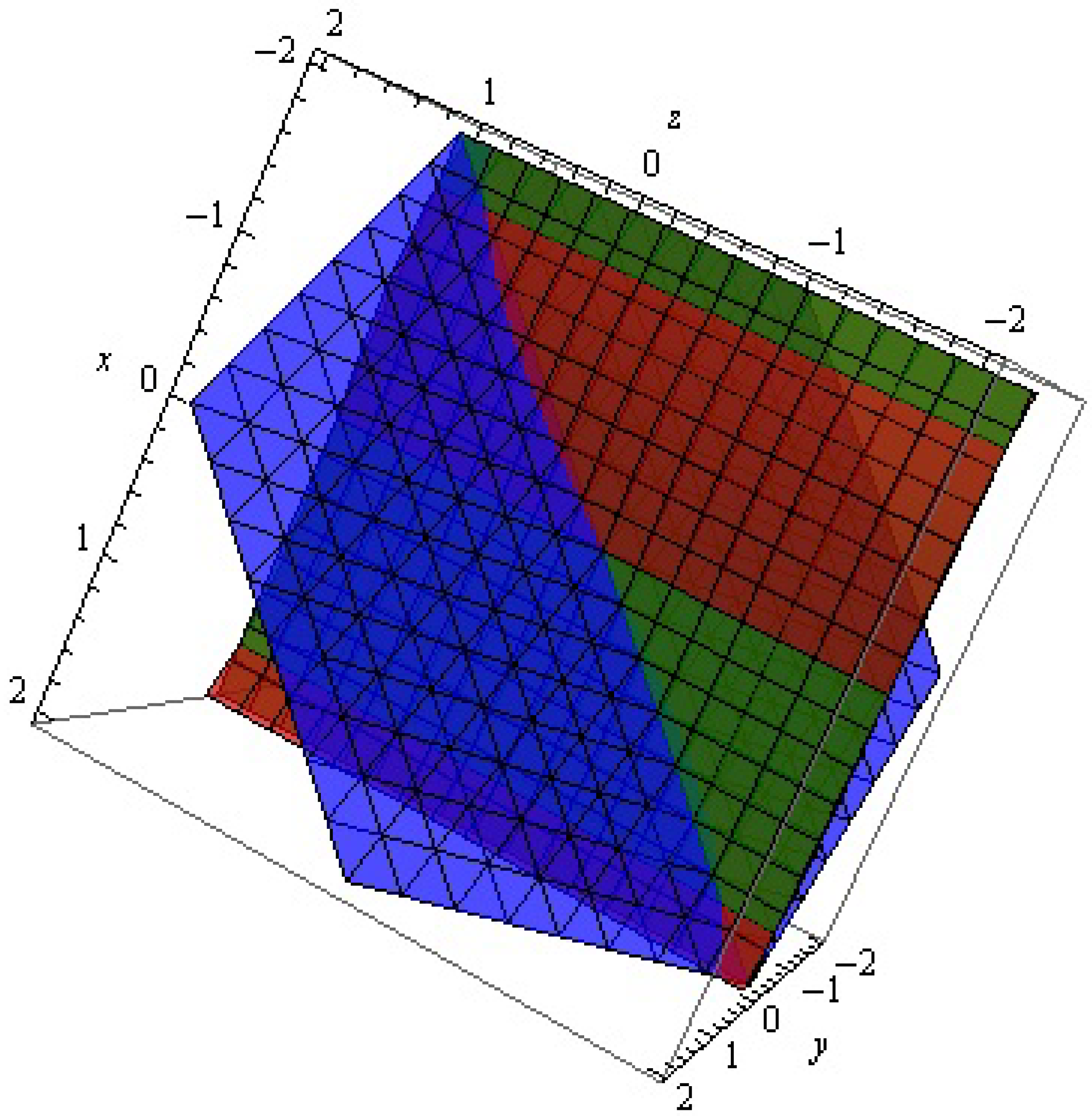
2.3. Linearized System

The linearized system for any critical point $(x^{*},y^{*},z^{*})$

$$\left\{\begin{array}{c}\hfill {\displaystyle u_1^{\prime }=-v_1{u}_1+{\mu }_1{w}_{11}{g}_1{u}_1+{\mu }_1{w}_{12}{g}_1{u}_2+{\mu }_1{w}_{13}{g}_1{u}_3,}\hfill \\ \hfill {\displaystyle u_2^{\prime }=-v_2{u}_2+{\mu }_2{w}_{21}{g}_2{u}_1+{\mu }_2{w}_{22}{g}_2{u}_2+{\mu }_2{w}_{23}{g}_2{u}_3,}\hfill \\ \hfill {\displaystyle u_3^{\prime }=-v_3{u}_3+{\mu }_3{w}_{31}{g}_3{u}_1+{\mu }_3{w}_{32}{g}_3{u}_2+{\mu }_3{w}_{33}{g}_3{u}_3,}\hfill \end{array}\right.$$

where

$$g_1=\frac{e^{-{\mu }_1(w_{11}{x}^{*}+w_{12}{y}^{*}+w_{13}{z}^{*}-{\theta }_1)}}{{[1+e^{-{\mu }_1(w_{11}{x}^{*}+w_{12}{y}^{*}+w_{13}{z}^{*}-{\theta }_1)}]}^2},$$

(9)

$$g_2=\frac{e^{-{\mu }_2(w_{21}{x}^{*}+w_{22}{y}^{*}+w_{23}{z}^{*}-{\theta }_2)}}{{[1+e^{-{\mu }_2(w_{21}{x}^{*}+w_{22}{y}^{*}+w_{23}{z}^{*}-{\theta }_2)}]}^2},$$

(10)

$$g_3=\frac{e^{-{\mu }_3(w_{31}{x}^{*}+w_{32}{y}^{*}+w_{33}{z}^{*}-{\theta }_3)}}{{[1+e^{-{\mu }_3(w_{31}{x}^{*}+w_{32}{y}^{*}+w_{33}{z}^{*}-{\theta }_3)}]}^2}.$$

(11)

One has

$$A-\lambda I=\left|\begin{array}{ccc}{\mu }_1{w}_{11}{g}_1-v_1-\lambda & {\mu }_1{w}_{12}{g}_1& {\mu }_1{w}_{13}{g}_1\\ {\mu }_2{w}_{21}{g}_2& {\mu }_2{w}_{22}{g}_2-v_2-\lambda & {\mu }_2{w}_{23}{g}_2\\ {\mu }_3{w}_{31}{g}_3& {\mu }_3{w}_{32}{g}_3& {\mu }_3{w}_{33}{g}_3-v_3-\lambda \end{array}\right|$$

and the characteristic equation is

$$\det |A-\lambda I|=-{\lambda }^3+{\lambda }^2(-v_1-v_2-v_3+{\mu }_1{w}_{11}{g}_1+{\mu }_2{w}_{22}{g}_2+{\mu }_3{w}_{33}{g}_3)+\lambda (g_1{v}_3{\mu }_1{w}_{11}+$$

$$+{\mu }_2{w}_{22}{g}_2{v}_3+g_1{g}_2{w}_{21}{\mu }_1{\mu }_2{w}_{12}-g_1{g}_2{w}_{11}{w}_{22}{\mu }_1{\mu }_2+g_1{g}_3{w}_{31}{w}_{13}{\mu }_1{\mu }_3-$$

$$-g_1{g}_3{w}_{11}{w}_{33}{\mu }_1{\mu }_3+g_2{g}_3{w}_{32}{w}_{23}{\mu }_2{\mu }_3-g_2{g}_3{w}_{22}{w}_{33}{\mu }_2{\mu }_3-v_1(v_2+v_3-g_2{w}_{22}{\mu }_2-g_3{w}_{33}{\mu }_3)+$$

$$+v_2(-v_3+g_1{w}_{11}{\mu }_1+g_3{w}_{33}{\mu }_3))+v_1(v_2(-v_3+g_3{w}_{33}{\mu }_3)+g_2{\mu }_2(v_3{w}_{22}+g_3{w}_{32}{w}_{23}{\mu }_3-$$

$$g_3{w}_{22}{w}_{33}{\mu }_3\left)\right)+g_1{\mu }_3(v_2(v_3{w}_{11}+g_3(w_{31}{w}_{13}-w_{11}{w}_{33}){\mu }_3)+g_2{\mu }_2(v_3(w_{21}{w}_{12}-w_{11}{w}_{22})+$$

$$+g_3(-w_{31}{w}_{22}{w}_{13}+w_{21}{w}_{32}{w}_{13}+w_{31}{w}_{12}{w}_{23}-w_{11}{w}_{32}{w}_{23}-w_{21}{w}_{12}{w}_{33}+w_{11}{w}_{22}{w}_{33}){\mu }_3\left)\right)=0.$$

The characteristic equation can be rewritten as

$$-{\lambda }^3+A{\lambda }^2+B\lambda +C=0,$$

(12)

where

$$A=-(v_1+v_2+v_3)+g_1{w}_{11}{\mu }_1+g_2{w}_{22}{\mu }_2+g_3{w}_{33}{\mu }_3,$$

$$\begin{array}{cc}\hfill B& ={\mu }_1{\mu }_2{w}_{31}{w}_{13}{g}_1{g}_3-{\mu }_2{\mu }_3{w}_{32}{w}_{23}{g}_2{g}_3+{\mu }_1{\mu }_2{w}_{21}{w}_{12}{g}_1{g}_2\hfill \\ \hfill & -({\mu }_2{w}_{22}{g}_2-v_2)({\mu }_3{w}_{33}{g}_3-v_3)-({\mu }_1{w}_{11}{g}_1-v_1)({\mu }_3{w}_{33}{g}_3-v_3)\hfill \\ \hfill & -({\mu }_1{w}_{11}{g}_1-v_1)({\mu }_2{w}_{22}{g}_2-v_2),\hfill \end{array}$$

$$\begin{array}{cc}\hfill C& =({\mu }_1{w}_{11}{g}_1-v_1)({\mu }_2{w}_{22}{g}_2-v_2)({\mu }_3{w}_{33}{g}_3-v_3)+{\mu }_1{\mu }_2{\mu }_3{w}_{21}{w}_{32}{w}_{23}{g}_1{g}_2{g}_3\hfill \\ \hfill & +{\mu }_1{\mu }_2{\mu }_3{w}_{31}{w}_{12}{w}_{23}{g}_1{g}_2{g}_3-{\mu }_1{\mu }_3{w}_{31}{w}_{13}{g}_1{g}_3({\mu }_2{w}_{22}{g}_2-v_2)\hfill \\ \hfill & -{\mu }_2{\mu }_3{w}_{32}{w}_{23}{g}_2{g}_3({\mu }_1{w}_{11}{g}_1-v_1)-{\mu }_1{\mu }_2{w}_{21}{w}_{12}{g}_1{g}_2({\mu }_3{w}_{33}{g}_3-v_3).\hfill \end{array}$$

Theorem 1.

The vector field $(f_1(x,y,z),f_2(x,y,z),f_3(x,y,z)),$ where $f_1,$$f_2$ and $f_3$ are the right sides of the equations in (7), is directed inward on the boundary of the domain $Q_3:=\{(x,y,z):0<x<\frac{1}{v_1},0<y<\frac{1}{v_2},0<z<\frac{1}{v_3}\}.$

Proof of Theorem 1.

Take one of faces of the parallelepiped $Q_3$, for example, $x=0$. The vector field there in the x direction is $f_1-v_1$, $x=f>0$. Take face ${\displaystyle x=\frac{1}{v_1}}$. The vector field in the x direction is $f_1-v_1$, $x=f_1-v_1$, ${\displaystyle \frac{1}{v_1}=f_1-1<0}$. In both cases, the vector field along the x axis is directed inside $Q_3$. Similarly, other faces of $Q_3$ can be considered. □

Theorem 2.

System (7) has at least one equilibrium (critical point). All equilibria are located in the open box $Q_3:=\{(x,y,z):0<x<\frac{1}{v_1},0<y<\frac{1}{v_2},0<z<\frac{1}{v_3}\}.$

This follows from the result of the mapping of a topological ball into itself. The second assertion follows from the fact that nullclines meet and can intersect only in $Q_3$.

3. Results

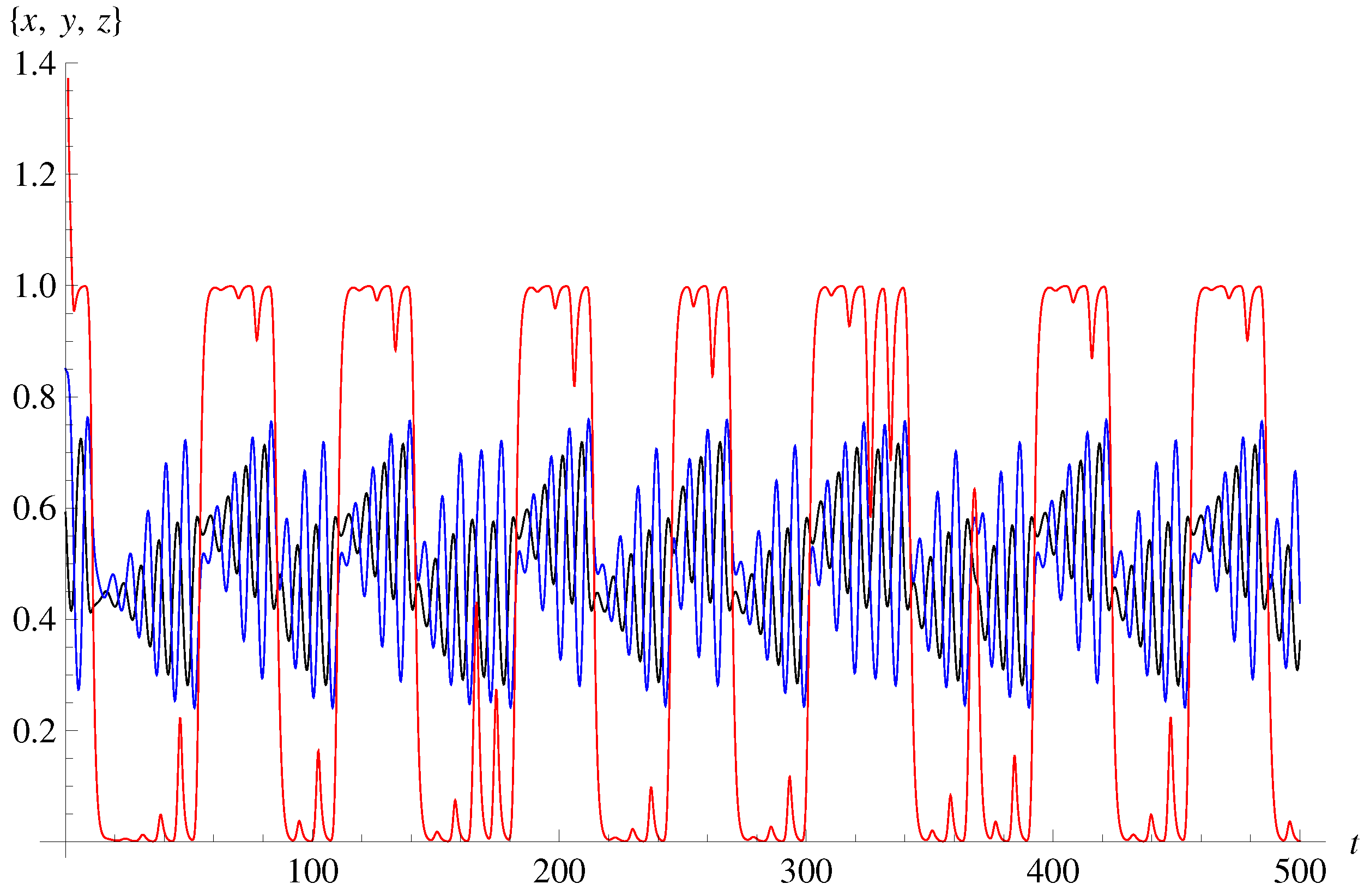
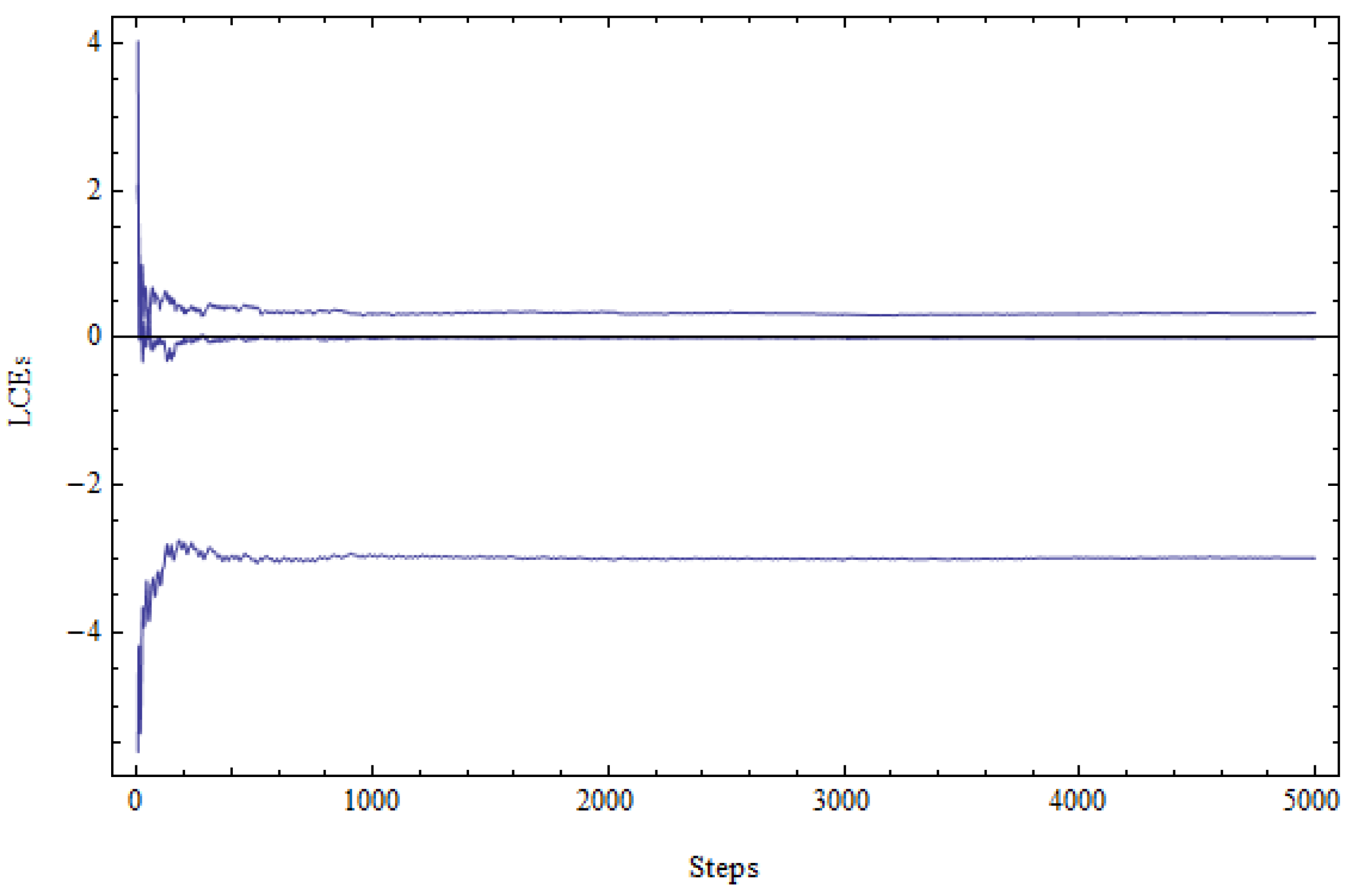
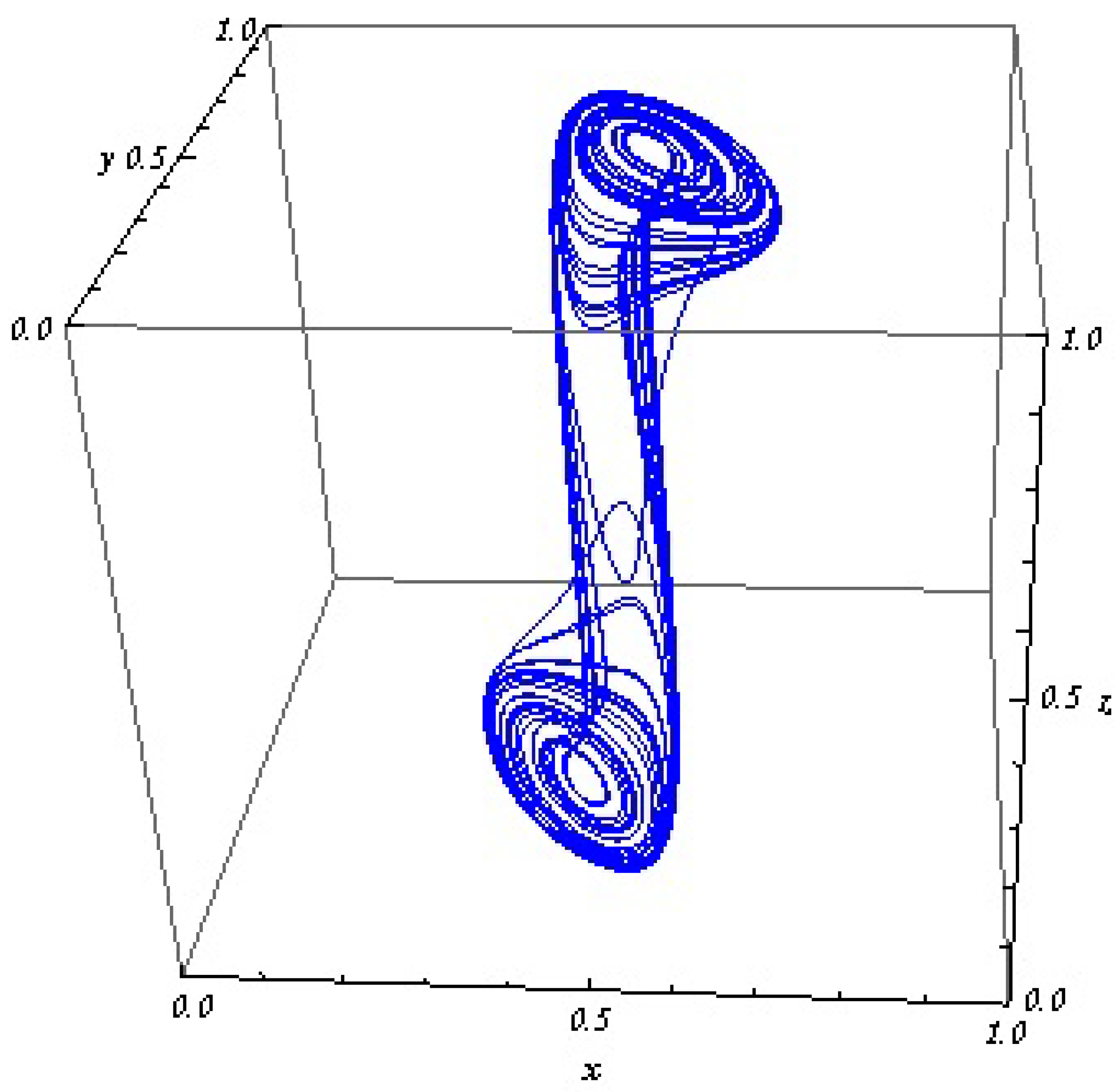
3.1. 3D Chaotic Attractor

The system (7) with the matrix

$$W=\left(\begin{array}{ccc}0.06& -0.825& 0.19\\ 1.915& 1.76& -0.32\\ 3.7& 0.128& 0.985\end{array}\right)$$

(13)

and ${\mu }_1=4,{\mu }_2=5.02,{\mu }_3=8$, $v_1=v_2=v_3=1$ and

$${\theta }_1=\frac{w_{11}+w_{12}+w_{13}}{2},$$

$${\theta }_2=\frac{w_{21}+w_{22}+w_{23}}{2},$$

$${\theta }_3=\frac{w_{31}+w_{32}+w_{33}}{2}$$

has three critical points. Linearization around these points provides us with the characteristic numbers $\lambda$.

The initial conditions are

$$x\left(0\right)=0.592;y\left(0\right)=0.85;z\left(0\right)=2.$$

(14)

The nullclines are depicted in Figure 5.

The characteristic equation for critical points is (12). The coefficients of characteristic Equation (12) are considered in

Table 2. Coefficients of characteristic Equation (12).

The Critical Point	A	B	C
$(0.4398,0.4545,0.0032)$	−0.725248	−0.557956	−0.787449
$(0.5,0.5,0.5)$	1.2388	0.195983	1.59353
$(0.5602,0.5455,0.9968)$	−0.725248	−0.557956	−0.787449

.

Characteristic numbers are considered in

Table 3. Characteristic numbers.

The Critical Point	${\mathit{\lambda }}_1$	${\mathit{\lambda }}_2$	${\mathit{\lambda }}_3$
$(0.4398,0.4545,0.0032)$	−0.9780	0.12638 − 0.888361 i	0.12638 + 0.888361 i
$(0.5,0.5,0.5)$	1.82477	−0.292985 − 0.887376 i	−0.292985 + 0.887376 i
$(0.5602,0.5455,0.9968)$	−0.9780	0.12638 − 0.888361 i	0.12638 + 0.888361 i

.

The type of two critical points is a saddle-focus with one-dimensional stable and two-dimensional unstable manifolds. The type of critical point $(0.5,0.5,0.5)$ is a saddle-focus with two-dimensional stable and one-dimensional unstable manifolds. The chaotic attractor is depicted in Figure 6 and Figure 7. The graph of solutions is depicted in Figure 8 and Figure 9.

Lyapunov exponents after 5000 steps were $L_1=0.0398$, $L_2=-0.0026$ and $L_3=-0.7665$. The largest Lyapunov exponent was greater than 0 as shown in Figure 10.

3.2. Bifurcation

The bifurcation theory of differential equation systems, first introduced in the works of Jules Henri Poincare (1854–1912), elucidates qualitative, abrupt alterations in the phase portraits of these systems as their parameters undergo continuous and smooth changes [36]. We take $w_{23}$ as a bifurcation parameter (that is, the third element in the second row) in the regulatory matrix (13). Computations are performed using Wolfram Mathematica. Results of calculations for the system (7) with regulatory matrix (13), changing the parameter $w_{23}$. are considered in

Table 4. Results of calculations for the system (7) with regulatory matrix (13), changing the parameter $w_{23}$.

${\mathit{w}}_{23}$	$\mathit{x}{}^{*},\mathit{y}{}^{*},\mathit{z}{}^{*}$	${\mathit{\lambda }}_1$	${\mathit{\lambda }}_2$	${\mathit{\lambda }}_3$
−0.569	(0.2673, 0.6735, 0.00002)	−0.9998	−0.0051 − 0.6838 i	−0.0051 − 0.6838 i
	(0.5, 0.5, 0.5)	2.0836	−0.4224 − 1.2107 i	−0.4224 + 1.2107 i
	(0.7327, 0.3265, 0.99998)	−0.9998	−0.0051 − 0.6838 i	−0.0051 + 0.6838 i
−0.5	(0.3190, 0.6015, 0.0001)	−0.9990	0.0849 − 0.7646 i	0.0849 + 0.7646 i
	(0.5, 0.5, 0.5)	−0.3913	−0.3913 − 1.1361	−0.3913 + 1.1361
	(0.6810, 0.3985, 0.9999)	−0.9990	0.0849 − 0.7646 i	0.0849 + 0.7646 i
−0.4	(0.3885, 0.5144, 0.0007)	−0.9941	0.1319 − 0.8505 i	0.1319 + 0.8505 i
	(0.5, 0.5, 0.5)	1.9197	−0.3404 − 1.0104 i	−0.3404 + 1.0104 i
	(0.6115, 0.4856, 0.9993)	−0.9941	0.1319 − 0.8505 i	0.1319 + 0.8505 i
−0.3	(0.4521, 0.4406, 0.0046)	−0.9698	0.1214 − 0.8932 i	0.1214 + 0.8932 i
	(0.5, 0.5, 0.5)	1.7985	−0.2799 − 0.8520 i	−0.2799 + 0.8520 i
	(0.5479, 0.5594, 0.9954)	−0.9698	0.1214 − 0.8932 i	0.1214 + 0.8932 i
−0.241	(0.4873, 0.4023, 0.0133)	−0.9247	0.1061 − 0.8937 i	0.1061 + 0.8937 i
	(0.5, 0.5, 0.5)	1.7130	−0.2371 − 0.7312 i	−0.2371 + 0.7312 i
	(0.5127, 0.5977, 0.9868)	−0.9247	0.1061 − 0.8937 i	0.1061 + 0.8937 i
−0.24	(0.4879, 0.4017, 0.0135)	−0.9235	0.1059 − 0.8935 i	0.1059 + 0.8935 i
	(0.5, 0.5, 0.5)	1.7114	−0.2363 − 0.7289 i	−0.2363 + 0.7289 i
	(0.5121, 0.5983, 0.9865)	−0.9235	0.1059 − 0.8935 i	0.1059 + 0.8935 i
0	(0.5, 0.5, 0.5)	−0.7071	0.9729 − 0.3612 i	0.9729 + 0.3612 i
8	(0.5, 0.5, 0.5)	−3.7550	2.4969 − 3.1062 i	2.4969 + 3.1062 i

.

Lyapunov exponents are considered in

Table 5. Lyapunov exponents.

${\mathit{w}}_{23}$	${\mathbf{LE}}_1$	${\mathbf{LE}}_2$	${\mathbf{LE}}_3$
$-0.569$	−0.0106	−0.0149	−0.9997
$-0.5$	−0.00002	−0.1529	−0.9907
$-0.4$	0.0026	−0.2235	−0.8975
$-0.3$	0.0309	−0.0127	−0.7389
$-0.241$	0.0512	−0.0062	−0.6901
$-0.24$	0.0020	−0.0260	−0.7109
0	−0.0029	−0.6131	−0.9340
8	0.0016	−0.9139	−1.5327

.

Periodic attractors are depicted in Figure 11, Figure 12 and Figure 13. Graphs of solutions are depicted in Figure 14, Figure 15 and Figure 16. The chaotic attractor is depicted in Figure 17 and the graph of solutions is depicted in Figure 18.

4. Discussion

A definite similarity was found between the Chua circuits and systems of the form (7), which are used in the mathematical modeling of genetic and neuronal networks. An analysis of critical points and their mutual positions in the Chua system motivated us to study similar configurations in GRN systems. The local analysis of critical points gave hints of what should be arranged in GRN systems to get similar behavior of trajectories as in the Chua system. For this, multiple parameters, built into GRN systems, were useful. The desired behavior can be reached by shifting the nullclines, changing $\theta$ parameters, or/and changing the elements of the regulatory matrix, and regulating the form of sigmoidal functions by changing $\mu$ parameters. Looking at the data being collected during the study, one may observe some properties that eventually lead to chaotic behavior. As an example, Table 1, Table 2 and Table 3 with the local characteristics of the critical points, should be mentioned. The bifurcation analysis made in the article concerns the varying of one parameter. The changes in the characteristics of critical points and fractal dimensionality of the chaotic attractor, give rise to conclusions and may indicate directions of further numerical experiments. Some questions arise. For instance, the monotone change in the parameter $w_{23}$ leads to generally non-monotone changes in characteristics of the critical points and KY fractal dimensionalities of the chaotic attractor. Analyzing the collected data may lead to the formulation of directions for further studies. The questions that should be answered: what is the minimal (or optimal) number of critical points needed for the birth of a strange attractor; what is the minimal configuration (positions, local characteristics) that ensures a transition to chaotic behavior; is the transition to chaotic behavior in the studied system possible without passing through the stable periodic solution stage; could sufficient conditions be formulated to ensure passage to chaotic behavior from a given configuration; what is the description of this configuration; what are the necessary conditions concerning passage to chaotic behavior; is it possible to pass from periodic attractors to chaotic ones through continuous change of KY dimensionality; generally, what is the role of jump changes in a system to go to the strange (chaotic) attractor?

This list can be continued and answering some, or all, of the formulated questions concerning the system (7) (with matrix (13), at least) would indicate the essential progress in understanding the process of formation of a chaotic attractor. So further investigations in this direction promise results, which may be relevant and important for the general theory of dynamical systems.