Abstract
The magneto-hydrodynamic dual convection stagnation flow pattern behavior of a Tangent Hyperbolic (TH) fluid has been reported in this study. The radiation, Joule heating, and heat generation/absorption impacts have also been analyzed. The flow-narrating differential equations, which are constrained by a thermal and solutal stratified porous medium, are transmuted into a system of nonlinear differential equations. To provide a numerical solution to the flow problem, a computational model is created. Numerical solutions are obtained using the fifth-order exactness program (Bvp5c), and for validation of the results, a comparison is also made with the methodology of the Runge–Kutta fourth order. The physical implications are appraised and depicted using diagrams or tables against flow-controlling parameters, such as Hartmann number, porosity parameter, solutal stratification, the parameter of curvature, temperature stratification, local Weissenberg number, Schmidt number, etc. It has been observed that in the appearance of Joule heating phenomena, the fluid temperature is a lowering function of thermal stratification. The findings are compared to the existing literature and found to be consistent with earlier research.
Keywords:
stagnation point flow; thermal stratification; solutal stratification; MHD tangent hyperbolic fluid; dual convection; Runge–Kutta fourth-order method; Bvp5c MSC:
65L06; 76D05; 76D50; 76S05; 76W05; 80A05
1. Introduction
In many engineering and industrial applications, the study of a viscous or non-Newtonian fluid’s stagnation-point flow is crucial. Transpiration cooling, developing thrust bearings, recovering thermal oil, reducing drag, and radial diffusers are all made easier with an understanding of the stagnation flow. Additionally, a stretching and contracting surface is frequently used to study stagnation-point flow. Nadeem et al. [1] described approaches for boundary layer motion using HAM in the vicinity of the stagnation point towards a stretching sheet, whereas Bachok et al. [2] examined the two-dimensional steady nanofluid stagnation-point flow in the existence of a sheet’s expansion or contraction. Pal and Mandal [3] numerically investigated the flow at the stagnation point across a stretching or contracting surface with heat emission and dissipation of viscous fluid in a pore media. In their study, Zaimi and Ishak [4] managed to prove the occurrence of two opposing flow solutions by examining partial slip and its consequences on the transmission of heat and stagnation-point flow caused by a sheet that extends vertically. Hayat et al. [5] studied Soret–Dufour’s implications on the flow over the stagnation point for a hyperbolic tangent fluid. According to Khan et al. [6], activation energy has an impact on the cross-nanofluid flow at nonlinear radiative stagnation points. On the issue of flow at the stagnation point in magnetohydrodynamics towards a surface that stretches and contracts in a permeable media, Khashi’ie et al. [7] looked into joint influences of double stratification (a system with two layers) and convection. Barnoon et al. [8] presented an entropy generation analysis of different nanofluid flows in the space between two concentric horizontal pipes in the presence of a magnetic field using single-phase and two-phase approaches simultaneously. When there are two separate layers in a pore media, Adigun et al. [9] studied the slip-flow of viscoelastic nanomaterials close to the stagnation point in the appearance of MHD across an angled stretched cylindrical surface. MHD flow of a fluid (hyperbolic tangent) at its stagnation point was explained by Arshad and Ashraf [10] using viscous dissipation and chemical reaction. By combining the consequences of Soret and Dufour, Ali et al. [11] examined the 3D flow of MHD hyperbolic tangent nano liquid in the form of a convective stretched sheet. Babu et al. [12] analyzed heat and mass transfer on unsteady magnetohydrodynamics (MHD) convective flow of Casson hybrid nanofluid over a permeable media with ramped wall temperature. Venkateswarlu et al. [13] elaborated MHD flow of MoS2 and MgO water-based nanofluid through a porous medium over a stretching surface with Cattaneo–Christov heat flux model and convective boundary condition.
When two layers of the same liquid flow independently at low velocities with significant temperature differences, a thermally stratified flow develops. The lower location along the surface is occupied by the colder (heavier) fluid, whereas the top position is occupied by the hotter (lighter) fluid. Thermal stratification has been observed in pressurized water reactors, nuclear power plants, lines for removing residual heat and cooling the core in case of emergency, and other applications. In the recent decade, Mukhopadhyay and Ishak [14] explored the issue of grouped convectional flow, considering a stretching cylindrical surface placed within a thermally stratified medium. Hayat et al. [15] summarized the effects of temperature and concentration stratifications on Jeffrey fluid motion caused by a sheet’s elongation under radiative conditions. Using the Keller box method, Malik et al. [16] performed a mathematical investigation on the MHD flow of TH-fluid across a cylinder due to its extending nature. By using a stretching cylinder, Rehman [17] addressed a numerical communication on magnetohydrodynamic, which is the movement of Casson fluid by dual convection within a system with distinct layers of temperature. Impacts of thermal and solutal stratification on Jeffrey magneto-nanofluid along an inclined stretching cylinder with thermal radiation and heat generation/absorption was discussed by Ramzan et al. [18]. Khan et al. [19] illustrated the flow of chemically reactive hyperbolic tangent fluid motion embedded in a permeable medium with thermal radiation and two-layer stratification. Nonlinear radiative nanofluidic hydrothermal unsteady bidirectional transport with thermal/mass convection characteristics was researched by Faisal et al. [20]. Miansari et al. [21] explained the numerical investigation of the effects of the groove on the thermal performance of a helically grooved shell and coil tube heat exchanger. Using stratification and non-Fourier heat flux theory, Kayikci et al. [22] explored the thermal characterization of radiative water and glycerin-based carbon nanotubes over a Riga plate.
One of the most notable models of non-Newtonian fluids is the tangent hyperbolic fluid. Such a structure accurately foretells the thinning characteristic resulting from shear in laboratory trials, according to the findings. To be more explicit, the tangent hyperbolic fluid model can be used to examine any substance that presents a picture of shear-thinning features. The four-constant fluid model is another name for this fluid model. Tangent hyperbolic fluids are typically employed in labs and industry. Whipped cream, ketchup, polymers, solutions, melts, paint and blood are some of the most common hyperbolic tangent model applications in the industry and biology. The mathematical modeling of fluid with the hyperbolic tangent flow within a curving channel was presented by Nadeem and Maraj [23]. The hyperbolic tangent fluid flow above an upright cylinder was examined by Naseer et al. [24] and the surface was assumed to be exponentially stretched. Salahuddin et al. [25] studied the tangent hyperbolic nanofluid stagnating point flow over a cylinder that stretches. Rehman et al. [26] gave a brief presentation on the thermophysical characteristics of fluid flow regimes with hyperbolic tangents. Rao et al. [27] used the spectrum relaxation approach to compute the boundary layer MHD flow of a TH-fluid with mass and heat transport across a stretching cylinder with pores on the surface. The implications of radiation on a tangent hyperbolic MHD nanofluid flow across an angled sheet were investigated by Saidulu et al. [28] and the sheet contained an exponentially stretching property. Ali et al. [29] established some graphical results for tangent hyperbolic fluid over a vertically stretched sheet and the consequence of an angled hydromagnetic field was also discussed. The mathematical model and technical flow characteristics of hyperbolic tangent nanofluid across a cone-shaped surface and a plate were investigated by Bilal et al. [30] under mixed convection and the implications of a chemical reaction. With the consideration of the TH-fluid over an extended cylinder’s surface, Salahuddin et al. [31] described homogeneous–heterogeneous reaction phenomena. Jat and Sharma [32] looked at the heat transfer assessment and tangent hyperbolic nanofluid unsteady MHD flow over an angled stretched sheet.
Mixed convection flow, also known as mixed free and forced convection flow, can be used in a variety of technical and industrial applications. Electrical instruments cooled by fans, wind-swept solar receivers, variations of flows in the ocean and atmosphere, and different thermal variations in the atmospheric flow are all examples of a mixed convection flow. In view of this, Patil et al. [33] discussed mixed convection flow over a vertical power-law stretching sheet. Ali et al. [34] examined mixed convection heat transfer in an incompressible viscous fluid over a vertical stretching sheet by taking the external magnetic field into account. Kumar et al. [35] discussed the effect of nonlinear thermal radiation on the double-diffusive mixed convection boundary layer flow of viscoelastic nanofluid over a stretching sheet. Abdul et al. [36] studied the mixed convection flow of the Powell–Eyring nanofluid near a stagnation point along a vertical stretching sheet. Barnoon [37] analyzed the numerical assessment of heat transfer and mixing quality of a hybrid nanofluid in a microchannel equipped with a dual mixer. Babu et al. [38] discussed the hall and ion-slip effects on MHD free convection flow of rotating Jeffrey fluid over an infinite vertical porous surface. Saeed et al. [39] described the mixed convective flow of a magnetohydrodynamic Casson fluid through a permeable stretching sheet with a first-order chemical reaction.
To date, the significance of dual convection stagnation-point flow of hyperbolic tangent fluid towards a smooth cylindrical surface has remained unknown. As a result, the goal of this analysis is to fill the void. In this analysis, thermally and solutally stratified porous medium is also taken into account. The novelty of the present study includes the following:
- Stagnation-point flow analysis for hyperbolic tangent fluid;
- Stratification phenomenon impacts on flow field with a stretched cylinder;
- Joule heating, thermal radiation, and heat source effect on the temperature profile;
- Mixed convection effect on velocity and temperature field.
Utilizing the MATLAB Bvp5c code, the numerical results are obtained. Many parameters and their graphical trends in relation to velocity, temperature, skin friction drag coefficient, and heat transfer rate are inspected and elaborated appropriately.
2. Mathematical Formulation
An incompressible tangent hyperbolic fluid movement has been considered, which is steady and two-dimensional, through a porous stratified media across a stretching cylindrical surface. The boundary layer flow in the neighboring region of the stagnation point is obtained in the presence of a magnetic field. Radiation and dual convection effects are also considered. A cylindrical surface with a radius is taken along the -axis. Fluid flow is only in the -direction, i.e., there is no flow in the -direction. The stretching of the surface enables a flow to develop along the -direction with velocity . The surface temperature of the cylinder’s wall is , while the temperature far away from the surface is (). The fluid concentration at the cylinder’s wall is , while the concentration far away from the surface is (). Here, a uniform magnetic field of strength is assumed normal to the path of the flow. At a great distance from the surface, the flow velocity is considered to be . Additionally, the contribution of dissipation of viscous fluid and induced magnetic field effects are considered insignificant in the present study. Since the induced magnetic field is negligible, the magnetic Reynolds number can be considered zero. The geometry of the problem is shown in Figure 1.
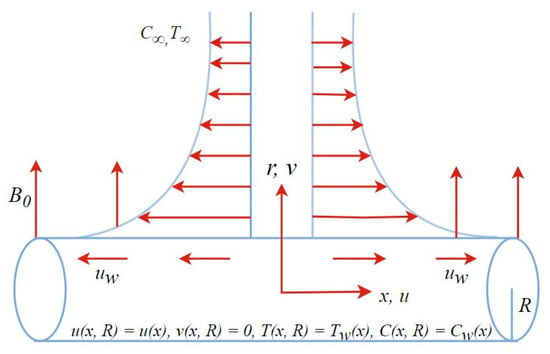
Figure 1.
Fluid Model.
The continuity equation for our mentioned model in cylindrical coordinates is written as follows:
The incompressible tangent hyperbolic fluid flow’s governing momentum equations are as follows:
In the tangent hyperbolic fluid model (Malik et al. [16], Ullah and Zaman [40]), the extra stress tensor expression is denoted as follows:
, where and is defined as:
Here, we assume because infinite shear rate viscosity prevents any meaningful discussion of the issue, and since, in this case, we have taken into account the tangent hyperbolic fluid, which specifies shear thinning. Thus, the required form of is expressed as the following:
Using this Formula (4) in Equation (2), we achieved the following expression of momentum equation:
Energy equation:
Concentration equation:
The boundary conditions are as follows:
The mode of expression of the velocity distribution of the stream is disclosed as follows:
Using Equation (9) in Equation (1), we conclude that the continuity equation is satisfied. Here, the following similarity transformations and expressions for (Rooseland approximation) are considered to perceive the velocity, temperature, and concentration outcome of the current research problem as shown below:
By applying these transformations to Equations (5)–(8), the reduced dimensionless model with boundary conditions is disclosed as follows:
In the above model, all the used non-dimensional parameters are defined as follows:
Additionally, the local skin friction coefficient, local Nusselt number, and local Sherwood number are expressed as follows:
where (rate of shear stress), (energy flow/heat flux) and (mass flux).
The dimensionless forms of all the physical quantities in Equation (16) are as follows:
where is the local Reynold number and is the local Weissenberg number.
3. Method of Solution
Equations (11)–(13) that govern the flow are numerically solved with the boundary conditions (14) on MATLAB using the Bvp5c program. This bvp5c function is designed using the 4-stage Lobatto IIIa formula under the finite difference scheme with fifth-order accuracy. The fundamental syntax programmed in this function is sol = bvp5c (@odefun, @bcfun, solinit, options) and the relative tolerance was set to 10−10. To solve the flow problem via Bvp5c, Equations (11)–(13) are reduced to a set of simultaneous equations of the first order as described below:
Let and , then
subjected to boundary conditions
Here, the additional boundary conditions are as follows:
We selected suitable guess values of , and , i.e., , so that the boundary conditions stated in Equation (20) are held absolutely when the integration of the above system of the first-order differential equations is performed. From a calculation point of view, we considered , where denotes . First, the interval [0,5] is subdivided using step size 0.0025. We created the initial boundary condition’s guesses using bvpinit command. First-order differential Equations (18) are encoded to differential functions using bvpfcn(x,y) command, and boundary conditions are encoded using bcfcn(ya,yb). Then, we solved the problem using sol=bvp5c(@bvpfcn, @bcfcn, solinit) and plotted the solution using plot(sol.x, sol.y). Computational procedure for finding the solution of our problem is as shown in Figure 2.
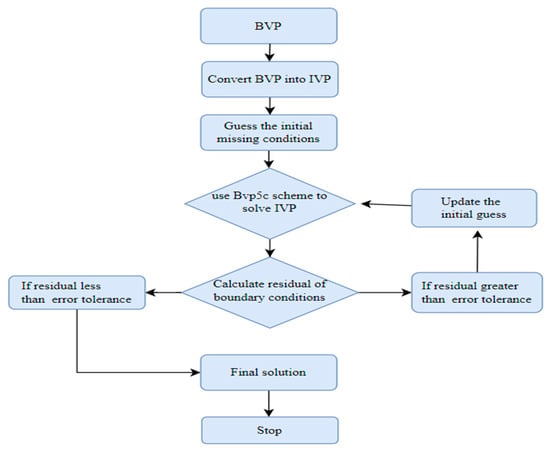
Figure 2.
Flow chart of computational procedure.
4. Results and Discussion
The physical features of magneto-hydrodynamic (MHD) flow with dual convection and stagnation pattern behavior of Tangent Hyperbolic (TH) fluid are discussed in this article. The subsequent control parameters are considered to obtain the numerical solutions as follows: Weissenberg number , power law index , curvature parameter , Prandtl number , Eckert number , Hartmann number , porosity parameter , heat source parameter , mixed convection parameter , buoyancy force parameter , velocity ratio parameter , Schmidt number , thermal stratification parameter , solute stratification parameter , and radiation parameter . For the computational purpose, , , , , or , , , , , , , , , , and are fixed unless stated separately. The impact of various physical parameters on the flow characteristics (velocity, temperature, and concentration) is graphically investigated.
Utilizing the MATLAB Bvp5c code and RK-4 approach, the local skin friction coefficient is obtained and shown in Table 1 for pertinent parameters, namely the power law index and the local Weissenberg number. Additionally, the computed findings for the coefficient of skin friction are compared to accessible literature (Rehman et al. [26]) and (Akbar et al. [41]), and a high similarity is seen in all datasets as indicated in Table 1.

Table 1.
Comparison for local skin friction coefficient.
4.1. Discussion of Momentum Profiles
Figure 3a–j depict the changes in flow control parameters, such as porosity parameter, curvature parameter, magnetic parameter, power law index, Weissenberg number, ratio of buoyancy, velocity ratio parameter, mixed convection parameter, and thermal parameter of solutal stratification. With rising porosity inputs, the flow speed profile decreases, as shown in Figure 3a. As the parameter , related to the curvature, is increased, the velocity profile increases near the surface of the cylinder (as seen Figure 3b). This behavior of velocity profiles changes as we move towards the free stream region. When the curvature parameter K is enhanced, the cylinder’s radius tends to lessen, and therefore the surface contact area decreases, resulting in reduced resistance for the fluid particles near the surface, thereby speeding up the fluid flow rate. Figure 3c,d show an inverse relationship between the magnetic parameter or power law index and the velocity pattern, i.e., the velocity profile decreases as the magnetic parameter or power law index increases. Figure 3e shows the fluid flow pattern as a subject of the local Weissenberg number . The velocity profile reduces for the local Weissenberg number. The reason for this is that when the Weissenberg number rises, the fluid’s relaxation time rises, creating the fluid’s resistance to flow and thus lowering the relative movement of particles in the fluid. The significance of the proportion of buoyancy forces on the velocity pattern is seen in Figure 3f. It is found that the fluid rate grows as increases. It is well-established that a rise in fluid motion is the result of a rise in buoyancy forces, with a concentration on buoyancy forces predominating. The consequence of the changing velocity ratio parameter is displayed in Figure 3g as a change in the flow field. The velocity field is shown to expand with bigger values of the velocity ratio parameter . Figure 3h is illustrating the influence of the mixed convection parameter on the velocity flow field. As the parametric value for mixed convection is increased, it is found that the resulting velocity field is more intense. It is the increased thermal buoyancy force that contributes to a greater velocity distribution as the parameter for mixed convection rises. Figure 3i displays the impacts of ; as the thermal stratification parameter is enhanced, the fluid velocity decreases. This is caused by the decrease in the convective potential between the cylinder’s surface and the adjacent heat. Figure 3j shows the distribution of the velocity profiles for solutal stratification parameter . It is clearly noticed from this figure that the profiles related to velocity decrease due to enhanced inputs of the solutal stratification parameter .
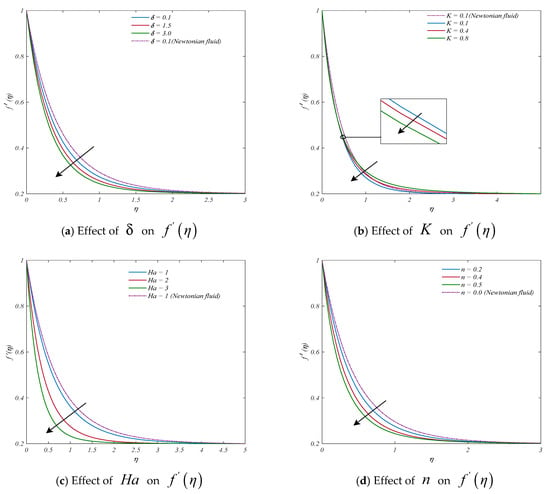
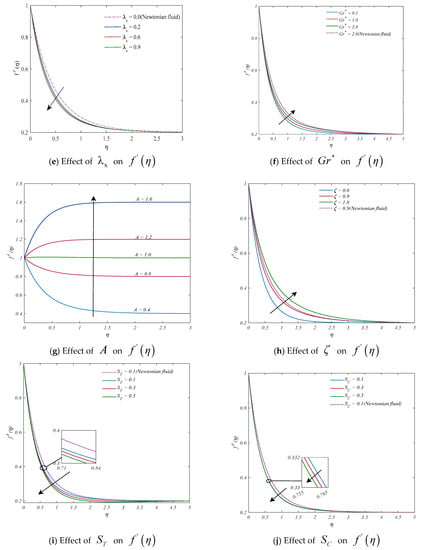
Figure 3.
Display of momentum profiles for different parameters: (a) , (b) , (c) , (d) , (e) , (f) , (g) , (h) , (i) , and (j) .
4.2. Discussion of Temperature Profiles
Figure 4a–l demonstrate the effects of the curvature parameter, Hartmann number, power law index, Eckert and Prandtl number, thermal stratification parameter, velocity ratio parameter, radiation parameter, heat source/sink parameter, local Weissenberg number, ratio of buoyancy forces, and mixed convection parameter. It is shown in Figure 4a that as the curvature parameter grows, the temperature distribution profiles are elevated. Since the Kelvin scale measures the average kinetic energy of a fluid, increasing the curvature of a cylinder causes the fluid’s velocity to increase, which in turn raises the fluid’s kinetic energy and hence its temperature. Figure 4b also suggests that the Hartmann number and the fluid temperature have a proportional relationship. Figure 4c shows that as the inputs of the power law index increase, the profiles related to temperature rise as well. For small readings of the Eckert number , temperature distribution has a proportional relationship, as shown in Figure 4d. Figure 4e represents the results of the Prandtl number investigation. The fluid’s heat conductivity has an opposite relationship with the Prandtl number ; increasing Prandtl numbers indicate weak energy diffusion. As a result, the Prandtl number going up indicates a significant decrease in the fluid’s temperature profiles. Figure 4f shows that the temperature distribution decreases as the inputs of the stratification parameter increase. The repercussion of changing the ratio parameter on the temperature distribution is displayed in Figure 4g. The width of the thermal and temperature boundary layer lessens as increases. The radiation parameter ’s effects on temperature distribution are indicated in Figure 4h. For a bigger value of the radiation parameter , the temperature increases. This is because the working fluid’s temperature field is enhanced as a result of higher heat production during the radiation phase. Figure 4i identifies the change of the heat generation/absorption parameter on the overall temperature pattern. It is noticeable that in the case of heat generation (), there is a rise in the temperature distribution and thermal boundary layer width, whereas in the context of heat absorption (), the opposite is visible. Naturally, more heat is generated during the heat-generating process when the parameter . This increases the temperature profile. It is true that the thermal width of the boundary layer grows very slightly with the increasing local Weissenberg number , as seen by the increased distribution of the temperatures in Figure 4j. Figure 4k depicts the influence of the ratio of buoyancy forces on temperature (θ). A higher value accelerates the convective cooling phenomenon of the system, resulting in a small decrease in the fluid temperature. From Figure 4l, a declining pattern for temperature distribution is observed when the values of mixed convection parameters are increased.
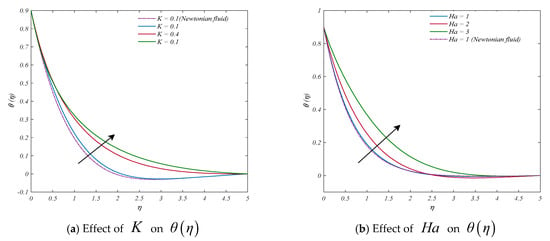
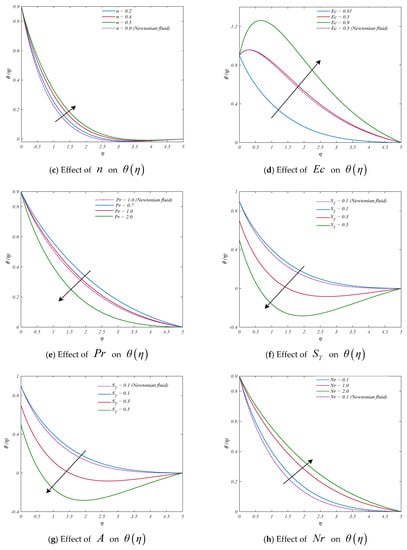
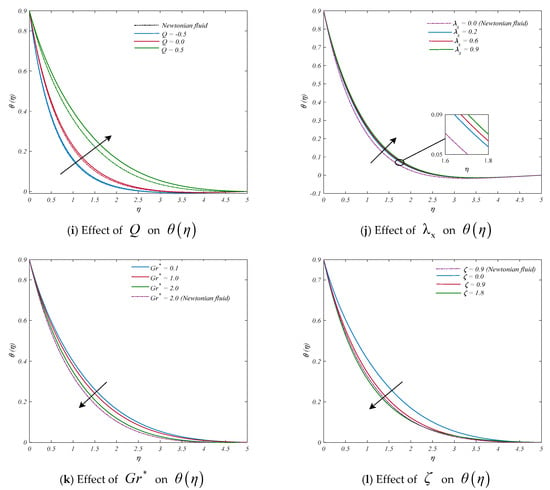
Figure 4.
Display of temperature profiles for different parameters: (a) , (b) , (c) (d) , (e) , (f) , (g) , (h) , (i) , (j) , (k) , and (l) .
4.3. Discussion of Concentration Profiles
Figure 5a–h demonstrate the effects of the Schmidt number, solutal stratification parameter, curvature parameter, Hartmann number, local Weissenberg number, velocity ratio parameter, mixed convection parameter, and the ratio of buoyancy forces. The effect that the Schmidt number has on the concentration profile is displayed in Figure 5a. As develops, the concentration profile flattens out. It is known that the Schmidt number is defined as the ratio of momentum diffusivity to mass diffusivity. In this case, a lower mass diffusivity, as indicated by a larger Schmidt number , reduces the concentration profile. Concentration changes based on the altering inputs of the solutal stratification parameter are shown in Figure 5b. It is also obvious that when increases, the fluid concentration decreases. Figure 5c indicates how the curvature parameter affects the concentration pattern. It can be seen that the concentration declines when the curvature parameter increases. For upsurging values of Hartmann and local Weissenberg number , the profiles for concentration is showing an increasing nature as shown in Figure 5d,e. A decreasing behavior is noticed in the concentration pattern for rising readings of the velocity ratio parameter , mixed convection parameter , and the ratio of buoyancy forces as depicted in Figure 5f–h).
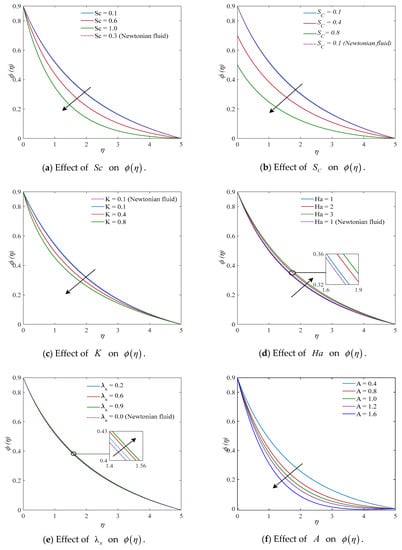
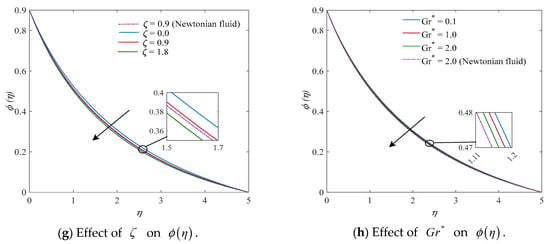
Figure 5.
Display of concentration profiles for different parameters: (a) , (b) , (c) , (d) , (e) , (f) , (g) , and (h) .
4.4. The Behavior of Surface Drag Coefficient, Nusselt Number, Sherwood Number, and Related Parameters
The outcomes of the local skin friction coefficient, Nusselt number and Sherwood number versus Hartmann number, porosity, mixed convection parameter, velocity ratio parameter, Eckert number, radiation parameter, heat generating/absorption parameter, and thermal stratification and Schmidt number have been shown in Figure 6, Figure 7 and Figure 8.
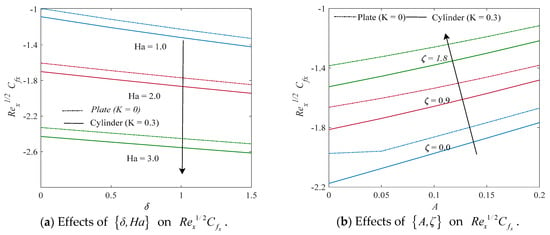
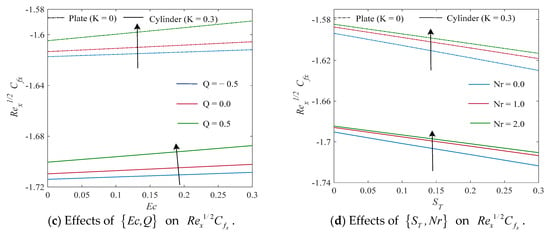
Figure 6.
Display of against (a) , (b) , (c) , and (d) .
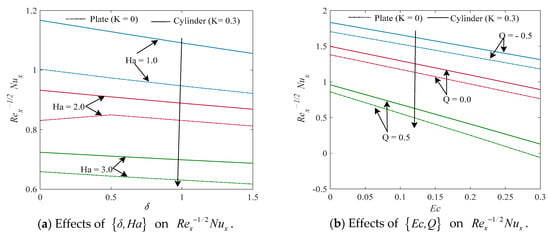
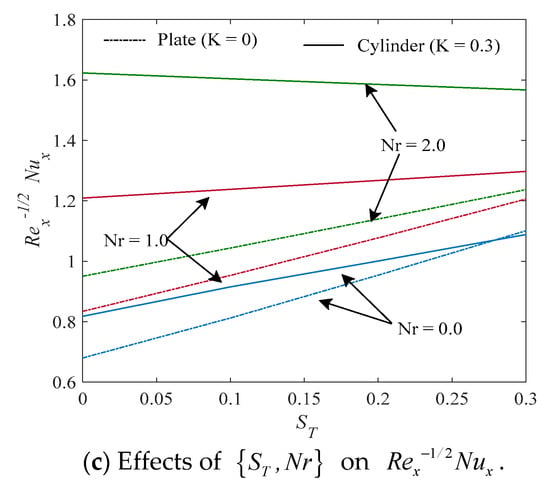
Figure 7.
Display of against (a) , (b) , and (c) .
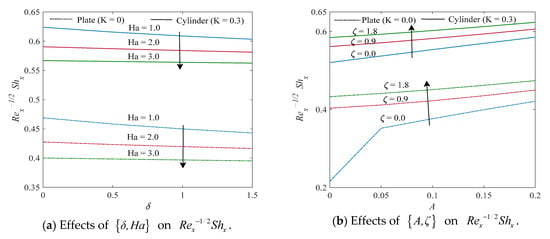
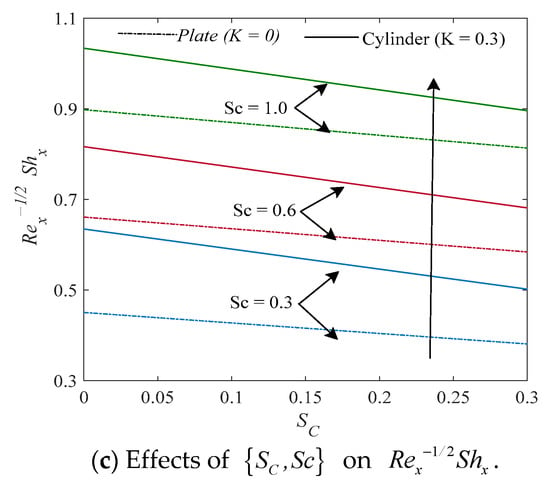
Figure 8.
Display of against (a) , (b) , and (c) .
The behavior of the local skin friction coefficient is displayed in Figure 6a–d. Changing inputs of Hartmann number , porosity parameter , and thermal stratification parameter reduce the friction coefficient while there is a rise in mixed convection parameter , velocity ratio parameter , heat generation/absorption parameter , Eckert number , and the radiation parameter enhances the skin friction coefficient. In all cases shown in Figure 6a–d, it is clear that the coefficient for skin friction is high for the plate and low for the cylinder.
Outcomes for the local Nusselt number against distinct parameters are portrayed in Figure 7a–c. These figures show the rising pattern of the local Nusselt number against the enhanced inputs of the radiation parameter and the thermal stratification parameter , whereas opposite nature is also observed from these figures for growing inputs of the Hartmann number , porosity parameter , heat generation/absorption parameter , and Eckert number . Additionally, the local Nusselt number is found to be significantly higher for a cylinder than a flat plate.
Figure 8a–c depict that the local Sherwood number dominates the cylindrical surface when it is compared to the plate. It can be clearly observed that Sherwood number profiles are declining with increasing inputs of the Hartmann number , porosity parameter , and solutal stratification parameter ; meanwhile, there is an enhancement with increasing values of the velocity ratio parameter , mixed convection parameter , and Schmidt number .
5. Conclusions
This paper deals with the magneto-hydrodynamic (MHD) flow with dual convection and stagnation pattern behavior of the Tangent Hyperbolic (TH) fluid. In this flow problem modeling radiation, Joule heating, and heat generation/absorption, their impacts have also been analyzed. Numerical solutions are obtained by using the fifth-order exactness program (Bvp5c) and for validation of the results, a comparison is also made with the fourth-order Runge–Kutta method from previously published data. The following major observations may be drawn from this analysis:
- For small values of the porosity parameter , the velocity pattern of the fluid decreases. It is found that the velocity reduces with , and thus the thickness of the momentum’s boundary layer is reduced. The cause behind this physical phenomenon is the pores of the porous material that reduces the velocity.
- For increases in the curvature parameter , the fluid temperature rises. Our observation indicates that the surface area of the contact decreases and the resistance provided by the cylindrical surface also decreases for greater values of the curvature parameter . Particle velocities rise as a result of this. The increased velocity is directly influenced by the kinetic energy. A higher kinetic energy is associated with a higher velocity. Higher temperatures are the outcome of a high average velocity value.
- The fluid features change from shear thinning to shear thickening as the power law index rises, and hence the fluid motion slows down. A boost in the local Weissenberg number appears to result in a decrease in the fluid velocity profiles. Since the local Weissenberg number is directly proportional to relaxation time, the internal resistance increases, and thus that velocity profiles exhibit a decreasing pattern. On the other hand, concentration and temperature profiles slightly increase.
- The conventional potential difference is diminished when the thermal stratification and the solutal stratification parameter are improved, causing the fluid temperature and concentration to decline, respectively, and when the Prandtl number rises, the fluid temperature decreases. Additionally, the effect of the Eckert number has a proportional relationship with the temperature profile.
- Higher values of the buoyancy parameter improve the velocity distribution. Physically, the buoyancy force increases with a significant increase of , hence causing the velocity to be higher. The temperature and concentration profiles show a declining pattern for higher values of .
- The local skin friction coefficient increases with the heat generation/absorption parameter and the local Nusselt number shows the opposite pattern for this parameter. The local Sherwood number has a rich profile for high values of the Schmidt number .
- Profile for the local skin friction coefficient is observed as high for the plate in comparison to the cylindrical surface; meanwhile, the reverse is true for the local Nusselt and Sherwood numbers.
Author Contributions
Conceptualization, S.C.; Methodology, P.C., N.A. and K.L.; Formal analysis, P.C.; Investigation, N.A. and K.L.; Resources, K.L.; Data curation, K.L.; Writing—original draft, P.C.; Writing—review & editing, S.C., K.L. and P.C.; Supervision, K.L.; Project administration, N.A.; Funding acquisition, N.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Princess Nourah Bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R59), Princess Nourah Bint Abdulrahman University, Riyadh, Saudi Arabia.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Princess Nourah Bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R59), Princess Nourah Bint Abdulrahman University, Riyadh, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Velocity ratio parameter | |
| Body force (kg m/) | |
| Temperature-dependent constants (K) | |
| Concentration-dependent constants | |
| Heat capacity at constant pressure (J/K) | |
| Hartmann number | |
| Schmidt number | |
| Dimensionless fluid velocity | |
| Identity tensor | |
| Curvature parameter | |
| Permeability of the medium () | |
| Radiation parameter | |
| Characteristic length (m) | |
| Cauchy stress tensor (N/) | |
| Power law index | |
| Pressure (N/) | |
| Prandtl number | |
| Radius of the cylindrical surface (m) | |
| Local Reynold number | |
| Solutal stratification parameter | |
| Thermal stratification parameter | |
| Reference temperature (K) | |
| Reference concentration | |
| Velocity components (m/s) | |
| Reference velocity (m/s) | |
| Local thermal Grashof number | |
| Local concentration Grashof number | |
| Mass diffusivity | |
| Mean absorption coefficient | |
| Cylindrical coordinates (m) | |
| Ratio of buoyancy forces | |
| Velocity vector (m/s) | |
| Parameter for heat generation/absorption | |
| Greek Symbols | |
| Dynamic viscosity (kg/m s) | |
| Infinite shear rate viscosity (kg/m s) | |
| Extra stress tensor (N/) | |
| Fluid density (kg/) | |
| Fluid electrical conductivity (K3A2/kg m3) | |
| Fluid temperature (K) | |
| Fluid concentration | |
| Kinematic viscosity () | |
| Porosity parameter | |
| Zero shear rate viscosity (kg/m s) | |
| Second invariant strain tensor | |
| Shear rate () | |
| Shear stress (N/) | |
| Similarity variable | |
| Stream function | |
| Local Weissenberg number | |
| Time-dependent material constant (s) | |
| Thermal conductivity (W/m K) | |
| Mixed convection parameter | |
| Stefan–Boltzmann constant | |
| Thermal expansion coefficient | |
| Concentration expansion coefficient | |
References
- Nadeem, S.; Hussain, A.; Khan, M. HAM solutions for boundary layer flow in the region of the stagnation point towards a stretching sheet. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 475–481. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Pop, I. Stagnation-point flow over a stretching/shrinking in a nanofluid. Nanoscale Res. Lett. 2011, 6, 623. [Google Scholar] [CrossRef] [PubMed]
- Pal, D.; Mandal, G. Mixed convection-radiation on stagnation point flow of nanofluid over a stretching/shrinking sheet in a porous medium with heat generation and viscous dissipation. J. Pet. Sci. Eng. 2015, 126, 16–25. [Google Scholar] [CrossRef]
- Zaimi, K.; Ishak, A. Stagnation-point flow towards a stretching vertical sheet with slip effects. Mathematics 2016, 4, 27. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Waqas, M.; Alsaedi, A. Stagnation point flow of hyperbolic tangent fluid with Soret-Dufour effects. Results Phys. 2017, 7, 2711–2717. [Google Scholar] [CrossRef]
- Khan, M.I.; Hayat, T.; Alsaedi, A. Activation energy impact in nonlinear radiative stagnation point flow of cross nanofluid. Int. Commun. Heat Mass Transf. 2018, 91, 216–224. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Rashidi, M.M.; Hafidzuddin, E.H.; Wahi, N. Magnetohydrodynamics (MHD) stagnation point flow past a shrinking/stretching surface with double stratification effect in a porous medium. J. Therm. Anal. Calorim. 2019, 139, 3635–3648. [Google Scholar] [CrossRef]
- Barnoon, P.; Toghraie, D.; Eslami, F.; Mehmandoust, B. Entropy generation analysis of different nanofluid flows in the space between two concentric horizontal pipes in the presence of magnetic field: Single-phase and two-phase approaches. Comput. Math. Appl. 2019, 77, 662–692. [Google Scholar] [CrossRef]
- Adigun, J.A.; Adeniyan, A.; Abiala, I.O. Stagnation point MHD slip-flow of viscoelastic nanomaterial over a stretched inclined cylindrical surface in a porous medium with dual stratification. Int. Commun. Heat Mass Transf. 2021, 126, 105479. [Google Scholar] [CrossRef]
- Arshad, K.; Ashraf, M. MHD stagnation point flow of hyperbolic tangent fluid with viscos dissipation and chemical reaction. J. Sci. Arts 2021, 21, 569–588. [Google Scholar] [CrossRef]
- Ali, F.; Reddy, C.S.; Zaib, A. 3D flow of MHD tangent hyperbloic nanoliquid with the combined effect of soret and dufour effect past a heated convective stretching sheet. Int. J. Hydrol. 2022, 6, 108–116. [Google Scholar] [CrossRef]
- Babu, B.H.; Rao, P.S.; Varma, S.V.K. Heat and Mass Transfer on Unsteady Magnetohydrodynamics (MHD) Convective Flow of Casson Hybrid Nanofluid Over a Permeable Media with Ramped Wall Temperature. J. Nanofluids 2022, 11, 552–562. [Google Scholar] [CrossRef]
- Venkateswarlu, S.; Varma, S.V.K.; Durga Prasad, P. MHD Flow of MoS2 and MgO water-based nanofluid through porous medium over a stretching surface with Cattaneo-Christov heat flux model and convective boundary condition. Int. J. Ambient. Energy 2022, 43, 2940–2949. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Ishak, A. Mixed convection flow along a stretching cylinder in a thermally stratified medium. J. Appl. Math. 2012, 2012, 491695. [Google Scholar] [CrossRef]
- Hayat, T.; Hussain, T.; Shehzad, S.A.; Alsaedi, A. Thermal and concentration stratifications effects in radiative flow of Jeffrey fluid over a stretching sheet. PLoS ONE 2014, 9, e107858. [Google Scholar] [CrossRef]
- Malik, M.Y.; Salahuddin, T.; Hussain, A.; Bilal, S. MHD flow of tangent hyperbolic fluid over a stretching cylinder: Using Keller box method. J. Magn. Magn. Mater. 2015, 395, 271–276. [Google Scholar] [CrossRef]
- Rehman, K.U.; Qaiser, A.; Malik, M.Y.; Ali, U. Numerical communication for MHD thermally stratified dual convection flow of Casson fluid yields by stretching cylinder. Chin. J. Phys. 2017, 55, 1605–1614. [Google Scholar] [CrossRef]
- Ramzan, M.; Bilal, M.; Chung, J.D. Effects of thermal and solutal stratification on Jeffrey magneto-nanofluid along an inclined stretching cylinder with thermal radiation and heat generation/absorption. Int. J. Mech. Sci. 2017, 131, 317–324. [Google Scholar] [CrossRef]
- Khan, M.; Rasheed, A.; Salahuddin, T.; Ali, S. Chemically reactive flow of hyperbolic tangent fluid flow having thermal radiation and double stratification embedded in porous medium. Ain Shams Eng. J. 2021, 12, 3209–3216. [Google Scholar] [CrossRef]
- Faisal, M.; Asogwa, K.K.; Alessa, N.; Loganathan, K. Nonlinear Radiative Nanofluidic Hydrothermal Unsteady Bidirectional Transport with Thermal/Mass Convection Aspects. Symmetry 2022, 14, 2609. [Google Scholar] [CrossRef]
- Miansari, M.; Darvishi, M.R.; Toghraie, D.; Barnoon, P.; Shirzad, M.; Alizadeh, A.A. Numerical investigation of grooves effects on the thermal performance of helically grooved shell and coil tube heat exchanger. Chin. J. Chem. Eng. 2022, 44, 424–434. [Google Scholar] [CrossRef]
- Kayikci, S.; Eswaramoorthi, S.; Postalcioglu, S.; Loganathan, K. Thermal analysis of radiative water-and glycerin-based carbon nanotubes past a Riga plate with stratification and non-Fourier heat flux theory. J. Therm. Anal. Calorim. 2023, 148, 533–549. [Google Scholar] [CrossRef]
- Nadeem, S.; Maraj, E.N. The mathematical analysis for peristaltic flow of hyperbolic tangent fluid in a curved channel. Commun. Theor. Phys. 2013, 59, 729. [Google Scholar] [CrossRef]
- Naseer, M.; Malik, M.Y.; Nadeem, S.; Rehman, A. The boundary layer flow of hyperbolic tangent fluid over a vertical exponentially stretching cylinder. Alex. Eng. J. 2014, 53, 747–750. [Google Scholar] [CrossRef]
- Salahuddin, T.; Malik, M.Y.; Hussain, A.; Awais, M.; Khan, I.; Khan, M. Analysis of tangent hyperbolic nanofluid impinging on a stretching cylinder near the stagnation point. Results Phys. 2017, 7, 426–434. [Google Scholar] [CrossRef]
- Rehman, K.U.; Alshomrani, A.S.; Malik, M.Y.; Zehra, I.; Naseer, M. Thermo-physical aspects in tangent hyperbolic fluid flow regime: A short communication. Case Stud. Therm. Eng. 2018, 12, 203–212. [Google Scholar] [CrossRef]
- Rao, M.V.S.; Gangadhar, K.; Lorenzini, G.A. Computational analysis for boundary layer flow of magneto hydrodynamic tangent hyperbolic fluid of heat and mass transfer past a stretching cylinder with suction/injection using spectral relaxation method. Math. Model. Eng. Probl. 2019, 6, 38–46. [Google Scholar] [CrossRef]
- Saidulu, N.; Gangaiah, T.; Lakshmi, A.V. Radiation effect on MHD flow of a tangent hyperbolic nanofluid over an inclined exponentially stretching sheet. Int. J. Fluid Mech. Res. 2019, 46, 277–293. [Google Scholar] [CrossRef]
- Ali, A.; Hussain, R.; Maroof, M. Inclined hydromagnetic impact on tangent hyperbolic fluid flow over a vertical stretched sheet. AIP Adv. 2019, 9, 125022. [Google Scholar] [CrossRef]
- Bilal, S.; Shah, Z.; Kumam, P.; Thounthong, P. Mathematical and Engineering Aspects of Chemically Reactive Tangent Hyperbolic Nanofluid over a Cone and Plate with Mixed Convection. Math. Probl. Eng. 2020, 2020, 9090185. [Google Scholar] [CrossRef]
- Salahuddin, T.; Tanveer, A.; Malik, M.Y. Homogeneous–heterogeneous reaction effects in flow of tangent hyperbolic fluid on a stretching cylinder. Can. J. Phys. 2020, 98, 125–129. [Google Scholar] [CrossRef]
- Jat, K.; Sharma, K. Unsteady MHD flow of Tangent Hyperbolic Nanofluid over an Inclined Stretching Sheet and Heat Transfer Analysis. NanoWorld J. 2022, 8 (Suppl. S1), S104–S110. [Google Scholar] [CrossRef]
- Patil, P.M.; Roy, S.; Chamkha, A.J. Mixed convection flow over a vertical power-law stretching sheet. Int. J. Numer. Methods Heat Fluid Flow 2010, 20, 445–458. [Google Scholar] [CrossRef]
- Ali, F.M.; Nazar, R.; Arifin, N.M.; Pop, I. Mixed convection stagnation-point flow on vertical stretching sheet with external magnetic field. Appl. Math. Mech. 2014, 35, 155–166. [Google Scholar] [CrossRef]
- Kumar, G.K.; Gireesha, B.J.; Manjunatha, S.; Rudraswamy, N.G. Effect of nonlinear thermal radiation on double-diffusive mixed convection boundary layer flow of viscoelastic nanofluid over a stretching sheet. Int. J. Mech. Mater. Eng. 2017, 12, 18. [Google Scholar] [CrossRef]
- Abdul Halim, N.; Mohd Noor, N.F. Mixed convection flow of Powell–Eyring nanofluid near a stagnation point along a vertical stretching sheet. Mathematics 2021, 9, 364. [Google Scholar] [CrossRef]
- Barnoon, P. Numerical assessment of heat transfer and mixing quality of a hybrid nanofluid in a microchannel equipped with a dual mixer. Int. J. 2021, 12, 100111. [Google Scholar] [CrossRef]
- Babu, B.; Srinivasa Rao, P.; Varma, S.V.K. Hall and ion-slip effects on MHD free convection flow of rotating Jeffrey fluid over an infinite vertical porous surface. Heat Transf. 2021, 50, 1776–1798. [Google Scholar] [CrossRef]
- Saeed, A.; Algehyne, E.A.; Aldhabani, M.S.; Dawar, A.; Kumam, P.; Kumam, W. Mixed convective flow of a magnetohydrodynamic Casson fluid through a permeable stretching sheet with first-order chemical reaction. PLoS ONE 2022, 17, e0265238. [Google Scholar] [CrossRef]
- Ullah, Z.; Zaman, G. Lie group analysis of magnetohydrodynamic tangent hyperbolic fluid flow towards a stretching sheet with slip conditions. Heliyon 2017, 3, e00443. [Google Scholar] [CrossRef]
- Akbar, N.S.; Nadeem, S.; Haq, R.U.; Khan, Z.H. Numerical solutions of magnetohydrodynamic boundary layer flow of tangent hyperbolic fluid towards a stretching sheet. Indian J. Phys. 2013, 87, 1121–1124. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).