A Novel Solution Approach for Time-Fractional Hyperbolic Telegraph Differential Equation with Caputo Time Differentiation

Abstract

In the current analysis, a specific efficient and applicable novel solution approach, based on a fractional power series technique and Laplace transform operator, is considered to predict certain accurate approximate solutions (ASs) for a time-fractional hyperbolic telegraph equation by aid of time-fractional derivatives in a Caputo sense. The solutions are obtained in a fractional Maclurian series formula by solving the original problem in the Laplace space aided by a limit concept having fewer small iterations than the classical fractional power series technique. To confirm applicability and feasibility of the proposed approach, three appropriate initial value problems are considered. Consequently, some simulations of gained outcomes are numerically and graphically implemented to support the effect of the fractional-order parameter on the geometric behavior of the obtained solutions. In addition, graphical representations are also fulfilled to verify the convergence analysis of the fractional series solutions of the classical solution. The proposed technique is therefore proposed to be a straightforward, accurate and powerful approach for handling varied time-fractional models in various physical phenomena.

1. Introduction

The fractional calculus (FC) has recently received a lot of dedication and appreciation in the area of mathematical analysis due to its ability to establish a precise depiction of diverse complex real-life phenomena that appear in physics [1] and its application of mathematics and engineering, including fluid mechanics [2], electromagnetism, viscoelasticity, signal processing, hydrology [3], fractional kinetics, electrochemistry, biomedicine, optics and robotics, etc. [4]. The FC is a generalization of the classical calculus having nonlocal and original consequences in the materiality features. It plays a prominent role in investigating and analyzing the above-mentioned problems, which can be successfully explained by creating models utilizing the theory of FC. During the growth of the FC theory, several operators of the fractional differentiation are discovered to define the behavior of many structures. Among these operators, we recall Atangana–Baleanu [5], Caputo–Fabrizio [6], Riemann–Liouville [7] and Caputo operators [8]. The latter-mentioned fractional operators give a high degree of freedom in modeling real-world problems compared with ordinary operators. Further, the inclusion of these operators in the process of modeling minimizes inaccuracy that is produced via the lack of knowledge of real components. The Caputo’s operator of the fractional differentiation is considered to be acceptable by the majority of scholars because it has a physical and practical sense without evolving operators. For this reason, the time-fractional hyperbolic telegraph equation (FHTE) is herein reconstituted using the Caputo fractional derivative.

Numerous scholars have solved various kinds of fractional models, e.g., the fractional diabetes model [9], fractal flow of traffic [10], time-fractional two-mode coupled Burgers equation [11], fractional Fokker–Planck equation [12], fractional-order of heat equations [13], fractional-order KdV–Kuramoto–Burger equation [14], Drinfeld–Sokolov–Wilson equation [15], third-order dispersive fractional PDEs [16] and the conformable evolution equations [17], etc.

In the era of technology that we live in today, the communication system is regarded as a robust system and is crucial to treat many difficulties in real-life phenomena. For instance, signal transmission from one place to another is one of the issues in engineering. The telegraph equation is a particular class of hyperbolic partial differential equations (PDEs) that describes the vibrations within objects and the phenomena of wave propagation in a medium [18]. Consideration of this kind of telegraph equation is widely used in the propagation of electrical circuits [19]. In this article, the time-fractional hyperbolic telegraph equation (FHTE) is taken into consideration in the following forms.

The one-dimensional time-FHTE is given by [19]

$${\partial }_t^{2\alpha }\omega \left(x,t\right)+\gamma {\omega }^2\left(x,t\right)+\mu {\partial }_t^{\alpha }\omega \left(x,t\right)=D_x^2\omega \left(x,t\right)+f\left(x,t\right),$$

(1)

The two-dimensional time-FHTE is given by [20,21]

$${\partial }_t^{2\alpha }\omega \left(x,y,t\right)+\gamma {\omega }^2\left(x,y,t\right)+\mu {\partial }_t^{\alpha }\omega \left(x,y,t\right)=D_x^2\omega \left(x,y,t\right)+g\left(x,y,t\right),$$

(2)

where $D_x^n=\frac{{\partial }^n}{\partial x^n}$, ${\partial }_t^{\alpha }$ is the $\alpha$-th time-fractional derivative in the Caputo sense, with $0<\alpha \le 1$ and $\mu ,\gamma \in {ℝ}^{+}$ when $\mu \in {ℝ}^{+},\gamma =0$; Equations (1) and (2) indicate damp wave equations, and in the case of $\mu >\gamma >0$, Equations (1) and (2) denote the telegraph equations. The parameter $\mathsf{\mu }$ represents the damping coefficient, which is a measure of the dissipation of energy in the medium. A non-zero value of $\mu$ indicates that the wave experiences some damping, which can be due to factors such as viscosity, friction or heat conduction. The parameter $\gamma$ represents the nonlinearity coefficient, which is a measure of the strength of the nonlinear interaction between the wave and itself. Overall, the values of $\mu$ and $\gamma$ determine the behavior of the wave in the medium and are often obtained from experimental measurements or via theoretical modeling of the system under consideration. The model has been widely employed in wave processes as well as signal analyses for the transmission and propagation of electrical impulses. This algorithm is used in reaction–diffusion designs in various areas of science and engineering. Additionally, in the field of medicine, some scientists have found the fractional model of the telegraph equation in a peristaltic flow system [22]. The diverse applications of this sort of model in biomedical and aerospace sciences have drawn scientists to solve the time-fractional problem. The classic PDEs are the specific instances of the fractional-order PDEs as they can be collected by letting the arbitrary-order become derivative to the classical order. The reaction of the fractional-order approach eventually converges to the result of the classical-order approach.

In the literature, there are numerous methods for studying fractional differential equations, such as the reproducing kernel algorithm [23], modified variational iteration method [24] and multistep generalized differential transform method [25]. One of the most recent analytic–numeric methods is the fractional power series method (FPSM). It is an amalgamation of residual error function and fractional Taylor’s series and is based on the presumption that the solution of the equation can be expanded as a fractional power series (FPS). Several problems are solved via this technique, such as the system of fractional PDEs [26], fractional Fokker–Planck models [27] and fuzzy fractional IVPs [28]. Many researchers have explored and debated analytical approximation solutions for linear and non-linear applications of many physical fractional problems via the FPSM, such as the time-fractional Korteweg–de Vries equation [29], fractional Cahn–Hilliard and Gardner equations [30], nonlinear fractional quantum mechanics problems [31] and pseudo-hyperbolic partial differential equations [32].

Finding accurate ASs for time-fractional PDEs indeed forms a difficult problem and is yet a crucial matter; therefore, many researchers turned to numerical algorithms to obtain these solutions, and there has been an insistent requirement for effective conventional analytical or semi-approximate schemes to find accurate ASs for such models. This gives us the incentive, in this analysis, to explore effective accurate ASs. Motivated by the previous discussion, our work purpose is to design a novel solution scheme that combines the FPSM and the Laplace transformation (LT) for generating accurate ASs to time-FHTEs (1) and (2). The novel scheme, called the Laplace FPSM, is proposed and seen as an excellent mathematical tool for improving the effectiveness of the FPSM for solving specific classes of coupled systems of both linear and non-linear time-fractional PDEs straightforwardly and effectively [33]. The Laplace FPSM provides a solution in the form of a fast convergence Maclaurin series, either exact or with ASs. It has been used to study a wide range of physical issues, including generating analytical data and for various systems of linear and non-linear fractional problems [34], studying a non-linear time-fractional generalized biological population model [35], solving temporal time-fractional gas dynamics equations [36], solving non-linear time-fractional Kolmogorov and Rosenau–Hyman models with suitable initial data [37] and investigating the ASs for a nonlinear fractional reaction–diffusion for a bacteria growth model [38].

The set of rules for the recommended approach relies on converting the studied equation into the LT space, creating an AS to the new Laplace equation and then obtaining an AS to the main equation by running the inverse LT. The new method can be used to produce FPS solutions for both linear and non-linear fractional PDEs, with no grand, unsanctified limitations. Different from the traditional FPSM, which neither necessitates comparing the components of the identical terms nor requires utilizing a recurrence relationship, the suggested method depends mainly on the concept of the limit in discovering the series components, not by using fractional derivatives, as the FPSM does. By including a fast convergence series, the suggested scheme can produce both a closed-form and accurate approximation solutions. The motivation of this analysis is to extend the Laplace FPSM for generating accurate ASs of multi-dimensional time-FHTEs in light of the time-fractional derivative in the Caputo sense.

The rest of this analysis is organized as follows. In Section 2, we revisited some primary notions from the fractional calculus theory and provided useful definitions, notations and basic properties utilized in the sequel of our work. In Section 3, a numeric–analytic Laplace FPSM has been described to investigate the solutions of nonlinear TFPDEs. In Section 4, three physical applications involving various kinds of non-linear TFPDEs are implemented to show the efficiency and applicability of the present scheme. Meanwhile, numerical outcomes and physical demonstrations are stated and followed by some conclusions in Section 5.

2. Preliminaries Results

In this section, we recall the mathematical preliminaries of some fractional operators and the Laplace transform operator, as well as review the essential theories and primary results related to fractional Taylor’s formula in the Laplace space.

Definition 1

([1]). The $\alpha$-th time fractional Riemann–Liouville integral operator of $\omega \left(x,t\right):I\times \left[0,1\right]\to ℝ,$ denoted by ${\mathcal{J}}_t^{\alpha },$is given by

$$\begin{gathered} {\mathcal{J}}_t^{\alpha }\omega \left(x,t\right)=\frac{1}{\Gamma \left(\alpha \right)}\underset{0}{\overset{t}{{\displaystyle \int }}}\frac{\omega \left(x,\vartheta \right)}{{\left(t-\vartheta \right)}^{1-\alpha }}d\vartheta , \alpha \in \left(n-1,n\right), n\in \mathbb{N}, \\ {\mathcal{J}}_t^0\omega \left(x,t\right)=\omega \left(x,t\right). \end{gathered}$$

(3)

Definition 2

([2]). The $\alpha$-th time fractional derivative in the Caputo sense of $\omega \left(x,t\right):I\times \left[0,1\right]\to ℝ,$ denoted by ${\partial }_t^{\alpha }$, is given by

$${\partial }_t^{\alpha }\omega \left(x,t\right)=\{\begin{array}{ll}\frac{{\partial }^n}{\partial x^n}\omega \left(x,t\right),\hfill & \alpha =0 \hfill \\ {\mathcal{J}}_t^{n-\alpha }\left(\frac{{\partial }^n}{\partial x^n}\omega \left(x,t\right)\right),\hfill & \alpha \in \left(n-1,n\right), n\in \mathbb{N}\hfill \end{array}.$$

(4)

Definition 3

([34]). Let $\omega \left(x,t\right):I\times \left[0,1\right]\to ℝ$. The LT of $\omega \left(x,t\right)$ is given by

$$\mathcal{W}\left(x,\zeta \right)=ℒ\left\{\omega \left(x,t\right)\right\}=\underset{0}{\overset{\infty }{{\displaystyle \int }}}\omega \left(x,t\right) e^{-\zeta t}dt, \zeta >\rho ,$$

(5)

and the inverse LT of $\mathcal{W}\left(x,\zeta \right)$ is given by

$$\omega \left(x,t\right)={ℒ}^{-1}\left\{\mathcal{W}\left(x,\zeta \right)\right\}=\underset{ϵ-i\infty }{\overset{ϵ+i\infty }{{\displaystyle \int }}}\mathcal{W}\left(x,\zeta \right) e^{\zeta t}ds, ϵ=\Re \mathfrak{e}\left(\zeta \right)>{ϵ}_0,$$

(6)

with the following characteristics:

• $ℒ\left\{t^{m\alpha }\right\}=\frac{\Gamma \left(m\alpha +1\right)}{{\zeta }^{m\alpha +1}},$ $\alpha >-1$;
• $\underset{\zeta \to \infty }{\lim }\zeta \mathcal{W}\left(x,\zeta \right)=\omega \left(x,0\right)$;
• $ℒ\left\{a\omega \left(x,t\right)+bv\left(x,t\right)\right\}=a\mathcal{W}\left(x,\zeta \right)+bV\left(x,\zeta \right)$, for any $a,b\in ℝ$;
• ${ℒ}^{-1}\left\{a\mathcal{W}\left(x,\zeta \right)+bV\left(x,\zeta \right)\right\}=a\omega \left(x,t\right)+bv\left(x,t\right)$;

where $\mathcal{W}\left(x,\zeta \right)=ℒ\left\{\omega \left(x,t\right)\right\}$, and $V\left(x,\zeta \right)=ℒ\left\{v\left(x,t\right)\right\}$.

Lemma 1.

Suppose that $\omega \left(x,t\right):I\times \left[0,1\right]\to ℝ$ be of an exponential order. Then, we have

(1)

$ℒ\left\{{\partial }_t^{\alpha }\omega \left(x,t\right)\right\}={\zeta }^{\alpha }\mathcal{W}\left(x,\zeta \right)-{\sum }_{k=0}^{n-1}{\zeta }^{\alpha -k-1}{\omega }_t^{\left(k\right)}\left(x,0\right),\alpha \in \left(n-1,n\right],n\in \mathbb{N}.$

(2)

$ℒ\left\{{\partial }_t^{m\alpha }\omega \left(x,t\right)\right\}=s^{m\alpha }\mathcal{W}\left(x,\zeta \right)-{\sum }_{k=0}^{m-1}{\zeta }^{\left(m-k\right)\alpha -1}{\partial }_t^{k\alpha }\omega \left(x,0\right),\alpha \in \left(0,1\right],m\in \mathbb{N}.$

Theorem 1

([33]). Assume that the transform function $\mathcal{W}\left(x,\zeta \right)=ℒ\left\{\omega \left(x,t\right)\right\}$ could be provided in the following Laplace series expansion (LSE).

$$\mathcal{W}\left(x,\zeta \right)={\displaystyle \sum }_{n=0}^{\infty }\frac{{\rho }_n\left(x\right)}{{\zeta }^{n\alpha +1}},\zeta >0,\alpha \in (0,1],$$

(7)

where the coefficients ${\rho }_n\left(x\right)={\partial }_t^{n\alpha }\omega \left(x,0\right).$

Theorem 2

([35]). Let the transform function $\mathcal{W}\left(x,\zeta \right)$ be expressed in the form of the LSE (7). If $\left| \zeta ℒ\left\{{\partial }_t^{\left(n+1\right)\alpha }\omega \left(x,t\right)\right\}\right|\le \ell \left(x\right)$, for $\alpha \in \left(0,1\right]$, then the remainder of the term of of the new expansion (7) satisfies the following:

$$\left|R_n\left(x,\zeta \right)\right|\le \frac{\ell \left(x\right)}{{\zeta }^{1+\left(n+1\right)\alpha }}, x\in I, {\eta }_1<\xi \le {\eta }_2.$$

(8)

Remark 1.

The inverse LT of $\mathcal{W}\left(x,\zeta \right)$ has the following multiple fractional series (MFS) form:

$${ℒ}^{-1}\left\{\mathcal{W}\left(x,\zeta \right)\right\}={\displaystyle \sum }_{n=0}^{\infty }\frac{{\partial }_t^{n\alpha }\omega \left(x,0\right)}{\Gamma \left(n\alpha +1\right)} t^{n\alpha }, t\ge 0, \alpha \in (0,1],$$

(9)

3. Construction of MFS-ASs via Laplace FPSM

The Laplace FPSM is an approximate–analytic notion specifically proposed to generate the MFS-ASs for various categories of FDEs and time-fractional PDEs arising in natural science. The present method is instituted based on using the principle of the LT, in which the main equation is solved in view of the FPSM after transforming it into a new space. The Laplace FPSM has great competence in solving the fractional phenomena due to being characterized by ease and speed in terms of the creation of the MFS expansions. The goal of this section is to explain the procedure of the Laplace FPSM in generating the MFS-ASs to a one-dimensional time-FHTE (1). More particularly, we will handle the following non-linear time-fractional initial value problem (IVP).

$${\partial }_t^{2\alpha }\omega \left(x,t\right)+\gamma {\omega }^2\left(x,t\right)+\mu {\partial }_t^{\alpha }\omega \left(x,t\right)=D_x^2\omega \left(x,t\right)+f\left(x,t\right),t\ge 0,0<\alpha \le 1,$$

(10)

with the IC’s

$$\omega \left(x,0\right)={\rho }_0\left(x\right),\mathrm{and}{\partial }_t^{\alpha }\omega \left(x,0\right)={\rho }_1\left(x\right),$$

(11)

where $\omega \left(x,t\right)$ is the unknown analytical function to be identified, and ${\rho }_0, {\rho }_1, f$ are continuous functions. The existence and the uniqueness of the solution are assumed.

Now, for generating the MFS-AS for IVPs (10) and (11), we do the subsequent iterations.

According to the Laplace FPSM [33,35], we convert the non-linear time-FHTE (10) to a Laplace space via performing the LT to both sides of the FHTE (10). With aid of the essential characteristics of the LT in Lemma 1, we obtain

$$\begin{array}{cc}\hfill \mathcal{W}\left(x,\zeta \right)-\frac{\omega \left(x,0\right)}{\zeta }& -\frac{{\partial }_t^{\alpha }\omega \left(x,0\right)}{{\zeta }^{\alpha +1}}+\frac{\mu }{{\zeta }^{\alpha }}\mathcal{W}\left(x,\zeta \right)-\frac{\mu \omega \left(x,0\right)}{{\zeta }^{\alpha +1}}+\frac{\gamma }{{\zeta }^{2\alpha }}ℒ\left\{{\left({ℒ}^{-1}\left[\mathcal{W}\left(x,\zeta \right)\right]\right)}^2\right\}\hfill \\ \hfill =& \frac{1}{{\zeta }^{2\alpha }}{D}_x^2\mathcal{W}\left(x,\zeta \right)+\frac{1}{{\zeta }^{2\alpha }}ℱ\left(x,\zeta \right),\hfill \end{array}$$

(12)

where $\mathcal{W}\left(x,\zeta \right)=ℒ\left\{\omega \left(x,t\right)\right\}$, and $ℱ\left(x,\zeta \right)=ℒ\left\{f\left(x,t\right)\right\}$.

Hence, by using ICs (11), the Laplace Equation (12) could be expressed as

$$\mathcal{W}\left(x,\zeta \right)-\frac{{\rho }_0\left(x\right)}{\zeta }-\frac{{\rho }_1\left(x\right)}{{\zeta }^{\alpha +1}}+\frac{\mu }{{\zeta }^{\alpha }}\mathcal{W}\left(x,\zeta \right)-\frac{\mu {\rho }_0\left(x\right)}{{\zeta }^{\alpha +1}}+\frac{\gamma }{{\zeta }^{2\alpha }}ℒ\left\{{\left({ℒ}^{-1}\left[\mathcal{W}\left(x,\zeta \right)\right]\right)}^2\right\}=\frac{1}{{\zeta }^{2\alpha }}{D}_x^2\mathcal{W}\left(x,\zeta \right)+\frac{1}{{\zeta }^{2\alpha }}ℱ\left(x,\zeta \right).$$

(13)

Next, the Laplace FPSM consists of expressing the solution of (13) as the following infinite (LSE):

$$\mathcal{W}\left(x,\zeta \right)={\displaystyle \sum }_{n=0}^{\infty }\frac{{\rho }_n\left(x\right)}{{\zeta }^{n\alpha +1}} \zeta >0,$$

(14)

and the $j$th-LSE takes the form

$${\mathcal{W}}_j\left(x,\zeta \right)=\frac{{\rho }_0\left(x\right)}{\zeta }+\frac{\rho \left(x\right)}{{\zeta }^{\alpha +1}}+{\displaystyle \sum }_{n=2}^j\frac{{\rho }_n\left(x\right)}{{\zeta }^{n\alpha +1}} \zeta >0,$$

(15)

where the unknown functions ${\rho }_n\left(x\right):n=2,3,\dots ,j$ could be determined by looking at the solution of $\underset{\zeta \to \infty }{\lim }{\zeta }^{1+j\alpha }ℒ\left\{Re{s}^j\left({\mathcal{W}}_j\left(x,\zeta \right)\right)\right\}=0$ so that $ℒ\left\{Re{s}^j\left({\mathcal{W}}_j\left(x,\zeta \right)\right)\right\}$ is identified as the $j$th-Laplace residual error (LRE) function of (13), given by

$$\begin{array}{c}ℒ\left\{Re{s}^j\left({\mathcal{W}}_j\left(x,\zeta \right)\right)\right\}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={\mathcal{W}}_j\left(x,\zeta \right)-\frac{{\rho }_0\left(x\right)}{\zeta }-\frac{{\rho }_1\left(x\right)}{{\zeta }^{\alpha +1}}+\frac{\mu }{{\zeta }^{\alpha }}{\mathcal{W}}_j\left(x,\zeta \right)-\frac{\mu {\rho }_0\left(x\right)}{{\zeta }^{\alpha +1}}+\frac{\gamma }{{\zeta }^{2\alpha }}ℒ\left\{{\left({ℒ}^{-1}\left[{\mathcal{W}}_j\left(x,\zeta \right)\right]\right)}^2\right\}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{1}{{\zeta }^{2\alpha }}{D}_x^2{\mathcal{W}}_j\left(x,\zeta \right)-\frac{1}{{\zeta }^{2\alpha }}ℱ\left(x,\zeta \right).\hfill \end{array}$$

(16)

The $\infty$-th LRE of (12) is therefore given by

$$\begin{array}{c}\underset{j\to \infty }{\lim }ℒ\left\{Re{s}^j\left({\mathcal{W}}_j\left(x,\zeta \right)\right)\right\}=ℒ\left\{Res\left(\mathcal{W}\left(x,\zeta \right)\right)\right\} \hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\mathcal{W}\left(x,\zeta \right)-\frac{{\rho }_0\left(x\right)}{\zeta }-\frac{{\rho }_1\left(x\right)}{{\zeta }^{\alpha +1}}+\frac{\mu }{{\zeta }^{\alpha }}\mathcal{W}\left(x,\zeta \right)-\frac{\mu {\rho }_0\left(x\right)}{{\zeta }^{\alpha +1}}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{\gamma }{{\zeta }^{2\alpha }}ℒ\left\{{\left({ℒ}^{-1}\left[\mathcal{W}\left(x,\zeta \right)\right]\right)}^2\right\}-\frac{1}{{\zeta }^{2\alpha }}{D}_x^2\mathcal{W}\left(x,\zeta \right)-\frac{1}{{\zeta }^{2\alpha }}ℱ\left(x,\zeta \right).\hfill \end{array}$$

(17)

Some useful results of the LRE function, which are basic for generating the MFS-ASs, are listed as:

▪

$\underset{j\to \infty }{\lim }ℒ\left\{Re{s}^j\left({\mathcal{W}}_j\left(x,\zeta \right)\right)\right\}=ℒ\left\{Res\left(\mathcal{W}\left(x,\zeta \right)\right)\right\}$, and $ℒ\left\{Res\left(\mathcal{W}\left(x,\zeta \right)\right)\right\}=0$ for $x\in ℝ$, and $\zeta >0$.

▪

$\underset{\zeta \to \infty }{\lim }\zeta ℒ\left\{Res\left(\mathcal{W}\left(x,\zeta \right)\right)\right\}=0$, and $\underset{\zeta \to \infty }{\lim }\zeta ℒ\left\{Re{s}^j\left({\mathcal{W}}_j\left(x,\zeta \right)\right)\right\}$ for $x\in ℝ$, and $\zeta >0$.

▪

$\underset{\zeta \to \infty }{\lim }{\zeta }^{1+j\alpha }ℒ\left\{Res\left(\mathcal{W}\left(x,\zeta \right)\right)\right\}=0$, and $\underset{\zeta \to \infty }{\lim }{\zeta }^{1+j\alpha }ℒ\left\{Re{s}^j\left({\mathcal{W}}_j\left(x,\zeta \right)\right)\right\}=0$, for $x\in ℝ$, $\zeta >0$, and $j=2,3,4\dots$.

Following, we show the method finding the second MFS-AS of the non-linear time FHTE (10).

Suppose that the first LSE of (11) takes the form ${\mathcal{W}}_1\left(x,\zeta \right)=\frac{{\rho }_0\left(x\right)}{\zeta }+\frac{{\rho }_1\left(x\right)}{{\zeta }^{\alpha +1}}.$ Therefore, the second LSE of (12) has the form

$${\mathcal{W}}_2\left(x,\zeta \right)=\frac{{\rho }_0\left(x\right)}{\zeta }+\frac{{\rho }_1\left(x\right)}{{\zeta }^{\alpha +1}}+\frac{{\rho }_2\left(x\right)}{{\zeta }^{2\alpha +1}}.$$

(18)

whilst the second LRE of (11) will be given as

$$\begin{array}{c}ℒ\left\{Re{s}^2\left({\mathcal{W}}_2\left(x,\zeta \right)\right)\right\}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\frac{{\rho }_2\left(x\right)}{{\zeta }^{2\alpha +1}}+\frac{\mu }{{\zeta }^{\alpha }}\left(\frac{{\rho }_0\left(x\right)}{\zeta }+\frac{{\rho }_1\left(x\right)}{{\zeta }^{\alpha +1}}+\frac{{\rho }_2\left(x\right)}{{\zeta }^{2\alpha +1}}\right)-\frac{\mu {\rho }_0\left(x\right)}{{\zeta }^{\alpha +1}}+\frac{\gamma }{{\zeta }^{2\alpha }}ℒ\left\{{\left({ℒ}^{-1}\left[\frac{{\rho }_0\left(x\right)}{\zeta }+\frac{{\rho }_1\left(x\right)}{{\zeta }^{\alpha +1}}+\frac{{\rho }_2\left(x\right)}{{\zeta }^{2\alpha +1}}\right]\right)}^2\right\}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{1}{{\zeta }^{2\alpha }}{D}_x^2\left(\frac{{\rho }_0\left(x\right)}{\zeta }+\frac{{\rho }_1\left(x\right)}{{\zeta }^{\alpha +1}}+\frac{{\rho }_2\left(x\right)}{{\zeta }^{2\alpha +1}}\right)-\frac{1}{{\zeta }^{2\alpha }}ℱ\left(x,\zeta \right).\hfill \end{array}$$

(19)

Then, one can multiply (19) by the factor ${\zeta }^{2\alpha +1}$ to obtain

$$\begin{array}{c}{\zeta }^{2\alpha +1}ℒ\left\{Re{s}^2\left({\mathcal{W}}_2\left(x,\zeta \right)\right)\right\}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\gamma {\rho }_0^2\left(x\right)+\mu {\rho }_1\left(x\right)+\frac{2\gamma {\rho }_0\left(x\right){\rho }_1\left(x\right)}{{\zeta }^{\alpha }}+\frac{\gamma \Gamma \left(2\alpha +1\right){\rho }_1^2\left(x\right)}{{\Gamma }^2\left(\alpha +1\right){\zeta }^{2\alpha }}+{\rho }_2\left(x\right)+\frac{\mu {\rho }_2\left(x\right)}{{\zeta }^{\alpha }}+\frac{2\gamma {\rho }_0\left(x\right){\rho }_2\left(x\right)}{{\zeta }^{2\alpha }}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{2\gamma \Gamma \left(3\alpha +1\right){\rho }_1\left(x\right){\rho }_2\left(x\right)}{\Gamma \left(3\alpha +1\right)\Gamma \left(2\alpha +1\right){\zeta }^{3\alpha }}+\frac{\gamma \Gamma \left(4\alpha +1\right){\rho }_2^2\left(x\right)}{{\Gamma }^2\left(\alpha +1\right){\zeta }^{4\alpha }}-{\rho }_0^{″}\left(x\right)-\frac{{\rho }_1^{″}\left(x\right)}{{\zeta }^{\alpha }}-\frac{{\rho }_2^{″}\left(x\right)}{{\zeta }^{2\alpha }}+\zeta ℱ\left(x,\zeta \right).\hfill \end{array}$$

(20)

Depending on the result $\underset{\zeta \to \infty }{\lim }{\zeta }^{1+j\alpha }ℒ\left\{Re{s}^j\left({\mathcal{W}}_j\left(x,\zeta \right)\right)\right\}=0$, for $j=2$, and using the fact $\underset{\zeta \to \infty }{\lim }\zeta ℱ\left(x,\zeta \right)=f\left(x,0\right)$, the solution of (20) will be as:

$${\rho }_2\left(x\right)={\rho }_0^{″}\left(x\right)-\mu {\rho }_1\left(x\right)-\gamma {\rho }_0^2\left(x\right)-f\left(x,0\right).$$

(21)

Thus, the second LSE of (13) could be written in the form of

$${\mathcal{W}}_2\left(x,\zeta \right)=\frac{{\rho }_0\left(x\right)}{\zeta }+\frac{{\rho }_1\left(x\right)}{{\zeta }^{\alpha +1}}+\frac{1}{{\zeta }^{2\alpha +1}}\left({\rho }_0^{″}\left(x\right)-\mu {\rho }_1\left(x\right)-\gamma {\rho }_0^2\left(x\right)-f\left(x,0\right)\right).$$

(22)

Correspondingly, by running the inverse LT on both sides of the second LSE (22), one can reach the second MFS-AS of the main Equation (10) with

$${\omega }_2\left(x,t\right)={\rho }_0\left(x\right)+{\rho }_1\left(x\right)\frac{t^{\alpha }}{\Gamma \left(\alpha +1\right)}+\left({\rho }_0^{″}\left(x\right)-\mu {\rho }_1\left(x\right)-\gamma {\rho }_0^2\left(x\right)-f\left(x,0\right)\right)\frac{t^{2\alpha }}{\Gamma \left(2\alpha +1\right)}.$$

(23)

Lemma 2.

Suppose that the transform function $\mathcal{W}\left(x,\zeta \right)$, in the form of LSE (15), is the AS of the Laplace Equation (13), then the non-linear term of (13) could be expressed as

$$ℒ\left\{{\left({ℒ}^{-1}\left[\mathcal{W}\left(x,\zeta \right)\right]\right)}^2\right\}={\displaystyle \sum }_{n=0}^{2j}\frac{\Gamma \left(n\alpha +1\right)}{{\zeta }^{n\alpha +1}}{\displaystyle \sum }_{i=max\left[0,n-j\right]}^{min\left[j,n\right]}\frac{{\rho }_i\left(x\right){\rho }_{n-i}\left(x\right)}{\Gamma \left(i\alpha +1\right)\Gamma \left(\left(n-i\right)\alpha +1\right)}, 0\le n\le j.$$

(24)

Theorem 3.

For $\alpha \in \left(0,1\right]$, let the AS of (13) have the form of LSE (7), then the variable coefficients ${\rho }_j\left(x\right)$, for $j\ge 2$, can be given using the recursive formula

$${\rho }_j\left(x\right)=-\gamma \Gamma \left(\left(j-2\right)\alpha +1\right){\displaystyle \sum }_{i=0}^{j-2}\frac{{\rho }_i\left(x\right){\rho }_{j-i-2}\left(x\right)}{\Gamma \left(i\alpha +1\right)\Gamma \left(\left(j-i-2\right)\alpha +1\right)}-\mu {\rho }_{j-1}\left(x\right)+{\rho }_{j-2}^{″}\left(x\right)+{\partial }_t^{\left(j-2\right)\alpha }f\left(x,0\right).$$

(25)

Proof. 

Suppose that the $\mathrm{j}$th-LSE takes the form ${\mathcal{W}}_{\mathrm{j}}\left(\mathrm{x},\mathsf{\zeta }\right)=\frac{{\mathsf{\rho }}_0\left(\mathrm{x}\right)}{\mathsf{\zeta }}+\frac{\mathsf{\rho }\left(\mathrm{x}\right)}{{\mathsf{\zeta }}^{\mathsf{\alpha }+1}}+\sum _{\mathrm{n}=2}^{\mathrm{j}}\frac{{\mathsf{\rho }}_{\mathrm{n}}\left(\mathrm{x}\right)}{{\mathsf{\zeta }}^{\mathrm{n}\mathsf{\alpha }+1}}\mathsf{\zeta }>0$. By using Lemma 2, the $\mathrm{j}$th-LRE function of (13) becomes

$$\begin{array}{c}ℒ\left\{Re{s}^j\left({\mathcal{W}}_j\left(x,\zeta \right)\right)\right\}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={\displaystyle {\displaystyle \sum }_{n=2}^j}\frac{{\rho }_n\left(x\right)}{{\zeta }^{n\alpha +1}}+\mu \left(\frac{\rho \left(x\right)}{{\zeta }^{2\alpha +1}}+{\displaystyle {\displaystyle \sum }_{n=2}^j}\frac{{\rho }_n\left(x\right)}{{\zeta }^{\left(n+1\right)\alpha +1}} \right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\gamma \left({\displaystyle {\displaystyle \sum }_{n=0}^{2j}}\frac{\Gamma \left(n\alpha +1\right)}{{\zeta }^{\left(n+2\right)\alpha +1}}{\displaystyle {\displaystyle \sum }_{i=\max \left[0,n-j\right]}^{\min \left[j,n\right]}}\frac{{\rho }_i\left(x\right){\rho }_{n-i}\left(x\right)}{\Gamma \left(i\alpha +1\right)\Gamma \left(\left(n-i\right)\alpha +1\right)}\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\left(\frac{{\rho }_0^{″}\left(x\right)}{{\zeta }^{2\alpha +1}}+\frac{{\rho }_1^{″}\left(x\right)}{{\zeta }^{3\alpha +1}}+{\displaystyle {\displaystyle \sum }_{n=2}^j}\frac{{\rho }_n^{″}\left(x\right)}{{\zeta }^{\left(n+2\right)\alpha +1}} \right)-\frac{1}{{\zeta }^{2\alpha }}ℱ\left(x,\zeta \right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\frac{\gamma }{{\zeta }^{2\alpha }}{\displaystyle {\displaystyle \sum }_{n=0}^{2j}}\frac{\Gamma \left(n\alpha +1\right)}{{\zeta }^{n\alpha +1}}{\displaystyle {\displaystyle \sum }_{i=\max \left[0,n-j\right]}^{\min \left[j,n\right]}}\frac{{\rho }_i\left(x\right){\rho }_{n-i}\left(x\right)}{\Gamma \left(i\alpha +1\right)\Gamma \left(\left(n-i\right)\alpha +1\right)}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{\mu }{{\zeta }^{\alpha }}{\displaystyle {\displaystyle \sum }_{n=0}^j}\frac{{\rho }_n\left(x\right)}{{\zeta }^{n\alpha +1}}+{\displaystyle {\displaystyle \sum }_{n=2}^j}\frac{{\rho }_n\left(x\right)}{{\zeta }^{n\alpha +1}}-\frac{1}{{\zeta }^{2\alpha }}{\displaystyle {\displaystyle \sum }_{n=0}^j}\frac{{\rho }_n^{″}\left(x\right)}{{\zeta }^{n\alpha +1}}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\mu \frac{{\rho }_0\left(x\right)}{{\zeta }^{\alpha +1}}-\frac{1}{{\zeta }^{2\alpha }}ℱ\left(x,\zeta \right).\hfill \end{array}$$

(26)

Multiplying both sides of (26) by the factor ${\zeta }^{j\alpha +1}$ yields

$$\begin{array}{c}{\zeta }^{j\alpha +1}ℒ\left\{Re{s}^j\left({\mathcal{W}}_j\left(x,\zeta \right)\right)\right\}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\gamma {\zeta }^{\left(j-2\right)\alpha +1}{\displaystyle {\displaystyle \sum }_{n=0}^{2j}}\frac{\Gamma \left(n\alpha +1\right)}{{\zeta }^{n\alpha +1}}{\displaystyle {\displaystyle \sum }_{i=\max \left[0,n-j\right]}^{\min \left[j,n\right]}}\frac{{\rho }_i\left(x\right){\rho }_{n-i}\left(x\right)}{\Gamma \left(i\alpha +1\right)\Gamma \left(\left(n-i\right)\alpha +1\right)}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\mu {\zeta }^{\left(j-1\right)\alpha +1}{\displaystyle {\displaystyle \sum }_{n=0}^j}\frac{{\rho }_n\left(x\right)}{{\zeta }^{n\alpha +1}}+{\zeta }^{j\alpha +1}{\displaystyle {\displaystyle \sum }_{n=2}^j}\frac{{\rho }_n\left(x\right)}{{\zeta }^{n\alpha +1}}-{\zeta }^{\left(j-2\right)\alpha +1}{\displaystyle {\displaystyle \sum }_{n=0}^j}\frac{{\rho }_n^{″}\left(x\right)}{{\zeta }^{n\alpha +1}}-\mu {\zeta }^{\left(j-1\right)\alpha }{\rho }_0\left(x\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-{\zeta }^{\left(j-2\right)\alpha +1}ℱ\left(x,\zeta \right).\hfill \end{array}$$

(27)

By aid of the fact $\underset{\zeta \to \infty }{\lim }{\zeta }^{1+j\alpha }ℒ\left\{Re{s}^j\left({\mathcal{W}}_j\left(x,\zeta \right)\right)\right\}=0$, and using Lemma 1, part (2), we conclude that

$$\begin{gathered} {\rho }_j\left(x\right)=-\gamma \Gamma \left(\left(j-2\right)\alpha +1\right){\displaystyle \sum }_{i=0}^{j-2}\frac{{\rho }_i\left(x\right){\rho }_{j-i-2}\left(x\right)}{\Gamma \left(i\alpha +1\right)\Gamma \left(\left(j-i-2\right)\alpha +1\right)}-\mu {\rho }_{j-1}\left(x\right) \\ +{\rho }_{j-2}^{″}\left(x\right)+{\partial }_t^{\left(j-2\right)\alpha }f\left(x,0\right), j=2,3,4,\dots \end{gathered}$$

(28)

 □

Corollary 1.

For $\alpha \in (0,1]$, the MFS-AS of the non-linear IVPs (10) and (11) has the following shape:

$$\begin{array}{c}\omega \left(x,t\right)={\rho }_0\left(x\right)+{\rho }_1\left(x\right)\frac{t^{\alpha }}{\Gamma \left(\alpha +1\right)}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\displaystyle {\displaystyle \sum }_{j=2}^{\infty }}({\partial }_t^{\left(j-2\right)\alpha }f\left(x,0\right)-\mu {\rho }_{j-1}\left(x\right)+{\rho }_{j-2}^{″}\left(x\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\gamma \Gamma \left(\left(j-2\right)\alpha +1\right){\displaystyle {\displaystyle \sum }_{i=0}^{j-2}}\frac{{\rho }_i\left(x\right){\rho }_{j-i-2}\left(x\right)}{\Gamma \left(i\alpha +1\right)\Gamma \left(\left(j-i-2\right)\alpha +1\right)})\frac{t^{j\alpha }}{\Gamma \left(j\alpha +1\right)},t\ge 0,\hfill \end{array}$$

(29)

Proof. 

Upon applying the Laplace FPSM in finding the MFS-AS of the target problem, and using Theorem 3, the series solution of (13) has the following LSE form:

$$\begin{array}{c}\mathcal{W}\left(x,\zeta \right)=\frac{{\rho }_0\left(x\right)}{\zeta }+\frac{{\rho }_1\left(x\right)}{{\zeta }^{\alpha +1}}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\displaystyle {\displaystyle \sum }_{j=2}^{\infty }}\frac{1}{{\zeta }^{j\alpha +1}}({\partial }_t^{\left(j-2\right)\alpha }f\left(x,0\right)-\mu {\rho }_{j-1}\left(x\right)+{\rho }_{j-2}^{″}\left(x\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-2\gamma \Gamma \left(\left(j-2\right)\alpha +1\right){\displaystyle {\displaystyle \sum }_{i=0}^{j-2}}\frac{{\rho }_i\left(x\right){\rho }_{j-i-2}\left(x\right)}{\Gamma \left(i\alpha +1\right)\Gamma \left(\left(j-i-2\right)\alpha +1\right)}), \zeta >0,\hfill \end{array}$$

(30)

By operating the inverse LT for both sides of the fractional expansion (30), this gives the MFS-AS of the nonlinear time-fractional IVP (10) and (11) in terms of the infinite series form.

$$\begin{array}{c}\omega \left(x,t\right)={\rho }_0\left(x\right)+{\rho }_1\left(x\right)\frac{t^{\alpha }}{\Gamma \left(\alpha +1\right)}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\displaystyle {\displaystyle \sum }_{j=2}^{\infty }}({\partial }_t^{\left(j-2\right)\alpha }f\left(x,0\right)-\mu {\rho }_{j-1}\left(x\right)+{\rho }_{j-2}^{″}\left(x\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\gamma \Gamma \left(\left(j-2\right)\alpha +1\right){\displaystyle {\displaystyle \sum }_{i=0}^{j-2}}\frac{{\rho }_i\left(x\right){\rho }_{j-i-2}\left(x\right)}{\Gamma \left(i\alpha +1\right)\Gamma \left(\left(j-i-2\right)\alpha +1\right)})\frac{t^{j\alpha }}{\Gamma \left(j\alpha +1\right)},t\ge 0.\hfill \end{array}$$

(31)

 □

4. Numerical Experiments

The time-fractional PDEs are excellent tools for modeling both linear and non-linear dispersed phenomena. In this section, we study and predict the MFSASs for three attractive time FHTEs subject to appropriate initial data to clarify the effectiveness and applicability of the Laplace FPSM. Here, all of the calculations and simulations were carried out using Mathematica 12.

Example 1.

Consider the following linear time-FHTE [19]:

$${\partial }_t^{2\alpha }\omega \left(x,t\right)+\omega \left(x,t\right)+2{\partial }_t^{\alpha }\omega \left(x,t\right)=D_x^2\omega \left(x,t\right)$$

(32)

which is subject to

$$\omega \left(x,0\right)=e^x,and{\partial }_t^{\alpha }\omega \left(x,0\right)=-2e^x$$

(33)

where $x\in R, t\ge 0, \alpha \in \left(0,1\right]$.

Now, applying the LT operator to (32), and owing to the fact $\left\{{\partial }_t^{2\alpha }\omega \left(x,t\right)\right\}={\zeta }^{2\alpha }\mathcal{W}\left(x,\zeta \right)+2e^x{\zeta }^{2\alpha -1}-e^x{\zeta }^{\alpha -1}$, we reach the Laplace equation:

$$\mathcal{W}\left(x,\zeta \right)+\frac{e^x}{\zeta }-\frac{2e^x}{{\zeta }^{\alpha +1}}+\frac{2}{{\zeta }^{\alpha }}\mathcal{W}\left(x,\zeta \right)-\frac{2e^x}{{\zeta }^{\alpha +1}}+\frac{1}{{\zeta }^{\alpha }}\mathcal{W}\left(x,\zeta \right)=\frac{1}{{\zeta }^{2\alpha }}{D}_x^3\mathcal{W}\left(x,\zeta \right).$$

(34)

The proposed AS $\mathcal{W}\left(x,\zeta \right)$ to (34) has the following LSE:

$$\mathcal{W}\left(x,\zeta \right)=\frac{e^x}{\zeta }-\frac{2e^x}{{\zeta }^{\alpha +1}}+{\displaystyle \sum }_{n=2}^{\infty }\frac{{\rho }_n\left(x\right)}{{\zeta }^{n\alpha +1}},$$

(35)

whereas the $j$th-LSE can be expressed as

$${\mathcal{W}}_j\left(x,\zeta \right)=\frac{e^x}{\zeta }-\frac{2e^x}{{\zeta }^{\alpha +1}}+{\displaystyle \sum }_{n=2}^j\frac{{\rho }_n\left(x\right)}{{\zeta }^{n\alpha +1}},$$

(36)

where the coefficients ${\rho }_n\left(x\right)$, for $n=2,3,\dots j$ are determined by looking at the solution of $\underset{\zeta \to \infty }{lim}{\zeta }^{1+j\alpha }ℒ\left\{Re{s}^j\left({\mathcal{W}}_j\left(x,\zeta \right)\right)\right\}=0$, $Re{s}^j$ being the $j$-th LRE function of (34) and defined by

$$\begin{array}{c}ℒ\left\{Re{s}^j\left({\mathcal{W}}_j\left(x,\zeta \right)\right)\right\}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={\displaystyle {\displaystyle \sum }_{n=2}^j}\frac{{\rho }_n\left(x\right)}{{\zeta }^{n\alpha +1}}+\frac{2}{{\zeta }^{\alpha }}\left(\frac{e^x}{\zeta }-\frac{2e^x}{{\zeta }^{\alpha +1}}+{\displaystyle {\displaystyle \sum }_{n=2}^j}\frac{{\rho }_n\left(x\right)}{{\zeta }^{n\alpha +1}}\right)-\frac{2e^x}{{\zeta }^{\alpha +1}}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{1}{{\zeta }^{\alpha }}\left(\frac{e^x}{\zeta }-\frac{2e^x}{{\zeta }^{\alpha +1}}+{\displaystyle {\displaystyle \sum }_{n=2}^j}\frac{{\rho }_n\left(x\right)}{{\zeta }^{n\alpha +1}}\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{1}{{\zeta }^{2\alpha }}{D}_x^3\left(\frac{e^x}{\zeta }-\frac{2e^x}{{\zeta }^{\alpha +1}}+{\displaystyle {\displaystyle \sum }_{n=2}^j}\frac{{\rho }_n\left(x\right)}{{\zeta }^{n\alpha +1}}\right).\hfill \end{array}$$

(37)

To determine the second variable coefficient ${\rho }_2\left(x\right)$, put $j=2$ into the 2nd-LRE function (37) to obtain

$$\begin{array}{c}ℒ\left\{Re{s}^2\left({\mathcal{W}}_2\left(x,\zeta \right)\right)\right\}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\frac{{\rho }_2\left(x\right)}{{\zeta }^{2\alpha +1}}+\frac{2}{{\zeta }^{\alpha }}\left(\frac{e^x}{\zeta }-\frac{2e^x}{{\zeta }^{\alpha +1}}+\frac{{\rho }_2\left(x\right)}{{\zeta }^{2\alpha +1}}\right)-\frac{2e^x}{{\zeta }^{\alpha +1}}+\frac{1}{{\zeta }^{\alpha }}\left(\frac{e^x}{\zeta }-\frac{2e^x}{{\zeta }^{\alpha +1}}+\frac{{\rho }_2\left(x\right)}{{\zeta }^{2\alpha +1}}\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{1}{{\zeta }^{2\alpha }}\left(\frac{e^x}{\zeta }-\frac{2e^x}{{\zeta }^{\alpha +1}}+\frac{{\rho }_2^{″}\left(x\right)}{{\zeta }^{2\alpha +1}}\right). \hfill \end{array}$$

(38)

Then, we multiply (38) by ${\zeta }^{\alpha +1}$ to receive

$${\zeta }^{2\alpha +1}ℒ\left\{Re{s}^2\left({\mathcal{W}}_2\left(x,\zeta \right)\right)\right\}={\rho }_2\left(x\right)-4e^x-\frac{2e^x}{{\zeta }^{\alpha }}\frac{3{\rho }_2\left(x\right)}{{\zeta }^{\alpha }}-\frac{e^x}{{\zeta }^{\alpha }}+\frac{2e^x\left(x\right)}{{\zeta }^{2\alpha }}.$$

(39)

Taking the limit to both sides of (39) as $\zeta \to \infty$, and by solving the obtained limit, this yield that ${\rho }_2\left(x\right)=4e^x$.

Again, for $j=3$, we have

$$\begin{array}{c}ℒ\left\{Re{s}^3\left({\mathcal{W}}_3\left(x,\zeta \right)\right)\right\}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\frac{{\rho }_3\left(x\right)}{{\zeta }^{3\alpha +1}}+\frac{4e^x}{{\zeta }^{2\alpha +1}}+\frac{2}{{\zeta }^{\alpha }}\left(\frac{e^x}{\zeta }-\frac{2e^x}{{\zeta }^{\alpha +1}}+\frac{4e^x}{{\zeta }^{2\alpha +1}}+\frac{{\rho }_3\left(x\right)}{{\zeta }^{3\alpha +1}}\right)-\frac{2e^x}{{\zeta }^{\alpha +1}}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{1}{{\zeta }^{\alpha }}\left(\frac{e^x}{\zeta }-\frac{2e^x}{{\zeta }^{\alpha +1}}+\frac{4e^x}{{\zeta }^{2\alpha +1}}+\frac{{\rho }_3\left(x\right)}{{\zeta }^{3\alpha +1}}\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{1}{{\zeta }^{2\alpha }}\left(\frac{e^x}{\zeta }-\frac{2e^x}{{\zeta }^{\alpha +1}}+\frac{4e^x}{{\zeta }^{2\alpha +1}}+\frac{{\rho }_3^{″}\left(x\right)}{{\zeta }^{3\alpha +1}}\right).\hfill \end{array}$$

(40)

Then, we multiply (40) by ${\zeta }^{3\alpha +1}$ to obtain

$${\zeta }^{3\alpha +1}ℒ\left\{Re{s}^3\left({\mathcal{W}}_3\left(x,\zeta \right)\right)\right\}=8e^x+{\rho }_3\left(x\right)+\frac{{\rho }_3\left(x\right)}{{\zeta }^{2\alpha }}+2\frac{{\rho }_3\left(x\right)}{{\zeta }^{\alpha }}-\frac{{\rho }_3^{″}\left(x\right)}{{\zeta }^{2\alpha }}.$$

(41)

Based upon the fact that $\underset{\zeta \to \infty }{lim}{\zeta }^{3\alpha +1}ℒ\left\{Re{s}^3\left({\mathcal{W}}_3\left(x,\zeta \right)\right)\right\}=0$, we recognized that ${\rho }_3\left(x\right)=-8e^x$.

Similarly, for $j=4$, we see that

$${\zeta }^{4\alpha +1}ℒ\left\{Re{s}^4\left({\mathcal{W}}_4\left(x,\zeta \right)\right)\right\}={\rho }_4\left(x\right)-16e^x+\frac{{\rho }_4\left(x\right)}{{\zeta }^{2\alpha }}+2\frac{{\rho }_4\left(x\right)}{{\zeta }^{\alpha }}-\frac{{\rho }_4^{″}\left(x\right)}{{\zeta }^{2\alpha }}.$$

(42)

Dependent on the fact that $\underset{\zeta \to \infty }{lim}{\zeta }^{4\alpha +1}ℒ\left\{Re{s}^4\left({\mathcal{W}}_4\left(x,\zeta \right)\right)\right\}=0$, we obtain that ${\rho }_4\left(x\right)=16e^x$.

Following the same procedure, the rest of the variable coefficients could be obtained for $j>4$, and the LSE solution of (34) could be written in terms of the following infinite series:

$$\mathcal{W}\left(x,\zeta \right)=\frac{e^x}{\zeta }-\frac{2e^x}{{\zeta }^{\alpha +1}}+\frac{4e^x}{{\zeta }^{2\alpha +1}}-\frac{8e^x}{{\zeta }^{3\alpha +1}}+\frac{16e^x}{{\zeta }^{4\alpha +1}}-\frac{32e^x}{{\zeta }^{5\alpha +1}}+\frac{64e^x}{{\zeta }^{6\alpha +1}}+\dots .$$

(43)

By applying the inverse LT on (43), we achieve the following MFS-AS of the linear time-FHTEs (32) and (33) in the terms of infinite series form:

$$\begin{array}{c}\omega \left(x,t\right)=e^x\left(1-\frac{2t^{\alpha }}{\Gamma \left(\alpha +1\right)}+\frac{4t^{2\alpha }}{\Gamma \left(2\alpha +1\right)}-\frac{8t^{3\alpha }}{\Gamma \left(3\alpha +1\right)}+\frac{16t^{4\alpha }}{\Gamma \left(4\alpha +1\right)}-\frac{32t^{5\alpha }}{\Gamma \left(5\alpha +1\right)}+\frac{64t^{6\alpha }}{\Gamma \left(6\alpha +1\right)}+\dots \right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=e^x{\displaystyle {\displaystyle \sum }_{n=0}^{\infty }}{\left(-1\right)}^n\frac{2^n{t}^{n\alpha }}{\Gamma \left(n\alpha +1\right)}=e^x{E}_{\alpha }\left(-2t^{\alpha }\right),\hfill \end{array}$$

(44)

where $E_{\alpha }(\ast )$ is well-known as the Mittag–Leffler function defined in [2].

If we put $\alpha =1$, then the AS of the linear time-FHTEs (32) and (33) takes the form of

$$\omega \left(x,t\right)=e^x\left(1-2t+{\left(2t\right)}^2-{\left(2t\right)}^3+{\left(2t\right)}^4-\dots \right),$$

(45)

which is equivalent to the exact solution $\omega \left(x,t\right)=e^{x-2t}$ of the classical Hyperbolic Telegraph equation [39].

Next, Table 1 illustrates some numerical simulations of the exact, 8th-MFS-AS and absolute errors $\mathbf{\left|}\mathit{\omega }\mathbf{\left(}\mathit{x}\mathbf{,}\mathit{t}\mathbf{\right)}\mathbf{-}{\mathit{\omega }}_{\mathit{j}}\mathbf{\left(}\mathit{x}\mathbf{,}\mathit{t}\mathbf{\right)}\mathbf{\right|}$, when $j=8, 10$ for time-FHTEs (32) and (33) at the standard-order of $\alpha =1$ for various values of $x$ and $t$. Some graphical representations are achieved for the Laplace FPSM outcomes, and the exact solutions of the considered problems (32) and (33) are shown in Figure 1 and Figure 2. Figure 1 displays the geometric behavior of the 8th-MFS-AS at some values of $\alpha \in \left(0,1\right)$ against the exact solution, whereas Figure 2 illustrates the effect of the fractional-order derivative on the behavior of the 8th-MFS-AS at different values of parameter $\alpha$ in a 3D-graph with a space-time domain $\left[-1,1\right]\times \left[0,1\right]$.

Table 1. Numerical simulations for Example 1, when $\alpha =1$.

$\left({\mathit{x}}_{\mathit{s}},{\mathit{t}}_{\mathit{s}}\right)$	$\mathit{\omega }\left(\mathit{x},\mathit{t}\right)$	${\mathit{\omega }}_8\left(\mathit{x},\mathit{t}\right)$	$\left|\mathit{\omega }\left(\mathit{x},\mathit{t}\right)-{\mathit{\omega }}_8\left(\mathit{x},\mathit{t}\right)\right|$	$\left|\mathit{\omega }\left(\mathit{x},\mathit{t}\right)-{\mathit{\omega }}_{10}\left(\mathit{x},\mathit{t}\right)\right|$
$\left(0.4,0.15\right)$	1.105171	1.105171	$7.86\times {10}^{-11}$	$6.46\times {10}^{-14}$
$\left(0.4,0.30\right)$	0.818731	0.818731	$3.91\times {10}^{-8}$	$1.29\times {10}^{-10}$
$\left(0.4,0.45\right)$	0.606531	0.606531	$1.46\times {10}^{-6}$	$1.09\times {10}^{-8}$
$\left(0.4,0.60\right)$	0.449329	0.449329	$1.89\times {10}^{-5}$	$2.52\times {10}^{-7}$
$\left(0.4,0.75\right)$	0.332871	0.332874	$1.37\times {10}^{-4}$	$2.87\times {10}^{-6}$
$\left(0.4,0.90\right)$	0.246597	0.246618	$6.90\times {10}^{-4}$	$2.09\times {10}^{-5}$
$\left(-0.4,0.15\right)$	0.496585	0.496585	$3.53\times {10}^{-11}$	$2.90\times {10}^{-14}$
$\left(-0.4,0.30\right)$	0.367879	0.367879	$1.76\times {10}^{-8}$	$5.80\times {10}^{-11}$
$\left(-0.4,0.45\right)$	0.272532	0.272532	$6.56\times {10}^{-7}$	$4.90\times {10}^{-9}$
$\left(-0.4,0.60\right)$	0.201897	0.201897	$8.50\times {10}^{-6}$	$1.13\times {10}^{-7}$
$\left(-0.4,0.75\right)$	0.149569	0.14957	$6.17\times {10}^{-5}$	$1.29\times {10}^{-6}$
$\left(-0.4,0.90\right)$	0.110803	0.110813	$3.10\times {10}^{-4}$	$9.37\times {10}^{-6}$

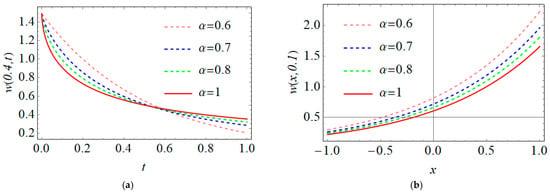
Figure 1. The MFS-AS for time-FHTEs (31) and (32) at various values of $\alpha$; (a) for $x=0.4$ and $t\in \left[0,1\right]$, (b) for $t=0.1$ and $x\in \left[-1,1\right]$.

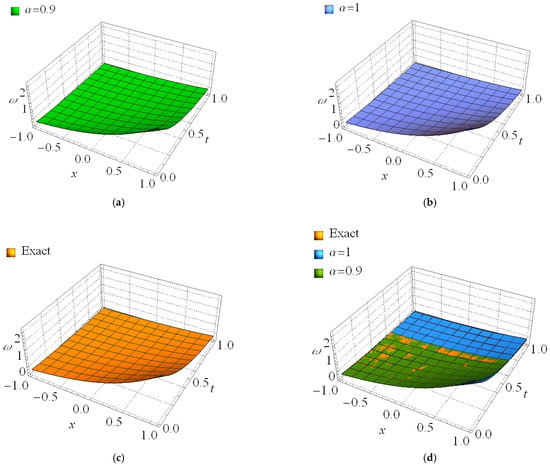
Figure 2. 3D graphs of the obtained solutions for Example 1; (a) MFS-ASs at $\alpha =0.9$; (b) MFS-ASs at $\alpha =1$; (c) Exact solution; (d) the exact solution against the MFS-ASs at $\alpha =1$ and $\alpha =0.9$.

Example 2.

Consider the following nonlinear time-FHTE [20,21]:

$${\partial }_t^{2\alpha }\omega \left(x,t\right)+{\omega }^2\left(x,t\right)+2{\partial }_t^{\alpha }\omega \left(x,t\right)=D_x^2\omega \left(x,t\right)+e^{2x-4t}-e^{x-2t},$$

(46)

which is subject to

$$\omega \left(x,0\right)=e^x,\mathrm{and}{\partial }_t^{\alpha }\omega \left(x,0\right)=-2e^x,$$

(47)

where $x\in R, t\ge 0, \alpha \in \left(0,1\right]$. For an integer case of $\alpha =1$, the exact solution of (46) and (47) is $\omega \left(x,t\right)=e^{x-2t}$.

According to the employment of the Laplace FPSM, we start by taking the LT operator to both sides of (46) and using the IC’s (47) to obtain

$$\begin{array}{c}\mathcal{W}\left(x,\zeta \right)-\frac{e^x}{\zeta }+\frac{2e^x}{{\zeta }^{\alpha +1}}+\frac{2}{{\zeta }^{\alpha }}\mathcal{W}\left(x,\zeta \right)-\frac{2e^x}{{\zeta }^{\alpha +1}}+\frac{1}{{\zeta }^{\alpha }}ℒ\left\{{\left[{ℒ}^{-1}\mathcal{W}\left(x,\zeta \right)\right]}^2\right\}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\frac{1}{{\zeta }^{2\alpha }}{D}_x^2\mathcal{W}\left(x,\zeta \right)+\frac{1}{{\zeta }^{2\alpha }}\left(\frac{e^x}{2+\zeta }-\frac{e^{2x}}{4+\zeta }\right).\hfill \end{array}$$

(48)

Suppose that the $j$-th LSE of (48), then the expansion form is

$${\mathcal{W}}_j\left(x,\zeta \right)=\frac{e^x}{\zeta }-\frac{2e^x}{{\zeta }^{\alpha +1}}+{\displaystyle \sum }_{n=2}^j\frac{{\rho }_n\left(x\right)}{{\zeta }^{n\alpha +1}}.$$

(49)

Next, the $j$-th LRE of (48) is defined as

$$\begin{array}{c}ℒ\left\{Re{s}^j\left({\mathcal{W}}_j\left(x,\zeta \right)\right)\right\}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={\displaystyle {\displaystyle \sum }_{n=2}^j}\frac{{\rho }_n\left(x\right)}{{\zeta }^{n\alpha +1}}+\frac{2}{{\zeta }^{\alpha }}\left(\frac{e^x}{\zeta }-\frac{2e^x}{{\zeta }^{\alpha +1}}+{\displaystyle {\displaystyle \sum }_{n=2}^j}\frac{{\rho }_n\left(x\right)}{{\zeta }^{n\alpha +1}}\right)-\frac{2e^x}{{\zeta }^{\alpha +1}}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{1}{{\zeta }^{\alpha }}ℒ\left\{{\left[{ℒ}^{-1}\left(\frac{e^x}{\zeta }-\frac{2e^x}{{\zeta }^{\alpha +1}}+{\displaystyle {\displaystyle \sum }_{n=2}^j}\frac{{\rho }_n\left(x\right)}{{\zeta }^{n\alpha +1}}\right)\right]}^2\right\}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{1}{{\zeta }^{2\alpha }}\left(\frac{e^x}{\zeta }-\frac{2e^x}{{\zeta }^{\alpha +1}}+{\displaystyle {\displaystyle \sum }_{n=2}^j}\frac{{\rho }_n^{″}\left(x\right)}{{\zeta }^{n\alpha +1}}\right)-\frac{1}{{\zeta }^{2\alpha }}\left(\frac{e^x}{2+\zeta }-\frac{e^{2x}}{4+\zeta }\right).\hfill \end{array}$$

(50)

Therefore, the variable coefficients ${\rho }_n\left(x\right)$, for $n=2,3,4,5,6$ could be determined with help of the recursive Formula (25) mentioned in Theorem 3, which is:

$${\rho }_2\left(x\right)=4e^x,$$

$${\rho }_3\left(x\right)=-8e^x,$$

$${\rho }_4\left(x\right)=\left(16e^x+16e^{2x}-\left(\frac{4e^{2x}}{{\Gamma }^2\left(\alpha +1\right)}+\frac{8e^{2x}}{\Gamma \left(2\alpha +1\right)}\right)\Gamma \left(2\alpha +1\right)\right),$$

$${\rho }_5\left(x\right)=8e^x\left(\frac{e^x\Gamma \left(2\alpha +1\right)}{{\Gamma }^2\left(\alpha +1\right)}+\frac{2e^x\Gamma \left(3\alpha +1\right)}{\Gamma \left(\alpha +1\right)\Gamma \left(2\alpha +1\right)}-8e^x-4\right),$$

$$\begin{array}{c}{\rho }_6\left(x\right)=\frac{8e^x}{{\Gamma }^2\left(\alpha +1\right)}(\frac{e^x\left(e^x-4\right){\Gamma }^3\left(2\alpha +1\right)}{{\Gamma }^2\left(\alpha +1\right)}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-2\left(\left(e^{2x}-24e^x-4\right){\Gamma }^2\left(2\alpha +1\right)+e^x\Gamma \left(4\alpha +1\right)\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{4e^x\Gamma \left(2\alpha +1\right)\left({\Gamma }^2\left(3\alpha +1\right)+\Gamma \left(2\alpha +1\right)\Gamma \left(4\alpha +1\right)\right)}{\Gamma \left(\alpha +1\right)\Gamma \left(3\alpha +1\right)}).\hfill \end{array}$$

So, the 6th-LSE of (48) could be expressed as the following expansion:

$${\mathcal{W}}_6\left(x,\zeta \right)=\frac{e^x}{\zeta }-\frac{2e^x}{{\zeta }^{\alpha +1}}+\frac{4e^x}{{\zeta }^{2\alpha +1}}-\frac{8e^x}{{\zeta }^{3\alpha +1}}+\frac{{\rho }_4\left(x\right)}{{\zeta }^{4\alpha +1}}+\frac{{\rho }_5\left(x\right)}{{\zeta }^{5\alpha +1}}+\frac{{\rho }_6\left(x\right)}{{\zeta }^{6\alpha +1}}.$$

(51)

Finally, by running the inverse LT to both sides of (51), one could reach the following 6th-MFS-AS for the non-linear time-FTHEs (46) and (47)

$$\begin{array}{c}\omega \left(x,t\right)=e^x(1-\frac{2t^{\alpha }}{\Gamma \left(\alpha +1\right)}+\frac{4t^{2\alpha }}{\Gamma \left(2\alpha +1\right)}-\frac{8e^x}{\Gamma \left(3\alpha +1\right)}{t}^{3\alpha }+\frac{{\rho }_4\left(x\right)}{\Gamma \left(4\alpha +1\right)}{t}^{4\alpha }\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{{\rho }_5\left(x\right)}{\Gamma \left(5\alpha +1\right)}{t}^{5\alpha }+\frac{{\rho }_6\left(x\right)}{\Gamma \left(6\alpha +1\right)}{t}^{6\alpha }).\hfill \end{array}$$

(52)

In the case of $\alpha =1$, the MFS expansion (52) reduces to the following infinite series:

$$\omega \left(x,t\right)=e^x\left(1-2t+2t^2-\frac{4t^3}{3}+\frac{2t^4}{3}-\frac{4t^5}{15}+\frac{4t^6}{45}\right),$$

(53)

which agrees with the first six Maclaurin series of the exact solution $\omega \left(x,t\right)=e^{x-2t}$.

Table 2 presents the numerical comparisons of the Laplace FPSM outcomes and the exact solution for the nonlinear time-FHTEs (46) and (47) at various values of $\alpha$. It also shows the achieved absolute errors of the studied equation at some values of $t$ on [0, 1] and a fixed value of $x$ when $\alpha =1$. Graphically, the geometric behaviour of the $j$th-MFS-ASs at different $j$th terms of the series against the exact solution is demonstrated in two dimensional plots, as shown in Figure 3. Clearly, the obtained MFS–AS curves are harmonic with each other at various values of the fractional-order derivative and converge to the exact solution curve at standard-order $\alpha =1$ by increasing the terms of the MFS-ASs.

Table 2. Numerical outcomes of the 6th-MFS-AS for Example 2.

${\mathit{x}}_{\mathit{s}}$	${\mathit{t}}_{\mathit{s}}$	$\mathit{\omega }\left(\mathit{x},\mathit{t}\right)$	${\mathit{\omega }}_6\left(\mathit{x},\mathit{t}\right)$	$\left|\mathit{\omega }\left(\mathit{x},\mathit{t}\right)-{\mathit{\omega }}_6\left(\mathit{x},\mathit{t}\right)\right|$	6th-MFS Solutions
					$\mathit{\alpha }=0.95$	$\mathit{\alpha }=0.85$	$\mathit{\alpha }=0.75$
$0.1$	0.1	0.904837	0.904837	$2.73814\times {10}^{-9}$	0.880178	0.825680	0.765968
	0.3	0.606536	0.606531	$5.70700\times {10}^{-6}$	0.583764	0.543398	0.515907
	0.5	0.406764	0.406570	$1.94636\times {10}^{-4}$	0.398782	0.398511	0.466931
	0.7	0.274494	0.272532	$1.96211\times {10}^{-3}$	0.286770	0.371405	0.745565
	0.9	0.193599	0.182684	$1.09150\times {10}^{-2}$	0.245210	0.556451	1.740233
$-0.1$	0.1	0.740818	0.740818	$2.24180\times {10}^{-9}$	0.720628	0.676004	0.627092
	0.3	0.496590	0.496585	$4.67250\times {10}^{-6}$	0.477923	0.444708	0.421253
	0.5	0.333030	0.332871	$1.59355\times {10}^{-4}$	0.326319	0.324557	0.371555
	0.7	0.224737	0.223130	$1.60644\times {10}^{-3}$	0.233829	0.294632	0.558375
	0.9	0.158505	0.149569	$8.93646\times {10}^{-2}$	0.196769	0.419641	1.253198

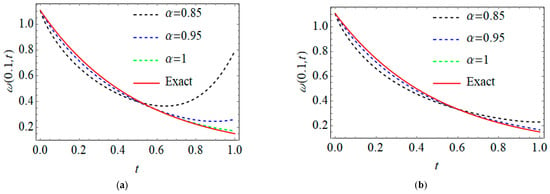
Figure 3. Profile solutions for the $j$th-MFS-ASs for IVPs (46) and (47) at various values of $\alpha$: (a) for $j=6$; (b) for $j=10$, for all $t\in \left[0,1\right]$.

Example 3.

Consider the following linear time-FHTE [20]

$${\partial }_t^{2\alpha }\omega \left(x,y,t\right)+2\omega \left(x,y,t\right)+3{\partial }_t^{\alpha }\omega \left(x,y,t\right)=D_x^2\omega \left(x,y,t\right)+D_y^2\omega \left(x,y,t\right),$$

(54)

which is subject to

$$\omega \left(x,y,0\right)=e^{x+y},and{\partial }_t^{\alpha }\omega \left(x,y,0\right)=-3e^{x+y}$$

(55)

where $x,y\in R, t\ge 0, \alpha \in \left(0,1\right]$. To construct the analytical AS of the linear time-FHTE (54) and (55), we firstly apply the LT operator on (54) and utilize the result of $\left\{{\partial }_t^{2\alpha }\omega \left(x,y,t\right)\right\}={\zeta }^{2\alpha }\mathcal{W}\left(x,y,\zeta \right)-{\zeta }^{2\alpha -1}\omega \left(x,y,0\right)-{\zeta }^{\alpha -1}{\partial }_t^{\alpha }\omega \left(x,y,0\right)$ to obtain the following Laplace equation:

$$\begin{array}{c}\mathcal{W}\left(x,y,\zeta \right)-\frac{\omega \left(x,y,0\right)}{\zeta }-\frac{{\partial }_t^{\alpha }\omega \left(x,y,0\right)}{{\zeta }^{\alpha +1}}+\frac{3}{{\zeta }^{\alpha }}\mathcal{W}\left(x,y,\zeta \right)-\frac{{\partial }_t^{\alpha }\omega \left(x,y,0\right)}{{\zeta }^{\alpha +1}}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{2}{{\zeta }^{\alpha }}\mathcal{W}\left(x,y,\zeta \right)-\frac{1}{{\zeta }^{2\alpha }}{D}_x^2\mathcal{W}\left(x,y,\zeta \right)-\frac{1}{{\zeta }^{2\alpha }}{D}_y^2\mathcal{W}\left(x,y,\zeta \right)=0.\hfill \end{array}$$

(56)

Since $\omega \left(x,y,0\right)=e^{x+y}$ and ${\partial }_t^{\alpha }\omega \left(x,y,0\right)=-3e^{x+y}$, Laplace Equation (56) can be rewritten as

$$\begin{array}{c}\mathcal{W}\left(x,y,\zeta \right)-\frac{e^{x+y}}{\zeta }+\frac{3e^{x+y}}{{\zeta }^{\alpha +1}}+\frac{3}{{\zeta }^{\alpha }}\mathcal{W}\left(x,y,\zeta \right)+\frac{3e^{x+y}}{{\zeta }^{\alpha +1}}+\frac{2}{{\zeta }^{\alpha }}\mathcal{W}\left(x,y,\zeta \right)-\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\frac{1}{{\zeta }^{2\alpha }}{D}_x^2\mathcal{W}\left(x,y,\zeta \right)-\frac{1}{{\zeta }^{2\alpha }}{D}_y^2\mathcal{W}\left(x,y,\zeta \right)=0.\hfill \end{array}$$

(57)

Suppose that the $j$-th LSE of (57) has the form

$${\mathcal{W}}_j\left(x,y,\zeta \right)=\frac{e^{x+y}}{\zeta }-\frac{3e^{x+y}}{{\zeta }^{\alpha +1}}+{\displaystyle \sum }_{n=2}^j\frac{{\rho }_n\left(x,y\right)}{{\zeta }^{n\alpha +1}} .$$

(58)

Then, consequently, the $j$-th LRE could be given by

$$\begin{array}{c}ℒ\left\{Re{s}^j\left({\mathcal{W}}_j\left(x,y,\zeta \right)\right)\right\}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={\displaystyle {\displaystyle \sum }_{n=2}^j}\frac{{\rho }_n\left(x,y\right)}{{\zeta }^{n\alpha +1}}+\frac{3}{{\zeta }^{\alpha }}\left(\frac{e^{x+y}}{\zeta }-\frac{3e^{x+y}}{{\zeta }^{\alpha +1}}+{\displaystyle {\displaystyle \sum }_{n=2}^j}\frac{{\rho }_n\left(x,y\right)}{{\zeta }^{n\alpha +1}} \right)+\frac{3e^{x+y}}{{\zeta }^{\alpha +1}}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{2}{{\zeta }^{\alpha }}\left(\frac{e^{x+y}}{\zeta }-\frac{3e^{x+y}}{{\zeta }^{\alpha +1}}+{\displaystyle {\displaystyle \sum }_{n=2}^j}\frac{{\rho }_n\left(x,y\right)}{{\zeta }^{n\alpha +1}} \right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{1}{{\zeta }^{2\alpha }}\left(\frac{e^{x+y}}{\zeta }-\frac{3e^{x+y}}{{\zeta }^{\alpha +1}}+{\displaystyle {\displaystyle \sum }_{n=2}^j}\frac{{\partial }_x^2{\rho }_n\left(x,y\right)}{{\zeta }^{n\alpha +1}} \right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{1}{{\zeta }^{2\alpha }}\left(\frac{e^{x+y}}{\zeta }-\frac{3e^{x+y}}{{\zeta }^{\alpha +1}}+{\displaystyle {\displaystyle \sum }_{n=2}^j}\frac{{\partial }_y^2{\rho }_n\left(x,y\right)}{{\zeta }^{n\alpha +1}}\right).\hfill \end{array}$$

(59)

For $j=2$, we have

$$\begin{array}{c}ℒ\left\{Re{s}^2\left({\mathcal{W}}_2\left(x,y,\zeta \right)\right)\right\}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\frac{{\rho }_2\left(x,y\right)}{{\zeta }^{2\alpha +1}}+\frac{3}{{\zeta }^{\alpha }}\left(\frac{e^{x+y}}{\zeta }-\frac{3e^{x+y}}{{\zeta }^{\alpha +1}}+\frac{{\rho }_2\left(x,y\right)}{{\zeta }^{2\alpha +1}}\right)+\frac{3e^{x+y}}{{\zeta }^{\alpha +1}}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{2}{{\zeta }^{\alpha }}\left(\frac{e^{x+y}}{\zeta }-\frac{3e^{x+y}}{{\zeta }^{\alpha +1}}+\frac{{\rho }_2\left(x,y\right)}{{\zeta }^{2\alpha +1}}\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{1}{{\zeta }^{2\alpha }}\left(\frac{e^{x+y}}{\zeta }-\frac{3e^{x+y}}{{\zeta }^{\alpha +1}}+\frac{{\partial }_x^2{\rho }_2\left(x,y\right)}{{\zeta }^{2\alpha +1}}\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{1}{{\zeta }^{2\alpha }}\left(\frac{e^{x+y}}{\zeta }-\frac{3e^{x+y}}{{\zeta }^{\alpha +1}}+\frac{{\partial }_y^2{\rho }_2\left(x,y\right)}{{\zeta }^{2\alpha +1}}\right).\hfill \end{array}$$

(60)

Then, by multiply (60) by the factor ${\zeta }^{2\alpha +1}$, and following some algebraic simplification, we obtain the following Laplace equation:

$${\zeta }^{2\alpha +1}ℒ\left\{Re{s}^2\left({\mathcal{W}}_2\left(x,y,\zeta \right)\right)\right\}={\rho }_2\left(x,y\right)-9e^{x+y}+\frac{2{\rho }_2\left(x,y\right)}{{\zeta }^{2\alpha }}+\frac{3{\rho }_2\left(x,y\right)}{{\zeta }^{\alpha }}-\frac{{\partial }_x^2{\rho }_2\left(x,y\right)}{{\zeta }^{2\alpha }}-\frac{{\partial }_y^2{\rho }_2\left(x,y\right)}{{\zeta }^{2\alpha }}.$$

(61)

Now, by computing the limit of the obtained Laplace Equation (61) when $\zeta$ tends to $\infty$, one concludes that ${\rho }_2\left(x,y\right)=9e^{x+y}$.

For $j=3$, we have

$$\begin{array}{c}ℒ\left\{Re{s}^3\left({\mathcal{W}}_3\left(x,y,\zeta \right)\right)\right\}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\frac{{\rho }_3\left(x,y\right)}{{\zeta }^{3\alpha +1}}+\frac{9e^{x+y}}{{\zeta }^{2\alpha +1}}+\frac{3}{{\zeta }^{\alpha }}\left(\frac{e^{x+y}}{\zeta }-\frac{3e^{x+y}}{{\zeta }^{\alpha +1}}+\frac{9e^{x+y}}{{\zeta }^{2\alpha +1}}+\frac{{\rho }_3\left(x,y\right)}{{\zeta }^{3\alpha +1}}\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{3e^{x+y}}{{\zeta }^{\alpha +1}}+\frac{2}{{\zeta }^{\alpha }}\left(\frac{e^{x+y}}{\zeta }-\frac{3e^{x+y}}{{\zeta }^{\alpha +1}}+\frac{9e^{x+y}}{{\zeta }^{2\alpha +1}}+\frac{{\rho }_3\left(x,y\right)}{{\zeta }^{3\alpha +1}}\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{1}{{\zeta }^{2\alpha }}\left(\frac{e^{x+y}}{\zeta }-\frac{3e^{x+y}}{{\zeta }^{\alpha +1}}+\frac{9e^{x+y}}{{\zeta }^{2\alpha +1}}+\frac{{\partial }_x^2{\rho }_3\left(x,y\right)}{{\zeta }^{3\alpha +1}}\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{1}{{\zeta }^{2\alpha }}\left(\frac{e^{x+y}}{\zeta }-\frac{3e^{x+y}}{{\zeta }^{\alpha +1}}+\frac{9e^{x+y}}{{\zeta }^{2\alpha +1}}+\frac{{\partial }_y^2{\rho }_3\left(x,y\right)}{{\zeta }^{3\alpha +1}}\right).\hfill \end{array}$$

(62)

Thus, by multiply (62) by the factor ${\zeta }^{3\alpha +1}$, and employing some algebraic simplification, we see that $\underset{\zeta \to \infty }{lim}{\rho }_3\left(x,y\right)+27e^{x+y}+\frac{2{\rho }_3\left(x,y\right)}{{\zeta }^{2\alpha }}+\frac{3{\rho }_3\left(x,y\right)}{{\zeta }^{\alpha }}-\frac{{\partial }_x^2{\rho }_3\left(x,y\right)}{{\zeta }^{2\alpha }}-\frac{{\partial }_y^2{\rho }_3\left(x,y\right)}{{\zeta }^{2\alpha }}=0$, and obtain ${\rho }_3\left(x,y\right)=-27e^{x+y}$.

Continuing in the same manner and using the MATHEMATICA Software Package 12, with the help of the result $\underset{\zeta \to \infty }{lim}{\zeta }^{j\alpha +1}ℒ\left\{Re{s}^j\left({\mathcal{W}}_j\left(x,y,\zeta \right)\right)\right\}=0$, we conclude that

$${\rho }_4\left(x,y\right)=81e^{x+y},$$

$${\rho }_5\left(x,y\right)=-243e^{x+y},$$

$${\rho }_6\left(x,y\right)=729e^{x+y}$$

$$⋮$$

Hence, the $j$th-LSE ${\mathcal{W}}_j\left(x,y,\zeta \right)$ of (57) can be expressed as follows:

$${\mathcal{W}}_j\left(x,y,\zeta \right)=e^{x+y}\left(\frac{1}{\zeta }-\frac{3}{{\zeta }^{\alpha +1}}+\frac{{\left(3\right)}^2}{{\zeta }^{2\alpha +1}}+\frac{{\left(-3\right)}^3}{{\zeta }^{3\alpha +1}}+\frac{{\left(3\right)}^4}{{\zeta }^{4\alpha +1}}+\dots +\frac{{\left(3\right)}^{j-1}}{{\zeta }^{\left(j-1\right)\alpha +1}}+\frac{{\left(3\right)}^j}{{\zeta }^{j\alpha +1}}\right).$$

(63)

Consequently, when $j\to \infty$, the LSE $\mathcal{W}\left(x,y,\zeta \right)$ of (57) could be written in terms of the infinite series:

$$\mathcal{W}\left(x,y,\zeta \right)=e^{x+y}\left(\frac{1}{\zeta }-\frac{3}{{\zeta }^{\alpha +1}}+\frac{{\left(3\right)}^2}{{\zeta }^{2\alpha +1}}+\dots +\frac{{\left(3\right)}^j}{{\zeta }^{j\alpha +1}}+\dots \right)=e^{x+y}{\displaystyle \sum }_{n=0}^{\infty }\frac{{\left(-3\right)}^n}{{\zeta }^{n\alpha +1}}.$$

(64)

Finally, converting the obtained LSE in (64) into the original space by running the inverse LT gives the MFS-AS to linear time-FHTEs (54) and (55), as shown below:

$$\begin{array}{c}\omega \left(x,y,t\right)=e^{x+y}\left(1-\frac{3t^{\alpha }}{\Gamma \left(\alpha +1\right)}+\frac{3^2{t}^{2\alpha }}{\Gamma \left(2\alpha +1\right)}-\frac{3^3{t}^{3\alpha }}{\Gamma \left(3\alpha +1\right)}+\dots \right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=e^{x+y}{\displaystyle {\displaystyle \sum }_{n=0}^{\infty }}\frac{{\left(-3\right)}^n{t}^{n\alpha }}{ \Gamma \left(n\alpha +1\right)}=e^{x+y}{E}_{\alpha }\left(-3t^{\alpha }\right).\hfill \end{array}$$

(65)

For $\alpha =1$, the MFS-AS (65) reduces to

$$\omega \left(x,y,t\right)=e^{x+y}\left(1-\frac{3t}{1!}+\frac{{\left(3t\right)}^2}{2!}+\frac{{\left(-3t\right)}^3}{3!}+\dots \right)=e^{x+y}{\displaystyle \sum }_{n=0}^{\infty }\frac{{\left(-3t\right)}^n}{ n!},$$

(66)

which converges to the exact solution of the classical Hyperbolic Telegraph Equations (55) and (56), $\omega \left(x,y,t\right)=e^{x+y-3t}$. Further, the obtained solution (66) is fully compatible with the solution investigated via the NDM [20].

Next, Table 3 presents some numerical comparisons of the outcomes obtained via the proposed method and NDM [20] when $\alpha =1$. The provided simulation in Table 3 confirms the superiority and efficiency of our technique, where the numerical results obtained via the Laplace FPSM approach and exact values being faster than the previously mentioned technique. Moreover, the solution curves of the $\alpha$th–time Caputo derivative of the MFS-ASs are displayed in 2D plots, as shown in Figure 4, for different values of $\alpha \in \left\{0.6, 0.7, 0.8, 1\right\}$. Additionally, the impact of the terms’ number of MFS-ASs on the geometric behaviour of our findings at various values of fractional-order, as well as on the obtained $j$th-MFS AS at integer-order $\alpha =1$ with the exact solution, is displayed in Figure 5. Moreover, the effect of the fractional-order derivative of the MFS-ASs on the geometric behaviour, shown in the 3D graph in Figure 6, is at a fixed value of $x=1$ when $\alpha \left\{1, 0.9\right\}$. Obviously, from these figures, in a homotopic manner, the behaviour of the solutions for different $\alpha$ curves is in harmony, with each converging continuously to the standard case $\alpha =1$, especially when increasing the terms of the MFS-ASs.

Table 3. Numerical comparison of 4th-MFS-ASs at $\alpha =1$, for Example 3.

$\mathit{t}$	$\mathit{\omega }\left(\mathit{x},\mathit{t}\right)$	Laplace FPSM		NDM [20]
		${\mathit{\omega }}_4\left(\mathit{x},\mathit{t}\right)$	$\left|\mathit{\omega }\left(\mathit{x},\mathit{t}\right)-{\mathit{\omega }}_4\left(\mathit{x},\mathit{t}\right)\right|$	${\mathit{\omega }}_4\left(\mathit{x},\mathit{t}\right)$	$\left|\mathit{\omega }\left(\mathit{x},\mathit{t}\right)-{\mathit{\omega }}_4\left(\mathit{x},\mathit{t}\right)\right|$
$0.12$	$1.271249$	$1.271336$	$8.6576\times {10}^{-5}$	$1.257167$	$1.40822\times {10}^{-2}$
$0.24$	$0.886920$	$0.889539$	$2.61872\times {10}^{-3}$	$0.776189$	$1.10732\times {10}^{-1}$
$0.36$	$0.618783$	$0.637623$	$1.88398\times {10}^{-2}$	$0.255066$	$3.63718\times {10}^{-1}$
$0.48$	$0.431711$	$0.507087$	$7.53761\times {10}^{-2}$	$-0.399716$	$8.31427\times {10}^{-1}$
$0.60$	$0.301194$	$0.520033$	$2.18838\times {10}^{-1}$	$-1.251067$	$1.55226098$

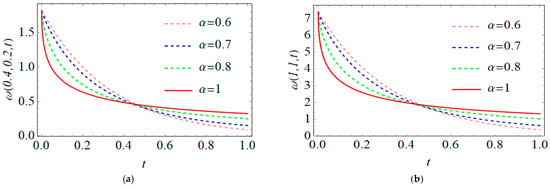
Figure 4. Profile solutions of the MFS-ASs for IVP (55, 56) at various values of $\alpha$: (a) for $x=0.2, y=0.4$; (b) for $x=y=1$, for all $t\in \left[0,1\right]$.

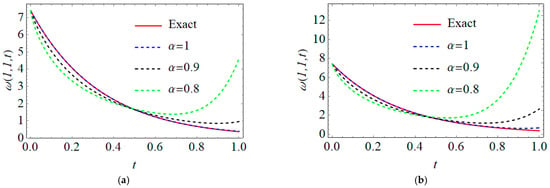
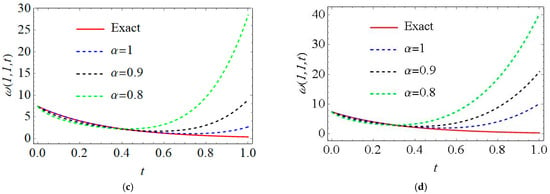
Figure 5. The geometric behaviour of the exact and $j$th-MFS-ASs for IVPs (55), (56) at various values of fractional-order $\alpha$: (a) $j=10$, (b) $j=8$, (c) $j=6$ and (d) $j=4$.

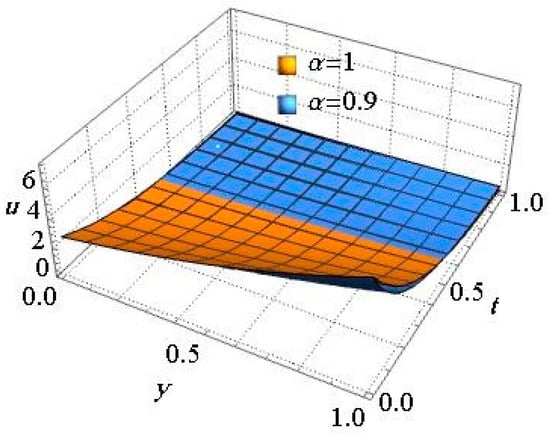
Figure 6. 3D graphs of the MFS-ASs at $\alpha =1$, $\alpha =0.9$, for Example 3.

5. Conclusions

In this article, the Laplace FPSM has been implemented to solve varied hyperbolic telegraph models of a fractional-order. The used method is an improvement of the traditional FPSM. It is a mixture between the LT operator and the FPSM that provides ASs with no unjustified physical constraints or linearization on the structure of the target problems. The novel approach features reduce the size of the computational requirements in finding the solutions as MPS forms, which are rapidly convergent to the exact solutions. The theoretical framework for the methodology in obtaining the variable coefficients values of the LSE based upon the limit concept is studied and analyzed by deriving recursive systematic formula. The accuracy and efficiency of the Laplace FPSM have been investigated by testing three various kinds of fractional hyperbolic telegraph models. The obtained solutions are illustrated by 2D and 3D graphs and numerically in limited domains. It was noted through graphical representation that the Laplace FPS solutions for the fractional-order models are compatible with each other, and that the solutions converge continuously to the classical case of $\alpha =1$. A numerical comparison between our findings with other numerical techniques in the literature is discussed. In summary, the results show that the novel approach is straightforward and highly accurate in creating a rapidly convergent AS with less computational cost.