Abstract
Seaweeds or seaweed Lie algebras are subalgebras of the full-matrix algebra introduced by Dergachev and Kirillov to give an example of algebras for which it is possible to compute the Dixmier index via combinatorial methods. It is worth noting that finding such an index for general Lie algebras is a cumbersome problem. On the other hand, Brauer configuration algebras are multiserial and symmetric algebras whose representation theory can be described using combinatorial data. It is worth pointing out that the set of integer partitions and compositions of a fixed positive integer give rise to Brauer configuration algebras. However, giving a closed formula for the dimension of these kinds of algebras or their centers for all positive integer is also a tricky problem. This paper gives formulas for the dimension of Brauer configuration algebras (and their centers) induced by some restricted compositions. It is also proven that some of these algebras allow defining seaweeds of Dixmier index one.
MSC:
05A17; 11P83; 16G20; 16G30; 16G60
1. Introduction
The Dixmier index (or simply the index) is an invariant algebra of a Lie algebra given by the following identity:
where f is a linear function on and is a corresponding skew-symmetric form for which with being the commutator of x and y [1,2,3,4,5].
It is well known that computing the index of a Lie algebra is very difficult. Advances to this problem were given by Tauvel and Yu [6], who gave an upper bound for the index of biparabolic subalgebras, which are intersections of two parabolic subalgebras of a Lie algebra , such that . Regarding this work, we recall that Joseph [7] proved their conjecture dealing with the index associated with a semisimple Lie algebra.
Another advance to the index problem associated with Lie algebras was proposed by Dergachev and Kirillov [1], who defined some subalgebras of the full-matrix algebra , where and are integer compositions of a fixed integer n giving the subalgebra structure. These subalgebras were named seaweed algebras (or seaweeds) by them. If , then the seaweed algebra is said to be parabolic. Seaweeds can be considered subalgebras of the Lie algebras or if endowed with the anti-commutative standard bracket.
Dergachev and Kirillov [1] associated a graph (called the meander) with each seaweed. They proved that the index associated with these algebras can be given via the number of cycles and paths in their corresponding meanders. Afterwards, Coll et al. [3,4,5] interpreted the formulas given by Dergachev and Kirillov for general algebras to subalgebras of ; according to them, the index of a seaweed Lie algebra is given by a sum of the form , where C (P) denotes the number of cycles (paths) in its meander.
Seaweeds and their meanders give rise to applications in different areas. For instance, Frobenius algebras give rise to the so-called skew solutions of the classical Yang–Baxter equation [8,9,10,11]. On the other hand, Coll at al. [3,4,5] and Seo and Yee [2] considered using the index associated with seaweeds to define statistics of integer partitions. In particular, they classified meanders to define families of Frobenius seaweed algebras, whose classification is an open problem.
This paper proves that some Brauer configuration algebras associated with integer compositions give rise to index one seaweeds. Green and Schroll [12,13] introduced Brauer configuration algebras to study multiserial symmetric algebras. However, their definitions based on combinatorial data have allowed applications in different science fields. For example, Brauer configuration algebras (BCAs) have been used to obtain solutions of the Yang–Baxter equation, to describe the key of the AES cryptosystem. BCAs allow for solving problems in the graph energy theory as well. For instance, they can be used to determine the trace norm of some -matrices [14,15,16,17].
It is worth noticing that finding a closed formula for the dimension of BCAs (and their centers) associated with integer partitions and compositions is generally a hard problem. To tackle this problem, we give formulas for the dimension of BCAs associated with integer compositions whose parts are triangular numbers, square numbers, pentagonal numbers, and octahedral numbers [18,19].
1.1. Motivations
This paper exploits interactions between Brauer configuration algebras, the theory of integer partitions, and the theory of Lie algebras to find Dixmier indices of some seaweed algebras and the dimensions of Brauer configuration algebras induced by integer compositions. It is worth noticing that the general problem of determining the index of seaweed algebras and dimensions of Brauer configuration algebras (and their centers) are problems of great difficulty whose solutions are far from being reached [2,3,4,5,14,15,16,17]. This paper provides advances to these problems by defining Brauer configuration algebras via some integer compositions whose enumeration theory deals with the Catalan numbers and Delannoy numbers [18,19].
1.2. Contributions
This paper defines Brauer configuration algebras induced by integer partitions and integer compositions. The main results of this paper are Theorems 7–13, along with Corollaries 2–4.
Theorem 7 gives formulas for valencies of vertices associated with compositions of type . Theorem 8 gives formulas for the dimension of the center of Brauer configuration algebras induced by compositions of type . Theorem 9 gives indices for seaweed algebras induced by compositions of type . Theorem 10 gives formulas for the valencies of vertices associated with Brauer configurations of type . Theorem 11 gives formulas for the dimension of the centers contained in these algebras. Theorems 12 and 13 give indices for seaweed algebras induced by compositions of type and .
Corollary 2 gives formulas for the dimensions of Brauer configuration algebras induced by compositions of type . Corollary 3 proves that Brauer configuration algebras induced by compositions of type are indecomposable. Corollary 4 gives formulas for the dimension of Brauer configuration algebras induced by compositions of type .
The organization of this paper is as follows: Section 2 is devoted to recalling the basic definitions and notation regarding seaweed algebras and integer partitions and compositions. Section 2.2 reminds about notation and basic definitions regarding seaweed algebras. In Section 3, we define Brauer configuration algebras induced by integer partitions and compositions (Section 3.1). Formulas for the Dixmier index and the dimensions of these algebras and their centers are given in this section as well. Conclusions with a description of future investigations regarding these subjects are given in Section 4. Appendix A includes tables giving the number of cycles and paths in meanders induced by compositions of type and .
2. Preliminaries
This section recalls some basic definitions and notation dealing with integer partitions and compositions, as well as seaweed algebras [3,4,5,18,19,20].
2.1. Integer Partitions and Compositions
This section is focused on giving basic definitions and results regarding integer partitions and compositions.
A set of ordered positive integers , such that
is said to be an integer partition of the integer number n, and numbers are called parts.
A composition of an integer n is an expression of n as an ordered sum of positive integers [21]. It is worth noting that according to Andrews [20], compositions are merely partitions in which the order of the summands is considered. For instance, there are three partitions and four compositions of the number three. Partitions are , , and , and the compositions are , , , and . It is worth pointing out that under controlled situations, 0 can be considered as a part of an integer n. For instance, in [20], ⌀ is regarded as the partition of 0.
The number of compositions of n with exactly m parts denoted is given by the following result.
Theorem 1
(Theorem 4.1, [20]).
The following theorem provides the Ramanujan–Hardy–Rademacher formula for the number of partitions of an integer number n.
Theorem 2
(Theorem 5.1, [20]).
where , with a certain 24th root of unity.
Stanley [21,22] introduced the theory of P-partitions as a generalization of the theory of partitions and compositions. According to him, a P-partition of an integer n is an order-reversing map (or preserving map), such that .
Stanley [21] proved that the number of P-partitions of an integer m is given by the formula:
where is the number of linear extensions induced by the poset P.
Cañadas et al. [18,19] defined P-partitions of type , , and as follows:
Let be a poset whose elements are compositions of an integer n satisfying the following conditions:
- 1.
- if and only if , .
- 2.
- At least two elements of c are positive.
- 3.
- and the difference .
- 4.
- if and only if , , and .
For , Cañadas et al. [19] proved the following result dealing with a problem proposed by Andrews regarding partitions.
Theorem 3
(Theorem 2, Corollary 3, [19]). Let be the number of compositions of type of the positive integer n, then
where () denotes the ith triangular number (the largest integer less than or equal to a number x), respectively.
We let denote the sum , where is the xth octahedral number.
If , and are fixed positive integers with , , and , then we say that a composition of a positive integer n is of type if and only if it satisfies the following conditions:
- 1.
- , for some , and .
- 2.
- with and for each for some positive integer .
- 3.
- If is the set of partial sums given in (7), then , . Actually, for all , it holds that , for some , . In such a case, , for all .
- 4.
- is a (trivial) composition of type for all , , and fixed.
Along with 39, the following are the compositions of type :
- ;
- ;
- ;
- ;
- ;
- ;
- .
Let () be the jth cube (pentagonal number) and fixed positive integers with , , .
A composition of a positive integer n is said to be of type if the following conditions hold:
- 1.
- , for some , .
- 2.
- where and for each , , for some . Furthermore, .
- 3.
- The following identity defines partial sums generated in (8).with , , for some positive integers , , . Note that
- 4.
- is also a composition of type for all , and fixed.
The following are the eight compositions of type of :
- 56.
- .
- .
- .
- .
- .
- .
- .
Cañadas and Angarita [18] proved the following result.
Theorem 4
(Theorem 19, [18]). For , let be the number of compositions of type of a positive number n, then , where
denotes the jth Catalan number, and , and are fixed positive integers such that , , , , and .
Compositions of type are defined as compositions of type and ; they are defined as follows [18]:
If are fixed positive integers with , , , then a composition of a positive integer n is of type if it satisfies the following rules for some fixed:
- 1.
- , for some , .
- 2.
- where , and for each , if , then .
- 3.
- Each partial sum in (12) has the form: with , for some positive integers , , . In this case: , and .
- 4.
- is a composition of type for all , , fixed.
We let denote the set of all compositions of type , , , and .
Corollary 1
(Corollary 20, [18]). Let be the number of compositions of type of a positive number δ, then , where , , , and are fixed positive integers such that , , , , and . In particular, , where denotes the uth Catalan number.
2.2. Seaweed Algebras
This section reminds about the basic definitions and results regarding seaweed algebras [2,3,4,5,23].
Given an arbitrary field , , the standard basis of , , and integer partitions of a fixed integer n, with and , then a subalgebra of (the full-matrix algebra) that preserves the vector spaces
is said to be a subalgebra of the seaweed type [1,2,3,4,5]. Figure 1 shows an example of a seaweed algebra shape.
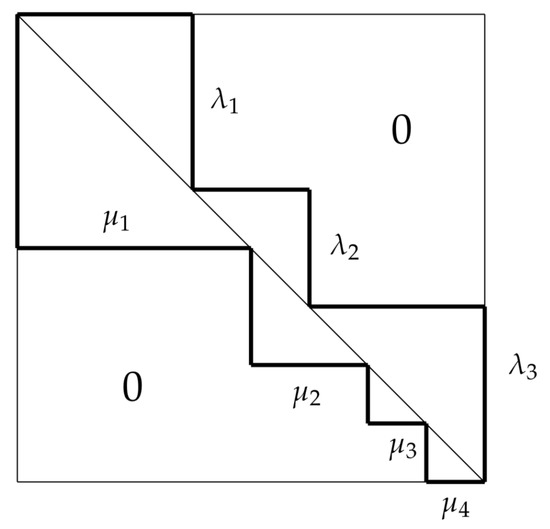
Figure 1.
Seaweed algebras are subalgebras of the full-matrix algebra.
Seaweed algebras are associative Lie subalgebras of or , if they are endowed with the bracket operation . If any of the partitions or has as its only part the number n, then the seaweed algebra is said to be maximal parabolic or parabolic [1].
According to Kirillov and Dergachev [1], the dimension of a seaweed algebra of type is given by the identity (14).
The meander graph is a helpful tool to compute the index of a seaweed algebra; it is built as follows [1,3,4,5]:
- 1.
- has n vertices.
- 2.
- Edges are constructed by partitioning the set of vertices into blocks () of size (), respectively. A vertex () is connected with the vertex () by a top (bottom) edge, respectively.
Figure 2 shows the meander graph associated with the seaweed algebra of type and its corresponding seaweed algebra. Note that partition is represented by the arcs , and and the vertex , whereas, partition is represented by the vertex and the arcs and .
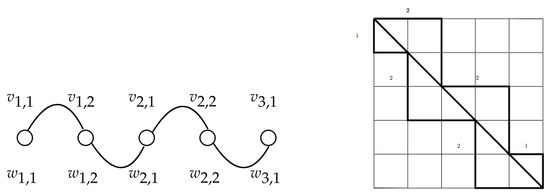
Figure 2.
Meander graph associated with the compositions {2, 2, 1} and {1, 2, 2} and the corresponding seaweed Lie algebra.
Dergachev and Kirillov [1] proved the following result regarding the index of seaweed algebras.
Theorem 5
(Theorem 5.1, [1]). The index of a seaweed algebra is equal to:
- Twice the number of circles in the associated meander plus the number of segments plus the number of isolated points.
- The number of cycles in the permutation corresponding to the associated meander.
For seaweed algebras of type , Coll et al. [2,3,4,5] interpreted Theorem 5 as an identity of the form:
where denotes the seaweed algebra defined by compositions and of a fixed integer n and C (P) denotes the number of cycles (paths) of its meander. In this case, isolated points are considered paths. For instance, Figure 2 allows inferring that , since the meander has just one path and it contains no cycles.
Henceforth, we use Identity (15) to compute the index of a seaweed algebra.
The following result proves that the index of a seaweed algebra can be obtained via some suitable moves of the meander, which keep the index value invariant. Such a sequence of moves is said to be the meander signature.
Lemma 1
(Lemma 4 (winding down), [3]). If M is a general meander of type , then we have the following cases:
- 1.
- Flip (F): If , then simply exchange a for b to obtain .
- 2.
- Component elimination: (C(c)) If , then .
- 3.
- Block elimination: (B) If , then .
- 4.
- Rotation contraction: (R) If , then .
- 5.
- Pure contraction: (P) If , then .
We note that component elimination is the only move that does not preserve the index of the associated seaweed algebra.
3. Main Results
This section describes Brauer configuration algebras induced by integer partitions and compositions. The dimensions of these algebras and their centers are given by compositions of type and . The index of seaweed algebras associated with compositions of type and are also given.
3.1. Brauer Configuration Algebras Defined by Integer Partitions and Compositions
This section follows the ideas of Green and Schroll [12,13] to define Brauer configuration algebras associated with integer partitions and compositions.
Let be a fixed integer, then any partition of n can be uniquely written as a sequence of the form , where only finitely many of the nonnegative integers are nonzero. We let denote the set of all integer partitions of n and .
For fixed, we endow with a linear order < in such a way that, if , then
If consists of all partitions for which a given positive integer i is a part, then the successor sequence associated with i has the form:
where is the number of times or frequency that i occurs as a part in the partition and denotes the kth copy of .
The valency of the part i is given by the following identity:
, successor sequences, and valencies associated with vertices define Brauer configurations, which are systems of the form , where:
- is the set of parts of the integer partitions of n whose parts differ from n.
- is a map such that , . We let denote the product , for any part .
- is an orientation defined by adding (for each ) to each successor sequence a relation of the form . This process builds a circular ordering in such a way that any partition can be assumed as the initial partition for the completed sequence . We assumed that all the successor sequences preserve the original order < defined for the integer partitions of n.
A part is said to be truncated (nontruncated) if (). Brauer configurations without truncated vertices are said to be reduced.
Instead of meanders, Brauer configurations define so-called Brauer quivers , which are directed graphs , defined as follows:
- The set of vertices is in bijective correspondence with the set of partitions .
- Coverings in circular orderings define arrows in , i.e., a covering gives rise to an arrow , with and . Copies of partitions in circular orderings define loops in .
- Circular orderings define so-called special cycles in Q.
Brauer Configuration Algebras Induced by Integer Partitions
The Brauer configuration algebra induced by the Brauer configuration is the bound quiver algebra , where I is an admissible ideal generated by the following relations:
- 1.
- (Relations of Type I) If is an integer partition of n and the parts , then the special cycles and are equivalent, where denotes the multiplication of copies of the special cycle .
- 2.
- (Relations of Type II) If f is the first arrow of a special cycle associated with a part i of an integer partition of n, then the relation .
- 3.
- (Relations of Type III) If is an arrow contained in a special cycle , is an arrow in another special cycle , and , then .
The following facts regarding Brauer configuration algebras induced by integer partitions are direct consequences of the results obtained by Green and Schroll and Sierra in [12,24] for general Brauer configuration algebras.
Theorem 6.
Let be the Brauer configuration algebra induced by the set of partitions of an integer n. Then:
- 1.
- There is a bijection between the set of indecomposable projective modules over Λ and .
- 2.
- If is an indecomposable projective module over Λ defined by a partition λ of n into r parts, then is the sum of r uniserial modules such that is either 0 or a simple Λ-module for any .
- 3.
- I is admissible Λ, and is multiserial symmetric algebra and indecomposable as an algebra.
- 4.
- If () denotes the radical (socle) of an indecomposable projective module P over the BCA induced by an integer partition λ of n and . Then, the number of summands in the heart of equals the number of parts in λ.
The dimension of the Brauer configuration algebra is given by the following formula.
where is the number of integer partitions of , is the jth triangular number, and .
The following is the formula of the center of the BCA .
where .
As an example, the following are the data associated with the partitions of the number four (see (18) and the notation below).
, where
Successor sequences and valencies are defined as follows:
The following Figure 3 shows the Brauer quiver induced by the Brauer configuration
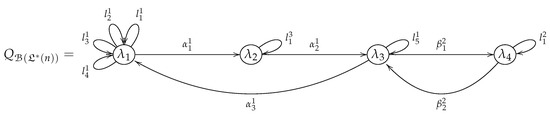
Figure 3.
Brauer quiver induced by the Brauer configuration (21).
The following relations generate the admissible ideal I such that :
- , for all possible values of i and j.
- , , , if .
- If is the kth special cycle associated with vertex and f is its first arrow, then . Furthermore, for all possible values of , and t.
Thus, the seaweed algebra is Frobenius.
The following results regard compositions of type (see Theorem 3 and Identity (6)).
Theorem 7.
For , , it holds that
- 1.
- 2.
- , for .
- 3.
- , for .
- 4.
- , for , where denotes the valency of the number (the set of parts in compositions of type of the number y).
Proof.
Note that , , and . Thus, if n is odd, then we can proceed by induction bearing in mind that each composition of type of gives rise to a composition of via a shift move of the form . The remaining compositions have the shape
For the even case, we note that if , then , , and .
, if and , for , provided that any composition of type of is obtained from a composition of by applying the shift described above. In such a case, any composition of containing three as a part gives rise to a composition of containing it as a part. has additional compositions of the form and , which gives three additional occurrences of the number. The same arguments can be used to note that , if , , and so on. If , then , (), and so on. We are done. □
Corollary 2.
Proof.
It is a consequence of Formulas (6) and (25) and Theorem 7, which gives formulas for the corresponding valencies. □
The following result gives formulas for , for .
Theorem 8.
If , then
where
Proof.
Note that . Thus, and
For each even number , define a partition of with the form , with , , . Then, the number of loops associated with vertices are given by the following identities:
According to the loops formulas, it holds that
If n is an odd number, then
Provided that, in this case, the number of loops associated with the vertices satisfies the following identities:
since (see Identity (6)). We are done. □
The following result regards seaweed algebras of type .
Theorem 9.
If , then .
Proof.
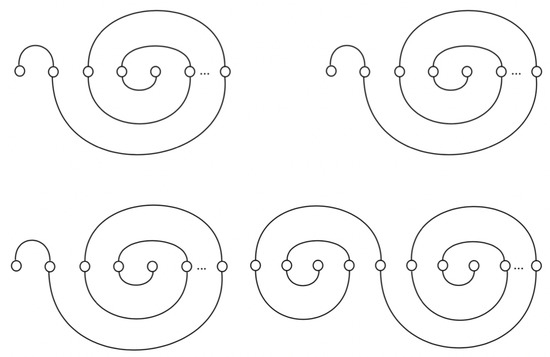
is a composition of type of the integer number . The general shape of the corresponding meander is shown in Figure 4 if n is even (odd). The result follows as a consequence of Lemma 1. □

Figure 4.
Meanders of the seaweed algebras for (even case, above) and for (odd case, below). Note that the corresponding meanders are not connected for even and odd numbers and that the components associated with the even case are identical.
Henceforth, we let denote the poset for which
In such a case, if and only if one of the following three conditions holds:
- and ;
- and ;
- and .
We denote by the number of lattice paths from the point to .
The following result regards Brauer configuration algebras induced by compositions of type . The Brauer configuration algebra is induced by a Brauer configuration , where
- .
- .
- consists of compositions of type of into parts of the form .
- , , and the corresponding Brauer configuration algebra are defined as in the general case.
Theorem 10.
For and , it holds that
Proof.
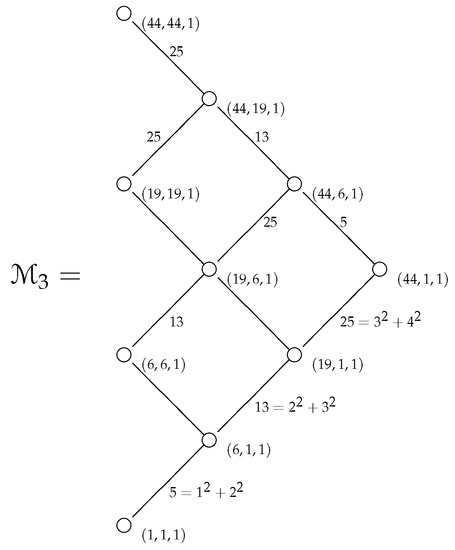
Note that, by definition for , it holds that , where . Each lattice path in corresponds to a unique polygon in . The result follows by labeling each edge () with a sum of the form (). A composition of type of is obtained by adding the number to each edge label of a fixed lattice path starting at , () and ending in . The following Figure 5 is the Hasse diagram of and its labeling of type . □

Figure 5.
The poset and its labeling giving compositions of type of the number 89.
The following result gives additional properties of Brauer configuration algebras induced by compositions of type .
Corollary 3.
For each fixed with , the Brauer configuration algebra is indecomposable as an algebra.
Proof.
By definition, has no truncated vertices. □
The following corollary gives a formula for the dimension of Brauer configuration algebras of type .
Corollary 4.
For fixed, , and , the dimension of the Brauer configuration algebras of type is given by the following identity:
Proof.
Note that as a consequence of Theorem 4. The valencies of the vertices (parts) are given in Theorem 10. □
The following result gives a formula for the dimension of the center of a Brauer configuration algebra of type .
Theorem 11.
If is fixed, then
where denotes the hth Catalan number.
Proof.
We note that , provided that gives the number of loops at a vertex , for any i, . There are no loops provided by vertices of the form . On the other hand, it holds that . Therefore, . Since there are vertices for which and there are vertices in , the result follows. We are done. □
The following result regards seaweeds induced by compositions of type , with and (see Corollary 1). and {4,2,3,2,3} are compositions of type associated with 14.
Theorem 12.
If and are compositions of type with and fixed, then
where l is the largest part of the compositions μ and λ. This sequence corresponds to the integer sequence encoded in the OEIS as A014209 [25].
Proof.
Suppose that l is the largest part of the compositions and . Each assignment of the form gives rise to cycles in the corresponding meander . Note that each cycle generated by an assignment of the form generates an isolated point in the meander, whereas, the assignment generates the unique non-trivial path contained in . Therefore, , twice the number of cycles is given by a recursion of the form , , , . Such recurrence gives rise to the integer sequence in the OEIS, for . . Thus, for , it holds that . We are done. □
Figure 6 and Figure 7 show cycles and paths in meander graphs induced by compositions of 158, 184, 2313, and 2939 (see Theorem 12).
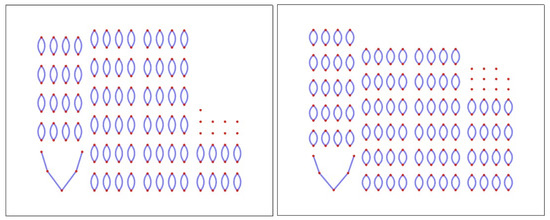
Figure 6.
Cycles and paths in meander graphs induced by compositions of type of 158 and 184.

Figure 7.
Cycles and paths in meander graphs induced by compositions of 2313 and 2939 of type .
The following result gives formulas for Dixmier indices associated with compositions of type .
Theorem 13.
If and are compositions of type of with and fixed, then
where () denotes the jth triangular number (octahedral number).
Proof.
We note that, as in Theorem 12, the assignments give rise to i-cycles and one path in the corresponding meander. Thus, if denotes the number of cycles in the meander of , then , and the number of paths . Therefore,
since . We are done. □
Table A1 and Table A2 in Appendix A give the number of cycles and paths in meanders induced by compositions () and () of type () described in Theorems 12 and 13.
4. Concluding Remarks
Compositions of type , , and dealing with Delannoy numbers, octahedral numbers, and triangular numbers, respectively, give rise to Brauer configuration algebras, whose dimensions, along with their centers, can be obtained by using suitable lattice paths. Compositions of type and induce Brauer configurations whose polygons are given by sums of Catalan numbers, whereas polygons in Brauer configurations induced by compositions of type are given by suitable triangular numbers. Such enumerations allow finding explicit formulas for the dimensions of Brauer configuration algebras induced by these compositions. In particular, seaweed algebras induced by some compositions of type have Dixmier index one, whereas Dixmier indices of seaweed algebras induced by compositions of type are given by the integer sequence encoded in the OEIS as A014209.
Future Work
- 1.
- To give formulas for the Dixmier index of any pair of compositions of type , , and of a fixed positive integer.
- 2.
- To give explicit formulas for the dimension of Brauer configuration algebras induced by partitions of an arbitrary integer number.
- 3.
- To give explicit formulas for the dimension of Brauer configuration algebras induced by compositions of an arbitrary integer number.
Author Contributions
Investigation, writing, review, and editing, A.M.C. and O.M.M. All authors have read and agreed to the published version of the manuscript.
Funding
Seminar Alexander Zavadskij on Representation of Algebras and their Applications, Universidad Nacional de Colombia.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BCA | Brauer configuration algebra |
| Dimension of a Brauer configuration algebra | |
| Dimension of the center of a Brauer configuration algebra | |
| Field | |
| Dixmier index of a seaweed algebra | |
| ; ith octahedral numbe | |
| OEIS | On-Line Encyclopedia of Integer Sequences |
| nth pentagonal number | |
| nth cubic number | |
| nth triangular number |
Appendix A
This section provides tables, which give the number of cycles and paths contained in meander graphs induced by the compositions of type and described in Theorems 12 and 13.

Table A1.
Number of cycles and paths in the meander induced by compositions of type of n.
Table A1.
Number of cycles and paths in the meander induced by compositions of type of n.
| n | Cycles | Paths | |
|---|---|---|---|
| 14 | 4 | 2 | |
| 22 | 8 | 2 | |
| 32 | 12 | 4 | |
| 44 | 18 | 4 | |
| 58 | 24 | 6 | |
| 74 | 32 | 6 | |
| 92 | 40 | 8 | |
| 112 | 50 | 8 | |
| 134 | 60 | 10 | |
| 158 | 72 | 10 | |
| 184 | 84 | 12 |

Table A2.
Number of cycles and paths in the meander induced by compositions of type of n.
Table A2.
Number of cycles and paths in the meander induced by compositions of type of n.
| n | Cycles | Paths | |
|---|---|---|---|
| 39 | 9 | 5 | |
| 89 | 33 | 7 | |
| 171 | 73 | 9 | |
| 293 | 133 | 11 | |
| 463 | 217 | 13 | |
| 689 | 329 | 15 | |
| 979 | 473 | 17 | |
| 1341 | 653 | 19 | |
| 1783 | 873 | 21 | |
| 2313 | 1137 | 23 | |
| 2939 | 1449 | 25 |
References
- Dergachev, V.; Kirillov, A.D. Index of Lie algebras of seaweed type. J. Lie Theory 2000, 10, 331–343. [Google Scholar]
- Seo, S.; Yee, A.J. Index of a seaweed algebra and integer partitions. Electron. J. Comb. 2020, 27, P1.47. [Google Scholar] [CrossRef] [PubMed]
- Coll, V.; Hyatt, M.; Magnant, C.; Wang, H. Meander graphs and Frobenius seaweed Lie algebras II. J. Gen. Lie Theory Appl. 2015, 9, 1000227. [Google Scholar]
- Coll, V.; Hyatt, M.; Magnant, C.; Wang, H. Meander graphs and Frobenius seaweed Lie algebras III. J. Gen. Lie Theory Appl. 2015, 9, 1000266. [Google Scholar] [CrossRef]
- Coll, V.; Mayers, W.; Mayers, N.W.; Wang, H. Statistics on partitions arising from seaweed algebras. Electron. J. Comb. 2020, 27, P3.1. [Google Scholar] [CrossRef] [PubMed]
- Tauvel, P.; Yu, R.W.T. Sur l’indice de certaines algèbres de Lie. Ann. Inst. Fourier. 2004, 54, 1793–1810. [Google Scholar] [CrossRef]
- Joseph, A. On semi-invariants and index for biparabolic (seaweed) algebras. J. Algebra 2006, 305, 487–515. [Google Scholar] [CrossRef]
- Stolin, A. On rational solutions of Yang–Baxter equation for . Math. Scand. 1991, 69, 57–80. [Google Scholar] [CrossRef]
- Gerstenhaber, M.; Giaquinto, A. Graphs, Frobenius functionals, and the classical Yang–Baxter equation. arXiv 2008, arXiv:0808.2423. [Google Scholar]
- Belavin, A.A.; Drinfeld, V.G. Solutions of the classical Yang–Baxter equations for simple Lie algebras. Funct. Anal. Appl. 1982, 16, 159–180. [Google Scholar] [CrossRef]
- Magnant, C.; Coll, V.; Giaquinto, A. Meander graphs and Frobenius seaweed algebras. J. Gen. Lie Theory Appl. 2011, 5, 1–7. [Google Scholar]
- Green, E.L.; Schroll, S. Brauer configuration algebras: A generalization of Brauer graph algebras. Bull. Sci. Math. 2017, 121, 539–572. [Google Scholar] [CrossRef]
- Schroll, S. Brauer Graph Algebras. In Homological Methods, Representation Theory, and Cluster Algebras; CRM Short Courses; Assem, I., Trepode, S., Eds.; Springer: Cham, Switzerland, 2018; pp. 177–223. [Google Scholar]
- Cañadas, A.M.; Ballester-Bolinches, A.; Gaviria, I.D.M. Solutions of the Yang–Baxter equation arising from Brauer configuration algebras. Computation 2022, 11, 2. [Google Scholar] [CrossRef]
- Cañadas, A.M.; Rios, G.B.; Serna, R.-J. Snake graphs arising from groves with an application in coding theory. Computation 2022, 10, 124. [Google Scholar] [CrossRef]
- Cañadas, A.M.; Angarita, M.A.O. Brauer configuration algebras for multimedia based cryptography and security applications. Multimed. Tools Appl. 2021, 80, 23485–23510. [Google Scholar]
- Agudelo, N.; Cañadas, A.M.; Gaviria, I.D.M.; Espinosa, P.F.F. {0,1}-Brauer configuration algebras and their applications in the graph energy theory. Mathematics 2021, 9, 3042. [Google Scholar] [CrossRef]
- Cañadas, A.M.; Angarita, M.A.O. On sums of three squares and compositions into squares and triangular numbers. JPANTA 2011, 23, 1677–1695. [Google Scholar]
- Cañadas, A.M.; Gaviria, I.D.M.; Giraldo, H. Representation of equipped posets to generate Delannoy numbers. FJMS 2017, 102, 1677–1695. [Google Scholar] [CrossRef]
- Andrews, G.E. The Theory of Partitions; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Stanley, R. Ordered structures and partitions. In Memoirs of the American Mathematical Society; American Mathematical Society: Providence, RI, USA, 1972; p. 119. [Google Scholar]
- Stanley, R. Enumerative Combinatorics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Panyushev, D.I. Inductive formulas for the index of seaweed Lie algebras. Moscow. Math. J. 2001, 2, 221–241. [Google Scholar] [CrossRef]
- Sierra, A. The dimension of the center of a Brauer configuration algebra. J. Algebra 2018, 510, 289–318. [Google Scholar] [CrossRef]
- OEIS Foundation Inc. Entry A248427. In The On-Line Encyclopedia of Integer Sequences; 2023; Available online: http://oeis.org/A014209 (accessed on 15 December 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).