Canards Oscillations, Noise-Induced Splitting of Cycles and Transition to Chaos in Thermochemical Kinetics
Abstract
1. Introduction
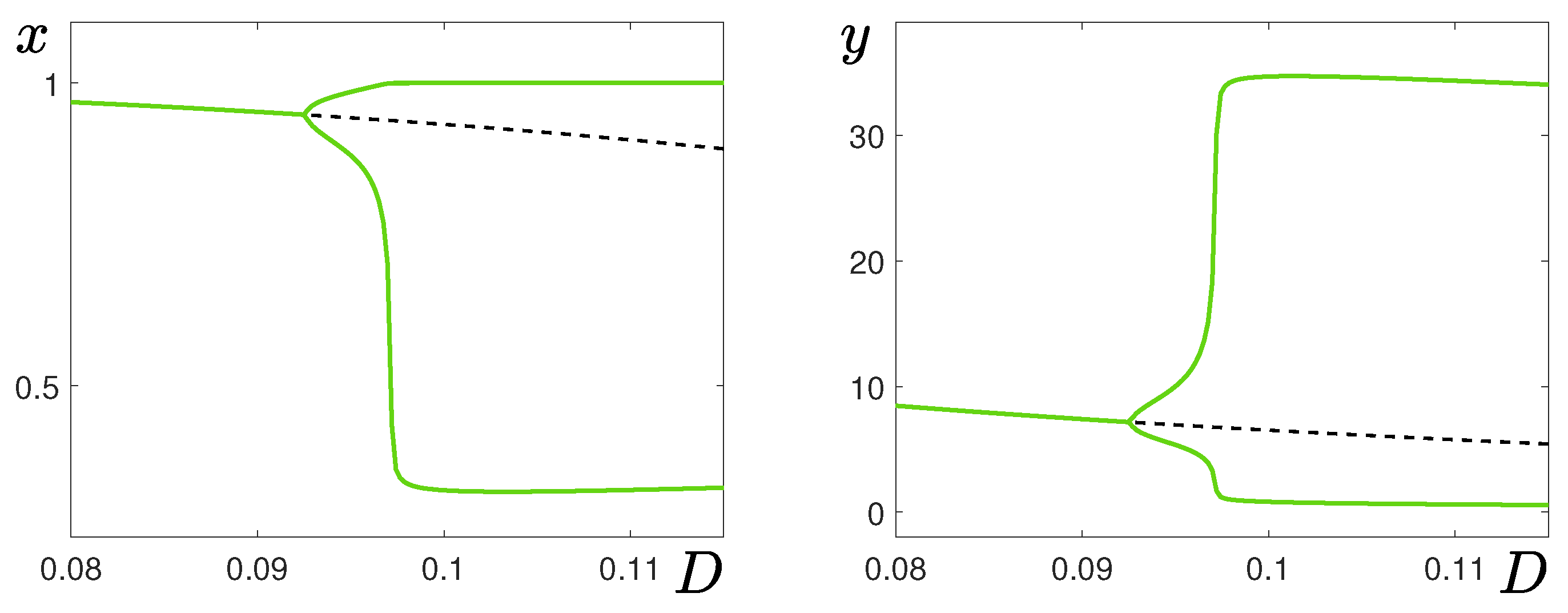
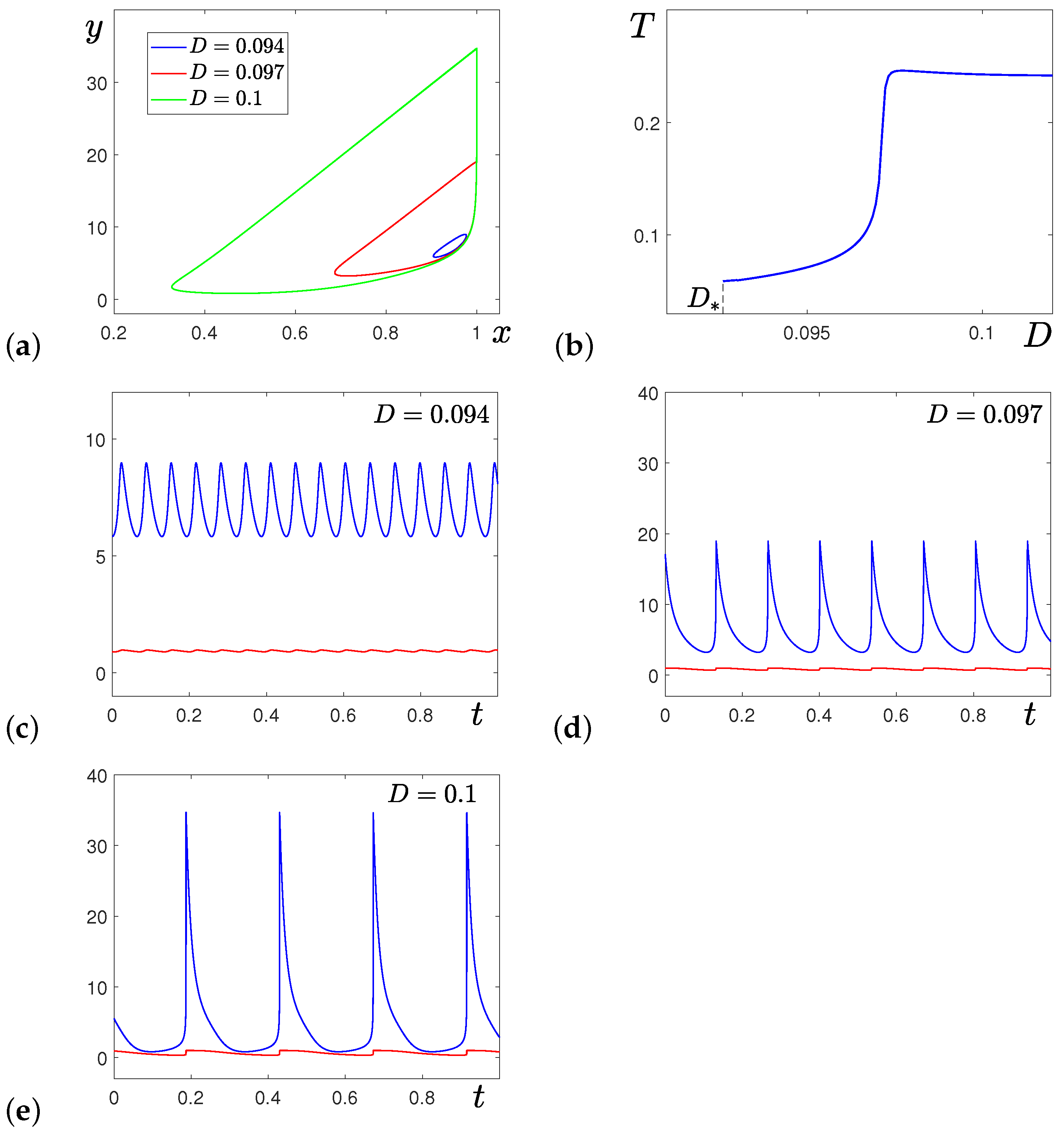
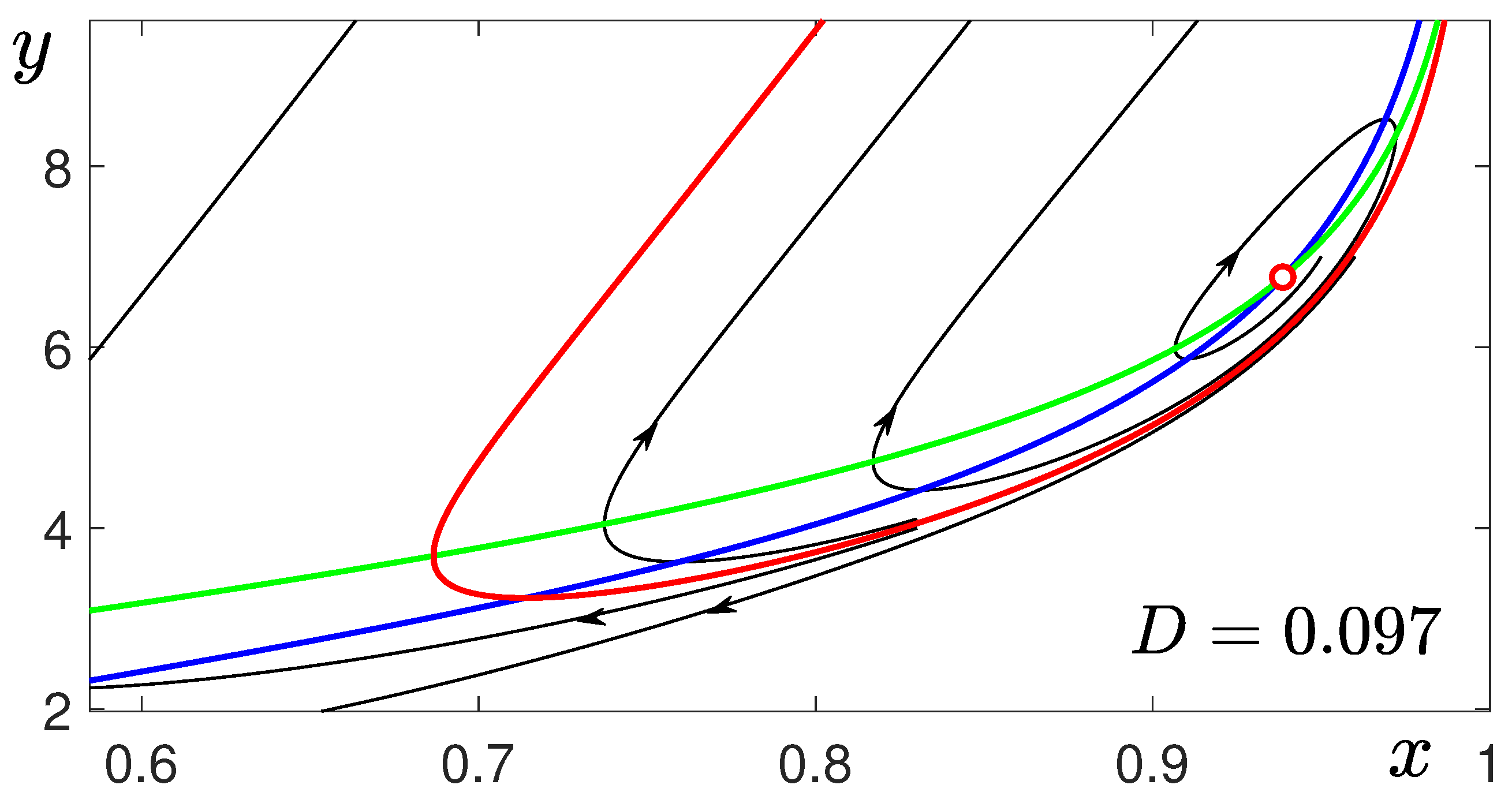
2. Canard Cycles in the Deterministic System
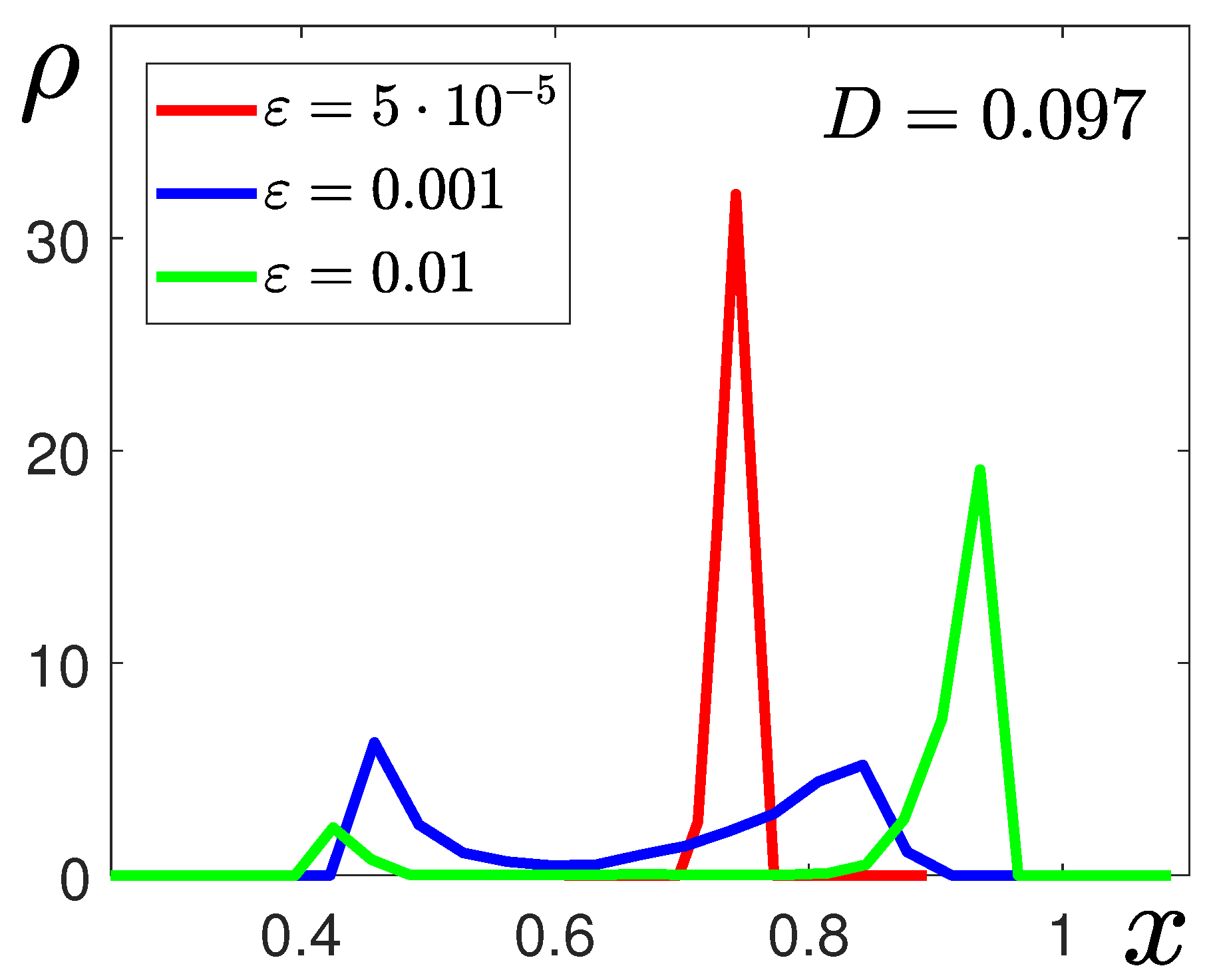
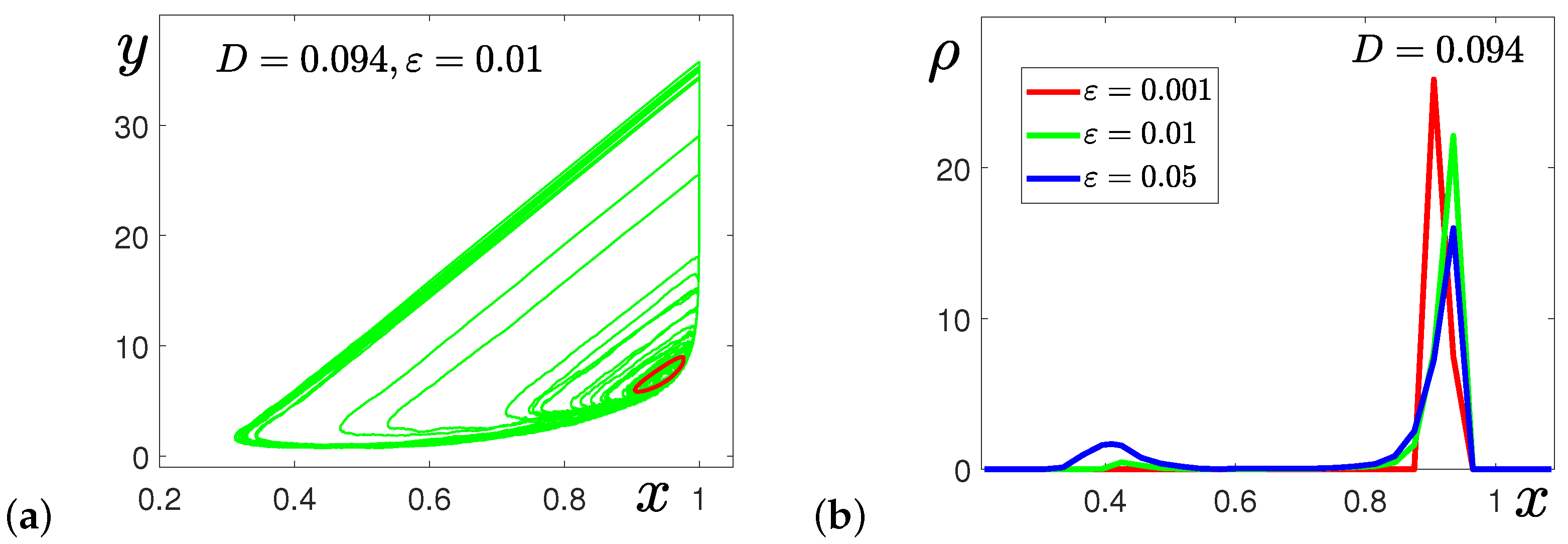
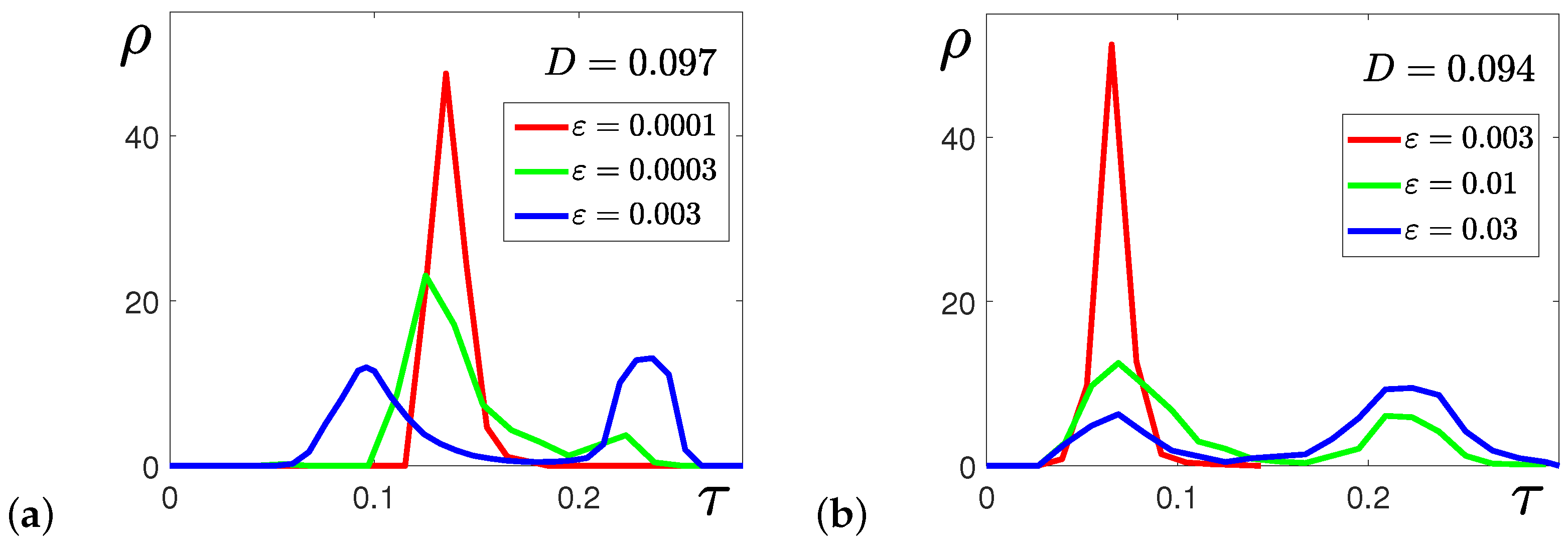
3. Noise-Induced Phenomena in the Stochastic Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer: Berlin/Heidelberg, Germany, 1983; p. 462. [Google Scholar]
- Kuramoto, Y. Chemical Oscillations, Waves, and Turbulence; Springer: Berlin/Heidelberg, Germany, 1984; p. 156. [Google Scholar]
- Field, R.J.; Burger, M. Oscillations and Traveling Waves in Chemical Systems; Wiley: Chichester, UK, 1985; p. 682. [Google Scholar]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; Wiley: New York, NY, USA, 1995; p. 720. [Google Scholar]
- Bazykin, A.D. Nonlinear Dynamics of Interacting Populations; World Scientific: Singapore, 1984; p. 216. [Google Scholar]
- Izhikevich, E.M. Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting; MIT Press: Cambridge, MA, USA, 2007; p. 521. [Google Scholar]
- Landa, P.S. Nonlinear Oscillations and Waves in Dynamical Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 360. [Google Scholar]
- Hayashi, C. Nonlinear Oscillations in Physical Systems; Princeton University Press: Princeton, NJ, USA, 2014; Volume 432. [Google Scholar]
- Uppal, A.; Ray, W.H.; Poore, A.B. The classification of the dynamic behavior of continuous stirred tank reactors—Influence of reactor resident time. Chem. Eng. Sci. 1976, 31, 205–214. [Google Scholar] [CrossRef]
- Vaganov, D.A.; Samoilenko, N.G.; Abramov, V.G. Periodic regimes of continuous stirred tank reactors. Chem. Eng. Sci. 1978, 33, 1131–1140. [Google Scholar] [CrossRef]
- Bykov, V.I.; Tsybenova, S.B. Parametric analysis of the simplest model of the theory of thermal explosion–the Zel’dovich–Semenov model. Combust. Explos. Shock Waves 2001, 37, 523–534. [Google Scholar] [CrossRef]
- Bykov, V.I.; Tsybenova, S.B.; Yablonsky, G. Chemical Complexity via Simple Models; De Gruyter: Berlin, Germany, 2018. [Google Scholar]
- Pérez, M.; Font, R.; Montava, M.A. Regular self-oscillating and chaotic dynamics of a continuous stirred tank reactor. Comput. Chem. Eng. 2002, 26, 889–901. [Google Scholar] [CrossRef]
- Ryashko, L.; Bashkirtseva, I. Stochastic bifurcations and excitement in the ZS-model of a thermochemical reaction. Mathematics 2022, 10, 960. [Google Scholar] [CrossRef]
- Shilnikov, L.P.; Shilnikov, A.L.; Turaev, D.V.; Chua, L.O. Methods of Qualitative Theory in Nonlinear Dynamics; World Scientific: Singapore, 1998; p. 416. [Google Scholar]
- Sun, J.Q.; Luo, A. Bifurcation and Chaos in Complex Systems; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Benoît, E.; Callot, J.L.; Diener, F.; Diener, M. Chasse au canards. Collect. Math. 1981, 31, 37–119. [Google Scholar]
- Krupa, M.; Szmolyan, P. Relaxation oscillation and canard explosion. J. Differ. Equ. 2001, 174, 312–368. [Google Scholar] [CrossRef]
- Rankin, J.; Desroches, M.; Krauskopf, B.; Lowenberg, M. Canard cycles in aircraft ground dynamics. Nonlinear Dyn. 2011, 66, 681–688. [Google Scholar] [CrossRef]
- Bashkirtseva, I.; Ryashko, L.; Zaitseva, S. Analysis of nonlinear stochastic oscillations in the biochemical Goldbeter model. Commun. Nonlinear Sci. Numer. Simul. 2019, 73, 165–176. [Google Scholar] [CrossRef]
- Bashkirtseva, I.; Ryashko, L. Canard oscillations in the randomly forced suspension flows. Chaos 2021, 31, 033129. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, P.R.; Petrovskii, S.; Banerjee, M. Effect of slow-fast time scale on transient dynamics in a realistic prey-predator system. Mathematics 2022, 10, 699. [Google Scholar] [CrossRef]
- Slepukhina, E.; Bashkirtseva, I.; Ryashko, L.; Kügler, P. Stochastic mixed-mode oscillations in the canards region of a cardiac action potential model. Chaos Solitons Fractals 2022, 164, 112640. [Google Scholar] [CrossRef]
- Sowers, R.B. Random perturbations of canards. J. Theoret. Probab. 2008, 21, 824–889. [Google Scholar] [CrossRef]
- Berglund, N.; Gentz, B.; Kuehn, C. Hunting French ducks in a noisy environment. J. Differ. Equ. 2012, 252, 4786–4841. [Google Scholar] [CrossRef]
- Bashkirtseva, I.; Nasyrova, V.; Ryashko, L. Analysis of noise effects in a map-based neuron model with Canard-type quasiperiodic oscillations. Commun. Nonlinear Sci. Numer. Simulat. 2018, 63, 261–270. [Google Scholar] [CrossRef]
- De Maesschalck, P.; Dumortier, F.; Roussarie, R. Canard Cycles From Birth to Transition; Springer International Publishing: New York, NY, USA, 2021; p. 408. [Google Scholar]
- Marsden, J.E.; McCracken, M. The Hopf bifurcation and Its Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 19. [Google Scholar]
- Higham, D.J. An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. 2001, 43, 525–546. [Google Scholar] [CrossRef]
- Arnold, L. Random Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 1998; p. 600. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bashkirtseva, I.; Ivanenko, G.; Mordovskikh, D.; Ryashko, L. Canards Oscillations, Noise-Induced Splitting of Cycles and Transition to Chaos in Thermochemical Kinetics. Mathematics 2023, 11, 1918. https://doi.org/10.3390/math11081918
Bashkirtseva I, Ivanenko G, Mordovskikh D, Ryashko L. Canards Oscillations, Noise-Induced Splitting of Cycles and Transition to Chaos in Thermochemical Kinetics. Mathematics. 2023; 11(8):1918. https://doi.org/10.3390/math11081918
Chicago/Turabian StyleBashkirtseva, Irina, Grigoriy Ivanenko, Dmitrii Mordovskikh, and Lev Ryashko. 2023. "Canards Oscillations, Noise-Induced Splitting of Cycles and Transition to Chaos in Thermochemical Kinetics" Mathematics 11, no. 8: 1918. https://doi.org/10.3390/math11081918
APA StyleBashkirtseva, I., Ivanenko, G., Mordovskikh, D., & Ryashko, L. (2023). Canards Oscillations, Noise-Induced Splitting of Cycles and Transition to Chaos in Thermochemical Kinetics. Mathematics, 11(8), 1918. https://doi.org/10.3390/math11081918









