1. Introduction
Chaos is a term that has many different interpretations based on the physical subject that generates it. If it relates to mathematical model expressed in the form of the ordinary differential equations, chaos can be understood as a long-term unpredictable evolution caused by the specific formation of vector field. The solution of chaotic system is very sensitive to small changes in initial conditions due to the exponential divergence of two neighboring state orbits. This feature of vector field is commonly denoted as stretching, while trajectory folding answers to intrinsic system nonlinearity and is responsible for strange attractor boundedness. The term strange attractor is also related to the subject of nonlinear dynamics, that is, we are speaking about the ω-limit set that comprises density and mixing.
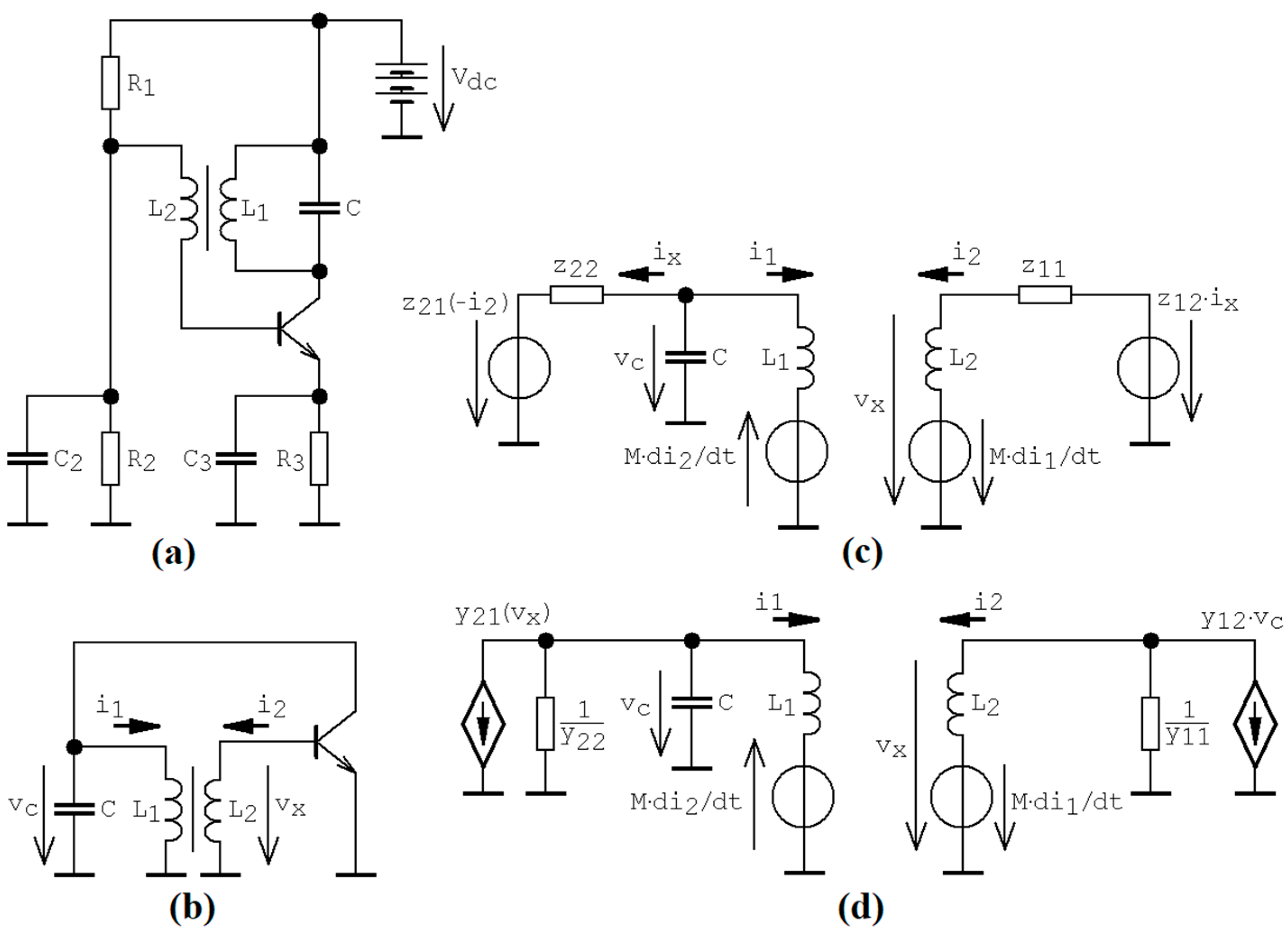
Chaos belongs to a complex motion that can be revealed within very simple circuits, both autonomous and driven. To mention the famous example, isolated Chua’s oscillator contains only four linear passive components and one piecewise-linear [
1] or cubic polynomial [
2] active resistor. The same number of the passive elements and active two-port working in the trans-admittance mode with quadratic polynomial transfer function can lead to the steady state chaotic oscillations as well, as indicated in the paper [
3]. These circuits belong to those that are deliberately constructed, with the knowledge of describing sets of ordinary differential equations as the robust chaos generators. However, chaos can be observed in the conventional non-chaotic building blocks dedicated for analogue signal processing. To find this kind of behavior, the initial step covers mathematical modeling of inspected dynamical system, considering an appropriately high level of abstraction. After that, elimination of nonessential parameters from the viewpoint of chaos evolution could be done. For example, fingerprints of deterministic chaos were reported in phase-locked loops [
4], power converters [
5], dc-dc converters [
6], switching regulators [
7], multi-state static memory cells [
8], switched capacitor circuits [
9], analog representation of simplified abandoned neuron [
10], and many others.
This paper extends a list of typical sinusoidal oscillators forced into chaotic steady state, such as Colpitts [
11], Hartley [
12], or Wien bridge-based [
13], Clapp [
14], RC phase shift [
15], by one additional case: single-stage tuned collector oscillator. Further text is organized as follows. The next section deals with numerical analysis of derived mathematical model which is, after removing parasitic properties of the generalized bipolar transistor, a third-order autonomous dynamical system in the dimensionless form. An active three-port, biased into hypothetical operating point, undergoes a multi-objective optimization routine. This results in a few sets of numerical values of internal parameters for which the oscillator becomes chaotic for all common perspectives: the positive largest Lyapunov exponent (LE), sensitivity to small changes of initial conditions, broad-band frequency spectrum, increased entropy of produced waveform, etc. Experimental construction and verification of flow-equivalent chaotic oscillator demonstrates, at least from the most interesting set of internal parameters, that chaos is neither a numerical artifact nor long transient behavior.
3. Searching for Chaos and Numerical Analysis
For further numerical analysis, the parameter constraints that reflect the conventional operational state of the sinusoidal oscillator should be considered. First of all, input and output impedance (case Z), as well as input and output admittance (case Y), will be positive numbers (zeroes are not excluded). Simultaneously, the backward trans-resistance (trans-conductance) should be as low as possible for case Z (case Y) dynamical system. Thanks to impedance and frequency rescaling, normalized values of all accumulation elements can be removed from the hyperspace of system parameters dedicated for optimization, i.e., we can keep them unified . Additionally, it is quite complicated to realize the coupling coefficient k of a feedback transformer close to unity. Since , high values of the mutual inductance are penalized during optimization. Because of the nature of the search engine, where the initial conditions in each optimization step are chosen randomly in the vicinity of the state space, all strange attractors discovered and mentioned in this paper belong to the group of the self-excited attractors. Therefore, the existence of the so-called hidden attractors is not excluded.
As pointed out in papers [
16,
17,
18,
19,
20], searching for the chaos process can be transformed into an optimization problem. In doing so, robust chaos was detected within the analyzed model of the tuned collector oscillator for the following mutual inductance and hypothetical bias point of the transistor modeled by impedance parameters
For these values, the fixed point located at origin is a full repeller with a stability index of zero, characterized by the following eigenvalues .
Within many runs of the search for chaos algorithm, another set of “chaotic system parameters” leading to geometrically different strange attractor was revealed, namely
In this case, origin is a fixed point with stability index two, i.e., different local vector field geometry if compared to system with parameter set (8). Eigenvalues can be established as .
For transistor modeled using admittance parameters, the following group of the internal system parameters that leads to robust chaos was discovered
Note that, in this case, the transistor behaves close to an ideal current source without backward trans-conductance. This is an interesting situation since it is rather close to the conventional operation regime of sinusoidal oscillator. Sinusoidal oscillations with quite low harmonic distortion can be excited if forward transconductance of generalized transistor .
In the upcoming two figures, numerical integration results were obtained by using a fourth order Runge–Kutta method with final time 10,000 s and step size 10 ms. Note that step size is much smaller than the time constant of dynamical system expressed in terms of the eigenvalues [
21].
Figure 2 brings selected results coming from the numerical analysis of case Z dynamical system. Namely,
Figure 2a shows the typical shape of a strange attractor generated by parameter set (12) in full 3D perspective. The sets of initial conditions leading to proposed chaotic motions are
for orange and blue trajectory respectively.
Figure 2b provides a typical strange attractor for parameter case (11). This plot also demonstrates the sensitive dependance of the solution to small perturbations of initial conditions. Small cubes with an edge of 0.01 (uniform distribution) containing 10
4 initial states were randomly generated (black dots). Following that, final states were stored after 2 s short-time evolution (blue dots), about 4 s average time evolution (green dots), and 10 s long-time evolution (red dots).
Figure 2c,d show all plane projections of the typical strange attractor, together with a one-dimensional curve of divergence of the vector field as a function of state variable
z(
t).
Figure 2d–m provide rainbow-scaled contour graphs of distribution of kinetic energy over the state space, calculated for time instance 100 ms and time step 1 ms. Cross-sections of generated attractors with individual horizontal planes of the state space were provided as well. Two-dimensional rainbow-scaled surface plots of the largest LE as function of bias point of the generalized transistor were provided via
Figure 2n–p. There, strong chaos is marked by red color, weak chaos by yellow, a limit cycle using a green color, and the blue area corresponds to the trivial solution. Each high-resolution plot contains 101 × 101 = 10,201 points. Of course, only a very small fragment of hyperspace of the system parameters investigated by an optimization routine is visualized here. For a slightly increased normalized value of the input impedance,
z11 = 0.33 Ω → 0.35 Ω of generalized transistor large attractor becomes separated into two funnel strange attractor, as illustrated in
Figure 2q. Finally,
Figure 2r,x provide basins of attraction for attractor generated by system (3) with parameter set (11). Each subplot represents horizontal planes where voltage across capacitor is constant,
i1∈(–10, 10) A and
i2∈(–10, 10) A. All initial states that eventually end up on the strange attractor are marked by red color, and the only other solution is unbounded (purple areas). Note that the basin for chaotic attractor fills an interestingly-shaped connected three-dimensional object in the state space.
Figure 3 provides selected results coming from the numerical analysis of case Y dynamical system. The figure begins by showing two mirrored typical strange attractors obtained for initial conditions
for purple trajectory and
, leading to state attractor plotted using an orange color. This subplot also demonstrates the sensitivity of system solution to small differences in initial conditions. In the beginning, a group of 10
4 initial conditions with uniform distribution were placed about origin, forming a cube with an edge size of 0.01 (black points). After 2 s short-time evolution (blue dots), 4 s evolution (green dots), and 10 s long-time evolution (red dots), the final states were visualized.
Figure 3b,g provide rainbow-scaled contour graphs showing distribution of kinetic energy over the state space, calculated for time instance 100 ms and time step 1 ms.
Figure 3h shows the colored plot of the largest LE as a two-dimensional function of two system parameters. The area visualized here represents only a tiny fragment of hyperspace investigated by an optimization routine. Strong chaos is marked by a red color, weak chaos is marked by yellow, limit cycle uses a green color, and the blue area corresponds to the trivial solution. Each high-resolution plot contains 101 × 101 = 10,201 points.
Adopting “the most chaotic” numerical values revealed, the Kaplan–Yorke dimension of corresponding strange attractor approximately equals
. The composition of plots in
Figure 3i,p can be understood as slices of the state space, showing interesting geometric structure of basins of attraction that lead to the chaotic (red area) or unbounded (purple region) behavior. Each subplot represents horizontal planes where voltage across capacitor is constant,
i1∈(–10, 10) A and
i2∈(–10, 10) A. Note that only slices for positive values of voltage
vC are provided. Because of vector field symmetry, the geometrical structure will be repeated for negative values.
4. Experimental Verification via Construction of Flow-Equivalent Oscillator
For research papers that present a new chaotic dynamical system, practical construction followed by experimental verification became the common standard long ago [
22]. There are several reasons for this:
The trajectory that originates in numerical integration is subject to inevitable errors and represents only an approximation of real behavior, regardless of the method chosen.
A smooth integration process instead of problem discretization is performed using an electronic circuit.
With a suitable choice of time constant, we can easily decide if observed motion is a long transient or a robust, structurally stable solution.
Since individual bifurcation parameters can be associated with variable resistors, a smooth and wide change of its value can reveal dynamical phenomena unobserved during the numerical analysis, i.e., the behavior of chaotic circuit can be thoroughly studied without time-consuming re-simulations.
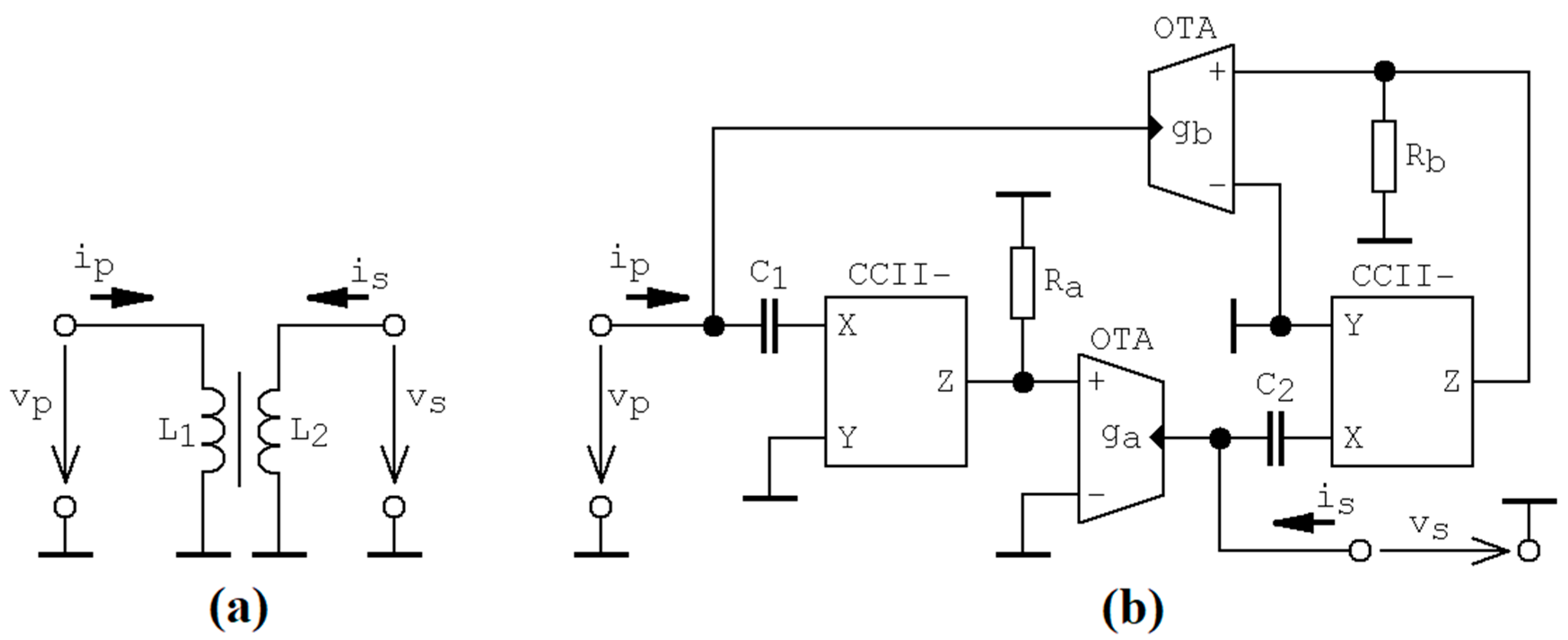
There are drawbacks that suggest that practical construction of transformer should be avoided: cumbersome realization of large values of self- and mutual inductances, hardly defined coupling coefficient, nonzero losses that can neither be precisely described nor included into the mathematical model. Assuming matrix Equation (1), the synthetic transformer suitable for our purposes can be designed, not directly, but considering ideal transformer´s dual circuit.
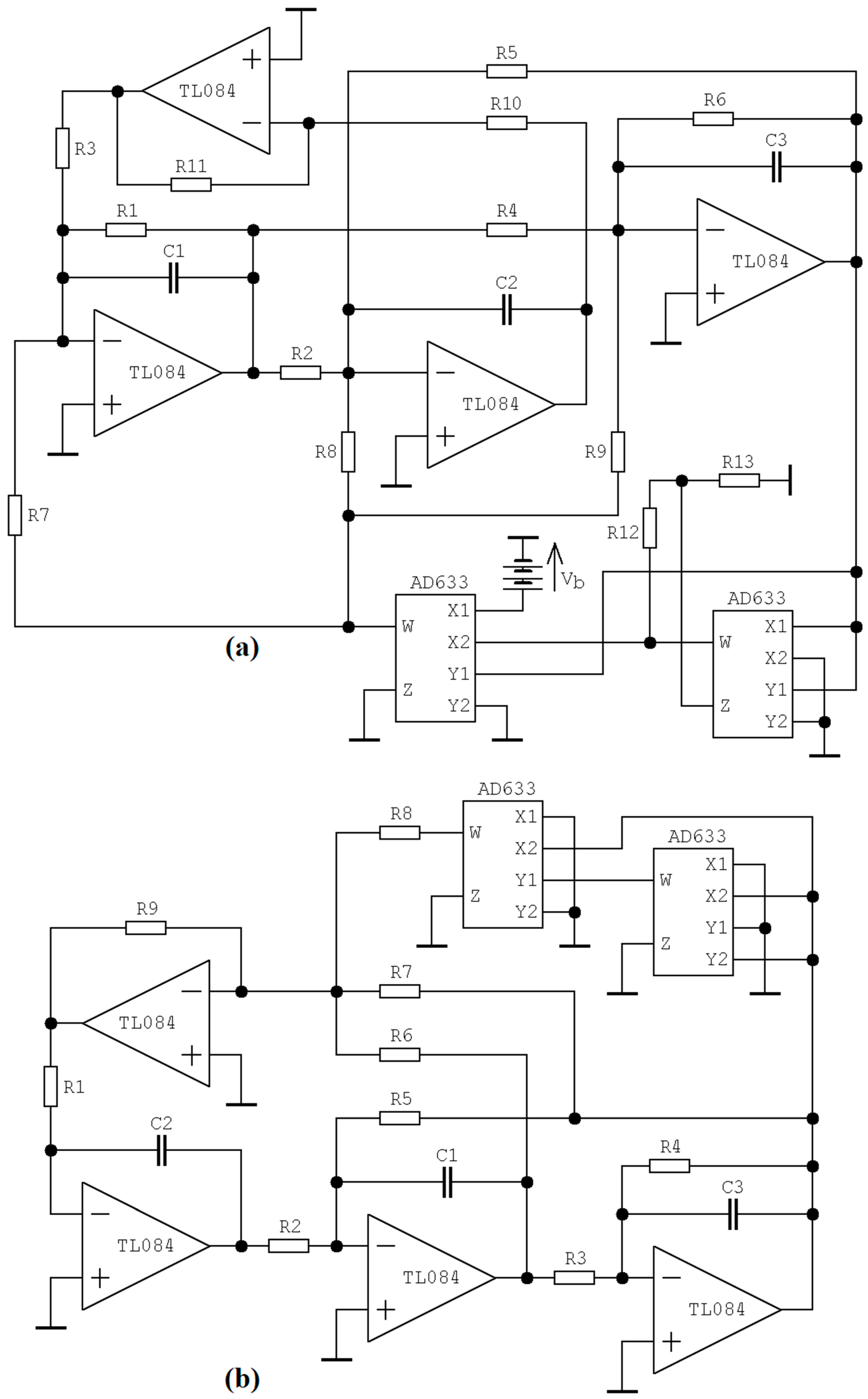
Figure 4 shows two port circuit that behaves close to ideal transformer´s dual circuit. Moreover, the coupling coefficient is adjustable (or even electronically tunable using external DC voltage) via the main transfer constant of both operational trans-conductance amplifiers (OTA). Since admittance and impedance two-port models of transistor are dual by definition, synthetic transformer could be connected directly between the base and collector of modeled bipolar transistor. Accordingly, to a given schematic, this active device can be described by the following port equations
where
α1,2 are the current tracking errors of second-generation current conveyors (CCII–),
ga and
gb are trans-conductance of first and second OTA, respectively.
Although a synthetic ideal transformer with arbitrary mutual inductances can be designed as mentioned above, the necessity of four active devices appears to be an overly complicated circuit solution. For both Z and Y cases of analyzed dynamical system, a more promising way to model associated dynamics using lumped electronic circuits is the so-called analog computer concept [
23,
24]. This universal method is based on the complete knowledge of differential equations, i.e., including numerical values of the internal parameters. Only three basic building blocks are required for design: lossless inverting integrator, inverting summation amplifier and two-port with prescribed nonlinear transfer function: polynomial, piecewise-linear, or digitally synthesized [
25]. For curious readers and design engineers, the latter publication source can be recommended; the cookbook is supported by complete documentation toward hybrid analog computer. Moreover, the time constant of the final circuit can be easily rescaled via simultaneous change of all capacitors.
A mathematical model (3) with numerical values (8) can be represented by a circuit provided in
Figure 5a. The behavior of this oscillator is uniquely determined by the following set of ordinary differential equations
where
K = 1/10 is internally trimmed transfer constant of the analog multiplier. State vector is composed by voltages measured at the outputs of inverting integrators. By comparing system (15) with model (3), together with parameters (11) and considering time constant
, we can establish numerical values of passive circuit components as
Note that resistors
R12 and
R13 do not appear in differential equations since their purpose is compensation of transfer constant of first analog multiplier in cascade. When choosing time constant, the frequency limitations described in [
26] associated with used active elements need to be considered.
Similarly, case Y dynamical system can be modeled by electronic network given in
Figure 5b, and the corresponding system of ordinary differential equations is
Numerical values of circuit elements can be calculated using direct comparison between system (17), with its mathematical model (8) having parameters (13) and considering the time scale
as follows
Note that both oscillators are quite simple, with only three integrated circuits fed by the symmetrical ±15 V supply voltage. A few examples coming from laboratory experiments can be found in
Figure 6, including breadboard photo (
Figure 6g) and waveforms captured in time domain (
Figure 6o,p). Designed chaotic oscillators proves useful for finding strange attractors that were unnoticed during numerical analysis (
Figure 6i–n).