Positive Periodic Solution for Pipe/Tank Flow Configurations with Friction
Abstract
1. Introduction
- (1)
- Using appropriate variable substitution, the second-order equation can be transformed into a low-order two-dimensional system so that the dynamic properties of the second-order equation can be conveniently studied.
- (2)
- Compared with the article [5], the existence and stability conditions of periodic solutions obtained in this paper are easier to verify.
- (3)
- In [2], strong mathematical analysis skills are required, while the method used in this paper does not require strong mathematical analysis skills.
2. Preliminaries
- (1)
- (2)
- (3)
- ,
3. Existence of a Positive Periodic Solution
4. Dynamic Properties of a Positive Periodic Solution
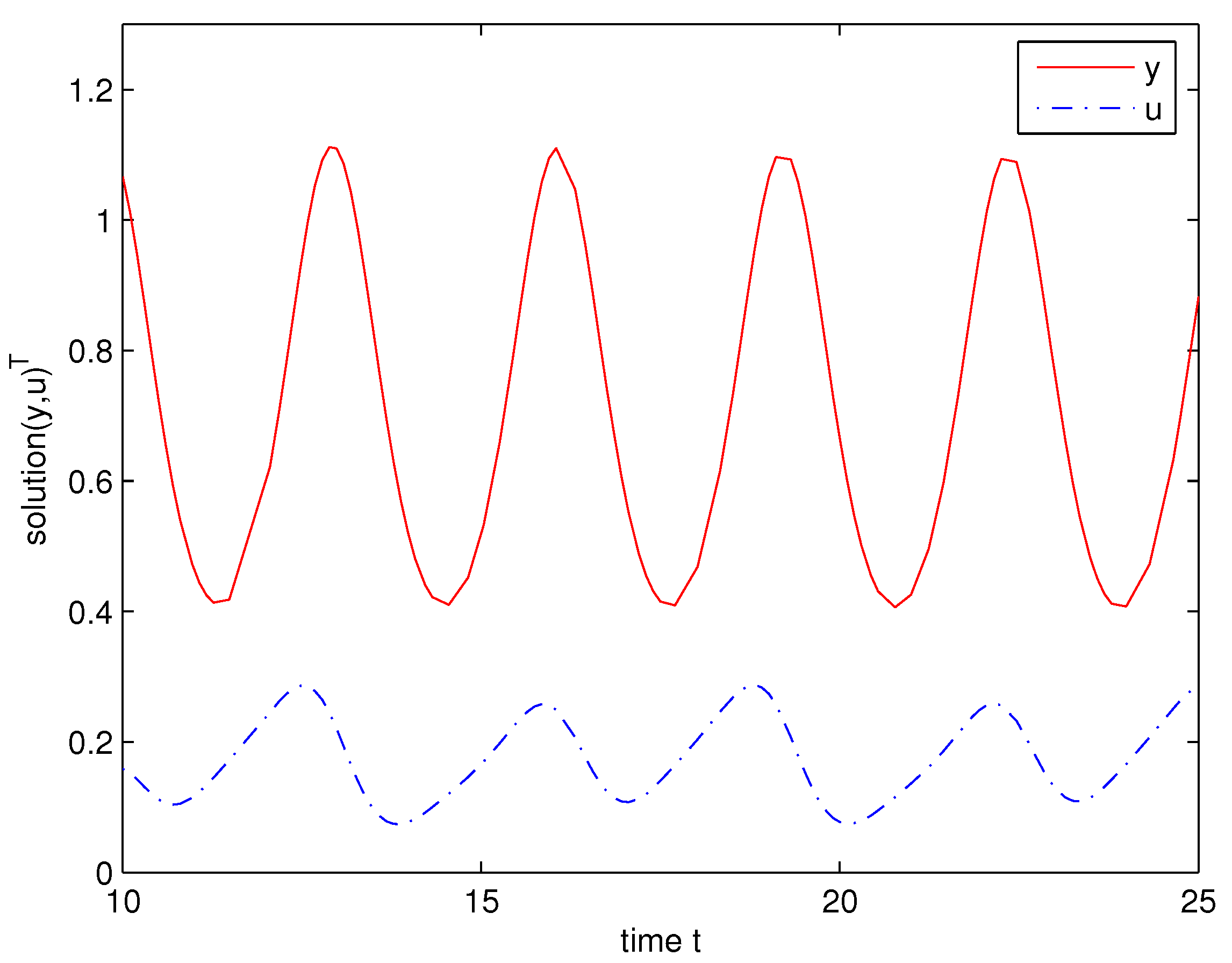
5. Example
6. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Propst, G. Pumping effects in models of periodically forced flow configurations. Phys. D Nonlinear Phenom. 2006, 217, 193–201. [Google Scholar] [CrossRef]
- Cid, J.Á.; Propst, G.; Tvrdý, M. On the pumping effect in a pipe/tank flow configuration with friction. Phys. D Nonlinear Phenom. 2014, 273, 28–33. [Google Scholar] [CrossRef]
- Hakl, R.; Torres, P.J.; Zamora, M. Periodic solutions of singular second order differential equations: The repulsive case. Topol. Methods Nonlinear Anal. 2012, 39, 199–220. [Google Scholar]
- Hakl, R.; Torres, P.J.; Zamora, M. Periodic solutions of singular second order differential equations: Upper and lower functions. Nonlinear Anal. 2011, 74, 7078–7093. [Google Scholar] [CrossRef]
- Dorociaková, B.; Michalková, M.; Olach, R.; Sága, M. Existence and Stability of Periodic Solution Related to Valveless Pumping. Math. Probl. Eng. 2018, 2018, 3982432. [Google Scholar] [CrossRef]
- Liu, W.; Huang, J.; Yao, Q. Stability analysis for quaternion-valued inertial memristor-based neural networks with time delays. Neurocomputing 2021, 448, 67–81. [Google Scholar] [CrossRef]
- Novaes, D.; Silva, F. Higher Order Analysis on the Existence of Periodic Solutions in Continuous Differential Equations via Degree Theory. Siam J. Math. Anal. 2021, 53, 2476–2490. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, P.; Ge, W. Periodic solutions of higher-order delay differential equations. Nonlinear Anal. TMA 2005, 63, 136–152. [Google Scholar] [CrossRef]
- Liu, J.; Liu, W.; Liu, B. Periodic solutions for fourth-order p-Laplacian functional differential equations with sign-variable coefficient. Electron. J. Differ. Equ. 2013, 205, 1–9. [Google Scholar]
- Djebali, I.; Guedda, L. Fractional multipoint boundary value problems at resonance with kernel dimension greater than one. Math. Methods Appl. Sci. 2021, 44, 2621–2636. [Google Scholar] [CrossRef]
- Rao, R.; Lin, Z.; Ai, X.; Wu, J. Synchronization of epidemic systems with Neumann boundary value under delayed impulse. Mathematics 2022, 10, 2064. [Google Scholar] [CrossRef]
- Li, G.; Zhang, Y.; Guan, Y.; Li, J. Stability analysis of multi-point boundary conditions for fractional differential equation with non-instantaneous integral impulse. Math. Biosci. Eng. 2023, 20, 7020–7041. [Google Scholar] [CrossRef]
- Zhu, Q.; Kong, F.; Cai, Z. Advanced Symmetry Methods for Dynamics, Control, Optimization and Applications. Symmetry 2023, 15, 26. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, L. Practical exponential stability of impulsive stochastic food chain system with time-varying delays. Mathematics 2023, 11, 147. [Google Scholar] [CrossRef]
- Li, K.; Li, R.; Cao, L.; Feng, Y.; Onasanya, B.O. Periodically intermittent control of Memristor-based hyper-chaotic bao-like system. Mathematics 2023, 11, 1264. [Google Scholar] [CrossRef]
- Xia, M.; Liu, L.; Fang, J.; Zhang, Y. Stability analysis for a class of stochastic differential equations with impulses. Mathematics 2023, 11, 1541. [Google Scholar] [CrossRef]
- Zhu, Q. Stabilization of stochastic nonlinear delay systems with exogenous disturbances and the event-triggered feedback control. IEEE Trans. Autom. Control 2019, 64, 3764–3771. [Google Scholar] [CrossRef]
- Gaines, R.; Mawhin, J. Coincidence Degree and Nonlinear Differential Equations; Springer: Berlin/Heidelberg, Germany, 1977. [Google Scholar]
- Lu, S. On the existence of positive peroiodic solutions for neutral functional differential equation with multiple deviating arguments. J. Math. Anal. Appl. 2003, 280, 321–333. [Google Scholar] [CrossRef]
- Yang, H.; Han, X. Existence of periodic solutions for the forced pendulum equations of variable length. Qual. Theory Dyn. Syst. 2023, 22, 20. [Google Scholar] [CrossRef]
- Shi, L.; Qi, L.; Zhai, S. Periodic and almost periodic solutions for a non-autonomous respiratory disease model with a lag effect. Acta Math. Sci. 2022, 42, 187–211. [Google Scholar] [CrossRef]
- Gao, F.; Zhang, W. Periodic solutions for a p-Laplacian-like NFDE system. J. Frankl. Inst. 2011, 348, 1020–1034. [Google Scholar] [CrossRef]
- Ge, W.; Ren, J. An extension of Mawhins continuation theorem and its application to boundary value problems with a p-Laplacain. Nonlinear Anal. 2004, 58, 477–488. [Google Scholar] [CrossRef]
- Hu, W.; Zhu, Q.; Karimi, H. Some improved Razumikhin stability criteria for impulsive stochastic delay differential systems. IEEE Trans. Autom. Control 2019, 64, 5207–5213. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, H.; Wang, X.; Du, B. Positive Periodic Solution for Pipe/Tank Flow Configurations with Friction. Mathematics 2023, 11, 1789. https://doi.org/10.3390/math11081789
Du H, Wang X, Du B. Positive Periodic Solution for Pipe/Tank Flow Configurations with Friction. Mathematics. 2023; 11(8):1789. https://doi.org/10.3390/math11081789
Chicago/Turabian StyleDu, Haiqing, Xiaojing Wang, and Bo Du. 2023. "Positive Periodic Solution for Pipe/Tank Flow Configurations with Friction" Mathematics 11, no. 8: 1789. https://doi.org/10.3390/math11081789
APA StyleDu, H., Wang, X., & Du, B. (2023). Positive Periodic Solution for Pipe/Tank Flow Configurations with Friction. Mathematics, 11(8), 1789. https://doi.org/10.3390/math11081789





