Automated Differential Equation Solver Based on the Parametric Approximation Optimization
Abstract
1. Introduction
- We stick to the known physical “blocks”, i.e., a pre-defined set of terms that appear in conventional equations. Moreover, we may impose a pre-defined form, such as in [4,5]. In this case, we should manually or automatically add additional terms, such as , covering all possible combinations. Separately, we manually add different types of non-linearities;
- We evolve the equation with manually added relatively small parameterized blocks; for example, all derivatives of the initial data field up to a certain order (within the optimization process) are combined in products to form the equation. An example of such an approach is [3]. In this case, we do not assume any form of the equation and may add the grid-variable coefficients to the search space. The evolutionary algorithm combines partial derivatives and other functions as building blocks to build various equations.
2. Related Work
2.1. Classical Differential Equation Solvers
2.2. Towards an Automated Solution
2.3. Neural Network Solvers
- Prepare equation and boundary conditions to a conventional form;
- Form a loss function for training;
- Train a model to minimize the loss function.
3. Mathematical Problem Overview
4. Proposed Approach
4.1. Theoretical Formulation
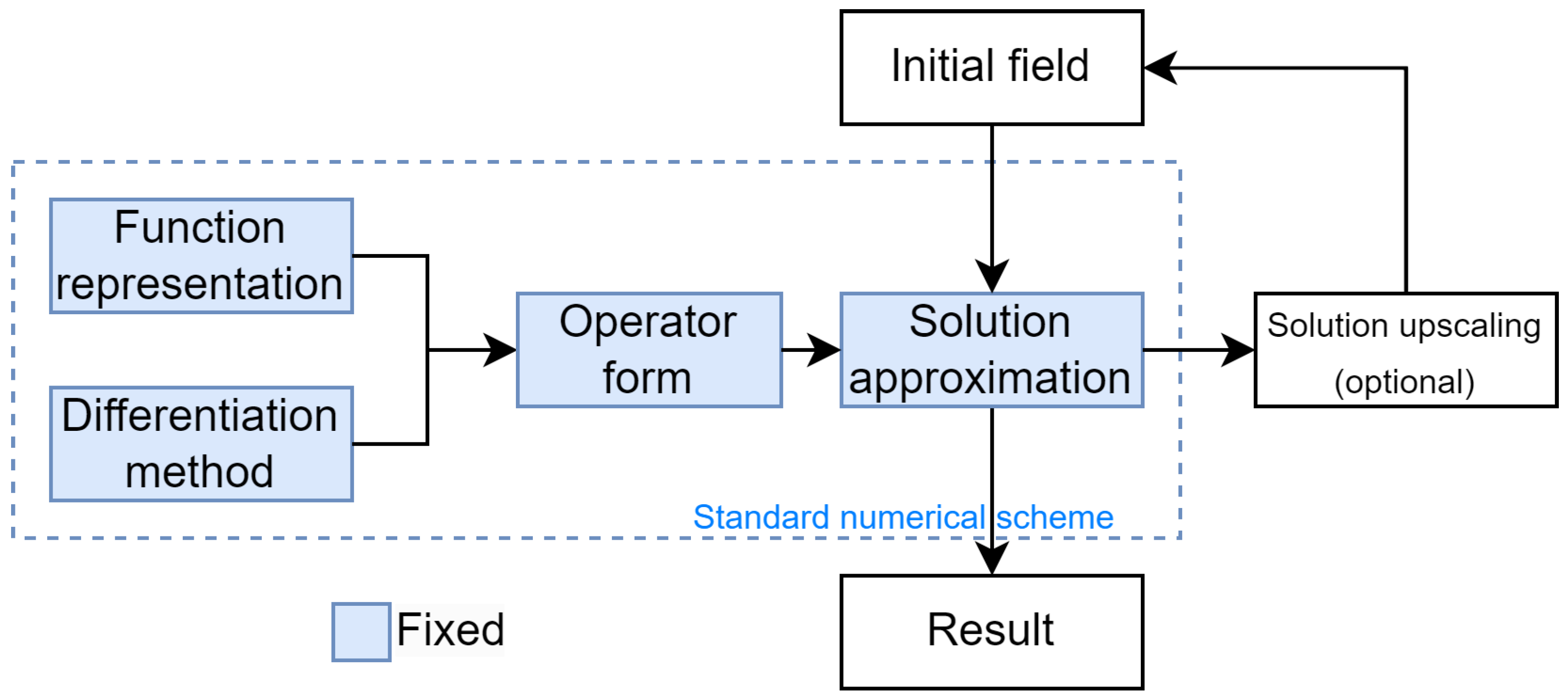
4.2. Numerical Realization
- How is the function represented?
- How do we take the derivative?
- How do we obtain the approximation parameters of the solution?
- (i)
- Parametric optimization. As the first component of the numerical solution, we attempt to approximate the solution of an equation with a continuous parameterized function that is represented by the parameterized model. The parameter set is an arbitrary set that determines the pre-defined function form. As the most straightforward example, represents a linear regression. Moreover, it could be a neural network. In this case, the method is an extension of PINN-like models.
- (ii)
- Model-agnostic differentiation. As the second component, we use finite-difference schemes, such as Equations (9) and (10), and automatic differentiation as equivalent choices. We explicitly build the finite difference schemes and combine them to apply operators for higher-dimensional derivatives in order to speed up computation.
- (iii)
4.3. Modular Approach
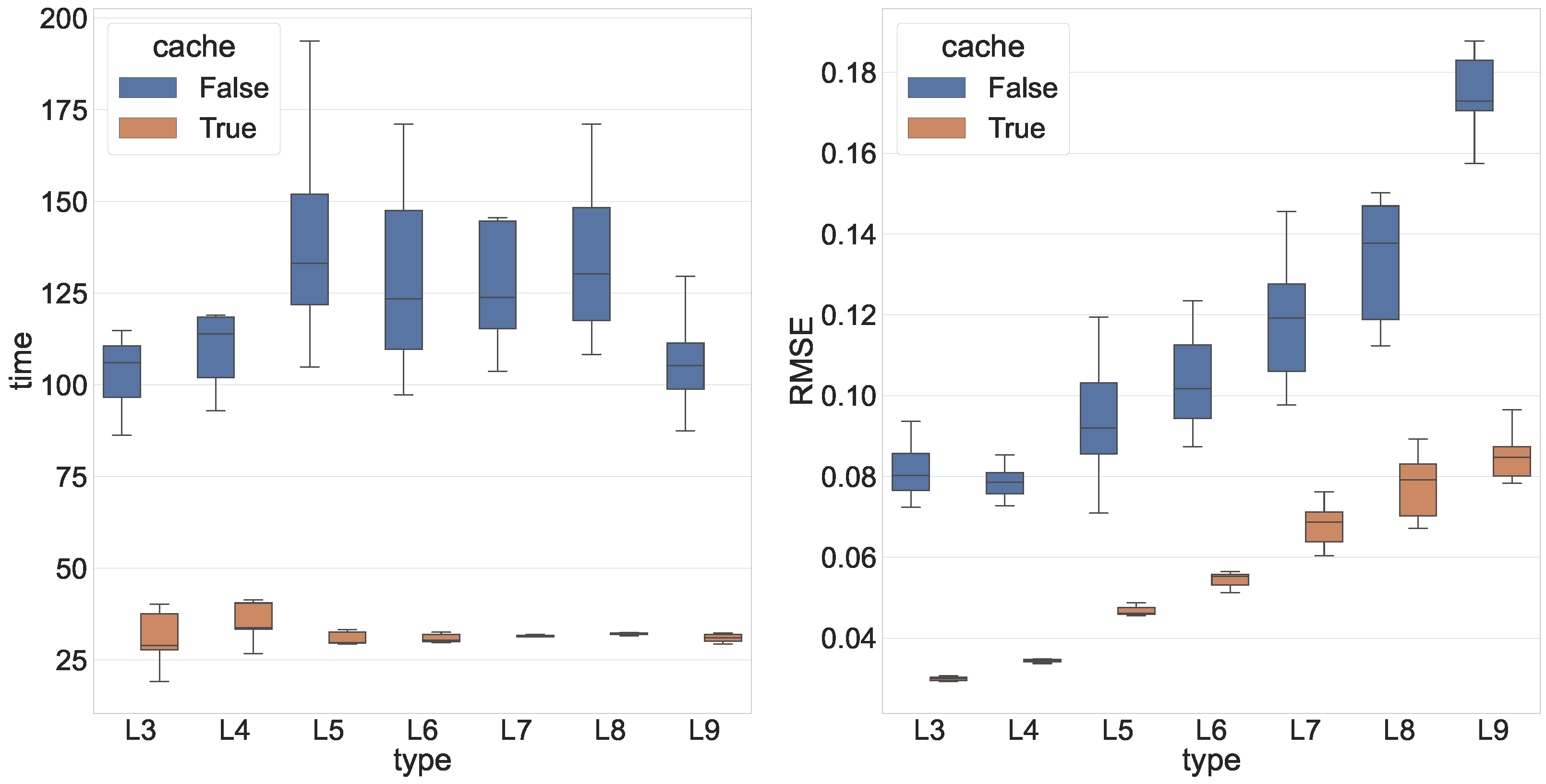
4.4. Caching of Approximate Models
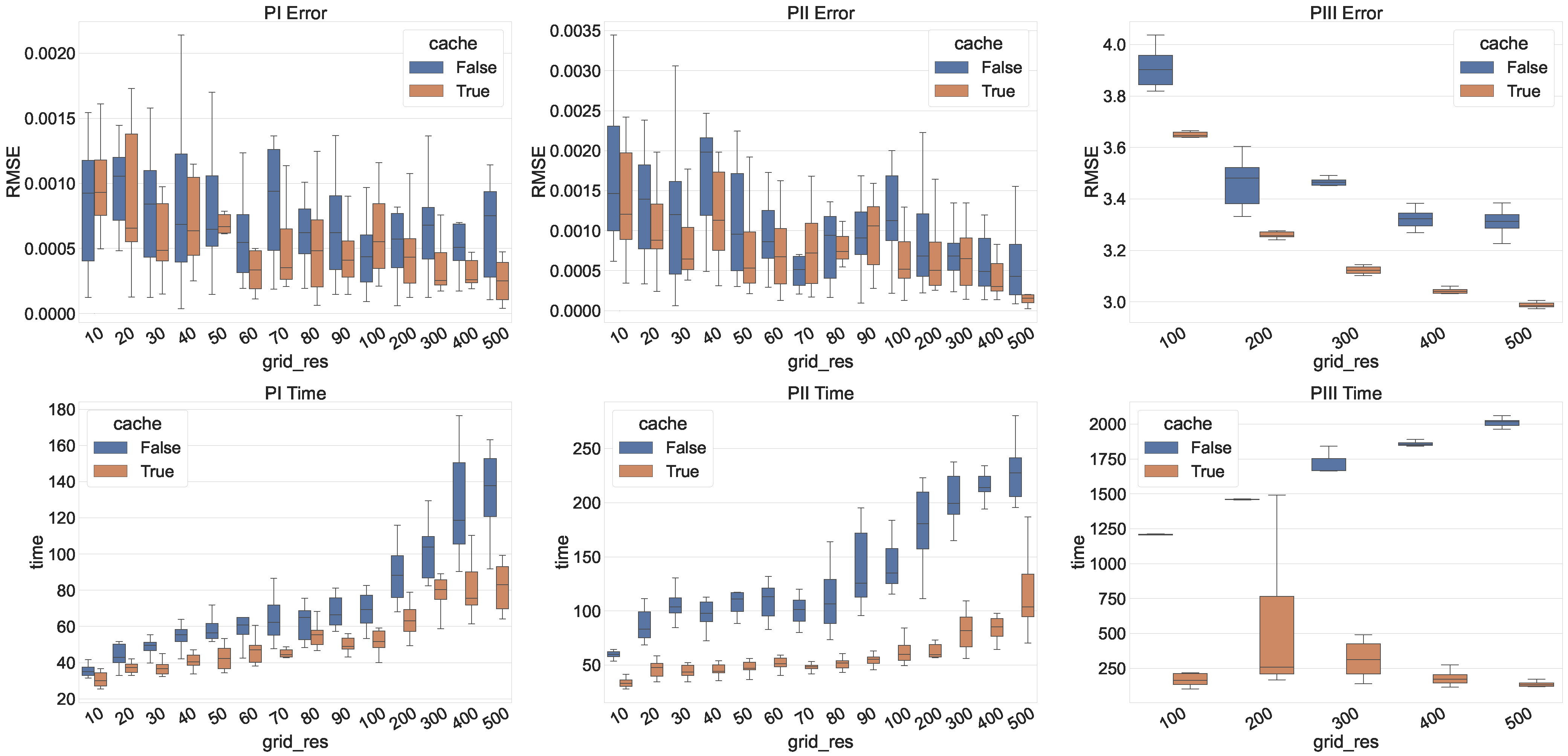
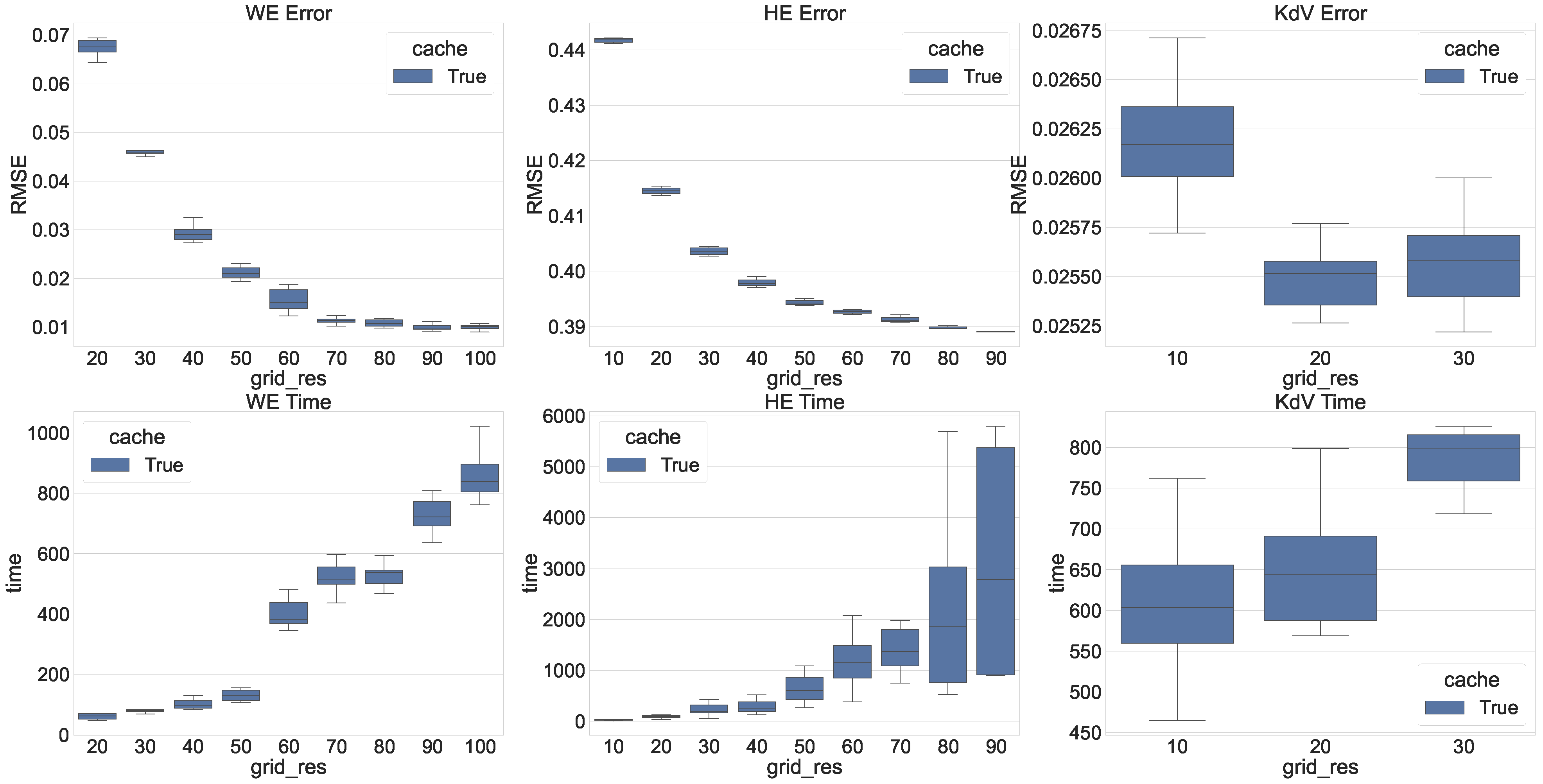
5. Numerical Experiments
- Cache allows converging faster;
- Adding points to the grid leads to a better solution;
- The error between the exact and obtained solutions is negligible for equation discovery application.
5.1. Ordinary Differential Equations
5.1.1. Legendre Equation
5.1.2. Painlevé Transcendents
5.2. Partial Differential Equations
5.2.1. Wave Equation
5.2.2. Heat Equation
5.2.3. Korteweg–de Vries Equation
6. Burgers Equation and DeepXDE Comparison
7. Conclusions
- It can solve ODE and PDE without the involvement of an expert after the algorithm launch, which is most useful for data-driven equation discovery methods;
- It has good precision for equation solution applications and has tools to trade the precision with integration time in both directions;
- It has a flexible modular structure. The modules could be replaced to achieve better speed or better precision.
- More machine learning approaches to differential equation initial-boundary value problems that allow solving non-canonical boundary-value problems, and a wider class of problems to move toward better equation discovery using automated solutions;
- Reduced optimization times;
- Possibility to use different parameterized models.
- Extended optimization time, which in some cases makes the discovery process non-viable;
- To work with physical problems, it is necessary to be able to work with models that allow reproducing special functions, including non-differentiable ones;
- To work with physical problems, the extension of boundary condition types is required.
- Use of the power of GPU to perform optimization using fast memory and built-in matrix instructions;
- Better usage of initial approximation;
- Usage of the “lazy computation” mode, i.e., the precompiled computational graph.
- The optimization problem statement using weak formulation to expand the possible class of solved equations;
- System solutions in strong and weak forms;
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Painlevé Boundary-Value Problems
Appendix B. Solution Plots
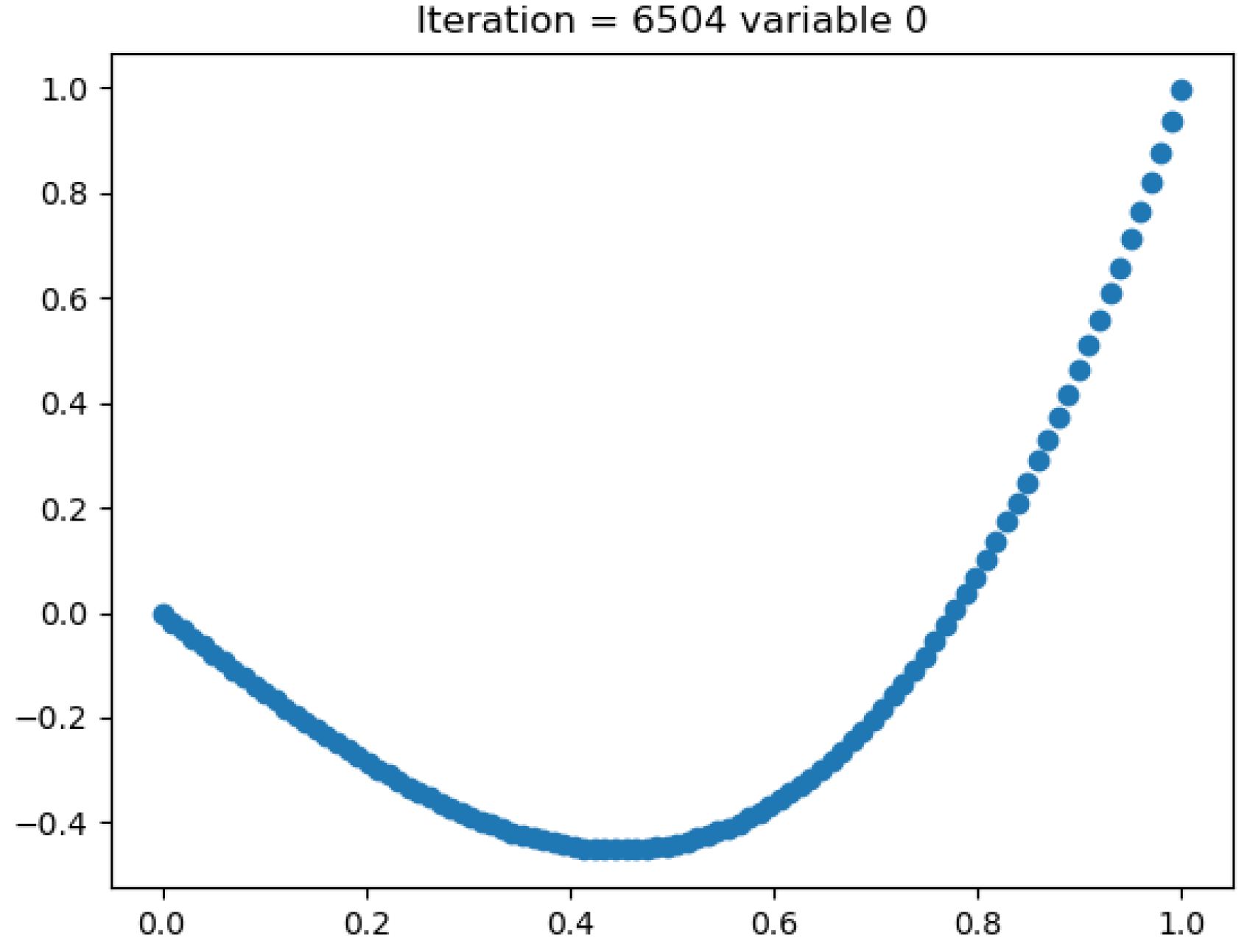

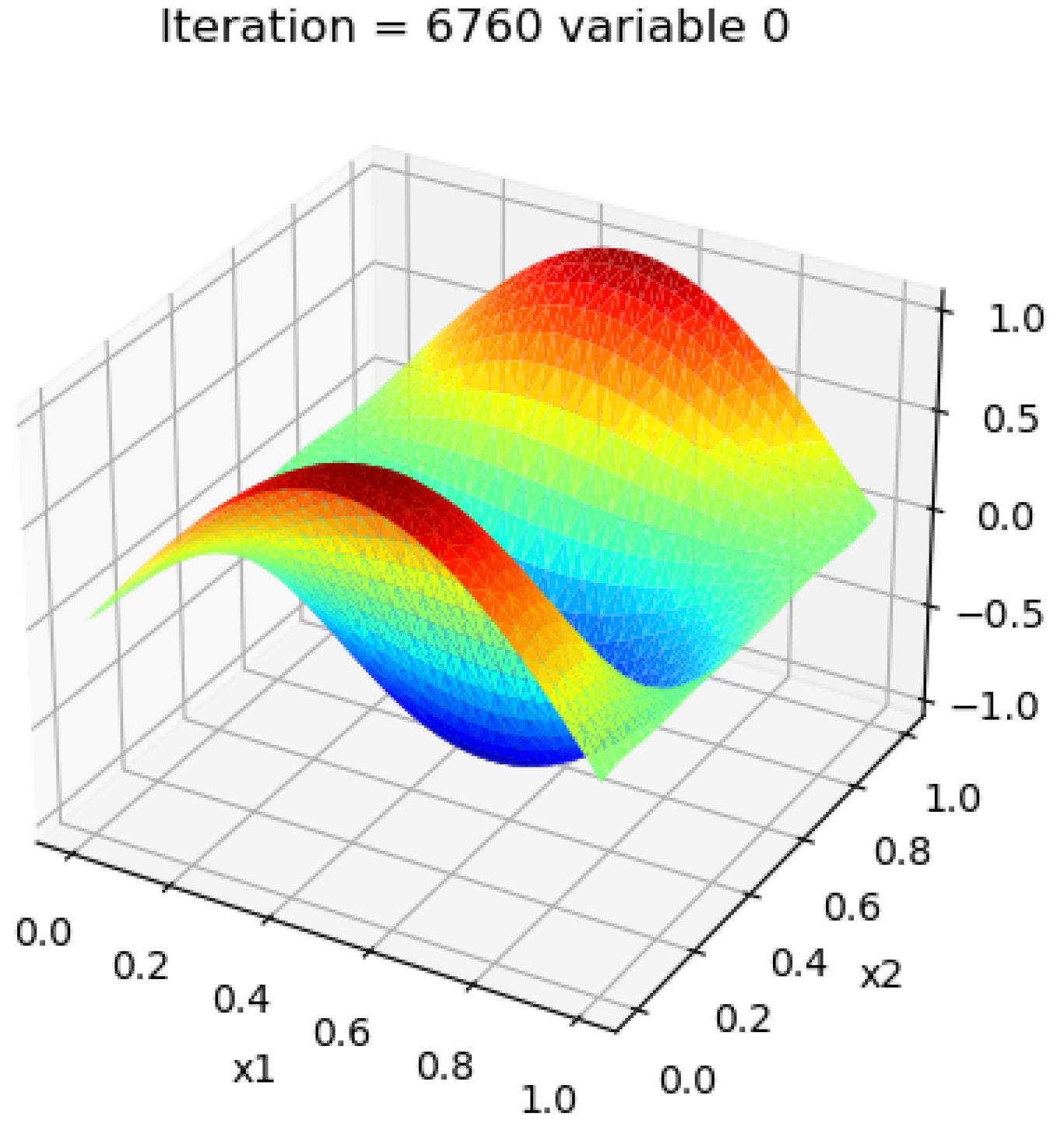
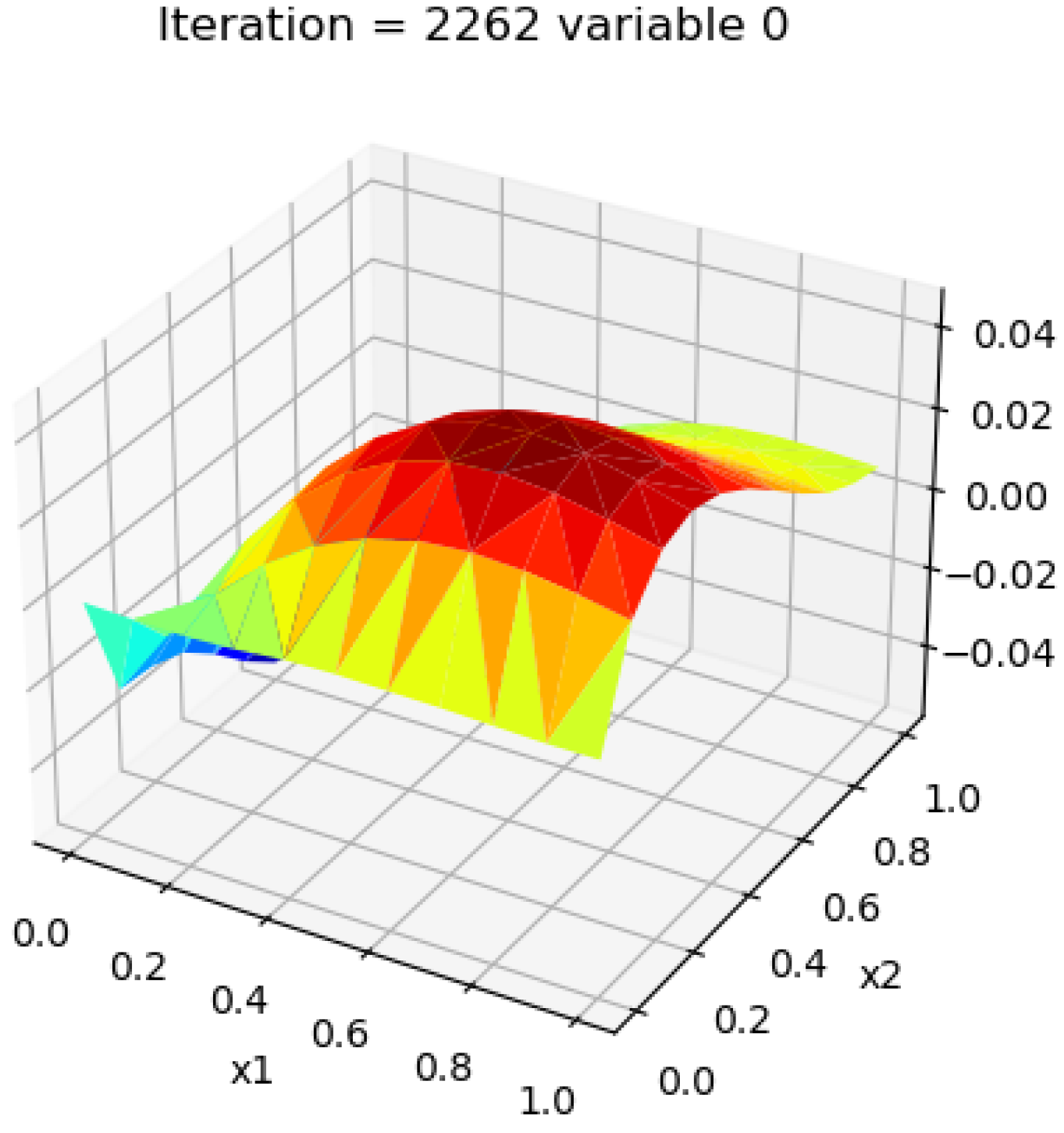
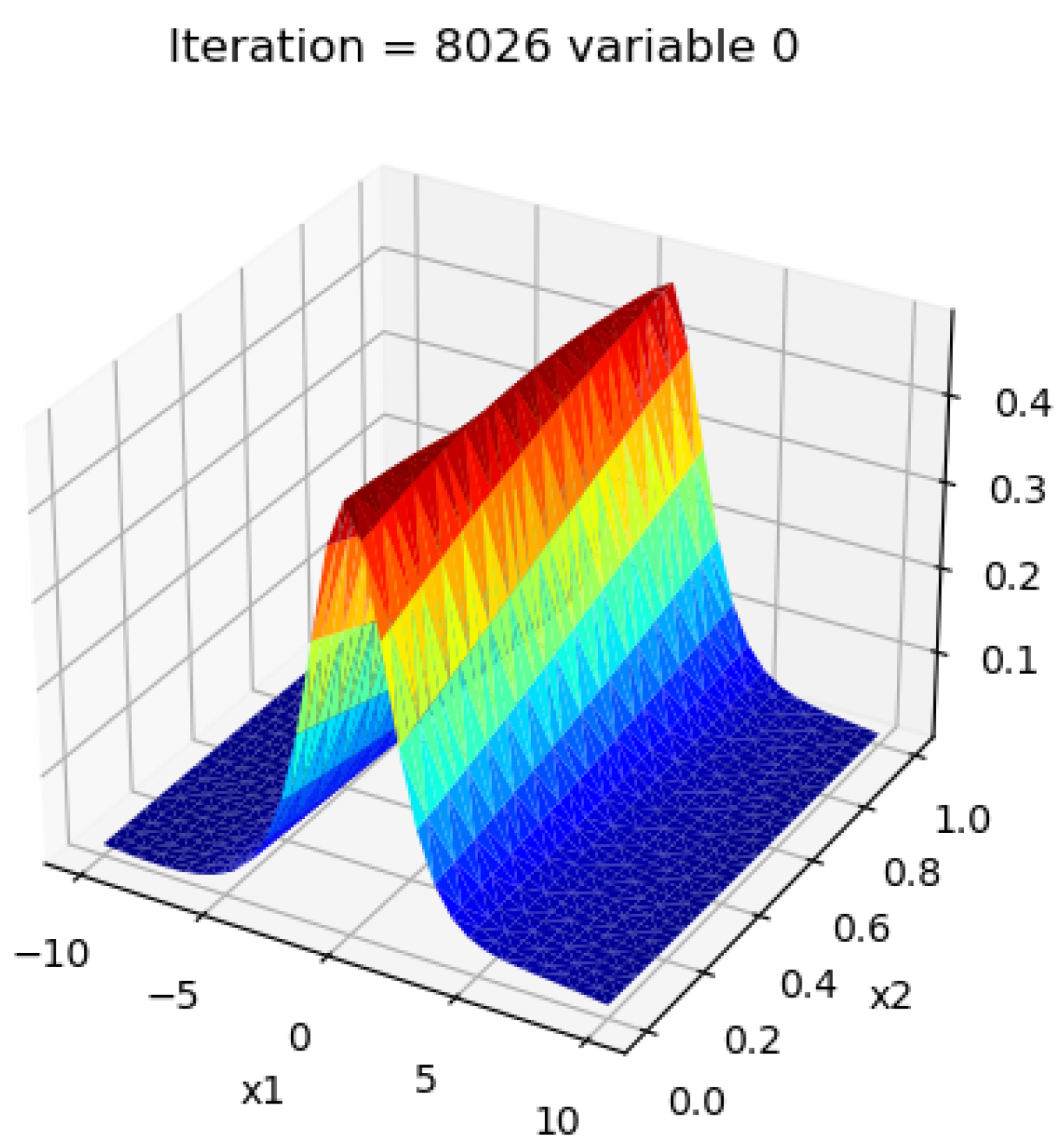
References
- Rao, R.; Lin, Z.; Ai, X.; Wu, J. Synchronization of epidemic systems with Neumann boundary value under delayed impulse. Mathematics 2022, 10, 2064. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, L. Practical Exponential Stability of Impulsive Stochastic Food Chain System with Time-Varying Delays. Mathematics 2023, 11, 147. [Google Scholar] [CrossRef]
- Maslyaev, M.; Hvatov, A.; Kalyuzhnaya, A.V. Partial differential equations discovery with EPDE framework: application for real and synthetic data. J. Comput. Sci. 2021, 53, 101345. [Google Scholar] [CrossRef]
- Rudy, S.H.; Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Data-driven discovery of partial differential equations. Sci. Adv. 2017, 3, e1602614. [Google Scholar] [CrossRef]
- Long, Z.; Lu, Y.; Dong, B. PDE-Net 2.0: Learning PDEs from data with a numeric-symbolic hybrid deep network. J. Comput. Phys. 2019, 399, 108925. [Google Scholar] [CrossRef]
- Rackauckas, C.; Nie, Q. Confederated modular differential equation APIs for accelerated algorithm development and benchmarking. Adv. Eng. Softw. 2019, 132, 1–6. [Google Scholar] [CrossRef]
- Hindmarsh, A.C.; Brown, P.N.; Grant, K.E.; Lee, S.L.; Serban, R.; Shumaker, D.E.; Woodward, C.S. SUNDIALS: Suite of nonlinear and differential/algebraic equation solvers. ACM Trans. Math. Softw. (TOMS) 2005, 31, 363–396. [Google Scholar] [CrossRef]
- Morton, K.W.; Mayers, D.F. Numerical Solution of Partial Differential Equations: An Introduction; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Thomas, J.W. Numerical Partial Differential Equations: Finite Difference Methods; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 22. [Google Scholar]
- Ŝolín, P. Partial Differential Equations and the Finite Element Method; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Pavlovic, A.; Fragassa, C. Geometry optimization by fem simulation of the automatic changing gear. Rep. Mech. Eng. 2020, 1, 199–205. [Google Scholar] [CrossRef]
- Scroggs, M.W.; Baratta, I.A.; Richardson, C.N.; Wells, G.N. Basix: A runtime finite element basis evaluation library. J. Open Source Softw. 2022, 7, 3982. [Google Scholar] [CrossRef]
- Burns, K.J.; Vasil, G.M.; Oishi, J.S.; Lecoanet, D.; Brown, B.P. Dedalus: A flexible framework for numerical simulations with spectral methods. Phys. Rev. Res. 2020, 2, 023068. [Google Scholar] [CrossRef]
- Li, Z.; Kovachki, N.; Azizzadenesheli, K.; Liu, B.; Bhattacharya, K.; Stuart, A.; Anandkumar, A. Neural operator: Graph kernel network for partial differential equations. arXiv 2020, arXiv:2003.03485. [Google Scholar]
- Li, Z.; Kovachki, N.; Azizzadenesheli, K.; Liu, B.; Bhattacharya, K.; Stuart, A.; Anandkumar, A. Fourier neural operator for parametric partial differential equations. arXiv 2020, arXiv:2010.08895. [Google Scholar]
- Zwillinger, D.; Dobrushkin, V. Handbook of Differential Equations; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Rackauckas, C.; Ma, Y.; Martensen, J.; Warner, C.; Zubov, K.; Supekar, R.; Skinner, D.; Ramadhan, A. Universal Differential Equations for Scientific Machine Learning. arXiv 2020, arXiv:2001.04385. [Google Scholar]
- Hindmarsh, A.C. ODEPACK, a systematized collection of ODE solvers. In Scientific Computing; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1983; pp. 55–64. [Google Scholar]
- Hindmarsh, A.C. ODEPACK: Ordinary Differential Equation Solver Library; Astrophysics Source Code Library: Record ascl:1905.021. May 2019. Available online: https://ui.adsabs.harvard.edu/abs/2019ascl.soft05021H (accessed on 7 February 2023).
- Ahnert, K.; Mulansky, M. Odeint–solving ordinary differential equations in C++. AIP Conf. Proc. 2011, 1389, 1586–1589. [Google Scholar]
- Rackauckas, C.; Innes, M.; Ma, Y.; Bettencourt, J.; White, L.; Dixit, V. Diffeqflux.jl-A julia library for neural differential equations. arXiv 2019, arXiv:1902.02376. [Google Scholar]
- Liu, S.; Wang, T.; Zhang, Y. A Functional Package for Automatic Solution of Ordinary Differential Equations with Spectral Methods. arXiv 2016, arXiv:1608.04815. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Lu, L.; Jin, P.; Karniadakis, G.E. Deeponet: Learning nonlinear operators for identifying differential equations based on the universal approximation theorem of operators. arXiv 2019, arXiv:1910.03193. [Google Scholar]
- Sirignano, J.; Spiliopoulos, K. DGM: A deep learning algorithm for solving partial differential equations. J. Comput. Phys. 2018, 375, 1339–1364. [Google Scholar] [CrossRef]
- Czarnecki, W.M.; Osindero, S.; Jaderberg, M.; Swirszcz, G.; Pascanu, R. Sobolev Training for Neural Networks. In Proceedings of the NIPS, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Lu, L.; Meng, X.; Mao, Z.; Karniadakis, G.E. DeepXDE: A deep learning library for solving differential equations. SIAM Rev. 2021, 63, 208–228. [Google Scholar] [CrossRef]
- Maslyaev, M.; Hvatov, A. Solver-Based Fitness Function for the Data-Driven Evolutionary Discovery of Partial Differential Equations. In Proceedings of the 2022 IEEE Congress on Evolutionary Computation (CEC), Padua, Italy, 18–23 July 2022; pp. 1–8. [Google Scholar]
- Nguyen, L.T.K. Modified homogeneous balance method: Applications and new solutions. Chaos Solitons Fractals 2015, 73, 148–155. [Google Scholar] [CrossRef]
- Arnold, D.N.; Winther, R. A superconvergent finite element method for the Korteweg-de Vries equation. Math. Comput. 1982, 38, 23–36. [Google Scholar] [CrossRef]
- Göküzüm, F.S.; Nguyen, L.T.K.; Keip, M.A. An artificial neural network based solution scheme for periodic computational homogenization of electrostatic problems. Math. Comput. Appl. 2019, 24, 40. [Google Scholar] [CrossRef]
- Wang, S.; Wang, H.; Perdikaris, P. On the eigenvector bias of Fourier feature networks: From regression to solving multi-scale PDEs with physics-informed neural networks. Comput. Methods Appl. Mech. Eng. 2021, 384, 113938. [Google Scholar] [CrossRef]
- Wang, S.; Yu, X.; Perdikaris, P. When and why PINNs fail to train: A neural tangent kernel perspective. J. Comput. Phys. 2022, 449, 110768. [Google Scholar] [CrossRef]


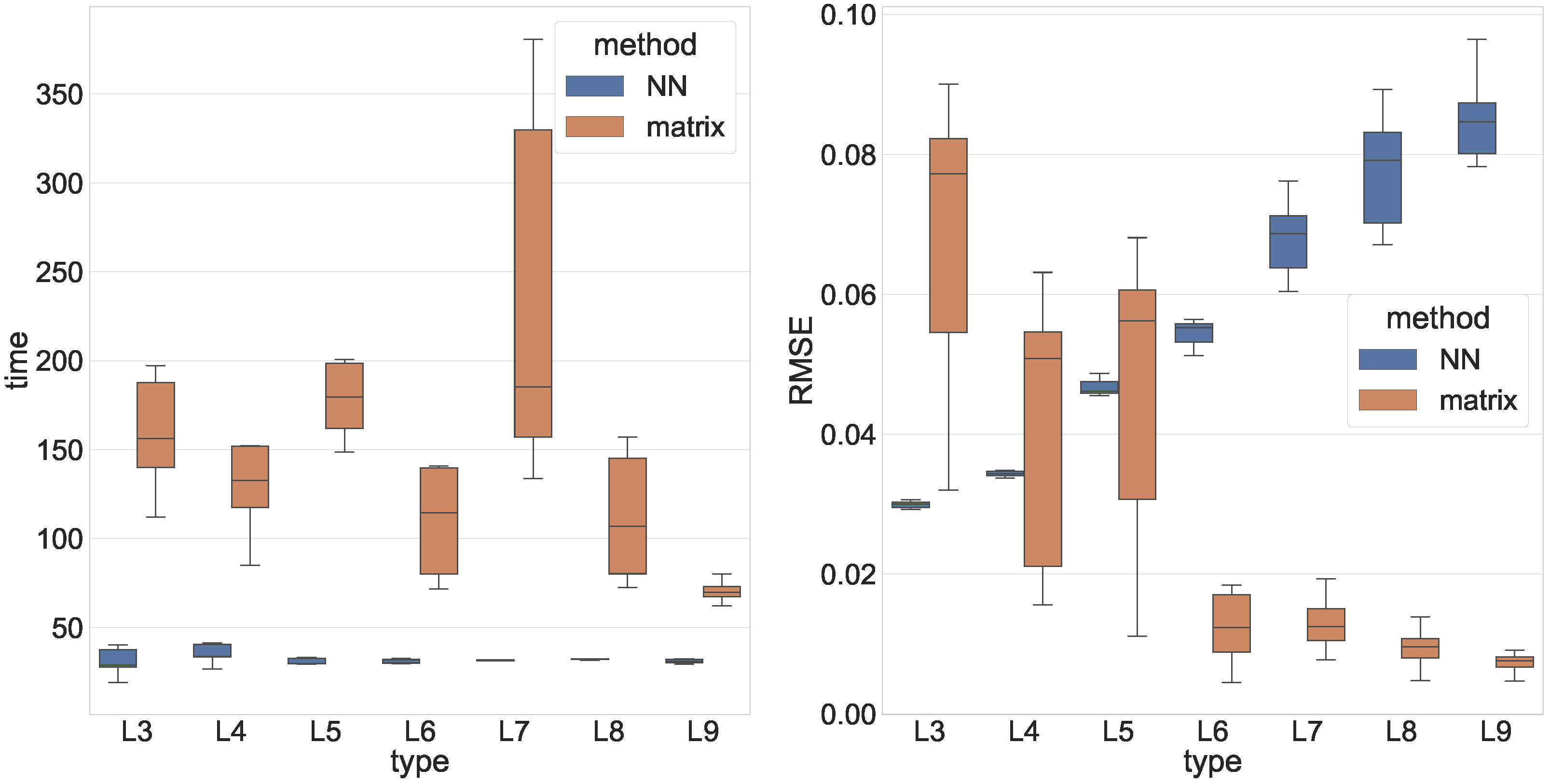


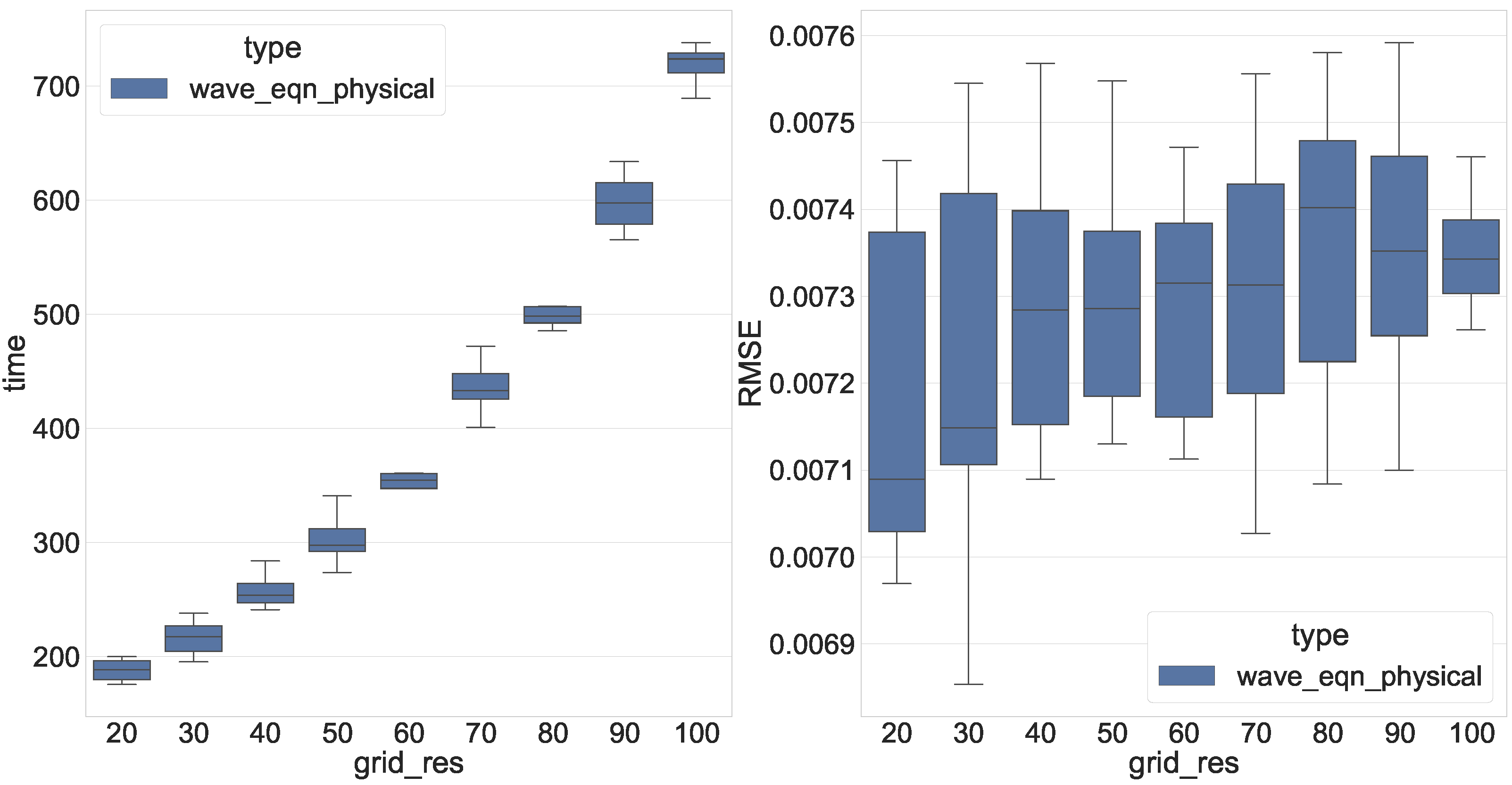

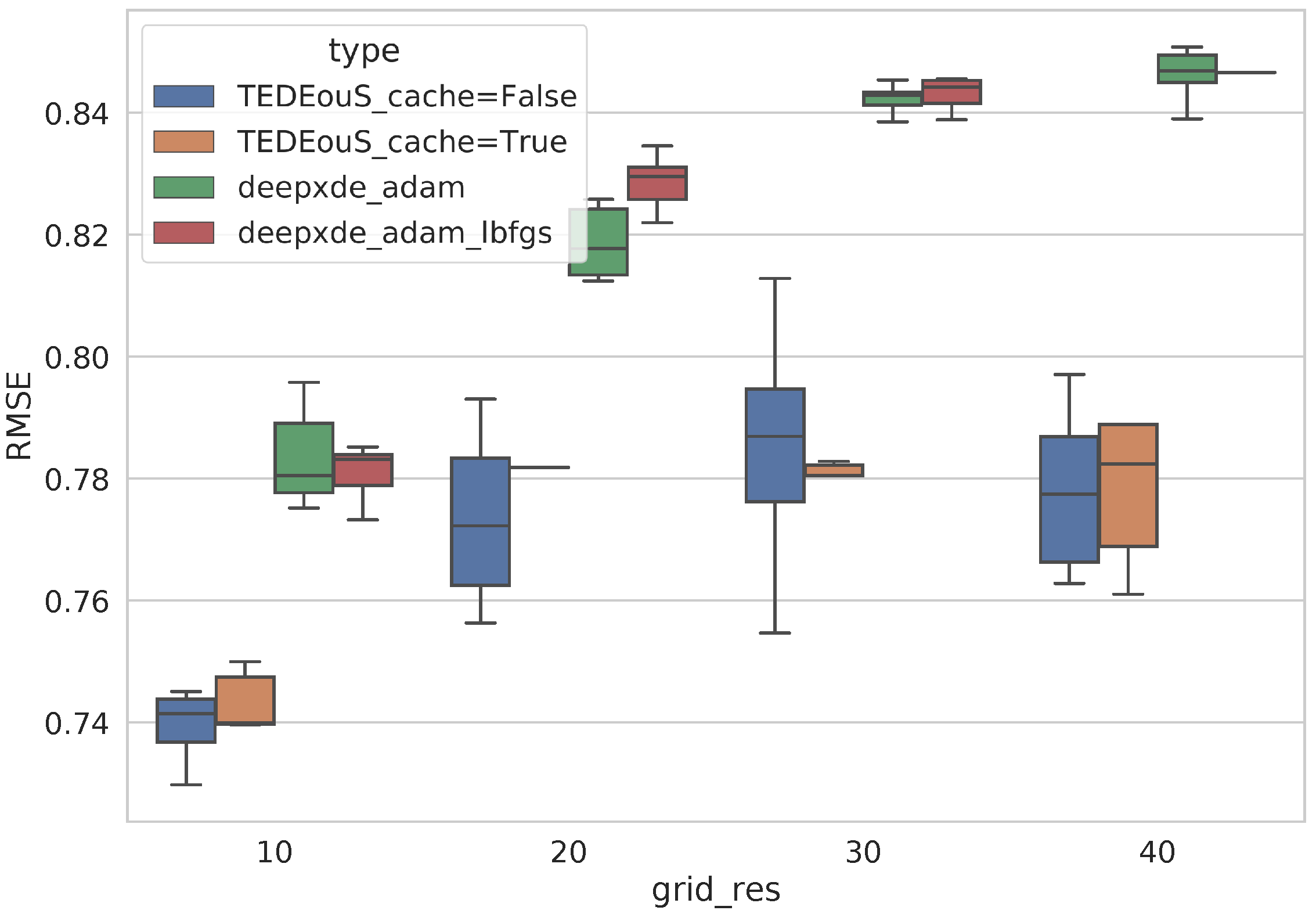

| Module | DeepXDE | Proposed Approach |
|---|---|---|
| Approximator | NN (TensorFlow—dense, Fourier kernel layers) | Parameterized model (PyTorch) |
| Differentiation | Autograd | Autograd, numerical differentiation |
| Operator form | Constant coefficients, variable coefficients (no examples) | Time- and spatial- variable coefficients |
| BC form | Dirichlet, Neumann, Robin, IC, GeneralBC (no examples) | Arbitrary |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hvatov, A. Automated Differential Equation Solver Based on the Parametric Approximation Optimization. Mathematics 2023, 11, 1787. https://doi.org/10.3390/math11081787
Hvatov A. Automated Differential Equation Solver Based on the Parametric Approximation Optimization. Mathematics. 2023; 11(8):1787. https://doi.org/10.3390/math11081787
Chicago/Turabian StyleHvatov, Alexander. 2023. "Automated Differential Equation Solver Based on the Parametric Approximation Optimization" Mathematics 11, no. 8: 1787. https://doi.org/10.3390/math11081787
APA StyleHvatov, A. (2023). Automated Differential Equation Solver Based on the Parametric Approximation Optimization. Mathematics, 11(8), 1787. https://doi.org/10.3390/math11081787






