Abstract
This study presents the claim that mathematics and logic are merely highly formalized reflections, grounded in the physical laws of conservation. The claim generally correlates with John Stuart Mill’s known stance, but unlike his general view, it specifies which elements of the natural kingdom are reflected by mathematical objects and statements. As the study claims one version of physicalism, it raises the question of the necessity vs. contingency of mathematics and concludes that the necessity of mathematical judgments depends on the necessity of the conservation laws themselves. Since the conservation laws are only certain, it follows that there is no basis to claim the necessity of mathematical statements themselves, and that it is only possible to speak of a conditional necessity in the sense that mathematics is necessarily such as it is only in a world governed by conservation laws. Such conditional necessity does not possess the being of absolute necessity. Mathematics can only be considered necessary to the extent that the reflected world described by it is necessary, which further implies the claim that mathematics is necessarily a posteriori and synthetic. The entire series of mathematical proof types, including the most commonly utilized reduction ad absurdum, ultimately derives its strength from experience.
MSC:
03A05
1. A Brief Introduction to the Ontology of Mathematics
Before attempting to make a specific theoretical contribution to mathematical realism (known as “Millianism”), it is useful to review existing schools of thought in the ontology of mathematics. This review simultaneously provides a list of key questions that the responses to constituting the different schools of thought. In the reviewing process, the division given in Balaguer (2009) [1] is schematically reconstructed. According to Balaguer, only two views of the metaphysics of mathematics manage to adequately answer all objections: these are Platonic set theory (as a form of realism) and fictionalism (as a form of anti-realism) (see Figure 1). Balaguer takes a relatively reserved stance towards the dilemma that one of these two perspectives is correct through three epistemic conclusions: (a) we have no reason to believe or not believe in abstract mathematical objects, (b) we can never in principle have a reason to believe or not believe in abstract mathematical objects, or (c) there is no material fact that could determine between Platonic set theory and fictionalism, although both adequately answer all objections (except, in a way, the question of proving the existence of abstract mathematical objects). The first key question that divides the metaphysics of mathematics into two domains, marked with (1) in Figure 1, is the question of whether mathematical theories represent truthful descriptions of some real part of the world. Realistic theories answer affirmatively, while anti-realistic theories answer negatively, claiming that mathematics has no ontology, or that its concepts are objectively empty. The question marked with (2) further divides the realist camp into two groups and is “are mathematical objects spatiotemporal?”. Platonic set theory answers negatively, while anti-Platonism answers affirmatively. The question marked with (3) further divides anti-Platonism into psychologism and physicalism and reads: “what is the nature of mathematical spatiotemporal objects?”. According to psychologism, the objects in question are mental objects, or mathematical statements represent truthful descriptions of mental objects, while according to physicalism, the subject of mathematical statements is non-mental parts of physical reality.
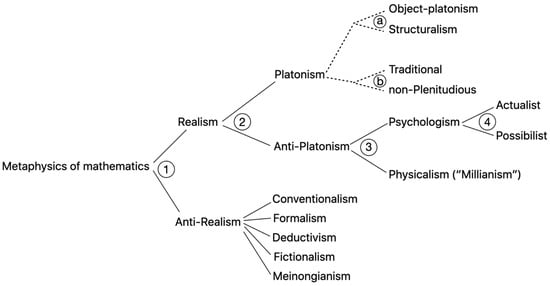
Figure 1.
Key branches of mathematical ontology, with nodes (1–4) formed by answers to several key questions discussed in further text. (a) and (b) represent two alternative divisions of Platonism. Physicalism is subscripted as some of its ideas, including the essence of the physical nature of mathematical objects, are being defended in this analysis, while Platonism of sets and fictionalism are emphasized as the only two that, according to Balaguer, are capable of answering all objections.
1.1. Realism
Anti-Platonism. John Stuart Mill (1853) [2] argued in the late 19th century that mathematics is an empirical science related to physical objects. According to Mill, abstract objects do not exist, and mathematics tells us nothing about them. The statement “2 + 1 = 3” simply means that when two objects are grouped together and a third is added, a group of three objects results. Psychologism, as another form of anti-Platonism, is divided into two groups: actualist psychologism and possible psychologism. Actualist psychologism sees mathematics as the science of real ideas in people’s heads, while possible psychologism sees it as the science of possible ideas. Although psychologism considers mathematical objects to be products of the subject’s consciousness, it is classified as a form of realism because it acknowledges the ontological content of these objects.
The strongest argument against anti-Platonism was provided by Frege (1953) [3]. It reduces to two statements: (a) the only way to respect the intuition of mathematical theories is to adopt Platonism, and (b) mathematical theories function in practice and are irreplaceable in empirical sciences, therefore they are true—Platonism is accurate and anti-Platonism is inaccurate. This can be answered from the standpoint of fictionalism, that it is meaningless to talk about the truth of the products of fiction (see Section 1.2), but also in other ways that go beyond the scope of this study.
Several objections can be raised against anti-Platonist physicalism (Millianism), which are significant for further discussion in this study, and therefore will be discussed in detail.
- (a)
- The poverty of the kingdom of real objects compared to the kingdom of mathematical objects. Millianism claims math is an empirical science, such as sets describing physical sets like Easter eggs. However, sets as mathematical objects pose a problem because an infinite number of sets can have the same physical equivalent. Sets are difficult to reduce to their physical equivalent because each set is its own subset, resulting in an infinite loop.
- (b)
- Overlap of physical equivalents of different mathematical objects in space–time. In the example of an egg, this would mean that infinitely many mathematical objects that can be constructed according to set theory over only one egg actually have one and the same physical equivalent—the egg. Thus, their difference must be based in the non-physical, non-space–time.
- (c)
- The Empirical Unfalsifiability of Mathematical Statements. If mathematics were a highly generalized empirical science, then its statements would at least in principle be falsifiable by empirical means. However, this does not happen. This means it is not an empirical science.
Each of these remarks will be analyzed in Section 3.4.
Psychologism and fictionalism both reject the objective nature of mathematical objects but differ in that psychologism sees mathematics as the study of the ideas of mathematical objects while fictionalism regards them as fiction. Frege [3] argued against psychologism, claiming that it cannot speak about mathematical objects such as the class of real numbers or numbers too large to be conceived. Psychologism also de-objectivizes mathematics as it depends on the existence of consciousness. Psychologism has not been able to address these issues and has been overshadowed by other theories.
Platonism. Platonism holds that math is an ontological science of non-physical, non-mental, and non-spatiotemporal objects. Famous proponents include Plato [4], Frege [5], Gödel [6], and Quine [7]. Platonism is divided into traditional and sets-based (Figure 1), with the latter acknowledging an infinite number of mathematical objects. Platonism is also divided into object-based and structuralism, with the latter holding that structures are more important than objects. Balaguer [1] defends sets-based Platonism, while Resnik and Shapiro [8,9] support structuralism (e.g., [10]) to respond to objections such as the non-uniqueness problem and epistemological objection.
The epistemological argument against Platonism can be formulated in several ways, but it most often comes down to the following series of statements:
- (1)
- Human beings are completely space–time-bound.
- (2)
- If there exists any abstract mathematical object, it is necessarily non-spatial–temporal.
- (3)
- If there exists any abstract mathematical object, then human beings cannot have knowledge of it.
- (4)
- If mathematical Platonism is correct, then human beings cannot have mathematical knowledge.
- (5)
- Human beings have mathematical knowledge.
- (6)
- Therefore, mathematical Platonism is not correct.
The key statements are (3) and (5), and they necessarily imply (6). The most common defense against the epistemological argument is that statements (1) and (2) do not imply (3), so even though human beings are completely space–time-bound and mathematical objects are non-spatial–temporal, knowledge of them is possible. The challenge that remains for Platonists in this way is how information is transferred from non-spatial–temporal to space–time. For example, Gödel, as a Platonist, challenged statement (1) by claiming that the human mind is capable of stepping into the non-spatial–temporal domain. Others have challenged (2), claiming that ordinary perception can provide knowledge about abstract mathematical objects, or that they are not non-spatiotemporal in any sense. The third strategy is to accept both (1) and (2) and still attempt to develop some non-contact epistemology based on the flow of information between the two domains, spatiotemporal and non-spatiotemporal. This path has been chosen by the majority of philosophers, including Quine, Resnik, Shapiro, Balaguer, etc. Each mentioned strategy to defend against the epistemological objection has its weaknesses, whose analysis goes beyond the scope of this study, so we will limit ourselves only to presenting the response of the pluralism of Platonism. The pluralism of Platonism abolished the boundary between possibility and existence by claiming that every mathematical object that can exist, exists, and thus, practically enabled each mathematical theory that is consistent to describe some part of the realm of mathematical objects. Its origin, whether it is dreamed, derived, imagined, etc., is completely irrelevant. What is important is that it is consistent, and this alone provides it with ontological content. A series of objections can be raised against this defense, for example, it is difficult to evaluate the consistency of mathematical theories without access to the world of mathematical objects, as well as even if consistent theories describe some part of the realm of mathematical objects, it is still not clear how we know which part it is, and whether it is exactly the desired object of investigation. Objectivity could also be challenged, as it is possible to accept two mathematical theories as true even though they are based on two different, incompatible hypotheses, as well as the possibility that following the ontology of pluralism of Platonism leads to contradiction.
In the non-uniqueness objection (b), Platonism is criticized for implying that mathematical theories describe unique sets of mathematical objects (e.g., natural numbers); however, this is not the case. Therefore, Platonism is incorrect. The usual argumentation goes as follows:
- (1)
- If there exists one sequence of abstract mathematical objects that satisfies the rules of Peano arithmetic, then there exists an infinite number of such sequences.
- (2)
- There is nothing metaphysically special about any of these sequences that would make it the sequence of natural numbers.
- (3)
- It follows that there is no unique sequence of mathematical objects that represents the natural numbers.
- (4)
- Platonism holds that there is a unique sequence of mathematical objects that represents the natural numbers.
- (5)
- Therefore, Platonism is incorrect.
To avoid the non-uniqueness objection, Platonism must either reject (2) by asserting that there is still something metaphysically unique about the sequence of natural numbers or abandon the idea that mathematical theories refer to unique sets of mathematical objects (4). Balaguer [1] argues that statement (4) is mistaken, and that Platonism has never been constituted as a direction that describes unique sets of mathematical objects. According to him, only Platonism of sets, by erasing the boundary between what is and what can be, and accepting the non-uniqueness of mathematical objects described by mathematical theories, deals with the two aforementioned objections and several other minor criticisms.
1.2. Anti-Realism
Anti-realism in mathematics comes in various forms, including conventionalism, formalism, deductivism, meinongianism and fictionalism. Conventionalism asserts that mathematical statements are true by convention, while formalism considers mathematical statements as theorems of the formal system. Deductivism holds that mathematical statements are deductions from basic axioms. Fictionalism regards mathematical objects as fictions, without any reference to the real world. Balaguer [1] criticizes fictionalism’s shallow explanation that mathematics is useful and aesthetically attractive. The debate resembles the materialist–idealist debates on the criterion of truth (see [11]). The challenge is to reconcile the emptiness of mathematics with its practical success.
Anti-realism faces a problem with the so-called Quine–Putnam indispensability argument [12], which states that we must acknowledge the ontological content of the smallest set of objects in our scientific theories, and since mathematical objects are contained in the smallest set of objects on which our scientific theories are based, we must also acknowledge their ontological content. The argument challenges all versions of anti-realism, and the responses to the objection are diverse and beyond the scope of this examination.
2. Analytic vs. Synthetic, a Priori vs. a Posteriori, and Necessary vs. Contingent
2.1. Some Observations on a Priori
What does a priori actually mean? A priori knowledge and justification is that which is independent of experience [13]. An interesting description of a priori was given by the British philosopher Galen Strawson. For him, an a priori argument is one for which you can know that it is true by lying on your couch, and for whose evaluation you do not need to stand up, leave, and examine things in the physical world, or engage in science [14]. The description does not specify whether the use of language in such consideration is allowed, because if it is, then this descriptive definition at least partially matches Kant’s concept of the analytic [15], which already creates confusion. That is, with the assumption of mastering language on the same couch, we could draw analytic judgments, for example, that the expert knows or the worker works, which are classic examples of analytic judgments. In addition, Strawson’s answer relates to the question of what a priori knowledge or argument means, while the question at the beginning of Section 2 was, however, what a priori means, not what a priori knowledge, justification or argument means, so his answer is not actually the correct answer to the question posed. The concept of a priori can possess at least three levels of meaning, which are usually used intuitively and insufficiently differentiated: (a) it is what we can know from pure conceptual analysis (analytic), (b) what does not require empirical verification (necessary), and (c) what exists prior to us (pre-experiential). In the following text, we further specify the way of using the concepts in this study.
2.2. Pairs of Notions Analytic/Synthetic, a Priori/a Posteriori, and Necessary/Contingent
The precision in demarcating the denotation of each of these concepts is necessary for understanding the idea of the possible contingency of mathematics. Of the three pairs mentioned, the components of the last pair are easiest to define. What cannot not be will be considered necessary in the following text, while what could not be, regardless of whether it is or not, will be considered contingent. Another way of understanding the contingent is that it is what does not contain within itself the reason for its existence, in which sense the term is used in the famous Russell–Copleston debate about the existence of the absolute/God [16]. The distinction between analytical and synthetic is built on the answer to the question of how to truthfully evaluate a statement. A statement that can only be evaluated based on the analysis of the concepts involved in it is analytical, while one for whose evaluation it is necessary to analyze the relationship between the concepts of the statement and the world is synthetic. From the definition, it appears that there are no analytical statements, as the concepts of analytical and synthetic refer to the relationship between knowledge, language, and experience, not just knowledge and experience, given that it is clear that statements must be formulated in a language that is itself necessarily learned, i.e., non-a priori. However, most philosophers consider this objection to be insufficient to destroy the kingdom of the analytical.
The visual representation of the relationship between analytical, a priori, and necessary, and their antipodes is given in Figure 2. There is a general consensus in the philosophical community about the relationship of these concepts, but there are also rare exceptions. In the following text, the use of these concepts will follow the pattern shown in Figure 2. Analytical statements are always a priori, accurate, and necessary, and a priori statements are always necessary.
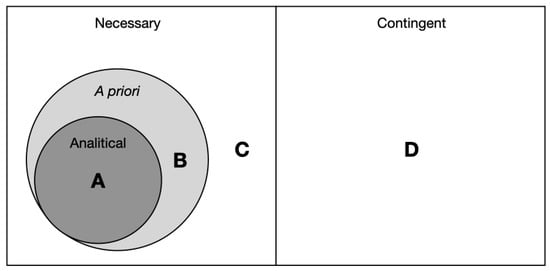
Figure 2.
The relationship of the concepts of analytical, a priori, necessary, and their antipodes. The diagram indicates that there are synthetic a priori judgments, as Kant claimed, that there are necessary a posteriori judgments (whose necessity is recognized through experience), and that analytical and a priori judgments can never be contingent. Where is mathematical knowledge located on this diagram, at position A, B, C, or D?
3. The Epistemological Status of Mathematical Knowledge
3.1. What Is Indubitably a Priori
The debate about whether the human mind is a tabula rasa at birth has been ongoing since Aristotle (De Anima), through the Stoics, Avicenna, and John Locke [17] who gave the debate a modern tone. What is difficult to dispute is that there is a neuro-physiological a priori mechanism that allows for the integration of sensory data into a meaningful experiential whole. Otherwise, sensory experience would remain a fragmented field of unrelated elements. This conclusion has implications for our understanding of the possible nature of mathematical knowledge, as it opens up the possibility that it is as a priori as that mechanism, or that it is its derivative. In other words, mathematical knowledge could be biologically necessary. This mechanism is pre-experiential from a personal perspective. Even if we accept that the organization of our primitive sensory data would be impossible without a pre-experiential ability to organize it (that is, a priori principles of thinking by which we systematize unconnected sensory experiences into meaningful wholes), is what is pre-experiential, strictly speaking, knowledge? Does this presumed ‘knowledge’ in the form of thinking principles meet the criteria of the classical three-part definition of knowledge [18], or some of its alternative formulations? It is difficult to say. If kidneys are not a priori knowledge, while filtering blood as a organ/mechanism, why would it be a biological mechanism that processes our neurophysiological responses to stimuli, that is, integrates experience? Information about its existence is a posteriori knowledge, but its existence is not. Thinking principles, as some have called this mechanism, are strictly not knowledge, because we neither believe in them nor do we do so justifiably. They simply are. In the preverbal stage, when we are already organizing primitive experience, we do not have concepts whose analysis would lead us to conclude about such principles, so they are not only not knowledge by the classical epistemological definition, but they are only pre-experiential and not a priori. Although knowledge can exist without the existence of concepts (for example, a seagull knows that when it drops a shell on a hard surface, it will break), the concepts of analytic and synthetic relate to the relationship between knowledge, language, and experience, not just knowledge and experience. Therefore, the first problem is how to view the principles of thinking in the context of the analytical–synthetic distinction, if they are presupposed. It is not disputed that young turtles when they hatch go towards the sea, but is it because they know that the sea is there? Or is it an instinctive genetically based impulse to which they submit without any belief or justification? We can treat that impulse as their collective knowledge, biologically encoded through generations, but accepting the validity of such individual knowledge is debatable. The past shows that many species have become extinct by following inherited instinctive patterns, which means that the sea may or may not have been there. What turtles actually possess is some structural property of their neuro-physiological apparatus, and at the same time, the structural property of their nucleic material, which stores and transmits this information. Therefore, we propose that what is “a priori”, serving to organize primitive personal experience, be understood as an inherent dispositional property of our biological organism, as a result of biological evolution, as something that is but is not knowledge; we propose that this be reduced to biological structure and function. Otherwise, we will end up in claims that existence is knowledge, and that spiders and turtles can believe. Therefore, the existence of a priori principles of thinking cannot be taken as a convincing proof of the a priori nature of mathematical knowledge, or of any knowledge at all—not even its possibilities.
3.2. Law of Identity: Description or Stipulation?
The Law of Identity represents the foundation of Aristotle’s bivalent logic and the basis of mathematics. In the history of the philosophy of mathematics, there have been several attempts to prove the necessity of the Law of Identity, among which are probably the most well-known proofs given by Ruth Barcan Marcus [19]), including the simplified proof published five years later by Fitch [20], and Kripke’s contribution to the proof [21], which are collectively referred to as the Barcan–Kripke proof. The Barcan–Kripke proof of the necessity of the Law of Identity requires only the validity of Leibniz’s Law (Leibniz’s Law is a bi-conditional that claims the following: Necessarily, for anything, x, and anything, y, x is identical to y if and only if for any property x has, y has, and for any property y has, x has. Because this is a bi-conditional, it is comprised of two conditional statements (i) and (ii): (i) If x is identical to y, then for any property x has, y has and for any property y has, x has. (ii) If for any property x has, y has, and for any property y has, x has, then x is identical to y), and the reflexivity. The formulation of this proof, translated into ordinary language from the formal statements of modal logic in which it was originally presented, and taken from Lowe (2002) [22], is as follows:
- (1)
- For any object x, it is necessarily the case that x is identical to x (reflexivity).
- (2)
- For any objects x and y, if x is identical to y, then whatever is true of x is true of y (Leibniz’s Law).
- (3)
- a is identical with b (assumption).
- (4)
- It is necessarily the case that a is identical with a (from (1)).
- (5)
- It is true of a that a is necessarily identical with a (from (4)).
- (6)
- If a is identical with b, then whatever is true of a is also true of b (from (2)).
- (7)
- Whatever is true of a is also true of b (from (3) and (6)).
- (8)
- It is true of b that it is necessarily identical with a (from (5) and (7)).
- (9)
- It is necessarily the case that a is identical with b (from (8)).
- (10)
- If a is identical with b, then it is necessarily the case that a is identical with b.
Although simple and without unnecessary assumptions, the Barcan–Kripke proof has been criticized. Lowe [22], while ultimately not rejecting the proof, notes that the transition from (4) to (5) assumes what it is trying to prove by stating that a is necessarily identical to a, rather than a being necessarily identical to itself. Replacing premises (5), (8), and (9) to reflect this revision results in (9) becoming “It is necessarily the case that b is identical with b,” which renders the truth of the conclusion questionable ([22], p. 87). The other argument against this proof is repeated in various forms in the literature and can be summarized as an objection that Kripke’s argument is circular because it only works for proper names or object constants construed as rigid designators in Kripke’s sense (In Kripke’s sense, a rigid designator is a term or expression that designates or refers to the same object in all possible worlds in which that object exists. This means that the referent of a rigid designator is necessarily the same entity, regardless of the specific circumstances or context in which it is referred to. For example, Kripke argues that proper names are rigid designators because they refer to the same individual in all possible worlds. So, if we consider the name “Joe Biden,” this name designates the same individual, Joe Biden, in every possible world in which he exists. Even if Joe Biden had not become President of the United States or had pursued a different career path, he would still be the same person referred to by the name “Joe Biden”. Kripke contrasts rigid designators with non-rigid or “accidental” designators, which are terms or expressions that may refer to different objects in different possible worlds. For example, the term “the current president of the United States” is a non-rigid designator, because it refers to different individuals in different possible worlds depending on who happens to hold that position in each world) (e.g., [23]. Leibniz’s Law, as previously stated, is biconditional and says nothing about the nature of a and b. Therefore, Dale [23] notes that “Kripke’s formalization of the argument for the necessity of identity overlooks identity relations involving non-rigidly designated relata, such as those expressed by means of definite descriptors, from which necessary identities cannot generally be inferred”.
To successfully challenge the necessity of the Law of Identity would mean automatically challenging the necessity of all its derivatives, all axioms and theorems that presuppose it. If it is anywhere possible to destroy the idea of unconditional necessity of mathematical knowledge with one move, then it is in the Law of Identity. In Section 3.1, we illustrated the way in which the assumption of the a priori nature of knowledge leads to a problem. Now, we could examine the reasons that led to certain knowledge being transferred to the domain of a priori. Let’s take, for example, the Law of Identity, A = A. If it is purely conventional, the argument could go as follows: We first stipulated a relationship with certain properties, including universality, which we denote with the symbol ‘=’, and which by definition expresses that each A is in this relationship with itself. Imagine that we adopted: “Let ‘=’ be a relationship that we will call identity, and in which each A is with itself”. Then, we stated that each A is in that relationship with itself. This argument is circular because it is imposed by the previous definition, and it represents a version of petitio principii. Furthermore, there is still a lack of evidence that such a relationship has any existential meaning. Each A is identical to itself because it has been axiomatized that each A is necessarily identical to itself, but this is a matter of decision and convention. Since we don’t know how to prove the claim here and now, we have transferred it to the realm of a priori. The essence of the meaning of a priori in this maneuver is to express “believe without proof”. If we had constituted this relationship in another way, then each A could not be identical to itself. The question arises: where does the need come from to constitute a supposedly universal relationship in such a way, and why does the assumption that it is valid have numerous positive experiential verifications? No a priori, but properties of this world provide such a solid foundation for the claim that identity is universal. Furthermore, note that A = A has the form of a definition ([24]). The question arises: what is this definition, logical, factual, or conventional, and how do we arrive at the knowledge of its necessity? Confirming the idea that it is a logical definition would have to reduce the Law under investigation to one of the logical axioms, which is a problem because we are currently investigating a logical axiom, so it cannot be adopted as a conclusion without being presupposed as a premise. So logically, it is unproven (which is the nature of an axiom). In general, it is pointless to logically prove logical axioms, and therefore the validation of the law of identity and other logical axioms is not within logic; but where is it, then? A trivial answer would be that it is self-evident, or a priori. In the same way, we could, by convention, axiomatize the reflexivity of any other relation, for example, A ≠ A. Its necessity, therefore, exists only to the extent that we axiomatize it, but isn’t that artificial, stipulated necessity? We do not believe that we would be happy to know that the basic foundation of mathematics is necessary simply because we agreed to consider it necessary. If the law of identity was a factual, descriptive definition, a highly confirmed generalization from experience, it would certainly not have the strength of necessity, but rather would be just a very likely, inductively created law, in the range of other experiential generalizations and scientific laws, which it actually is. A favorite refuge from this problem is the realm of the a priori. Transferring axiomatized claims to the realm of the a priori is a sure mask for unprovability. The law of identity is, they say, ‘a priori’. In order for this law to be a priori, it would first be necessary to prove such a problematic claim as the existence of a priori laws, second, we would all have to recognize the a priori necessity of this law. The author of these lines does not recognize such an emotion towards the law of identity in the world, in himself.
Therefore, the law of identity can only be a highly confirmed generalization from experience, it is certain but not necessary. Perhaps a comparison with ethics is striking. In ethics, the fundamental problem is how to derive ought from is. How did we derive must from is in the case of the law of identity, if we dare not derive ought from is, or cannot derive it from isn’t? How do we claim the necessity of the law of identity, when it is obviously just a generalization from experience to which general importance has been attributed by convention? The conclusion is that the law of identity is in the world, but not necessarily. It may be necessary in this world, because if it did not exist, it would be a different world. Or, it might not exist at all. The principle of universality, though, says that it is necessary in all worlds, which seems to be a strong statement.
At the end of this section, it might be appropriate to also point out a syntax inconsistency in mathematics. Namely, the relationship “=” is used in two very different ways. Take the following two statements as an example:
A: X = X
B: X = 3
Thus, does the symbol “=” in these two statements have the same meaning? No. While the first represents a comparison operator, conveying identity, and can be truthfully evaluated as accurate (at least conditionally, by convention), the second symbol “=” represents something entirely different. It can represent either a comparison operator or an assignment operator. For example, if X already exists and “=” represents a comparison operator, then this statement can be truthfully evaluated. If X exists and “=” represents an assignment operator, then X takes on a new value. If X has no value and “=” represents an assignment operator, then X is constituted by this statement. In the case where X has no value and “=” represents a comparison operator, the statement represents nonsense. This syntactic confusion in mathematics has been successfully resolved in programming languages where different symbols have been adopted for comparison and assignment operators.
3.3. Principium Contradictionis
Problems similar to those related to the law of identity also apply to the other three basic principles of reasoning. For example, the second principle of reasoning, the principle of non-contradiction (principle of contradictionis), is often formulated as: “Two opposing statements cannot be true in the same sense at the same time,” or formally, statements “A = B” and “A ≠ B” exclude each other.
Aristotle observed in his Metaphysics that the principle of non-contradiction has a special status, namely, that it cannot be rejected without prior acceptance. Philosophers later concluded from this that it was a priori and necessary. However, this conclusion is not entirely correct. Let’s consider two statements:
P: The principle of non-contradiction is
Q: If the principle of non-contradiction is, it is necessarily (cannot not be)
Did Aristotle assert P, or P => Q? Namely, what interests us is only P, not P => Q, and therefore the right question is not: “Can the law of non-contradiction be rejected, but not accepted?”, but rather: “Can the law of non-contradiction not be accepted, but not accepted?”. The premise, not the conclusion, is problematic here. The impossibility of rejection here resembles a Constitution in which one of the members stipulates that this Constitution cannot be changed; in a similar way, the principle of non-contradiction appears to stipulate its own existence, once it exists—but does it exist?
Although the world is obviously asymmetrical in terms of providing evidence of the validity of the principle of non-contradiction, and any alternatives, there are still rare examples that can show that this principle is not necessary. For example, in Leszek Kołakowski’s Philosophical Essays [25], although in a different context, the author states that the three notions, consistent inconsistency, inconsistent inconsistency, and consistent inconsistency, resist the application of the principle of non-contradiction in a specific way. Kołakowski argues that consistent inconsistency cannot truly be consistent inconsistency because it excludes the principle of inconsistency from the realm of the inconsistent, and therefore, it cannot be consistent. Hence, in order for inconsistency to be consistent, it must be inconsistent! Formally expressed, this observation leads to two expressions that virtually opposes the principle of non-contradiction:
1: Consistent inconsistency ≠ Consistent inconsistency
2: Inconsistent inconsistency = Consistent inconsistency
Further, examples of questioning and some other axioms of logic can also be found, for example, the principle of the exclusion of the third (principium ehclusi tertii sine medii). Take the concept of “totality”. Totality as a concept represents both one and many. It is simultaneously A and non-A. Proponents of dialectical logic believe that the concept of “totality” is at a higher evolutionary level than non-veridical Cartesian dualism. The entire classical formal–logical system is an idealization of the world, its necessity is artificially stipulated and as such may not be, and its practical value is highly confirmed. This is an axiomatized, closed system, which is absolutely consistent in its self-sufficiency. Its internal properties are not problematic, they are stipulated, conventionally necessary, and what is problematic is the connection to the world. This connection actually means an answer to the question: why is the axiomatized system of binary Aristotelian logic privileged in some way? Are the rules of logic necessary in the world, just as they are “necessary” in the axiomatized logical system? Is it an idealization, just as a mathematical cube is a nonexistent idealization, to which reality corresponds more or less approximately?
The above-mentioned weaknesses directly affect one of the most common methods of proof, reductio ad absurdum. Namely, if the necessity of the law of identity is challenged, then contradictions also lose their destructive power and no longer have the force of necessity. All mathematical theorems proven by reduction to contradiction become only as necessary as the law of identity itself. This means they become only contingent, a posteriori, and nothing more.
3.4. The Criticism of Realism and Empiricism
If the basic logical principles are not necessary, as we believe, then surely their derivatives are not necessary either. However, the Quine–Putnam argument imposes the need for a mathematical knowledge ontology, an ontology that is, in our opinion, fundamentally realist, that is, mathematical knowledge is located on scheme 2 under (d). However, regardless of whether we support the classical Mill thesis (see Section 1.1), or some other form of mathematical ontological realism and empiricism, objections to nominalism represent the first obstacle and so we will first deal with them.
- (a)
- The Poverty of the Realm of Reality Objection. In our opinion, this objection is artificial and arose as a result of syntactic inconsistencies. For example, take the previously mentioned egg as a physical object and the infinite set of sets that contain the mathematical correlate of the egg as a subset. Formally written, if we represent the egg as “E,” then the objection actually means the following: there is a whole series of mathematical objects {E}, {{E}}, {{{E}}}, {{{{E}}}}, etc., all of which have only one real correlate—the egg. So, it seems that the infinite series of mathematical objects corresponds to only one physical one, thereby supposedly destroying the realist mathematical ontology because it is too impoverished for the unending realm of mathematical objects. The problem with this proof is the following, in the theory of sets it is known that every set contains itself as a subset. In other words, writing {E} either means being syntactically inconsistent with the definition of a set or already taking into account the fact that the curly brace symbol replaces the set of all sets that contain themselves as a subset, ad infinitum. In the first case, what should be written is an infinite series of “{” or “}” with the symbol “E” on the left and right side, and in the second, adding another symbol that implicitly replaces an infinite number of brackets has no significance. For feasibility, in the first case, we decide to write only one bracket on each side, which strictly speaking does not reflect the properties of the set. Then, in this particular “proof”, we partially deviate from the initial decision and write an arbitrary number of brackets artificially generating “new mathematical objects.” What we actually generate are new symbols for one and the same mathematical object with one real equivalent—the egg. The question is whether there is such a mathematical statement in which the mathematical equivalents of the egg cannot be changed salvatically with an arbitrary number of brackets? No, there is not. It follows that, at least in the case of the egg problem, the proof of the unviability of the realist ontology is a farce.
- (b)
- The physical equivalence of different mathematical objects and the overlap of space–time. This objection falls along with the previous one, as it has been shown that there is no overlap of physical equivalence of mathematical objects in space–time, but rather, an unnecessary syntactical inconsistency that denotes the same mathematical objects with different symbols. This is like generating an arbitrarily large number of names for the same object and then being surprised that there are not as many objects as the number of names generated.
- (c)
- The empirical invincibility of mathematical statements. This is probably the weakest objection to mathematical realism. Let us start with geometry. Poincaré in his famous work “Science and Hypothesis” [26] derived the assumption that the geometry he knew, the geometry of a homogeneous three-dimensional Euclidean space, parasitizes on the certainty of the world of solid bodies in which we live, and that the geometry would be completely different if we lived in some fluid world. He actually claimed the contingency of geometry. The rejection of Euclid’s fifth postulate, which produced new geometries, then Riemann’s and Lobachevsky’s space, and then the discovery of adequate empirical evidence for these geometries, shows that mathematics is subject to revision. The most striking example of mathematical–logical revisionism comes from new logics, modal, modern, polyvalent, and “fuzzy”, each of which has practical applications. Mathematical and logical statements are not only not invulnerable, but are de facto already overthrown.
In addition, confusion has been made in the argument between what is and what could be. The fact that mathematics is allegedly not overthrown by empiricism does not yet mean that it could not be overthrown by empiricism, which would be necessary to overthrow realism.
3.5. On the Origin and Content of Mathematical and Logical Knowledge
Criticisms of realism are not as devastating as they appeared at first glance, as seem in the previous section. So, where does mathematical knowledge come from? In our opinion, mathematical and logical knowledge is nothing but a highly formalized reflection, grounded in the physical laws of conservation. It is a picture of the physics of this nature. It relates to this world. Its necessity is conditional, that is, mathematical knowledge is just as much as the world is. It is a statement about the contingent; even if it is a necessary statement about the contingent, its necessity is limited by the contingency of the subject of the statement. This is a conditional necessity, and a conditional necessity is not necessity. The law of identity is a generalization of the observation that I am, that I am in a series of moments t0 … tn, that I am sustained in time, that the objects of my perceptions are sustained, that they last, that they are not multiplied, that they do not arise from nothing, that they do not disappear (but only transform). The whole world of conservation laws tells us about identity from the first moment—(matter and) energy, momentum, angular momentum, electrification are sustained. The world is sustained. The world is. The world is the world. A is A. The parallelism we proclaim here may seem counterintuitive, but it can be approached through a thought experiment. Let us imagine an extremely simplified version of our world (a world in which all conservation laws hold): an elastic ball bouncing off the walls of a closed rectangular container (Figure 3a). Although simplified, this representation of the world contains almost all conservation laws, and by observing it, the same laws of conservation could be inductively derived as in the case of our world. The conservation of mass and energy, momentum, and other conservation laws implies a series of regularities in the motion of this ball, including its inertial properties, the identity of the incident and outgoing angles, regularity in the evolution of its spatiotemporal coordinates, etc. In this experimental model-world, deriving the necessity of the law of identity would be just as justified or expected as in the real world. However, if we were to initiate a series of sequential suspensions of conservation laws, for example, remove momentum conservation, then energy conservation, etc., it would lead to seemingly “irregular” (compared to the rules of the real world to which we are accustomed) motion of the ball; it would begin bouncing at different angles, accelerating and decelerating, disappearing and reappearing, changing shape, size, and the number of copies of the ball (Figure 3b). Complete degradation of the laws of conservation would lead to a situation where the result of the model-world evolution becomes absolute chaos. All continuities and regularities would be eliminated, and all physical laws, in addition to the laws of conservation, would no longer apply. This suggests that the laws of conservation are a prerequisite for the possibility of physical laws, but this topic goes beyond the scope of this study. In order to consistently apply the suspension of the laws of conservation, we would also have to apply it to the observer–world system, not just the world, because we too are subject to its rules in this world. Even the observer would become temporary, losing the continuity of their physical existence and consciousness, including the consciousness of the experiment itself (in an idealistic interpretation, the elimination of consciousness would actually eliminate the model-world) (Figure 3c). Everything would disappear. The question is: would the law of identity still hold true in this new, chaotic, and unstable world? What would it refer to? It would not apply to any element in the model-world, even the model-world taken as a whole, because there would no longer be A and A, either in the sense of two separate objects or in the sense of one object observed continuously at different points in time. In the absence of introspective self-perception of the continuity of the observer’s consciousness, the law of identity could not even abstractly reflect that. Binary logic and its necessity would become pure convention, an abstract game of symbols devoid of any ontology. Binary logic would not contain in itself the power of its own applicability to this model-world, as apparently it is not its intrinsic property—it draws that power from the regularities which ultimately have their origin in the laws of conservation. In a completely different experiment, where we would not degrade the laws of conservation in the model-world, but instead replace them with alternatives of a completely different nature, say the rule that in successive moments of time the shape of a ball always changes to that of a cube, writing A = A would no longer have the same meaning.
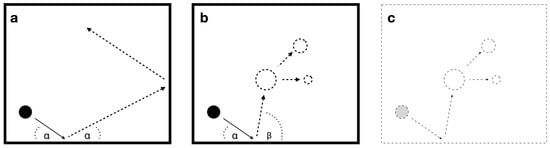
Figure 3.
(a) Model-world in which the same laws of conservation apply as in the real world, (b) Model-world degraded by gradually abolishing the laws of conservation, whose evolution becomes increasingly chaotic, and (c) By completely suspending the laws of conservation, the continuity of the observer is also abolished, as part of the integral observer-world system.
Therefore, mathematics (and logic) is a reflection of the world. This world. So, the question of the necessity of mathematics reduces to the question of the possibility of another world, a world in which there would be no laws of conservation. The problem is that that world in which there would be no laws of conservation would also be—unsustainable. It could be temporary, sporadic, localized, but it could not be in every sense. Would we be able to show its temporariness in a temporarily sustainable world? Hardly. It could look as sustainable as an unconditionally sustainable world; and that could or could not be.
3.6. Implications for Number Theory
Given that our study advocates a realistic view of the ontology of logic and mathematics, it would be appropriate to address some of the problems that a realistic interpretation encounters in the field of number theory, especially with numbers beyond natural numbers. Realistic ontology of mathematics and logic have implications for the theory of complex numbers, quaternions, and other number types beyond natural numbers, which are often considered to be purely abstract and theoretical, suggesting a non-realistic ontology of mathematics. The answer could be that physicalistic interpretations of the ontology of complex and other numbers beyond natural (or real) numbers are not obvious, but not impossible. For example, in the case of complex numbers, one could argue that the concept of a complex number was developed to explain certain physical phenomena, such as electrical circuits and electromagnetic waves. The use of complex numbers in physics suggests that there may be a connection between the mathematical structure of complex numbers and the behavior of physical systems. In the past, the use of complex numbers in physical theories often caused discomfort because it was intuitively believed to undermine the realistic character of theoretical constructs and to be difficult to interpret physical correlates of complex numbers. A paradigmatic example of a physical theory that uses complex numbers is quantum mechanics. In his letter to Lorenzo in 1926, one of the founders of quantum mechanics, Schrödinger [27] writes: “What is unpleasant here, and indeed directly to be objected to, is the use of complex numbers. Ψ [wave function] is surely fundamentally a real function”, clearly demonstrating his own spontaneous realistic standpoint in the interpretation of quantum mechanics formalisms. One response could be that complex numbers are used out of convenience, not out of necessity [28]. The debate on whether complex numbers can be replaced by real numbers in the Hilbert space formulation of quantum theory without limiting its predictions has been ongoing until recently. In a recent study, it has been shown that quantum theory without complex numbers can be experimentally falsified [27], refuting the results of some other studies that claimed the opposite (e.g., [29]). This key study has provided a direct connection between the ontology of complex numbers and experimental evidence, confirming the existence of empirical correlates of complex numbers, or the incompleteness of a mathematical apparatus that would be devoid of complex numbers in describing physical reality. Therefore, although the physicalist interpretation of the ontology of numbers beyond natural numbers is not obvious, and not without challenges, it is possible, and lately, it is experienceing its experimental verification.
4. Conclusions
In this study, the following claims are made:
A: If “the world is necessary” => “mathematics is necessary”
B: If “the world is contingent” => “mathematics is contingent”
The discussion of the necessity of mathematics reduces to a discussion of the necessity of the world, which is a completely different terrain from that on which discussions about the epistemological status of mathematical statements, and the ontological status of mathematical objects, are usually conducted. Therefore, the question of whether mathematics is necessary is a question of whether a sustainable or unsustainable world is possible, or whether it is possible for a necessary statement to be made about a contingent world. Our world could otherwise not be, and we cannot know that.
Mathematical knowledge is a reflection of this world, which, if it were not at least temporarily sustainable, would not be, therefore it is at least conditionally sustainable and the law of identity prevails as a reflection of its sustainability. If it were not sustainable, we would not necessarily be able to observe it, because we as observers could also not be. Therefore, we could only describe it contingently. What would happen if we had temporary sustainability in such a contingent world? Would it seem to us that the world was necessary, and with it, mathematics? Probably yes, because during the time the world lasts, it would seem to be sustainable, and when it no longer exists, and us in it, then it would be too late for theoretical revisions. Mathematics is only conditionally necessary, if there is a set of statements about a necessary world. It is not possible to prove the necessity of the world from the inside, and therefore not the necessity of mathematics. The formal logical system, as well as mathematics derived from it, parasitizes on the certainty of the laws of conservation in nature.
In conclusion, although peripherally related to the topic being discussed, Leibniz’s definition of necessity as something that holds true in all possible worlds appears to be flawed. According to this definition, what holds true in every possible world, including a contingent world, would possess the attribute of necessity. However, the contingency of the world undermines the existence of absolute necessity. Therefore, necessity should not only be defined as something that holds true in all possible worlds, but also in all non-worlds, meaning something that is independent of the existence of the world. How to conceive such existence is another question.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
The author would like to thank the anonymous referees for valuable comments that improved the quality of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Balaguer, M.; Irvine, A. Realism and anti-realism in mathematics. Philos. Math. 2009, 13, 45–69. [Google Scholar]
- Mill, J.S. A System of Logic. Book II, Chapters 5 and 6. 1843. Available online: http://www.sparknotes.com/philosophy/mill/section1.rhtml (accessed on 31 March 2023).
- Frege, G. The Foundations of Arithmetic; Basic Blackwell: Oxford, UK, 1953. [Google Scholar]
- Sedley, D. (Ed.) Plato: Meno and Phaedo; Cambridge Texts in the History of Philosophy; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar] [CrossRef]
- Frege, G. Grundgesetze der Arithmetik [The Basic Laws of Arithmetic]. In Jena: Verlag Hermann Pohle, Band I/II; Furth, M., Translator; University of California Press: Berkeley, CA, USA, 1964. [Google Scholar]
- Gödel, K. What is Cantor’s Continuum Problem. Am. Math. Mon. 1947, 54, 515–525, Reprinted in Philosophy of Mathematics; Benacerraf, P., Putnam, H., Eds.; Blackwell: Oxford, UK, 1964. [Google Scholar] [CrossRef]
- Quine, W.V.O. On What There Is. In From a Logical Point of View; Harvard University Press: Cambridge, MA, USA, 1953. [Google Scholar]
- Resnik, M. Mathematics as a Science of Patterns; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Shapiro, S. Philosophy of Mathematics: Structure and Ontology; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Steiner, M. Mathematical Knowledge; Cornell University Press: Ithaka, NY, USA, 1975. [Google Scholar]
- Lenin, V.I. Materialism and Empirio-Criticism; Wellred Books: London, UK, 1972. [Google Scholar]
- Colyvan, M. Indispensability Arguments in the Philosophy of Mathematics. In The Stanford Encyclopedia of Philosophy, Spring 2015 ed.; Zalta, E.N., Ed.; 2015; Available online: http://plato.stanford.edu/archives/spr2015/entries/mathphil-indis/ (accessed on 1 April 2023).
- Russell, B. A Priori Justification and Knowledge. In The Stanford Encyclopedia of Philosophy, Summer 2014 ed.; Zalta, E.N., Ed.; 2014; Available online: http://plato.stanford.edu/archives/sum2014/entries/apriori/ (accessed on 1 April 2023).
- Sommers, T. Galen Strawson (Interview). In Believer Magazine; Jarman, C., Ed.; McSweeney’s McMullens: San Francisco, CA, USA, 2003; Volume 1. [Google Scholar]
- Kant, I. Critique of pure reason, 1781. In Modern Classical Philosophers; Houghton Mifflin: Cambridge, MA, USA, 1908; pp. 370–456. [Google Scholar]
- Russell-Copleston, A Debate on the Argument from Contingency. Available online: http://www.ditext.com/russell/debate.html (accessed on 1 April 2023).
- John, L. An Essay Concerning Human Understanding; Kay & Troutman: Philadelphia, PA, USA, 1847. [Google Scholar]
- Dansi, D. Uvod u Savremenu Epistemologiju; Plato: Beograd, Serbia, 2006. [Google Scholar]
- Barcan, R.C. The identity of individuals in a strict functional calculus of second order. J. Symb. Log. 1947, 12, 12–15. [Google Scholar] [CrossRef]
- Fitch, F.B. Symbolic Logic, An Introduction. Am. J. Phys. 1953, 21, 237. [Google Scholar] [CrossRef]
- Saul, K. Naming and Necessity. In Semantics of Natural Language; Davidson, D., Harman, G., Eds.; D. Riedel: Dordrecht, The Netherlands, 1972; pp. 253–355. [Google Scholar]
- Lowe, E.J. A Survey of Metaphysics; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Jacquette, D. Kripke on the Necessity of Identity. Anal. Metaphys. 2014, 13, 7–26. [Google Scholar]
- Borisavljević, M. Uvod u Logiku I [Introduction to Logic I]; Saobraćajni Fakultet: Beograd, Serbia, 2009. [Google Scholar]
- Kolakovski, L. Filozofski Eseji [Philosophical Essays]; Nolit: Beograd, Serbia, 1964. [Google Scholar]
- Poincaré, H. Science and Hypothesis; Science Press: New York, NY, USA, 1905. [Google Scholar]
- Einstein, A.; Przibram, K.; Klein, M. Letters on Wave Mechanics: Correspondence with H. A. Lorentz, Max Planck, and Erwin Schrödinger; Philosophical Library/Open Road: New York, NY, USA, 2011. [Google Scholar]
- Renou, M.O.; Trillo, D.; Weilenmann, M.; Le, T.P.; Tavakoli, A.; Gisin, N.; Acín, A.; Navascués, M. Quantum theory based on real numbers can be experimentally falsified. Nature 2021, 600, 625–629. [Google Scholar] [CrossRef] [PubMed]
- Wootters, W.K. Complexity, Entropy, and the Physics of Information; Zurek, W.H., Ed.; Addison-Wesley: Boston, MA, USA, 1990; pp. 39–46. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).