Abstract
Despite recent advances in the mathematical modeling of biological processes and real-world situations raised in the day-to-day life phase, some phenomena such as immune cell populations remain poorly understood. The mathematical modeling of complex phenomena such as immune cell populations using nonlinear differential equations seems to be a quite promising and appropriate tool to model such complex and nonlinear phenomena. Fractional differential equations have recently gained a significant deal of attention and demonstrated their relevance in modeling real phenomena rather than their counterpart, classical (integer) derivative differential equations. We report in this paper a mathematical approach susceptible to answering some relevant questions regarding the side effects of ionizing radiation (IR) on DNA with a particular focus on double-strand breaks (DSBs), leading to the destruction of the cell population. A theoretical elucidation of the population memory was carried out within the framework of fractional differential equations (FODEs). Using FODEs, the mathematical approach presented herein ensures connections between fractional calculus and the nonlocal feature of the fractional order of immune cell populations by taking into account the memory trace and genetic qualities that are capable of integrating all previous actions and considering the system’s long-term history. An illustration of both fractional modeling, which provides an excellent framework for the description of memory and hereditary properties of immune cell populations, is elucidated. The mathematics presented in this research hold promise for modeling real-life phenomena and paves the way for obtaining accurate model parameters resulting from the mathematical modeling. Finally, the numerical simulations are conducted for the analytical approach presented herein to elucidate the effect of various parameters that govern the influence of ionizing irradiation on DNA in immune cell populations as well as the evolution of cell population dynamics, and the results are presented using plots and contrasted with previous theoretical findings.
MSC:
26A33
1. Introduction
Nowadays, it is well established that ionizing radiation damage may cause side effects including the changing of the chemistry of the nucleotides and the breaking of the sugar-phosphate backbone, as well as the hydrogen bonds breaking between bases [1,2,3,4,5]. Most of the in vitro investigations and the studies dealing with anecdotal evidence have shown that the ionizing radiation may generate DNA damage, susceptible to the development of cancer if the DNA structure is not properly repaired. Moreover, numerous clinical studies have addressed the effects of ionizing radiation on immune cell populations, thereby enabling the scientific community to a comprehensive elucidation of the instantaneous and overdue aspects of ionizing radiation on the immune system [6,7].
One of the basic functionalities of the immune system is its aptitude to preserve the memory of previous infections, hence allowing this sophisticated system the ability to distinguish and identify this antigen if an anterior infection arises and then support a sturdier attack on this particular antigen [8,9].
It is crucial to note that the development of theoretical tools must appropriately convey the rising interest in understanding the operation of the immune system. By means of such theoretical tools, mathematicians and biologists will be capable of gathering both experimental findings and theoretical results in a feasible way to perceive more suitable schemes for studying cancer growth and treatment. Most of the recent studies constitute a fragment of such a methodology and it becomes crucial nowadays to simulate this strategy, especially in the study of the immune system by developing appropriate mathematical models. Over the last decade, numerous mathematical approaches have been developed within the framework of conventional integer-order differential equations to initiate the functioning of the immune system. However, most of the obtained results do not reproduce the experimental findings because they are unfit to take into consideration the memory influences in immune systems [9,10,11,12,13]. It has been elucidated that the approaches established with fractional-order differential equations (FODEs) provide more advantages and are considered more harmonious with reality when matched with integer-order mathematical approaches due to the fact that most biological processes endure to function employing hereditary properties, after-affects, and memory. The advantages of the FODEs consist mainly in taking into account the hereditary traits and memory trace that are adept at assimilating all past events and considering the long-term history of the biological process. Within such circumstances, it can be elucidated that the dynamics of the memory trace are decidedly time-dependent processes. Once decreased from the unit, the fractional-order α trains an augmentation of the memory trace nonlinearly from zero. Consequently, the dynamics of a fractional-order system will be quite different from the dynamics elucidated by integer-order approaches, thereby suggesting that FODEs provide more accurate results that can mimic reality better than those obtained by its counterpart, integer-order differential equations [9]. For instance, Mukhopadhyay and Bhattacharyya [10] provided an investigation on tumor and macrophage cells using an integer-order differential equations model. Their results show that the conversion rate of malignant cells to normal cells is quite different to those provided by the experimental data. In other interesting work, Khajanchi et al. [11] have treated the tumor–immune competitive system by extending the model developed by Sarkar and Banerjee [12] and by using an integer-order differential equations model. Khajanchi et al. [11] concluded that the conversion of hunting cells to resting cells, and the degradation caused by hunting cells on the resting cells, are both not the same and provide different results compared to the experimental data. In another work, Hu and Jang [13] proposed a mathematical approach dealing with the effect of CD4+T on tumor dynamics by focusing particularly on the tumor–immune cell interconnection using integer-order mathematical models. Hu and Jang’s approach was extended by Özköse et al. [9] by taking into account the fractionality and better compatibility with the experimental results.
Within this methodology, the used integer differentiation is a local operator, and hence it appears not to be suitable for describing the immunological memory mechanism [14]. Thus, most of the recent mathematical models have used fractional-order approaches, which are more satisfactory to describe the hereditary and memory properties of real phenomena than classical integer-order models [15,16]. Moreover, it should be underlined that even though fractional derivatives do not possess physical and geometric interpretation, fractional differential equations are, however, well established to provide a satisfactory mathematical modeling of biological processes and real-world situations raised in the day-to-day life phase [17]. This is mainly because these equations are generally nonlocal operators, suggesting thereby that the determination at a given point of the fractional temporal derivative necessitates the knowledge of all preceding points [18]. Memory processes are found to be present in numerous biological organisms, especially in the immune system [19,20,21]. Moreover, the advantage of fractional models is that they can help us to reduce the errors arising from the parameters of modeling real-life phenomena by their multi-skilling nature and better fitting to the data, as well as they can provide better descriptions of the evolution of organisms over time taking in consideration their history or memory [22].
The most important property of FODEs is their nonlocal property, which is not an intrinsic property of integer differential equations (IDEs) [23,24]. Nonlocal property signifies that the next state of a model does not rely only on its current state but also depends on all of its historical states [25]. FODEs actually constitute the most powerful tool for incorporating memory effects as well as the hereditary properties in molecular biological problems in contrast with the integer-based models where such effects are neglected to be incorporated [26]. FODEs are commonly utilized in various biological systems such as the immune system, spread of HIV in the human body, glioblastoma multiforme, cancer tumor, oncolytic virus cancer, blood cancer, and several other types of cancer, because their capability to be related in a natural way to systems with memory [27,28,29,30,31]. Moreover, when fitting data, the model described by FODEs seems to be more appropriate than that of its counterpart described by IDEs because of its multi-degree-of-freedom character [23,24,25]. Nevertheless, the numerical calculation of fractional derivatives necessitates a large number of computations because of their nonlocal character [23,26]. Predominantly, the numerical effort and the storage requirements explode in situations dealing with multi-degree-of-freedom phenomena such as immunological memories, which lead to a search for alternative appropriate mathematical modeling to surmount such difficulties encountered with such biological phenomena. For this purpose, new approaches dealing with the numerical evaluation of fractional derivatives should considerably decrease the numerical effort of multi-degree-of-freedom systems [23,24,25,26].
FODEs based on the Caputo operator will be employed in this study in order to elucidate the memory effects mechanism. This omnipresent mechanism effect is evident in immune cell populations and can be studied using fractional derivatives susceptive to be interpreted physically when describing the memory effect, for which the order of fractional derivatives is considered as an index of memory [15,16]. This property enables the estimation of the model parameters more accurately. A fractional derivative provides the memory effect by the integration of FODE based on the Caputo operator from 0 to . The Caputo operator has different properties, making it more convenient for real phenomena by implementing a model of FODE using the well-known Caputo operator [24]. Using the Caputo operator to solve fractional differential equations leads to zero for the constant function derivation. Furthermore, we will be using, in the present study, the Linear Quadratic (LQ) Model to elucidate the effect of ionizing radiations [32,33]. The cell survival curve and its connection to dosage may be represented using the LQ formula in logarithm form. Cell survival curves such as single target model and multi-target model have been widely used to evaluate and predict in vitro and in vivo reactions to ionizing irradiation. In this context, the LQ model, which takes into consideration the total dose and the dose per fraction, is the most commonly used. The LQ model presumes the implementation of two components related to cell killing: the first component is proportional to the radiation dose, whereas the second one is proportional to the square of the dose [32,33]. Cell survival curve in the LQ model is depicted by an exponential function, given by:
where D represents the radiation dose, S represents the fraction of surviving cells for the corresponding dose D, and α and β are, respectively, the linear and quadratic components of cell killing. This formula offers a direct link between the survival of cells and a given dosage [32].
The ultimate motivation of the present work is to derive a fractional-order IR effect model from an integer-order IR effects model developed by Siam et al. [34]. The model can describe a realistic mechanistic model of the effects of ionizing irradiation on immune cell populations and interpret new complex behaviors via numerical simulations explanation. The aim of the present study is to develop a realistic model that describes the dynamic process of the effects of ionizing radiation on immune cell populations. This model will be formulated using a fractional differential equations (FODEs) system. According to [23], fractional derivatives exhibit five basic properties, which include the fractional derivative of an analytic function is analytic; if the order of the fractional derivative is a positive integer, then it is called an ordinary derivative; while for a negative integer, it is called an integral (backward compatibility).
A new fractional-order model describing the dynamics of the IR effects elucidated using the Caputo operator and Mittag-Leffler function for solving fractional derivatives will be developed. The work is based on the pioneering work performed by Siam et al. [34]. The mathematical modeling framework of the present work will introduce the complex behavior of ionizing irradiation effects on immune cells. Particularly, the study presented herein aims to provide valuable information that will help to better understand the complex behavior of the ionizing irradiation effect on immune cell populations. The significant contribution of the present study resides in introducing a new fractional-order IR model within the spirit of the pioneering mathematical model developed by Siam et al. [34]. The study reveals the principal mathematical parameter having major control impacts on the survival of immune cells by elucidating the appropriate fraction cell sensitivity rate, repair, and death rate. The main impact of the present work resides in providing a new parameter, namely, the fractional-order parameter susceptive to add a remarkable impact that helps the capture of the neglected memory effect in the proposed model of Siam et al. [34]. Numerical simulations will be carried out to serve as an efficient platform for reducing the death of cells affected effectively, and by providing a better understanding of the behavior dynamics of ionizing irradiation effects on immune cell populations. A MATLAB algorithm is used for the mathematical computation and graph plotting to elucidate the ability of the model to explain the effect of IR on immune cell populations by evaluating the sensitivity rate of fraction cells as well as repair, and death rates.
The paper is organized as follows: Section 2 contains an overview of the research background, the problem statement, and the objectives as well as the scopes of the present study. In Section 3, an illustration of the relevant literature dealing with biological and mathematical approaches in connection with the present study is provided. In Section 4, we present and discuss the methodology of the proposed research. In Section 5, a detailed theoretical elucidation of the population memory within the framework of fractional differential equations (FODEs) is presented. A physical discussion of the obtained results is illustrated in Section 6, and concluding remarks are made in Section 7.
2. Mathematical Modeling of Immune System
The ultimate objective of the present study is to investigate the influence of ionizing irradiation on immune cell populations. Herein, we should emphasize that the mathematical approaches dealing with the most harmful health effects caused by exposure to the ionizing irradiation process on immune cell populations are disentangled into two main general models, namely, the deterministic and stochastic models [35,36,37,38,39,40].
The application of fractional differential equations within the context of a stochastic model necessitates cautious attention because of the memory effects and the rise in calculation time as compared to the required computation time for classic random differential equations. In this sense, the mathematical models of IR effects introduced within the framework of integer-order differential equations (IDEs) [41,42,43,44], classified as a deterministic mathematical model, seem to be non-appropriate since the model does not take into consideration the effects of memory that exist in real-life diseases [45]. Despite this inconvenience, these models have shown their aptitude to be easy to use and susceptible to be applied in modeling, especially with cancer growth, readily available numerical methods, and well-developed dynamical systems theory. The utilization of fractional-order differential equations in molecular biological problems may fill this gap [45].
Recently, Siam et al. [34] proposed a mathematical approach involving structured cell populations for modeling DSBs and misrepair cells succeeding in ionizing irradiation. The model is described by the IDE system. This model illustrates the dynamics process of cell populations succeeding in ionizing irradiation, and the probability that the cell is correctly repaired, including repair rate, and death rate. Nevertheless, this approach only takes into account the primary electrons of ionizing irradiation as the main origin of DSB formation, which induces DNA damage. Siam et al. [46] proposed a mathematical model using IDEs that describes the role of radio-sensitizers such as gold nanoparticles in radiotherapy to increase the number of cancer cell deaths. Mathematically, the approach was built within the framework of IDEs. The authors managed to explain that gold nanoparticles increase secondary electron production after exposure to primary irradiation that causes DNA damage. Therefore, a radio-sensitizer such as gold nanoparticles may be a promising and important factor in radiotherapy. This study aims to investigate the influence of radio-sensitizers on radiotherapy to clarify their role in reducing the damage to neighboring healthy cells. This study was conducted by incorporating the dose function deposited by gold nanoparticles into the model used for the effects of ionizing irradiation.
2.1. Merits of Modeling Biological Processes with Fractional Derivatives
Fractional derivatives have been used in many scientific areas, including biology, physics, chemistry, biochemistry, hydrology, medicine, and finance [47,48,49]. Biological processes are also very reliant on the ultimate state of the dependent variable, and all preceding stages throughout time. This is regarded as a memory effect of the dependent variable in time. There are several examples of biological systems with memory effects that have used nonlocal fractional-order differential equations to study their dynamics, for example: modeling immune systems based on Atangana–Baleanu fractional derivatives, fractional-order mathematical modeling of cancer cell–cancer stem cell–immune system interaction with chemotherapy, and dynamical behavior of HIV immunology model with non-integer time fractional derivatives [50,51,52]. In the aforementioned examples, the memory of the systems is governed by the immunized cells and their corresponding dynamics have thereby been studied with nonlocal fractional differential equations. The concept of fractional calculus is embedded into a larger theory of nonlocal operators, leading to a successful generalization of the fractional derivative operator that results in a promising concept of memory effects. The influence of memory effects on a distinguished set of biological processes is usually elucidated with nonlocal models.
2.2. Fractional Integrals and Fractional Derivatives
Even though fractional calculus is almost as old as conventional calculus, it has long been used and sporadically discussed by only a few scientists. Multiple definitions for fractional derivatives exist in the literature. There are various definitions for fractional derivatives; the most popular ones are the Riemann–Liouville and the Caputo fractional derivatives [53,54]. However, the Riemann–Liouville fractional derivative of a constant is not zero, but that of the Caputo fractional derivative is zero. Hence, the Caputo fractional derivative is more commonly used for mathematical modeling than the Riemann–Liouville fractional derivative [55]. Moreover, Riemann’s definition requires the knowledge of the initial conditions for the integration of the function, whereas the Caputo fractional derivative needs the initial conditions of the function and its normal derivatives. Caputo fractional derivative requirements are closer to reality, and they can be dealt with more easily [56,57,58].
Special calculus functions have become important as solutions to FODEs and refined mathematical models for various natural problems. In an innovative study, Mainardi [59] tried to answer a central question by implementing the relationship between the Mittag-Leffler function and fractional calculus. Several authors have investigated the solutions of linear and nonlinear fractional differential equations by the Mittag-Leffler function in recent years [60,61].
3. Mathematical Formulation
The primary goal of this work is to explain the effects of ionizing radiation on a memory cell population using a system of fractional differential equations based on the IDE model proposed by Siam et al. [34], in which the population of cells is structured by the number of DNA double-strand breaks (DSBs) due to ionizing irradiation. More precisely, the cell population is structured into different cohorts, which contain DSBs and misrepaired of DSBs. The death rate function in the model proposed by [34] depends on the number of k DSBs and misrepairs, . The authors considered two primary events in the population, which are cell death , and the repair process for DSBs with the probability of a successful repair cell, and an unsuccessful repair cell defined as . The Michaelis–Menten equation is implemented to describe the repair rate of DNA damage. The model has FODEs, where depends on a maximum number of DSBs, . The number of cells with DSBs is produced immediately after ionizing radiation following Poisson distribution with mean . Refer to [34] for further details.
Working in the same spirit and motivation as the recent work conducted by Siam et al. [34], the current model is estimated to provide an improvement in the description of the cell population under the effects of ionizing irradiation. However, it should be underlined that the mathematical model developed herein is based on fractional-order differential equations (FODEs), whereas the model of Siam et al. [34] used a system of linear differential equations susceptible to describe the evolution of the irradiated population of cells over time. The model of FODEs is given as follows:
For and with . From the last inequality represents the maximum number of DSBs arising in a population of cells from ionizing irradiation. The operator represents the Caputo derivative with respect to time and . The α means the memory index of the cell. Its value is maintained until it is changed, thereby leading to changing the solution by the system. The integration from to corresponds with the history of the memory effect of the cell, which ranges from to . It is interesting to note herein that the integer derivation equation considers only the instantaneous dynamic evaluated at the instant time . The parameters , and correspond, respectively, to the repair rate, death rate, and probability of effective repair. The death rate, of cells is illustrated owing to the interaction between two DSBs. Furthermore, death rate, is elucidated herein with aid from the lethal chromosomal aberration, and the misrepair of DSBs. Consequently, the cell death rate, arising from ionizing irradiation, is presented as:
where is a lethal misrepair rate constant, whereas corresponds to the lethal damage rate constant. The function is inspired by the Siam et al. [34] approach by taking into consideration that the DSB damage that occurs in DNA arises in cells. It is widely accepted that DSBs are among the most deleterious forms of DNA lesions. The occurrence of a large number of DSBs induces an important probability of obtaining unrepaired or misrepaired DSBs, as well as a considerable probability of obtaining lethal chromosomal aberrations, thereby leading to a high probability of cell death. The repair rate, is an ensemble of cells having DSBs, whereas the repair procedure of DSBs can be expressed by Michaelis–Menten saturating function [62]:
where represents the DSBs number, is the Michaelis–Menten constant and is the maximum repair rate. The Michaelis–Menten constant shows that the number corresponding to the repair rate has reached half of the maximum number.
We consider an initial population of on cells being exposed to a dose of irradiation , and resulting in cells with DSBs. Thus, the initial and the total cell population satisfies:
Distribution of Initial Number of DSBs
Let us suppose that new DSBs are formed directly after being subject of ionizing radiation [63]. Following the work conducted by [64], which gave strong support that the phosphorylation–dephosphorylation radiation-induced foci are considered to be a direct biomarker of DSBs, we presume that the probability of a cell obtaining k DSBs can be expressed by the Poisson distribution, as follows:
with the mean is given by:
is the radiation dose, and is a measure of the radiosensitivity of cells.
Fractional calculus theories have undergone significant and even intense progress, being predominantly developed by pure mathematicians. In the last decade, engineers and researchers have managed to demonstrate that differential equations modeled with the aid of fractional derivatives can efficiently provide a mathematical modeling of real problems, such as signal processing, viscoelastic systems, control processing, diffusion processes, radiology in biology, and ecology [64,65,66].
Different types of definitions for fractional derivatives are available in the literature, which are typically not equivalent to each other. Different from integer-order (or classical) derivatives, some relevant fractional derivative definitions are introduced herein. The choice of these definitions, among others, is their aptitude to be used for modeling immune cell populations. The Grunwald–Letnikov derivative is simply an expansion of the general definition of an ordinary derivative that permits the derivation of a non-integer number of times. This extension establishes a more general equation of the fractional derivative with the interesting feature of nonlocality generally employed for the explanation of the memory feature of real-life cases. The Grunwald–Letnikov definition is considered a reference definition, into which the memory feature is typically integrated with all definitions of fractional derivatives. The Caputo fractional derivative is commonly used in expressing the enhanced model of radiotherapy cancer treatments, which mainly possess a feature memory.
Definition 1.
The definition of a derivative, as well as the establishment of the fractional derivative based on the Grunwald–Letnikov definition, is provided by the following equations:
where
It implies that Equation (4) can be represented as:
by replacing Equation (12) with Equation (8), we obtain:
Consequently, any
power derivative, where
, can be provided by:
For an interval
with step size
, then Equation (11) becomes:
where and
The definition of the fractional derivative illustrated by Grunwald–Letnikov is provided by Equation (16). As can be depicted from Equations (8)–(18), the derivative becomes local and the expansion terminates in case the parameter is considered as integer (q) (i.e., m = q), giving rise to an ordinary derivative of order . Nevertheless, in case the integer is taken to be negative, the expansion fails to terminate and continues during the whole interval . In this particular case, Equations (17) and (18) become integral and the derivative obtains a nonlocal character. Moreover, in cases where is considered a fractional number, the expansion also continues along with the entire interval , enabling Equations (17) and (18) to possess a fractional derivative character. Due to this nonlocality, both the fractional and integral derivatives treat the totality of the points within the interval, and, as a result, the integral and fractional derivatives expose the so-called memory effect [41,46].
4. Fractional Differential Equations Model Formulation
The mathematical model considered herein is used to reproduce the effects of ionizing irradiation on immune cell populations. For this purpose, we extend the pioneering mathematical model proposed by Siam et al. [34], by taking into account fractional differential modeling to better describe and understand immune cell population phenomena rather than its counterpart, classical (integer) derivative differential equations. In addition, the fractional differential equations introduced herein are very promising tools since they are very efficient methods for reducing errors arising from the parameters of modeling real-world phenomena. Moreover, the choice of using fractional modeling in our model is mainly due to the fractality nature of the problem, which ensures links between fractal structures and fractional calculus, such as those encountered in immune cell populations. The mathematical model proposed by Siam et al. [34] is adapted herein by substituting the exponential decay component with the generalized Mittag-Leffler function, which leads to a mathematical approach with nonlocal characteristics. To solve the system, we used an approach that involves the conversion of the model to an integral equation with fractional differential equations. Accordingly, the derived solution takes the following expression:
For and with and is the maximum number of DSBs created following IR in the population of immune cells. represents the Caputo derivative with respect to time. The parameter figuring in the Caputo derivative which refers to the memory index of the cell, designs the fractional-order derivative that satisfies the condition . The means the memory index of the cell. Its value is maintained until it is changed, thereby leading to changing the solution by the system. The integration from to corresponds to the history of the memory effect of the cell, which ranges from to . It is interesting to note herein that the integer derivation equation considers only the instantaneous dynamic evaluated at the instant time . Equation (19) contains some rate functions:
is the death rate of cells, which is considered in two ways, and is due to misrepair of DSBs; is also due to the interaction of two DSBs located in spatial proximity formed a lethal chromosomal aberration, .
where is the repair rate of immune cells, and in Equation (21) is the probability of successful repair. Note that is not fixed, but random, based on a Poison distribution. The value of parameters: and are chosen randomly only as an example. As an example, we consider Equation (19) for three different cases, which depend on .
Case 1. When , , and are taken to be equal to 1, the population can be structured into three groups of immune cells, which are . Then, Equation (19) is reduced to a system of FODEs, which is given as follows:
Using the parameter values, the above equations become:
To make biological sense, the population is eliminated when . The system of FODEs can be rewritten into a matrix form:
Case 2. When , then the possible and are taken as and . The population is structured into groups of immune cells, . Then, Equation (21) is reduced to a system of FODEs, which is given as follows:
Using the parameter values and eliminating the value of misrepair immune cells, , the equations become
with does not make sense. The system can be rewritten into a matrix form:
Case 3. When and and are taken as and then the population is structured into groups of immune cells, which are . In this case, Equation (21) is reduced to a system of FODEs, which is given as follows:
Using the parameter values and eliminating the value of misrepair immune cells, the equations become:
The system can be rewritten into a matrix form:
The value of is randomly generated by the Poisson distribution function in MATLAB (see Equation (7)). It can be concluded that the general form of the FODE system with a maximum number of DSBs in a population of cells can be rewritten into a matrix form:
where N is a matrix that represents groups of immune cells having DSBs and misrepair DSBs and A is a square matrix.
The matrix N and the size of matrix A are derived based on the value of , which is the maximum number of DSBs in a population of cells. The number of FODEs that exists in the system is with the dimension of matrix N is matrix given by:
4.1. Solution of the FODE Model
The solution for Equation (22) with the initial population, is as follows:
The initial condition, , is explained in Section 3. It should be emphasized, herein, that the rational approximation, which has proven its capability to provide an excellent estimation of the Mittag-Leffler function, constitutes an appropriate solution [67,68]. Furthermore, within the frame of this approximation, the problem requires only solving linear systems rather than matrix inversions [68]. This is an efficient method even for small matrix arguments, and direct approaches can be involved in solving the resulting linear systems. In this case, we consider a large matrix argument and several alternatives can be applied and, herein, the iterative method will be used. Indeed, in controlling large matrices, iterative procedures are the most suitable compared to direct schemes, as they are less vulnerable to numerical errors and robust [69]. A scheme using iterative procedures is implemented in MATLAB and, hence, this routine will be performed for the numerical evaluation of the Mittag-Leffler function. The initial distribution of the random Poisson distribution only generates the number of DSBs in immune cells. Therefore, for all values of because there is no cell with misrepair DSBs in the initial condition, as the repair process has not started yet.
For the example of how the initial condition is computed here, suppose that there is a population of immune cells and the number of DSBs produced by Poisson distribution on each cell is . Observe the number of maximum DSBs, to groups of immune cells. Therefore, the initial condition, is as follows:
The survival fraction of immune cells for the solution is given as:
4.2. Model Simulation Algorithm
In the model simulation, we generate 31 simulation data points for the fixed value of model parameters. MATLAB R2021a is used to perform the simulation of the model. The algorithm to compute the survival fraction with respect to dose is as follows:
- Generate random initial conditions, . The dose is incorporated into the system via initial conditions. This is achieved by fixing dose , to compute the mean to obtain the initial conditions.
- Solve the system up to time for h. We chose the number to ensure that the repair process is completed [70].
- Compute the fraction of surviving immune cells
- Plot lnS versus the dose D. Due to the randomness of the initial conditions, we repeat steps (1)–(3) for twenty runs in order to obtain the averaged value of the surviving fraction in logarithmic scale,. This step shows the completion of the loop for a single dose , corresponding to a single data point. To obtain many data points on the survival curve, steps (1)–(3) and the averaged value of surviving fraction in a logarithmic scale, need to be repeated for each dose D.
- Fit the obtained data to the LQ (see Equation (1)) relation using fmin-search in MATLAB. This method employs the search method of Lagarias et al. [71], which determines the minimum of our unconstrained multivariable function using derivative-free. A flowchart of the model simulation algorithm is provided in Figure 1.
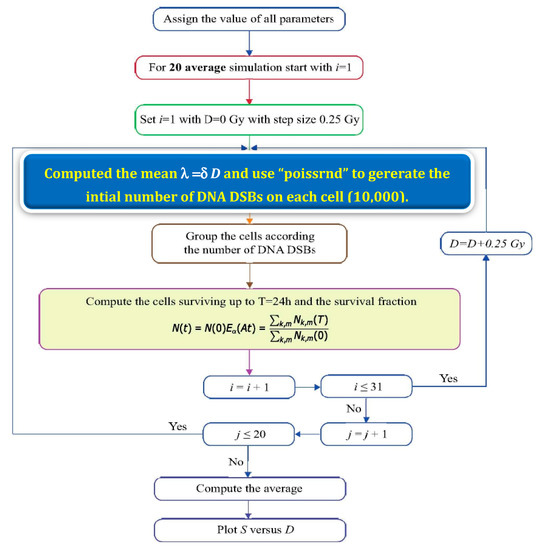 Figure 1. Flowchart of model simulation algorithm.
Figure 1. Flowchart of model simulation algorithm.
4.3. Simulation of the Model
We generate 31 simulation data points for the value of model parameters, . These values and the total number of data are chosen only as an example. For the model simulation, the proposed boundaries’ value ranges are listed in Table 1.

Table 1.
The parameter space is restricted to the range of values.
An illustration of the obtained results relative to the model simulation with the variation in the memory index values is plotted in Figure 2.
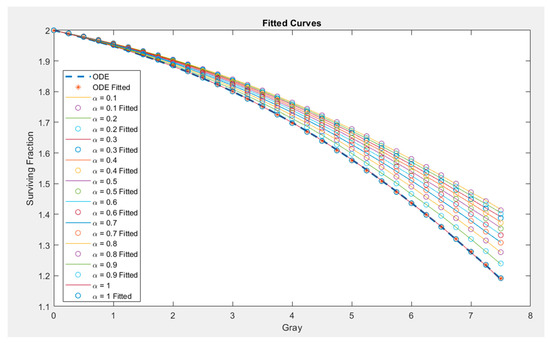
Figure 2.
The cell survival curves for memory index .
5. Comparison between Current Model and Previous Model Proposed by Siam et al. [34]
Various forms of fractional derivatives have been employed to pattern many problems in biological science [63,64]. In this research, the Caputo fractional-order derivative will be employed. Caputo fractional-order derivatives are another suitable alternative for calculating fractional derivatives, featured by the fact that the searching solution of the differential equations does not require the definition of the fractional-order initial conditions. Furthermore, in cases where real-world diseases are considered, the Caputo fractional differential allows the utilization of the initial and boundary conditions [29]. Here, we present a generalization of Siam’s model in [34], in which we transform from the integer derivative (IDE) model to the fractional derivative (FODE) model (see Table 2).

Table 2.
Modification of current model from previous model.
In the following, we show the differences between previous and current models. The system of fractional differential equations (FODEs) is given by:
where is the cell population following ionizing radiation. matrix is defined by Equation (2), and then the solution for this system (19) above is given by:
is the initial population of cells being subjected to a dose of ionizing radiation following a Poisson distribution. is Mittag-Leffler function with .
6. Results Discussion and Summary
Despite the recent advances in mathematical modeling of biological processes and real-world situations raised in the day-to-day life phase, some phenomena such as immune response phenomena remain poorly understood. The mathematical modeling of complex systems for these phenomena using nonlinear differential equations seems to be quite promising with appropriate tools to model such complex and nonlinear complex systems. Fractional differential equations recently have gained a significant deal of attention and demonstrated their relevance in modeling real-world problems. Several publications mention the involvement of fractional modeling to better describe and understand real-world problems rather than their counterpart, classical (integer) derivative differential equations. In addition, fractional differential equations are very promising tools since they are very efficient methods for reducing errors arising from the parameters of modeling real-world phenomena. Moreover, the literature brings another reason to choose fractional modeling in our model aiming to describe the biological aspects of immune cell populations and blood tumor treatment and growth: fractality, which ensures links between fractal structures and fractional calculus, revealing patterns in nature, such as immune cell populations and blood tumor growth or treatment.
The systematic investigation of the immune cell populations provided herein uses a mathematical model that deals with the effects of ionizing radiation and involves, in its structure, nonlinear differential equations. Interestingly, a comprehensive investigation using fractional differential equations to describe the biological aspects of immune cell populations and blood tumor treatment and growth is provided. Fractality, which ensures the link between fractal structures and fractional calculus, also reveals patterns in nature, such as those involving memory effects, which constitute the foundation of the mathematical formulation used in conducting this work. We report herein a realistic mechanistic model of the influence of ionizing irradiation on DNA in immune cell populations using fractional order of derivatives. In order to elucidate the evolution of cell population dynamics following ionizing radiation, the present mechanistic model is developed within the framework of fractional differential equations by taking into account the Mittag-Leffler function as well as the Caputo derivative. The choice of using some definitions among others is their aptitude to be used for modeling such biological processes. The common definition of a derivative is proposed by Grünwald–Letnikov, which is simply an expansion of the general definition of an ordinary derivative that permits the derivation of a non-integer number of times. This extension establishes a more general equation of the fractional derivative with the interesting feature of nonlocality generally employed for the explanation of the memory features such as those observed in immune cell populations. This is typically what happens in some real-life processes, particularly dealing with biological processes. For instance, the treatment of immune cell populations depends on all the points in the interval because this biological process exhibits a memory effect [65,66]. Hence, the employment of fractional derivatives for modeling biological processes will provide more realistic results than its counterpart, ordinary derivatives. Because cancer cure is a purely natural process, it is therefore more appropriate and precise to employ fractional derivatives. The Caputo fractional derivative constitutes the most useful scheme for defining a fractional derivative. The Caputo fractional derivative treats the differentiation in the entire interval, thereby allowing the derivative to be nonlocal. The differentiation consequence considers all the interval points, hence providing a great advantage compared to classical derivatives that consider only the initial and final points or a finite number of points, having a limited local character.
We now present the results of our realistic mechanistic model on the influence of ionizing irradiation on DNA in an immune cell population using fractional order of derivatives. Our results are compared and contrasted with those provided by Siam et al. [34]. The parameter estimation approach used herein qualifies the death rate coefficient of the model species, giving rise to a value of parameters that best fits the model simulation to the experimental data collected for this purpose. Global optimization algorithms are used to obtain the minimum value of the sum of squares error (SSE). The simulation results are performed using the system of fractional-order derivatives derived herein for a memory index ranging from 0 to 1 (0 < 𝛼 < 1). The FODE model is implemented to explain the dynamics process of the irradiation effects on immune cell populations.
In Figure 2, we plot the steady-state surviving fraction obtained using various values of the memory index 𝛼. It is interesting to disentangle herein that the fractional order refers also to the memory index 𝛼. The convergence criteria considered herein is to proceed with an absolute difference between two consecutive terms less than 10−9, i.e., |an−an−1| < 10−9. Moreover, in order to describe the evolution of cell population dynamics following ionizing radiation, the mechanistic model presented herein is developed within the framework of the fractional differential equations by taking into account the Mittag-Leffler Function as well as the Caputo derivative. The parameter estimation approach used herein qualifies the death rate coefficient of the model species, giving rise to a value of parameters that best fits the model simulation to the previous theoretical model [34] as well as the experimental data that will be collected for this purpose. Global optimization algorithms are used to obtain the minimum value of the sum of squares error (SSE), derived within the least square method, which supposes that the appropriate fit line of the experimental data is the one having the minimum value of the least square error.
As can be depicted from the figure, for a memory index, 𝛼 is equal to the unit (𝛼 = 1), and the obtained survival curve is perfectly superimposed with its corresponding curve obtained within the framework of the IDE model developed in the pioneering work proposed by Siam et al. [34]. Interestingly, when the memory index 𝛼 = 1, the FODE model exhibits the expected identical results compared to the IDE model. When the fractional order is reduced between 0 and 1, the immune cell surviving fraction is increased due to the manifestation of the nonlocality and memory effect, thereby suggesting that when the previous history of the immune cells is considered, more cells will survive the irradiation effects. These observations indicate that fractional-order effects are important in the surviving fraction dynamics across a complex wide range of memory effects and hereditary traits. Furthermore, it is shown in this context that the memory trace dynamics are strongly reliant on time [72]. When the fractional order is reduced to between 0 and 1, the immune cells’ survival rises owing to the memory trace that provides strong support for the immune cells having the ability to repair the DNA damage effectively [72,73]. Hence, fractional-order system dynamics yields more sophisticated results, giving rise to a significant divergence from those obtained from integer-order dynamics. Moreover, in cases where α is considered as a fractional number between 0 and 1, the Caputo derivative also continues to possess a fractional derivative character. Due to this nonlocality, both the fractional and integral derivatives treat the totality of the points within the interval, and, as a result, the integral and fractional derivatives expose the so-called memory effect. This is typically what happens in some real-life processes, particularly dealing with biological processes. For instance, the treatment of immune cell populations depends on all the points in the interval because this biological process exhibits a memory effect. Hence, the employment of fractional derivatives for modeling biological processes with a memory index satisfying 0 < α < 1 will provide more realistic results than its counterpart ordinary derivatives.
It should be noted that the effects of ionizing radiation on cell populations while accounting for memory effect/hereditary traits are typically scarcely studied and to our knowledge, no such study in the literature has addressed the effects of ionizing radiation by taking into account the memory effects and hereditary traits. Moreover, we should emphasize that the results obtained herein are in line with the experimental facts elucidated in nonlocal memory effect phenomena, which affirm that the cells of the immune system have the ability to remember (or adapt) a previous response to irradiation damage. Particularly, the immune cells can respond more effectively to the irradiation damage [74,75]. This is illustrated once the immune cells are exposed to environmental hazards such as ionizing radiation and, consequently, activation of the cells’ immune response will be triggered.
7. Conclusions
The mathematical approach adopted in this study has been applied for the first time to develop a fractional-order mathematical model of DNA damage response to ionizing radiation. The model is based on the use of fractional-order differential equations inherently connected to systems with memory, which are predominantly present in cancer cell–immune system interactions. Within the context of this model, the nonlocality character of such disease dynamics is employed, thereby leading to the development of a mathematical approach dealing with fractional-order differential equations. Mathematical models based on ordinary differential equations of integer order have proven useful in understanding disease dynamics. However, when compared to fractional-order derivatives, they are several restrictions. The immediate biological events are solely described by integer-order derivatives. The nonlocal feature of fractional order asserts that the next step of a model depends not only on its present state but also on all of its prior stages. Using this model, we have explained the effects of ionizing radiation on a cell population using a system of fractional differential equations based on the IDE pioneering model proposed by the Siam et al. [34], in which the population of cells is structured by the number of DNA double-strand breaks due to ionizing irradiation. More precisely, the cell population is structured into different cohorts, which contain k DSBs and misrepaired of DSBs. We have taken into consideration that the death rate function depends on the number of k DSBs and misrepairs, . We also considered two primary events in the population, which are cell death and the repair process for DSBs, with the probability of successfully repairing a cell, and an unsuccessful repair cell defined as and finally, we implemented the Michaelis–Menten equation for the elucidation of the repair rate of DNA damage. Our model presents a set of FODEs, which are mainly dependent on the maximum number of DSBs. The number of cells with the elucidated number of DSBs is produced immediately after ionizing radiation using Poisson distribution. The theoretical results illustrated in this investigation, dealing with the fractional-order mathematical model of DNA damage response to ionizing radiation developed with the aid of the above theoretical considerations, permit the following important conclusions and observations:
(i) For a memory index, 𝛼 is equal to the unit (𝛼 = 1), the obtained survival curve is excellently superimposed with the results obtained within the framework of the IDE model proposed by Siam et.al. [34].
(ii) When the fractional order is reduced to between 0 and 1, the immune cells surviving fraction is increased due to the manifestation of the nonlocality and memory effect. Hence, more cells will survive the irradiation effects, and a significant deviation from the results obtained by the model of Siam et al. [34] is elucidated.
(ii) Mathematical models based on ordinary differential equations of integer order have proven useful in understanding disease dynamics. However, when compared to fractional-order derivatives, they have several restrictions.
(iv) The nonlocal characteristic of the mathematical models dealing with fractional-order differential equations is crucial, as it does not exist in integer-order differential operators. Fractionality is inherently connected to systems with memory, and is present in cancer cell–immune system interactions.
(v) Mathematical models with fractional-order differential equations outperform integer-order mathematical models. Both fractional modeling and the estimated value of model parameters have been evaluated in this investigation,
(vi) Fractional-order modeling is also very susceptible to taking into account memory trace and genetic qualities, which are capable of integrating all previous actions, taking into account the system’s long-term history.
Finally, it is important to emphasize that the inclusion of fractional-order differential equations is intended to better mimic the real world when dealing with real-life phenomena with memory such as those involved in biological applications. We are persuaded that the extension of theoretical mathematical approaches must appropriately convey their rising importance in cancer growth and treatment. By using such mathematical models, biologists and academics will be capable of linking both experimental findings and theoretical results in a sustainable way to consider more appropriate methodology for a comprehensive understanding of such diseases by elucidating the memory trace and genetic qualities that are capable of integrating all previous actions, taking into account the system’s long-term history. The mathematical model presented herein institutes a fragment of such an approach.
Author Contributions
Conceptualization, D.Y.A., F.M.S. and F.A.A.; methodology, D.Y.A., F.M.S. and F.A.A.; validation, D.Y.A., F.M.S. and F.A.A.; formal analysis, D.Y.A., F.M.S. and F.A.A.; resources, D.Y.A.; data curation, D.Y.A.; writing—original draft preparation, D.Y.A.; writing—review and editing, F.M.S. and F.A.A.; visualization, F.M.S. and F.A.A.; supervision, F.M.S. and F.A.A.; project administration, F.M.S. and F.A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Universiti Teknologi Malaysia (UTM).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to acknowledge the financial support from the Universiti Teknologi Malaysia (UTM) Encouragement Research Grant Scheme, grant number: Q.J130000.3854.20J20.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sowa, P.; Rutkowska-Talipska, J.; Sulkowska, U.; Rutkowski, K.; Rutkowskie, R. Ionizing and non-ionizing electromagnetic radiation in modern medicine. Pol. Ann. Med. 2012, 19, 134–138. [Google Scholar] [CrossRef]
- Woodside, G. Environmental, Safety, and Health Engineering; John Wiley & Sons: Hoboken, NJ, USA, 1997; p. 476. [Google Scholar]
- Ryan, J. Ionizing Radiation: The Good, the Bad, and the Ugly. J. Investig. Dermatol. 2012, 132, 985–993. [Google Scholar] [CrossRef]
- L’Annunziata, M.; Baradei, M. Handbook of Radioactivity Analysis; Academic Press: Cambridge, MA, USA, 2003; p. 58. ISBN 978-0-12-436603-9. [Google Scholar]
- Grupen, C.; Cowan, G.; Eidelman, S.; Stroh, T. Astroparticle Physics; Springer: Berlin/Heidelberg, Germany, 2005; p. 109. ISBN 978-3-540-25312-9. [Google Scholar]
- Siegel, R.L.; Miller, K.D.; Jemal, A. Cancer statistics. CA Cancer J. Clin. 2018, 68, 7–30. [Google Scholar] [CrossRef]
- Belpomme, D.; Hardella, L.; Belyaevade, I.; Burgioa, E.O.; Carpenteragh, D. Thermal and non-thermal health effects of low intensity non-ionizing radiation: An international perspective. Environ. Pollut. 2018, 242, 643–658. [Google Scholar] [CrossRef] [PubMed]
- Barrea, A.; Hernandez, M.E. Optimal control of a delayed breast cancer stem cells nonlinear model. Optim. Control Appl. Methods 2016, 37, 248–258. [Google Scholar] [CrossRef]
- Özköse, F.; Yılmaz, S.; Yavuz, M.; Öztürk, İ.; Şenel, M.T.; Bağcı, B.Ş.; Doğan, M.; Önal, Ö. A Fractional Modeling of Tumor–Immune System Interaction Related to Lung Cancer with Real Data. Eur. Phys. J. Plus 2022, 137, 40. [Google Scholar] [CrossRef]
- Mukhopadhyay, R.; Bhattacharyya, T. Spatio temporal variations in mathematical model of macrophage-tumorinteraction. Nonlinear Anal. Hybrid Syst. 2008, 2, 819–831. [Google Scholar] [CrossRef]
- Khajanchi, J.; Nieto, J. Mathematical modeling of tumor-immune competitive system, considering the role of time delay. Appl. Math. Comput. 2019, 340, 180–205. [Google Scholar] [CrossRef]
- Sarkar, R.R.; Sandip, B. Cancer self-remission and tumor stability—A stochastic approach. Math. Biosci. 2005, 196, 65–81. [Google Scholar] [CrossRef]
- Hu, X.; Jang, S.R.-J. Dynamics of tumor-CD4T+-cytokines-host cells interactions with treatments. Appl. Math. Comput. 2018, 1, 700–720. [Google Scholar] [CrossRef]
- Lei, G.; Zhang, Y.; Koppula, P.; Liu, X.; Zhang, J.; Lin, S.H.; Gan, B. The role of ferroptosis in ionizing radiation-induced cell death and tumor suppression. Cell Res. 2020, 30, 146–162. [Google Scholar] [CrossRef] [PubMed]
- Prakasha, D.G.; Veeresha, P. Analysis of lakes pollution model with mittag-leffer kernel. J. Ocean. Eng. Sci. 2020, 5, 310–322. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G. A reliable analytical technique for fractional Caudrey-Dodd-gibbon equation with Mittag-Leer kernel. Nonlinear Eng. 2020, 9, 319–328. [Google Scholar] [CrossRef]
- Tavassoli, M.H.; Tavassoli, A.; Rahimi, M.R.O. The geometric and physical interpretation of fractional order derivatives of polynomial functions. Differ. Geom.-Dyn. Syst. 2013, 15, 93–104. [Google Scholar]
- Farayola, M.F.; Shae, S.S.; Siam, F.M.; Khan, I. Mathematical modeling of radiotherapy cancer treatment using Caputo fractional derivative. Comput. Methods Programs Biomed. 2020, 188, 105306. [Google Scholar] [CrossRef]
- Pimentel, V.O.; Rekers, N.H.; Yaromina, A.; Lieuwes, N.G.; Biemans, R.; Zegers, C.M.L.; Germeraad, W.T.V.; Van Limbergen, E.J.; Neri, D.; Dubois, L.J.; et al. Radiotherapy causes long-lasting antitumor immunological memory when combined with immunotherapy. Radiother. Oncol. 2018, 127, S22. [Google Scholar]
- Qureshi, S. Real life application of Caputo fractional derivative for measles epidemiological autonomous dynamical system. Chaos Solitons Fractals 2020, 134, 109744. [Google Scholar] [CrossRef]
- Sopasakis, P.; Sarimveis, H.; Macheras, P.; Dokoumetzidis, A. Fractional calculus in pharmacokinetics. J. Pharmacokinet. Phar. 2018, 45, 107125. [Google Scholar] [CrossRef]
- Ahmed, N.; Shah, N.A.; Taherifar, S.; Zaman, F.D. Memory effects and of the killing rate on the tumor cells concentration for a one-dimensional cancer model. Chaos Solitons Fractals 2021, 144, 110750. [Google Scholar] [CrossRef]
- Machado, J.T.; Kiryakova, V. Recent history of the fractional calculus: Data and statistics. Handb. Fract. Calc. Appl. 2019, 1, 1–21. [Google Scholar]
- Bisci, G.M.; Rădulescu, V.D.; Servadei, R. Variational Methods for Nonlocal Fractional Problems; Cambridge University Press: Cambridge, UK, 2016; Volume 162. [Google Scholar]
- Kumar, S.; Kuma, A.; Momani, S.; Aldhaifallah, M.; Nisar, K.S. Numerical solutions of nonlinear fractional model arising in the appearance of the strip patterns in two-dimensional systems. Adv. Differ. Equ. 2019, 2019, 413. [Google Scholar] [CrossRef]
- Abdelaziz, M.A.; Ismail, A.I.; Abdullah, F.A.; Mohd, M.H. Bifurcations and chaos in a discrete SI epidemic model with fractional order. Adv. Differ. Equ. 2018, 1, 44. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. Solving smoking epidemic model of fractional order using a modified homotopy analysis transform method. Math. Sci. 2019, 13, 115–128. [Google Scholar] [CrossRef]
- Abdelaziz, M.A.; Ismail, A.I.; Abdullah, F.A.; Mohd, M.H. Codimension one and two bifurcations of a discrete-time fractional-order SEIR measles epidemic model with constant vaccination. Chaos Solitons Fractals 2020, 140, 110104. [Google Scholar] [CrossRef]
- Al-Khedhairi, A.; Elsadany, A.A.; Elsonbaty, A. On the Dynamics of a Discrete Fractional-Order Cournot-Bertrand Competition Duopoly Game. Math. Probl. Eng. 2022, 2022, 8249215. [Google Scholar] [CrossRef]
- Rashid, S.; Jarad, F.; Ahmad, A.G.; Abualnaja, K.M. New numerical dynamics of the heroin epidemic model using a fractional derivative with Mittag-Leffler kernel and consequences for control mechanisms. Results Phys. 2022, 35, 105304. [Google Scholar] [CrossRef]
- Lu, Z.; Yu, Y.; Chen, Y.; Ren, G.; Xu, C.; Wang, S. Stability analysis of a nonlocal SIHRDP epidemic model with memory effects. Nonlinear Dyn. 2022, 109, 121–141. [Google Scholar] [CrossRef]
- Bazan, J.G.; Le, Q.-T.; Zips, D. Radiobiology of Lung Cancer. In IASLC Thoracic Oncology, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 330–336. [Google Scholar]
- Loan, M.; Bhat, A. Effect of Over dispersion of Lethal Lesions on Cell Survival Curves. arXiv 2021. [Google Scholar] [CrossRef]
- Siam, F.M.; Grinfeld, M.; Bahar, A.; Rahman, H.A.; Ahmad, H.; Johar, F. A mechanistic model of high dose irradiation damage. Math. Comput. Simul. 2018, 151, 156–168. [Google Scholar] [CrossRef]
- Williams, J.P.; McBride, W.H. After the bomb drops: A new look at radiation-induced multiple organ dysfunction syndrome (MODS). Int. J. Irradiat. Biol. 2011, 87, 851–868. [Google Scholar] [CrossRef] [PubMed]
- Baar, M.; Coquille, L.; Mayer, H.; Hölzel, M.; Rogava, M.; Tüting, T.; Bovier, A. A stochastic model for immunotherapy of cancer. Sci. Rep. 2016, 6, 24169. [Google Scholar] [CrossRef] [PubMed]
- Eftimie, R.; Bramson, J.; Earn, D. Interactions between the immune system and cancer: A brief review of non-spatial mathematical models. Bull. Math. Biol. 2011, 73, 232. [Google Scholar] [CrossRef] [PubMed]
- Gupta, P.B.; Fillmore, C.M.; Jiang, G.; Shapira, S.D.; Tao, K.; Kuperwasser, C.; Lander, E.S. Stochastic state transitions give rise to phenotypic equilibrium in populations of cancer cells. Cell 2011, 146, 633644. [Google Scholar] [CrossRef] [PubMed]
- Durrett, R. Cancer modeling: A personal perspective. Not. AMS 2013, 60, 304309. [Google Scholar] [CrossRef]
- Mohseni-Salehi, F.S.; Zare-Mirakabad, F.; Sadeghi, M.; Ghafouri-Fard, S. A Stochastic Model of DNA Double-Strand Breaks Repair Throughout the Cell Cycle. Bull. Math. Biol. 2020, 82, 11. [Google Scholar] [CrossRef]
- Huether, S.E.; McCance, K.L. Understanding Pathophysiology-E-Book; Elsevier Health Sciences: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Li, L.; Chen, X.C.; Li, X.J.; Li, Z.H.; Jian, Y.; Wu, Y.Z.; Zhang, J.P.; Ren, M.; Zhang, B. Analytical model for total ionizing dose-induced excess base current in PNP BJTs. Microelectron. Reliab. 2020, 113, 113939. [Google Scholar] [CrossRef]
- Sazykina, T.G.; Kryshev, A.I. Simulation of population response to ionizing irradiation in an ecosystem with a limiting resource Model and analytical solutions. J. Environ. Radioact. 2016, 151, 50–57. [Google Scholar] [CrossRef]
- Widdicombe, T.; Borrelli, R.A. MCNP modelling of irradiation effects of the Dragonfly missions RTG on Titan II: Atmospheric ionization effects. Acta Astronaut. 2021, 186, 517–522. [Google Scholar] [CrossRef]
- Saeedian, M.; Khalighi, M.; Azimi-Tafreshi, N.; Jafari, G.R.; Ausloos, M. Memory effects on epidemic evolution: The susceptible-infected recovered epidemic model. Phys. Rev. E 2017, 95, 022409. [Google Scholar] [CrossRef]
- Rashid, H.; Siam, F.M.; Maan, N.; Abd Rahman, W.N.W. Ionizing Irradiation Effects Modelling in Cells Population with Gold Nanoparticles. Malays. J. Fundam. Appl. Sci. 2021, 17, 659–669. [Google Scholar] [CrossRef]
- Chakraverty, S.; Jena, R.M.; Jena, S.K. Time-fractional order biological systems with uncertain parameters. In Synthesis Lectures on Mathematics and Statistics; Springer: Berlin/Heidelberg, Germany, 2020; Volume 12, 160p. [Google Scholar]
- Anderson, D.R.; Camrud, E.; Ulness, D.J. On the nature of the conformable derivative and its applications to physics. arXiv 2018. [Google Scholar] [CrossRef]
- Jena, R.M.; Chakraverty, S.; Rezazadeh, H.; Domiri Ganji, D. On the solution of time-fractional dynamical model of Brusselator reaction-diffusion system arising in chemical reactions. Math. Methods Appl. Sci. 2020, 43, 3903–3913. [Google Scholar] [CrossRef]
- Al-khedhairi, A.; Elsadany, A.A.; Elsonbaty, A. Modelling immune systems based on Atangana-Baleanu fractional derivative. Chaos Solitons Fractals 2019, 129, 25–39. [Google Scholar] [CrossRef]
- Azkase, F.; Aženel, M.T.; Habbireeh, R. Mathematical Fractional-order mathematical modelling of cancer cells-cancer stem cells-immune system interaction with chemotherapy. Model. Numer. Simul. Appl. 2021, 1, 67–83. [Google Scholar]
- Ashraf, F.; Ahmad, A.; Saleem, M.U.; Farman, M.; Ahmad, M.O. Dynamical behavior of HIV immunology model with non-integer time fractional derivatives. Int. J. Adv. Appl. Sci. 2018, 5, 39–45. [Google Scholar] [CrossRef]
- Petras, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Kilbs, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Kumar, S.; Kumar, A.; Odibat, Z.M. A nonlinear fractional model to describe the population dynamics of two interacting species. Math. Methods Appl. Sci. 2017, 40, 4134–4148. [Google Scholar] [CrossRef]
- Zou, C.; Zhang, L.; Hu, X.; Wang, Z.; Wik, T.; Pecht, M. A review of fractional-order techniques applied to lithium-ion batteries, lead-acid batteries, and supercapacitors. J. Power Sources 2018, 390, 286–296. [Google Scholar] [CrossRef]
- Teodoro, G.S.; Machado, J.T.; De Oliveira, E.C. A review of definitions of fractional derivatives and other operators. J. Comput. Phys. 2019, 388, 195–208. [Google Scholar] [CrossRef]
- Abdeljawad, T. On Riemann and Caputo fractional differences. Comput. Math. Appl. 2011, 62, 1602–1611. [Google Scholar] [CrossRef]
- Mainardi, F. Why the Mittag-Leffler function can be considered the queen function of the fractional calculus? Entropy 2020, 22, 1359. [Google Scholar] [CrossRef]
- Ahmadova, A.; Huseynov, I.T.; Fernandez, A.; Mahmudov, N.I. Trivariate Mittag-Leffler functions used to solve multi-order systems of fractional differential equations. Commun. Nonlinear Sci. Numer. Simul. 2021, 97, 105735. [Google Scholar] [CrossRef]
- Erdelyi, A. Higher Transcendental Functions; McGRAW-HILL Book Company: New York, NY, USA, 1953; p. 59. [Google Scholar]
- Nasir, M.H.; Siam, F.M. Simulation and sensitivity analysis on the parameter of non-targeted irirradiation effects model. J. Teknol. 2019, 81, 133–142. [Google Scholar] [CrossRef]
- Singh, S.K.; Wang, M.; Staudt, C.; Iliakis, G. Post-irradiation chemical processing of DNA damage generates double-strand breaks in cells already engaged in repair. Nucleic Acids Res. 2011, 39, 8416–8429. [Google Scholar] [CrossRef] [PubMed]
- Antonelli, F.; Campa, A.; Esposito, G.; Giardullo, P.; Belli, M.; Dini, V.; Tabocchini, M.A. Induction and repair of DNA DSB as revealed by H2AX phosphorylation foci in human fibroblasts exposed to low-and high-LET irradiation: Relationship with early and delayed reproductive cell death. Irradiat. Res. 2015, 183, 417–431. [Google Scholar] [CrossRef] [PubMed]
- Herrera Ortiz, A.F.; Fernandez Beaujon, L.J.; Garcia Villamizar, S.Y.; Fonseca Lpez, F.F. Magnetic resonance versus computed tomography for the detection of retroperitoneal lymph node metastasis due to testicular cancer: A systematic literature review. Eur. J. Radiol. Open 2021, 8, 100372. [Google Scholar] [CrossRef]
- Understanding Cancer, National Cancer Institute. Available online: https://www.cancer.gov/publications/dictionaries/geneticsdictionary/def/chromosome (accessed on 21 February 2023).
- Garrappa, R.; Giusti, A.; Mainardi, F. Variable-order fractional calculus: A change of perspective. Commun. Nonlinear Sci. Numer. Simul. 2021, 102, 105904. [Google Scholar] [CrossRef]
- Brandibur, O.; Garrappa, R.; Kaslik, E. Stability of Systems of Fractional-Order Differential Equations with Caputo Derivatives. Mathematics 2021, 9, 914. [Google Scholar] [CrossRef]
- Haghani, F.K.; Soleymani, F. An improved Schulz-type iterative method for matrix inversion with application. Trans. Inst. Meas. Control 2014, 36, 983–991. [Google Scholar] [CrossRef]
- Anelone, A.J.; Spurgeon, S.K. Modelling and Simulation of the Dynamics of the Antigen-Specific T Cell Response Using Variable Structure Control Theory. PLoS ONE 2016, 18, e0166163. [Google Scholar] [CrossRef] [PubMed]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Kusunoki, Y.; Hayashi, T. Long-lasting alterations of the immune system by ionizing radiation exposure: Implications for disease development among atomic bomb survivors. Int. J. Radiat. Biol. 2008, 84, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Manda, K.; Glasow, A.; Paape, D.; Hildebrandt, G. Effects of ionizing radiation on the immune system with special emphasis on the interaction of dendritic and T cells. Front. Oncol. 2012, 2, 102. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, D.; Coates, P.J.; Lorimore, S.A.; Wright, E.G. Responses to ionizing radiation mediated by inflammatory mechanisms. J. Pathol. 2014, 232, 289–299. [Google Scholar] [CrossRef] [PubMed]
- Derer, A.; Frey, B.; Fietkau, R.; Gaipl, U.S. Immune-modulating properties of ionizing radiation: Rationale for the treatment of cancer by combination radiotherapy and immune checkpoint inhibitors. Cancer Immunol. Immunother. 2016, 65, 779–786. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).