Analyzing Both Fractional Porous Media and Heat Transfer Equations via Some Novel Techniques

Abstract

It has been increasingly obvious in recent decades that fractional calculus (FC) plays a key role in many disciplines of applied sciences. Fractional partial differential equations (FPDEs) accurately model various natural physical phenomena and many engineering problems. For this reason, the analytical and numerical solutions to these issues are seriously considered, and different approaches and techniques have been presented to address them. In this work, the FC is applied to solve and analyze the time-fractional heat transfer equation as well as the nonlinear fractional porous media equation with cubic nonlinearity. The idea of solving these equations is based on the combination of the Yang transformation (YT), the homotopy perturbation method (HPM), and the Adomian decomposition method (ADM). These combinations give rise to two novel methodologies, known as the homotopy perturbation transform method (HPTM) and the Yang tranform decomposition method (YTDM). The obtained results show the significance of the accuracy of the suggested approaches. Solutions in various fractional orders are found and discussed. It is noted that solutions at various fractional orders lead to an integer-order solution. The application of the current methodologies to other nonlinear fractional issues in other branches of applied science is supported by their straightforward and efficient process. In addition, the proposed solution methods can help many plasma physics researchers in interpreting the theoretical and practical results.

1. Introduction

Fractional calculus (FC) has a significant advantage when it comes to simulating physical problems with whole-memory effects. In applied mathematics, fractional derivatives are a useful tool for relating non-integer-order derivatives as well as integrals. Numerous studies have been conducted in many fields of science, physics, and engineering concerning this branch due to its importance in modeling many realistic problems. In reality, the novel features of this distinguished branch appear in several disciplines, including fluid dynamics, chemistry, applied mathematics, physics of plasma, astrophysics, mathematical biology, control theory, image processing, controlled thermonuclear fusion, and many other fields. Fractional-order integrals and derivatives have become a significant new mathematical tool that helps in solving many problems that arise in engineering, physics, and nature. Podlubny [1] provided comprehensive details on arbitrary-order differential equations (DEs). A great book on the basics and details of FC and DEs was written by Miller and Ross [2]. There are also many research works on this very important topic in modeling several nonlinear phenomena in physics, especially the physics of plasmas. Singh [3] investigated a fractional-order blood alcohol model. Caputo presented the basic characteristics of the FC [4]. The topic of singular kernels connected to fractional derivatives was studied by Caputo, and Fabrizio [5]. New aspects of fractional derivatives were explained by Caputo, and Fabrizio [4].

Both nonlinear ordinary DEs (ODEs) and partial DEs (PDEs) are primarily applied to describe most physical phenomena, either simple or complex, that appear in reality [6,7,8] via mathematical modeling, such as many nonlinear phenomena that have been studied and analyzed in different models of plasma physics [9,10,11,12,13,14]. The mathematical modeling of numerous natural processes benefits greatly from the use of nonlinear fractional DEs (NLFDEs). The essential feature of fractional derivatives is their nonlocality, which emphasizes how the future state arises from both current and all previous states [15,16,17]. The investigation of nonlinear ODEs is an essential way of determining the behavior of the system, which has attracted the interest of many researchers (including scientists and engineers). Fractional PDEs are significant mathematical models that accurately represent a variety of complex processes in numerous scientific disciplines, such as fractional diffusion equations occurring in oil pollution [18], fractional Fornberg–Whitham equations [19], fractional Helmholtz equations [20], local fractional modified Zakharov–Kuznetsov (mZK) equations [21], fractional local damped wave and dissipative equations [22], fractional nonlinear Boussinesq Equations [23], time-fractional Navier–Stokes equations [24], fractional third-order Burgers and Korteweg–De Vries (KdV) equations [25], nonlinear Schrodinger (NLS) equations [26], Maxwell’s equations [27], fractional advection–dispersion equations [27], time-fractional Fisher’s equations [28], nonlinear biological predator–prey population systems [29], fractional-order Kaup–Kupershmidt equations [30], and fractional-order Gardner and Cahn–Hilliard equations [31].

Mathematicians have constructed many numerical and analytical strategies for solving and analyzing integer order DEs and FPDEs because of the aforementioned applications [32,33,34,35,36]. For example, Mehdi Dehghan et al., in [37], applied the homotopy analysis method (HAM) for solving the fractional KdV, Burgers, BBM–Burgers, coupled KdV, cubic Boussinesq, and Boussinesq-like equations. Mohamed et al. [38] applied Elzaki Transformation HPM (ETHPM) to determine a series form of solutions of different NLFDEs. Similarly, Mounirah Areshi et al. [39] applied the variational iteration transform method (VITM) to solve fractional-order Newell–Whitehead–Segel equations. An optimal HAM has been applied by Randhir Singh [40] to solve non-isothermal reaction–diffusion model equations with a spherical catalyst. With the help of the modified trial equation method, Hasan Bulut and Yusuf Pandir [41] solved the time-fractional Sharma–Tasso–Olever (STO) equation. Sheng Zhang et al. [42] used the modified extended Fan sub-equation technique to solve the (3+1)-dimensional Kadomstev–Petviashvili (KP) equation. Analytic results of the fractional-order diffusion equation have been investigated by applying the Yang transformation (YT) decomposition technique [43]. Furthermore, the numerical solutions of the multi-dimensional time-fractional telegraphic equation have been analyzed and discussed using the reduced differential transform method [44]. Moreover, Azzh Saad Alshehry et al. [45] developed natural transformation based on the decomposition method for analyzing a fractional Kuramoto–Sivashinsky equation.

In nonlinear flow studies concerning heat and mass transfer, diffusion, porous media flow, biology, and viscosity, as well as other related subjects, boundary-layer theory is a crucial component; for example, the porous media equation, sometimes known as a nonlinear heat equation, commonly exists, and more effort is needed to analyze them via simplified mathematical approaches [46,47,48,49]. Current research aims to present novel methods for solving the fractional porous media equation and the non-linear time-fractional heat transfer equation that features cubic non-linearity using the combination between YT, HPM, and ADM. Adomian introduced the ADM in 1980 as a powerful tool for resolving differential equations describing physical phenomena [50]. ADM is additionally altered using the YT. As a result, the Yang transformation decomposition method (YTDM), a novel technique, has been constructed.

The fundamental elements of both YT and ADM are included in the YTDM. This method is useful and effective for analyzing PDEs of initial and boundary value problems. He [51,52] created HPM by combining conventional homotopy and perturbation to address a variety of physical issues. It is important to note that the HPM is applied without any discretization, restricted assumptions, or transformation and is error-free concerning rounding. Due to the challenges raised by the nonlinear variables, the YT is completely unable to handle nonlinear equations. The well-known YT method is paired with the homotopy perturbation approach to develop a highly efficient method known as the homotopy perturbation transform method (HPTM) for dealing with numerous nonlinear issues. The advantages of the proposed techniques are their capability of combining two powerful approaches for obtaining exact and approximate analytical solutions to nonlinear equations. It is important to keep in mind that the suggested methods can perform better in general as they need less computational work than the alternative methods while keeping a high level of numerical precision; the size reduction amounts to an improvement in the performance of the approaches.

The following summarises this work’s structure: In Section 2, we present a few fundamental elements of calculus theory. In Section 3 and Section 4, the general solution is obtained using the HPTM and YTDM algorithms, and Section 5 provides the convergence analysis of these suggested techniques. In Section 6, we demonstrate the reliability and efficacy of both strategies. In Section 7, the conclusion is presented.

2. Preliminary Concepts

Definition 1.

The The Caputo definition of order ς is described as [39,53]

$$\begin{array}{c}\hfill D_{\vartheta }^{\varsigma }\zeta (ß)=\frac{1}{\mathsf{\Gamma }(ı-\varsigma )}{\int }_0^{ß}{(ß-j)}^{ı-\varsigma -1}{\zeta }^{\left(ı\right)}\left(j\right)dj,ı-1<\varsigma \le ı,ı\in N.\end{array}$$

(1)

Definition 2.

YT is defined by [43,54]

$$Y\left\{\zeta (ß)\right\}=M\left(u\right)={\int }_0^{\infty }{e}^{\frac{-ß}{u}}\zeta (ß)dß,ß>0,$$

(2)

and its inverse reads

$$Y^{-1}\left\{M\left(u\right)\right\}=\zeta (ß).$$

(3)

Definition 3.

The YT inverse reads [43,54]

$$Y^{-1}\left[Y\left(u\right)\right]=\zeta (ß)=\frac{1}{2\pi \iota }{\int }_{\varsigma -\iota \infty }^{\varsigma +\iota \infty }\zeta \left(\frac{1}{u}\right)e^{uß}udu=\mathsf{\Sigma }residuesof\zeta \left(\frac{1}{u}\right)e^{uß}u.$$

Definition 4.

The derivative of fractional order in YT reads [43,54]

$$Y\left\{{\zeta }^{\varsigma }(ß)\right\}=\frac{M\left(u\right)}{u^{\varsigma }}-\sum _{ı=0}^{n-1}\frac{{\zeta }^{ı}\left(0\right)}{u^{\varsigma -(ı+1)}},n-1<\varsigma \le n.$$

(4)

3. Fundamental Plan of HPTM

To discuss the main plan of the suggested scheme, we examine the following FPDE related to the Caputo derivative:

$$D_{ß}^{\varsigma }\zeta (\chi ,ß)={\mathcal{M}}_1\left[\chi \right]\zeta (\chi ,ß)+{\mathcal{N}}_1\left[\chi \right]\zeta (\chi ,ß),0<\varsigma \le 1,$$

(5)

with initial solution

$$\zeta (\chi ,0)=\xi \left(\chi \right).$$

Here, $D_{ß}^{\varsigma }=\frac{{\partial }^{\varsigma }}{\partial {ß}^{\varsigma }}$ denotes the fractional derivative in a Caputo manner, and ${\mathcal{M}}_1\left[\chi \right]$ and ${\mathcal{N}}_1\left[\chi \right]$ represent the general differential operators.

Applying the YT, we obtain

$$Y\left[D_{ß}^{\varsigma }\zeta (\chi ,ß)\right]=Y[{\mathcal{M}}_1\left[\chi \right]\zeta (\chi ,ß)+{\mathcal{N}}_1\left[\chi \right]\zeta (\chi ,ß)],$$

(6)

$$\frac{1}{u^{\varsigma }}\{M\left(u\right)-u\zeta (\chi ,0)\}=Y[{\mathcal{M}}_1\left[\chi \right]\zeta (\chi ,ß)+{\mathcal{N}}_1\left[\chi \right]\zeta (\chi ,ß)].$$

(7)

The simplified form reads

$$M\left(u\right)=u\zeta (\chi ,0)+u^{\varsigma }Y[{\mathcal{M}}_1\left[\chi \right]\zeta (\chi ,ß)+{\mathcal{N}}_1\left[\chi \right]\zeta (\chi ,ß)].$$

(8)

By employing the inverse of YT, we have

$$\zeta (\chi ,ß)=\zeta (\chi ,0)+Y^{-1}\left[u^{\varsigma }Y[{\mathcal{M}}_1\left[\chi \right]\zeta (\chi ,ß)+{\mathcal{N}}_1\left[\chi \right]\zeta (\chi ,ß)]\right].$$

(9)

In terms of HPM, the basic solution in a power series reads

$$\zeta (\chi ,ß)=\sum _{ı=0}^{\infty }{ϵ}^{ı}{\zeta }_{ı}(\chi ,ß).$$

(10)

with homotopy parameter $ϵ\in [0,1]$.

The nonlinear term reads

$${\mathcal{N}}_1\left[\chi \right]\zeta (\chi ,ß)=\sum _{ı=0}^{\infty }{ϵ}^{ı}{H}_{ı}\left(\zeta \right).$$

(11)

Accordingly, the following polynomials are obtained

$$H_{ı}({\zeta }_0,{\zeta }_1,\cdots ,{\zeta }_n)=\frac{1}{\mathsf{\Gamma }(n+1)}{D}_{ϵ}^{ı}{\left[{\mathcal{N}}_1\left(\sum _{ı=0}^{\infty }{ϵ}^i{\zeta }_i\right)\right]}_{ϵ=0},$$

(12)

where $D_{ϵ}^{ı}=\frac{{\partial }^{ı}}{\partial {ϵ}^{ı}}.$

Substituting Equations (10) and (11) into Equation (9), we obtain

$$\sum _{ı=0}^{\infty }{ϵ}^{ı}{\zeta }_{ı}(\chi ,ß)=\zeta (\chi ,0)+ϵ\times \left(Y^{-1}\left[u^{\varsigma }Y\{{\mathcal{M}}_1\sum _{ı=0}^{\infty }{ϵ}^{ı}{\zeta }_{ı}(\chi ,ß)+\sum _{ı=0}^{\infty }{ϵ}^{ı}{H}_{ı}\left(\zeta \right)\}\right]\right).$$

(13)

Equating similar coefficients of $ϵ$ in the above equation, we have

$$\begin{array}{cc}\hfill & {ϵ}^0:{\zeta }_0(\chi ,ß)=\zeta (\chi ,0),\hfill \\ \hfill & {ϵ}^1:{\zeta }_1(\chi ,ß)=Y^{-1}\left[u^{\varsigma }Y({\mathcal{M}}_1\left[\chi \right]{\zeta }_0(\chi ,ß)+H_0\left(\zeta \right))\right],\hfill \\ \hfill & {ϵ}^2:{\zeta }_2(\chi ,ß)=Y^{-1}\left[u^{\varsigma }Y({\mathcal{M}}_1\left[\chi \right]{\zeta }_1(\chi ,ß)+H_1\left(\zeta \right))\right],\hfill \\ \hfill & .\hfill \\ \hfill & .\hfill \\ \hfill & .\hfill \\ \hfill & {ϵ}^{ı}:{\zeta }_{ı}(\chi ,ß)=Y^{-1}\left[u^{\varsigma }Y({\mathcal{M}}_1\left[\chi \right]{\zeta }_{ı-1}(\chi ,ß)+H_{ı-1}\left(\zeta \right))\right],\hfill \\ \hfill ı>0,ı\in N.\end{array}$$

(14)

Finally, we approximate the analytical solution in the following series form:

$$\zeta (\chi ,ß)=\underset{M\to \infty }{lim}\sum _{ı=1}^M{\zeta }_{ı}(\chi ,ß).$$

(15)

4. The Fundamental Idea of the YTDM

The principal scheme of the current approach is based on studying the FPDE associated with the Caputo derivative as follows:

$$D_{ß}^{\varsigma }\zeta (\chi ,ß)={\mathcal{M}}_1(\chi ,ß)+{\mathcal{N}}_1(\chi ,ß),0<\varsigma \le 1,$$

(16)

with initial source

$$\zeta (\chi ,0)=\xi \left(\chi \right).$$

Here, the fractional derivative in the Caputo manner is denoted by $D_{ß}^{\varsigma }=\frac{{\partial }^{\varsigma }}{\partial {ß}^{\varsigma }}$, and the general differential operators are represented by ${\mathcal{M}}_1$ and ${\mathcal{N}}_1$.

Applying the YT, we obtain

$$\begin{array}{cc}\hfill & Y\left[D_{ß}^{\varsigma }\zeta (\chi ,ß)\right]=Y[{\mathcal{M}}_1(\chi ,ß)+{\mathcal{N}}_1(\chi ,ß)],\hfill \\ \hfill & \frac{1}{u^{\varsigma }}\{M\left(u\right)-u\zeta (\chi ,0)\}=Y[{\mathcal{M}}_1(\chi ,ß)+{\mathcal{N}}_1(\chi ,ß)].\hfill \end{array}$$

(17)

The simplified form reads

$$M\left(u\right)=u\zeta (\chi ,0)+u^{\varsigma }Y[{\mathcal{M}}_1(\chi ,ß)+{\mathcal{N}}_1(\chi ,ß)],$$

(18)

By employing the inverse of the YT, we obtain

$$\zeta (\chi ,ß)=\zeta (\chi ,0)+Y^{-1}[u^{\varsigma }Y[{\mathcal{M}}_1(\chi ,ß)+{\mathcal{N}}_1(\chi ,ß)].$$

(19)

The series form solution of $\zeta (\chi ,ß)$ reads

$$\zeta (\chi ,ß)=\sum _{m=0}^{\infty }{\zeta }_m(\chi ,ß).$$

(20)

In Equation (19), the nonlinear term is put in as

$${\mathcal{N}}_1(\chi ,ß)=\sum _{m=0}^{\infty }{\mathcal{A}}_m\left(\zeta \right).$$

(21)

with

$${\mathcal{A}}_m\left({\zeta }_0,{\zeta }_1,{\zeta }_2,\cdots ,{\zeta }_m\right)=\frac{1}{m!}{\left[\frac{{\partial }^m}{\partial {\ell }^m}\left\{{\mathcal{N}}_1\left(\sum _{m=0}^{\infty }{\ell }^m{\zeta }_m\right)\right\}\right]}_{\ell =0},m=0,1,2,\cdots$$

(22)

The substitution of Equations (20) and (21) into Equation (19) yields

$$\sum _{m=0}^{\infty }{\zeta }_m(\chi ,ß)=\zeta (\chi ,0)+Y^{-1}{u}^{\varsigma }\left[Y\left\{{\mathcal{M}}_1\left(\sum _{m=0}^{\infty }{\zeta }_m(\chi ,ß)\right)+\sum _{m=0}^{\infty }{\mathcal{A}}_m\left(\zeta \right)\right\}\right].$$

(23)

Similarly,

$${\zeta }_0(\chi ,ß)=\zeta (\chi ,0),$$

(24)

$${\zeta }_1(\chi ,ß)=Y^{-1}\left[u^{\varsigma }Y\{{\mathcal{M}}_1\left({\zeta }_0\right)+{\mathcal{A}}_0\}\right],$$

Generally, for $m\ge 1$, we obtain

$${\zeta }_{m+1}(\chi ,ß)=Y^{-1}\left[u^{\varsigma }Y\{{\mathcal{M}}_1\left({\zeta }_m\right)+{\mathcal{A}}_m\}\right].$$

5. Convergence Analysis

In this part, the suggested techniques of convergence analysis are discussed

Theorem 1.

Suppose that the exact solution to Equation (5) is $G(\chi ,ß)$, and let $G(\chi ,ß)$, $G_n(\chi ,ß)\in H$ and $\alpha \in (0,1)$, where H represents the Hilbert space. The obtained solution ${\sum }_{q=0}^{\infty }{G}_q(\chi ,ß)$ converges $G(\chi ,ß)$ if $G_q(\chi ,ß)\le G_{q-1}(\chi ,ß)\forall q>A$, i.e., for any $\omega >0\exists A>0$, such that $\left|\right|G_{q+n}(\chi ,ß)\left|\right|\le \beta ,\forall m,n\in N.$

Proof. 

We take a sequence of ${\sum }_{q=0}^{\infty }{G}_q(\chi ,ß).$

$$\begin{array}{cc}\hfill C_0(\chi ,ß)=& G_0(\chi ,ß),\hfill \\ \hfill C_1(\chi ,ß)=& G_0(\chi ,ß)+G_1(\chi ,ß),\hfill \\ \hfill C_2(\chi ,ß)=& G_0(\chi ,ß)+G_1(\chi ,ß)+G_2(\chi ,ß),\hfill \\ \hfill C_3(\chi ,ß)=& G_0(\chi ,ß)+G_1(\chi ,ß)+G_2(\chi ,ß)+G_3(\chi ,ß),\hfill \\ \hfill & ⋮\hfill \\ \hfill C_q(\chi ,ß)=& G_0(\chi ,ß)+G_1(\chi ,ß)+G_2(\chi ,ß)+\cdots +G_q(\chi ,ß),\hfill \end{array}$$

(25)

We must demonstrate that $C_q(\chi ,ß)$ forms a “Cauchy sequence” in order to achieve the desired outcome. Additionally, let us take

$$\begin{array}{cc}\hfill \left|\right|C_{q+1}(\chi ,ß)-C_q(\chi ,ß)\left|\right|& =\left|\right|G_{q+1}(\chi ,ß)\left|\right|\le \alpha \left|\right|G_q(\chi ,ß)\left|\right|\le {\alpha }^2\left|\right|G_{q-1}(\chi ,ß)\left|\right|\le {\alpha }^3\left|\right|G_{q-2}(\chi ,ß)\left|\right|\cdots \hfill \\ \hfill & \le {\alpha }_{q+1}\left|\right|G_0(\chi ,ß)\left|\right|.\hfill \end{array}$$

(26)

For $q,n\in N$, we have

$$\begin{array}{cc}\hfill \left|\right|C_q(\chi ,ß)-C_n(\chi ,ß)\left|\right|=& \left|\right|G_{q+n}(\chi ,ß)\left|\right|=\left|\right|C_q(\chi ,ß)-C_{q-1}(\chi ,ß)+(C_{q-1}(\chi ,ß)-C_{q-2}(\chi ,ß))\hfill \\ \hfill & +(C_{q-2}(\chi ,ß)-C_{q-3}(\chi ,ß))+\cdots +(C_{n+1}(\chi ,ß)-C_n(\chi ,ß))\left|\right|\hfill \\ \hfill \le & \left|\right|C_q(\chi ,ß)-C_{q-1}(\chi ,ß)\left|\right|+\left|\right|(C_{q-1}(\chi ,ß)-C_{q-2}(\chi ,ß))\left|\right|\hfill \\ \hfill & +\left|\right|(C_{q-2}(\chi ,ß)-C_{q-3}(\chi ,ß))\left|\right|+\cdots +\left|\right|(C_{n+1}(\chi ,ß)-C_n(\chi ,ß))\left|\right|\hfill \\ \hfill \le & {\alpha }^q\left|\right|G_0(\chi ,ß)\left|\right|+{\alpha }^{q-1}\left|\right|G_0(\chi ,ß)\left|\right|+\cdots +{\alpha }^{q+1}\left|\right|G_0(\chi ,ß)\left|\right|\hfill \\ \hfill =& \left|\right|G_0(\chi ,ß)\left|\right|({\alpha }^q+{\alpha }^{q-1}+{\alpha }^{q+1})\hfill \\ \hfill =& \left|\right|G_0(\chi ,ß)\left|\right|\frac{1-{\alpha }^{q-n}}{1-{\alpha }^{q+1}}{\alpha }^{n+1}.\hfill \end{array}$$

(27)

As $0<\alpha <1$, and $G_0(\chi ,ß)$ are bound, we take $\beta =1-\alpha /(1-{\alpha }_{q-n}){\alpha }^{n+1}\left|\right|G_0(\chi ,ß)\left|\right|$, and we obtain

$$\left|\right|G_{q+n}(\chi ,ß)\left|\right|\le \beta ,\forall q,n\in N.$$

(28)

Hence, ${\left\{G_q(\chi ,ß)\right\}}_{q=0}^{\infty }$ makes a “Cauchy sequence” in H. It proves that the sequence ${\left\{G_q(\chi ,ß)\right\}}_{q=0}^{\infty }$ is a convergent sequence with the limit ${lim}_{q\to \infty }{G}_q(\chi ,ß)=G(\chi ,ß)$ for $\exists G(\chi ,ß)\in \mathcal{H}$, which completes the proof. □

Theorem 2.

Let us assume that ${\sum }_{h=0}^k{G}_h(\chi ,ß)$ is finite and that $G(\chi ,ß)$ reflects the series solution that was found. Assuming $\alpha >0$ such that $\left|\right|G_{h+1}(\chi ,ß)\left|\right|\le \left|\right|G_h(\chi ,ß)\left|\right|$, the maximum absolute error is given by the following relation.

$$\left|\right|G(\chi ,ß)-\sum _{h=0}^k{G}_h(\chi ,ß)\left|\right|<\frac{{\alpha }^{k+1}}{1-\alpha }\left|\right|G_0(\chi ,ß)\left|\right|.$$

(29)

Proof. 

Suppose ${\sum }_{h=0}^k{G}_h(\chi ,ß)$ is finite which implies that ${\sum }_{h=0}^k{G}_h(\chi ,ß)<\infty$.

Let us consider

$$\begin{array}{cc}\hfill \left|\right|G(\chi ,ß)-\sum _{h=0}^k{G}_h(\chi ,ß)\left|\right|=& \left|\right|\sum _{h=k+1}^{\infty }{G}_h(\chi ,ß)\left|\right|\hfill \\ \hfill \le & \sum _{h=k+1}^{\infty }\left|\right|G_h(\chi ,ß)\left|\right|\hfill \\ \hfill \le & \sum _{h=k+1}^{\infty }{\alpha }^h\left|\right|G_0(\chi ,ß)\left|\right|\hfill \\ \hfill \le & {\alpha }^{k+1}(1+\alpha +{\alpha }^2+\cdots )\left|\right|G_0(\chi ,ß)\left|\right|\hfill \\ \hfill \le & \frac{{\alpha }^{k+1}}{1-\alpha }\left|\right|G_0(\chi ,ß)\left|\right|.\hfill \end{array}$$

(30)

which completes the proof of theorem. □

Theorem 3.

The result of (16) is unique when $0<({\phi }_1+{\phi }_2)\left(\frac{{ß}^{\varsigma }}{\mathsf{\Gamma }(\varsigma +1)}\right)<1.$

Proof. 

Let $H=\left(C\right[J],||.|\left|\right)$ with the norm $\left|\right|\varphi (ß)\left|\right|={max}_{ß\in J}\left|\varphi (ß)\right|$ be Banach space, which is ∀-continuous function on J. Let $I:H\to H$ be a non-linear mapping, where

$${\zeta }_{l+1}^C={\zeta }_0^C+Y^{-1}\left[p(\varsigma ,\upsilon ,\varpi )Y[\mathcal{M}\left({\zeta }_l(\chi ,ß)\right)+\mathcal{N}\left({\zeta }_l(\chi ,ß)\right)]\right],l\ge 0.$$

Suppose that $|\mathcal{M}\left(\zeta \right)-\mathcal{M}\left({\zeta }^{*}\right)|<{\phi }_1|\zeta -{\zeta }^{*}|$ and $|\mathcal{N}\left(\zeta \right)-\mathcal{N}\left({\zeta }^{*}\right)|<{\phi }_2|\zeta -{\zeta }^{*}|$, where $\zeta :=\zeta (\chi ,ß)$ and ${\zeta }^{*}:={\zeta }^{*}(\chi ,ß)$ are are two different function values and ${\phi }_1$,${\phi }_2$ are Lipschitz constants.

$$\begin{array}{cc}\hfill \left|\right|I\zeta -I{\zeta }^{*}\left|\right|& \le ma{x}_{t\in J}|Y^{-1}[p(\varsigma ,\upsilon ,\varpi )Y[\mathcal{M}\left(\zeta \right)-\mathcal{M}\left({\zeta }^{*}\right)]\hfill \\ \hfill & +p(\varsigma ,\upsilon ,\varpi )Y[\mathcal{N}\left(\zeta \right)-\mathcal{N}\left({\zeta }^{*}\right)]\left|\right]\hfill \\ \hfill & \le ma{x}_{ß\in J}[{\phi }_1{Y}^{-1}\left[p(\varsigma ,\upsilon ,\varpi )Y\right[|\zeta -{\zeta }^{*}\left|\right]]\hfill \\ \hfill & +{\phi }_2{Y}^{-1}\left[p(\varsigma ,\upsilon ,\varpi )Y\right[|\zeta -{\zeta }^{*}\left|\right]\left]\right]\hfill \\ \hfill & \le ma{x}_{t\in J}({\phi }_1+{\phi }_2)\left[Y^{-1}\left[p(\varsigma ,\upsilon ,\varpi )Y\right|\zeta -{\zeta }^{*}\left|\right]\right]\hfill \\ \hfill & \le ({\phi }_1+{\phi }_2)\left[Y^{-1}\left[p(\varsigma ,\upsilon ,\varpi )Y\right||\zeta -{\zeta }^{*}\left|\right|]\right]\hfill \\ \hfill & =({\phi }_1+{\phi }_2)\left(\frac{{ß}^{\varsigma }}{\mathsf{\Gamma }(\varsigma +1)}\right)\left|\right|\zeta -{\zeta }^{*}\left|\right|,\hfill \end{array}$$

(31)

where I is a contraction as $0<({\phi }_1+{\phi }_2)\left(\frac{{ß}^{\varsigma }}{\mathsf{\Gamma }(\varsigma +1)}\right)<1$. From Banach’s fixed-point theorem, the result of (16) is unique. □

Theorem 4.

The result of (16) is convergent.

Proof. 

Let ${\zeta }_m={\sum }_{r=0}^m{\zeta }_r(\chi ,ß)$. To show that ${\zeta }_m$ is a Cauchy sequence in H, let

$$\begin{array}{cc}\hfill \left|\right|{\zeta }_m-{\zeta }_n\left|\right|& =ma{x}_{ß\in J}\left|\sum _{r=n+1}^m{\zeta }_r\right|,n=1,2,3,\cdots \hfill \\ \hfill & \le ma{x}_{ß\in J}\left|Y^{-1}\left[p(\varsigma ,\upsilon ,\varpi )Y\left[\sum _{r=n+1}^m(\mathcal{M}\left({\zeta }_{r-1}\right)+\mathcal{N}\left({\zeta }_{r-1}\right))\right]\right]\right|\hfill \\ \hfill & =ma{x}_{ß\in J}\left|Y^{-1}\left[p(\varsigma ,\upsilon ,\varpi )Y\left[\sum _{r=n+1}^{m-1}(\mathcal{M}\left({\zeta }_r\right)+\mathcal{N}\left({\zeta }_r\right))\right]\right]\right|\hfill \\ \hfill & \le ma{x}_{ß\in J}\left|Y^{-1}\left[p(\varsigma ,\upsilon ,\varpi )Y\left[(\mathcal{M}\left({\zeta }_{m-1}\right)-\mathcal{M}\left({\zeta }_{n-1}\right)+\mathcal{N}\left({\zeta }_{m-1}\right)-\mathcal{N}\left({\zeta }_{n-1}\right))\right]\right]\right|\hfill \\ \hfill & \le {\phi }_{1}ma{x}_{ß\in J}\left|Y^{-1}\left[p(\varsigma ,\upsilon ,\varpi )Y\left[(\mathcal{M}\left({\zeta }_{m-1}\right)-\mathcal{M}\left({\zeta }_{n-1}\right))\right]\right]\right|\hfill \\ \hfill & +{\phi }_{2}ma{x}_{ß\in J}\left|Y^{-1}\left[p(\varsigma ,\upsilon ,\varpi )Y\left[(\mathcal{N}\left({\zeta }_{m-1}\right)-\mathcal{N}\left({\zeta }_{n-1}\right))\right]\right]\right|\hfill \\ \hfill & =({\phi }_1+{\phi }_2)\left(\frac{{ß}^{\varsigma }}{\mathsf{\Gamma }(\varsigma +1)}\right)\left|\right|{\zeta }_{m-1}-{\zeta }_{n-1}\left|\right|.\hfill \end{array}$$

(32)

Let $m=n+1$; then,

$$\begin{array}{c}\hfill \left|\right|{\zeta }_{n+1}-{\zeta }_n\left|\right|\le \phi \left|\right|{\zeta }_n-{\zeta }_{n-1}\left|\right|\le {\phi }^2\left|\right|{\zeta }_{n-1}{\zeta }_{n-2}\left|\right|\le \cdots \le {\phi }^n\left|\right|{\zeta }_1-{\zeta }_0\left|\right|,\end{array}$$

(33)

where $\phi =({\phi }_1+{\phi }_2)\left(\frac{{ß}^{\varsigma }}{\mathsf{\Gamma }(\varsigma +1)}\right)$. Similarly, we have

$$\begin{array}{cc}\hfill \left|\right|{\zeta }_m-{\zeta }_n\left|\right|& \le \left|\right|{\zeta }_{n+1}-{\zeta }_n\left|\right|+\left|\right|{\zeta }_{n+2}{\zeta }_{n+1}\left|\right|+\cdots +\left|\right|{\zeta }_m-{\zeta }_{m-1}\left|\right|,\hfill \\ \hfill & ({\phi }^n+{\phi }^{n+1}+\cdots +{\phi }^{m-1})\left|\right|{\zeta }_1-{\zeta }_0\left|\right|\hfill \\ \hfill & \le {\phi }^n\left(\frac{1-{\phi }^{m-n}}{1-\phi }\right)\left|\right|{\zeta }_1\left|\right|,\hfill \end{array}$$

(34)

As $0<\phi <1$, we obtain $1-{\phi }^{m-n}<1$. Therefore,

$$\begin{array}{c}\hfill \left|\right|{\zeta }_m-{\zeta }_n\left|\right|\le \frac{{\phi }^n}{1-\phi }ma{x}_{ß\in J}\left|\right|{\zeta }_1\left|\right|.\end{array}$$

(35)

Since $\left|\right|{\zeta }_1\left|\right|<\infty ,\left|\right|{\zeta }_m-{\zeta }_n\left|\right|\to 0$ when $n\to \infty$. As a result, ${\zeta }_m$ is a Cauchy sequence in H, implying that the series ${\zeta }_m$ is convergent. □

6. Numerical Problems

Example 1.

Here, we consider the following fractional porous media Equation [55]:

$$\frac{{\partial }^{\varsigma }\zeta (\chi ,ß)}{\partial {ß}^{\varsigma }}=\frac{\partial }{\partial \chi }\left(\zeta (\chi ,ß)\frac{\partial \zeta (\chi ,ß)}{\partial \chi }\right),$$

(36)

with the initial condition

$$\zeta (\chi ,0)=\chi$$

Applying the YT yields

$$Y\left(\frac{{\partial }^{\varsigma }\zeta }{\partial {ß}^{\varsigma }}\right)=Y\left[\frac{\partial }{\partial \chi }\left(\zeta (\chi ,ß)\frac{\partial \zeta (\chi ,ß)}{\partial \chi }\right)\right],$$

(37)

The simplified form reads

$$\frac{1}{u^{\varsigma }}\{M\left(u\right)-u\zeta (\chi ,0)\}=Y\left[\frac{\partial }{\partial \chi }\left(\zeta (\chi ,ß)\frac{\partial \zeta (\chi ,ß)}{\partial \chi }\right)\right],$$

(38)

$$M\left(u\right)=u\zeta (\chi ,0)+u^{\varsigma }Y\left[\frac{\partial }{\partial \chi }\left(\zeta (\chi ,ß)\frac{\partial \zeta (\chi ,ß)}{\partial \chi }\right)\right].$$

(39)

By employing the inverse of the YT, we obtain

$$\begin{array}{cc}\hfill & \zeta (\chi ,ß)=\zeta (\chi ,0)+Y^{-1}\left[u^{\varsigma }\left\{Y\left[\frac{\partial }{\partial \chi }\left(\zeta (\chi ,ß)\frac{\partial \zeta (\chi ,ß)}{\partial \chi }\right)\right]\right\}\right],\hfill \\ \hfill & \zeta (\chi ,ß)=\chi +Y^{-1}\left[u^{\varsigma }\left\{Y\left[\frac{\partial }{\partial \chi }\left(\zeta (\chi ,ß)\frac{\partial \zeta (\chi ,ß)}{\partial \chi }\right)\right]\right\}\right].\hfill \end{array}$$

(40)

In terms of HPM, we have

$$\begin{array}{cc}\hfill & \sum _{ı=0}^{\infty }{ϵ}^{ı}{\zeta }_{ı}(\chi ,ß)=\chi +\left(Y^{-1}\left[u^{\varsigma }Y\left[\frac{\partial }{\partial \chi }\left(\sum _{ı=0}^{\infty }{ϵ}^{ı}{H}_{ı}\left(\zeta \right)\right)\right]\right]\right).\hfill \end{array}$$

(41)

Here, the nonlinear term reads

$$\begin{array}{cc}\hfill & H_0\left(\zeta \right)={\zeta }_0{\zeta }_{0\chi },\hfill \\ \hfill & H_1\left(\zeta \right)={\zeta }_0{\zeta }_{1\chi }+{\zeta }_1{\zeta }_{0\chi },\hfill \\ \hfill & H_2\left(\zeta \right)={\zeta }_0{\zeta }_{2\chi }+{\zeta }_1{\zeta }_{1\chi }+{\zeta }_2{\zeta }_{0\chi },\hfill \\ \hfill & ⋮.\hfill \end{array}$$

Now, by equating the coefficient of ϵ, we have

$$\begin{array}{cc}\hfill & {ϵ}^0:{\zeta }_0(\chi ,ß)=\chi ,\hfill \\ \hfill & {ϵ}^1:{\zeta }_1(\chi ,ß)=Y^{-1}\left[u^{\varsigma }Y\left[\frac{\partial }{\partial \chi }\left(\sum _{ı=0}^{\infty }{ϵ}^{ı}{H}_0\left(\zeta \right)\right)\right]\right]=\frac{{ß}^{\varsigma }}{\mathsf{\Gamma }(\varsigma +1)},\hfill \\ \hfill & {ϵ}^2:{\zeta }_2(\chi ,ß)=Y^{-1}\left[u^{\varsigma }Y\left[\frac{\partial }{\partial \chi }\left(\sum _{ı=0}^{\infty }{ϵ}^{ı}{H}_1\left(\zeta \right)\right)\right]\right]=0,\hfill \\ \hfill ⋮.\end{array}$$

Finally, we approximate the analytical solution in the form of the following series"

$$\begin{array}{cc}\hfill & \zeta (\chi ,ß)={\zeta }_0(\chi ,ß)+{\zeta }_1(\chi ,ß)+{\zeta }_2(\chi ,ß)+\cdots ,\hfill \\ \hfill & \zeta (\chi ,ß)=\chi +\frac{{ß}^{\varsigma }}{\mathsf{\Gamma }(\varsigma +1)}+\cdots .\hfill \end{array}$$

Now, in terms of YTDM and by applying the YT, we obtain

$$Y\left\{\frac{{\partial }^{\varsigma }\zeta }{\partial {ß}^{\varsigma }}\right\}=Y\left[\frac{\partial }{\partial \chi }\left(\zeta (\chi ,ß)\frac{\partial \zeta (\chi ,ß)}{\partial \chi }\right)\right],$$

(42)

The simplified form reads

$$\frac{1}{u^{\varsigma }}\{M\left(u\right)-u\zeta (\chi ,0)\}=Y\left[\frac{\partial }{\partial \chi }\left(\zeta (\chi ,ß)\frac{\partial \zeta (\chi ,ß)}{\partial \chi }\right)\right],$$

(43)

$$M\left(u\right)=u\zeta (\chi ,0)+u^{\varsigma }Y\left[\frac{\partial }{\partial \chi }\left(\zeta (\chi ,ß)\frac{\partial \zeta (\chi ,ß)}{\partial \chi }\right)\right].$$

(44)

By employing the inverse of the YT, we obtain

$$\begin{array}{cc}\hfill & \zeta (\chi ,ß)=\zeta (\chi ,0)+Y^{-1}\left[u^{\varsigma }\left\{Y\left[\frac{\partial }{\partial \chi }\left(\zeta (\chi ,ß)\frac{\partial \zeta (\chi ,ß)}{\partial \chi }\right)\right]\right\}\right],\hfill \\ \hfill & \zeta (\chi ,ß)=(-\frac{15}{8}{sech}^2\left(\frac{\chi }{2}\right))+Y^{-1}\left[u^{\varsigma }\left\{Y\left[\frac{\partial }{\partial \chi }\left(\zeta (\chi ,ß)\frac{\partial \zeta (\chi ,ß)}{\partial \chi }\right)\right]\right\}\right].\hfill \end{array}$$

(45)

The series form solution of $\zeta (\chi ,ß)$ reads

$$\zeta (\chi ,ß)=\sum _{m=0}^{\infty }{\zeta }_m(\chi ,ß),$$

(46)

with $\zeta (\chi ,ß)\frac{\partial \zeta (\chi ,ß)}{\partial \chi }={\sum }_{m=0}^{\infty }{\mathcal{A}}_m$, showing the nonlinear term in terms of Adomian polynomial, and

$$\begin{array}{cc}\hfill & \sum _{m=0}^{\infty }{\zeta }_m(\chi ,ß)=\zeta (\chi ,0)+Y^{-1}\left[u^{\varsigma }\left\{Y\left[\frac{\partial }{\partial \chi }\left(\sum _{m=0}^{\infty }{\mathcal{A}}_m\right)\right]\right\}\right],\hfill \\ \hfill & \sum _{m=0}^{\infty }{\zeta }_m(\chi ,ß)=\chi +Y^{-1}\left[u^{\varsigma }\left\{Y\left[\frac{\partial }{\partial \chi }\left(\sum _{m=0}^{\infty }{\mathcal{A}}_m\right)\right]\right\}\right].\hfill \end{array}$$

(47)

Here, the nonlinear terms read

$$\begin{array}{cc}\hfill & A_0={\zeta }_0{\zeta }_{0\chi },\hfill \\ \hfill & A_1={\zeta }_0{\zeta }_{1\chi }+{\zeta }_1{\zeta }_{0\chi },\hfill \\ \hfill & A_2={\zeta }_0{\zeta }_{2\chi }+{\zeta }_1{\zeta }_{1\chi }+{\zeta }_2{\zeta }_{0\chi },\hfill \\ \hfill & ⋮.\hfill \end{array}$$

Similarly,

$${\zeta }_0(\chi ,ß)=\chi ,$$

for $m=0$

$${\zeta }_1(\chi ,ß)=\frac{{ß}^{\varsigma }}{\mathsf{\Gamma }(\varsigma +1)},$$

for $m=1$

$${\zeta }_2(\chi ,ß)=0,$$

Finally, we approximate the analytical solution in the form of the following series:

$$\zeta (\chi ,ß)=\sum _{m=0}^{\infty }{\zeta }_m(\chi ,ß)={\zeta }_0(\chi ,ß)+{\zeta }_1(\chi ,ß)+{\zeta }_2(\chi ,ß)+\cdots ,$$

$$\begin{array}{cc}\hfill & \zeta (\chi ,ß)=\chi +\frac{{ß}^{\varsigma }}{\mathsf{\Gamma }(\varsigma +1)}+\cdots .\hfill \end{array}$$

The exact result at $\varsigma =1$ reads

$$\zeta (\chi ,ß)=\chi +ß.$$

(48)

Example 2.

Here, we consider the following fractional heat-transfer equation [55]

$$\frac{{\partial }^{\varsigma }\zeta (\chi ,ß)}{\partial {ß}^{\varsigma }}=\frac{{\partial }^2\zeta (\chi ,ß)}{\partial {\chi }^2}-2{\zeta }^3(\chi ,ß),$$

(49)

with the initial condition

$$\zeta (\chi ,0)=\frac{1+2\chi }{{\chi }^2+\chi +1}.$$

Applying the YT yields

$$Y\left(\frac{{\partial }^{\varsigma }\zeta }{\partial {ß}^{\varsigma }}\right)=Y\left[\frac{{\partial }^2\zeta (\chi ,ß)}{\partial {\chi }^2}-2{\zeta }^3(\chi ,ß)\right],$$

(50)

The simplified form reads

$$\frac{1}{u^{\varsigma }}\{M\left(u\right)-u\zeta (\chi ,0)\}=Y\left[\frac{{\partial }^2\zeta (\chi ,ß)}{\partial {\chi }^2}-2{\zeta }^3(\chi ,ß)\right],$$

(51)

$$M\left(u\right)=u\zeta (\chi ,0)+u^{\varsigma }Y\left[\frac{{\partial }^2\zeta (\chi ,ß)}{\partial {\chi }^2}-2{\zeta }^3(\chi ,ß)\right].$$

(52)

By employing the inverse of the YT, we obtain

$$\begin{array}{cc}\hfill & \zeta (\chi ,ß)=\zeta (\chi ,0)+Y^{-1}\left[u^{\varsigma }\left\{Y\left[\frac{{\partial }^2\zeta (\chi ,ß)}{\partial {\chi }^2}-2{\zeta }^3(\chi ,ß)\right]\right\}\right],\hfill \\ \hfill & \zeta (\chi ,ß)=\frac{1+2\chi }{{\chi }^2+\chi +1}+Y^{-1}\left[u^{\varsigma }\left\{Y\left[\frac{{\partial }^2\zeta (\chi ,ß)}{\partial {\chi }^2}-2{\zeta }^3(\chi ,ß)\right]\right\}\right].\hfill \end{array}$$

(53)

In terms of HPM, we have

$$\begin{array}{cc}\hfill & \sum _{ı=0}^{\infty }{ϵ}^{ı}{\zeta }_{ı}(\chi ,ß)=\frac{1+2\chi }{{\chi }^2+\chi +1}+\left(Y^{-1}\left[u^{\varsigma }Y\left[\frac{{\partial }^2\zeta (\chi ,ß)}{\partial {\chi }^2}-\sum _{ı=0}^{\infty }{ϵ}^{ı}{H}_{ı}\left(\zeta \right)\right]\right]\right).\hfill \end{array}$$

(54)

Here, the nonlinear terms read

$$\begin{array}{cc}\hfill & H_0\left(\zeta \right)=2{\zeta }_0^3(\chi ,ß),\hfill \\ \hfill & H_1\left(\zeta \right)=6{\zeta }_0^2(\chi ,ß){\zeta }_1(\chi ,ß),\hfill \\ \hfill & H_2\left(\zeta \right)=6{\zeta }_0(\chi ,ß){\zeta }_1^2(\chi ,ß)+6{\zeta }_0^2(\chi ,ß){\zeta }_2(\chi ,ß),\hfill \\ \hfill & ⋮.\hfill \end{array}$$

Now, by equating the coefficient of ϵ, we have

$$\begin{array}{cc}\hfill & {ϵ}^0:{\zeta }_0(\chi ,ß)=\frac{1+2\chi }{{\chi }^2+\chi +1},\hfill \\ \hfill & {ϵ}^1:{\zeta }_1(\chi ,ß)=Y^{-1}\left(u^{\varsigma }Y\left[\frac{{\partial }^2\zeta (\chi ,ß)}{\partial {\chi }^2}-\sum _{ı=0}^{\infty }{ϵ}^{ı}{H}_0\left(\zeta \right)\right]\right)=\frac{-6(1+2\chi )}{{({\chi }^2+\chi +1)}^2}\frac{{ß}^{\varsigma }}{\mathsf{\Gamma }(\varsigma +1)},\hfill \\ \hfill & {ϵ}^2:{\zeta }_2(\chi ,ß)=Y^{-1}\left(u^{\varsigma }Y\left[\frac{{\partial }^2\zeta (\chi ,ß)}{\partial {\chi }^2}-\sum _{ı=0}^{\infty }{ϵ}^{ı}{H}_1\left(\zeta \right)\right]\right)=\frac{72(1+2\chi )}{{({\chi }^2+\chi +1)}^3}\frac{{ß}^{2\varsigma }}{\mathsf{\Gamma }(2\varsigma +1)},\hfill \\ \hfill & {ϵ}^3:{\zeta }_3(\chi ,ß)=Y^{-1}\left(u^{\varsigma }Y\left[\frac{{\partial }^2\zeta (\chi ,ß)}{\partial {\chi }^2}-\sum _{ı=0}^{\infty }{ϵ}^{ı}{H}_2\left(\zeta \right)\right]\right)=(-\frac{1296(1+2\chi )}{{({\chi }^2+\chi +1)}^4}+\frac{432{(1+2\chi )}^3}{{({\chi }^2+\chi +1)}^5}-\hfill \\ \hfill & \frac{216{(1+2\chi )}^3}{{({\chi }^2+\chi +1)}^5}·\frac{\mathsf{\Gamma }(2\varsigma +1)}{{\mathsf{\Gamma }}^2(\varsigma +1)})\frac{{ß}^{3\varsigma }}{\mathsf{\Gamma }(3\varsigma +1)},\hfill \\ \hfill ⋮.\end{array}$$

Finally, we approximate the analytical solution in the form of the following series

$$\begin{array}{cc}\hfill & \zeta (\chi ,ß)={\zeta }_0(\chi ,ß)+{\zeta }_1(\chi ,ß)+{\zeta }_2(\chi ,ß)+{\zeta }_3(\chi ,ß)+\cdots \hfill \\ \hfill & \zeta (\chi ,ß)=\frac{1+2\chi }{{\chi }^2+\chi +1}+\frac{-6(1+2\chi )}{{({\chi }^2+\chi +1)}^2}\frac{{ß}^{\varsigma }}{\mathsf{\Gamma }(\varsigma +1)}+\frac{72(1+2\chi )}{{({\chi }^2+\chi +1)}^3}\frac{{ß}^{2\varsigma }}{\mathsf{\Gamma }(2\varsigma +1)}+(-\frac{1296(1+2\chi )}{{({\chi }^2+\chi +1)}^4}+\hfill \\ \hfill & \frac{432{(1+2\chi )}^3}{{({\chi }^2+\chi +1)}^5}-\frac{216{(1+2\chi )}^3}{{({\chi }^2+\chi +1)}^5}·\frac{\mathsf{\Gamma }(2\varsigma +1)}{{\mathsf{\Gamma }}^2(\varsigma +1)})\frac{{ß}^{3\varsigma }}{\mathsf{\Gamma }(3\varsigma +1)}\hfill \\ \hfill +\cdots .\end{array}$$

Now, in terms of YTDM and applying the YT yields

$$Y\left\{\frac{{\partial }^{\varsigma }\zeta }{\partial {ß}^{\varsigma }}\right\}=Y\left[\frac{{\partial }^2\zeta (\chi ,ß)}{\partial {\chi }^2}-2{\zeta }^3(\chi ,ß)\right].$$

(55)

Upon simplification, we have

$$\frac{1}{u^{\varsigma }}\{M\left(u\right)-u\zeta (\chi ,0)\}=Y\left[\frac{{\partial }^2\zeta (\chi ,ß)}{\partial {\chi }^2}-2{\zeta }^3(\chi ,ß)\right],$$

(56)

$$M\left(u\right)=u\zeta (\chi ,0)+u^{\varsigma }Y\left[\frac{{\partial }^2\zeta (\chi ,ß)}{\partial {\chi }^2}-2{\zeta }^3(\chi ,ß)\right].$$

(57)

By employing the inverse of YT, we obtain

$$\begin{array}{cc}\hfill & \zeta (\chi ,ß)=\zeta (\chi ,0)+Y^{-1}\left[u^{\varsigma }\left\{Y\left[\frac{{\partial }^2\zeta (\chi ,ß)}{\partial {\chi }^2}-2{\zeta }^3(\chi ,ß)\right]\right\}\right],\hfill \\ \hfill & \zeta (\chi ,ß)=\frac{1+2\chi }{{\chi }^2+\chi +1}+Y^{-1}\left[u^{\varsigma }\left\{Y\left[\frac{{\partial }^2\zeta (\chi ,ß)}{\partial {\chi }^2}-2{\zeta }^3(\chi ,ß)\right]\right\}\right].\hfill \end{array}$$

(58)

The series form solution of $\zeta (\chi ,ß)$ reads

$$\zeta (\chi ,ß)=\sum _{m=0}^{\infty }{\zeta }_m(\chi ,ß),$$

(59)

with $2{\zeta }^3(\chi ,ß)={\sum }_{m=0}^{\infty }{\mathcal{A}}_m$, showing the nonlinear term in terms of Adomian polynomial

$$\begin{array}{cc}\hfill & \sum _{m=0}^{\infty }{\zeta }_m(\chi ,ß)=\zeta (\chi ,0)-Y^{-1}\left[u^{\varsigma }\left\{Y\left[\frac{{\partial }^2\zeta (\chi ,ß)}{\partial {\chi }^2}-\sum _{m=0}^{\infty }{\mathcal{A}}_m\right]\right\}\right],\hfill \\ \hfill & \sum _{m=0}^{\infty }{\zeta }_m(\chi ,ß)=\frac{1+2\chi }{{\chi }^2+\chi +1}-Y^{-1}\left[u^{\varsigma }\left\{Y\left[\frac{{\partial }^2\zeta (\chi ,ß)}{\partial {\chi }^2}-\sum _{m=0}^{\infty }{\mathcal{A}}_m\right]\right\}\right].\hfill \end{array}$$

(60)

Here, the nonlinear terms read

$$\begin{array}{cc}\hfill & A_0=2{\zeta }_0^3(\chi ,ß),\hfill \\ \hfill & A_1=6{\zeta }_0^2(\chi ,ß){\zeta }_1(\chi ,ß),\hfill \\ \hfill & A_2=6{\zeta }_0(\chi ,ß){\zeta }_1^2(\chi ,ß)+6{\zeta }_0^2(\chi ,ß){\zeta }_2(\chi ,ß),\hfill \\ \hfill & ⋮.\hfill \end{array}$$

Similarly,

$${\zeta }_0(\chi ,ß)=\frac{1+2\chi }{{\chi }^2+\chi +1},$$

for $m=0$

$${\zeta }_1(\chi ,ß)=\frac{-6(1+2\chi )}{{({\chi }^2+\chi +1)}^2}\frac{{ß}^{\varsigma }}{\mathsf{\Gamma }(\varsigma +1)},$$

for $m=1$

$${\zeta }_2(\chi ,ß)=\frac{72(1+2\chi )}{{({\chi }^2+\chi +1)}^3}\frac{{ß}^{2\varsigma }}{\mathsf{\Gamma }(2\varsigma +1)},$$

for $m=2$

$${\zeta }_3(\chi ,ß)=\left(-\frac{1296(1+2\chi )}{{({\chi }^2+\chi +1)}^4}+\frac{432{(1+2\chi )}^3}{{({\chi }^2+\chi +1)}^5}-\frac{216{(1+2\chi )}^3}{{({\chi }^2+\chi +1)}^5}·\frac{\mathsf{\Gamma }(2\varsigma +1)}{{\mathsf{\Gamma }}^2(\varsigma +1)}\right)\frac{{ß}^{3\varsigma }}{\mathsf{\Gamma }(3\varsigma +1)}.$$

Finally, we approximate the analytical solution in the form of the following series:

$$\zeta (\chi ,ß)=\sum _{m=0}^{\infty }{\zeta }_m(\chi ,ß)={\zeta }_0(\chi ,ß)+{\zeta }_1(\chi ,ß)+{\zeta }_2(\chi ,ß)+{\zeta }_3(\chi ,ß)+\cdots ,$$

$$\begin{array}{cc}\hfill & \zeta (\chi ,ß)=\frac{1+2\chi }{{\chi }^2+\chi +1}+\frac{-6(1+2\chi )}{{({\chi }^2+\chi +1)}^2}\frac{{ß}^{\varsigma }}{\mathsf{\Gamma }(\varsigma +1)}+\frac{72(1+2\chi )}{{({\chi }^2+\chi +1)}^3}\frac{{ß}^{2\varsigma }}{\mathsf{\Gamma }(2\varsigma +1)}+(-\frac{1296(1+2\chi )}{{({\chi }^2+\chi +1)}^4}+\hfill \\ \hfill & \frac{432{(1+2\chi )}^3}{{({\chi }^2+\chi +1)}^5}-\frac{216{(1+2\chi )}^3}{{({\chi }^2+\chi +1)}^5}·\frac{\mathsf{\Gamma }(2\varsigma +1)}{{\mathsf{\Gamma }}^2(\varsigma +1)})\frac{{ß}^{3\varsigma }}{\mathsf{\Gamma }(3\varsigma +1)}+\cdots .\hfill \end{array}$$

The obtained results agree with the result in Ref. [56]. For $\varsigma =1,$ the above can be rearranged as

$$\zeta (\chi ,ß)=\frac{1+2\chi }{{\chi }^2+\chi +1}-\frac{6(1+2\chi )}{{({\chi }^2+\chi +1)}^2}ß+\frac{36(1+2\chi )}{{({\chi }^2+\chi +1)}^3}{ß}^2-\frac{216(1+2\chi )}{{({\chi }^2+\chi +1)}^4}{ß}^3+\cdots .$$

(61)

Numerical Simulation Studies

Here, we have presented the numerical simulations of the time-fractional heat transfer equation as well as the nonlinear fractional porous media equation with cubic nonlinearity of fractional order by applying the proposed methodologies. We used graphs and tables to show how the obtained solution behaves. Maple was used to complete all of the computational work for the problems stated. The behavior of the exact and suggested approaches’ solutions at $\varsigma =1$ is depicted in the graphs in Figure 1. Figure 2 displays the results of proposed methodologies at various fractional orders of $\varsigma =1,0.75,0.50,0.25,$ within the domain $1\le \chi ,$$ß\le 0$ for Example 1.

Table 1. A comparison between our approach and the actual outcome with a $\varsigma$ value of 1, including the calculation of the absolute error (AE).

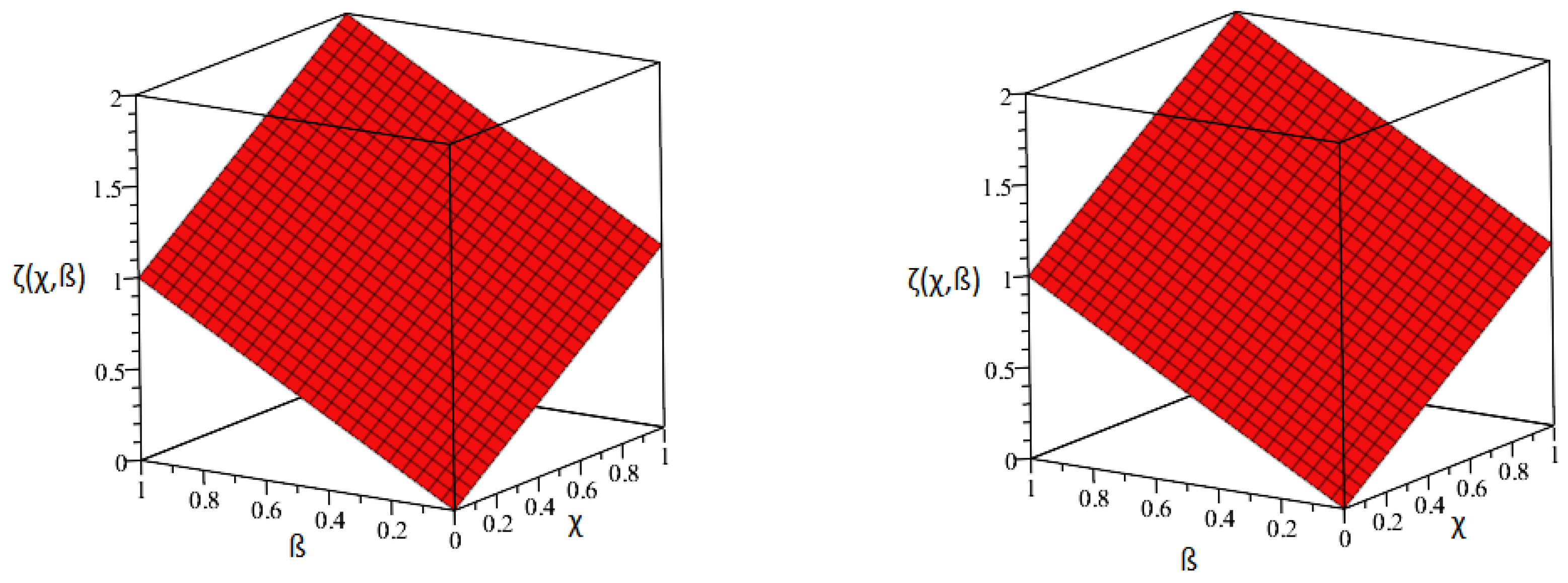
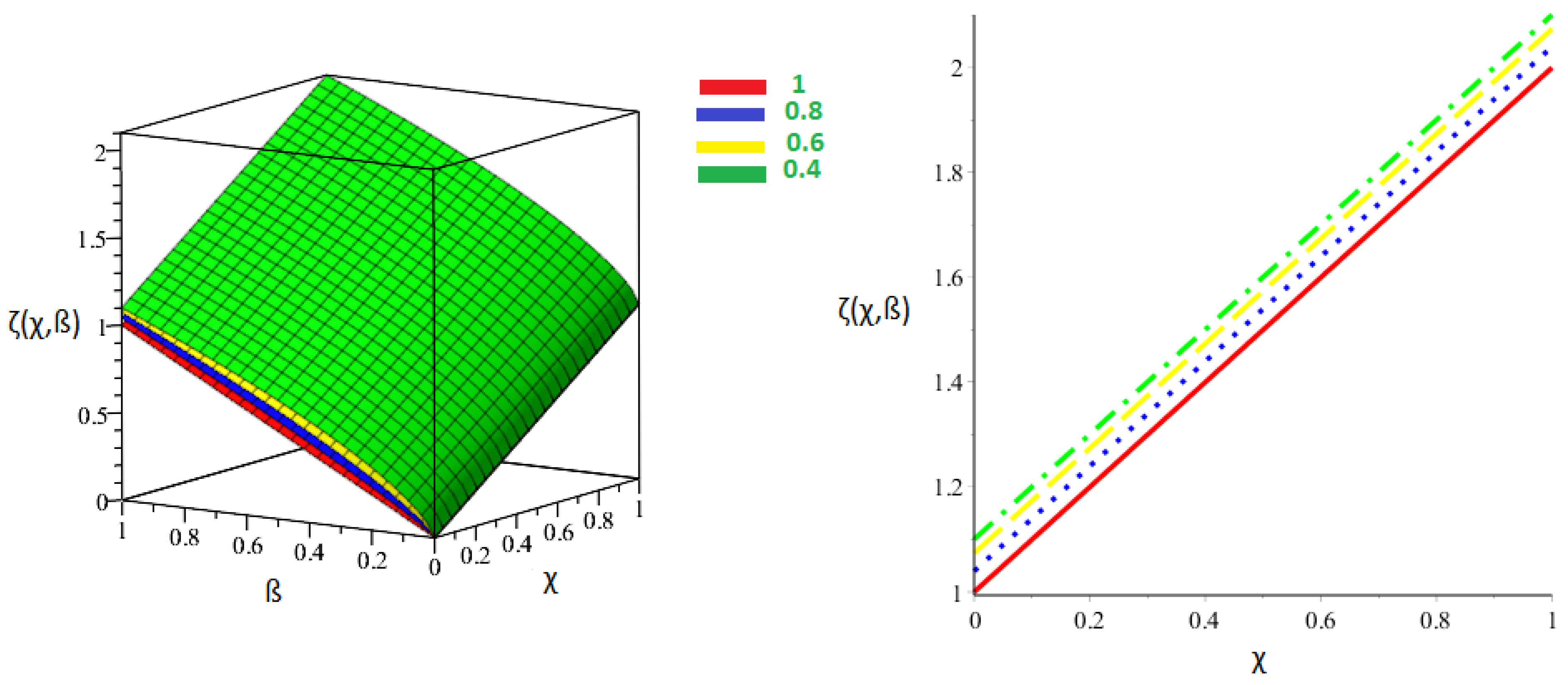
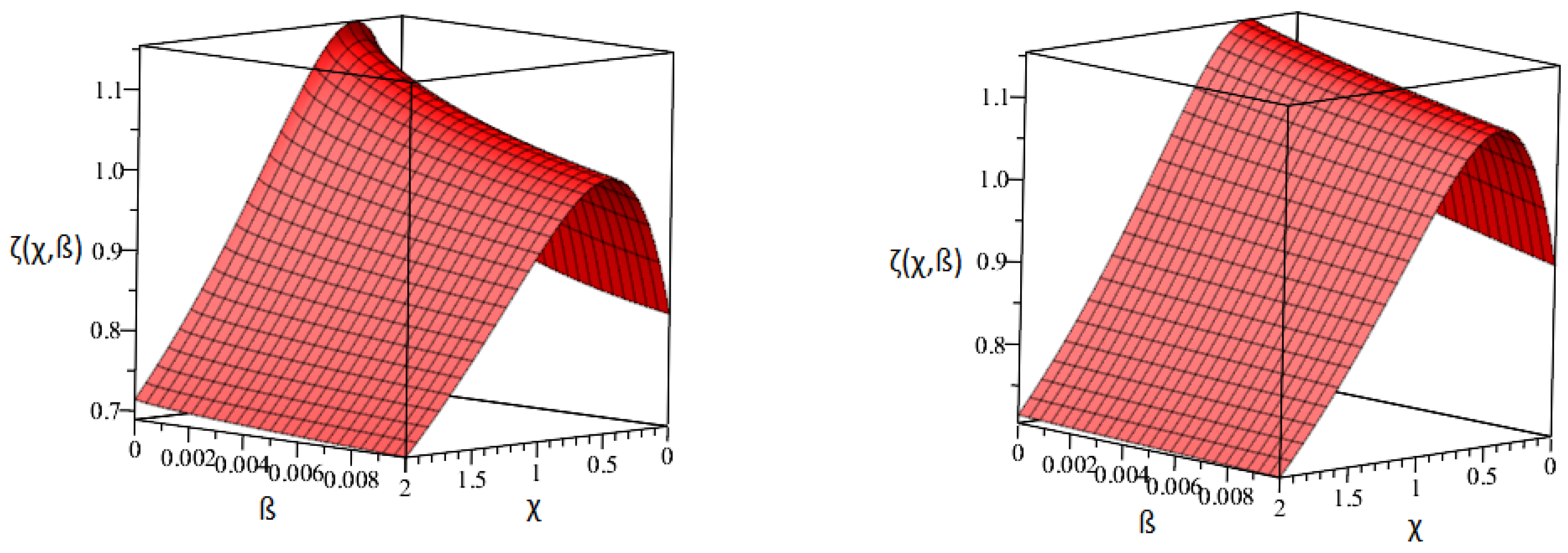
$ß=0.01$	Exact Result	Our Techniques’ Result	AE of Our Techniques
$\mathbf{\chi }$	$\mathbf{\varsigma }=\mathbf{1}$	$\mathbf{\varsigma }=\mathbf{1}$	$\mathbf{\varsigma }=\mathbf{1}$
1	1.01000000000	1.01000000000	0.0000000000 $\times {10}^{+00}$
2	2.01000000000	2.01000000000	0.0000000000 $\times {10}^{+00}$
3	3.01000000000	3.01000000000	0.0000000000 $\times {10}^{+00}$
4	4.01000000000	4.01000000000	0.0000000000 $\times {10}^{+00}$
5	5.01000000000	5.01000000000	0.0000000000 $\times {10}^{+00}$
6	6.01000000000	6.01000000000	0.0000000000 $\times {10}^{+00}$
7	7.01000000000	7.01000000000	0.0000000000 $\times {10}^{+00}$
8	8.01000000000	8.01000000000	0.0000000000 $\times {10}^{+00}$
9	9.01000000000	9.01000000000	0.0000000000 $\times {10}^{+00}$
10	10.01000000000	10.01000000000	0.0000000000 $\times {10}^{+00}$

compares the accurate as well as proposed methods’ solutions with the aid of absolute error for Example 1. The approximate solutions $\zeta (\chi ,ß)$ for various fractional-order $\varsigma$ values are shown in Figure 3 and Figure 4, respectively. This illustrates how the graphical behavior varies on the order of the fractional derivative.

Table 2. A solution is presented through the proposed method, which involves the use of different values of $\chi$ and ß for varying fractional orders $\varsigma$ in Example 2.

$\mathit{\chi }$	ß	$\mathit{\varsigma }=0.50$	$\mathit{\varsigma }=0.75$	$\mathit{\varsigma }=1$
1	0.25	0.900577	0.796350	0.750000
2		0.577330	0.583104	0.594023
3		0.467902	0.475540	0.483500
4		0.390528	0.395451	0.400145
5		0.332537	0.335639	0.338499
1	0.50	1.612625	1.255979	1.000000
2		0.578917	0.552933	0.539358
3		0.438141	0.439283	0.442876
4		0.369207	0.372329	0.376093
5		0.318621	0.321125	0.323822
1	0.75	2.825667	0.321125	1.750000
2		0.655398	0.595920	0.550291
3		0.427756	0.420533	0.416590
4		0.355017	0.355164	0.356413
5		0.307995	0.309167	0.310806
1	1	4.448532	3.692364	3.000000
2		0.7910888	0.703748	0.626822
3		0.432096	0.416896	0.404642
4		0.346044	0.342991	0.341107
5		0.299696	0.299287	0.299452

compares the approximations for the solutions to Example 2 for various values of $\chi$ and ß. The demonstrated plots help us to better understand the nature of the proposed equations when temporal-spatial variables vary in comparison with arbitrary order. The comparison of absolute errors demonstrates that our methods converge more quickly than other methods. Additionally, the graphical depiction demonstrates a good agreement between the exact solution and the suggested approaches solution.

7. Conclusions

In this work, both the nonlinear fractional porous media equation and time-fractional heat transfer equation have been solved by implementing HPTM and YTDM, an elegant combination of the hybrid Yang transformation (YT) with the homotopy perturbation method (HPM) and the Adomian decomposition method (ADM). Both He’s polynomials and Adomian polynomials have been applied to express the nonlinear terms in the targeted issues. The suggested hybrid methods feature simpler and clearer steps for determining the solutions to fractional problems. To make the offered approaches more understandable and to assess their applicability, various numerical problems were solved. The obtained results demonstrate a strong association between the suggested strategy and the actual solution. Plots of the fractional solutions depict the behavior of different dynamics of the specified physical phenomenon. The fractional solution rapidly approaches the integer-order ones. In conclusion, we recommend that these methods be applied to solving several other nonlinear fractional problems in various scientific fields because they are easy to implement and lead to the actual solution. The proposed methods can also address many evolution equations that govern different nonlinear phenomena in plasma physics [57,58,59,60].