Abstract
There is a manufacturing system where several parts are processed through machining workstations and later assembled to form final products. In the event of disruptions such as machine failure, the original flow-shop schedule needs to be revised and/or rescheduled. In such a scenario, rescheduling methods based on right-shift rescheduling and affected operations rescheduling work very well. Here in this study, the deviation of the make-span of the revised schedule from the original schedule is used as a performance measure. We have proposed three rescheduling methods. There are multiple factors that influence the performance of the rescheduling methodology. One of them is the make-span deviation of the schedule, and the factors influencing it are optimality of the initial solution, failure duration, deviation of make-span, rescheduling method, size, and instant of failure. The initial schedule and problem size depend on the flow-shop manufacturing system for which scheduling is performed, but the method of rescheduling depends on the decision as to which rescheduling methodology is to be selected. Computations are performed using full factorial experimentation. We also observed that right-shift rescheduling is the preferred rescheduling method in the majority of situations. In contrast, the affected operation rescheduling method is also equally suitable when the initial solution is created using modified bottleneck minimum idleness.
Keywords:
scheduling; right-shift rescheduling; affected operations rescheduling; genetic algorithm; heuristics MSC:
90B50
1. Introduction
Schedules are prepared in advance to lead production operations and assist with other planning activities. However, disruptions, which are inevitable for manufacturing installations, result in unacceptable performance changes to the pre-decided schedules. These disruptions compel rescheduling the operations for optimum performance, which involves modifying an already-planned, possibly optimal schedule to take the disturbance into account. Furthermore, it needs to be prepared in a short time, accommodate unforeseen or urgent events, and adapt to the original schedule.
Nowadays, with multiple product lines consisting of multiple parts requiring different workstations, the manufacturing parameters are far more complicated. This complexity is strongly influenced by the product structure and manufacturing system. Although, according to the product requirements, product structures can be simple or complex based on the relationship between the parts and/or subassemblies and the final assembly in a hierarchical manner (refer to the two examples presented in Figure 1). It is important to take into account the type of production system available, whether it is a job-shop, open-shop, or flow-shop system [1]. In the open-shop system, there are no restrictions on the flow of each work through the ‘m’ machines, whereas each job has a separate flow pattern in the job-shop. The jobs can be processed either in a permutational way, where jobs are processed by a series of ‘m’ machines in the same order, or in a non-permutational way, where jobs are processed by a series of ‘m’ machines but not in the same order [2].
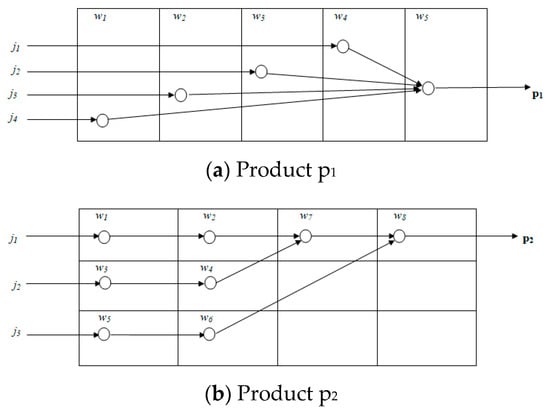
Figure 1.
Assembly job-shop process operations.
In the case of the assembly job-shop problem with Product p1, only one operation is performed on every part, parts j1, j2, j3, and j4 (refer to Figure 1a). Conversely, with Product p2, these parts are processed simultaneously on multiple workstations: w1, w2, w3, and w4. The complexity of the assembly job-shop problem increases with the number of operations. From this example (refer to Figure 1b), it is evident that only one operation, before assembly, is assumed for every part in the case of Product p1, whereas in the complex product structure of Product p2, there could be more than two operations. Thus, any manufacturing system that assembles multiple products (p1, p2 … so on) needs several parts (j1, j2 … so on) and/or subassemblies that subsequently require a series of machining/sub-assemblies at multiple work stations: w1, w2, … wn. Due to design and technological constraints, machining operations are performed in the first stage, whereas assembly operations are performed at later stages. Final assembly or sub-assembly may have to wait not only for the machines but for their sub-components as well. However, the problem of production planning for the job- and/or flow-shop with the machining and assembly operations is called the assembly flow-shop problem. Similar complex structures in the assembly job-shop problem are common in special and unique capital goods.
In the case of the assembly flow-shop problem, the workstation can be used to perform exactly similar or different operations for multiple products (refer to Figure 2). Here, parts are processed serially through the same set of workstations (w1, w2, … wn) to manufacture products (p1, p2 … so on); these products need several parts (j1, j2 … so on) and/or subassemblies that subsequently require a series of machining/sub-assemblies at multiple work stations: w1, w2, … wn. For example [3,4], in gearbox processing, milling machines at the first stage perform roughing operations, and then machining centers at the next stage perform finishing operations. Finally, the product is assembled on the last workstation with the remaining parts (say a team of workers assembles them with other parts, such as casing, shaft, etc.), forming the final product. A consolidated survey of categories of assembly flow-shop models and their solution methodologies is available in the literature [4,5]. There are huge avenues for research in this area [5], as it has received less attention than other areas of scheduling.
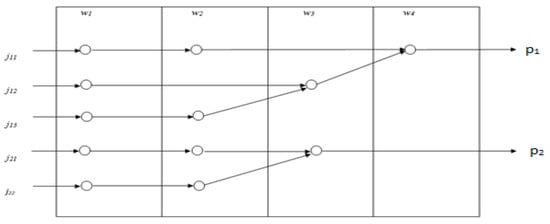
Figure 2.
Processing of parts in the assembly flow-shop problem.
Thus, there is a need to study and analyze the appropriate techniques for scheduling and rescheduling of such assembly flow-shop problems in any manufacturing system. Earlier studies [6,7,8,9,10] presented an analysis of scheduling techniques by considering the largest possible size (nearly 1520) of number of operations [4] to minimize the make-span. The objective of the present work is to study and analyze the appropriate technique for rescheduling in the event of a system disruption. In this study, the performance measure of percent deviation of make-span between the disrupted schedule and the new schedule generated by the proposed rescheduling methods is performed. Thus, our main contribution is to study the influence of factors such as failure duration, rescheduling method, size, and instant of failure that impact the make-span deviation of the disrupted reschedule. Additionally, another objective is to study the interactions between the rescheduling method and the optimality of the initial solution for managing disruptions in a flow-shop manufacturing system. Subsequently, we propose right-shift, break down machine heuristics, and the use of a genetic algorithm in order to accommodate disruptions in the manufacturing and/or assembly processes.
The manuscript presents, in Section 2, a brief background review on rescheduling strategies. Section 3 presents the details of flow-shops with assembly operations. Next, Section 4 describes the proposed three methods: right-shift, affected operations, and a genetic algorithm for rescheduling flow-shops with assembly operations under system disruptions. Subsequently, Section 5 and Section 6 present the computational experiments conducted for larger-sized problems and discuss the combined effects of rescheduling methods having different combination factors and their interaction effects, respectively. Lastly, Section 7 concludes our findings with the limitations of this and its future scope.
2. Background Review
Two common strategies for controlling production environments with disruptions are dynamic (normal) and predictive–reactive (nominal) scheduling. Ouelhadj and Petrovic [11] have described dynamic scheduling as complete reactivity. Even though dynamic scheduling is more popular for dealing with disruptions, it is not about optimizing scheduling. Whereas, the original/initial schedule given is standard. Heuristics and optimization concepts are typically the foundation of initial schedules. As a result, any strategy for correction or repair will result in a departure from the initially planned schedule. Zhang et al. [12] and Ghaleb et al. [13] presented the option to update schedules using right-shift rescheduling (RSR), affected operation rescheduling (AOR), and total rescheduling (TR). They selected the best rescheduling based on evaluation of different performance measures such as schedule efficiency (i.e., make-span, mean tardiness, mean flow time, average resource utilization, and maximum lateness), schedule stability (i.e., robustness and nervousness), and cost (i.e., computational, setup, and transportation costs). The right-shift rescheduling method delays or reschedules each affected task by the disruption, keeping the initial sequence, and by the time required to make the reschedule plan workable. Thus, there is no sequence deviation between schedule and reschedule. In affected operation rescheduling, operations affected directly or indirectly by disruption are only rescheduled. In order to maintain stability, affected operations rescheduling preserves the initial schedule as much as possible. In total rescheduling, all job operations—those not processed before disruptions and those not affected—are rescheduled.
From published literature, it is evident that researchers adopted different performance measures while evaluating rescheduling methods. Table 1 summarizes selected literature and the adopted rescheduling strategies. Please refer to Appendix A for details regarding the researchers adopted performance measures, the production system used for the study, and the types of disruptions in the manufacturing system.

Table 1.
Initial Schedule and Rescheduling Strategies.
From Table 1, it is evident that AOR is the most preferred rescheduling approach due to its stability and potential savings in CPU time. It is also evident that AOR finds more applications in most of the heuristics developed to date. RSR can also be regarded as a special case of AOR, where scheduled repair or recovery is very practical as it saves CPU time and maintains the stability of the manufacturing system. Similarly, though TR might, in principle, be better capable of maintaining optimality, its main disadvantage is excessive computational effort and CPU time. However, this approach is discouraged in the industry as the new schedule is likely to differ considerably from the old one, and it is not desirable since many other decisions, such as the assignment of personnel, the delivery of raw materials, and the subsequent processing of jobs in other facilities, may be severely disrupted. It is found that AOR demonstrates competitive performance for both efficiency and stability measures [15,16,20,21,22,23]. TR uses a rescheduling procedure that is the same as that used at the predictive stage for scheduling; it showed better performance for efficiency measures. However, it is achieved at the expense of computation time [21]. From Table 1, it is also evident that most researchers adopted machine failure as a disruption. This may be due to the fact that a disruption due to machine failure includes other uncertainties like disruption in the processing of operations on the machine for a period of time. The scheduling complexity of AJSP and AFSP systems is mainly characterized by the number of operations, the precedence relationship among operations (product structure), and computing time. Only one instance of rescheduling work on such a manufacturing system is seen in the literature [43]. In this paper, rescheduling methods are presented for the assembly flow-shop problem (AFSP), which has machining operations in the first stage and assembly operations at a later stage. Thus, in order to accommodate for disruptions in the manufacturing process, the rescheduling process needs to have the facility to change the initial schedule as and when the event occurs. The initially adopted assembly flow-shop operation and the required scheduling as a problem on hand are discussed in the following section.
3. Problem on Hand: Flow-Shop with Assembly Operation
The objective of the present work is to study and analyze the appropriate technique for rescheduling in the event of a system disruption in any flow-shop with part manufacturing and their subsequent assembly operations. Thus, the flow-shop manufacturing system combined with the adopted assembly operations is presented in Figure 3. Where, the beginning and end of the flow-shop are shown by dummy operations O1 and O38, respectively. Operations O12, O26, and O37 performed on w5 represent final assembly and three products: Product 1, Product 2, and Product 3. Each product is made up of several parts, and each part is processed on workstations in a technological sequence. For example, Product 1 is made up of parts J11, J12, and J13, where the operations of the first part J11 follow the sequence O2, O3, and O4 machining operations; O11 is a subassembly operation, and O12 is an assembly operation of the product. Machining operations are performed on all workstations except the last two, which perform only assembly operations. Thus, the system on hand has H total products and Jh parts per product with J total parts. The directed graph of the operation-based representation of AFSP is shown, where O1 and O38 are dummy sets of operations, O2 to O37 stand for actual operations as per the predefined manufacturing flow, J11 to J33 represent parts, and w1 to w5 represent workstations (refer to Figure 3).
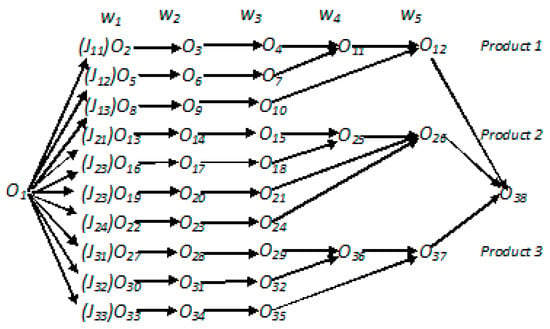
Figure 3.
Operation-based representation of the assembly flow-shop problem.
In order to decide the start and finish times of each of the operations (machining, subassembly, and assembly), first the order of parts for each product is decided, and then the order of products is determined on the basis of the minimum completion time. Scheduling the manufacturing system aims to minimize the completion time (make-span) for all products by finding the optimal sequence of parts at each workstation. In this study, the performance, i.e., percent deviation of make-span between the disrupted schedule and the new schedule generated by the proposed rescheduling methods, is evaluated. Here in this study, the initial schedule is generated using heuristics based on the genetic algorithm (GA) and modified bottleneck minimum idleness (MBMI) heuristics developed for AFSP with the objective of minimizing make-span time [5]. The problems are generated by varying the number of operations (NOP), number of products (H), parts per product (Jh), and number of workstations (W), as shown in Table 2.

Table 2.
Problem sizes for the initial schedule.
The initial schedule is generated using MBMI and GA methods, which are addressed in earlier work [44]. In brief, the details on how these methods work are presented here below.
3.1. Genetic Algorithm
The genetic algorithm mechanism starts by encoding the feasible schedule to produce a list of genes (parent chromosomes) as the initial solution space (refer to Figure 4). Where each gene represents an operation and a chromosome (list of genes) represents a set of operations for all workstations (the entire schedule). For deciding the sequence of operations, the operations for each product are structured in a specific sequence (refer to Figure 3) and are reproduced as chromosome structure. Such a chromosome structure for the first product (h = 1) is depicted in Figure 4a, where each chromosome is divided into subchromosomes that correspond to the sequence of operations on the wj workstation. Similarly, for deciding the sequence of products, see Figure 3, and the operations corresponding to the final assembly of all products are reproduced as a chromosome structure, as shown in Figure 4b. In the first phase, the sequence of operations on all workstations is decided for every individual product to minimize the make-span of each one. In the second phase, the sequence of the product is decided by obtaining the minimum make-span of all products. The adopted procedure to generate the initial schedule using a genetic algorithm-based heuristic for both phases is presented in Figure 5.
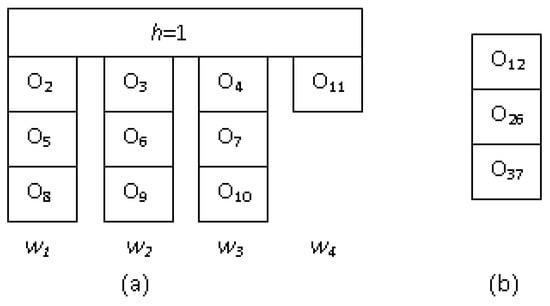
Figure 4.
Genetic algorithm chromosome. (a) For first product. (b) Final assembly of all products.
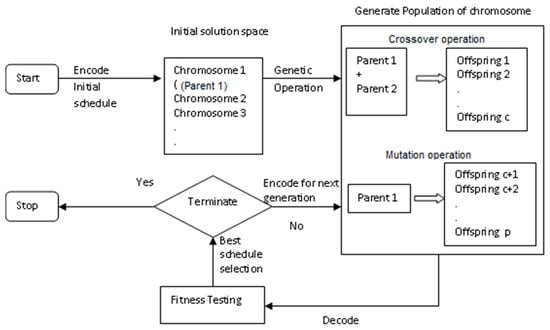
Figure 5.
Procedure to set the initial schedule using a genetic algorithm.
3.2. Modified Bottleneck Minimal Idleness
Here, the order of the parts (refer to Figure 3) to be processed for all products on every workstation is collectively decided. Initially, the set of operations for every workstation is identified for all products, and subsequently, the bottleneck workstation that consumes the most processing time is identified. Secondly, for each part of the bottleneck station, the sum of the processing times of the remaining operations, called the tail, is estimated. Subsequently, the total processing time at the bottleneck station for every product is calculated, and the sequence of the products is determined in decreasing order of time. Followed and continued to club, the operations on parts at the bottleneck station belonging to each product and arranging them in sequence is determined earlier. Thus, for each product, the operations at the bottleneck station are sorted in decreasing order of closeness to the secondary bottleneck workstation upstream. Finally, the schedule is set by aligning the remaining operations before and after the bottleneck station and determining the make-span.
4. Proposed Approach
For the above-stated assembly flow-shop problem with machining operations in the first stage and assembly operations at a later stage, in order to accommodate disruptions in the manufacturing and assembly processes, the rescheduling process needs to have the facility to change the initial schedule as and when the event occurs. The framework of the whole proposed approach begins with the given assembly flow-shop problem. The schedule is generated using the MBMI and GA methods, the performances of which are decided on the basis of the deviation of the make-span from the lower bound [44]. These schedules are rescheduled in the event of a disruption (machine failure: instant and duration) using the proposed rescheduling methods. The deviation of the make-span of the new schedule from the original schedule is used to measure the performance of these proposed rescheduling methods. The proposed three methods—right-shift, break down machine heuristics, and genetic algorithms—are presented below.
4.1. Right-Shift Rescheduling (RSR)
RSR simply postpones (shifts) all the affected operations by the amount equal to the disruption duration by retaining the original sequence of operations on all workstations, thereby maintaining the schedule’s stability. The procedural steps are as follows:
Step A1: Determine the breakdown or disrupted workstation (DW), time of failure (Tf), and duration of failure (Df).
Step A2: Determine the two sets of operations from the initial schedule for each workstation, first S1 before Tf and another S2 after Tf. If operation is interrupted, the DW during disruption is incomplete and is added to set S1.
Step A3: In the case of an incomplete interrupted operation, modify the processing time of the interrupted operation by adding a failure duration as P(Jhi, DW) = Df + P(Jhi, DW). Else, add an idle time of Df after a disrupted operation.
Step A4. Combine the operations of the workstations of sets S1 and S2.
Step A5: Determine the start and finish times of each operation for the combined set with the same sequence of operations as the initial schedule.
4.2. Break down Machine Heuristics
After the rescheduling of the operations at the disrupted workstation is completed, corresponding changes in the operations at another workstation are necessitated. Thus, sequence stability is disturbed to some extent. In this scenario, two heuristics (a break down machine and a genetic algorithm) are adopted. In this case, the sequence of parts in each product may change, but the sequence of products in the flow-shop is maintained to ensure system stability to the maximum possible extent. In the case of a disrupted break down workstation, the operations on the subsequent workstations are rearranged accordingly. This rearrangement is based on the break down machine heuristic and is performed step by step as follows:
Step B1: Determine the breakdown or disrupted workstation, time of failure, and duration of failure. It is the same procedure as mentioned above in Step A1.
Step B2: Determine two sets of operations from the initial schedule for each workstation, the first set of operations S1 being before time failure Tf and another set of operations S2 being after time failure Tf. An interrupted incomplete operation, if any, on DW during disruption is added to set S1 and modifies the processing time of an interrupted operation by adding the failure duration Df (same as the above Step A3).
Step B3: Group the set of operations S2 after the time of failure for each product and sort these operations product-wise on the disrupted workstation in increasing order of processing time.
Step B4: Perform the aligning of the corresponding operations S2 of the parts on the non-disrupted workstation.
Step B5: Finally, combine the operations on workstations from sets S1 and S2 and determine the start and finish times of each operation for the combined set.
4.3. Use of Genetic Algorithm
Here, the use of a genetic algorithm is to treat the sequence of operations on disrupted workstations as a representation scheme of chromosome structure. The number of generations is decided based on the time required for execution of the program, which is maintained to a reasonable extent. The rearrangement/reschedule is based on a genetic algorithm heuristic performed step by step as follows:
Step C1: Determine the breakdown or disrupted workstation (DW), time of failure (Tf), and duration of failure (Df) (same as the above Step B1).
Step C2: Determine the two sets of operations from the initial schedule for each workstation, first S1 before Tf and another S2 after Tf. An interrupted, incomplete operation, if any, on DW during disruption is added to set S1 (same as the above Step B2).
Step C3: In the case of an incomplete operation, modify the processing time of the interrupted operation by adding a failure duration, i.e., P (Jhi, DW) = Df + P(Jhi, DW) (same as the above Step B2).
Step C4: For the operation set S2, generate two parent chromosomes, where the first chromosome is generated as the sequence of operations of a disruptive machine using the breakdown rescheduling approach and another chromosome is generated randomly. These two parent chromosomes will be used for the first generation.
Step C5: If the generation number has not reached the maximum set limit, use the genetic operator as a one-point crossover to generate sequences of operation for a disruptive machine and the shift mutation operator on the parent chromosomes to form the population.
Step C6: Align the corresponding operations of the parts in non-disruptive workstations with the set of operations obtained for the disruptive workstation for the entire population.
Step C7: Combine the operations of the workstations related to operation sets S1 and S2 and determine the start and finish times of each operation for the combined set.
Step C8: Finally, from the population, select two schedules with the least make-span and determine their sequences of operations in the disruptive workstation, which will be used as parent chromosomes in the next generation.
Step C9: Reach step C5, in the case that the generation number has not reached the maximum limit.
In the above-proposed approach, the following assumptions are made and listed as follows:
- Each part can handle up to one workstation at a time. All parts are stand-alone, available for zero-time processing, and may or may not require all workstations.
- A workstation is continuously available and processes parts in the same order; for example, if part jhi is processed on a workstation before part jhi+1, then all workstations proceed in the same way.
- Setup times for the parts and assemblies are negligible and therefore ignored.
- It is permissible to keep inventory during the process.
- Transit time is zero, which makes a part available on a workstation wj+1 as soon as it leaves workstation wj.
- All products have the same delivery dates.
- All the parts and machines immediately resume their execution once the reschedule is made available.
- The duration of the breakdown is known as soon as it occurs.
- A machining workstation other than the first fails in a random manner.
- After rescheduling, an interrupted, incomplete operation, if any, will be completed on the same machine.
- Disruption occurs only at machining workstations. Disruption at assembly workstations is assumed to be negligible as the number of operations at these workstations is less than those at machining workstations.
The affected operation rescheduling is found to be the most suitable as it gives a better performance in the efficiency and stability measures. Further, right-shift rescheduling being a special case of the affected operation rescheduling requisites a comparative analysis of the results obtained using these two methods, presented with machine failure as a disruption. When studying the affected operation rescheduling method, two heuristics (BDM and genetic algorithms) have evolved based on the concept of the affected operation rescheduling method. Sequence deviation, a stability measure, is prevented in the procedure of the affected operation rescheduling and right-shift rescheduling. Thus, only schedule efficiency needs to be measured when comparing these methods. The schedule efficiency is estimated on the basis of the percent deviation of the make-span (%DM) between the disrupted and new schedules. The %DM is calculated using the following Equation (1): where Mr is the make-span obtained by the rescheduling method and Mo is the make-span of the original (disrupted) schedule.
%DM = [(Mr − Mo)/Mo] × 100
5. Performance of Rescheduling: Design of Experiments
Using the proposed right-shift, affected operations, and genetic algorithm, computational experiments are conducted on larger-sized problems in order to study the performance as the percent deviation of the make-span between the disrupted workstation schedule and the new schedule generated by the above-proposed three rescheduling methods (refer to Section 4). There are multiple factors that influence the effectiveness of rescheduling. The selected details are presented herewith.
The size of the manufacturing system [15] refers to its problem size and is expressed as the number of operations (NOP). The NOP in turn is decided by the number of products (H), parts per product (Jh), and number of workstations (W). The NOP has already been established as an important factor in scheduling and can range up to 1520. In order to cover the entire range of sizes, two levels are considered in this experiment.
Extent of the optimality of the initial schedule [15]: The schedule is referred to as optimal if it gives the least deviation from the lower bounds. In this work, the optimality of the initial schedule (OSI) depends on the deviation of the make-span from the lower bound of the initial schedule method, viz., the GA, Disjunctive, and MBMI methods, which are found to be least, moderate, and highest, respectively [5]. To cover the entire range, the two extreme levels are selected for OSI, i.e., GA and MBMI.
A number of disruptions occur and workstations fail, which, in the manufacturing system, results in parts being processed sequentially through several workstations. Disrupted workstation (DW) refers to the workstation(s) where break down occurs. Idle time available on each workstation varies, and hence workstations where disruptions occur affect the rescheduling performance. Break down occurs on any one or more workstations simultaneously. However, in this work, we only considered failures that occur one at a time in a workstation. The selection level for disrupted workstations depends on the number of machining workstations in the manufacturing system. A disrupted workstation is a continuous variable, and the two levels are set, viz., an earlier or later machining workstation. For a small-sized problem, i.e., 290 NOP, as shown in Table 1, only three machining workstations exist, of which the first one is assumed not to be failing. Hence, in the earlier workstation, failure begins in workstation two, and workstation three is the later failing machining workstation. However, in the large size problem, i.e., NOP 1440, eight machining workstations are considered. When defining earlier DW, it is assumed to lie between two and four, and workstations five and onward are considered later. In such cases, selection of failure workstation is made by generating random number as Earlier DW [2~4] and Later DW [5~8].
The instant of disruption [15] is an instant (Tf) at which a failure occurs. The instant can occur anywhere in the entire make-span period of a schedule. The earlier the failure (Tf), the more the number of operations are affected, which extends the make-span of the revised schedule significantly. If Mo is the make-span of the initial schedule, then the available range for Tf is zero to Mo. Thus, the levels for continuous factor Tf are set, i.e., early and late, which are selected randomly in the following two intervals: Early Tf [0.05 Mo~0.4 Mo] and Late Tf [0.6 Mo~0.9 Mo].
The failure duration [15] is the time period (duration) for which the workstation is not available and depends on the time required (Df) to repair the workstation. Workstation failures that only occur during the make-span period result in the values of Df being taken in proportion to Mo. As it is a continuous factor, the factor is set at two levels, and the values are generated using random numbers of short or long duration as follows: short duration Df [0.005 Mo~0.025 Mo] and long duration Df [0.04 Mo~0.06 Mo].
The rescheduling method [15], of which three methods, i.e., RSR, BDM, and GA, have been proposed. Owing to the discrete nature of a factor and the necessity of considering all the methods so as to assess their effect on the performance measure, the factor is set for three levels.
The above multiple factors and their levels are summarized in Table 3. As one factor is set at three levels and the remaining five factors at two levels, the experimental plan works out to be a 31 × 25 statistical factorial design. A full factorial design, therefore, necessitates 2 × 2 × 2 × 2 × 2 × 3 = 96 experimental combinations. For the experimental combinations of each of these levels in a full factorial experimental design, refer to Appendix B. The proposed rescheduling methods are required to produce revised schedules with the start and finish times of each operation, along with a sequence of operations on workstations. The appropriateness of the schedules generated by these methods is illustrated by a numerical example tabulated in Table 4.

Table 3.
Levels of rescheduling factors.

Table 4.
Numerical data.
Though the data for disruption is generated randomly, for illustration, it is taken as Tf = 20, and Df = 15 (refer arrow in the below Figure 6a) for the numerical example as referred in the above Table 4. The data given in Table 4 is processed on the computational programs for each of the three rescheduling methodologies, i.e., RSR, BDM, and GA, developed for generating a new schedule. The computational program is coded in MATLAB for each of the methodologies considered. Computations are executed on a system with the Windows operating environment. The number of generations in GA is kept at ten, as it does not show any significant improvement after ten generations. The original schedule generated by the initial method and the rescheduled schedule generated by the three rescheduling methods are represented using a Gantt chart (refer to Figure 4). The arrow position in Figure 6a denotes the instant of failure, and the hatched region (refer to Figure 6b–d) denotes the failure duration on the breakdown workstation (w2).
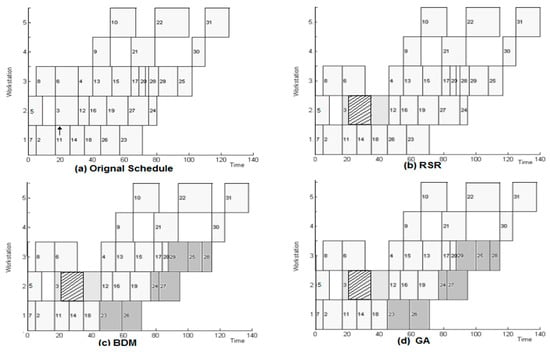
Figure 6.
Gantt chart for operations rescheduling.
From Figure 6b–d, the processing time of the incomplete operation (O3: operation number 3), interrupted during the disruption, is modified, and the processing of the operation is resumed after the disruption. While Figure 6b shows the sequence of operations on workstations remains the same with RSR, in the case of AOR methods, Figure 6c,d show the sequences of some operations are changed (shaded region). This verifies that the programming codes developed for the methods are working properly. Experimentation is performed with different failures of the workstation, the instant of failure, and the duration of failure. From these experiments, the methods are able to generate results for all the variation among disruption data as discussed above. The make-span of the original schedule and the make-span obtained by three rescheduling methods for various disruptions are presented in Table 5.

Table 5.
Make-span obtained by rescheduling.
6. Discussion and Interpretation of Results
This experiment yields values for the performance measures as well as the make-span and computation time for each design of the experiment. With three replications, there will be 288 observations for each performance measure. The results of the computational experiment include the original make-span (the make-span of the schedule before disruption occurs), the make-span obtained in ith replication, and the percent deviation of make-span. The effects of the factors on the percent deviation of the make-span are determined using statistical techniques, such as the plotting method and the analysis of variance, as discussed below [45]. The plotting method is used to study the influence of individual factors and the interaction effects of the different factors on the performance measure. The plot obtained using the mean percent deviation of make-span values for all factors is shown in Figure 7, which shows that the least slope of the plot is for Tf, whereas OIS indicates the highest slope.
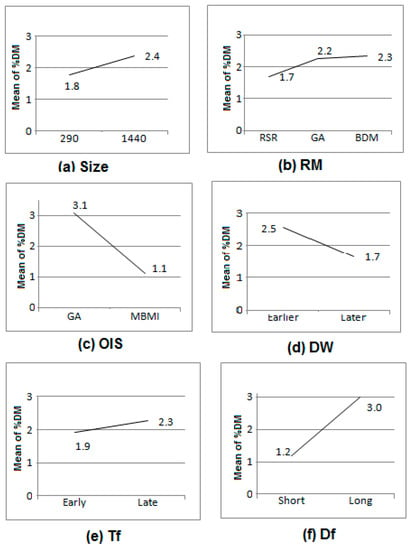
Figure 7.
Effect of the levels of factors on the mean percent deviation of the make-span.
The mean percent deviation of the make-span is lower in the case of smaller-sized problems and increases with greater problem size, which is expected. Disruptions that occur at earlier workstations affect the mean percent deviation of the make-span more than those that occur later. An earlier disruption affects the entire schedule, thereby increasing the mean percent deviation of the make-span. The duration of failure at that particular workstation affects the percent deviation of the make-span to a greater extent, which is highly expected. Though the genetic algorithm is preferred over the bottleneck minimum idleness in scheduling problems, the modified bottleneck minimum idleness indicates a lower mean percent deviation of the make-span. Since the genetic algorithm, in itself, has a lesser idle time than the modified bottleneck minimum idleness. Hence, the modified bottleneck minimum idleness can accommodate disruption more than the genetic algorithm. RSR performs better than the other two methods used for rescheduling (refer to Figure 8). In order to study the combined effect of rescheduling methods with different combinations of other factors, interaction effects are evaluated. The interaction effects of combinations of factors, i.e., RM x OIS, RM x Df, RM x DW, RM x size, and RM x Tf, are studied. The plot obtained for the interaction of RM x OIS using the mean percent deviation of the make-span values is shown in Figure 8a. As the effect of RM is to be studied on OIS, plots obtained for OIS are for the three RM levels separately. Similarly, plots obtained for the other interactions are shown in Figure 8a–e. The horizontal plots of right-shift rescheduling with respect to size and Tf (refer to Figure 8d) indicate that the percent deviation of the make-span remains unaffected, irrespective of level. The interaction effects of Df x RM, Tf x RM, DW x RM, and size x RM are not significant. The intersection of the lines in Figure 6a is an indication of a major interaction effect between the levels of factors OIS and DM. Once the initial schedule is obtained by the modified bottleneck minimum idleness method, affected operation rescheduling methods improve schedule performance. Thus, the right-shift rescheduling, as indicated in above Figure 8b, performs better when the initial schedule is prepared using a modified bottleneck minimum idleness approach. This is because when the initial schedule is suboptimal, there is more idle time available on the machining workstation to accommodate disruptions and reduce the make-span. However, the differences seen between the performances of right-shift rescheduling and affected operation rescheduling are quite negligible. Subsequently, an ANOVA is used to do statistical analysis of the results, and the FEst value and estimated FTab value are compared, as shown in Table 6. The FEst values are higher than the corresponding FTab values at a 95% confidence level for all factors except for the factor Tf. Therefore, the size, RM, OIS, Df, and DW contribute significantly to the %DM variation. Among these interactions, only the RM x OIS interaction is found to be significant.
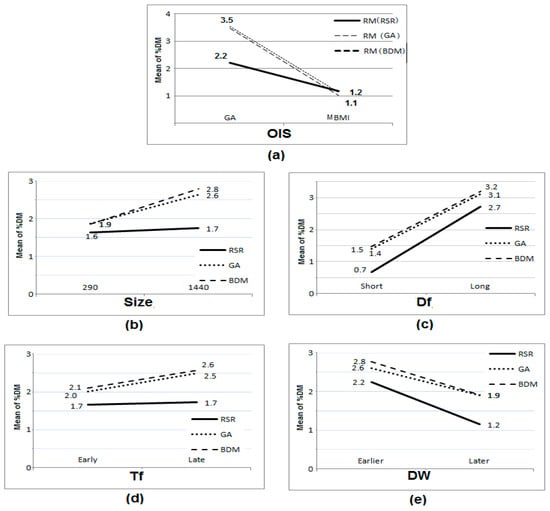
Figure 8.
Interaction effect of factors with RM on mean %DM, where (a) interaction of RM x OIS (b) interaction of RM x Size (c) interaction of RM x Df (d) interaction of RM x Tf and (e) interaction of RM vs. DW.

Table 6.
Statistical analysis of the factors influencing disruptions and their interactions.
7. Conclusions
On the occurrence of disruptions like machine failure, the original schedule of the flow-shop needs to be revised and/or rescheduled. In such a scenario, rescheduling methods based on right-shift rescheduling and the affected operations rescheduling strategy work very well. Here in this study, the deviation of the make-span of the revised schedule from the original schedule is used as a performance measure. The severity of the influence of different factors on the percent deviation, i.e., the extent to which make-span of the original schedule is natural, where factors influencing make-span deviation of the schedule are optimality of the initial solution; failure duration; deviation of make-span; and rescheduling method, size, and instant of failure. The initial schedule and problem size depend on the manufacturing system for which scheduling is performed, but the method of rescheduling depends on the decision as to which rescheduling approach is to be selected. The higher severity of effect of duration of failure is quite natural. However, the considerable influence of the make-span deviation and instant of failure is worth noting. Similarly, the percent deviation of make-span is directly proportional to failure duration, instant of failure, rescheduling method, and problem size, whereas it is inversely proportional to the optimality of the initial solution and disrupted workstation. The investigation into the interactions revealed that a major interaction exists between the rescheduling method and the optimality of the initial solution. They indicate that, though right-shift rescheduling is the preferred method in the majority of situations, the affected operation rescheduling method is also equally suitable when the initial solution is created using modified bottleneck minimum idleness. The setup time, changeover time, and transport time are not considered in this work. Our method can be applied to other performance measures, such as due dates. This work may be extended to include other disruptions, such as alterations in order priority, multiple machine failures, new orders, the modification or cancellation of orders, etc.
Author Contributions
Conceptualization, A.S.B. and P.M.K.; Data curation, M.D.N. and P.D.P.; Formal analysis, P.M.K. and M.D.N.; Funding acquisition, A.U.R.; Investigation, A.S.B. and P.D.P.; Methodology, A.S.B., P.M.K., M.D.N. and P.D.P.; Project administration, A.S.B. and A.U.R.; Software, A.S.B. and A.U.R.; Supervision, P.M.K. and A.U.R.; Validation, A.U.R. and P.S.; Visualization, A.S.B., P.S. and A.U.R.; Writing—original draft, A.S.B. and P.M.K.; Writing—review and editing, A.S.B., P.S. and A.U.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Researchers Supporting Project number (RSPD2023R701), King Saud University, Riyadh, Saudi Arabia.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within this article.
Acknowledgments
The authors are thankful to the King Saud University for funding this work through the Researchers Supporting Project number (RSPD2023R701), King Saud University, Riyadh, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Rescheduling overview.
Table A1.
Rescheduling overview.
| Ref. | Initial Schedule | Rescheduling Strategy * | Performance Measure | Disruptions ** | Production System | Findings/Remarks |
|---|---|---|---|---|---|---|
| [14] | Nominal | AOR | Flow time, tardiness, and machine utilization | MF, NJ, JC, urgent job | Flexible manufacturing system (FMS) | Shortlisted dispatching rules performed better than the early due date for rescheduling |
| [15] | Nominal | RSR/AOR/TR | Efficiency and stability | MF | Job-shop | AOR demonstrated superior performance over all other methods in most situations |
| [16] | Nominal | RSR/AOR | Earliness, tardiness, and stability | MF | Flow-shop | Used the embedded dominance rule for rescheduling |
| [17] | Nominal | AOR | Robustness | MF | Flow-shop | Determined trigger value for deciding rescheduling |
| [18] | Nominal | AOR | Machine utilization, setup, and rescheduling frequency | MF | Parallel machine | Used periodic, event-driven, and hybrid rescheduling strategies |
| [19] | Normal | AOR | Tardiness | MF, NJ, JC | Job-shop FMS | An adaptive genetic algorithm is applied |
| [20] | Nominal | RSR/AOR | Make-span and deviation of the start times | MF, NJ, PT vary, urgent job | Job-shop | AOR performed better. Experimented with up to 500 operations for various sizes and incidences of disruptions |
| [21] | Nominal | RSR/AOR/TR | Total weighted tardiness | MF | Job-shop | TR outperformed other methods. Used a modified shifting bottleneck method for scheduling and rescheduling. |
| [22] | No schedule | AOR | make-span, tardiness, and start time deviation | NJ | Job-shop | Used the genetic local search method for periodic rescheduling |
| [23] | Nominal | AOR | Total flow time and number of disrupted jobs | MF | Parallel machine | Used the shortest processing time for rescheduling |
| [24] | Nominal | AOR | Cost deviation related to part and machine preparation | MF, NJ | FMS/Job-shop | Used an agent-based approach |
| [25] | Dispatching rule | RSR/AOR | Tardiness and degree of similarity | MF | Job-shop | The proposed method of message passing and the local search algorithm performed well |
| [26] | Normal | AOR | Efficiency | NJ | Job-shop | Genetic algorithm-based reactive scheduling |
| [27] | Robust | RSR | Robustness and deviation of completion times | MF | Single machine | Applied to the predictive schedule |
| [28] | Nominal | RSR AOR | Make-span and lateness | NJ, delay in processing time | Flow-shop with parallel machines | Initial schedule was generated with a commercial constraint programming solver and a low impact rescheduling algorithm was proposed |
| [29] | Nominal | RSR AOR | Earliness, tardiness, and cost and deviation of completion time | MF | Parallel machine | A linear programming model for scheduling and a minimum-cost network flow algorithm were used for reactive scheduling. |
| [30] | Nominal | AOR | Flowtime and stability in tooling cost | MF | Unrelated parallel machines | Used algorithms by incorporating powerful reduction and bounding mechanisms |
| [31] | Nominal | AOR | Tardiness, flowtime, and make-span and stability in start times | MF | Job-shop | Dispatching rules generated an initial schedule |
| [32] | Nominal | AOR/RSR | Tardiness, number of tardy jobs, setup time, total idle time of machines, total flow time, start time deviation, and change in operations sequence | NJ | Job-shop | The match-up algorithms proposed performed well |
| [33] | Normal | AOR | Make-span and tardiness, start time and process sequence deviation, and change in machine allocation | NJ | FMS | A genetic algorithm was proposed for match up scheduling with a non-reshuffle strategy and performed better than the reshuffle and TR methods |
| [34] | Nominal | RSR AOR TR | Make-span and deviation of the start times | MF, NJ, Job ready time variation | Flow-shop | An iterated greedy algorithm was used for predictive and reactive scheduling. It performed better than the local search and repair method |
| [35] | Nominal | RSR/AOR | No. of disrupted jobs and cost due to additional resources | MF | Unidentical parallel machines | Heuristics for the initial schedule and improvement used the local search algorithm |
| [36] | Normal | Periodic/event driven | Make-span, tardiness, and start time deviation, and cost | NJ | Job-shop | A non-dominated sorting algorithm was used. Length of the scheduling interval, no. of jobs added, and shop utilization showed influence on efficiency measures |
| [37] | Normal | AOR | Make-span and energy consumption | Job-shop | Applied match-up and memetic algorithms in a sustainable environment | |
| [38] | Normal | AOR/RSR | Equipment utilization and degree of similarity | MF | Job-shop with parallel machines | The concept of match-up scheduling was used for single and group machines, for partial repair of affected segment(s) of the schedule |
| [39] | Normal | Selection from trained data | Tardiness | NJ | Job-shop | The knowledge gathered with the deep learning reinforcement method was used for the optimal sequence and repair of operations |
| [40] | Normal | AOR | Make-span and deviation of no. of job allocations | Hybrid flow-shop | A multi-objective evolutionary algorithm was employed | |
| [41] | Normal | RSR/AOR | Make-span, computational time, energy consumption, and setup time | MF | Unidentical parallel machines | Used greedy heuristics and metaheuristics |
| [42] | Normal | Simulation | Delivery due dates | Change in delivery plan | Hybrid flow-shop | Multimethod modeling was used, which involved simulation of interacting agents with any logic software |
| [43] | Nominal | Simulation | Make-span and completion time | MF | Assembly flow-shop | Used an adaptive evolutionary algorithm on a two-stage assembly flow-shop scheduling problem with random breakdowns |
* Note: RSR—right-shift rescheduling, AOR—affected operation rescheduling, and TR—total rescheduling. ** Note: MF—Machine failure, NJ—New job, OC—Order cancellation, PT—processing time.
Appendix B

Table A2.
Full factorial experimental design.
Table A2.
Full factorial experimental design.
| # | F1 $ | F2 | F3 | F4 | F5 | F6 | # | F1 | F2 | F3 | F4 | F5 | F6 | # | F1 | F2 | F3 | F4 | F5 | F6 | # | F1 | F2 | F3 | F4 | F5 | F6 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 25 | 1 | 2 | 1 | 1 | 1 | 2 | 49 | 2 | 1 | 1 | 1 | 1 | 1 | 73 | 2 | 2 | 1 | 1 | 1 | 2 |
| 2 | 1 | 1 | 2 | 1 | 1 | 1 | 26 | 1 | 2 | 2 | 1 | 1 | 2 | 50 | 2 | 1 | 2 | 1 | 1 | 1 | 74 | 2 | 2 | 2 | 1 | 1 | 2 |
| 3 | 1 | 1 | 1 | 1 | 2 | 1 | 27 | 1 | 2 | 1 | 1 | 2 | 2 | 51 | 2 | 1 | 1 | 1 | 2 | 1 | 75 | 2 | 2 | 1 | 1 | 2 | 2 |
| 4 | 1 | 1 | 2 | 1 | 2 | 1 | 28 | 1 | 2 | 2 | 1 | 2 | 2 | 52 | 2 | 1 | 2 | 1 | 2 | 1 | 76 | 2 | 2 | 2 | 1 | 2 | 2 |
| 5 | 1 | 1 | 1 | 2 | 1 | 1 | 29 | 1 | 2 | 1 | 2 | 1 | 2 | 53 | 2 | 1 | 1 | 2 | 1 | 1 | 77 | 2 | 2 | 1 | 2 | 1 | 2 |
| 6 | 1 | 1 | 2 | 2 | 1 | 1 | 30 | 1 | 2 | 2 | 2 | 1 | 2 | 54 | 2 | 1 | 2 | 2 | 1 | 1 | 78 | 2 | 2 | 2 | 2 | 1 | 2 |
| 7 | 1 | 1 | 1 | 2 | 2 | 1 | 31 | 1 | 2 | 1 | 2 | 2 | 2 | 55 | 2 | 1 | 1 | 2 | 2 | 1 | 79 | 2 | 2 | 1 | 2 | 2 | 2 |
| 8 | 1 | 1 | 2 | 2 | 2 | 1 | 32 | 1 | 2 | 2 | 2 | 2 | 2 | 56 | 2 | 1 | 2 | 2 | 2 | 1 | 80 | 2 | 2 | 2 | 2 | 2 | 2 |
| 9 | 1 | 2 | 1 | 1 | 1 | 1 | 33 | 1 | 1 | 1 | 1 | 1 | 3 | 57 | 2 | 2 | 1 | 1 | 1 | 1 | 81 | 2 | 1 | 1 | 1 | 1 | 3 |
| 10 | 1 | 2 | 2 | 1 | 1 | 1 | 34 | 1 | 1 | 2 | 1 | 1 | 3 | 58 | 2 | 2 | 2 | 1 | 1 | 1 | 82 | 2 | 1 | 2 | 1 | 1 | 3 |
| 11 | 1 | 2 | 1 | 1 | 2 | 1 | 35 | 1 | 1 | 1 | 1 | 2 | 3 | 59 | 2 | 2 | 1 | 1 | 2 | 1 | 83 | 2 | 1 | 1 | 1 | 2 | 3 |
| 12 | 1 | 2 | 2 | 1 | 2 | 1 | 36 | 1 | 1 | 2 | 1 | 2 | 3 | 60 | 2 | 2 | 2 | 1 | 2 | 1 | 84 | 2 | 1 | 2 | 1 | 2 | 3 |
| 13 | 1 | 2 | 1 | 2 | 1 | 1 | 37 | 1 | 1 | 1 | 2 | 1 | 3 | 61 | 2 | 2 | 1 | 2 | 1 | 1 | 85 | 2 | 1 | 1 | 2 | 1 | 3 |
| 14 | 1 | 2 | 2 | 2 | 1 | 1 | 38 | 1 | 1 | 2 | 2 | 1 | 3 | 62 | 2 | 2 | 2 | 2 | 1 | 1 | 86 | 2 | 1 | 2 | 2 | 1 | 3 |
| 15 | 1 | 2 | 1 | 2 | 2 | 1 | 39 | 1 | 1 | 1 | 2 | 2 | 3 | 63 | 2 | 2 | 1 | 2 | 2 | 1 | 87 | 2 | 1 | 1 | 2 | 2 | 3 |
| 16 | 1 | 2 | 2 | 2 | 2 | 1 | 40 | 1 | 1 | 2 | 2 | 2 | 3 | 64 | 2 | 2 | 2 | 2 | 2 | 1 | 88 | 2 | 1 | 2 | 2 | 2 | 3 |
| 17 | 1 | 1 | 1 | 1 | 1 | 2 | 41 | 1 | 2 | 1 | 1 | 1 | 3 | 65 | 2 | 1 | 1 | 1 | 1 | 2 | 89 | 2 | 2 | 1 | 1 | 1 | 3 |
| 18 | 1 | 1 | 2 | 1 | 1 | 2 | 42 | 1 | 2 | 2 | 1 | 1 | 3 | 66 | 2 | 1 | 2 | 1 | 1 | 2 | 90 | 2 | 2 | 2 | 1 | 1 | 3 |
| 19 | 1 | 1 | 1 | 1 | 2 | 2 | 43 | 1 | 2 | 1 | 1 | 2 | 3 | 67 | 2 | 1 | 1 | 1 | 2 | 2 | 91 | 2 | 2 | 1 | 1 | 2 | 3 |
| 20 | 1 | 1 | 2 | 1 | 2 | 2 | 44 | 1 | 2 | 2 | 1 | 2 | 3 | 68 | 2 | 1 | 2 | 1 | 2 | 2 | 92 | 2 | 2 | 2 | 1 | 2 | 3 |
| 21 | 1 | 1 | 1 | 2 | 1 | 2 | 45 | 1 | 2 | 1 | 2 | 1 | 3 | 69 | 2 | 1 | 1 | 2 | 1 | 2 | 93 | 2 | 2 | 1 | 2 | 1 | 3 |
| 22 | 1 | 1 | 2 | 2 | 1 | 2 | 46 | 1 | 2 | 2 | 2 | 1 | 3 | 70 | 2 | 1 | 2 | 2 | 1 | 2 | 94 | 2 | 2 | 2 | 2 | 1 | 3 |
| 23 | 1 | 1 | 1 | 2 | 2 | 2 | 47 | 1 | 2 | 1 | 2 | 2 | 3 | 71 | 2 | 1 | 1 | 2 | 2 | 2 | 95 | 2 | 2 | 1 | 2 | 2 | 3 |
| 24 | 1 | 1 | 2 | 2 | 2 | 2 | 48 | 1 | 2 | 2 | 2 | 2 | 3 | 72 | 2 | 1 | 2 | 2 | 2 | 2 | 96 | 2 | 2 | 2 | 2 | 2 | 3 |
Note: $ Refer to Table 3; #: Experiment number.
References
- Pinedo, M.L. Scheduling: Theory, Algorithms and Systems, 3rd ed.; Springer International Publisher: Cham, Switzerland, 2022. [Google Scholar]
- Rooyani, D.; Defersha, F. A Two-Stage Multi-Objective Genetic Algorithm for a Flexible Job Shop Scheduling Problem with Lot Streaming. Algorithms 2022, 15, 246. [Google Scholar] [CrossRef]
- Mahdavi, I.; Komaki, G.M.; Kayvanfar, V. Aggregate Hybrid Flowshop Scheduling with Assembly Operations. In Proceedings of the 2011 IEEE 18th International Conference on Industrial Engineering and Engineering Management, Changchun, China, 3–5 September 2011; Volume 1, pp. 663–667. [Google Scholar]
- Khodke, P.M.; Bhongade, A.S. Real-Time Scheduling in Manufacturing System with Machining and Assembly Operations: A State of Art. Int. J. Prod. Res. 2013, 51, 4966–4978. [Google Scholar] [CrossRef]
- Komaki, G.M.; Sheikh, S.; Malakooti, B. Flow Shop Scheduling Problems with Assembly Operations: A Review and New Trends. Int. J. Prod. Res. 2019, 57, 2926–2955. [Google Scholar] [CrossRef]
- Jabbari, M.; Tavana, M.; Fattahi, P.; Daneshamooz, F. A Parameter Tuned Hybrid Algorithm for Solving Flow Shop Scheduling Problems with Parallel Assembly Stages. Sustain. Oper. Comput. 2022, 3, 22–32. [Google Scholar] [CrossRef]
- Yokoyama, M. Flow-Shop Scheduling with Setup and Assembly Operations. Eur. J. Oper. Res. 2008, 187, 1184–1195. [Google Scholar] [CrossRef]
- Lagodimos, A.G.; Mihiotis, A.N.; Kosmidis, V.C. Scheduling a Multi-Stage Fabrication Shop for Efficient Subsequent Assembly Operations. Int. J. Prod. Econ. 2004, 90, 345–359. [Google Scholar] [CrossRef]
- Shokrollahpour, E.; Zandieh, M.; Dorri, B. A Novel Imperialist Competitive Algorithm for Bi-Criteria Scheduling of the Assembly Flowshop Problem. Int. J. Prod. Res. 2011, 49, 3087–3103. [Google Scholar] [CrossRef]
- Hatami, S.; Ebrahimnejad, S.; Tavakkoli-Moghaddam, R.; Maboudian, Y. Two Meta-Heuristics for Three-Stage Assembly Flowshop Scheduling with Sequence-Dependent Setup Times. Int. J. Adv. Manuf. Technol. 2010, 50, 1153–1164. [Google Scholar] [CrossRef]
- Ouelhadj, D.; Petrovic, S. A Survey of Dynamic Scheduling in Manufacturing Systems. J. Sched. 2009, 12, 417–431. [Google Scholar] [CrossRef]
- Zhang, X.; Han, Y.; Królczyk, G.; Rydel, M.; Stanislawski, R.; Li, Z. Rescheduling of Distributed Manufacturing System with Machine Breakdowns. Electronics 2022, 11, 249. [Google Scholar] [CrossRef]
- Ghaleb, M.; Zolfagharinia, H.; Taghipour, S. Real-Time Production Scheduling in the Industry-4.0 Context: Addressing Uncertainties in Job Arrivals and Machine Breakdowns. Comput. Oper. Res. 2020, 123, 105031. [Google Scholar] [CrossRef]
- Duan, J.; Wang, J. Robust Scheduling for Flexible Machining Job Shop Subject to Machine Breakdowns and New Job Arrivals Considering System Reusability and Task Recurrence. Expert Syst. Appl. 2022, 203, 117489. [Google Scholar] [CrossRef]
- Valledor, P.; Gomez, A.; Priore, P.; Puente, J. Modelling and Solving Rescheduling Problems in Dynamic Permutation Flow Shop Environments. Complexity 2020, 2020, e2862186. [Google Scholar] [CrossRef]
- Kim, Y.-I.; Kim, H.-J. Rescheduling of Unrelated Parallel Machines with Job-Dependent Setup Times under Forecasted Machine Breakdown. Int. J. Prod. Res. 2021, 59, 5236–5258. [Google Scholar] [CrossRef]
- Guo, B.; Nonaka, Y. Rescheduling and Optimization of Schedules Considering Machine Failures. Int. J. Prod. Econ. 1999, 60, 503–513. [Google Scholar] [CrossRef]
- Vieira, G.E.; Herrmann, J.W.; Lin, E. Predicting the Performance of Rescheduling Strategies for Parallel Machine Systems. J. Manuf. Syst. 2000, 19, 256–266. [Google Scholar] [CrossRef]
- Honghong, Y.; Zhiming, W. The Application of Adaptive Genetic Algorithms in FMS Dynamic Rescheduling. Int. J. Comput. Integr. Manuf. 2003, 16, 382–397. [Google Scholar] [CrossRef]
- Subramaniam, V.; Raheja, A.S. MAOR: A Heuristic-Based Reactive Repair Mechanism for Job Shop Schedules. Int. J. Adv. Manuf. Technol. 2003, 22, 669–680. [Google Scholar] [CrossRef]
- Mason, S.J.; Jin, S.; Wessels, C.M. Rescheduling Strategies for Minimizing Total Weighted Tardiness in Complex Job Shops. Int. J. Prod. Res. 2004, 42, 613–628. [Google Scholar] [CrossRef]
- Rangsaritratsamee, R.; Ferrell, W.G.; Kurz, M.B. Dynamic Rescheduling That Simultaneously Considers Efficiency and Stability. Comput. Ind. Eng. 2004, 46, 1–15. [Google Scholar] [CrossRef]
- Azizoǧlu, M.; Alagöz, O. Parallel-Machine Rescheduling with Machine Disruptions. IIE Trans. (Inst. Ind. Eng.) 2005, 37, 1113–1118. [Google Scholar] [CrossRef]
- Wong, T.N.; Leung, C.W.; Mak, K.L.; Fung, R.Y.K. Integrated Process Planning and Scheduling/Rescheduling—An Agent-Based Approach. Proc. Int. J. Prod. Res. 2006, 44, 3627–3655. [Google Scholar] [CrossRef]
- Cheng, M.; Sugi, M.; Ota, J.; Yamamoto, M.; Ito, H.; Inoue, K. A fast rescheduling method in semiconductor manufacturing allowing for tardiness and scheduling stability. In Proceedings of the 2006 IEEE International Conference on Automation Science and Engineering, Shanghai, China, 8–10 October 2006. [Google Scholar]
- Sakaguchi, T.; Kamimura, T.; Shirase, K.; Tanimizu, Y. GA Based Reactive Scheduling for Aggregate Production Scheduling. In Manufacturing Systems and Technologies for the New Frontier; Mitsuishi, M., Ueda, K., Kimura, F., Eds.; Springer: London, UK, 2008; pp. 275–278. [Google Scholar]
- Liu, L.; Gu, H.Y.; Xi, Y.G. Robust and Stable Scheduling of a Single Machine with Random Machine Breakdowns. Int. J. Adv. Manuf. Technol. 2007, 31, 645–654. [Google Scholar] [CrossRef]
- Caricato, P.; Grieco, A. An Online Approach to Dynamic Rescheduling for Production Planning Applications. Int. J. Prod. Res. 2008, 46, 4597–4617. [Google Scholar] [CrossRef]
- Turkcan, A.; Akturk, M.S.; Storer, R.H. Predictive/Reactive Scheduling with Controllable Processing Times and Earliness-Tardiness Penalties. IIE Trans. (Inst. Ind. Eng.) 2009, 41, 1080–1095. [Google Scholar] [CrossRef]
- Özlen, M.; Azizoĝlu, M. Generating All Efficient Solutions of a Rescheduling Problem on Unrelated Parallel Machines. Int. J. Prod. Res. 2009, 47, 5245–5270. [Google Scholar] [CrossRef]
- Dong, Y.H.; Jang, J. Production Rescheduling for Machine Breakdown at a Job Shop. Int. J. Prod. Res. 2012, 50, 2681–2691. [Google Scholar] [CrossRef]
- Moratori, P.; Petrovic, S.; Vázquez-Rodrguez, J.A. Match-up Approaches to a Dynamic Rescheduling Problem. Int. J. Prod. Res. 2012, 50, 261–276. [Google Scholar] [CrossRef]
- Zakaria, Z.; Petrovic, S. Genetic Algorithms for Match-up Rescheduling of the Flexible Manufacturing Systems. Comput. Ind. Eng. 2012, 62, 670–686. [Google Scholar] [CrossRef]
- Katragjini, K.; Vallada, E.; Ruiz, R. Flow Shop Rescheduling under Different Types of Disruption. Int. J. Prod. Res. 2013, 51, 780–797. [Google Scholar] [CrossRef]
- Gürel, S.; Cincioğlu, D. Rescheduling with Controllable Processing Times for Number of Disrupted Jobs and Manufacturing Cost Objectives. Int. J. Prod. Res. 2015, 53, 2751–2770. [Google Scholar] [CrossRef]
- Jin, L.; Zhang, C.; Shao, X.; Yang, X. A Study on the Impact of Periodic and Event-Driven Rescheduling on a Manufacturing System: An Integrated Process Planning and Scheduling Case. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2017, 231, 490–504. [Google Scholar] [CrossRef]
- Salido, M.A.; Escamilla, J.; Barber, F.; Giret, A. Rescheduling in Job-Shop Problems for Sustainable Manufacturing Systems. J. Clean. Prod. 2017, 162, S121–S132. [Google Scholar] [CrossRef]
- Qiao, F.; Ma, Y.; Zhou, M.; Wu, Q. A Novel Rescheduling Method for Dynamic Semiconductor Manufacturing Systems. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 1679–1689. [Google Scholar] [CrossRef]
- Palombarini, J.A.; Martínez, E.C. Automatic Generation of Rescheduling Knowledge in Socio-Technical Manufacturing Systems Using Deep Reinforcement Learning. In Proceedings of the 2018 IEEE Biennial Congress of Argentina (ARGENCON), San Miguel de Tucuman, Argentina, 6–8 June 2018; pp. 1–8. [Google Scholar]
- Zhang, B.; Pan, Q.; Gao, L.; Zhao, Y. MOEA/D for Multi-Objective Hybrid Flowshop Rescheduling Problem. In Proceedings of the IEEE Congress on Evolutionary Computation, CEC 2008, (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2018; Volume 4. [Google Scholar]
- Ferrer, S.; Nicolò, G.; Salido, M.A.; Giret, A.; Barber, F. Dynamic Rescheduling in Energy-Aware Unrelated Parallel Machine Problems. In IFIP Advances in Information and Communication Technology; Springer New York LLC: New York, NY, USA, 2018; Volume 536, pp. 232–240. [Google Scholar]
- Uhlmann, I.R.; Zanella, R.M.; Frazzon, E.M. Hybrid Flow Shop Rescheduling for Contract Manufacturing Services. Int. J. Prod. Res. 2022, 60, 1069–1085. [Google Scholar] [CrossRef]
- Seidgar, H.; Rad, S.T.; Shafaei, R. Scheduling of Assembly Flow Shop Problem and Machines with Random Breakdowns. Int. J. Oper. Res. 2017, 29, 273–293. [Google Scholar] [CrossRef]
- Bhongade, A.S.; Khodke, P.M. A Genetic Algorithm for Flow Shop Scheduling with Assembly Operations to Minimize Makespan. J. Inst. Eng. (India) Ser. C 2014, 95, 89–96. [Google Scholar] [CrossRef]
- Mitra, A. The Taguchi Method. WIREs Comput. Stat. 2011, 3, 472–480. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).