Abstract
Graph regularized non-negative matrix factorization (GNMF) is widely used in feature extraction. In the process of dimensionality reduction, GNMF can retain the internal manifold structure of data by adding a regularizer to non-negative matrix factorization (NMF). Because Ga NMF regularizer is implemented by local preserving projections (LPP), there are small sample size problems (SSS). In view of the above problems, a new algorithm named robust exponential graph regularized non-negative matrix factorization (REGNMF) is proposed in this paper. By adding a matrix exponent to the regularizer of GNMF, the possible existing singular matrix will change into a non-singular matrix. This model successfully solves the problems in the above algorithm. For the optimization problem of the REGNMF algorithm, we use a multiplicative non-negative updating rule to iteratively solve the REGNMF method. Finally, this method is applied to AR, COIL database, Yale noise set, and AR occlusion dataset for performance test, and the experimental results are compared with some existing methods. The results indicate that the proposed method is more significant.
Keywords:
graph regularization non-negative matrix factorization (GNMF); non-negative matrix factorization (NMF); local preserving projections (LPP); feature extraction; SSS problems MSC:
68Q99
1. Introduction
In recent years, technologies such as computer vision and pattern recognition have been widely used in all walks of life. In many application scenarios, the dimension of the data matrix that needs to be calculated is very high. For example, a photo of 100 × 100 pixels has 10,000 dimensions in the computer, which enormously increases the difficulty of data processing. For dealing with the problem of the “dimensionality curse” [1], many dimensionality reduction algorithms have been proposed, for instance, principal component analysis (PCA) [2] and linear discriminant analysis (LDA) [3], in the literature [4]. The linear dimensionality reduction algorithm has the advantages of being simple to operate and easy to analyze, but it is no longer effective when the data have non-linear structure. However, in reality, high-dimensional data are usually non-linear structures. When using linear dimensionality reduction methods to extract features from high-dimensional data, we often cannot get a good effect.
For dealing with high-dimensional non-linear data, manifold learning algorithms show an ideal result. Scholars have paid attention to the fact that in practical applications, the neighborhood relationship of data plays an important role, considering that different datasets have different manifold structures. The structure of the data is embedded in the projected function, which can achieve more efficient dimensionality reduction. Examples such as Laplacian Eigenmaps (LE) [5,6], local linear embedding (LLE) [7,8], local preserving projections (LPP) [9,10], neighborhood preserving embedding (NPE) [11,12] and supervised low-rank embedded regression (SLRER) [13] are all classical manifold learning algorithms. LPP retains the local neighborhood information between sample points on the database by constructing the neighborhood map of the sample points. After projection, the nearest neighbor relationship of sample data in high-dimensional space is still maintained in the low-dimensional subspace.
In addition to manifold learning algorithms, matrix factorization can also achieve the purpose of dimensionality reduction. The matrix decomposition method hopes to seek out two or more low-dimensional matrices so that their product can approximate the original matrix. Typical matrix factorization technologies consist of singular value decomposition (SVD) [14], NMF [15], etc. The NMF method is based on the principle of physiology that the overall perception of human beings is composed of local perceptions (purely additive) and is introduced into data processing to form global data by accumulating various parts of the data [16,17]. The idea of the NMF algorithm is to represent the whole by the part. NMF is a partial-based linear representation of non-negative data. Due to the strong constraint of NMF on the non-negativity of the factor matrices, the NMF algorithm has better interpretability and is more in line with human cognition. For any matrix A, NMF can discover two non-negative factor matrices U and V, so that A is equal to the product of U and V. Therefore, NMF can decompose a matrix into the form of the product of left and right non-negative matrices. Different from SVD, the matrices obtained by SVD can be positive or negative, whereas the matrices obtained by NMF are both non-negative, and NMF only allows addition but not subtraction.
Nevertheless, traditional NMF methods have some problems, such as poor robustness to noise and outliers, lack of discriminative information, etc. In recent years, the improvement of the NMF algorithm has become a research hotspot. Lu et al. proposed low-rank non-negative factorization (LRNF) [18], which learns low-rank representations of data and performs non-negative matrix factorization at the same time, eliminating the effect of noisy data on dimensionality reduction. On the basis of LRNF, Lu et al. introduced structural inconsistency and then proposed a new model, i.e., structurally incoherent low-rank NMF (SILR-NMF) [19]. SILR-NMF is able to learn the global structure of samples and introduced sample label information so as to ensure that the clean data points of different categories shall be independent as far as possible. The semi-supervised NMF (SSNMF) method proposed in reference [20] merges the label information and sample matrix into the traditional NMF framework. Robust semi-supervised NMF (RSSNMF) [21] adopts the L2,1 norm as the loss function and incorporates discriminant information into extra conditions. The algorithm is better to accommodate noise and outliers. A semi-supervised non-negative matrix factorization method [22] is proposed for dissimilarity and similarity regularization, which can better utilize label information by introducing a pair of complementary regularizers for matrix factorization.
However, the above NMF algorithms do not take the geometric structure into account in the initial data space when performing matrix decomposition. However, the geometric structure inside the data plays an important part in practical applications. For the sake of improving the recognition rate of NMF, a form of graph regularization is introduced. GNMF [23] combines NMF with the objective function of LPP and adds a regularization parameter on the basis of the original NMF. According to GNMF, robust manifold NMF (RMNMF) [24] is proposed, which adopts the L1 norm to increase the constraints on the noise matrix. Yi et al. [25] propose NMF with locality constrained adaptive graph (NMF-LCAG), in which two local constraints are used to adaptively optimize the graph composition. NMF-LCAG can learn the weight matrix of the graph and the low-dimensional properties of the samples at the same time. The combination of NMF and graph embedding can greatly improve the dimensionality reduction effect and bring both into full play, maintaining the geometric structure of data while exploiting a parts-based linear representation of non-negative information.
Most of the current non-negative matrix factorization algorithms for graph embedding do not consider the problem of matrix singularity, therefore, graph embedding often causes SSS problems [26]. In the past few decades, the analysis method according to matrix index to solve the SSS problems has received extensive concern, for example, exponential locality preserving projection (ELPP) [27], exponential elasticity preserving projection (EEPP) [28], exponential local discriminant embedding (ELDE) [29], exponential discriminant analysis (EDA) [30], exponential semi-spervised discriminant embedding (ESDE) [31], Krylov-EDA [32], exponential marginal Fisher analysis (EMFA) [33], etc. The exponential operation of matrices is also related to much scientific computing work and is widely used in nuclear magnetic resonance spectroscopy, control theory, Markov chain analysis, and other fields. For example, in boundary Fisher analysis, Guo et al. [34] transformed the inverse matrix into a matrix exponent inverse matrix for training support vector machines (SVM) and successfully solved the matrix singularity problem in the process of data optimization. Ivanovs et al. [35] analyzed the number of zero points of the determinant composed of the matrix index of the Markov addition process (MAP) with the unilateral jump, and the theoretical model obtained was widely used in the financial field. MEDLPP [36] introduced the matrix index into DLPP to solve its SSS problems and made corresponding improvements to shorten the running time. Reference [37] proposed the exponential form framework of the dimensionality reduction algorithm, and it pointed out that the index of the matrix is non-singular, so the method based on the matrix index can effectively solve the SSS problems. Many results show that the matrix index discriminant analysis method often has a stronger discriminative ability than the original method.
To sum up, in GNMF, LPP will have the SSS problem, which greatly affects the dimensionality reduction effect. To handle the aforementioned problem, we propose a novel method, i.e., a robust exponential graph regularization NMF algorithm (REGNMF). In REGNMF, the matrix exponent is added to the objection function so that the original Laplacian matrix is not singular. The optimal solution of the model is obtained by the non-greedy iterative method of Lagrangian, which successfully solves the SSS problems. Experiments with this algorithm on multiple databases show that its image feature extraction effect is better than some other algorithms.
The main contributions of this article are as follows:
- (1)
- A new robust graph embedding algorithm, i.e., REGNMF, for unsupervised subspace learning is proposed in this article. On the basis of Euclidean distance and exponential Laplacian matrix as robustness criteria, we introduce an iterative algorithm to address optimization problems.
- (2)
- Different from the traditional GNMF algorithm, REGNMF can not only successfully solve the SSS problems by introducing the matrix exponent but gain a part-based representation of data. Test sample points are mapped into a novel subspace by learning the base matrix without being affected by singular matrices.
- (3)
- REGNMF improves the robust capacity of existing NMF algorithms based on graph embedding. In the contrast to existing methods, REGNMF can recode part-based geometric information of samples to classify. Extensive experiments show that our proposed methods runs well and outperforms existing algorithms on most occasions, especially on noisy and corrupted databases.
The remainder of the paper is organized as follows: For the convenience of understanding, Section 2 describes some related work. Section 3 clarifies some details of REGNMF, including the objective function, optimization process, etc. Section 4 gives the operation results of relevant algorithms on different databases. Section 5 summarizes the article.
2. Related Work
Suppose is a sample dataset of the original space, is the projection dataset, and is the subspace dimension. Then we can obtain the formula as follows:
2.1. Matrix Exponent [27]
The exponential operation of matrices is also related to much scientific computing work and is widely used in nuclear magnetic resonance spectroscopy, control theory, Markov chain analysis, and other fields. In this section, we give the definition of the matrix exponent and its properties. Suppose D is a square matrix of , the matrix exponent formula of D is defined below:
where I indicates an identity matrix of n × n. According to the Taylor series expansion theorem, we can convert the matrix index into the form of infinite matrix series. By proving the convergence and divergence of infinite matrix series, we get that is convergent. In other words, is a definite matrix. Matrix exponents have the following properties:
- (1)
- is a full rank matrix;
- (2)
- If the matrices M and N are commutative, that is , then ;
- (3)
- For any matrix M, exists, and ;
- (4)
- Suppose that T is a non-singular matrix, then ;
- (5)
- Assuming that are the eigenvectors of D, and the corresponding to eigenvalues are , then still are the eigenvectors corresponding to the eigenvalues of matrix .
2.2. Graph Regularization Non-Negative Matrix Factorization (GNMF) [23]
By combining NMF with a geometry-based regularizer, GNMF learns the geometric structure between sample points while projecting.
The goal of NMF is to calculate two non-negative matrices U and V so that the product of two factor matrices is as approximate as possible to X, i.e., . The loss after matrix factorization is represented by Euclidean distance, so the calculation formula of NMF is
The regularizer part of GNMF is implemented by LPP. LPP is a linear approximation of non-linear Laplacian characteristic projection. The ultimate aim of LPP is to obtain a projection matrix V that can map high-dimensional sample points into a low-dimensional subspace. LPP requires that the points with the nearest neighborhood relationship in the original high-dimensional space are still maintained after mapping into low-dimensional space. The calculated function of the LPP is
The W is a graph containing information about the neighborhood of the dataset
where represents the set of K nearest neighbors of , and t is a real number. After calculation, it can be simplified to
where , D is a diagonal matrix, and the elements on the diagonal are the sum of each column in the weight matrix W, i.e., . represents the trace of matrix.
Compared with traditional NMF, GNMF still maintains the underlying geometry of the original data space when performing dimensionality reduction. GNMF integrates NMF and LPP into a framework, and the calculation formula is as follows:
where is the regularization parameter.
2.3. Low Rank Non-Negative Factorization (LRNF) [18]
Because NMF is based on Euclidean distance, it has poor robustness to data containing noise and corruption. For the purpose of decreasing the sensitivity of NMF to noise and occlusion, LRNF utilizes low rank to learn the global structure of the sample points. In the problem of image classification, compared with the local information contained in noise data, the global geometry structure of the sample is provided with more robustness.
LRNF divides original data X into clean data A and noise data E. The low-rank constraint on matrix A can learn the global structure of the original matrix X. Therefore, A can replace X and act as a matrix that needs to be decomposed. We use the L1 norm to realize the sparsity of the noise matrix and propose the objective function of LRNF as below:
where Z is a low-rank matrix with a block diagonal structure, and are two regularization parameters, and both of them are greater than zero.
3. Robust Exponential Graph Regularization Non-Negative Matrix Factorization
In this section, we first describe the reason for our proposed method, then detail the principle of the REGNMF algorithm and obtain an optimized solution by the Lagrange multiplier iterative method.
3.1. The Motivation of REGNMF
NMF as a non-linear and non-negative constraint matrix factorization dimensionality reduction method has the advantages of interpretability, simple calculation, physical meaning, large-scale data processing, and small storage space, so it is extensively applied to blind source separation, pattern recognition, time series segmentation, document clustering [38], recommender systems [39], gene detection, and other fields [40]. Hence, the study of NMF has a profound impact.
NMF measures the approximation of the original matrix and decomposed matrix based on Euclidean distance, which indirectly results in a strong level of sensitivity of NMF to noise and outliers. How to increase the robustness of NMF is the primary problem we have to face. There are many ways to increase robustness, such as low rank representation (LRR) [41], which learns the global structure of the samples through low rank and dictionary; LRNF utilizes low rank to increase the robustness of the original NMF; latent low rank representation (LatLRR) [42] divides original data into observed and unobserved data; literature [43] separates clean data from noisy data; sparse preserving projection (SPP) [44] uses sparsity to filter out redundant information; and MEDLPP [36] introduces matrix exponents to solve the SSS problems. In the NMF of graph embedding, although the internal structure of the data is considered, according to the above analysis, it can be seen that graph embedding will cause SSS problems, so the combination of graph embedding and NMF requires a method to increase the robustness of the algorithm.
The small sample size is also a problem that researchers need to consider. When the samples are insufficient, how to improve the dimensionality reduction effect has attracted extensive attention. There are many solutions to the SSS problems, such as feature transfer, metric learning, and others. The introduction of a matrix exponent is also an effective solution. Compared with other methods, matrix exponent is more convenient and concise.
For example, as a classical supervised matrix dimensionality reduction method, LDE’s [45] key idea is to maximize the similarity between similar sample points and the divergence between different sample points. For overcoming the boundedness of the LDE algorithm, the LDE algorithm with matrix exponent, namely ELDE [29], emerged as the times required. In the extension algorithm of LDE, researchers added label information and proposed a semi-supervised version of LDE, named SDE [46]. Although SDE has a high discriminative ability, without regularization, SDE may encounter the SSS problems when the number of samples is insufficient. For the purpose of addressing the above problems, Dornaika et al. proposed the exponential SDE (ESDE) [31] method by exploiting the property of the matrix exponent. Except for solving the SSS problems, ESDE expands the gap between different categories of samples to increase the discrimination ability.
According to the above analysis, the matrix index can solve the SSS problems. For the sake of dealing with SSS problems of NMF in graph embedding, we use a form of matrix index to transform the possible singular matrix into a non-singular one and make the best of the information of the null space to increase the robustness and discriminative power of the algorithm.
3.2. Problem Formulation for REGNMF
In order to deal with the problems in real life and production, we need to obtain certain data for analysis. However, in many scenarios, due to the difficulties in data collection and the high cost of sample labeling, the data we obtain are not always sufficient or effective, but often a small amount of data with little effective information, which makes the scale of training samples small and will lead to overfitting of the model. Therefore, the SSS problems have proved to be one of the most important exploration interests in the field of artificial intelligence.
We know that graph embedding will cause the SSS problems. Although the traditional GNMF method based on Euclidean distance considers the manifold structure of the sample, the problem of small sample size will also occur in the procedure of matrix dimensionality reduction. In the above analysis, we know that the matrix exponent is an effective means to address SSS problems. Therefore, we adopt the form of introducing the matrix exponent to solve the SSS problems in GNMF. Based on this, we make improvements on the basis of the original GNMF, introduce the matrix exponent, and propose the REGNMF method. The objective function of our proposed method is displayed as follows:
In the above formulation, matrix X is composed of training samples arranged in columns. An additional condition restricts two matrix factors U and V to both non-negative matrices: U is a base matrix, and V is a coefficient matrix. The product of U and V is used to approximate X. The parameter is a regularization parameter to avoid over-fitting in the proceeding of data dimensionality reduction. The expression adds a matrix exponent to the objective function of the LPP algorithm; and L is a Laplacian matrix of sample data, i.e., .
The Laplacian matrix in traditional LPP may be singular. When a matrix exponent is added, according to the properties of the matrix exponent, it can be seen that is a full-rank matrix. Therefore, must be a non-singular matrix, which greatly solves the SSS problems in LPP. The first item in model (9) represents the reconstruction error of the decomposed matrix and the original matrix. In practical applications, the smaller the reconstruction error is, the more decomposed matrices retain the information of the original data. The second term indicates the manifold structure of samples introduced by a regularizer, and the matrix exponent is mixed to increase the robust ability of our method.
Therefore, in the progress of data dimensionality reduction, REGNMF not only maintains the internal geometric structure between sample points, but reduces the sensitivity to noise and outlier data. The next subsection shows how to solve model (9) with an iterative algorithm.
3.3. The Optimal Solution
As both U and V in the objective function (9) of REGNMF are not convex, we cannot expect to find an algorithm to get a global minimum solution; instead we use a gradient descent method [47] to obtain local minimum values, so we can obtain the following rules:
where and represent the learning rate, which determines the step size of each gradient descent, and when the choice of and are both small enough, it can be guaranteed that each iteration is decreasing until the objective function converges to a stationary point. Thus, we set , . Then the update rules for and are
According to the convergence proof of NMF in the paper of Lee and Seung [17], the objective function in formulation (7) is not increasing under the update rule in formulations (11) and (12). Our proof of convergence basically follows the thought of the original NMF in Lee and Seung’s paper, which will not be repeated here. However, many studies have shown that the multiplication algorithm of the original NMF cannot guarantee convergence to a stable point. In order to make our algorithm converge, we further demand that each column vector in the matrix U (or V) has a Euclidean distance of length 1. The matrix V (or U) updates automatically to prevent U from changing. The implementation is as follows:
This strategy is also adopted in GNMF, and it is still the same after adding the matrix exponent. After the multiplicative update process has converged, this paper fits the length of Euclidean distance of every column vector in matrix U to 1 and tunes up matrix V to ensure that U is invariant. We prove the convergence of our proposed REGNMF through experiments, as displayed in Figure 1. It can be seen that on different databases, when the number of algorithmic iterations to 200 times, the reconstruction error of the objective function is almost unchanged. Therefore, 200 is used as the number of iterations of the experiment in this paper.
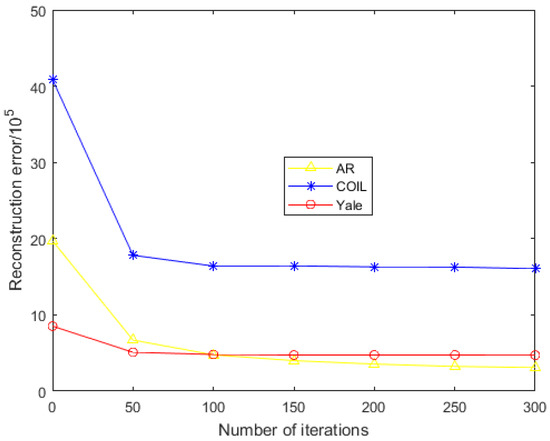
Figure 1.
Relationship between reconstruction error and iteration times.
According to our derivation process, the following solution algorithm (Algorithm 1) is obtained.
| Algorithm 1 REGNMF Algorithm. |
Input: Training set X, subspace dimensions d, the number of iterations iter, the current iteration number s, the regularization term coefficient , the matrices U and V, the weight matrix W, and the Laplacian matrix L. Initialization: The number of sample rows m and sample columns n, , , iter = 200, , ; 1. Use random functions to generate U and V factor matrices, , ; 2. Use the K-nearest neighbor algorithm to select the neighbor points of the to construct a neighborhood graph W; 3. According to , construct the Laplacian matrix L; 4. When s <= iter, loop: ➀ Iterate and Update U: ; ➁ Iterate and Update V: ; ➂ ; 5. If s > iter: end the loop; 6. Normalize matrices U and V: . Output: base matrix U and coefficient matrix V |
4. Experiment
For the purpose of testing the ability of REGNMF’s feature extraction and its robustness to noise and outliers, REGNMF, GNMF, NMF, LPP, ELPP, LRR, and LRNF are used to extract main features on the AR, COIL, and Yale databases with random noise and AR database with occlusion for recognition experiments. We use MATLAB to carry out our experiments, the device processor used in the experiment is Intel Core i5-7200U, 64-bit Windows operating system, and the running memory is 4G. During the experiments, we use the kNN method for classification. In this paper, we fix the parameter k (number of nearest neighbor nodes of each data instance) in the kNN method to 10, so that the graph structure constructed by the model is consistent each time, thus avoiding the influence of irrelevant parameters on the model performance.
4.1. The AR Database Experiment
The AR face database includes more than 4000 images of 70 men and 56 women, totaling 126 people. The characteristics of these images are that the faces in the front view have different facial expressions, lighting conditions, and occlusion (sunglasses, etc.). Each image is 50 × 40 pixels. Figure 2 shows a partial image from the AR database. From the AR database, we randomly select 24 images in each category as the training set. The recognition rate curve of diverse face recognition algorithms under different feature dimensions is displayed in Figure 3.

Figure 2.
A partial image from the AR database.
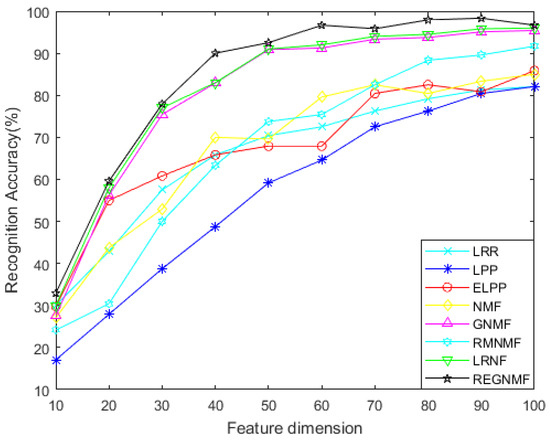
Figure 3.
Comparison of face recognition rate curves of diverse feature extraction algorithms for the AR database.
4.2. The COIL Database Experiment
The COIL database consists of 20 objects, each with 72 images, which are collected from distinct angles of the object. Each image is 128 × 128 pixels. A partial image from the COIL database is shown in Figure 4. From the COIL database, we randomly select 60 images in each class as the training set and the remaining 12 images as the test set. Figure 5 shows the comparison of the recognition rates of each algorithm under different feature dimensions. We know that the number of samples in the COIL database is less than the sample dimension, and we can see from Figure 5 that our model is effective and performs far better than other models, which indicates that REGNMF successfully solves the SSS problem.

Figure 4.
A partial image from the COIL database.
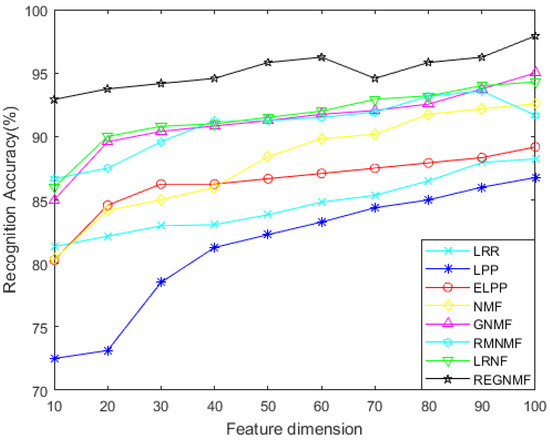
Figure 5.
Comparison of face recognition rate curves of different feature extraction methods for the COIL database.
4.3. Robustness Test for Random Pixel Destruction
In order to further evaluate the robust capability of the REGNMF algorithm to noise and outliers, this paper adds Gaussian noise with a density of 0.2 and salt and pepper noise with a density of 0.1, respectively, to the Yale database. Figure 6 shows, respectively, a Yale clean image and after adding different noise Yale images. The Yale dataset includes 165 images in 15 categories, and each category contains 11 images from different lighting, expressions, and shooting angles, and the resolution of each image is 80 × 100. In this paper, different train sample numbers (2, 3, 4, 5, 6) are casually chosen as train sets to test the robustness of each algorithm when reduced to the same dimension (six dimensions). Table 1 gives the face recognition rate of each algorithm. It can be proved that our model can perfectly solve the SSS problem.

Figure 6.
A partial image of Yale database. (a) Yale clean image; (b) Yale image with Gaussian noise density = 0.2; (c) Yale image with salt and pepper noise density = 0.1.

Table 1.
Face recognition rate of each algorithm under different noise densities.
4.4. Robustness Test of Continuous Pixel Occlusion
For the sake of testing the sensitivity of the REGNMF method to occlusion data, we add the 5 × 5 and 10 × 10 occlusion blocks to the AR database for the face recognition rate experiment. Figure 7a,b are the images after adding different occlusion blocks to the AR database. This paper selects 24 samples as the training set and then assesses the robustness of each algorithm under different feature dimensions. Figure 8 and Figure 9, respectively, show the face recognition rates of each algorithm under different occlusions.
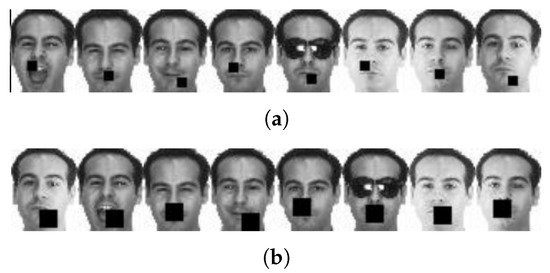
Figure 7.
(a,b) AR images with 5 × 5 and 10 × 10 occlusion blocks, respectively.
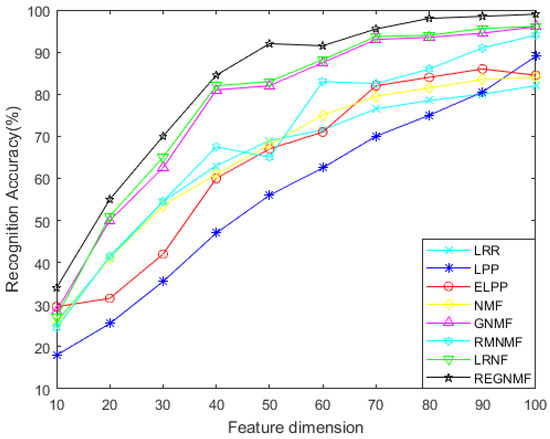
Figure 8.
Classification accuracy of different feature dimensions for the AR database based on 5 × 5 occlusion.
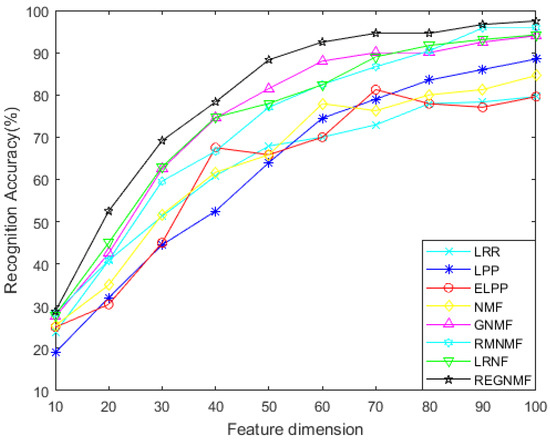
Figure 9.
Classification accuracy of different feature dimensions for the AR database based on 10 × 10 occlusion.
4.5. Analysis of Results
- (1)
- For the noiseless data, Figure 2 and Figure 4 show the variation of each algorithm with the feature dimension for the AR and COIL databases. It can be seen that in most cases, the effect of REGNMF is significantly better than other algorithms, and the experiment on the COIL database indicates that the SSS problems are successfully solved.
- (2)
- In the experiment of adding noise, as shown in Table 1, the effect of the REGNMF method is far more effective than other algorithms under different noise densities, and the classification accuracy of image recognition is about 1–4% higher than other algorithms.
- (3)
- In the experiment with occlusion, it is clear from Figure 8 and Figure 9 that the REGNMF algorithm has better robustness and a higher face recognition rate, so it is more discriminative. In most cases, the classification accuracy of REGNMF and GNMF is much higher than that of other algorithms. This is because REGNMF, RMNMF, and GNMF join a graph regularizer, which takes the structure of the data into account while reducing the dimension. Therefore, the accuracy is higher.
5. Conclusions
Manifold learning and matrix factorization methods are effective in feature extraction, and the GNMF is a generalization based on manifold learning. On this basis, this paper proposes an improved model for the GNMF, i.e., REGNMF. REGNMF integrates the manifold learning model with the NMF model together and still maintains the manifold geometry of data space in the progress of dimension reduction. At the same time, considering the impact of SSS problems caused by matrix singularity on face recognition rate, the author successfully solves the SSS problems by introducing a matrix index to make the Laplacian matrix into a non-singular matrix, which greatly increases the robustness and discrimination of the method. In this paper, the iterative update optimization algorithm is used to derive and certificate the formulation of the proposed REGNMF method, and the optimal solution is obtained. The algorithm is applied to image databases such as AR, Yale Salt and Pepper, Yale Gaussian, and COIL. A large number of experimental results indicate that, in comparison with traditional algorithms, image features extracted by REGNMF have higher recognition rates when used for classification and recognition, especially on datasets with noise and occlusion.
Author Contributions
Writing—review & editing: M.W. Writing—original draft: M.C. Resources: G.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work is partially supported by Postgraduate Research & Practice Innovation Program of Jiangsu Province No. KYCX22_2221; the National Science Foundation of China under Grant Nos. 61876213, 61991401, 62172229, 61976118; the Key R&D Program Science Foundation in Colleges and Universities of Jiangsu Province Grant No. 20KJA520002; the Natural Science Fund of Jiangsu Province under Grants Nos. BK20201397, BK20191409, BK20211295; and Jiangsu Key Laboratory of Image and Video Understanding for Social Safety of Nanjing University of Science and Technology under Grants J2021-4. This work was funded by the Future Network Scientific Research Fund Project SRFP-2021-YB-25 and China’s Jiangxi Province Natural Science Foundation (No. 20202ACBL202007).
Data Availability Statement
Data available on request due to restrictions eg privacy or ethical The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hart, P.E.; Stork, D.G.; Duda, R.O. Pattern Classification; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Turk, M.; Pentland, A. Eigenfaces for recognition. J. Cogn. Neurosci. 1991, 3, 71–86. [Google Scholar] [CrossRef] [PubMed]
- Belhumeur, P.N.; Hespanha, J.P.; Kriegman, D.J. Eigenfaces vs. fisherfaces: Recognition using class specific linear projection. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 711–720. [Google Scholar] [CrossRef]
- Wan, M.; Li, M.; Yang, G.; Gai, S.; Jin, Z. Feature extraction using two-dimensional maximum embedding difference. Inf. Sci. 2014, 274, 55–69. [Google Scholar] [CrossRef]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps and spectral techniques for embedding and clustering. Adv. Neural Inf. Process. Syst. 2001, 14, 585–591. [Google Scholar]
- Wan, M.; Lai, Z.; Yang, G.; Yang, Z.; Zhang, F.; Zheng, H. Local graph embedding based on maximum margin criterion via fuzzy set. Fuzzy Sets Syst. 2017, 318, 120–131. [Google Scholar]
- Roweis, S.T.; Saul, L.K. Nonlinear Dimensionality Reduction by Locally Linear Embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef]
- Wan, M.; Chen, X.; Zhan, T.; Yang, G.; Tan, H.; Zheng, H. Low-rank 2D Local Discriminant Graph Embedding for Robust Image Feature Extraction. Pattern Recognit. 2023, 133, 109034. [Google Scholar]
- He, X. Locality preserving projections. Adv. Neural Inf. Process. Syst. 2003, 16, 186–197. [Google Scholar]
- Wang, A.; Zhao, S.; Liu, J.; Yang, J.; Liu, L.; Chen, G. Locality adaptive preserving projections for linear dimensionality reduction. Expert Syst. Appl. 2020, 151, 113352. [Google Scholar] [CrossRef]
- He, X.; Cai, D.; Yan, S.; Zhang, H.J. Neighborhood preserving embedding. In Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV’05), Washington, DC, USA, 17–21 October 2005; Volume 1, pp. 1208–1213. [Google Scholar]
- Gui, J.; Sun, Z.; Jia, W.; Hu, R.; Lei, Y.; Ji, S. Discriminant sparse neighborhood preserving embedding for face recognition. Pattern Recognit. 2012, 45, 2884–2893. [Google Scholar] [CrossRef]
- Wan, M.; Yao, Y.; Zhan, T.; Yang, G. Supervised Low-Rank Embedded Regression (SLRER) for Robust Subspace Learning. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 1917–1927. [Google Scholar] [CrossRef]
- Abdi, H. Singular value decomposition (SVD) and generalized singular value decomposition. Encycl. Meas. Stat. 2007, 907, 912. [Google Scholar]
- Lee, D.; Seung, H.S. Algorithms for non-negative matrix factorization. Adv. Neural Inf. Process. Syst. 2001, 13, 556–562. [Google Scholar]
- Palmer, S.E. Hierarchical structure in perceptual representation. Cogn. Psychol. 1977, 9, 441–474. [Google Scholar] [CrossRef]
- Logothetis, N.K.; Sheinberg, D.L. Visual object recognition. Annu. Rev. Neurosci. 1996, 19, 577–621. [Google Scholar] [CrossRef]
- Lu, Y.; Lai, Z.; Li, X.; Zhang, D.; Wong, W.K.; Yuan, C. Learning parts-based and global representation for image classification. IEEE Trans. Circuits Syst. Video Technol. 2017, 28, 3345–3360. [Google Scholar] [CrossRef]
- Lu, Y.; Yuan, C.; Zhu, W.; Li, X. Structurally incoherent low-rank non-negative matrix factorization for image classification. IEEE Trans. Image Process. 2018, 27, 5248–5260. [Google Scholar] [CrossRef]
- Lee, H.; Yoo, J.; Choi, S. Semi-supervised non-negative matrix factorization. IEEE Signal Process. Lett. 2009, 17, 4–7. [Google Scholar]
- Wang, J.; Tian, F.; Liu, C.H.; Wang, X. Robust semi-supervised non-negative matrix factorization. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–17 July 2015; pp. 1–8. [Google Scholar]
- Jia, Y.; Kwong, S.; Hou, J.; Wu, W. Semi-supervised non-negative matrix factorization with dissimilarity and similarity regularization. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 2510–2521. [Google Scholar] [CrossRef]
- Cai, D.; He, X.; Han, J.; Huang, T.S. Graph regularized non-negative matrix factorization for data representation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 1548–1560. [Google Scholar]
- Huang, J.; Nie, F.; Huang, H.; Ding, C. Robust manifold nonnegative matrix factorization. ACM Trans. Knowl. Discov. Data (TKDD) 2014, 8, 1–21. [Google Scholar]
- Yi, Y.; Wang, J.; Zhou, W.; Zheng, C.; Kong, J.; Qiao, S. Non-negative matrix factorization with locality constrained adaptive graph. IEEE Trans. Circuits Syst. Video Technol. 2019, 30, 427–441. [Google Scholar]
- Kuo, B.C.; Chang, K.Y. Feature extractions for small sample size classification problem. IEEE Trans. Geosci. Remote Sens. 2007, 45, 756–764. [Google Scholar] [CrossRef]
- Wang, S.J.; Chen, H.L.; Peng, X.J.; Zhou, C.G. Exponential locality preserving projections for SSS problems. Neurocomputing 2011, 74, 3654–3662. [Google Scholar] [CrossRef]
- Yuan, S.; Mao, X. Exponential elastic preserving projections for facial expression recognition. Neurocomputing 2018, 275, 711–724. [Google Scholar] [CrossRef]
- Dornaika, F.; Bosaghzadeh, A. Exponential local discriminant embedding and its application to face recognition. IEEE Trans. Cybern. 2013, 43, 921–934. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Fang, B.; Tang, Y.Y.; Shang, Z.; Xu, B. Generalized discriminant analysis: A matrix exponential approach. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2009, 40, 186–197. [Google Scholar] [CrossRef]
- Dornaika, F.; El Traboulsi, Y. Matrix exponential based semi-supervised discriminant embedding for image classification. Pattern Recognit. 2017, 61, 92–103. [Google Scholar] [CrossRef]
- Wu, G.; Feng, T.T.; Zhang, L.J.; Yang, M. Inexact implementation using Krylov subspace methods for large scale exponential discriminant analysis with applications to high dimensionality reduction problems. Pattern Recognit. 2017, 66, 328–341. [Google Scholar] [CrossRef]
- He, J.; Ding, L.; Cui, M.; Hu, Q.H. Marginal Fisher analysis based on matrix exponential transformation. Chin. J. Comput. 2014, 37, 2196–2205. [Google Scholar]
- Yaqin, G. Support vectors classification method based on matrix exponent boundary fisher projection. In Proceedings of the 2019 IEEE International Conference on Mechatronics and Automation (ICMA), Tianjin, China, 4–7 August 2019; pp. 957–961. [Google Scholar]
- Ivanovs, J.; Boxma, O.; Mandjes, M. Singularities of the matrix exponent of a Markov additive process with one-sided jumps. Stoch. Process. Their Appl. 2010, 120, 1776–1794. [Google Scholar] [CrossRef]
- Lu, G.F.; Wang, Y.; Zou, J.; Wang, Z. Matrix exponential based discriminant locality preserving projections for feature extraction. Neural Netw. 2018, 97, 127–136. [Google Scholar] [CrossRef]
- Wang, S.J.; Yan, S.; Yang, J.; Zhou, C.G.; Fu, X. A general exponential framework for dimensionality reduction. IEEE Trans. Image Process. 2014, 23, 920–930. [Google Scholar] [CrossRef] [PubMed]
- Shahnaz, F.; Berry, M.W.; Pauca, V.P.; Plemmons, R.J. Document clustering using nonnegative matrix factorization. Inf. Process. Manag. 2006, 42, 373–386. [Google Scholar] [CrossRef]
- Luo, X.; Zhou, M.; Xia, Y.; Zhu, Q. An efficient non-negative matrix-factorization-based approach to collaborative filtering for recommender systems. IEEE Trans. Ind. Inform. 2014, 10, 1273–1284. [Google Scholar]
- Wang, Y.X.; Zhang, Y.J. Nonnegative matrix factorization: A comprehensive review. IEEE Trans. Knowl. Data Eng. 2012, 25, 1336–1353. [Google Scholar]
- Liu, G.; Lin, Z.; Yu, Y. Robust subspace segmentation by low-rank representation. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Liu, G.; Yan, S. Latent low-rank representation for subspace segmentation and feature extraction. In Proceedings of the 2011 International Conference on Computer Vision, Washington, DC, USA, 6–13 November 2011; pp. 1615–1622. [Google Scholar]
- Wan, M.; Chen, X.; Zhao, C.; Zhan, T.; Yang, G. A new weakly supervised discrete discriminant hashing for robust data representation. Inf. Sci. 2022, 611, 335–348. [Google Scholar]
- Qiao, L.; Chen, S.; Tan, X. Sparsity preserving projections with applications to face recognition. Pattern Recognit. 2010, 43, 331–341. [Google Scholar] [CrossRef]
- Chen, H.T.; Chang, H.W.; Liu, T.L. Local discriminant embedding and its variants. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–26 June 2005; pp. 846–853. [Google Scholar]
- Huang, H.; Liu, J.; Pan, Y. Semi-supervised marginal fisher analysis for hyperspectral image classification. Isprs Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 3, 377–382. [Google Scholar] [CrossRef]
- Kivinen, J. Additive versus exponentiated gradient updates for linear prediction. Inf. Comput. 1997, 132, 1–64. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).