Solitary Wave Solution of a Generalized Fractional–Stochastic Nonlinear Wave Equation for a Liquid with Gas Bubbles
Abstract
1. Introduction
2. CD and SWP
- 1.
- is continuous for ,
- 2.
- has a normal distribution .
- 3.
- 4.
- is independent for ,
3. Wave Equation for GFSNWE
4. Exact Solutions of GFSNWE
4.1. -Expansion Method
4.2. JEF Method
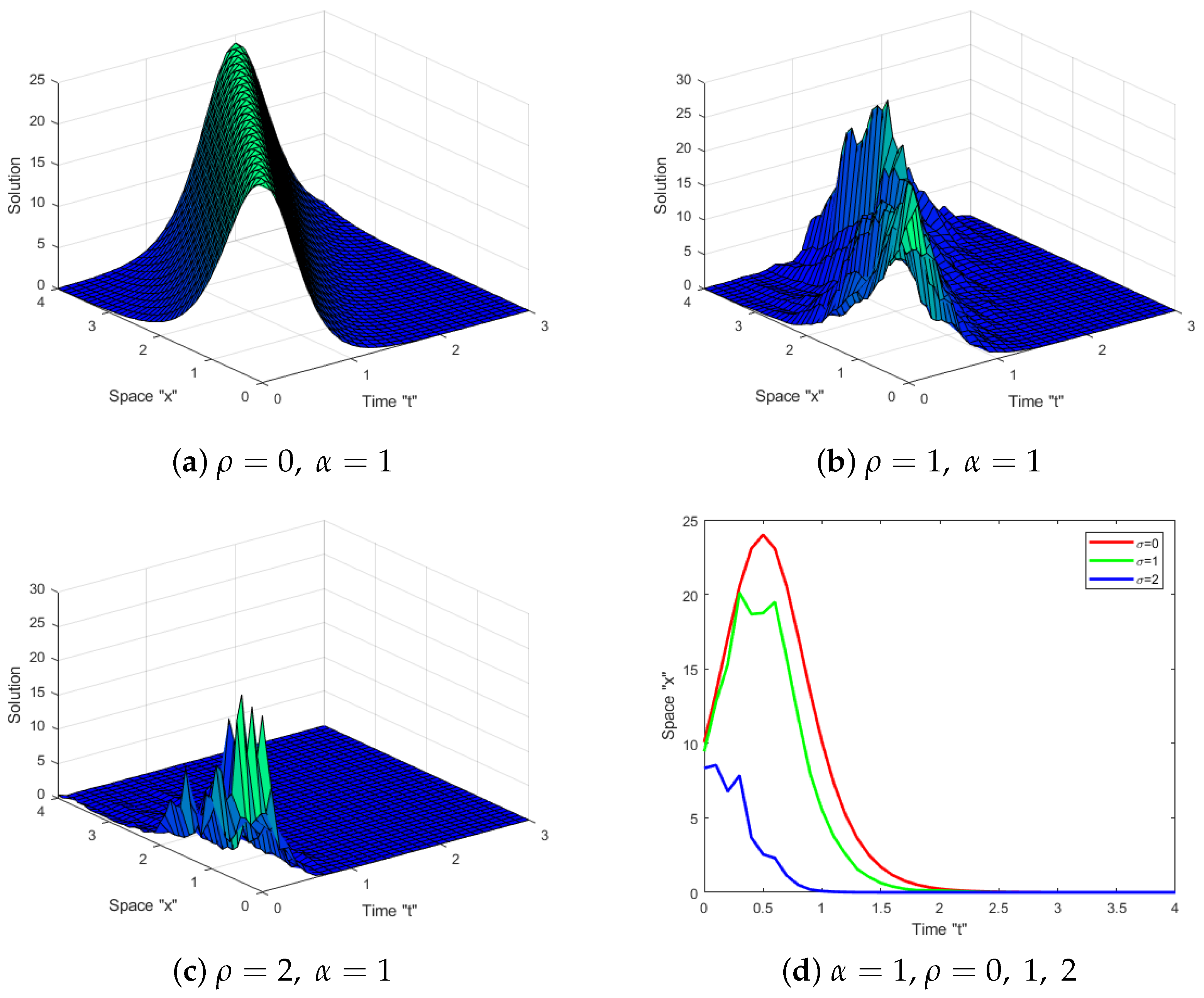
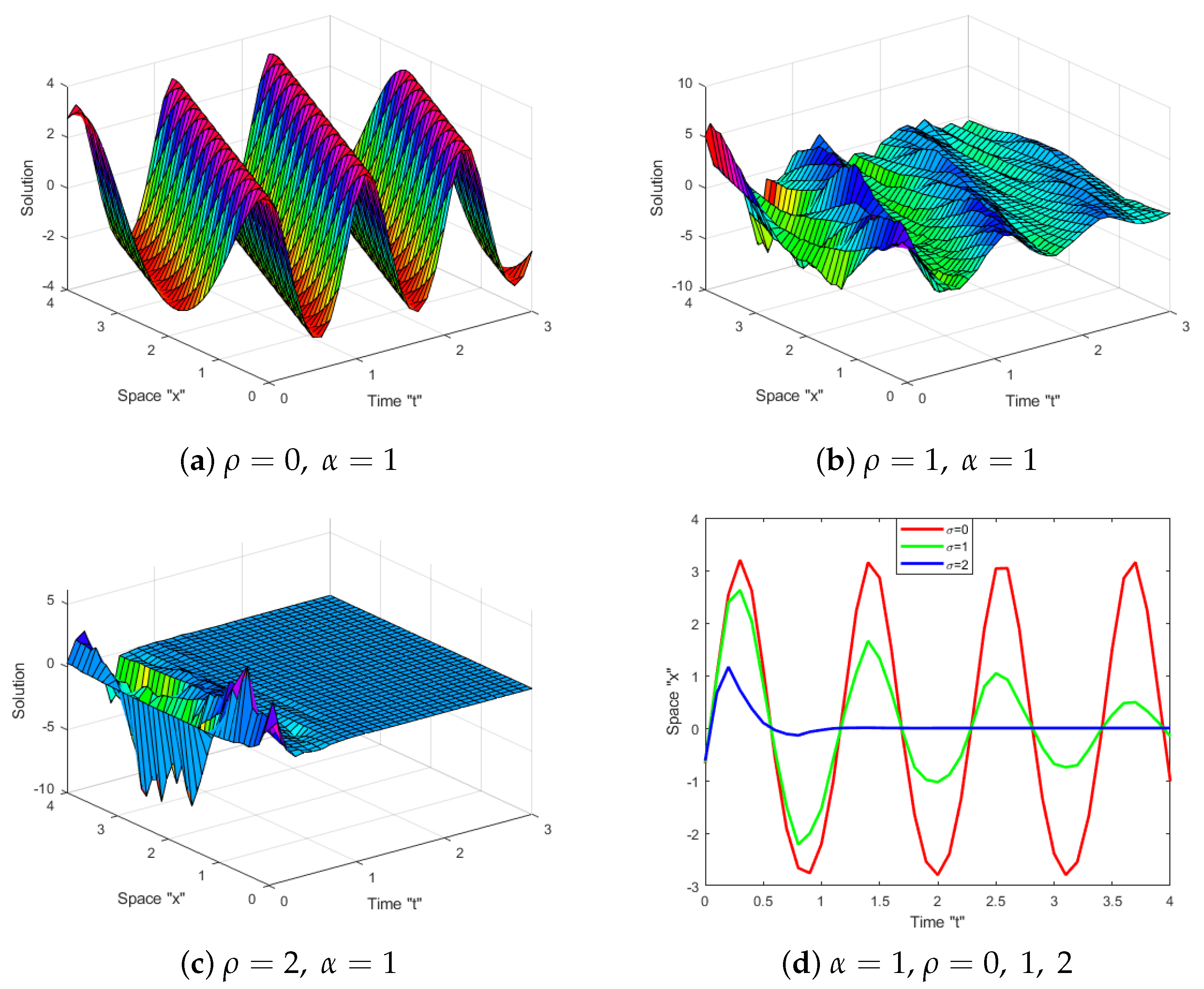
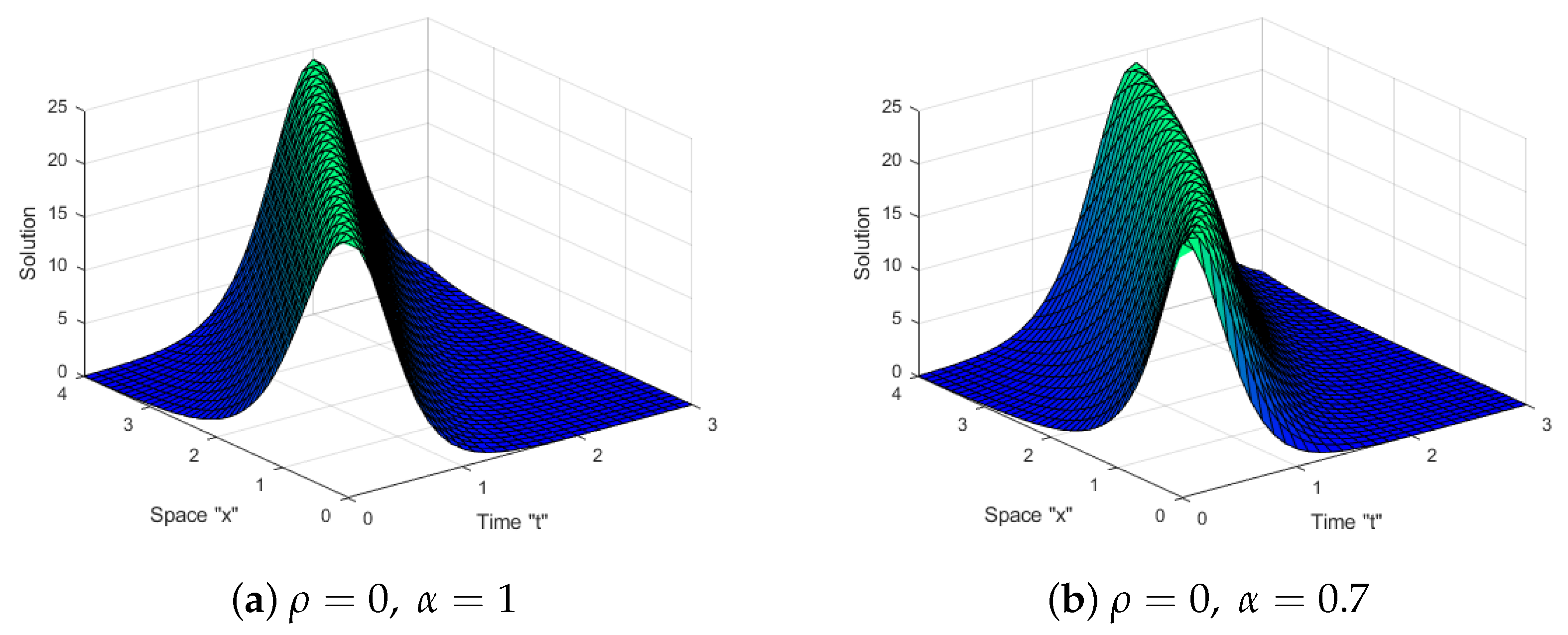
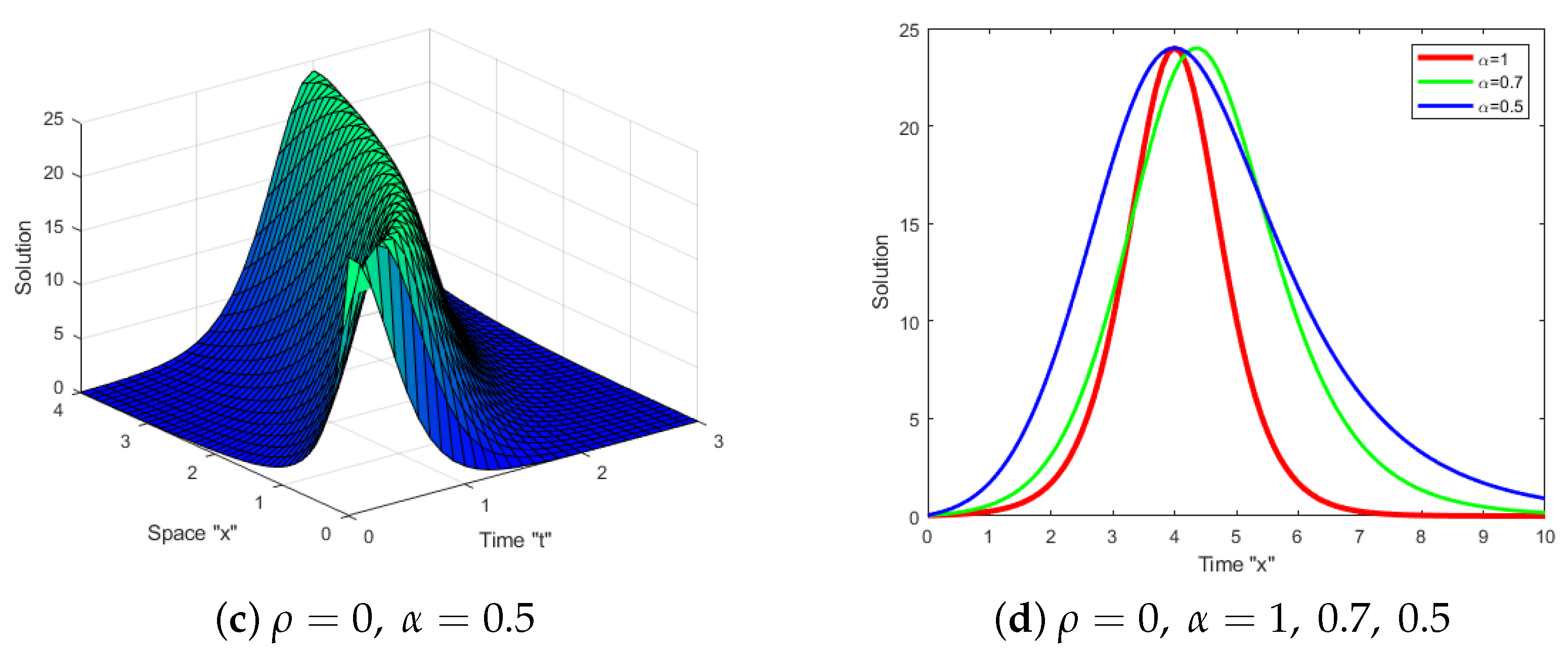
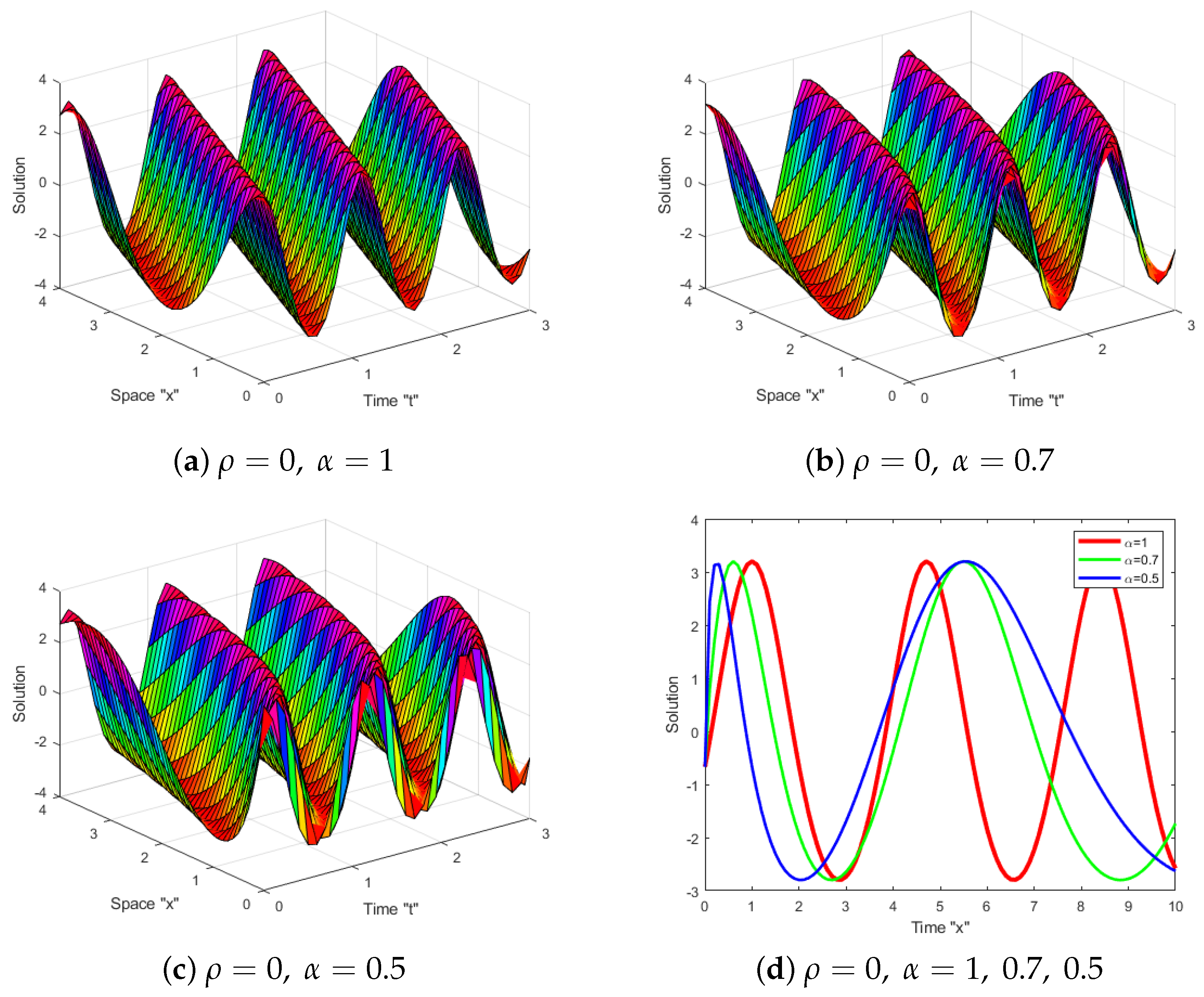
5. Impacts of SWP and the Fractional Derivative
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: San Diego, CA, USA, 2006. [Google Scholar]
- Podlubny, I. Fractional Differential Equations, Vol. 198 of Mathematics in Science and Engineering; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Bouloudene, M.; Manar, A.; Alqudah, M.A.; Jarad, F.; Adjabi, Y.; Abdeljawad, T. Nonlinear singular P-Laplacian boundary value problems in the frame of conformable derivative. Discret. Contin. Dyn. S 2021, 14, 3497–3528. [Google Scholar] [CrossRef]
- Abdeljawad, T. On conformable fractional calculus. J. Comput. Appl. Math. 2015, 279, 57–66. [Google Scholar] [CrossRef]
- Arnold, L. Random Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Imkeller, P.; Monahan, A.H. Conceptual stochastic climate models. Stoch. Dynam. 2002, 2, 311–326. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Al-Askar, F.M.; Cesarano, C.; EL-Morshedy, M. Solitary Wave Solutions of the Fractional-Stochastic Quantum Zakharov–Kuznetsov Equation Arises in Quantum Magneto Plasma. Mathematics 2023, 11, 488. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Cesarano, C.; Al-Askar, F.M. Solutions to the (4 + 1)-Dimensional Time-Fractional Fokas Equation with M-Truncated Derivative. Mathematics 2023, 11, 194. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Mohammed, W.W.; Aly, E.S.; EL-Morshedy, M. Exact solutions of the stochastic Maccari system forced by multiplicative noise. Zamm-J. Appl. Math. Mech. Angew. Math. Und Mech. 2022, 10, e202100199. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Al-Askar, F.M.; Cesarano, C. The analytical solutions of the stochastic mKdV equation via the mapping method. Mathematics 2022, 10, 4212. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Cesarano, C.; Mohammed, W.W. The analytical solutions of stochastic-fractional Drinfel’d-Sokolov-Wilson equations via (G’/G)-expansion method. Symmetry 2022, 14, 2105. [Google Scholar] [CrossRef]
- Rayleigh, R. On the pressure developed in a liquid during the collapse of a spherical cavity. Philos. Mag. Ser. 1917, 6, 94–98. [Google Scholar] [CrossRef]
- Shen, G.; Manafian, J.; Huy, D.T.N.; Nisar, K.S.; Abotaleb, M.; Trung, N.D. Abundant soliton wave solutions and the linear superposition principle for generalized (3 + 1)-D nonlinear wave equation in liquid with gas bubbles by bilinear analysis. Results Phys. 2022, 32, 105066. [Google Scholar] [CrossRef]
- Wang, M.; Tian, B.; Sun, Y.; Zhang, Z. Lump, mixed lump-stripe and rogue wave-stripe solutions of a (3 + 1)-dimensional nonlinear wave equation for a liquid with gas bubbles. Comput. Math. Appl. 2020, 79, 576–587. [Google Scholar] [CrossRef]
- Guo, Y.R.; Chen, A.H. Hybrid exact solutions of the (3 + 1)-dimensional variable-coefficient nonlinear wave equation in liquid with gas bubbles. Results Phys. 2021, 23, 103926. [Google Scholar] [CrossRef]
- Tu, J.M.; Tian, S.F.; Xu, M.J.; Song, X.Q.; Zhang, T.T. Bäcklund transformation, infinite conservation laws and periodic wave solutions of a generalized (3 + 1)-dimensional nonlinear wave in liquid with gas bubbles. Nonlinear Dyn. 2016, 83, 1199–1215. [Google Scholar] [CrossRef]
- Zhou, X.; Ilhan, O.A.; Zhou, F.; Sutarto, S.; Manafian, J.; Abotaleb, M. Lump and Interaction Solutions to the (3 + 1)-Dimensional Variable-Coefficient Nonlinear Wave Equation with Multidimensional Binary Bell Polynomials. J. Funct. Spaces 2021, 2021, 4550582. [Google Scholar] [CrossRef]
- Zhao, Y.H.; Mathanaranjan, T.; Rezazadeh, H.; Akinyemi, L.; Inc, M. New solitary wave solutions and stability analysis for the generalized (3 + 1)-dimensional nonlinear wave equation in liquid with gas bubbles. Results Phys. 2022, 43, 106083. [Google Scholar] [CrossRef]
- Akbulut, A.; Arnous, A.H.; Hashemi, M.S.; Mirzazadeh, M. Solitary waves for the generalized nonlinear wave equation in (3+1) dimensions with gas bubbles using the Nnucci’s reduction, enhanced and modified Kudryashov algorithms. J. Ocean. Eng. Sci. 2022. accepted. [Google Scholar] [CrossRef]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives, Theory and Applications; Gordon and Breach: Yverdon, Switzerland, 1993. [Google Scholar]
- Katugampola, U.N. New approach to a generalized fractional integral. Appl. Math. Comput. 2011, 218, 860–865. [Google Scholar] [CrossRef]
- Katugampola, U.N. New approach to generalized fractional derivatives. Bull. Math. Anal. Appl. 2014, 6, 1–15. [Google Scholar]
- Calin, O. An Informal Introduction to Stochastic Calculus with Applications; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2015. [Google Scholar]
- Fan, E.; Zhang, J. Applications of the Jacobi elliptic function method to special-type nonlinear equations. Phys. Lett. A 2002, 305, 383–392. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammed, W.W.; Al-Askar, F.M.; Cesarano, C.; El-Morshedy, M. Solitary Wave Solution of a Generalized Fractional–Stochastic Nonlinear Wave Equation for a Liquid with Gas Bubbles. Mathematics 2023, 11, 1692. https://doi.org/10.3390/math11071692
Mohammed WW, Al-Askar FM, Cesarano C, El-Morshedy M. Solitary Wave Solution of a Generalized Fractional–Stochastic Nonlinear Wave Equation for a Liquid with Gas Bubbles. Mathematics. 2023; 11(7):1692. https://doi.org/10.3390/math11071692
Chicago/Turabian StyleMohammed, Wael W., Farah M. Al-Askar, Clemente Cesarano, and Mahmoud El-Morshedy. 2023. "Solitary Wave Solution of a Generalized Fractional–Stochastic Nonlinear Wave Equation for a Liquid with Gas Bubbles" Mathematics 11, no. 7: 1692. https://doi.org/10.3390/math11071692
APA StyleMohammed, W. W., Al-Askar, F. M., Cesarano, C., & El-Morshedy, M. (2023). Solitary Wave Solution of a Generalized Fractional–Stochastic Nonlinear Wave Equation for a Liquid with Gas Bubbles. Mathematics, 11(7), 1692. https://doi.org/10.3390/math11071692







