Exploring the Dynamics of COVID-19 with a Novel Family of Models
Abstract
1. Introduction
2. The New Family of Distributions
2.1. Asymptotics
2.2. Useful Representation
2.3. Order Statistics (OS)
2.4. Entropy
2.4.1. Rényi Entropy
2.4.2. Tsallis Entropy
2.4.3. Havrda and Charvat Entropy
2.5. Inference
3. Mathematical Characteristics of Sub-Model
3.1. Useful Representation
3.2. Moments and Related Measures
3.3. Residuals and Related Measures
3.3.1. Mean Residual and Mean Inactivity Time
3.4. Entropy
3.4.1. Rényi Entropy
3.4.2. Tsallis Entropy
3.4.3. Havrda and Charvat Entropy
3.5. Order Statistics (OS)
4. Inference
4.1. Maximum Likelihood Estimation Method (MLE)
4.2. Anderson–Darling Estimation Method (ADE-M)
4.3. Cram’er–Von Mises Estimation Method (CVME-M)
4.4. Least Squares Estimation Method (LSE-M)
4.5. Weighted Least-Squares Estimation Method (WLSE-M)
4.6. Maximum Product of Spacings Estimation Method (MPSE-M)
5. Simulation Study
- We set the beginning values for the parameters of our suggested model.
- From our suggested model, we have produced random data sets using the inverse of cdf.
- Use several estimate techniques to find estimators for our proposed model.
- Calculate the bias, MSE, and MRE for each estimator using each estimating technique.
- Repeat steps 1 through 4, 500 times.
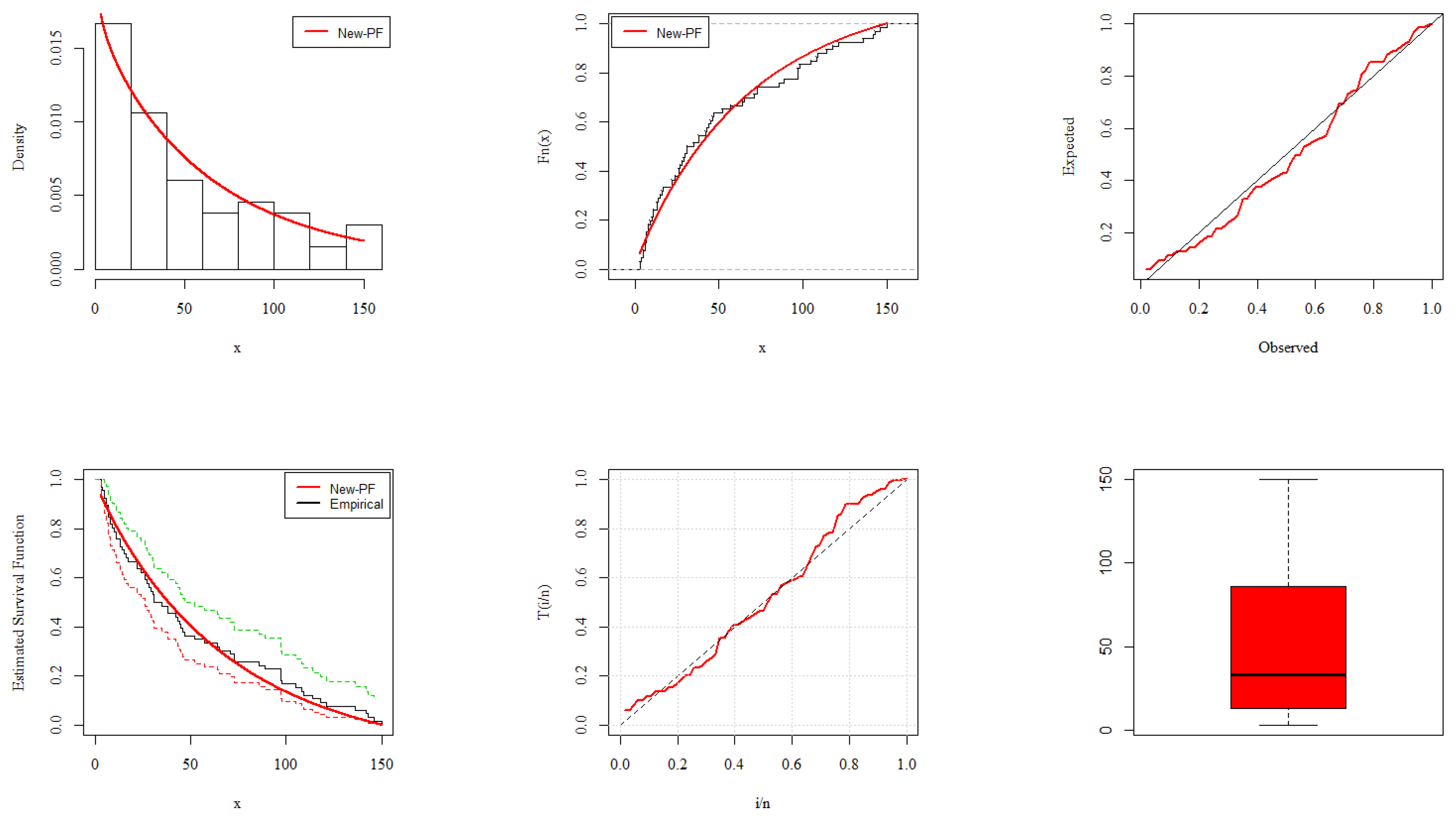
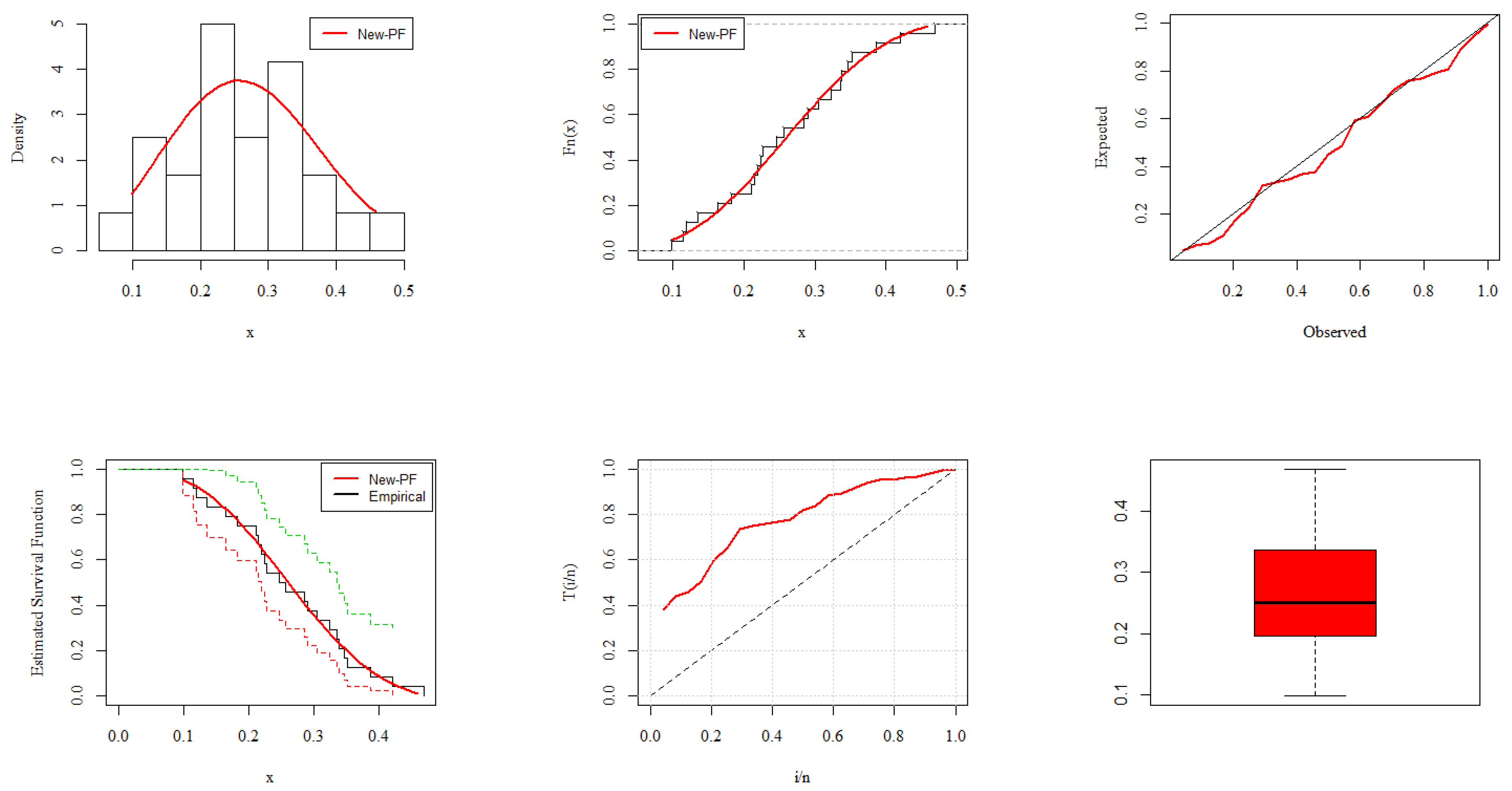
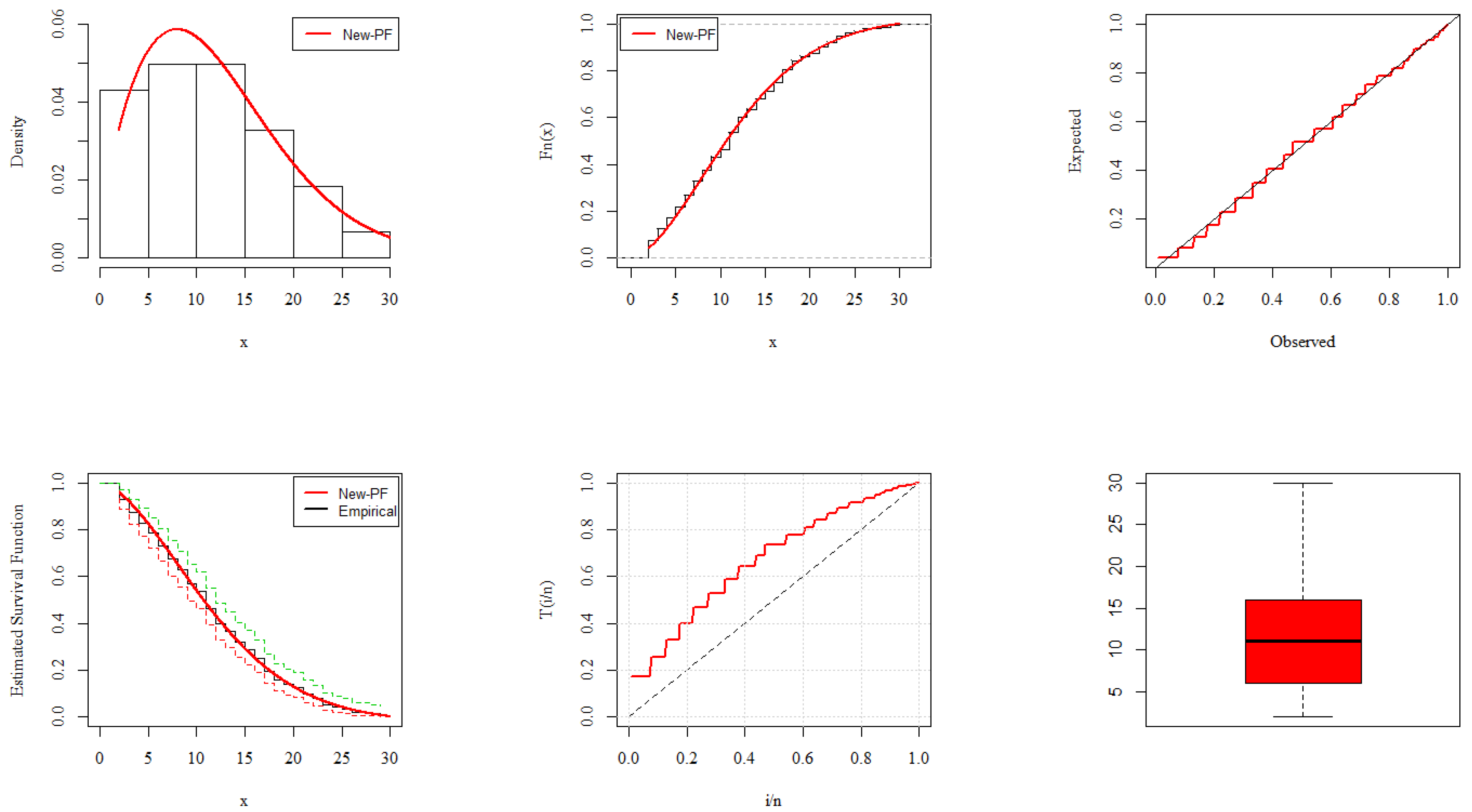
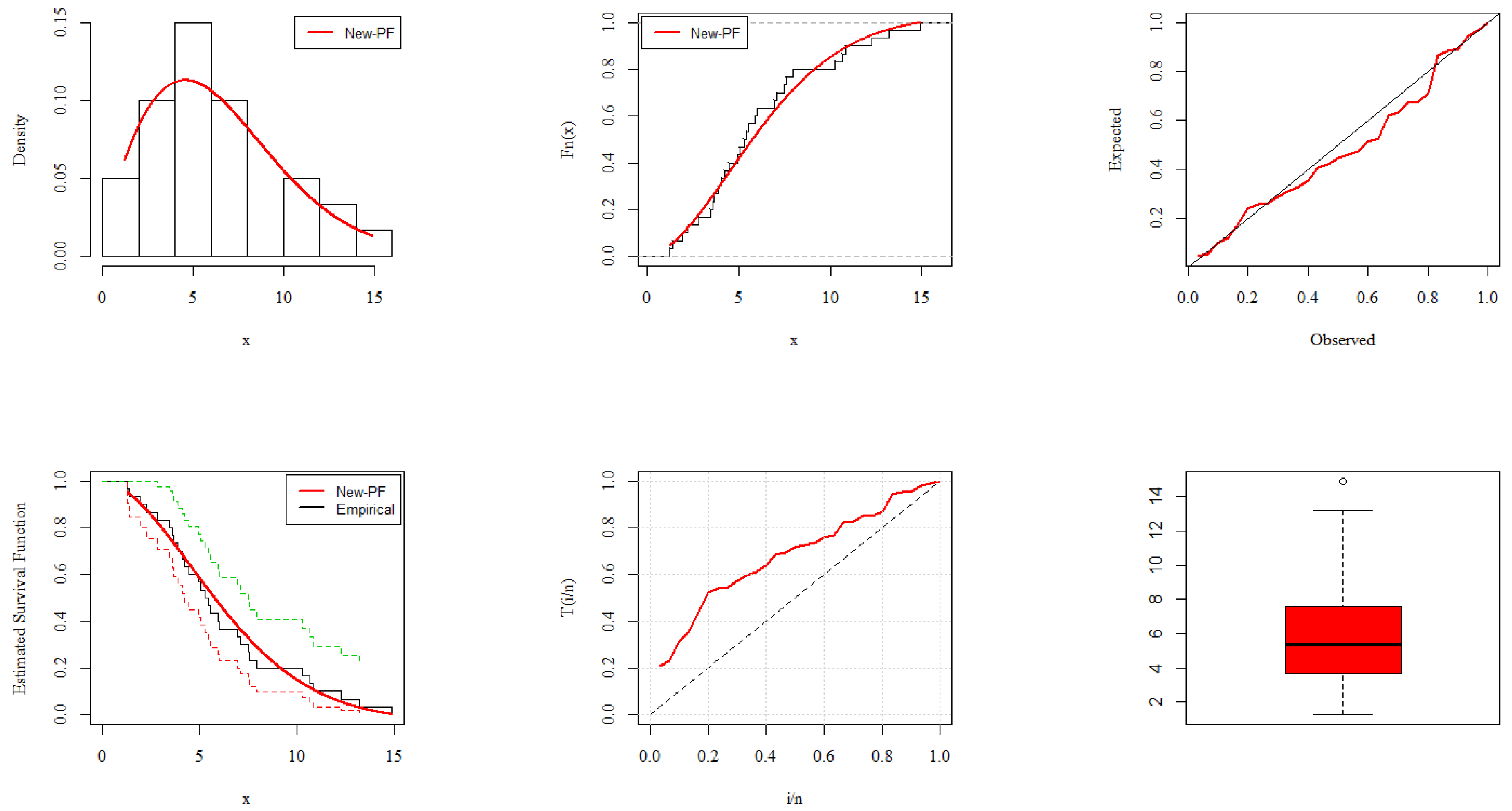
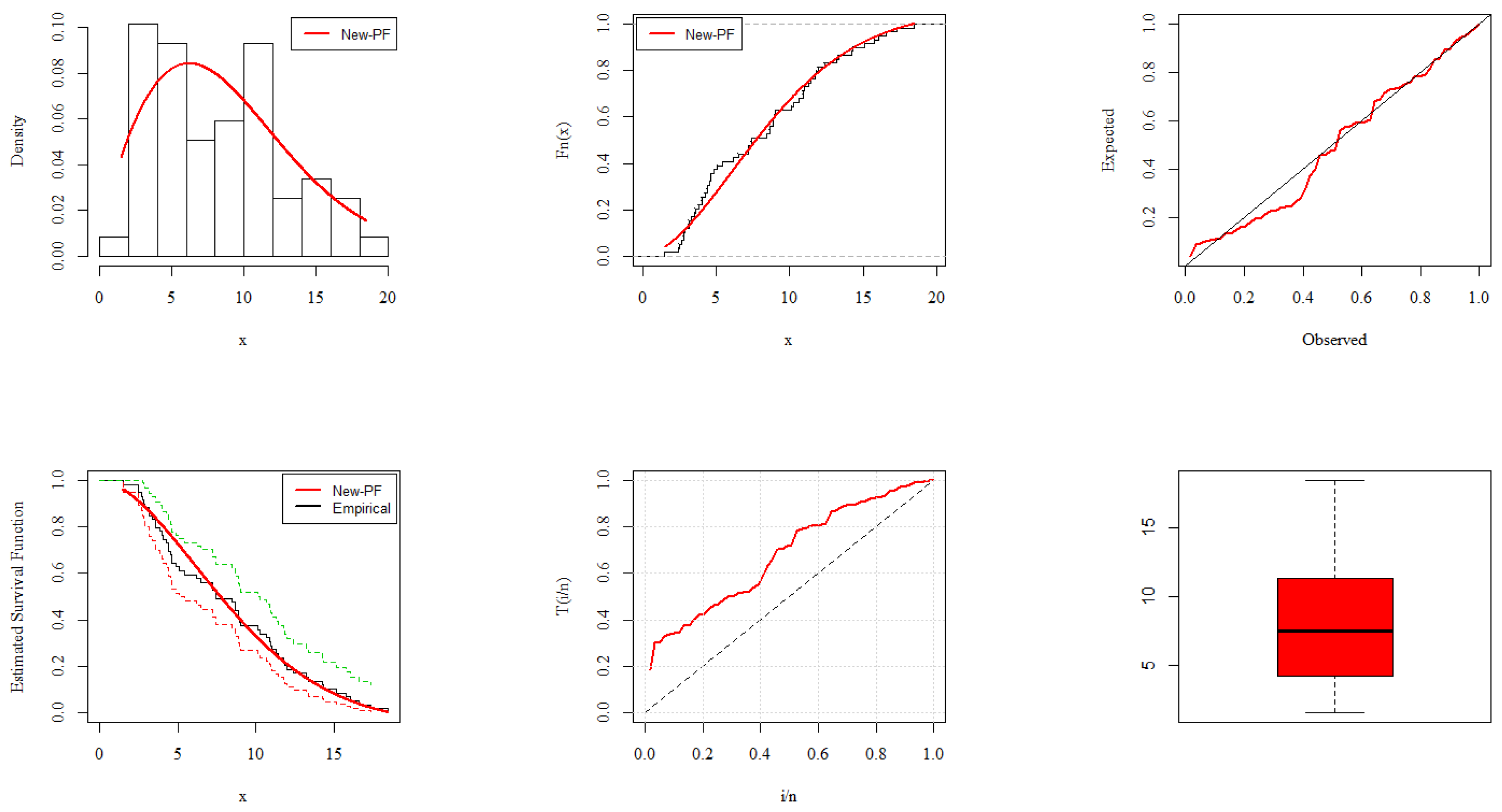
6. Analysis of COVID-19 Data
7. Summary and Conclusions
8. Future Recommendations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- Application I: United Kingdom COVID-19 Mortality Rate
- Application II: Europe COVID-19 Mortality Rate
- Application III: China COVID-19 Mortality Rate
- Application IV: United Kingdom COVID-19 Mortality Rate
- Application V: Nepal COVID-19 Mortality Rate
- Application VI: Netherland COVID-19 Mortality Rate
- Application VII: Italy COVID-19 Mortality Rate
References
- Dallas, A.C. Characterizing the Pareto and power distributions. Ann. Math. Stat. 1976, 28, 491–497. [Google Scholar] [CrossRef]
- Saran, J.; Pandey, A. Estimation of parameters of power function distribution and its characterization by the kth record values. Statistica. 2004, 14, 523–536. [Google Scholar]
- Zaka, A.; Akhter, A.S.; Jabeen, R. The new reflected power function distribution: Theory, simulation & application. AIMS Math. 2020, 5, 5031–5054. [Google Scholar]
- Tahir, M.H.; Alizadeh, M.; Mansoor, M.; Cordeiro, G.M.; Zubair, M. The Weibull-power function distribution with applications. Hacet. J. Math. Stat. 2016, 45, 245–265. [Google Scholar] [CrossRef]
- Ahsan-ul-Haq, M.; Butt, N.S.; Usman, R.M.; Fattah, A.A. Transmuted power function distribution. Gazi Univ. J. Sci. 2016, 29, 177–185. [Google Scholar]
- Okorie, I.E.; Akpanta, A.C.; Ohakwe, J.; Chikezie, D.C. The modified power function distribution. Cogent Math. 2017, 4, 1319592. [Google Scholar] [CrossRef]
- Hassan, A.S.; Assar, S.M. A new class of power function distribution: Properties and applications. Ann. Data Sci. 2021, 8, 205–225. [Google Scholar] [CrossRef]
- Meniconi, M.; Barry, D. The power function distribution: A useful and simple distribution to assess electrical component reliability. Microelectron. Reliab. 1996, 36, 1207–1212. [Google Scholar] [CrossRef]
- Marshall, A.W.; Olkin, I. A new method for adding a parameter to a family of distributions with application to the exponential and Weibull families. Biometrika 1997, 84, 641–652. [Google Scholar] [CrossRef]
- Shaw, W.T.; Buckley, I.R. Alchemy of Probability Distributions: Beyond Gram-Charlier and Cornish-Fisher Expansions, and Skewed-kurtotic Normal Distribution from a Rank Transmutation Map. arXiv 2009, arXiv:0901.0434. [Google Scholar]
- Eugene, N.; Lee, C.; Famoye, F. Beta-normal distribution and its applications. Commun. Stat.-Theory Methods 2002, 31, 497–512. [Google Scholar] [CrossRef]
- Pourreza, H.; Jamkhaneh, E.B.; Deiri, E. A family of Gamma-generated distributions: Statistical properties and applications. Stat. Methods Med. Res. 2021, 30, 1850–1873. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; de Castro, M. A new family of generalized distributions. J. Stat. Comput. Simul. 2011, 81, 883–898. [Google Scholar] [CrossRef]
- Alzaatreh, A.; Lee, C.; Famoye, F. A new method for generating families of continuous distributions. Metron 2013, 71, 63–79. [Google Scholar] [CrossRef]
- Bourguignon, M.; Silva, R.B.; Cordeiro, G.M. The Weibull-G family of probability distributions. Data Sci. J. 2014, 12, 53–68. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Alizadeh, M.; Diniz Marinho, P.R. The type I half-logistic family of distributions. J. Stat. Comput. Simul. 2016, 86, 707–728. [Google Scholar] [CrossRef]
- Al-Shomrani, A.; Arif, O.; Shawky, A.; Hanif, S.; Shahbaz, M.Q. Topp–Leone family of distributions: Some properties and application. Pak. J. Stat. Oper. Res. 2016, 12, 443–451. [Google Scholar] [CrossRef]
- Al Mutairi, A.; Iqbal, M.Z.; Arshad, M.Z.; Afify, A.Z. A New Class of the Power Function Distribution: Theory and Inference with an Application to Engineering Data. J. Math. 2022, 2022, 1206254. [Google Scholar] [CrossRef]
- Al-Babtain, A.A.; Gemeay, A.M.; Afify, A.Z. Estimation methods for the discrete Poisson-Lindley and discrete Lindley distributions with actuarial measures and applications in medicine. J. King Saud Univ. Sci. 2021, 33, 101224. [Google Scholar] [CrossRef]
- Liu, X.; Ahmad, Z.; Gemeay, A.M.; Abdulrahman, A.T.; Hafez, E.H.; Khalil, N. Modeling the survival times of the COVID-19 patients with a new statistical model: A case study from China. PLoS ONE 2021, 16, e0254999. [Google Scholar] [CrossRef] [PubMed]
- Nagy, M.; Almetwally, E.M.; Gemeay, A.M.; Mohammed, H.S.; Jawa, T.M.; Sayed-Ahmed, N.; Muse, A.H. The new novel discrete distribution with application on covid-19 mortality numbers in Kingdom of Saudi Arabia and Latvia. Complexity 2021, 2021, 7192833. [Google Scholar] [CrossRef]
- Hossam, E.; Abdulrahman, A.T.; Gemeay, A.M.; Alshammari, N.; Alshawarbeh, E.; Mashaqbah, N.K. A novel extension of Gumbel distribution: Statistical inference with covid-19 application. Alex. Eng. J. 2022, 61, 8823–8842. [Google Scholar] [CrossRef]
- Riad, F.H.; Alruwaili, B.; Gemeay, A.M.; Hussam, E. Statistical modeling for COVID-19 virus spread in Kingdom of Saudi Arabia and Netherlands. Alex. Eng. J. 2022, 61, 9849–9866. [Google Scholar] [CrossRef]
- Alsuhabi, H.; Alkhairy, I.; Almetwally, E.M.; Almongy, H.M.; Gemeay, A.M.; Hafez, E.H.; Aldallal, R.A.; Sabry, M. A superior extension for the Lomax distribution with application to Covid-19 infections real data. Alex. Eng. J. 2022, 61, 11077–11090. [Google Scholar] [CrossRef]
- Meriem, B.; Gemeay, A.M.; Almetwally, E.M.; Halim, Z.; Alshawarbeh, E.; Abdulrahman, A.T.; Abd El-Raouf, M.M.; Hussam, E. The Power XLindley Distribution: Statistical Inference, Fuzzy Reliability, and COVID-19 Application. J. Funct. Spaces 2022, 2022, 9094078. [Google Scholar] [CrossRef]
- Abdul-Moniem, I.B. The Kumaraswamy power function distribution. J. Stat. Appl. Pro. 2017, 6, 81–90. [Google Scholar] [CrossRef]
- Tahir, M.H.; Cordeiro, G.M.; Alizadeh, M.; Mansoor, M.; Zubair, M.; Hamedani, G.G. The odd generalized exponential family of distributions with applications. JSDA 2015, 2, 1–28. [Google Scholar] [CrossRef]
- Hassan, A.S.; Nassr, S.G. A new generalization of power function distribution: Properties and estimation based on censored samples. Thail. Stat. 2020, 18, 215–234. [Google Scholar]
- Okorie, I.E.; Akpanta, A.C.; Ohakwe, J.; Chikezie, D.C.; Onyemachi, C.U.; Rastogi, M.K. Zero-truncated Poisson-power function distribution. Ann. Data Sci. 2021, 8, 107–129. [Google Scholar] [CrossRef]
- Okorie, I.E.; Akpanta, A.C.; Ohakwe, J. Marshall-Olkin extended power function distribution. FJPS 2017, 5, 16–29. [Google Scholar]
| Model | Base Model | New Model |
|---|---|---|
| Exponential | ||
| Weibull | ||
| Rayleigh | ||
| Gompertz | ||
| Lomax | ||
| Burr | ||
| Pareto | ||
| Half Log-Logistic | ||
| Kumaraswamy | ||
| Power Function | ||
| Uniform |
| Est. | Par. | MLE-M | ADE-M | CVME-M | MPSE-M | LSE-M | WLSE-M | |
|---|---|---|---|---|---|---|---|---|
| 20 | BIAS | 0.3769 | 0.3296 | 0.3288 | 0.3120 | 0.3697 | 0.3932 | |
| 0.3723 | 0.3683 | 0.3915 | 0.3293 | 0.3241 | 0.4479 | |||
| MSE | 0.2035 | 0.1671 | 0.1498 | 0.1352 | 0.1689 | 0.1946 | ||
| 0.2903 | 0.2374 | 0.3020 | 0.1866 | 0.1949 | 0.4083 | |||
| MRE | 0.7538 | 0.6593 | 0.6576 | 0.6240 | 0.7394 | 0.7864 | ||
| 0.2482 | 0.2455 | 0.2610 | 0.2196 | 0.2161 | 0.2986 | |||
| 40 | BIAS | 0.3226 | 0.3177 | 0.2933 | 0.2955 | 0.3218 | 0.3115 | |
| 0.2652 | 0.2654 | 0.2669 | 0.2128 | 0.2719 | 0.2403 | |||
| MSE | 0.1698 | 0.1469 | 0.1170 | 0.1294 | 0.1392 | 0.1394 | ||
| 0.1128 | 0.1173 | 0.1192 | 0.0843 | 0.1251 | 0.1109 | |||
| MRE | 0.6451 | 0.6354 | 0.5865 | 0.5910 | 0.6435 | 0.6229 | ||
| 0.1768 | 0.1770 | 0.1780 | 0.1419 | 0.1813 | 0.1602 | |||
| 80 | BIAS | 0.2865 | 0.2372 | 0.2258 | 0.2450 | 0.2577 | 0.2499 | |
| 0.1836 | 0.1790 | 0.1891 | 0.1689 | 0.1741 | 0.1767 | |||
| MSE | 0.1457 | 0.0925 | 0.0828 | 0.0998 | 0.1098 | 0.1059 | ||
| 0.0632 | 0.0521 | 0.0550 | 0.0538 | 0.0547 | 0.0535 | |||
| MRE | 0.5730 | 0.4744 | 0.4516 | 0.4901 | 0.5154 | 0.4999 | ||
| 0.1224 | 0.1193 | 0.1261 | 0.1126 | 0.1161 | 0.1178 | |||
| 100 | BIAS | 0.2538 | 0.2231 | 0.2604 | 0.2140 | 0.2631 | 0.2727 | |
| 0.1768 | 0.1661 | 0.1741 | 0.1501 | 0.1812 | 0.1577 | |||
| MSE | 0.1142 | 0.0816 | 0.1062 | 0.0832 | 0.1109 | 0.1151 | ||
| 0.0556 | 0.0482 | 0.0519 | 0.0413 | 0.0528 | 0.0449 | |||
| MRE | 0.5076 | 0.4462 | 0.5207 | 0.4279 | 0.5262 | 0.5455 | ||
| 0.1178 | 0.1107 | 0.1161 | 0.1001 | 0.1208 | 0.1051 | |||
| 150 | BIAS | 0.2357 | 0.2039 | 0.2321 | 0.2295 | 0.2092 | 0.2634 | |
| 0.1523 | 0.1357 | 0.1600 | 0.1158 | 0.1319 | 0.1414 | |||
| MSE | 0.1210 | 0.0779 | 0.0974 | 0.1005 | 0.0906 | 0.1184 | ||
| 0.0479 | 0.0300 | 0.0528 | 0.0248 | 0.0431 | 0.0302 | |||
| MRE | 0.4713 | 0.4078 | 0.4641 | 0.4590 | 0.4183 | 0.5269 | ||
| 0.1015 | 0.0905 | 0.1067 | 0.0772 | 0.0879 | 0.0942 | |||
| 200 | BIAS | 0.2177 | 0.1687 | 0.2269 | 0.1551 | 0.2126 | 0.2236 | |
| 0.1270 | 0.1073 | 0.1115 | 0.0926 | 0.1097 | 0.1222 | |||
| MSE | 0.1030 | 0.0600 | 0.0978 | 0.0514 | 0.0872 | 0.0980 | ||
| 0.0273 | 0.0193 | 0.0217 | 0.0159 | 0.0200 | 0.0248 | |||
| MRE | 0.4353 | 0.3375 | 0.4538 | 0.3101 | 0.4251 | 0.4472 | ||
| 0.0847 | 0.0715 | 0.0743 | 0.0617 | 0.0731 | 0.0815 |
| Est. | Par. | MLE-M | ADE-M | CVME-M | MPSE-M | LSE-M | WLSE-M | |
|---|---|---|---|---|---|---|---|---|
| 20 | BIAS | 0.4524 | 0.3208 | 0.3965 | 0.2681 | 0.3433 | 0.3426 | |
| 0.1327 | 0.1265 | 0.1600 | 0.1030 | 0.1352 | 0.1349 | |||
| MSE | 0.2718 | 0.1350 | 0.1910 | 0.1034 | 0.1455 | 0.1650 | ||
| 0.0383 | 0.0277 | 0.0426 | 0.0238 | 0.0330 | 0.0374 | |||
| MRE | 0.6032 | 0.4278 | 0.5287 | 0.3575 | 0.4577 | 0.4568 | ||
| 0.2655 | 0.2529 | 0.3199 | 0.2060 | 0.2705 | 0.2698 | |||
| 40 | BIAS | 0.3773 | 0.2905 | 0.3601 | 0.2529 | 0.3060 | 0.3293 | |
| 0.0824 | 0.0786 | 0.1078 | 0.0616 | 0.0942 | 0.0795 | |||
| MSE | 0.2131 | 0.1143 | 0.1548 | 0.1018 | 0.1112 | 0.1374 | ||
| 0.0141 | 0.0115 | 0.0183 | 0.0083 | 0.0152 | 0.0106 | |||
| MRE | 0.5031 | 0.3873 | 0.4802 | 0.3372 | 0.4080 | 0.4390 | ||
| 0.1649 | 0.1572 | 0.2157 | 0.1231 | 0.1884 | 0.1590 | |||
| 80 | BIAS | 0.2763 | 0.2139 | 0.3093 | 0.2312 | 0.2794 | 0.2613 | |
| 0.0497 | 0.0542 | 0.0661 | 0.0419 | 0.0647 | 0.0602 | |||
| MSE | 0.1272 | 0.0754 | 0.1120 | 0.0938 | 0.0978 | 0.0858 | ||
| 0.0053 | 0.0061 | 0.0081 | 0.0035 | 0.0078 | 0.0062 | |||
| MRE | 0.3684 | 0.2852 | 0.4125 | 0.3083 | 0.3725 | 0.3484 | ||
| 0.0993 | 0.1084 | 0.1321 | 0.0838 | 0.1293 | 0.1203 | |||
| 100 | BIAS | 0.2598 | 0.1988 | 0.2691 | 0.1739 | 0.2452 | 0.2783 | |
| 0.0428 | 0.0445 | 0.0514 | 0.0311 | 0.0547 | 0.0606 | |||
| MSE | 0.1216 | 0.0647 | 0.0946 | 0.0633 | 0.0823 | 0.0992 | ||
| 0.0045 | 0.0043 | 0.0045 | 0.0024 | 0.0047 | 0.0065 | |||
| MRE | 0.3464 | 0.2650 | 0.3589 | 0.2318 | 0.3270 | 0.3711 | ||
| 0.0856 | 0.0890 | 0.1028 | 0.0623 | 0.1094 | 0.1212 | |||
| 150 | BIAS | 0.2659 | 0.1839 | 0.2481 | 0.1731 | 0.2767 | 0.2420 | |
| 0.0446 | 0.0318 | 0.0465 | 0.0334 | 0.0446 | 0.0439 | |||
| MSE | 0.1286 | 0.0632 | 0.0792 | 0.0642 | 0.0901 | 0.0779 | ||
| 0.0046 | 0.0022 | 0.0035 | 0.0027 | 0.0033 | 0.0031 | |||
| MRE | 0.3546 | 0.2453 | 0.3307 | 0.2308 | 0.3690 | 0.3227 | ||
| 0.0893 | 0.0636 | 0.0930 | 0.0668 | 0.0891 | 0.0879 | |||
| 200 | BIAS | 0.2047 | 0.1354 | 0.2469 | 0.1375 | 0.2556 | 0.2536 | |
| 0.0317 | 0.0268 | 0.0484 | 0.0223 | 0.0428 | 0.0427 | |||
| MSE | 0.0950 | 0.0386 | 0.0761 | 0.0481 | 0.0814 | 0.0781 | ||
| 0.0030 | 0.0018 | 0.0037 | 0.0013 | 0.0029 | 0.0032 | |||
| MRE | 0.2730 | 0.1805 | 0.3292 | 0.1833 | 0.3408 | 0.3381 | ||
| 0.0633 | 0.0536 | 0.0967 | 0.0446 | 0.0856 | 0.0854 |
| Est. | Par. | MLE-M | ADE-M | CVME-M | MPSE-M | LSE-M | WLSE-M | |
|---|---|---|---|---|---|---|---|---|
| 20 | BIAS | 1.1442 | 0.2833 | 0.3719 | 0.3823 | 0.4131 | 0.3160 | |
| 0.1602 | 0.1293 | 0.1434 | 0.1475 | 0.1504 | 0.1414 | |||
| MSE | 1.6432 | 0.1557 | 0.2312 | 0.2903 | 0.2905 | 0.1607 | ||
| 0.0408 | 0.0307 | 0.0316 | 0.0331 | 0.0361 | 0.0305 | |||
| MRE | 0.4577 | 0.1133 | 0.1488 | 0.1529 | 0.1653 | 0.1264 | ||
| 0.2136 | 0.1724 | 0.1912 | 0.1967 | 0.2005 | 0.1885 | |||
| 40 | BIAS | 0.8187 | 0.1869 | 0.3060 | 0.2338 | 0.3459 | 0.2289 | |
| 0.1534 | 0.0950 | 0.1106 | 0.0853 | 0.1104 | 0.1052 | |||
| MSE | 1.1100 | 0.0648 | 0.1467 | 0.1348 | 0.2198 | 0.0965 | ||
| 0.0428 | 0.0135 | 0.0195 | 0.0115 | 0.0204 | 0.0181 | |||
| MRE | 0.3275 | 0.0747 | 0.1224 | 0.0935 | 0.1384 | 0.0916 | ||
| 0.2045 | 0.1267 | 0.1474 | 0.1138 | 0.1473 | 0.1402 | |||
| 80 | BIAS | 0.5424 | 0.1206 | 0.1838 | 0.1014 | 0.1968 | 0.1544 | |
| 0.1142 | 0.0673 | 0.0815 | 0.0586 | 0.0770 | 0.0759 | |||
| MSE | 0.6064 | 0.0286 | 0.0564 | 0.0168 | 0.0653 | 0.0417 | ||
| 0.0250 | 0.0072 | 0.0104 | 0.0057 | 0.0090 | 0.0082 | |||
| MRE | 0.2170 | 0.0483 | 0.0735 | 0.0406 | 0.0787 | 0.0618 | ||
| 0.1523 | 0.0897 | 0.1087 | 0.0781 | 0.1027 | 0.1012 | |||
| 100 | BIAS | 0.5402 | 0.0992 | 0.1572 | 0.0818 | 0.1865 | 0.1131 | |
| 0.1370 | 0.0632 | 0.0556 | 0.0457 | 0.0674 | 0.0526 | |||
| MSE | 0.5514 | 0.0184 | 0.0420 | 0.0111 | 0.0506 | 0.0200 | ||
| 0.0362 | 0.0064 | 0.0051 | 0.0037 | 0.0075 | 0.0046 | |||
| MRE | 0.2161 | 0.0397 | 0.0629 | 0.0327 | 0.0746 | 0.0452 | ||
| 0.1826 | 0.0843 | 0.0741 | 0.0609 | 0.0898 | 0.0702 | |||
| 150 | BIAS | 0.3914 | 0.0701 | 0.1261 | 0.0587 | 0.1387 | 0.0879 | |
| 0.0915 | 0.0393 | 0.0524 | 0.0397 | 0.0517 | 0.0486 | |||
| MSE | 0.3582 | 0.0099 | 0.0252 | 0.0066 | 0.0318 | 0.0118 | ||
| 0.0172 | 0.0025 | 0.0043 | 0.0026 | 0.0040 | 0.0038 | |||
| MRE | 0.1566 | 0.0281 | 0.0504 | 0.0235 | 0.0555 | 0.0352 | ||
| 0.1221 | 0.0523 | 0.0699 | 0.0530 | 0.0690 | 0.0648 | |||
| 200 | BIAS | 0.2187 | 0.0536 | 0.1108 | 0.0354 | 0.1192 | 0.0755 | |
| 0.0579 | 0.0378 | 0.0487 | 0.0299 | 0.0453 | 0.0406 | |||
| MSE | 0.0880 | 0.0064 | 0.0195 | 0.0022 | 0.0225 | 0.0082 | ||
| 0.0068 | 0.0025 | 0.0035 | 0.0017 | 0.0031 | 0.0027 | |||
| MRE | 0.0875 | 0.0215 | 0.0443 | 0.0142 | 0.0477 | 0.0302 | ||
| 0.0772 | 0.0504 | 0.0649 | 0.0398 | 0.0604 | 0.0542 |
| Est. | Par. | MLE-M | ADE-M | CVME-M | MPSE-M | LSE-M | WLSE-M | |
|---|---|---|---|---|---|---|---|---|
| 20 | BIAS | 0.6551 | 0.5539 | 0.5667 | 0.5194 | 0.5117 | 0.5046 | |
| 0.5853 | 0.5147 | 0.5672 | 0.5333 | 0.5370 | 0.5565 | |||
| MSE | 0.8185 | 0.4264 | 0.4388 | 0.3312 | 0.3496 | 0.3353 | ||
| 0.5296 | 0.4334 | 0.5226 | 0.3938 | 0.4555 | 0.4805 | |||
| MRE | 0.4367 | 0.3693 | 0.3778 | 0.3463 | 0.3411 | 0.3364 | ||
| 0.2341 | 0.2059 | 0.2269 | 0.2133 | 0.2148 | 0.2226 | |||
| 40 | BIAS | 0.4699 | 0.4312 | 0.4480 | 0.4797 | 0.4561 | 0.4303 | |
| 0.4674 | 0.4015 | 0.4695 | 0.4247 | 0.3905 | 0.4035 | |||
| MSE | 0.2956 | 0.2428 | 0.2840 | 0.3135 | 0.2724 | 0.2252 | ||
| 0.3515 | 0.2245 | 0.3717 | 0.2447 | 0.2339 | 0.2738 | |||
| MRE | 0.3133 | 0.2875 | 0.2987 | 0.3198 | 0.3041 | 0.2869 | ||
| 0.1870 | 0.1606 | 0.1878 | 0.1699 | 0.1562 | 0.1614 | |||
| 80 | BIAS | 0.3615 | 0.3707 | 0.3991 | 0.3688 | 0.3920 | 0.3369 | |
| 0.3561 | 0.2647 | 0.3746 | 0.3453 | 0.3465 | 0.2991 | |||
| MSE | 0.1906 | 0.1830 | 0.2170 | 0.1995 | 0.2006 | 0.1527 | ||
| 0.1944 | 0.1216 | 0.2243 | 0.1818 | 0.1802 | 0.1374 | |||
| MRE | 0.2410 | 0.2471 | 0.2661 | 0.2459 | 0.2613 | 0.2246 | ||
| 0.1424 | 0.1059 | 0.1498 | 0.1381 | 0.1386 | 0.1197 | |||
| 100 | BIAS | 0.3808 | 0.3453 | 0.3706 | 0.4104 | 0.3278 | 0.3254 | |
| 0.3515 | 0.2927 | 0.3085 | 0.3352 | 0.2728 | 0.2765 | |||
| MSE | 0.1986 | 0.1607 | 0.1639 | 0.2329 | 0.1525 | 0.1499 | ||
| 0.1995 | 0.1271 | 0.1579 | 0.1677 | 0.1200 | 0.1195 | |||
| MRE | 0.2539 | 0.2302 | 0.2470 | 0.2736 | 0.2185 | 0.2170 | ||
| 0.1406 | 0.1171 | 0.1234 | 0.1341 | 0.1091 | 0.1106 | |||
| 150 | BIAS | 0.2997 | 0.2534 | 0.3034 | 0.3213 | 0.3070 | 0.3110 | |
| 0.2417 | 0.2349 | 0.2779 | 0.2508 | 0.2770 | 0.2720 | |||
| MSE | 0.1447 | 0.1010 | 0.1283 | 0.1701 | 0.1295 | 0.1376 | ||
| 0.0890 | 0.0881 | 0.1206 | 0.0988 | 0.1082 | 0.1020 | |||
| MRE | 0.1998 | 0.1689 | 0.2023 | 0.2142 | 0.2047 | 0.2073 | ||
| 0.0967 | 0.0940 | 0.1112 | 0.1003 | 0.1108 | 0.1088 | |||
| 200 | BIAS | 0.2640 | 0.2652 | 0.3074 | 0.3507 | 0.2594 | 0.2394 | |
| 0.2121 | 0.2225 | 0.2266 | 0.2427 | 0.2349 | 0.2063 | |||
| MSE | 0.1234 | 0.1032 | 0.1193 | 0.1943 | 0.0987 | 0.0902 | ||
| 0.0762 | 0.0796 | 0.0746 | 0.0966 | 0.0821 | 0.0654 | |||
| MRE | 0.1760 | 0.1768 | 0.2050 | 0.2338 | 0.1729 | 0.1596 | ||
| 0.0848 | 0.0890 | 0.0906 | 0.0971 | 0.0940 | 0.0825 |
| Model | Estimates | Fitted Measures | |||||||
|---|---|---|---|---|---|---|---|---|---|
| AIC | CVM | AD | KS | p-Value | SS | ||||
| New-PFD | 0.0314 | 0.4012 | - | 283.6512 | 0.1934 | 1.2679 | 0.0777 | 0.7488 | 0.1147 |
| Tr-PF | 0.7647 | - | 1.5949 | 291.6001 | 0.3140 | 1.9964 | 0.1329 | 0.1367 | 0.3548 |
| Kum-PF | 1.1071 | 0.4754 | 1.3700 | 302.9045 | 0.4286 | 2.6819 | 0.1582 | 0.0446 | 0.5521 |
| OGE-PF | 6.4256 | 0.0690 | 2.0309 | 309.0742 | 0.3635 | 2.3533 | 0.1959 | 0.0058 | 0.9499 |
| PF-I | 0.4375 | - | - | 302.9309 | 0.4179 | 2.6213 | 0.1976 | 0.0053 | 0.9699 |
| NG-PF | 0.6775 | 0.0727 | 5.8366 | 305.8946 | 0.3440 | 2.1834 | 0.0777 | 0.0038 | 1.0395 |
| Gen-PF | 2.2790 | - | - | 332.1345 | 0.3500 | 2.1641 | 0.3180 | 0.0000 | 3.0369 |
| Model | Estimates | Fitted Measures | |||||||
|---|---|---|---|---|---|---|---|---|---|
| AIC | CVM | AD | KS | p-Value | SS | ||||
| New-PFD | 0.1921 | 0.3262 | - | 470.1407 | 0.1433 | 0.9490 | 0.1232 | 0.6889 | 0.0760 |
| ZTP-PF | 2.8368 | 0.7329 | - | 476.5421 | - | - | 0.1728 | 0.2790 | 0.1924 |
| Kum-PF | 1.2485 | 0.2696 | 0.6369 | 467.5365 | 0.1976 | 1.2621 | 0.1797 | 0.2393 | 0.2962 |
| OGE-PF | 4.7180 | 0.0646 | 0.0047 | 475.6623 | 0.1195 | 0.8823 | 0.2213 | 0.0818 | 0.4595 |
| Gen-PF | 1.0351 | - | - | 494.4784 | 0.1204 | 0.7690 | 0.3991 | 0.0001 | 1.8877 |
| Model | Estimates | Fitted Measures | |||||||
|---|---|---|---|---|---|---|---|---|---|
| AIC | CVM | AD | KS | p-Value | SS | ||||
| New-PFD | 0.1044 | 0.4908 | - | 642.4877 | 0.1217 | 0.8393 | 0.0814 | 0.7740 | 0.0924 |
| Tr-PF | 0.5604 | - | 1.7920 | 643.7063 | 0.1588 | 1.0521 | 0.1032 | 0.4836 | 0.1446 |
| NG-PF | 1.1644 | 17.2847 | 0.0531 | 648.6244 | 0.1868 | 1.2314 | 0.0814 | 0.2892 | 0.1946 |
| Kum-PF | 0.3894 | 1.6505 | 1.0472 | 650.1455 | 0.2125 | 1.3840 | 0.1464 | 0.1182 | 0.2983 |
| PF-I | 0.6247 | - | - | 646.2304 | 0.2118 | 1.3797 | 0.1521 | 0.0945 | 0.3314 |
| Model | Estimates | Fitted Measures | |||||||
|---|---|---|---|---|---|---|---|---|---|
| AIC | CVM | AD | KS | p-Value | SS | ||||
| New-PFD | 0.0287 | 1.3984 | - | −41.7665 | 0.0255 | 0.2089 | 0.0835 | 0.9910 | 0.0199 |
| NG-PF | 1.5971 | 18.5499 | 0.2342 | −38.5436 | 0.0361 | 0.3030 | 0.0835 | 0.9651 | 0.0265 |
| Kum-PF | 0.9756 | 2.1057 | 1.7528 | −36.7425 | 0.0532 | 0.4306 | 0.1276 | 0.7836 | 0.0555 |
| Tr-PF | 0.8341 | - | 1.0780 | −39.9779 | 0.0382 | 0.3138 | 0.1277 | 0.7826 | 0.0522 |
| PF-I | 1.4845 | - | - | −37.2526 | 0.0498 | 0.4067 | 0.2310 | 0.1311 | 0.2499 |
| Estimates | Fitted Measures | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | AIC | CVM | AD | KS | p-Value | SS | |||
| New-PFD | 0.0205 | 0.8481 | - | 993.5991 | 0.0471 | 0.4678 | 0.0519 | 0.8044 | 0.0531 |
| W-PF | 4.2216 | 8.4898 | 0.2024 | 996.1838 | 0.0597 | 0.5134 | 0.0548 | 0.7468 | 0.0594 |
| ZTP-PF | 4.3987 | 1.7816 | - | 998.4550 | 0.1012 | 0.8065 | 0.0679 | 0.4803 | 0.1028 |
| MOE-PF | 0.1416 | 1.9682 | - | 994.8340 | 0.0874 | 0.7155 | 0.0681 | 0.4774 | 0.0815 |
| Gen-PF | 1.7756 | - | - | 979.7377 | 0.5117 | 3.7593 | 0.0716 | 0.4132 | 0.1176 |
| Kum-PF | 0.4168 | 3.0564 | 1.9823 | 1012.3107 | 0.1206 | 0.9920 | 0.0790 | 0.2948 | 0.1706 |
| Tr-PF | 0.9380 | - | 1.2519 | 1002.0116 | 0.0784 | 0.6836 | 0.0819 | 0.2563 | 0.1993 |
| OGE-PF | 7.6256 | 0.1239 | 2.8673 | 1035.8485 | 0.2114 | 1.5872 | 0.1621 | 0.0006 | 1.0577 |
| PF-I | 0.8615 | - | - | 1039.2363 | 0.1050 | 0.8905 | 0.1992 | 0.0000 | 1.6514 |
| Model | Estimates | Fitted Measures | |||||||
|---|---|---|---|---|---|---|---|---|---|
| AIC | CVM | AD | KS | p-Value | SS | ||||
| New-PFD | 0.0253 | 0.8957 | - | 156.8105 | 0.1062 | 0.6493 | 0.1070 | 0.8467 | 0.0522 |
| PF-Poi | −3.5098 | 1.7625 | - | 156.8312 | 0.1076 | 0.6575 | 0.1093 | 0.8283 | 0.0549 |
| Tr-PF | 0.8025 | - | 1.3066 | 160.1585 | 0.1701 | 1.0188 | 0.1617 | 0.3725 | 0.1589 |
| NG-PF | 1.3880 | 164.1245 | 0.1819 | 1.1150 | 0.1070 | 0.3563 | 0.1619 | ||
| Kum-PF | 0.4400 | 2.4843 | 1.2740 | 167.1066 | 0.2316 | 1.4057 | 0.2097 | 0.1232 | 0.2811 |
| OGE-PF | 9.8176 | 0.1003 | 2.8782 | 168.6015 | 0.1665 | 0.9571 | 0.2378 | 0.0562 | 0.3771 |
| Model | Estimates | Fitted Measures | |||||||
|---|---|---|---|---|---|---|---|---|---|
| AIC | CVM | AD | KS | p-Value | SS | ||||
| New-PFD | 0.0442 | 0.8961 | - | 335.7237 | 0.0979 | 0.7027 | 0.1128 | 0.4103 | 0.1011 |
| Tr-PF | 0.8247 | - | 1.4090 | 338.2626 | 0.1176 | 0.8627 | 0.1162 | 0.3742 | 0.1269 |
| Kum-PF | 0.5666 | 2.2183 | 1.4513 | 345.9732 | 0.1472 | 1.1037 | 0.1172 | 0.3639 | 0.1927 |
| NG-PF | 1.4465 | 27.0812 | 0.0996 | 341.4392 | 0.1092 | 0.8408 | 0.1128 | 0.3496 | 0.1173 |
| OGE-PF | 8.7252 | 0.1239 | 2.8958 | 349.0370 | 0.1462 | 1.0418 | 0.1414 | 0.1718 | 0.3554 |
| ZTP-PF | 3.8076 | 1.9272 | - | 339.4020 | 0.1315 | 0.7659 | 0.1450 | 0.1514 | 0.1789 |
| PF-I | 1.0090 | - | - | 346.1583 | 0.1420 | 1.0706 | 0.1694 | 0.0598 | 0.4853 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alghamdi, A.S.; Abd El-Raouf, M.M. Exploring the Dynamics of COVID-19 with a Novel Family of Models. Mathematics 2023, 11, 1641. https://doi.org/10.3390/math11071641
Alghamdi AS, Abd El-Raouf MM. Exploring the Dynamics of COVID-19 with a Novel Family of Models. Mathematics. 2023; 11(7):1641. https://doi.org/10.3390/math11071641
Chicago/Turabian StyleAlghamdi, Abdulaziz S., and M. M. Abd El-Raouf. 2023. "Exploring the Dynamics of COVID-19 with a Novel Family of Models" Mathematics 11, no. 7: 1641. https://doi.org/10.3390/math11071641
APA StyleAlghamdi, A. S., & Abd El-Raouf, M. M. (2023). Exploring the Dynamics of COVID-19 with a Novel Family of Models. Mathematics, 11(7), 1641. https://doi.org/10.3390/math11071641






