Applied and Computational Mathematics for Digital Environments

1. Introduction

Currently, digitalization and digital transformation are actively expanding into various areas of human activity, and researchers are identifying urgent problems and offering new solutions regarding digital environments in industry [1,2], economics [3,4], medicine [5,6], ecology [7,8], education [9,10], etc.

The advanced principles and technologies of applied and computational mathematics should be used to address challenges faced by the global community. The application of such principles and technologies enables the study and modeling of various phenomena of the real world using intelligent software and hardware platforms and corresponding modules.

In this regard, topics of interest in this Special Issue, “Applied and Computational Mathematics for Digital Environments”, include but are not limited to scientific research, applied tasks and problems in the following areas:

• Construction of mathematical and information models of intelligent computer systems for monitoring and controlling the parameters of digital environments;
• Development of intelligent optimization algorithms that search for optimal parameters values of mathematical and information models in digital environments;
• Software and mathematical technologies in the implementation of intelligent monitoring and computer control of the parameters of digital environments;
• Development and application of mathematical and information models, machine learning methods, and artificial intelligence for the analysis and processing of big data in digital environments.

2. Statistics of the Special Issue

A total of 12 papers were submitted to this Special Issue, of which 11 were published (91.67%) [11,12,13,14,15,16,17,18,19,20,21] and only 1 was rejected (8.33%), indicating the very high quality of the original submissions.

These 11 papers were accepted for publication in this Special Issue after a careful, comprehensive and iterative peer-review process based on criteria related to their high quality and novelty.

The geographical distribution of the authors of the submitted papers is presented in Figure 1, and the published papers are represented by 26 authors from 5 different countries.

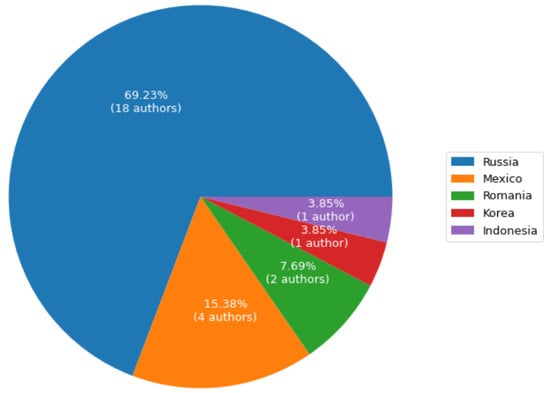
Figure 1. The geographical distribution of the authors of the papers.

We also note that three papers were written by one author each, three papers were written by teams of two authors, three papers were written by teams of three authors, one paper was written by a team of four authors, and one paper was written by a team of five authors.

At the same time, many papers were written as collaborations between authors from different countries, cities and scientific organizations.

3. Authors of the Special Issue

The authors of this Special Issue and their affiliations are shown in Table 1.

Table 1. Affiliations and bibliometric indicators for authors.

Author	Affiliation	References
Evgeny Nikulchev	Department of Intelligent Information Security Systems, MIREA—Russian Technological University, 119454 Moscow, Russia	[11]
Dmitry Ilin	Department of Intelligent Information Security Systems, MIREA—Russian Technological University, 119454 Moscow, Russia	[11]
Alexander Gusev	Data Center, Russian Academy of Education, Moscow 119121, Russia; Kuban State Technological University, 350072 Krasnodar, Russia	[11]
Ilya E. Tarasov	Institute of Informational Technologies, RTU MIREA, Vernadsky pr. 78, 119454 Moscow, Russia	[12]
Anton Aleshkin	Department of Systems Management and Modelling, MIREA—Russian Technological University, 78 Vernadsky Prospect, 119454 Moscow, Russia	[13]
Natanael Karjanto	Department of Mathematics, University College, Natural Science Campus, Sungkyunkwan University, Suwon 16419, Korea	[14]
Husty Serviana Husain	Department of Mathematics Education, Faculty of Mathematics and Natural Science Education, Indonesia University of Education, Bandung 40154, Indonesia	[14]
Bogdan Aman	Institute of Computer Science, Romanian Academy, 700505 Iaşi, Romania; Faculty of Computer Science, Alexandru Ioan Cuza University, 700506 Iaşi, Romania	[15]
Gabriel Ciobanu	Faculty of Computer Science, Alexandru Ioan Cuza University, 700506 Iaşi, Romania	[15]
Dmitry Zhukov	Institute of Cybersecurity and Digital Technologies, MIREA—Russian Technological University, 78 Vernadsky Avenue, 119454 Moscow, Russia	[16]
Julia Perova	Institute of Radio Electronics and Computer Science, MIREA—Russian Technological University, 78 Vernadsky Avenue, 119454 Moscow, Russia	[16]
Vladimir Kalinin	Institute of Cybersecurity and Digital Technologies, MIREA—Russian Technological University, 78 Vernadsky Avenue, 119454 Moscow, Russia	[16]
Juan-Jose Cardenas-Cornejo	Electronics Engineering Department, DICIS, University of Guanajuato, Carr. Salamanca-Valle de Santiago KM. 3.5 + 1.8 Km., Salamanca 36885, Mexico	[17]
Mario-Alberto Ibarra-Manzano	Electronics Engineering Department, DICIS, University of Guanajuato, Carr. Salamanca-Valle de Santiago KM. 3.5 + 1.8 Km., Salamanca 36885, Mexico	[17]
Daniel-Alberto Razo-Medina	Electronics Engineering Department, DICIS, University of Guanajuato, Carr. Salamanca-Valle de Santiago KM. 3.5 + 1.8 Km., Salamanca 36885, Mexico	[17]
Dora-Luz Almanza-Ojeda	Electronics Engineering Department, DICIS, University of Guanajuato, Carr. Salamanca-Valle de Santiago KM. 3.5 + 1.8 Km., Salamanca 36885, Mexico	[17]
Vladimir Krutikov	Department of Applied Mathematics, Kemerovo State University, Krasnaya Street 6, 650043 Kemerovo, Russia	[18]
Svetlana Gutova	Department of Applied Mathematics, Kemerovo State University, Krasnaya Street 6, 650043 Kemerovo, Russia	[18]
Elena Tovbis	Institute of Informatics and Telecommunications, Reshetnev Siberian State University of Science and Technology, Prosp. Krasnoyarskiy Rabochiy 31, 660031 Krasnoyarsk, Russia	[18]
Lev Kazakovtsev	Institute of Informatics and Telecommunications, Reshetnev Siberian State University of Science and Technology, Prosp. Krasnoyarskiy Rabochiy 31, 660031 Krasnoyarsk, Russia	[18]
Eugene Semenkin	Institute of Informatics and Telecommunications, Reshetnev Siberian State University of Science and Technology, Prosp. Krasnoyarskiy Rabochiy 31, 660031 Krasnoyarsk, Russia	[18,20]
Askhat Diveev	Federal Research Center “Computer Science and Control”, the Russian Academy of Sciences, 119333 Moscow, Russia	[19]
Elizaveta Shmalko	Federal Research Center “Computer Science and Control”, the Russian Academy of Sciences, 119333 Moscow, Russia	[19]
Aleksei Vakhnin	Department of System Analysis and Operations Research, Reshetnev Siberian State University of Science and Technology, 660037 Krasnoyarsk, Russia	[20]
Evgenii Sopov	Department of System Analysis and Operations Research, Reshetnev Siberian State University of Science and Technology, 660037 Krasnoyarsk, Russia	[20]
Liliya A. Demidova	Institute of Information Technologies, Federal State Budget Educational Institution of Higher Education, MIREA—Russian Technological University, 78, Vernadsky Avenue, 119454 Moscow, Russia	[21]

4. Overview of the Contributions to the Special Issue

Nikulchev et al. [11] evaluated the efficiency of integrating information technology solutions into digital platforms by developing a mathematical model and methodology based on the use of fuzzy logic.

Tarasov [12] studied the application of an approximation method of experimental data using functional dependencies. The author introduced an independent parameter “scale of the error probability distribution function” that considers the architecture and practical approaches to its implementation.

Aleshkin [13] proposed an approach to modeling and managing traffic flows based on percolation theory. The author studied the properties of transport networks and proposes algorithms for building planar random networks and calculating their percolation thresholds.

The study by Karjanto et al. [14] is dedicated to a computer algebra system (CAS) wxMaxima for calculus teaching and learning at a tertiary level. The authors study the strengths and limitations of the software under consideration.

Aman et al. [15] address the behavior of multi-agent systems. The authors consider how knowledge is handled and exchanged between agents, and study the evolution of the system that is caused by these exchanges.

Zhukov et al. [16] consider distributions of news items via the number of comments, including both comments at the first level and comments under these. The authors state that under certain assumptions the law for the stationary probability distribution can be derived from the Fokker–Planck differential equation.

Cardenas-Cornejo et al. [17] propose a new chromatic segmentation approach for detecting and classifying objects in urban environments. This approach yields centroids of patches on the color image, which are subsequently classified using a convolutional neural network (CNN) with a high accuracy score.

The study by Krutikov et al. [18] is dedicated to a new relaxation subgradient minimization method (RSMM). The computational experiments conducted by the authors confirmed the effectiveness of the proposed algorithm, showing that it outperforms currently known methods.

Diveev et al. [19] propose a universal numerical approach to solving the problem of optimal control with feedback using machine learning methods based on symbolic regression. First, authors introduce and discuss such notions as machine learning control, stability, optimality and feasibility of machine-made control systems. Then, they provide a substantiation for the machine learning feedback control approach based on symbolic regression and evolutionary algorithms.

Vakhnin et al. [20] address large-scale global black-box optimization (LSGO). The authors propose a self-adaptive approach that combines ideas from state-of-the-art algorithms and implements Coordination of Self-adaptive Cooperative Co-evolution algorithms with Local Search (COSACC-LS1).

Demidova [21] proposes an approach for diagnosing oncological diseases based on blood protein markers, new features generated using non-linear dimensionality reduction algorithm UMAP, formulas for various entropies and fractal dimensions. The author used resulting datasets with various combinations of features to develop multiclass kNN and SVM classifiers.

The published papers cover a wide range of tasks and problems in various fields of human activity and offer solutions by applying modern tools to analyze and process data in digital environments.

5. Acknowledgments to the Authors and Reviewers

As Guest Editor of the Special Issue, “Applied and Computational Mathematics for Digital Environments”, I am grateful to all contributing authors. I also express my gratitude to all the reviewers for their painstaking work and valuable comments that helped to improve the quality of the submitted papers.

6. Conclusions

The purpose of this Special Issue was to attract high-quality new papers in the field of applied and computational mathematics for digital environments, offering original solutions to various problems that are relevant and in demand in various fields of human activity.

I hope that these selected research papers are recognized as important and meaningful by the international scientific community and can form the basis for further research in the field of applied and computational mathematics for digital environments, solving complex problems in various disciplines and application areas.