Curves Related to the Gergonne Point in an Isotropic Plane

Abstract

The notion of the Gergonne point of a triangle in the Euclidean plane is very well known, and the study of them in the isotropic setting has already appeared earlier. In this paper, we give two generalizations of the Gergonne point of a triangle in the isotropic plane, and we study several curves related to them. The first generalization is based on the fact that for the triangle $ABC$ and its contact triangle $A_i{B}_i{C}_i$, there is a pencil of circles such that each circle $k_m$ from the pencil the lines $A{A}_m$, $B{B}_m$, $C{C}_m$ is concurrent at a point $G_m$, where $A_m$, $B_m$, $C_m$ are points on $k_m$ parallel to $A_i,B_i,C_i$, respectively. To introduce the second generalization of the Gergonne point, we prove that for the triangle $ABC$, point I and three lines $q_1,q_2,q_3$ through I there are two points $G_{1,2}$ such that for the points $Q_1,Q_2,Q_3$ on $q_1,q_2,q_3$ with $d(I,Q_1)=d(I,Q_2)=d(I,Q_3)$, the lines $A{Q}_1,B{Q}_2$ and $C{Q}_3$ are concurrent at $G_{1,2}$. We achieve these results by using the standardization of the triangle in the isotropic plane and simple analytical method.

1. Introduction

An isotropic plane is a projective plane with an absolute figure $(f,F)$ consisting of a real line f and a real point $F\in f$. Isotropic lines are all lines incident with F, and isotropic points are all points incident with f. Two lines intersecting at an isotropic point are called parallel lines. Analogously, any pair of distinct points joined by an isotropic line is said to be parallel. The standard affine model of the isotropic plane is obtained by setting $x_0=0$ for the equation of f, and $(0,0,1)$ for the coordinates of F. In this model, the coordinates of points are defined by $x={\displaystyle \frac{x_1}{x_0}}$, $y={\displaystyle \frac{x_2}{x_0}}$. The isotropic lines are given by the equations $x=const.$ The points $A=(x_A,y_A)$ and $B=(x_B,y_B)$ are parallel if $x_A=x_B$. The isotropic distance $d(A,B)$ of a pair of non-parallel points is defined by $d(A,B)=x_B-x_A$, as explained in [1].

We say that a triangle in the isotropic plane is allowable if all its sides are non-isotropic lines. It was shown in [2] that each allowable triangle can be set in the standard position by choosing an appropriate coordinate system. Such a triangle $ABC$ is inscribed into the circle with the equation $y=x^2$ and has vertices of the form

$$A(a,a^2),B(b,b^2),C(c,c^2),$$

(1)

with $a+b+c=0$.

The following abbreviations

$$p=abc,q=ab+bc+ca,$$

(2)

together with their repercussions

$$a^2+b^2+c^2=-2q,a^3+b^3+c^3=3p,$$

(3)

will be useful. In order to prove that some geometric fact is valid for each allowable triangle, it is sufficient to prove it for a standard triangle.

The Gergonne point of a triangle in the isotropic plane was studied in [3], where it was shown that the incircle (excircle) of the standard triangle $ABC$ has the equation

$$k_i...y=\frac{1}{4}{x}^2-q,$$

(4)

and the contact points are given by

$$A_i(-2a,bc-2q),B_i(-2b,ca-2q),C_i(-2c,ab-2q).$$

(5)

The common intersection point

$$\Gamma \left(-\frac{3p}{q},-\frac{4q}{3}\right)$$

(6)

of the lines $A{A}_i$, $B{B}_i$, and $C{C}_i$ is called the Gergonne point of the triangle $ABC$.

We study some curves related to the Gergonne point in the isotropic plane, and we present a sort of generalizations of the Gergonne point in the Euclidean case.

2. Materials and Methods

The Gergonne point of the triangle $ABC$ in the Euclidean plane is the intersection point of three lines $A{A}_i$, $B{B}_i$, $C{C}_i$, where $A_i,B_i,C_i$ are the contact points of the triangle and its incircle. In [4], the following generalization is given: let c be a circle concentric to the inscribed circle with the center I and let ${\overline{A}}_i,{\overline{B}}_i,{\overline{C}}_i$ be the intersections of c with $I{A}_i,I{B}_i,I{C}_i$, respectively. Then, the lines $A{\overline{A}}_i$, $B{\overline{B}}_i$, and $C{\overline{C}}_i$ are concurrent. The analogous situation in the isotropic plane is described in Theorem 1. In order to make the proofs simpler, we use the standardization of triangles. The calculation tool is purely analytical.

3. Results

Let $K\left(m\right)$ be the pencil of circles $k_m$ with the equation of the form

$$k_m...y=\frac{1}{4}{x}^2+m,$$

(7)

where $m\in \mathbb{R}$. The inscribed circle $k_i$ belongs to the pencil $K\left(m\right)$.

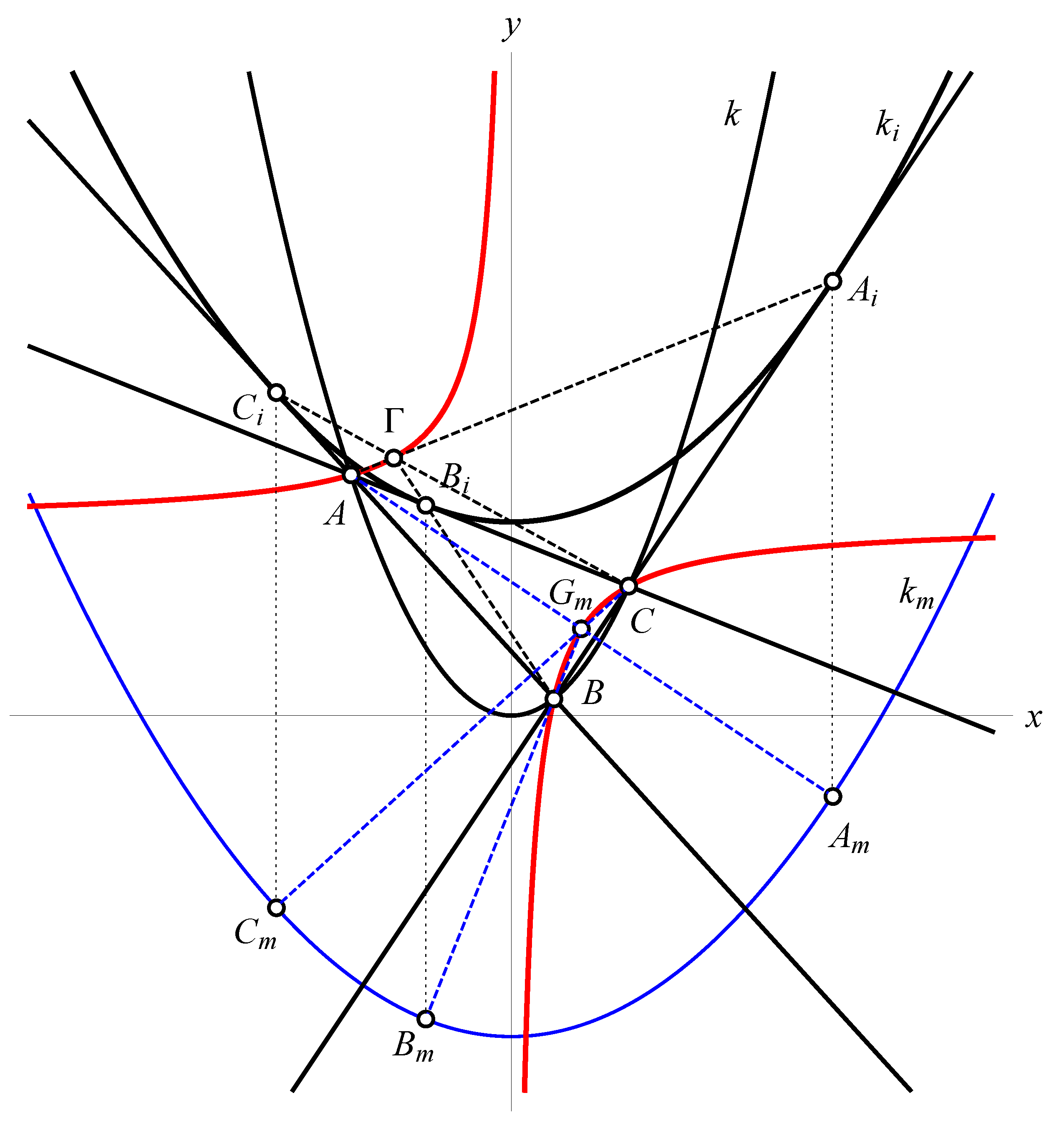
Theorem 1.

Let $ABC$ be the standard triangle, $A_i{B}_i{C}_i$ its contact triangle, and $k_m$ a circle of the pencil $K\left(m\right)$ given by the Equation (7). Let $A_m,B_m,C_m$ be the points of $k_m$ parallel to $A_i,B_i,C_i$, respectively. The lines $A{A}_m$, $B{B}_m$, $C{C}_m$ are concurrent at a point $G_m$.

When the circle $k_m$ runs through the pencil $K\left(m\right)$, the points $G_m$ form a special hyperbola.

Proof of Theorem 1.

The points $A_m,B_m,C_m\in k_m$ parallel to $A_i,B_i,C_i$ have the coordinates

$$A_m(-2a,a^2+m),B_m(-2b,b^2+m),C_m(-2c,c^2+m).$$

Therefore, the lines $A{A}_m$, $B{B}_m$, $C{C}_m$ have the equations

$$y=-\frac{m}{3a}x+a^2+\frac{m}{3},y=-\frac{m}{3b}x+b^2+\frac{m}{3},y=-\frac{m}{3c}x+c^2+\frac{m}{3}.$$

They all pass through the point

$$G_m\left(\frac{3p}{m},-q+\frac{m}{3}\right).$$

(8)

Indeed, the calculation ${\displaystyle -\frac{m}{3a}\frac{3p}{m}+a^2+\frac{m}{3}=-\frac{abc}{a}+a(-b-c)+\frac{m}{3}=-q+\frac{m}{3}}$ gives a proof for the line $A{A}_m$.

All points $G_m$ lie on the conic

$$xy+qx-p=0,$$

which is according to [1], a special hyperbola, see Figure 1. □

The point $G_m$ from Theorem 1 can be called the generalized Gergonne point for the triangle $ABC$ and the circle $k_m$.

The Gergonne point $\Gamma$ of the triangle $ABC$ is identical to $G_{-q}$.

The locus of generalized Gergonne points also passes through the vertices of the triangle $ABC$ since $G_{3bc}=A$, $G_{3ca}=B$, and $G_{3ab}=C$.

In [5,6], the authors gave some further generalizations of the concept of Gergonne point in the Euclidean case. Here, we study some analogues of these results in the isotropic case.

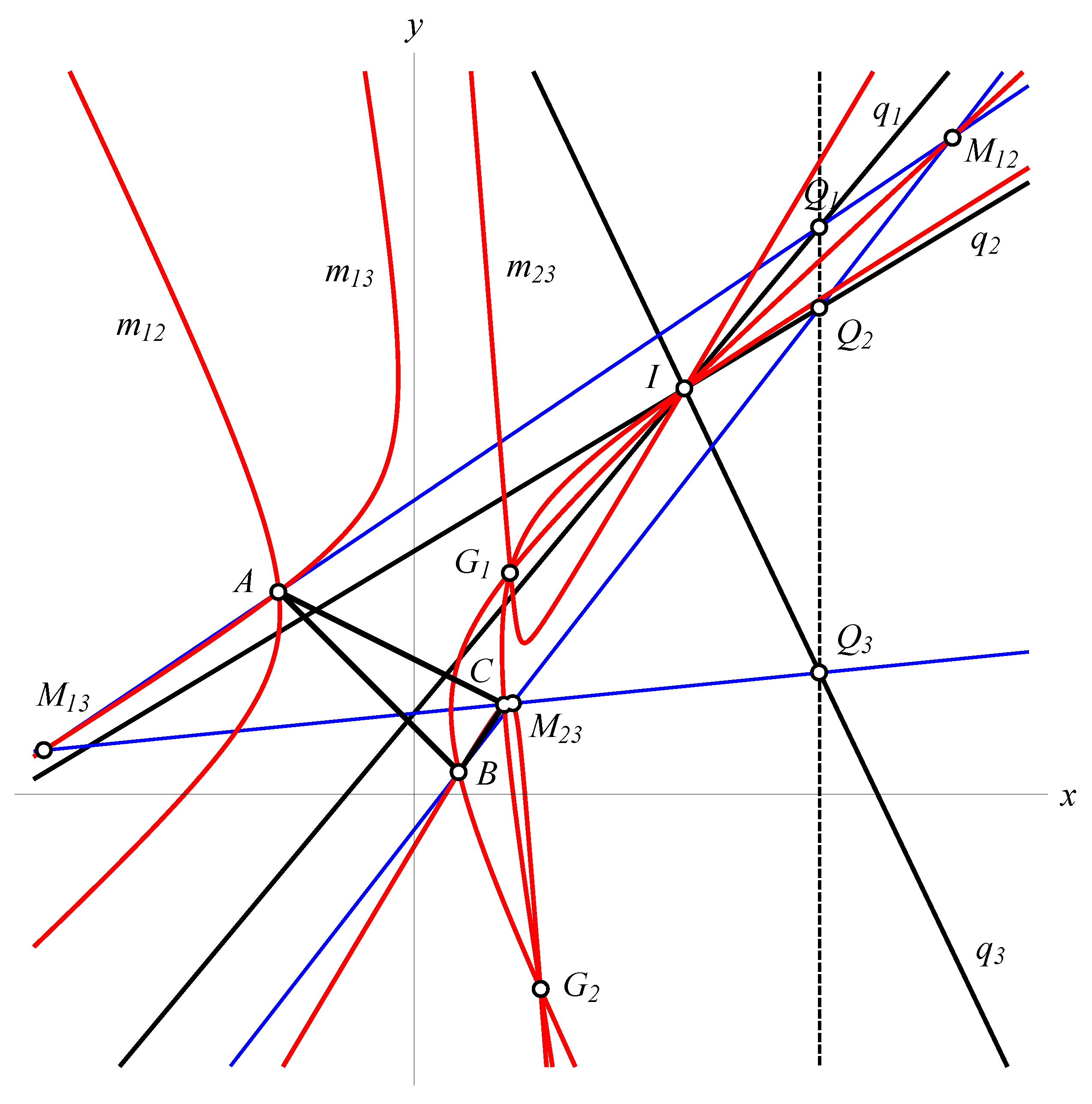
Theorem 2.

Let $ABC$ be the standard triangle, I a point in the isotropic plane and $q_1,q_2,q_3$ three lines through I. There are at most two values $d\in \mathbb{R}/\left\{0\right\}$ such that for points $Q_1,Q_2,Q_3$ on $q_1,q_2,q_3$ with $d(I,Q_1)=d(I,Q_2)=d(I,Q_3)=d$, the lines $A{Q}_1,B{Q}_2$ and $C{Q}_3$ are concurrent.

Proof of Theorem 2.

Let I be given by the coordinates $(\overline{x},\overline{y})$, and let $q_i$ have the equations $y=k_i(x-\overline{x})+\overline{y}$, $i=1,2,3$. All points T such that $d(I,T)=d$ lie on the isotropic line with the equation $x=\overline{x}+d$. Therefore, points $Q_i$ have coordinates $(d+\overline{x},k_{i}d+\overline{y})$, see Figure 2.

Thus,

$$\begin{array}{c}\hfill A{Q}_1...y=\frac{k_{1}d+\overline{y}-a}{d+\overline{x}-a}(x-a)+a^2,\\ \hfill B{Q}_2...y=\frac{k_{2}d+\overline{y}-b}{d+\overline{x}-b}(x-b)+b^2,\\ \hfill C{Q}_3...y=\frac{k_{3}d+\overline{y}-c}{d+\overline{x}-c}(x-c)+c^2.\end{array}$$

(9)

Let $M_{12}=A{Q}_1\cap B{Q}_2$, $M_{23}=B{Q}_2\cap C{Q}_3$, $M_{13}=A{Q}_1\cap C{Q}_3$. Some trivial but long calculations deliver the following values of d for which these three points coincide

$$d_{1,2}=\frac{-\mathcal{B}\pm \sqrt{{\mathcal{B}}^2-4\mathcal{A}\mathcal{C}}}{2\mathcal{A}},$$

(10)

where

$$\begin{array}{ccc}\hfill \mathcal{A}& =& k_1(c^2-b^2)+k_2(a^2-c^2)+k_3(b^2-a^2)+k_1{k}_2(b-a)+k_2{k}_3(c-b)+k_1{k}_3(a-c),\hfill \\ \hfill \mathcal{B}& =& k_1(c^3-b^3)+k_2(a^3-c^3)+k_3(b^3-a^3)+(k_1{k}_2+2k_3\overline{x})(b^2-a^2)\hfill \\ & & +(k_1{k}_3+2k_2\overline{x})(a^2-c^2)+(k_2{k}_3+2k_1\overline{x})(c^2-b^2)+(k_1{k}_2\overline{x}-k_3\overline{y})(b-a)\hfill \\ & & +(k_2{k}_3\overline{x}-k_1\overline{y})\left(c-b\right)+\left(k_1{k}_3\overline{x}-k_2\overline{y}\right)(a-c),\hfill \\ \hfill \mathcal{C}& =& \left(p-\overline{x}\overline{y}\right)\left[k_1(c-b)+k_2(a-c)+k_3(b-a)\right]+\overline{x}\left[k_1(c^3-b^3)+k_2(a^3-c^3)+k_3(b^3-a^3)\right]\hfill \\ & & +({\overline{x}}^2-\overline{y})\left[k_1(c^2-b^2)+k_2(a^2-c^2)+k_3(b^2-a^2)\right].\hfill \end{array}$$

The numbers $d_{1,2}$ are real and different, real and identical, or a pair of complex conjugate numbers depending on the value of ${\mathcal{B}}^2-4\mathcal{A}\mathcal{C}$. □

The values $d_{1,2}$ determine the points $G_{1,2}$, the common points of the lines $A{Q}_1,B{Q}_2$, and $C{Q}_3$. The points $G_1$ and $G_2$ can be real and different, complex conjugate, or coinciding depending on the value of ${\mathcal{B}}^2-4\mathcal{A}\mathcal{C}$. They are called generalized Gergonne points for the triangle $ABC$ and point I and lines $q_1$, $q_2$, $q_3$, through it.

Remark: By eliminating the parameter d from the first two equations of (9), we obtain the equation

$$\frac{(\overline{y}-a)(x-a)-(\overline{x}-a)(y-a^2)}{y-a^2-k_1(x-a)}=\frac{(\overline{y}-b)(x-b)-(\overline{x}-b)(y-b^2)}{y-b^2-k_2(x-b)}.$$

(11)

It represents the locus $m_{12}$ of points $M_{12}$ when d runs through $\mathbb{R}$. The curve $m_{12}$ is obviously a conic. In the same manner, we conclude that the loci of $M_{13}$ and $M_{23}$ are conics as well. According to Theorem 2, three loci $m_{12}$, $m_{13}$ and $m_{23}$ share two further common points $G_{1,2}$ except the fixed point I, see Figure 2.

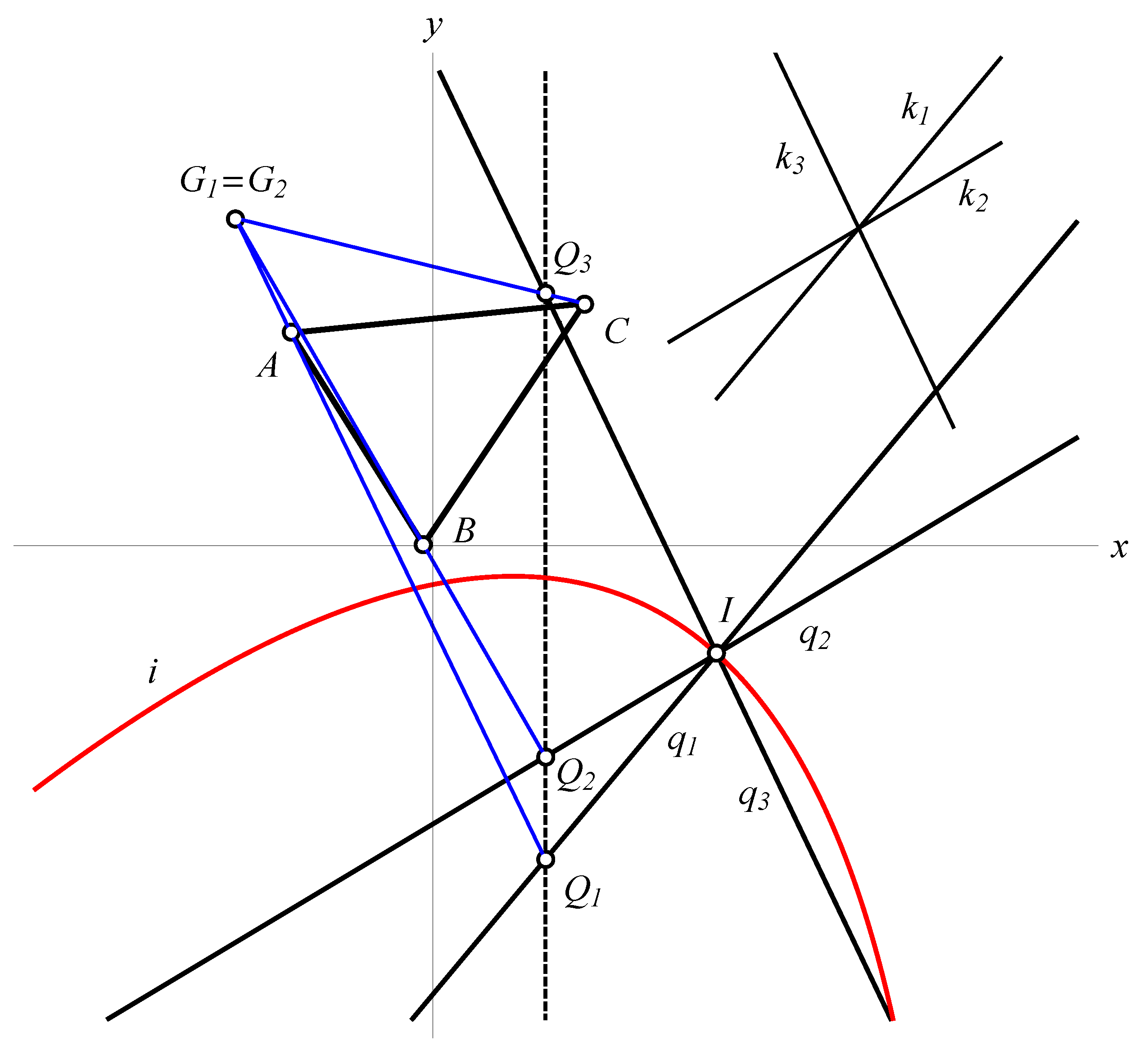
Note that, if directions $k_1,k_2,k_3$ are given, ${\mathcal{B}}^2-4\mathcal{A}\mathcal{C}$ from (10) is a quadratic function of $I(\overline{x},\overline{y})$. This means that there will be two, one, or none real points $G_{1,2}$ depending on whether the point I is located outside, on or inside the conic i with the equation ${\mathcal{B}}^2-4\mathcal{A}\mathcal{C}=0$, see Figure 3.

Now, we can also state:

Theorem 3.

Let $ABC$ be the standard triangle and $k_1,k_2,k_3$ three directions. All points I for which there is a unique value $d\in \mathbb{R}/\left\{0\right\}$ such that for points $Q_1,Q_2,Q_3$ on lines $q_1,q_2,q_3$ in directions $k_1,k_2,k_3$ with $d(I,Q_1)=d(I,Q_2)=d(I,Q_3)=d$ the lines $A{Q}_1,B{Q}_2$, and $C{Q}_3$ are concurrent lie on a parabola.

Proof of Theorem 3.

It is left to prove that the conic i with the equation ${\mathcal{B}}^2-4\mathcal{A}\mathcal{C}=0$ is a parabola. After replacing $\overline{x},\overline{y}$ with $x,y$ and introducing notations

$$\begin{array}{ccc}\hfill \mathcal{D}& =& k_1(c^2-b^2)+k_2(a^2-c^2)+k_3(b^2-a^2),\hfill \\ \hfill \mathcal{F}& =& k_1(c-b)+k_2(a-c)+k_3(b-a),\hfill \end{array}$$

the terms of the highest degree in the equation of i are

$${\left[(\mathcal{A}-\mathcal{D})x-\mathcal{F}y\right]}^2.$$

Thus, the conic i touches the absolute line in one point, the isotropic point of the line $y={\displaystyle \frac{\mathcal{A}-\mathcal{D}}{\mathcal{F}}}x$. □

4. Discussion and Conclusions

This study gives a contribution to the very rich base of triangle properties in the isotropic plane. We have proved that for a triangle $ABC$ and its contact triangle $A_i{B}_i{C}_i$, there is a pencil of circles $K_m$ such that for each circle $k_m$ from the pencil the lines $A{A}_m$, $B{B}_m$, $C{C}_m$ are concurrent at a point $G_m$, where $A_m$, $B_m$, $C_m$ are points on $k_m$ parallel to $A_i,B_i,C_i$, respectively. When $k_m$ runs through $K\left(m\right)$, the generalized Gergonne points $G_m$ form a special hyperbola.

Further on, to each triangle $ABC$, a point I and three lines $q_1,q_2,q_3$ through I we have associated three conics intersecting at I and two generalized Gergonne points $G_1$ and $G_2$. The existence of $G_1$ and $G_2$ follows from the existence of two values d such that for points $Q_1,Q_2,Q_3$ on $q_1,q_2,q_3$ with $d(I,Q_1)=d(I,Q_2)=d(I,Q_3)=d$ the lines $A{Q}_1,B{Q}_2$ and $C{Q}_3$ are concurrent. For arbitrary directions, the points I, such that $G_1,G_2$ coincide, lie on a parabola.

In the papers [7,8], the authors studied some further curves related to Gergonne points; they studied the loci of Gergonne points in different pencils of triangles in the isotropic plane. Hence, this paper completes the investigations given there.