A Machine-Learning-Based Model for Buckling Analysis of Thermally Affected Covalently Functionalized Graphene/Epoxy Nanocomposite Beams
Abstract
1. Introduction
2. Theory & Formulation
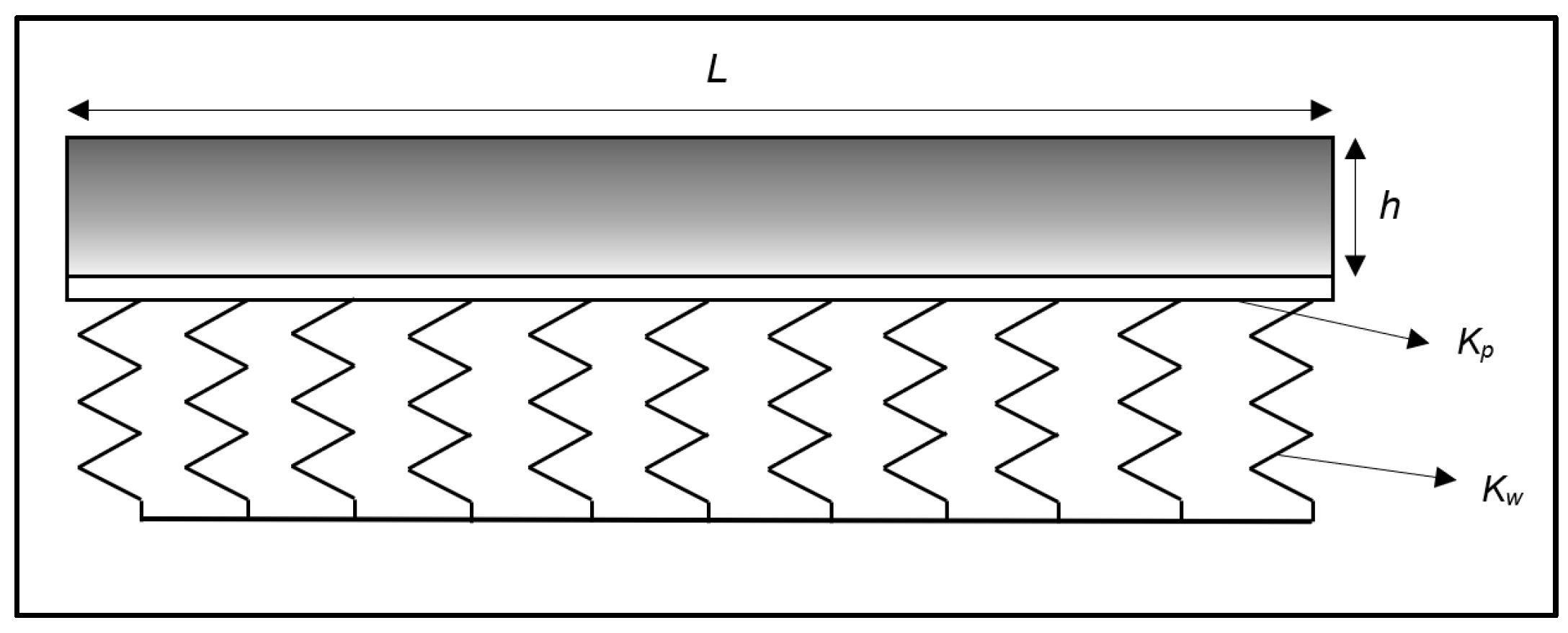
2.1. Problem Definition
2.2. Estimation of the Temperature-Dependent Young’s Moduli
2.3. The Governing Equation for Thermally Affected Buckling Problem
3. Analytical Solution
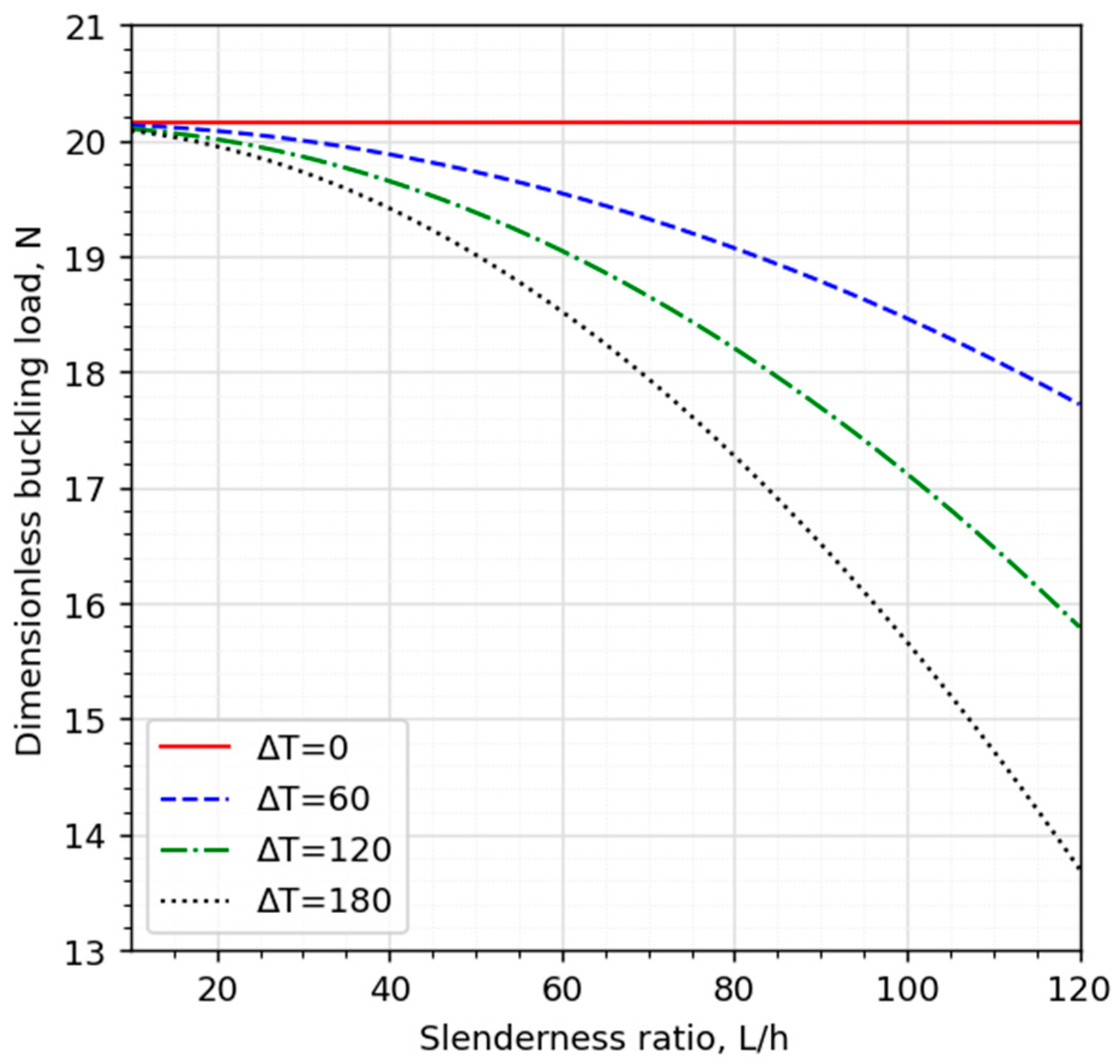
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tang, L.-C.; Wan, Y.-J.; Yan, D.; Pei, Y.-B.; Zhao, L.; Li, Y.-B.; Wu, L.-B.; Jiang, J.-X.; Lai, G.-Q. The effect of graphene dispersion on the mechanical properties of graphene/epoxy composites. Carbon 2013, 60, 16–27. [Google Scholar]
- Song, L.; Khoerunnisa, F.; Gao, W.; Dou, W.; Hayashi, T.; Kaneko, K.; Endo, M.; Ajayan, P.M. Effect of high-temperature thermal treatment on the structure and adsorption properties of reduced graphene oxide. Carbon 2013, 52, 608–612. [Google Scholar]
- Yadav, S.K.; Cho, J.W. Functionalized graphene nanoplatelets for enhanced mechanical and thermal properties of polyurethane nanocomposites. Appl. Surf. Sci. 2013, 266, 360–367. [Google Scholar]
- Naebe, M.; Wang, J.; Amini, A.; Khayyam, H.; Hameed, N.; Li, L.H.; Chen, Y.; Fox, B. Mechanical property and structure of covalent functionalised graphene/epoxy nanocomposites. Sci. Rep. 2014, 4, 4375. [Google Scholar]
- Chandrasekaran, S.; Sato, N.; Tölle, F.; Mülhaupt, R.; Fiedler, B.; Schulte, K. Fracture toughness and failure mechanism of graphene based epoxy composites. Compos. Sci. Technol. 2014, 97, 90–99. [Google Scholar]
- Ahmadi-Moghadam, B.; Taheri, F. Influence of graphene nanoplatelets on modes I, II and III interlaminar fracture toughness of fiber-reinforced polymer composites. Eng. Fract. Mech. 2015, 143, 97–107. [Google Scholar]
- Sun, Z.; Li, Y.-Q.; Huang, P.; Cao, H.-J.; Zeng, W.; Li, J.; Li, F.; Sun, B.-G.; Shi, H.-Q.; Zhou, Z.-l. Temperature-dependent mechanical properties of polyetherimide composites reinforced by graphene oxide-coated short carbon fibers. Compos. Struct. 2021, 270, 114075. [Google Scholar]
- Khoei, A.; Khorrami, M. Mechanical properties of graphene oxide: A molecular dynamics study. Fuller. Nanotub. Carbon Nanostruct. 2016, 24, 594–603. [Google Scholar] [CrossRef]
- Lin, F.; Xiang, Y.; Shen, H.-S. Temperature dependent mechanical properties of graphene reinforced polymer nanocomposites–a molecular dynamics simulation. Compos. Part B Eng. 2017, 111, 261–269. [Google Scholar]
- Feng, C.; Kitipornchai, S.; Yang, J. Nonlinear free vibration of functionally graded polymer composite beams reinforced with graphene nanoplatelets (GPLs). Eng. Struct. 2017, 140, 110–119. [Google Scholar]
- Kitipornchai, S.; Chen, D.; Yang, J. Free vibration and elastic buckling of functionally graded porous beams reinforced by graphene platelets. Mater. Des. 2017, 116, 656–665. [Google Scholar] [CrossRef]
- Yas, M.; Samadi, N. Free vibrations and buckling analysis of carbon nanotube-reinforced composite Timoshenko beams on elastic foundation. Int. J. Press. Vessel. Pip. 2012, 98, 119–128. [Google Scholar] [CrossRef]
- Barati, M.R.; Zenkour, A.M. Post-buckling analysis of refined shear deformable graphene platelet reinforced beams with porosities and geometrical imperfection. Compos. Struct. 2017, 181, 194–202. [Google Scholar] [CrossRef]
- Shen, H.-S.; Lin, F.; Xiang, Y. Nonlinear vibration of functionally graded graphene-reinforced composite laminated beams resting on elastic foundations in thermal environments. Nonlinear Dyn. 2017, 90, 899–914. [Google Scholar] [CrossRef]
- Yang, B.; Kitipornchai, S.; Yang, Y.-F.; Yang, J. 3D thermo-mechanical bending solution of functionally graded graphene reinforced circular and annular plates. Appl. Math. Model. 2017, 49, 69–86. [Google Scholar]
- Song, M.; Yang, J.; Kitipornchai, S. Bending and buckling analyses of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos. Part B Eng. 2018, 134, 106–113. [Google Scholar] [CrossRef]
- Yang, J.; Chen, D.; Kitipornchai, S. Buckling and free vibration analyses of functionally graded graphene reinforced porous nanocomposite plates based on Chebyshev-Ritz method. Compos. Struct. 2018, 193, 281–294. [Google Scholar]
- Yang, J.; Dong, J.; Kitipornchai, S. Unilateral and bilateral buckling of functionally graded corrugated thin plates reinforced with graphene nanoplatelets. Compos. Struct. 2019, 209, 789–801. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Dabbagh, A.; Civalek, Ö. Vibration analysis of magnetically affected graphene oxide-reinforced nanocomposite beams. J. Vib. Control 2019, 25, 2837–2849. [Google Scholar] [CrossRef]
- Moayedi, H.; Aliakbarlou, H.; Jebeli, M.; Noormohammadiarani, O.; Habibi, M.; Safarpour, H.; Foong, L. Thermal buckling responses of a graphene reinforced composite micropanel structure. Int. J. Appl. Mech. 2020, 12, 2050010. [Google Scholar] [CrossRef]
- Mao, J.-J.; Zhang, W. Buckling and post-buckling analyses of functionally graded graphene reinforced piezoelectric plate subjected to electric potential and axial forces. Compos. Struct. 2019, 216, 392–405. [Google Scholar]
- Amani, M.A.; Ebrahimi, F.; Dabbagh, A.; Rastgoo, A.; Nasiri, M.M. A machine learning-based model for the estimation of the temperature-dependent moduli of graphene oxide reinforced nanocomposites and its application in a thermally affected buckling analysis. Eng. Comput. 2021, 37, 2245–2255. [Google Scholar]
- Yas, M.-H.; Rahimi, S. Thermal buckling analysis of porous functionally graded nanocomposite beams reinforced by graphene platelets using Generalized differential quadrature method. Aerosp. Sci. Technol. 2020, 107, 106261. [Google Scholar]
- Shokrgozar, A.; Ghabussi, A.; Ebrahimi, F.; Habibi, M.; Safarpour, H. Viscoelastic dynamics and static responses of a graphene nanoplatelets-reinforced composite cylindrical microshell. Mech. Based Des. Struct. Mach. 2020, 50, 509–536. [Google Scholar] [CrossRef]
- Liu, J.; Deng, X.; Wang, Q.; Zhong, R.; Xiong, R.; Zhao, J. A unified modeling method for dynamic analysis of GPL-reinforced FGP plate resting on Winkler-Pasternak foundation with elastic boundary conditions. Compos. Struct. 2020, 244, 112217. [Google Scholar]
- Qian, W.-M.; Vahid, M.H.; Sun, Y.-L.; Heidari, A.; Barbaz-Isfahani, R.; Saber-Samandari, S.; Khandan, A.; Toghraie, D. Investigation on the effect of functionalization of single-walled carbon nanotubes on the mechanical properties of epoxy glass composites: Experimental and molecular dynamics simulation. J. Mater. Res. Technol. 2021, 12, 1931–1945. [Google Scholar]
- Eyvazian, A.; Sebaey, T.A.; Żur, K.K.; Khan, A.; Zhang, H.; Wong, S.H. On the dynamics of FG-GPLRC sandwich cylinders based on an unconstrained higher-order theory. Compos. Struct. 2021, 267, 113879. [Google Scholar]
- Zhao, S.; Zhang, Y.; Chen, D.; Yang, J.; Kitipornchai, S. Enhanced thermal buckling resistance of folded graphene reinforced nanocomposites with negative thermal expansion: From atomistic study to continuum mechanics modelling. Compos. Struct. 2022, 279, 114872. [Google Scholar]
- Jiang, Y.; Li, L.; Hu, Y. A compatible multiscale model for nanocomposites incorporating interface effect. Int. J. Eng. Sci. 2022, 174, 103657. [Google Scholar]
- Le, T.-T. Prediction of tensile strength of polymer carbon nanotube composites using practical machine learning method. J. Compos. Mater. 2021, 55, 787–811. [Google Scholar] [CrossRef]
- Garg, A.; Belarbi, M.-O.; Tounsi, A.; Li, L.; Singh, A.; Mukhopadhyay, T. Predicting elemental stiffness matrix of FG nanoplates using Gaussian Process Regression based surrogate model in framework of layerwise model. Eng. Anal. Bound. Elem. 2022, 143, 779–795. [Google Scholar]
- Rahman, A.; Deshpande, P.; Radue, M.S.; Odegard, G.M.; Gowtham, S.; Ghosh, S.; Spear, A.D. A machine learning framework for predicting the shear strength of carbon nanotube-polymer interfaces based on molecular dynamics simulation data. Compos. Sci. Technol. 2021, 207, 108627. [Google Scholar] [CrossRef]
- Samui, P.; Roy, S.S.; Balas, V.E. Handbook of Neural Computation; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Ebrahimi, F.; Barati, M.R. Hygrothermal buckling analysis of magnetically actuated embedded higher order functionally graded nanoscale beams considering the neutral surface position. J. Therm. Stress. 2016, 39, 1210–1229. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Dabbagh, A. On thermo-mechanical vibration analysis of multi-scale hybrid composite beams. J. Vib. Control 2019, 25, 933–945. [Google Scholar]



| Neat epoxy (C = 2121.54893) | |||||
| α1 | α2 | α3 | α4 | α5 | α6 |
| 7.80627389 | −1.81533262 × 10−1 | 5.99054633 × 10−4 | −9.41097233 × 101 | −1.87784478 × 102 | −1.82985862 × 102 |
| α7 | α8 | α9 | α10 | α11 | |
| −8.19707494 × 101 | −1.86225844 × 102 | −1.30992530 × 102 | −6.71379619 × 101 | −8.64014610 × 101 | |
| Epoxy/Graphene (C = 2394.51308) | |||||
| α1 | α2 | α3 | α4 | α5 | α6 |
| 4.33776820 | −1.66278050 × 10−1 | 6.11193348 × 10−4 | −2.42975958 × 101 | −7.63626419 × 101 | −1.33970188 × 102 |
| α7 | α8 | α9 | α10 | α11 | |
| −2.37603975 × 102 | −3.43333229 × 102 | −2.32259096 × 102 | −1.12062166 × 102 | −3.60855758 × 101 | |
| Epoxy/Functionalized graphene (C = 2968.22288) | |||||
| α1 | α2 | α3 | α4 | α5 | α6 |
| −1.22978891 × 101 | 2.27421386 × 10−2 | 1.09216658 × 10−5 | 1.61387358 × 101 | −1.34988115 × 101 | −1.25826021 × 101 |
| α7 | α8 | α9 | α10 | α11 | |
| −1.15675331 × 101 | −9.50302118 × 101 | −2.01753507 × 102 | −5.76713858 × 102 | −6.21085483 × 102 | |
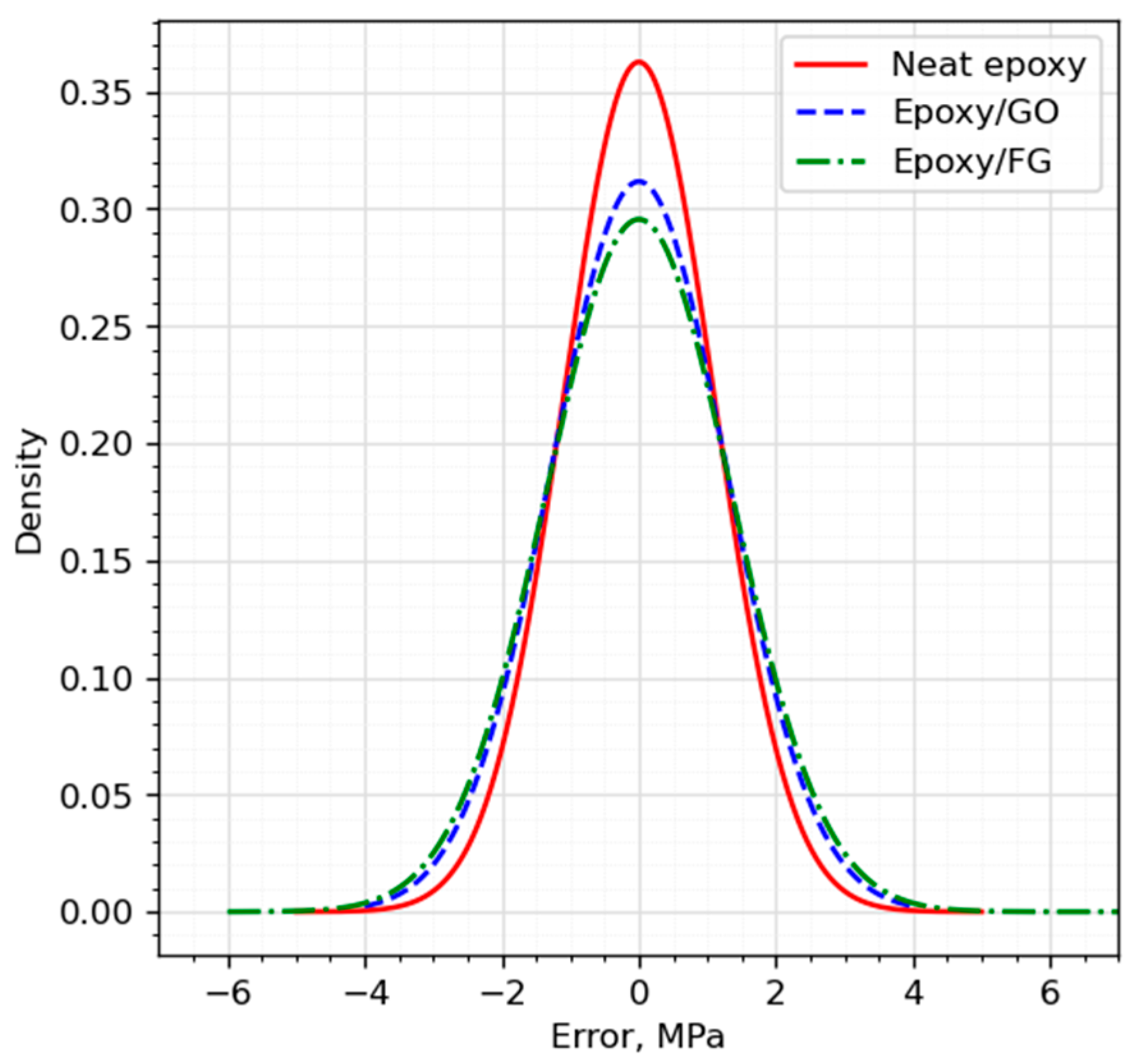
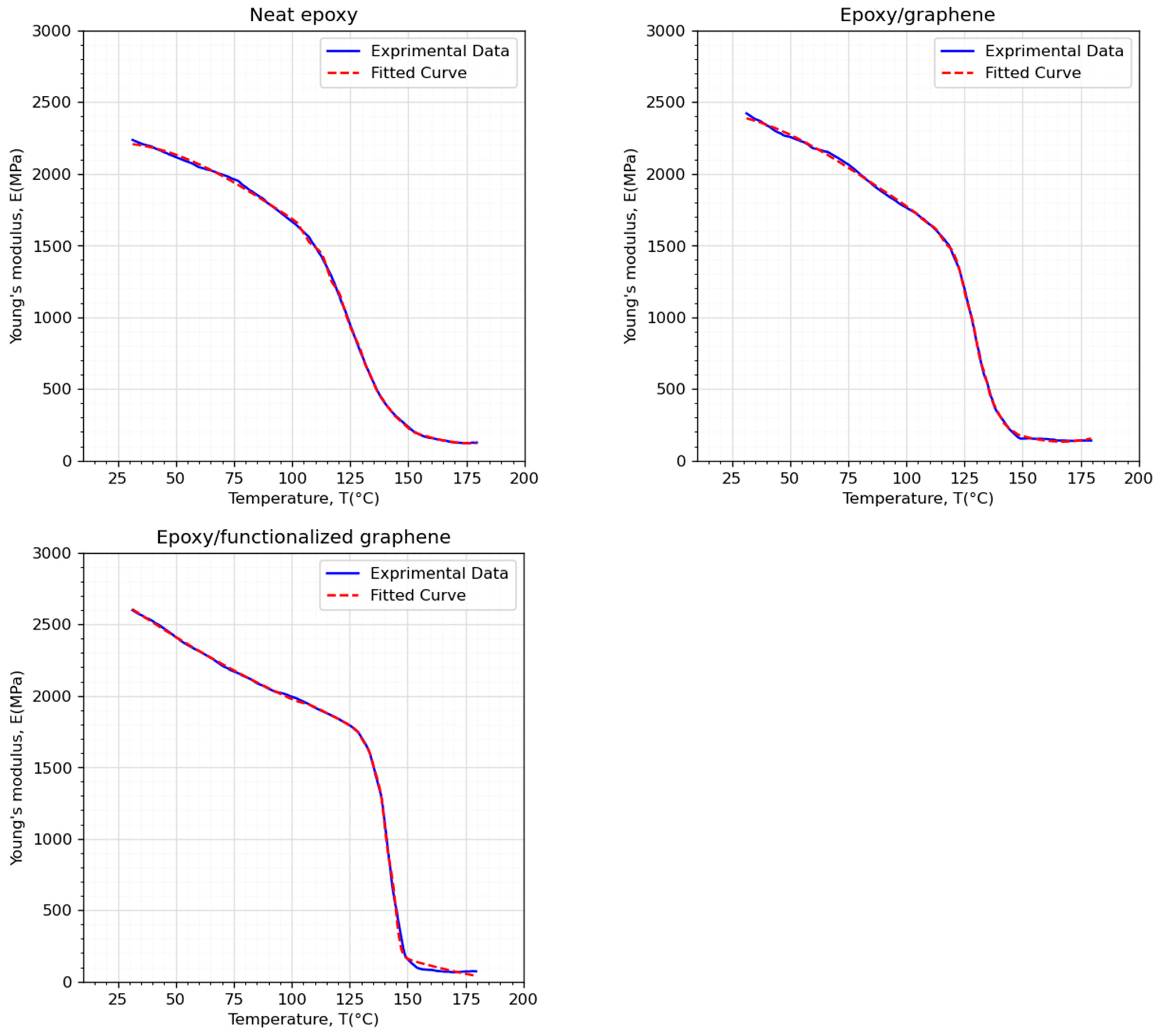
| Material | R2 | MRE | ||
|---|---|---|---|---|
| Training Dataset | Test Dataset | Training Dataset | Test Dataset | |
| Neat epoxy | 0.9997 | 0.9994 | 0.0006 | 0.0006 |
| Epoxy/Graphene | 0.9997 | 0.9996 | 0.0006 | 0.0005 |
| Epoxy/Functionalized graphene | 0.9992 | 0.9987 | 0.0007 | 0.0006 |
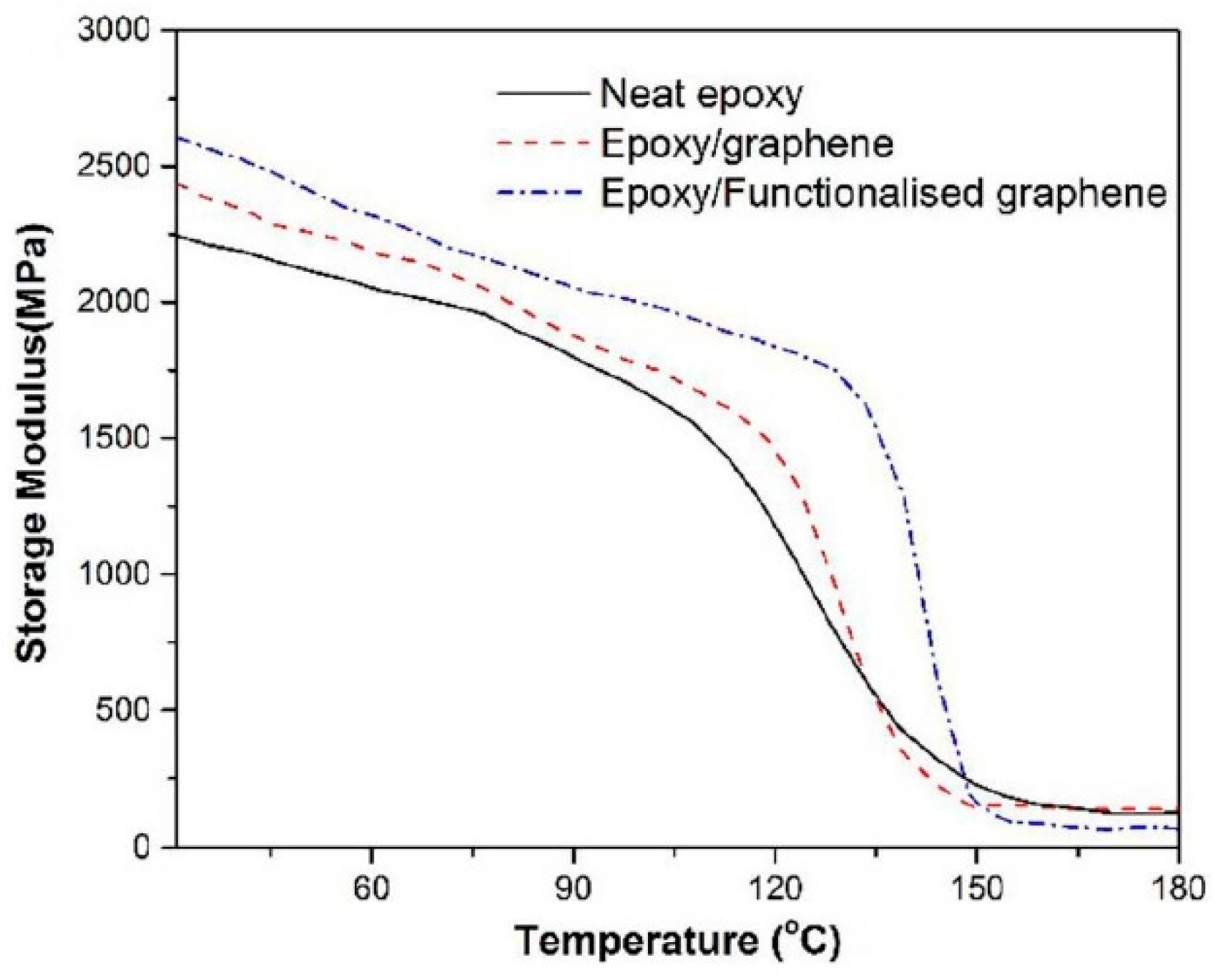
| Neat Epoxy | Epoxy/Graphene | Epoxy/Functionalized Graphene | ||||
|---|---|---|---|---|---|---|
| Temp | Actual [4] | Fitted | Actual [4] | Fitted | Actual [4] | Fitted |
| 40 | 2180.7 | 2179.3 | 2337.5 | 2341.5 | 2514.1 | 2513.4 |
| 50 | 2131.5 | 2129.0 | 2273.8 | 2274.4 | 2410.7 | 2411.5 |
| 60 | 2066.2 | 2067.3 | 2186.8 | 2188.1 | 2313.0 | 2314.6 |
| 70 | 1980.0 | 1977.9 | 2089.1 | 2090.4 | 2217.3 | 2222.5 |
| 80 | 1902.4 | 1886.5 | 1986.6 | 1986.5 | 2135.7 | 2135.7 |
| 90 | 1784.8 | 1785.8 | 1874.5 | 1877.6 | 2054.4 | 2053.6 |
| 100 | 1678.6 | 1683.4 | 1774.4 | 1776.5 | 1985.2 | 1976.8 |
| 110 | 1485.6 | 1483.7 | 1647.3 | 1648.5 | 1918.8 | 1921.1 |
| 120 | 1185.5 | 1181.7 | 1457.9 | 1459.0 | 1840.1 | 1839.8 |
| 130 | 741.7 | 740.3 | 848.0 | 847.2 | 1707.8 | 1707.5 |
| 140 | 402.4 | 407.0 | 317.4 | 317.3 | 1121.0 | 1112.7 |
| 150 | 214.3 | 213.6 | 164.8 | 170.9 | 159.4 | 160.1 |
| 160 | 156.7 | 160.0 | 150.2 | 139.3 | 97.7 | 111.4 |
| 170 | 124.1 | 126.4 | 135.5 | 133.3 | 65.9 | 72.4 |
| 180 | 120.4 | 120.7 | 139.1 | 146.4 | 54.8 | 39.0 |
| Volume Fraction of CNT, | Reference | |
|---|---|---|
| Yas and Samadi [12] | Present | |
| 0.12 | 0.213958 | 0.213564 |
| 0.17 | 0.344251 | 0.342843 |
| 0.28 | 0.455602 | 0.460245 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ebrahimi, F.; Ezzati, H. A Machine-Learning-Based Model for Buckling Analysis of Thermally Affected Covalently Functionalized Graphene/Epoxy Nanocomposite Beams. Mathematics 2023, 11, 1496. https://doi.org/10.3390/math11061496
Ebrahimi F, Ezzati H. A Machine-Learning-Based Model for Buckling Analysis of Thermally Affected Covalently Functionalized Graphene/Epoxy Nanocomposite Beams. Mathematics. 2023; 11(6):1496. https://doi.org/10.3390/math11061496
Chicago/Turabian StyleEbrahimi, Farzad, and Hosein Ezzati. 2023. "A Machine-Learning-Based Model for Buckling Analysis of Thermally Affected Covalently Functionalized Graphene/Epoxy Nanocomposite Beams" Mathematics 11, no. 6: 1496. https://doi.org/10.3390/math11061496
APA StyleEbrahimi, F., & Ezzati, H. (2023). A Machine-Learning-Based Model for Buckling Analysis of Thermally Affected Covalently Functionalized Graphene/Epoxy Nanocomposite Beams. Mathematics, 11(6), 1496. https://doi.org/10.3390/math11061496






