Demographic Factors Affecting Fuzzy Grading: A Hierarchical Linear Regression Analysis

Abstract

Several factors affect students’ mathematics grades and standardized test results. These include the gender of the students, their socio-economic status, the type of school they attend, and their geographic region. In this work, we analyze which of these factors affect assessments of students based on fuzzy logic, using a sample of 29,371 Italian high school students from the 2018/19 academic year. To combine grades assigned by teachers and the students’ results in the INVALSI standardized tests, a hybrid grade was created using fuzzy logic, since it is the most suitable method for analyzing qualitative data, such as teacher-given grades. These grades are analyzed with a hierarchical linear regression. The results show that (1) boys have higher hybrid grades than girls; (2) students with higher socio-economic status achieve higher grades; (3) students from scientific lyceums have the highest grades, whereas students from vocational schools have the lowest; and (4) students from Northern Italy have higher grades than students from Southern Italy. The findings suggest that legislators should investigate appropriate ways to reach equity in assessment and sustainable learning. Without proper interventions, disparities between students might lead to unfairness in students’ future career and study opportunities.

1. Introduction

In recent decades, the topic of assessing students’ knowledge with the aid of fuzzy logic has been extensively researched, and different assessment models have been proposed [1,2,3,4,5,6,7,8,9,10,11,12,13]. The popularity of using fuzzy logic in assessment is due to the fact that fuzzy logic deals with uncertain quantities and qualitative descriptions of everyday phenomena [14,15,16], of which school grades and evaluations are an example [17,18,19,20]. Despite often being numerical, teacher-given grades are generally verbal/linguistic variables: for example, a teacher might convert the grade “good” into 7/10 or 8/10, depending on how “good” the student is. Therefore, computing an average or combining grades of different assessments (e.g., an oral exam and a practical one) might require fuzzy logic [21].

There is no unique way of using fuzzy logic to assess students’ knowledge and competencies: a range of different methods have been proposed. For instance, educators might want to include in the students’ final grades their competencies in completing and presenting their project work [22], their class attendance [23], a combination of their attainments in two or more exams [1], their attainments in two or more semesters [3], or a combination of multiple factors [4,24]. Literature on the topic of the applications of fuzzy logic for assessment has tested the efficiency of different models and investigated whether grades obtained using fuzzy logic (hereon, fuzzy or hybrid grades) significantly differ from teacher-given grades [9,23,25,26]. The findings are mixed, since some studies have found that fuzzy grades are significantly lower than teacher-given grades [23], whereas some researchers have found no differences between the two assessment methods [9,26].

Despite the increasing interest in using fuzzy logic to assess students’ knowledge and competencies, little is known about the factors that might affect fuzzy grades. Namely, the literature is consistent in stating that different factors affect teacher-given grades, including students’ genders [27,28,29,30], their economic, social, and cultural status (hereon, ESCS) [31,32], the type of school they attend (e.g., vocational schools, technical schools) [33,34], the geographic region [33], and other non-cognitive factors (e.g., anxiety, teachers’ expectations) [35,36,37]. The corresponding literature on fuzzy grades is scarce, and it is not clear yet whether the same factors that affect teacher-given grades also affect fuzzy grades. It might be hypothesized that since fuzzy grades are a combination of different evaluations (e.g., several written and oral examinations, students’ attendance, the quality of lab work and/or project work), they will be affected by the same factors as teacher-given grades. On the other hand, combining teacher-given grades with more objective measurements of students’ knowledge and competencies, such as national assessments [38], might reduce the influence of individual factors or even eclipse some of them.

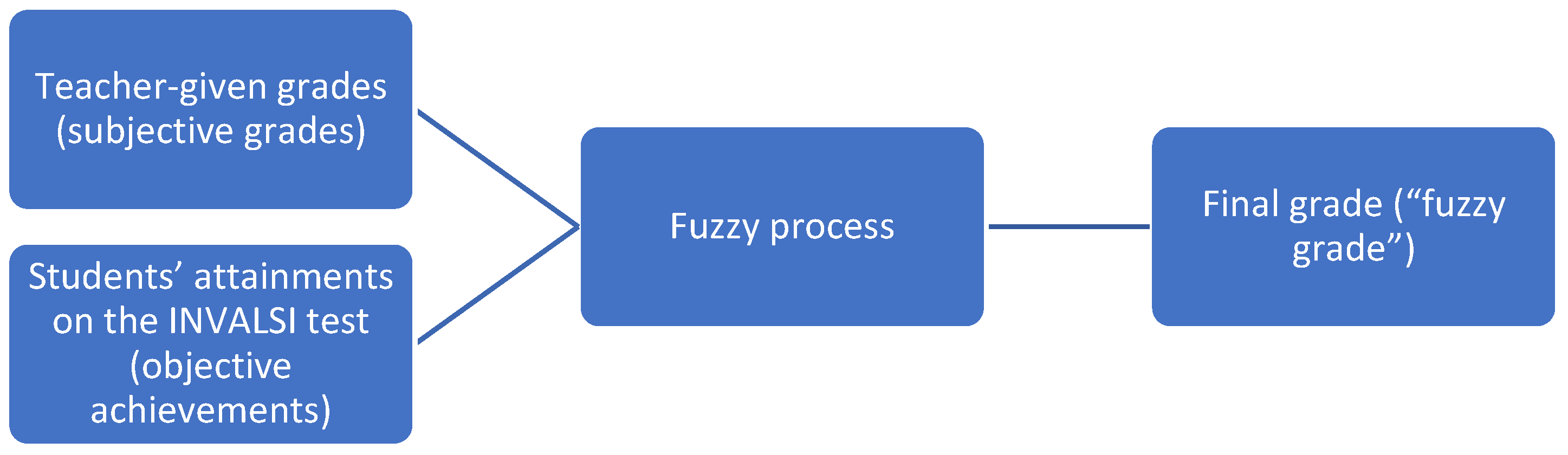
Addressing this research question is important, since it might give educators and researchers new insight into the possibility of using fuzzy grades. Namely, knowing which factors affect fuzzy grades might help researchers to develop a fairer way of evaluating students’ knowledge [9]. In the present paper, we focus on the assessment of students’ mathematical knowledge and competencies in Italy. In particular, a combination of (1) teacher-given grades and (2) students’ attainments in the national assessment is considered. Through a fuzzy process, the two variables are combined to create a fuzzy grade. The aim is to investigate how (1) students’ gender, (2) students’ ESCS, (3) the typology of the school attended by the students, and (4) the geographic location of the school (i.e., the geographic region) affect fuzzy grades. To answer this question, a hierarchical linear regression is used.

The present paper is one of the first that explores how external factors, namely, students’ demographic factors, might impact fuzzy grades. In fact, despite recent efforts to promote the usage of fuzzy logic for the assessment of students’ knowledge and competencies, little is known about whether fuzzy assessment methods might be considered fairer or more objective. Therefore, the aim of this research is to explore the effect that several external factors might have on fuzzy grades.

2. Related Work

2.1. The Italian Context

The National Institute for the Evaluation of the Educational System (Istituto nazionale per la valutazione del sistema educativo di istruzione e formazione—INVALSI) takes care of national tests [39].

Knowledge tests, which are objective and standardized, take place in the second and fifth grades of primary school, in the third grade of lower secondary school, and in the second and, from the 2018/19 school year, also in the fifth grade of upper secondary school [39]. INVALSI tests have a formative role, as the results are used to obtain additional information about students’ knowledge, progress, and competencies and to determine the quality of teaching. The test is mandatory for all students.

Each student receives a descriptive indicator of their knowledge, which is expressed as a level from 1 to 5, where 1 is the lowest level, and 5 is the highest. The level achieved is and then recorded in the student’s competence certificate [39].

Students in the third year of lower secondary school and students in the second and fifth years of upper secondary school receive a computerized version of the test (the computer-based test). Each student takes a different test, which is automatically generated by the INVALSI system based on a database of questions. The system randomly selects a few questions from each section of the database. Insofar as the questions are of equal difficulty and test the same constructs, the INVALSI test results can be compared with each other [39].

The mathematical content tested by the INVALSI tests in upper secondary schools is presented in the documents Indicazioni nazionali per i Licei (National Guidelines for Lyceums; D. 211/2010) and in the Linee Guida per gli Istituti tecnici e professionali (Guidelines for Technical and Vocational Institutes; D. M. 16 January 2012), that is, in the documents that determine the contents at the national level that need to be processed in different types of schools [39]. The contents are divided into the following groups:

• Data and predictions (i.e., statistics, probability theory, data analysis and interpretation);
• Numbers (i.e., arithmetic and algebra);
• Relations and functions;
• Space and shapes (i.e., geometry).

Each test consists of a certain number of questions, which may have additional sub-questions. The total number of questions changes every year. The questions are of open and closed type. In the case of computer-based tests, open-ended and closed-ended questions require the student to choose the correct answer, move the answer to the correct cell, or type their answer using the keyboard, for example. Closed-type questions can be of the multiple-choice type, the correct–incorrect type, or other types of choice (e.g., the student must insert the object into the cell). Open-ended questions can be shorter (e.g., insert the correct number or letter) or longer (e.g., justify the answer, write down the procedure).

2.2. Factors Affecting Teacher Grading Standards and INVALSI Assessments

Standardized tests of mathematics knowledge are used to measure students’ achievement, but the results of these tests might be affected by several factors, such as gender, geographic region, school type, and ESCS [36,40,41,42].

Regarding gender, studies have shown that, on average, boys tend to score higher on high-stakes mathematics tests than girls [43,44]. However, this gender gap in achievement is not consistent across all countries and cultures [45,46]. Research suggests that the gender gap in mathematics can be attributed to several factors, including social expectations, stereotypes, access to resources and opportunities, and teaching methods [47].

Official INVALSI documents and research relying on official data [44] have confirmed that a gender gap is present in national assessments of mathematics, especially in high schools.

In addition, reports from the INVALSI Institute and research based on official data [33,48] have shown that there are systematic differences between students in different Italian macroregions: students from Northern Italy have the highest achievements in mathematics, whereas students from Southern Italy have the worst achievements, which may simply be the result of different socio-economic factors [33].

The connection between a student’s ESCS and their achievement on the INVALSI test is positive and statistically significant [48,49,50]: students with a higher ESCS score higher on the INVALSI test. The INVALSI Institute measures students’ ESCS in the same way as PISA [51], with a coefficient that is strongly correlated with other measures of socio-economic factors. The ESCS is based on three indicators, namely [52]:

• Parents’ employment status (HISEI indicator);
• Level of education of residents (PARED indicator);
• The presence of certain material resources that encourage and strengthen learning (HOMEPOS indicator).

The final ESCS is calculated by performing a principal component analysis of the above indicators; it is defined such that it has mean M = 0 and standard deviation SD = 1. Thus, students who have a positive ESCS have a higher socioeconomic status than the Italian average.

The INVALSI institute obtains data on a student’s ESCS through a questionnaire that they receive while taking INVALSI knowledge tests; additional information is provided by the schools themselves.

In addition to the differences mentioned above, official reports and research [53] show that students from different types of upper secondary schools attain different scores on the INVALSI knowledge test. The reports state that students of scientific lyceums have the highest achievements, followed by students at technical institutes, other lyceums, and, finally, students at vocational institutes. Systematic differences in achievements between students attending different types of schools are also present in international tests of mathematics knowledge, such as PISA [54].

2.3. Fuzzy Logic and Its Applications for the Assessment of Students’ Knowledge

Among various applications of fuzzy logic (see, e.g., [55,56]), the recent literature has investigated the possibility of using it for the assessment of students’ knowledge, competencies, skills, and abilities [5,6,7,8,9,17]. Numerous reasons have been cited for using fuzzy logic to assess students. First, teacher-given grades are normally verbal (linguistic) variables, and the assessment is a non-linear, complex, and uncertain process [57]. Furthermore, although students’ grades might be expressed as numbers or percentages, these are translations of qualitative descriptors [9,57]. Traditional assessment methods are based primarily on teachers’ judgments and tend to be subjective [58]. Therefore, traditional methods rely on crisp criteria, which might lead to biased or erroneous evaluations [57]. Second, a fuzzy-based assessment method might include more information than quantitative teacher-given grades, thus representing a fairer and more complete evaluation of knowledge [9,57].

For the abovementioned reasons, the assessment of students’ knowledge, which includes imprecise data and opinions, might be performed with the aid of fuzzy logic. In this case, the students’ characteristics under assessment are represented as fuzzy subsets of linguistic labels, which characterize their performance [4] (see also Section 3.6).

3. Materials and Methods

3.1. Aims of the Research

Teacher-given grades describe a student’s quality of knowledge and competencies but are not certain quantities. When we sort students, we do so considering the criteria of fuzzy logic. The fuzzy process allows us to calculate with data that include verbal variables. Many researchers [1,2,3,4,6,18,59,60,61,62,63] have considered using fuzzy logic for the purpose of assessing students’ knowledge with several input variables. In these studies, the final grade was obtained using a fuzzy process. However, although researchers have investigated the possibility of using fuzzy logic to assess students’ knowledge and competencies, little is known about the factors that might affect fuzzy grades. Therefore, the aim of the present research is to explore which factors (e.g., gender, school typology, ESCS) significantly affect fuzzy grades. To do so, we considered a model of assessing students’ mathematical knowledge considering (1) teacher-given grades and (2) students’ achievements on the national assessment of knowledge INVALSI (see Section 3.2). We combined these two achievements using fuzzy logic, and the final hybrid grade was produced.

Research has shown that boys tend to have higher achievements on standardized assessments than girls [43,44]; therefore, it is reasonable to think that this pattern will also be present in hybrid grades obtained using fuzzy logic. Studies have also found that students with lower ESCS have lower achievements [48,49,50]. Therefore, we hypothesize that students’ ESCS will play a non-negligible role in predicting their hybrid grade. Moreover, research [53] has found that students from different school types (i.e., scientific lyceums, other lyceums, professional schools, and vocational schools) have significantly different achievements, in favor of students from scientific lyceums. Hence, we hypothesize that the same result will be obtained if fuzzy grades are considered. Finally, the literature is consistent in stating that students from Northern Italy have higher achievements than students from Southern Italy [33,48]. Therefore, we expect that hybrid grades of students from Northern Italy will be higher than those from Southern Italy. Our hypotheses are, hence, the following:

H1. 

Boys have higher fuzzy grades than girls.

H2. 

Students with higher ESCS have higher fuzzy grades than students with lower ESCS.

H3. 

Students from scientific lyceums have the highest fuzzy grades.

H4. 

Students from Northern Italy have higher fuzzy grades than students from Southern Italy.

3.2. Proposed Model

The proposed model is shown in Figure 1. The hybrid assessment considers two forms of student evaluation:

• Teacher-given grades, which are more subjective in nature and might include more factors (e.g., students’ participation in class activities, regularity of turning in homework, academic knowledge);
• Students’ achievements on the national assessment of mathematical knowledge INVALSI, which is a more objective way of assessing students’ knowledge, but does not include some psychometric variables, which might affect students’ performance.

These two achievements are combined using the fuzzy process described in Section 3.6, and a final grade (i.e., “fuzzy grade”) is produced.

3.3. Methodology

To verify the validity of our hypotheses, we applied a non-experimental quantitative research methodology. Both descriptive and inferential statistical methods are used. The fuzzy process is applied to produce the students’ final (fuzzy) grades.

3.4. Sample

The sample was retrieved from the official INVALSI statistical page [64]. A sample of 35,802 grade 10 Italian high school students who took the INVALSI national assessment of mathematical knowledge in the school year 2018/19 was considered. Before analyzing the available data, the sample was filtered, and missing data were removed. The final sample comprised 29,371 students. Among them, there were 13,712 (46.7%) males. In

Table 1. The description of the sample.

Description	Frequency (f)	%f
Year of birth
2000 or before	100	0.3
2001	566	1.9
2002	2799	9.5
2003	23,556	80.2
2004 or later	2350	8.0
Attended school
Scientific lyceum	7639	26.0
Other lyceum	10,856	37.0
Technical school	7462	25.4
Vocational school	3414	11.6
Geographic macroregion
Northwestern Italy	5563	18.9
Northeastern Italy	6326	21.5
Central Italy	6442	21.9
Southern Italy	5845	19.9
Southern Italy and Isles	5195	17.7

, we present the description of the sample. The sample comprised 3465 (11.8%) students born in 2002 or before and 2350 (8.0%) students born in 2004 or later. Younger students started attending school a year or more in advance, and older students started school one or more years later or failed one or more classes in the past.

3.5. Data Analysis

The data were analyzed statistically using the Jamovi software. The Fuzzy Logic Toolbox in MATLAB was used to combine teacher-given grades with students’ attainments on the INVALSI assessment through fuzzy logic [65,66].

Both descriptive and inferential statistical tools were used. In particular, an analysis of the frequencies permitted us to describe the sample. Means, standard deviations, and medians were used to analyze students’ achievements.

To answer the research hypotheses, hierarchical linear modeling was used [67]: this is a test in which different linear regressions are performed, and it is measured how independent variables predict the dependent variable. In particular, hierarchical linear modeling is a form of ordinary least-squares regression that is used to analyze the variance in the dependent variables when the independent variables are at different hierarchical levels [68]. The use of hierarchical linear regression (HLR) was justified by the fact that the data are organized hierarchically: students are nested in schools [68,69,70]. We considered two levels. The first was the students’ level (independent variables were the students’ gender and ESCS), and the second was the school level (independent variables were the school type and the geographic macroregion of the school) [69].

Several models were considered in the HLR; in all models, the method of maximum likelihood was used. The initial (empty or null) model evaluates whether HLR is needed [68]. The equation of the first model is:

1st level (student level):

$${\mathrm{GRADE}}_{ij}={\beta }_{0j}+r_{ij},$$

2nd level (school level):

$${\beta }_{0j}={\gamma }_{00}+u_{0j},$$

where ${\mathrm{GRADE}}_{ij}$ represents the dependent variable of the i-th student in the j-th school. The coefficient ${\beta }_{0j}$ represents the mean of the dependent variable in the j-th school, and $r_{ij}$ represents the random effect of the i-th student in the j-th school [70]. The coefficient ${\gamma }_{00}$ in the second level represents the grand mean of the j-th school, and the coefficient $u_{0j}$ is the random effect of the j-th school.

The first model is the model of random coefficients. It includes variables on the student level: the students’ gender (${\mathrm{gender}}_{ij}$) and ESCS (${\mathrm{ESCS}}_{ij}$). The equations in this model are:

1st level (student level):

$${\mathrm{GRADE}}_{ij}={\beta }_{0j}+{\beta }_{1j}{\mathrm{gender}}_{ij}+{\beta }_{2j}{\mathrm{ESCS}}_{ij}+r_{ij},$$

2nd level (school level):

$$\begin{array}{c}{\beta }_{0j}={\gamma }_{00}+u_{0j},\\ {\beta }_{1j}={\gamma }_{10}+u_{1j},\\ {\beta }_{2j}={\gamma }_{20}+u_{2j}.\end{array}$$

The second (final) model captures the variability of regression coefficients with the aid of slopes and initial values [71,72]. In this model, we added variables related to students’ schools: the school type (${\mathrm{school}\mathrm{type}}_{ij}$) and geographic macroregion (${\mathrm{macroregion}}_{ij}$). The equations of the model are

1st level (student level):

$${\mathrm{GRADE}}_{ij}={\beta }_{0j}+{\beta }_{1j}{\mathrm{gender}}_{ij}+{\beta }_{2j}{\mathrm{ESCS}}_{ij}+r_{ij},$$

2nd (school level):

$$\begin{array}{c}{\beta }_{0j}={\gamma }_{00}+{\gamma }_{01}{\left(\mathrm{school}\mathrm{type}\right)}_{ij}+{\gamma }_{02}{\mathrm{macroregion}}_{ij}+u_{0j},\\ {\beta }_{1j}={\gamma }_{10}+u_{1j},\\ {\beta }_{2j}={\gamma }_{20}+u_{2j}.\end{array}$$

In hierarchical modeling with two levels, the total variance includes the variance between students and that between schools [73]. To check whether the hierarchical linear regression is suitable, the interclass correlation coefficient (ICC) of the null model is calculated:

$$ICC=\frac{{\tau }_{00}}{{\tau }_{00}+{\sigma }^2},$$

where ${\tau }_{00}$ is the variance of residuals at the 2nd level (school level), and ${\sigma }^2$ is the variance of residuals at the 1st level (student level). The ICC represents the total variance that is explained by the variables on the school level [73,74]. If ICC > 0.10, the use of the HLR is justified [75,76].

The model fit is evaluated with the R² coefficient [68]. In the present research, the Akaike information criterion (AIC) is also calculated: when comparing different models, the one with the lowest AIC should be preferred [77].

The assumptions for the HLR are the normality of the residuals on both levels and the independence of the residuals on both levels [68]. The assumptions are checked using the Kolmogorov–Smirnov test and by checking the Q–Q plots. Since the residuals are not normally distributed, additional caution should be applied when interpreting the coefficients. Nevertheless, the estimated parameters are sufficiently precise and reliable [78].

3.6. Procedure

The proposed model (Figure 1) takes into account two measurements of students’ mathematical knowledge: (1) teacher-given grades and (2) students’ attainments on the Italian national assessment INVALSI. In the present study, only students’ oral grades, that is, the collection of all oral examinations, assessments of homework, and written tests, are considered.

Crisp information is fuzzified using membership functions. After the fuzzification of both sets of input data, each student receives two fuzzified grades. Fuzzified data are combined using inference rules, and the final crisp grade is produced through defuzzification. Hereafter, the final grade produced using fuzzy logic is referred to as the fuzzy grade (see Figure 2).

The fuzzification of crisp teacher-given grades was performed using the membership functions presented in

Table 2. The fuzzification of teacher-given grades.

Level of Mathematical Knowledge	Membership Function
Very low (VL)	$\mathrm{Trian} \left(x,1,1,3\right)$
Low (L)	$\mathrm{Trian} \left(x,1,3,5\right)$
Medium (M)	$\mathrm{Trap} \left(x,3,5,6,8\right)$
High (H)	$\mathrm{Trian} \left(x,6,8,10\right)$
Very high (VH)	$\mathrm{Trian} \left(x,8, 10, 10\right)$

. Each membership function was either a triangular or a trapezoidal one. Figure 3 shows plots of these membership functions.

Students’ attainments on the national assessment INVALSI were fuzzified using Gaussian membership functions (see

Table 3. The fuzzification of students’ achievements in the INVALSI test.

Level of Mathematical Knowledge	Membership Function
Very low (VL)	$\mathrm{Gauss} \left(x,120,40\right)$
Low (L)	$\mathrm{Gauss} \left(x,160,40\right)$
Medium (M)	$\mathrm{Gauss} \left(x,200,40\right)$
High (H)	$\mathrm{Gauss} \left(x,240,40\right)$
Very high (VH)	$\mathrm{Gauss} \left(x,280,40\right)$

and Figure 4).

The inference rules are presented in

Table 4. The inference rules.

		Teacher-Given Grade
		VL	L	M	H	VH
INVALSI	VL	VL	VL	L	L	M
	L	VL	L	L	M	M
	M	L	L	M	M	M
	H	M	M	M	H	H
	VH	M	M	H	H	VH

. These are similar to the ones presented in the study [1], with the following differences:

• A student reaches the VH level if and only if they have both evaluations at VH;
• A student reaches the H level only if no evaluation is lower than M;
• A student reaches the H level if both evaluations are H, or one is VH and the other is at least M.

For the defuzzification, the same five membership functions as in Table 2 were applied. The fuzzy grade was produced using the mean of maxima (MoM) defuzzification method:

$$\overline{x}=\frac{1}{\left|M\right|}·{\displaystyle \sum }_{x_i\in M}{x}_i,$$

where $M$ is the set defined as $M=\left\{x_i:{\mu }_A\left(x_i\right) \mathrm{is}\mathrm{maximal}\right\}$, and $\left|M\right|$ is its cardinality. Fuzzy grades were rounded to the nearest integer.

3.7. Cross-Validation

The model was cross-validated using Geisser’s k-fold cross-validation [79,80]. Cross-validation gives an estimation of how our model would perform if we trained it on a random sample from our distribution, of a similar size to the training fold. The aim of the cross-validation is to assess how the results of our statistical analysis will generalize to an independent dataset. The k-fold cross-validation is a resampling method that uses portions of the data to train and test a model on different iterations. The original sample is randomly partitioned into k (almost) equal-sized subsamples; a subsample is retained as the validation data for the model testing. The remaining k − 1 subsamples are used as training data. The validation process is repeated k times; the results are then averaged, and a final estimation is produced. The 10-fold cross-validation is the most commonly used. For more details, see ref. [81].

In the present research, the dataset was partitioned into k = 10 nearly equal-sized subsets. The cross-validation was performed in R and JASP. The root mean square error (RMSE), R², mean square error (MSE), and mean absolute error (MAE) are reported [82]. If the RMSE and MAE have a value close to 0, the linear regression model fits the data perfectly [83].

4. Results

4.1. Preliminary Analyses

In the sample, there were 29,371 grade 10 Italian high school students who took the INVALSI mathematics test in the school year 2018/19. The descriptive statistics for the sample are presented in

Table 5. The descriptive statistics for the variables.

Variable	M (SD)	Mdn	Min	Max	Skew (SE)	Kurt (SE)
Teacher-given grade	6.19 (1.45)	6	1	10	−0.133 (0.0143)	−1.98 (0.0286)
Achievements on the INVALSI	208 (38.8)	206	72.3	314	0.218 (0.0143)	−0.0500 (0.0286)
ESCS	0.0972 (0.991)	0.0664	−3.93	1.93	−0.220 (0.0143)	−0.389 (0.0286)
Fuzzy grades	5.61 (1.58)	6	1	10	−0.317 (0.0143)	0.135 (0.0286)

. The correlations between the variables are presented in

Table 6. Spearman’s correlation coefficients between the variables.

Variable	1.	2.	3.	4.
1. Fuzzy grades	-	0.577 ***	0.817 ***	0.225 ***
2. Teacher-given grades		-	0.416 ***	0.136 ***
3. Achievements on the INVALSI			-	0.260 ***
4. ESCS				-

Note: *** p < 0.001.

.

In

Table 7. The descriptive statistics divided among variables.

Variable	M (SD)	Mdn	Min	Max	U/W	Effect Size
Gender					1.03 × 108 ***	0.0387
Male	5.67 (1.57)	6	1	10
Female	5.56 (1.43)	6	1	10
School type					4418 ***	0.140
SL	6.43 (1.37)	6	1	10
OL	5.54 (1.41)	6	1	10
TS	5.39 (1.48)	6	1	10
VS	4.48 (1.48)	5	1	10
Macroregion					1934 ***	0.0659
NW	5.93 (1.44)	6	1	10
NE	6.06 (1.39)	6	1	10
C	5.72 (1.51)	6	1	10
S	5.22 (1.66)	6	1	10
SI	5.01 (1.62)	6	1	10

Note: OL = other lyceums; SL = scientific lyceums; TS = technical schools; VS = vocational schools; NE = Northeastern Italy; NW = Northwestern Italy; C = Central Italy; S = Southern Italy; SI = Southern Italy and Isles. *** p < 0.001.

, we present the descriptive statistics of the fuzzy grades divided among variables. In the last three columns of the table, we present the Mann–Whitney U-test or the Wilcoxon W-test for independent samples, with their respective p-values and the effect size (the biserial rank correlation coefficient for the Mann–Whitney test and the ε² coefficient for the Wilcoxon test).

4.2. Hierarchical Linear Regression

From Table 7, it can be concluded that fuzzy grades differ among gender, school type, and geographic macroregion, and from Table 6, it can be inferred that fuzzy grades are significantly correlated with ESCS. To evaluate how these demographic factors affect students’ fuzzy grades, HLR was used. As a preliminary step, the normality of the residuals was checked using the Kolmogorov–Smirnov test, which found that they are not normally distributed (D = 0.0545; p < 0.001), even though from the Q–Q plot (Figure 5), it can be seen that they are almost normally distributed. The variance inflation factors (VIF) indicated almost no correlation between independent variables, ranging from 1.01 to 1.14.

In

Table 8. The coefficients of the hierarchical linear regression (HLR).

Variable	Null Model		1st Model		2nd Model
	β	SE	β	SE	β	SE
Intercept	5.49 ***	0.031	5.50 **	0.030	5.43 ***	0.018
Student level
Gender
Female–Male			−0.055 ***	0.019	−0.039 **	0.018
ESCS			0.13 ***	0.009	0.11 ***	0.009
School level
School type
OL–SL					−0.85 ***	0.038
TS–SL					−1.00 ***	0.042
VS–SL					−1.84 ***	0.052
Macroregion
NE–NW					0.12 **	0.057
C–NW					−0.24 ***	0.056
S–NW					−0.70 ***	0.057
SI–NW					−0.92 ***	0.058
Random components
Variance on the school level ${\tau }_{00}$	0.736		0.658		0.199
Variance on the student level ${\sigma }^2$	1.817		1.808		1.785
Information parameters of the model
AIC	103,083.56		102,859.33		101,664.98
R2	0.000		0.007		0.206
ICC	0.288		0.267		0.100

Note: SE = standard error; OL = other lyceums; SL = scientific lyceums; TS = technical schools; VS = vocational schools; NE = Northeastern Italy; NW = Northwestern Italy; C = Central Italy; S = Southern Italy; SI = Southern Italy and Isles. ** p < 0.01; *** p < 0.001.

, we present the coefficients of the HLR.

The HLR shows that all factors on the student level (i.e., gender and ESCS) are significant predictors of the students’ fuzzy grades (p < 0.001). On the school level, both school type and geographic macroregion are significant predictors of the students’ fuzzy grades (p < 0.01). The second model is the one that best fits the data (AIC = 101,664.98).

4.3. k-Fold Cross-Validation

The model was validated using k-fold cross-validation. We used k = 10 folds. The data were split into an n_train = 23,497 training set and an n_test = 5874 test set (i.e., 20% of the sample was used to test the model). The evaluation coefficients were found to be RMSE = 0.891, MAE = 0.683, R² = 0.216, and MSE = 0.793. Regarding the relative influence, ESCS had the greatest influence (44.9), followed by school typology (33.5), macroregion (21.5), and gender (0.04). In Figure 6, we present a decision tree plot (test MSE = 0.830).

From the fit coefficient, we conclude that the model has poor prediction validity. In particular, the students’ demographic factors explain around 20% of the variance in the fuzzy grades. Consequently, other factors that were not considered might have a greater impact on fuzzy grades. From the decision tree (Figure 6), it follows that gender has an almost negligible impact on fuzzy grades (see also Table 7). For students with lower ESCS, the macroregion has a larger impact on fuzzy grades, whereas for students with higher ESCS, the school typology predicts fuzzy grades better.

5. Discussion

The assessment of mathematical knowledge is often problematic, as teachers’ assessments are subjective and may not reflect the students’ actual knowledge [38]. The assessments given by the teachers may vary among genders [50], school types [33], ESCS [52], and geographic regions [33,48]. In the present work, we investigated which of these factors affected assessments of students’ mathematical knowledge that were based on fuzzy logic. Because fuzzy grades are composed of teacher-given grades and students’ achievements on the INVALSI test (see Section 3.3), it is reasonable to assume that hybrid scores differ based on the factors mentioned above, but it is not clear to what extent. For example, teacher ratings are statistically higher for girls, whereas boys have significantly higher achievements on the national assessment of mathematical knowledge, INVALSI.

First, starting with gender, we found that fuzzy grades are higher for boys than for girls. This can be partially explained by looking at the correlations between teacher-given grades, fuzzy grades, and achievement on the INVALSI. Our analyses showed that hybrid grades are positively and strongly correlated with student achievement on the INVALSI, but less so with teacher grades. The process of combining the teacher’s grades and INVALSI achievements (via inference rules and focusing with the mean of maxima method) led to the fact that within the hybrid grades, the students’ achievements on the INVALSI had more weight than the teacher’s grades. In the model used to obtain the hybrid scores, the characteristics of the INVALSI tests are therefore more apparent, and it is understandable that boys have higher hybrid scores than girls. We therefore confirm hypothesis H1.

Additional analyses have shown that gender has only a small effect on predicting the students’ fuzzy grades. This means that fuzzy grades are less affected by this variable than their achievements on the INVALSI test, and possibly their grades. Since some studies have found that girls generally have higher teacher-given grades and lower achievements on standardized tests, the proposed method of combining these two evaluations might lead to a fairer way of assessing both boys and girls. Nevertheless, it is important that further research investigates the phenomenon further. Explaining gender differences is particularly difficult [84], as the literature does not seem to have found a definitive answer. Some research has attributed the fact that girls have lower grades than boys to the theory of gender stereotypes [27], which states that girls have a lower self-concept [85] and higher anxiety [86] when dealing with mathematics. Given that girls generally have higher levels of test anxiety and mathematical anxiety than boys, one might explain the disparity in standardized test results by looking at these results.

Second, students with higher ESCS also have higher fuzzy grades. This result is not surprising; it is nevertheless important to investigate this phenomenon further. We confirm hypothesis H2.

Understanding the role that socio-economic status plays in the assessment of mathematical skills and knowledge is of paramount importance in making future decisions about education policies. In particular, having demonstrated that pupils with higher ESCS also have higher grades, this could create further disadvantage and inequity in the world of work [87]. For example, lower-performing students may not have as high a chance of being hired as higher-performing students. In this regard, school authorities should invest more resources to ensure that everyone has the same opportunities. Our findings suggest that students’ ESCS has the greatest impact on fuzzy grades. Therefore, although the proposed assessment model might represent a more objective way of assessing students’ knowledge and competencies (cf. [38]), it is non-negligibly affected by an external factor that might cause disparities (cf. [33,48]) and, consequently, unequal possibilities.

In addition, we have shown that students of scientific lyceums have the highest hybrid scores, followed by students at technical schools, other lyceums, and vocational schools. It was found that the fuzzy grades of students at vocational schools are significantly lower than the grades of students of scientific lyceums, which is again a consequence of the fact that the INVALSI national test has more weight within the hybrid grades. We hence confirm hypothesis H3.

These findings are consistent with previous studies [33]. To fully understand the reasons why students from scientific lyceums have higher fuzzy grades, additional research is needed. However, based on the current programs and the nature of these schools, we might notice that students from scientific lyceums have 4 to 5 h per week of mathematics lessons, whereas students from some vocational schools and other lyceums have 2 to 3 h. Students from scientific lyceums also study other scientific subjects, such as physics, from the first school year, which might contribute to their mathematical literacy.

Fuzzy grades also differ across macroregions: students in Northern Italy have significantly higher scores than those in Southern Italy. We can therefore confirm hypothesis H4.

These disparities among various Italian macroregions have also been found in previous studies [33,48], which have highlighted the importance of reducing such disparities, as they could create further discrimination in employment or university. Further research is needed to find efficient policies to reduce these differences between Northern and Southern Italy.

6. Limitations and Conclusions

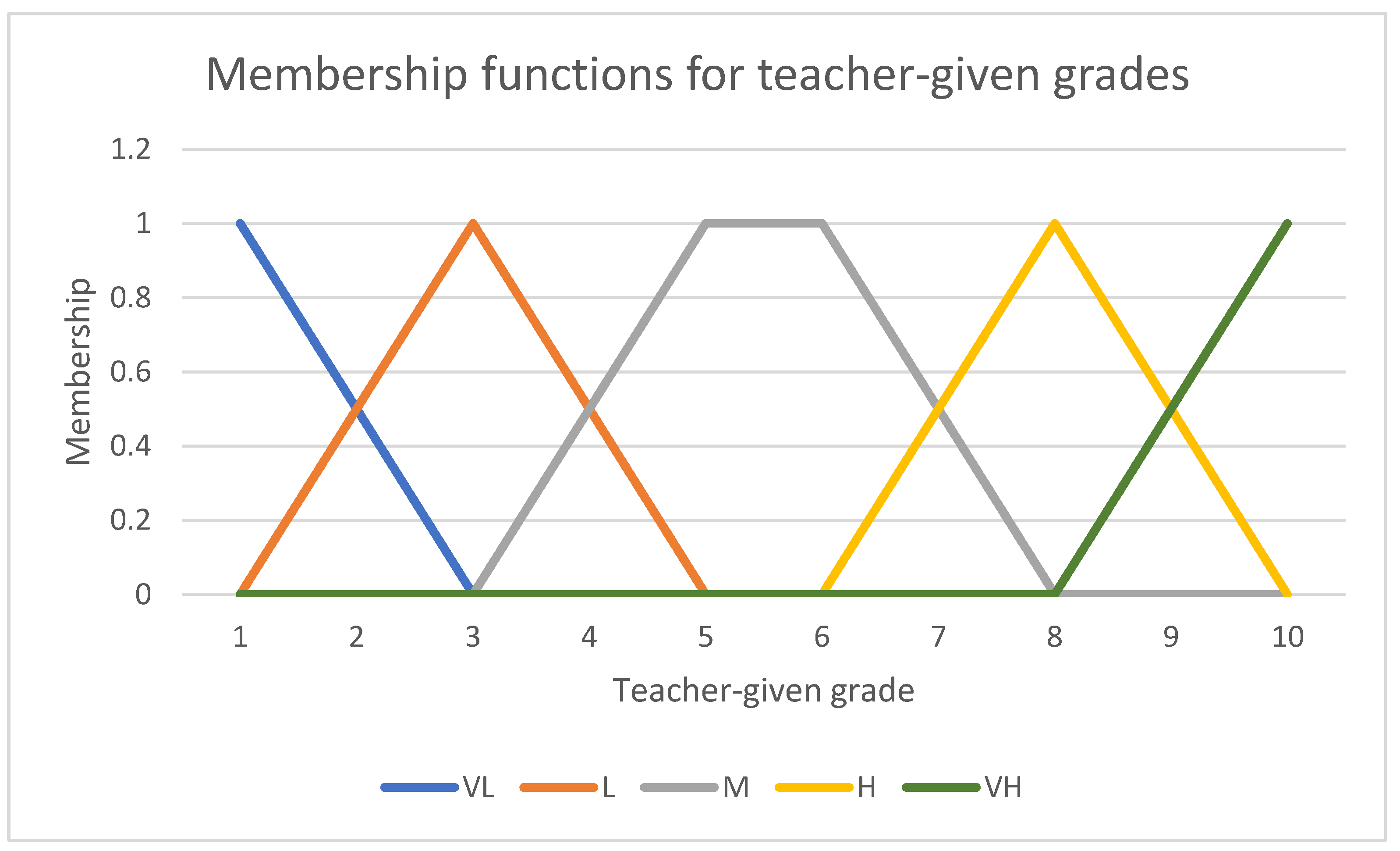
The present research has some limitations. First: the selected membership functions are the result of experience [21], so additional research is needed to standardize them. By this, we mean that future quantitative and qualitative studies should explore the opinions of experts, teachers, and students about what grades should be considered “very high,” “high,” “medium,” “low,” and “very low.” As an example of an attempt at standardization, we mention the criteria set by INVALSI [88], but it is necessary to extend them to the teacher’s evaluations. How this can be done remains an open question, so it would be appropriate to carry out both quantitative and qualitative research to find out which standardization best suits school authorities, students, and teachers.

Second: the final evaluations are strongly influenced by the chosen defuzzification methods, so different methods could lead to significantly different results and interpretations [21]. Therefore, we recommend that this topic be explored with additional research. In this case, it would also be appropriate to triangulate the quantitative data with the qualitative opinions of experts, teachers, and students. With the help of focus groups, it should be possible to determine the best method of defuzzifying the data.

Third: the residuals in the HLR are not normally distributed, which raises questions about the validity of the findings [89]. Additional caution is therefore needed when interpreting the results. Moreover, additional analysis of the model fit coefficients has shown that the model does not fit the data closely. This means that demographic factors can predict just a small portion of the variance of the fuzzy grades. The majority of the variance cannot be explained by considering only the students’ gender, school typology, ESCS, and macroregion. Therefore, other factors have a stronger impact on fuzzy grades. Future studies might investigate this question and try to quantify their effects.

Fourth: the sample used in this study is only a small share of the population of Italian students. It is likely that the results of the study are representative of the population; however, additional care should be taken when generalizing our findings [90].

Despite these limitations, the research is one of the first in the international literature to examine the factors affecting fuzzy grades based on teachers’ assessments and students’ achievements in national tests. Although some international research has already dealt with the possibility of using fuzzy logic in the assessment of students’ skills, abilities, achievements, and final grades, little is known about the impact of demographic factors on the resulting fuzzy grades. Dealing with this question is important, since our results show that even though the described model gives educators and policymakers a more complete view of students’ knowledge and competencies, fuzzy grades still differ among genders, ESCSs, geographic regions, and school typologies. Therefore, when developing and proposing new assessment methods that rely on fuzzy logic, researchers and educators should consider the fairness of the proposed method and, specifically, how is it affected by demographic factors.

Our research has some practical implications. Since gender was found to have an almost negligible effect on the fuzzy grades, the proposed method might be considered as a way of reducing the gender gap in assessment in mathematics. In particular, since boys seem to have lower teacher-given grades than girls, but higher achievements on standardized tests, fuzzy grading might help to reduce the disparities in assessment by creating a more objective way of assessing mathematical knowledge. Nevertheless, other demographic factors seem to have an important impact on fuzzy grades; therefore, additional effort is needed to develop a more sustainable and objective way of assessing students’ knowledge.