Abstract
Recently, due to the growth in machine learning and data mining, for scheduling applications in China’s industrial intelligence, we are quite fortunate to witness a paradigm of evolutionary scheduling via learning, which includes a new tool of evolutionary transfer optimization (ETO). As a new subset in ETO, single-objective to multi-objective/many-objective optimization (SMO) acts as a powerful, abstract and general framework with wide industrial applications like shop scheduling and vehicle routing. In this paper, we focus on the general mechanism of selection that selects or gathers elite and high potential solutions towards gathering/transferring strength from single-objective problems, or gathering/transferring storms of knowledge from solved tasks. Extensive studies in vehicle routing problems with time windows (VRPTW) on well-studied benchmarks validate the great universality of the SMO framework. Our investigations (1) contribute to a deep understanding of SMO, (2) enrich the classical and fundamental theory of building blocks for genetic algorithms and memetic algorithms, and (3) provide a completive and potential solution for VRPTW.
Keywords:
evolutionary transfer optimization; green scheduling; transfer learning; data analytics; system optimization; carbon neutrality MSC:
05-04
1. Introduction
First of all, let us begin with “knowledge and building-block based scheduling” (KAB2S), which is empowered with AI [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54]. According to our paper [5] “Towards KAB2S: learning key knowledge from single-objective problems to multi-objective problem”, KAB2S is also witnessed as a paradigm shift of evolutionary scheduling via learning [1,2,3,4,16,19,22,29]. In KAB2S, we mainly concern with evolutionary transfer optimization (ETO), with knowledge transfer across two or more tasks/problems.
This paper on ETO-based routing in logistic systems, or “double gathering”, is the second in the planned series to be issued as an engineering part of KAB2S. (Notes: (1). a piece of our title, “gathering strength, gathering storms”, actually is borrowed from Stanford AI100 [1], (2). the third part, or the scientific part, is [6]).
Then, we move forward with “ETO meeting scheduling” for complex optimization or “SMO meeting scheduling” (for readability, the abbreviation SMO is used for single-objective to multi/many-objective optimization).
Scheduling in logistics includes a type of problem, vehicle routing problem with time windows (VRPTW). Therefore, “SMO meeting scheduling” for VRPTW is formulated as “SMO meeting routing”.
Lastly, “SMO meeting routing” via selection is highlighted. We tend to believe that SMO is a powerful, abstract and general framework, which will boost both shop scheduling problems and vehicle routing problems. We shall devote this paper to operators and techniques that are not problem-dependent or application-dependent, such as selection.
Actually, selection is the key component or core mechanism for the evolutionary algorithm (EA) [48], and for the whole ETO family, not only for SMO (the mainstream of ETO is multitasking optimization or MTO, while SMO is new. The continuous version of SMO was firstly invented by [10] and the combinatorial case of SMO was firstly proposed by our group [5,49]). In other words, selection weeds out maladaptive genetic material, selects/gathers elite and high-potential solutions, and therefore gathers strength and storms of knowledge in solutions and/or tasks.
The main contributions are as follows:
1. To our best knowledge, it is the first work to extend SMO for VRPTW. (To our best knowledge, Ref. [55] is the first work of MTO for VRPTW).
2. Another firm step toward China’s international appeal for carbon neutrality via an attempt to avoid routing operations in logistic systems from scratch. (Our first step is [53]).
3. An extensive investigation of different operator combinations shows the functional modules of our SMO in VRPTW.
4. An extension of [7,8,9,24,25,26,27]’s classical building block (BB) hypothesis via ETO learning setups within routing towards the enrichment of the fundamental genetic algorithm (GA) and the memetic algorithm (MA).
Related works are given as follows: The most related paper to ours is [10]. To the best of their knowledge, their work serves as the first work to boost evolutionary multi-objective optimization via knowledge transferred from corresponding single-objective problems. Furthermore, their problems are continuous, not discrete. For example, the quadratic assignment problem (QAP), linear ordering problem (LOP), traveling salesman problem (TSP), job shop scheduling problem (JSP) and permutation flow shop scheduling problem (PFSP) are discrete. In our work, we roughly follow the same framework as [10], such as transferring experience by direct injection of external populations from source task of all single objective problems to the corresponding multi-objective problem (target task) “every G generation, where G is the gap” [49]. Fundamental dissimilarities between continuous and discrete cases prevent us from directly following their deployment of “mapping/connection between populations in source task and target task via denoising autoencoder” [49]. The mapping lacks physical meaning for permutation representation in the case of PFSP. Instead, that mapping or connection is constructed in our work as follows: we add the design of intra-task learning via clustering which is not deployed in their work to select potential elite solutions with potentially good positional BBs, then directly inject the external population (which may include those elite solutions) from the source task to the target one.
In the following, another four important related works are given. The first is ETO for MTO in the combinatorial case of TSP, QAP, LOP, and JSP. A multifactorial evolutionary algorithm was designed to explore the power of evolutionary multi-tasking, which can act as the engine for the simultaneous optimization of multiple permutation-based combinatorial problems in supply chain networks [11]. In order to “achieve the adaptive ability, a unified representation design and selection operator are applied” [49]. Secondly, ETO for MTO in a combinatorial case of routing. In [12], a memetic computing framework is developed, which can evolve and learn knowledge memes that traverse two different but related domains for the enhancement of evolutionary search performance. For the discrete case, a realization is implemented on two NP-hard vehicle routing domains, the capacitated arc routing problem and the capacitated vehicle routing problem. Thirdly, “machine learning based intelligent optimization (MA) for PFSP” [49]. In [13], machine learning-based MA is designed for PFSP in the multi-objective setting. The algorithm is called ML-MOMA, whose main development is the design of a local search operator via machine learning. In ML-MOMA, historical data during the search optimization of PFSP are fully utilized. Furthermore, the clustering method is also introduced to select better permutation solutions that are representative ones for refinement in local search. Duplicated searches are thus effectively avoided on similar individual permutation solutions. Besides MA above, another method in the whole family of intelligent optimization, such as simulated annealing (SA), can also tackle PFSP as follows. Lastly, “residual learning based intelligent optimization (SA) for PFSP” [49]. To solve the optimization of PFSP, [14] introduces an improved method of SA which is armed with a residual learning setting. The neighborhood is defined in PFSP. Furthermore, “the trained/learned/fitted parameters are further stored in the SA for greater search efficiency” [14,49].
Gathering/highlighting the strength and storms of some important abbreviations at the end of the introduction will help you grasp the introduction better.
KAB2S means “knowledge and building block based scheduling”. That is an abstract idea architecture, a big picture, which contains “1 + 3” works (“1”, is our conference paper, our root, “3”, are [5,6], and this paper, branches and leaves). Furthermore, “double gathering” stands for this paper because of its title.
ETO is short for evolutionary transfer optimization. ETO is the main tool we use in KAB2S.
SMO is single-objective to multi/many-objective optimization, which is a new subset of ETO.
VRPTW is the abbreviation for the vehicle routing problem with time windows.
In a word, in our paper or “double gathering”, we study an ETO or SMO-based VRPTW to enrich the abstract idea of the architecture of KAB2S, which will contribute to system optimization [2] in engineering management for smart industry.
2. Materials and Methods
2.1. Test Problem: VRPTW, Two Objectives of Total Travel Cost and Total Customer Dissatisfaction
VRPTW [37] is an extension of capacitated vehicle routing problem, where the service must start within a time window and the vehicle must remain at the location of the customer during service.
A mathematical programming formulation of VRPTW is defined on a network flow model, which involves two types of variables: one is the flow variable, and another is the time variable. Variables and parameters are set as follows (same as [36]):
- : Arrival time at node ;
- : Wait time at node ;
- if there is no arc from node to node , and 1 otherwise. ;
- Total number of vehicles;
- Total number of customers;
- : Any arbitrary real number;
- : Euclidean distance between node and ;
- : Cost incurred on arc from node to ;
- : Travel time between node and ;
- : Demand at node ;
- : Capacity of vehicle ;
- : Earliest arrival time at node ;
- : Latest arrival time at node ;
- : Service time at node ;
- : Maximum route time allowed for vehicle .
In the following, Formula (1) is the main optimization objective function of total travel cost (in our SMO, sometimes we test total travel cost or total customer dissatisfaction alone, sometimes both. Total travel cost is the basic objective, so we only discuss it here). Constraint (2) specifies that there exist maximum K routes, which go out of the central depot. Furthermore, Equation (3) makes sure that each route begins and ends at the depot. Equations (4) and (5) define that each node can be visited by one vehicle only once. Equation (6) constructs the capacity constraint. Equation (7) gives the maximum constraint of travel time. Constraint (8)–(10) constitute the time windows. Those formulas specify the feasibility of solution space completely for VRPTW.
s. t.:
2.2. BB Hypothesis: Goldberg’s Decomposition Theory (7 Steps) and BB Processing Pipeline (5 Steps)
The BB hypothesis (an example of BBs can be seen in Figure 1) is mainly constructed via Goldberg’s [21] decomposition theory, which includes 7 steps as follows:
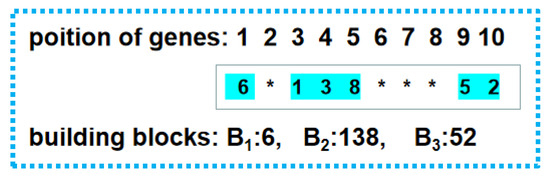
Figure 1.
An example of building blocks (those “*”s can be anyone in 4, 7, 9 and 10, however, the whole list should be a permutation.) in PFSP, inspired by [9].
(1) “Know what GAs process” [21]—BBs. This step states the idea that GA performs via structures that are quasi-invariant, highly fit or via “components of good solutions” identified as BB by Holland.
(2) Solve optimization problems that have bounded BB difficulty. Competent GAs can solve optimization problems reliably if the order of BBs is low. Some problems are hard in that deep or complex building blocks exist, or in that BBs are hard to separate, or in that low order BBs “are misleading or deceptive” [21].
(3) Ensure that the supply of raw BBs is adequate. This step emphasizes that for GAs to tackle problems successfully, the whole necessary raw BBs should be not only available but also sufficient. The size of the initial population should be large enough so that the supply is adequate enough for the optimization from the start.
(4) Ensure that the “market share” [21] of superior BBs increases. During the evolutionary process, the proportion of good BBs should continue to grow for the continuous supply of good BBs. When cooperating with step 3, which ensures the supply from the beginning, GAs can yield more and more copies of good BBs for the creation of promising solutions.
(5) Know “BB takeover” [21] and the models of convergence times. Although in the previous step the market share for superior BBs “has to grow and cannot grow too slowly over the generations, the growth rate of the portion of superior building blocks in the population should not be too fast, either” [21], if the growth of the proportion of BBs is too fast, there is no enough time for a GA to work on both exchange and recombination of raw BBs before no alternative BBs are left for effective recombination. Such a condition may lead to premature convergence or result in the domination of deceptive BBs.
(6) Ensure that GAs make the BB decisions well. Because GAs work on the fitness value of an individual solution including multiple BBs, there is a statistical decision problem for choosing among competing BBs. In some cases, GAs may select a bad BB and abandon competitors of that bad BB, in that the bad one is with other good BBs in the same solution. For a particular BB, the fitness contribution via the BBs from other partitions in the solution can be regarded as something like noise to the fitness. Therefore, it also suggests that the size of the population should be set sufficiently large for GAs to make statistically correct decisions among the competing BBs.
(7) Ensure that the mixing of BBs is good. After the supply, growth and decision of BBs in step 3, step 4, and step 6, respectively, GAs need to combine and assemble these BBs efficiently and effectively towards the creation of high-quality individuals.
Based on the proposed decomposition theory, they present the pipeline for BB processing with 5 steps: (1) creation, which creates the raw BB supply, (2) identification, which identifies the good BBs, (3) separation, that devotes to the separation of superior BBs, (4) preservation, that focus on the maintenance of good BBs, and (5) mixing, which reassembles good BBs [21].
2.3. The Framework across Tasks: SMO
2.3.1. Typical 3 Tasks: 2 Subtasks Boost the Core Task
SMO belongs to the decomposition style, it roughly divides the pipeline into 3 typical components: two boosts one.
2.3.2. In total, 4 bags, 4 × 2 Groups, 4 × 2 × 4 Tasks: E.g., Bag 00: Group 1, t1_wc (t_wc 1.0, t_wc 1.1), t2_wc and t2e_wc; Group 2, t1_nc (t_nc 1.0, t_nc 1.1), t2_nc and t2e_nc…
An overview is in Figure 2 (Bag 00 serves as an example). In SMO, for each bag, we set 2 groups. Furthermore, each group contains 4 tasks. Bag and group are special terms of units of measurement for tasks.
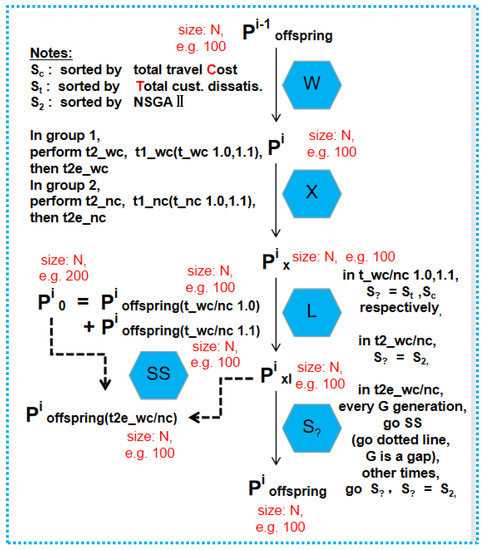
Figure 2.
Overview. For generation i, from parent Pi to Pioffspring.
Bag 00 (example or mother bag) is full of groups 1 and 2.
Group 1 owns 4 tasks, namely, t1_wc including two sub-tasks (t_wc 1.0, t_wc 1.1), t2_wc and t2e_wc, where “wc” means with clustering and “e” is external transferring from t1_wc, sharing the same toolkit of W-X-L (only L varies, t_wc 1.0 chooses total customer dissatisfaction, while t_wc 1.1, t2_wc and t2e_wc choose total travel cost).
The above is the same for group 2 of t1_nc (t_nc 1.0, t_nc 1.1), t2_nc and t2e_nc, except that no clustering (named “nc”) is in W [49].
Based on Bag 00, we get the next 4 child bags.
Bag 9 stores groups 3 and 4, which are the same as groups 1 and 2 in Bag 00.
Then, Bag 10 owns groups 5 and 6. Just remove L from groups 1 and 2 in Bag 00 to achieve the groups for Bag 10.
Furthermore, Bag 11 contains groups 7 and 8. Simply remove X from groups in Bag 00.
At last, Bag 12 gets groups 9 and 10. Just remove S from the mother bag of Bag 00.
Because our goal is to test selection and Bags 1, 2, 3, 4, 5, 6, 7, and 8 (in [53] or “eMeets”, we test Bag 1, 2, 3, and 4, and for [54] or “iMeets”, Bags 5, 6, 7, and 8 are investigated. The “Meets” series is firstly named in [54]. This paper is “rMeets”) provide us useful experiences and key guidelines, so in this paper, we only focus on Bag 10 and Bag 12.
In the overview in Figure 2, W-X-L deploys a special operator (W) to choose parents, a crossover (X) operator and a local search (L) operator. It is worth mentioning that the family of tasks above shares the same initial (I) population (random) for a fair comparison. Selection (S) differs. In S, we use NSGA II, some sorting methods by total customer dissatisfaction or total travel cost, etc. Therefore, so many shared parts above from both the problem and algorithm sides are elaborately constituted toward a harmonious and well-defined test bed of SMO. More of the test bed can be seen in the next 4 figures (Figure 3, Figure 4, Figure 5 and Figure 6), and 3 details (WC, XL, SS).
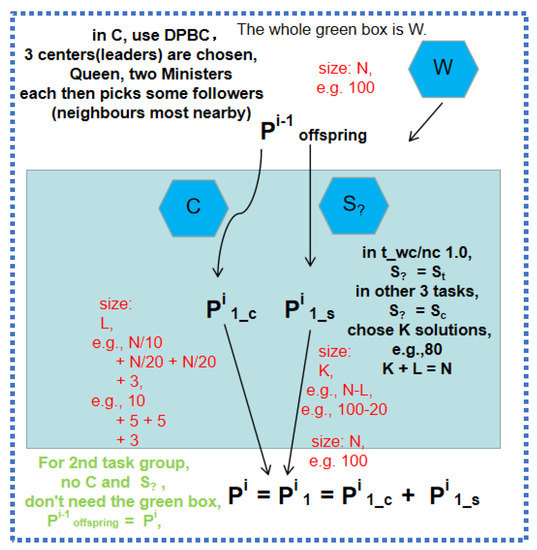
Figure 3.
Details of W. Here, we choose parents Pi. Furthermore, DPBC is in C.
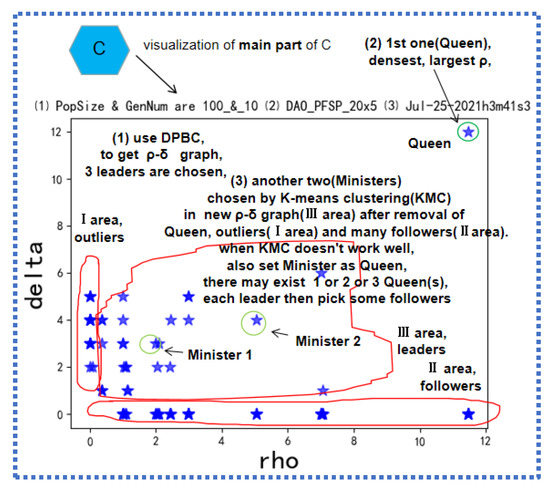
Figure 4.
Details of C. You can see a typical ρ-δ (rho-delta) graph in the simulation of PFSP (the same for VRPTW), where ρ denotes local density, and δ denotes “the minimum distance between one sample point and any other one with higher density” [49].
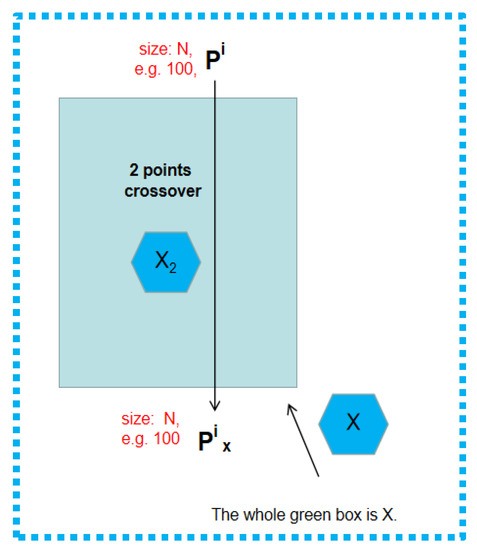
Figure 5.
Details of X.
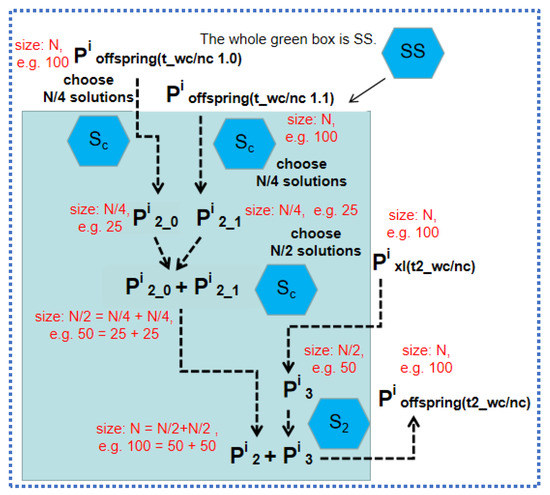
Figure 6.
Details of SS.
Details of WC (Figure 3 and Figure 4). For W, we choose parents Pi with S? and C. In C, we develop the key component, density peak-based clustering (DPBC) [54].
For DPBC, “science clustering” (because it was published at science, so we named it “science clustering”) is based on the deep observation that centers of clusters in sample space are characterized by both “a relatively higher density than points in their neighborhoods” [6,49] and “a relatively long distance from points that have higher densities” [6,49].
To apply DPBC for VRPTW, we implement science clustering via the hamming distance metric, which is widely accepted and used in evolutionary computation research. To our surprise, hamming distance also focuses on the work of mining the positional BBs. Quite obviously and intuitively, the measure of “hamming distance (dissimilarity) and positional BB (similarity) work from opposite sides to the same characterization” [6,49].
Details of XL, especially X, are presented in Figure 5. L is just an ordinary insertion operator.
Details of SS in S can be seen in Figure 6. “t1_wc/nc and t2_wc/nc have no Pi0, only t2e_wc/nc needs Pi0 every G generation” [49]. Both t_wc/nc 1.0 and 1.1 establish the selection pressure via settings of single objectives, and t2_wc/nc and t2e_wc/nc use both objectives via NSGA II.
3. Results
3.1. Experimental Setup
To test the validation of the framework of SMO, we carry out extensive simulation on some VRPTW instances in well-studied (Solomon) benchmarks, that is, C101, R101 and RC101.
Furthermore, in our simulation, SMO is coded by Python 3.8.8 and is run on servers.
The following parameters of SMO are set: N is 100, and the number of generations is 100. In t1_wc/nc 1.0 and 1.1, crossover and local search probabilities [px2, pls] are [0.80, 0.60] and [0.90, 0.60], respectively. For t2_wc/nc and t2e_wc/nc, it is [0.85, 0.60]. For reference, C101 takes range (30,000, 100,000) to normalize total travel cost, and (0, 800) to normalize total customer dissatisfaction; R101 uses (10,000, 80,000) and (0, 800); and instance 3 picks the same as R101. For those two objectives, the unit cost is 8.0, the initial cost is set 100.0, the wait for cost is 1.0 and the value of delay cost is 1.5. “The gap G is 2. The baseline size of Pi2 is 50, modified by a factor K1. For Pi1, the base line size is 20 + H. Furthermore, 20 is also adapted by K2, H may be 0, 1, 2 or 3, depending on the solutions with equal distance at cutting distance” [49].
Varying the setup of [K1, K2] from vectors of [1, 0.6], [0.6, 0.6] to [1, 1] in each instance (3), we get 9 cases in each bag, and each case owns total 20 independent runs. In each run, we perform a simulation of 8 tasks, that is, 2 task groups in Section 2.3.2.
3.2. Simulations and Comparisons
In every case, both t2_wc and t2e_wc work with clustering methods, and both t2_nc and t2e_nc are performed without (no) clustering.
In Bag 10 and 12, we evolve overall 2 (bags) × 100 (generations per task) × 4 (4 tasks in each group) × 2 (wc/nc, that is wc or nc) × 20 (independent runs) = 32,000 generations!
Then, in Bag 10 and 12, we will give a systematic study of key operators, like our selection, which is robust and is believed to be the transfer core.
For Bag 10 (Figure 7) below, we will focus on the systems based on Bag 9, but without a local search (L) or memes, that is, we study operator X. Because the evolutionary algorithm or population-based global search is the main body of our SMO, so it is necessary to study Bag 10.
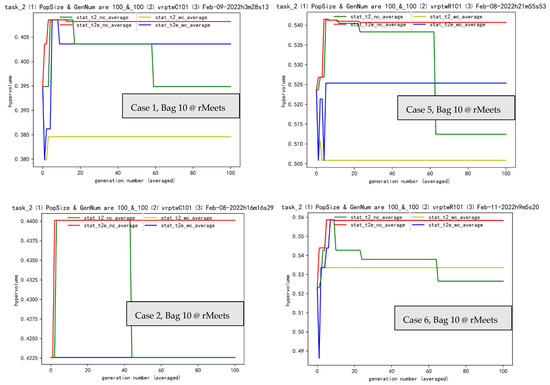
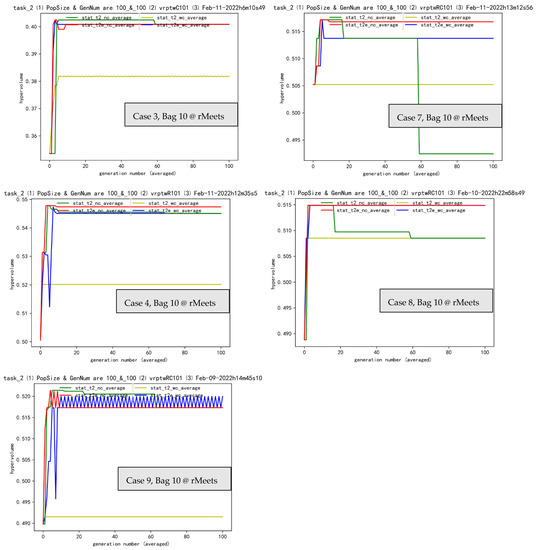
Figure 7.
Cases 1, 2, …, 9 in Bag 10. “stat” denotes statistics of hypervolume. Besides, t2_nc is the baseline NSGA II, without clustering and transferring. Those lines in the picture are colored, so you should read them in colored presentation. We choose dark green lines as baseline tasks or algorithms of t2_nc.
As for Bag 10, between t2_wc and t2e_wc, there is always obvious positive transferring effectiveness (except case 2) in Figure 7, which tends to validate great effectiveness (ee) in SMO, whereas for t2_nc and t2e_nc, both effectiveness (ee, e) and ineffectiveness (ie) exist. More observations of those examples can be found in Table 1.

Table 1.
Comparisons in Bag 10 for SMO framework.
Then, let us go to Bag 12.
Here, we will explore W, L and S operators, where we hope to find selection effectiveness in the transfer core for SMO.
Bag 12 (Figure 8) tells us that between t2_wc and t2e_wc, and the pair of t2_nc and t2e_nc, you can see some rules about selection in SMO.
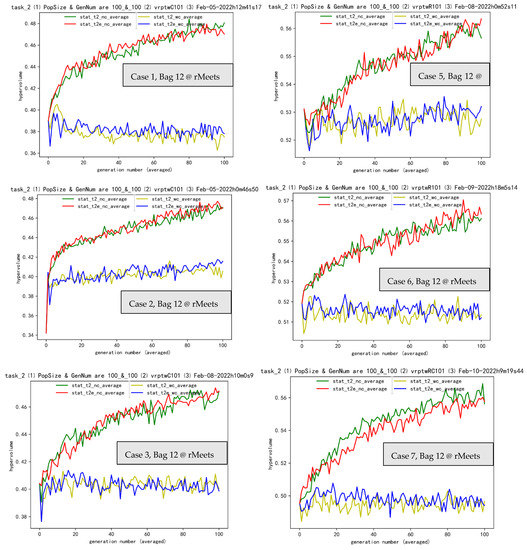
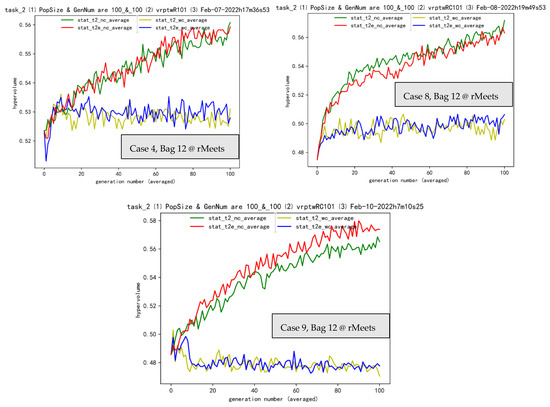
Figure 8.
Cases 1, 2, …, 9 are shown above, respectively. Notes: (1) “stat” means statistics of hypervolume. (2) Actually, t2_nc (dark green) is the baseline NSGA II, without clustering and transferring.
Without selection S, both the red line and dark green line can reach higher and higher (like the Beijing 2022 Olympics winter games), which means that the L operator also acts as a small role of selection, and a positive role.
Without selection S, the red and dark green lines beat blue and light green lines, which tells us that the W operator serves a bad role for selection here. (As we already pointed out in our paper [53], W is also a selection operator.)
With selection S in complete Bag 9, we get a further comparison. The united selection or gathering effectiveness of W, L and S can be seen in Bag 9. Without a loss of generality, we choose case 1 (Figure 9) and 3 (Figure 10) in Bag 9 as representative. With fine control/harness of overall selection, like settings in t2_nc and t2e_nc (the red and dark green lines), transfer effectiveness of SMO can be achieved.
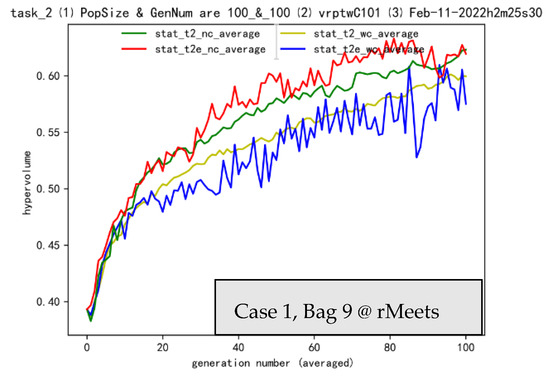
Figure 9.
Cases 1 in Bag 9.
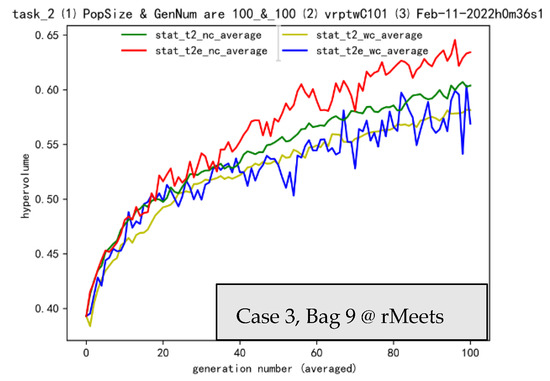
Figure 10.
Cases 3 in Bag 9.
Those observations above are again summed up in Table 2.

Table 2.
Comparisons in Bag 12 for SMO framework.
4. Discussion
4.1. Transferring and Learning between Key Bag 9, 10 and 12: Common Operator of Insertion, Core Function of Selection
We tend to conclude that the transfer effectiveness of the SMO framework is always quite obvious, especially without clustering conditions (t2e_nc VS t2_nc, for case 1 and 3 in Bag 9).
What we should highlight here are “two Cs, two tions”, that is, the common operator of insertion and the core function of the selection.
First, we try to prove the generality of SMO via a typical pipeline of three MAs armed with insertion. Why do we choose insertion? No matter for PFSP or VRPTW, or any permutation-based discrete problem, we tend to believe that insertion is the atom local search operator, and usually constitutes a complete local search operator base for any local search operator, whether simple or complicated! Thus, great generality is proved to exist by insertion. Simple yet not simple, it is the whole world (a set of any local search operator) in a dewdrop (atom, base of insertion)!
Secondly, just as we point out in the Introduction, selection is the core mechanism for traditional EA [46,48] and ETO. For example, in MTO [44] or in the picture below (Figure 11), MTO is defined or characterized by selection.
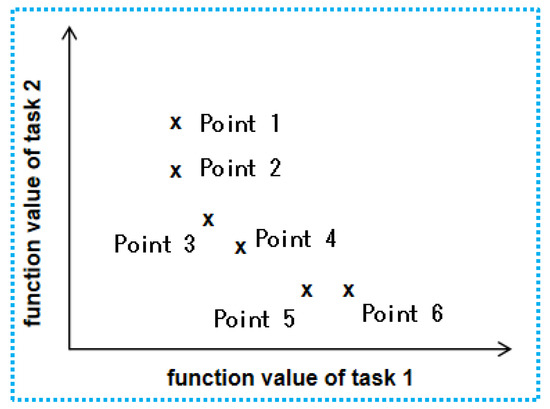
Figure 11.
Multi-objective optimization (MOO) and MTO chose different selection pressure. For MOO, points 2, 3, 4, and 5 are better than 1, and 6. However, points 1, 2, 5, and 6 are more preferable than 3 and 4 in the MTO case.
4.2. State of the Art via Two Steps: Gathering Inner Strength (1, Core Task Is Strong Enough), Gathering Outer Storms (2, Boost Core Task via Transferring)
As we already stated in our paper [49], “transferring from one task to another task, does not necessarily lead to the state of the art (SOTA) performance of the latter task (as usually observed in transfer learning community)”.
We need two steps of gathering both inner strength (step 1) and outer storms (step 2) to reach our goal of SOTA. In PFSP, W or science clustering serves as a positive transferring or gathering tool. However, it acts as a negative gathering selection for VRPTW here, failing to gather benefit storms! Partly because positional building blocks exist in [27] PFSP, but do not exist in VRPTW, building block theory needs to be refined for exploration of VRPTW.
What we should highlight here again is that W belongs to unsupervised learning and serves as a learning module, where three clustering centers are named as Queen(s) and Ministers. The learning and selection roles of W matter little for VRPTW but matters more for PFSP. What really matters should be the transfer/boost core between tasks, which is the key learning/gathering mechanism for SMO and has deep connections with selection (such as the SS operator).
4.3. On the General Spectrum: Gathering Core Tasks beyond MAs Here, like Iterated Greedy Algorithms, Reinforcement Learning Based EA
Our SMO tests GAs, MAs (GAs + local search), GAs + W and MAs + W here.
How about other algorithms, whether heuristic or not, such as iterated greedy algorithms [35], which are quite powerful for PFSP, reinforcement learning based EA, cuckoo search, fractal search…?
Like the Beijing 2022 Olympics winter games, we shall head “Together for a Shared Future” of SMO. We anticipate fruitful answers from gathering those types of core tasks toward a clearer discovery of the mystery in SMO, which may constrain or extend its general spectrum.
5. Conclusions
Considering the pledge of China’s carbon neutrality, our framework SMO attempts to avoid scheduling [33,38,45] production and logistics operations from scratch towards a happy medium of efficiency and effectiveness.
Concerning new frontier evolutionary computation [41,52] and machine learning [50,51], our solution of SMO can reduce the computational complexity of multi-objective and even many-objective problems, providing great potential scientific and academic values.
In the future, many directions are attractive and inspiring. For example, to disentangle [54] the knowledge is quite important [39,41], which somehow is like the disentanglement of different features/representations [5,15,34,51] in deep learning/transfer learning towards interpretability [17,18,19,20,21,23,28,29,30,31,32,39,40,42,43,47] of black box based artificial intelligence (AI).
Author Contributions
Conceptualization, D.H., W.X., Q.G. and X.W.; methodology, R.Z., X.S. and G.Z.; software, X.W., X.S. and G.Z.; validation, R.Z., X.S. and G.Z.; formal analysis, X.W., X.S. and G.Z.; investigation, Y.Y., T.X. and G.Z.; resources, Y.Y., T.X. and G.Z.; data curation, Y.Y., T.X. and G.Z.; writing—original draft preparation, X.W. and G.Z.; writing—review and editing, D.H., W.X., Q.G., R.Z., X.S. and X.W.; visualization, Y.Y., T.X. and G.Z.; supervision, D.H., W.X., Q.G., Y.Y., R.Z. and T.X.; project administration, D.H. and W.X.; funding acquisition, W.X., D.H. and Q.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Fundamental Research Funds for the Central Universities, N2128001.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors thank Han Zhou (also, in our group of DAO, NEU) for her useful support and kindly help, and thank Lijie Su and Yun Dong (they are in our group of DAO, NEU) for their useful comments. Wendi Xu (one of the authors), also thanks Zuocheng Li (also, in our group), for his useful discussion of building block theory. At last, Wendi Xu expresses his thank to Yingping Chen (from National Yang Ming Chiao Tung University) for his insights on linkage learning genetic algorithms, which helps him (Wendi Xu) understand the building block theory better. The anonymous reviewers have also contributed considerably to the publication of this paper. In addition, we would like to thank anonymous reviewers who have helped us to improve the paper, to reach for new horizons, and to forge new partnerships that are mutually beneficial like what we have seen behind Olympics games.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Littman, M.; Ajunwa, I.; Berger, G.; Boutilier, C.; Currie, M.; Velez, F.; Hadfield, G.; Horowitz, M.; Isbell, C.; Kitano, H.; et al. Gathering Strength, Gathering Storms: The One Hundred Year Study on Artificial Intelligence (AI100) Study Panel Report; Stanford University: Stanford, CA, USA, 2021; Available online: http://ai100.stanford.edu/2021-report (accessed on 14 July 2022).
- Tang, L.; Meng, Y. Data analytics and optimization for smart industry. Front. Eng. Manag. 2021, 8, 157–171. [Google Scholar] [CrossRef]
- Tan, K.; Feng, L.; Jiang, M. Evolutionary transfer optimization—A new frontier in evolutionary computation research. IEEE Comput. Intell. Mag. 2021, 16, 22–33. [Google Scholar] [CrossRef]
- Xu, W.; Zhang, M. Towards WARSHIP: Combining brain-inspried computing of RSH for image super resolution. In Proceedings of the 2018 5th IEEE International Conference on Cloud Computing and Intelligence Systems, Nanjing, China, 23–25 November 2018. [Google Scholar]
- Xu, W.; Wang, X.; Guo, Q.; Song, X.; Zhao, R.; Zhao, G.; Yang, Y.; Xu, T.; He, D. Towards KAB2S: Learning key knowledge from single-objective problems to multi-objective problem. arXiv 2022, arXiv:2206.12906. [Google Scholar]
- Xu, W.; Wang, X.; Guo, Q.; Song, X.; Zhao, R.; Zhao, G.; Yang, Y.; Xu, T.; He, D. Towards KAB2S (ΙΙΙ): A proposal on ETO interpretability to disentangle the knowledge. arXiv 2022, arXiv:2206.12906. [Google Scholar]
- Harik, G. Learning Gene Linkage to Efficiently Solve Problems of Bounded Difficulty Using Genetic Algorithms. Ph.D. Thesis, The University of Michigan, Ann Arbor, MI, USA, 1997. [Google Scholar]
- Chen, Y. Extending the Scalability of Linkage Learning Genetic Algorithms: Theory & Practice; Part of the Studies in Fuzziness and Soft Computing Book Series; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Chang, P.; Huang, W.; Wu, J.; Cheng, T. A block mining and recombination enhanced genetic algorithm for the permutation flow-shop scheduling problem. Int. J. Prod. Econ. 2013, 141, 45–55. [Google Scholar] [CrossRef]
- Huang, L.; Feng, L.; Wang, H.; Hou, Y.; Liu, K.; Chen, C. A preliminary study of improving evolutionary multi-objective optimization via knowledge transfer from single-objective problems. In Proceedings of the 2020 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Toronto, ON, Canada, 11–14 October 2020. [Google Scholar]
- Yuan, Y.; Ong, Y.; Gupta, A.; Tan, P.; Xu, H. Evolutionary multitasking in permutation-based combinatorial optimization problems: Realization with TSP, QAP, LOP, and JSP. In Proceedings of the 2016 IEEE Region 10 Conference (TENCON), Singapore, 22–25 November 2016. [Google Scholar]
- Feng, L.; Ong, Y.-S.; Lim, M.-H.; Tsang, I.W. Memetic Search with Interdomain Learning: A Realization between CVRP and CARP. IEEE Trans. Evol. Comput. 2014, 19, 644–658. [Google Scholar] [CrossRef]
- Wang, X.; Tang, L. A machine-learning based memetic algorithm for the multi-objective permutation flowshop scheduling problem. Comput. Oper. Res. 2016, 79, 60–77. [Google Scholar] [CrossRef]
- Li, Y.; Wang, C.; Gao, L.; Song, Y.; Li, X. An improved simulated annealing algorithm based on residual network for permutation flow shop scheduling. Complex Intell. Syst. 2020, 7, 1173–1183. [Google Scholar] [CrossRef]
- Shi, J.; Zhao, L.; Wang, X.; Zhao, W.; Hawbani, A.; Huang, M. A Novel Deep Q-Learning-Based Air-Assisted Vehicular Caching Scheme for Safe Autonomous Driving. IEEE Trans. Intell. Transp. Syst. 2020, 22, 4348–4358. [Google Scholar] [CrossRef]
- Wang, L.; Wang, J.; Wu, C. Advances in green shop scheduling. Control. Decis. 2018, 33, 385–391. [Google Scholar]
- Lei, N.; An, D.; Guo, Y.; Su, K.; Liu, S.; Luo, Z.; Yau, S.-T.; Gu, X. A Geometric Understanding of Deep Learning. Engineering 2020, 6, 361–374. [Google Scholar] [CrossRef]
- Bronstein, M.; Bruna, J.; Cohen, T.; Velikovi, P. Geometric deep learning: Grids, groups, graphs, geodesics, and gauges. arXiv 2021, arXiv:2104.13478. [Google Scholar]
- Zhu, Y.; Gao, T.; Fan, L.; Huang, S.; Edmonds, M.; Liu, H.; Gao, F.; Zhang, C.; Qi, S.; Wu, Y.N.; et al. Dark, Beyond Deep: A Paradigm Shift to Cognitive AI with Humanlike Common Sense. Engineering 2020, 6, 310–345. [Google Scholar] [CrossRef]
- Weinan, E. A Proposal on Machine Learning via Dynamical Systems. Commun. Math. Stat. 2017, 5, 1–11. [Google Scholar]
- Li, D. Ten questions for the new generation of artificial intelligence. CAAI Trans. Intell. Sys. 2020. [Google Scholar] [CrossRef]
- Wu, F.; Yang, C.; Lan, X.; Ding, J.; Zheng, N.; Gui, W.; Gao, W.; Chai, T.; Qian, F.; Li, D.; et al. Artificial intelligence: Review and future opportunities. Bull. Natl. Nat. Sci. Found. China 2018, 32, 243–250. [Google Scholar]
- Stone, P.; Brooks, R.; Brynjolfsson, E.; Calo, R.; Etzioni, O.; Hager, G.; Hirschberg, J.; Kalyanakrishnan, S.; Kamar, E.; Kraus, S.; et al. Artificial Intelligence and Life in 2030. Available online: http://ai100.stanford.edu/2016-report (accessed on 14 July 2022).
- Chen, Y.-P.; Chuang, C.-Y.; Huang, Y.-W. Inductive linkage identification on building blocks of different sizes and types. Int. J. Syst. Sci. 2012, 43, 2202–2213. [Google Scholar] [CrossRef]
- Krasnogor, N.; Smith, J. A Tutorial for Competent Memetic Algorithms: Model, Taxonomy, and Design Issues. IEEE Trans. Evol. Comput. 2005, 9, 474–488. [Google Scholar] [CrossRef]
- Yazdani, D.; Cheng, R.; Yazdani, D.; Branke, J.; Jin, Y.; Yao, X. A Survey of Evolutionary Continuous Dynamic Optimization over Two Decades—Part B. IEEE Trans. Evol. Comput. 2021, 25, 630–650. [Google Scholar] [CrossRef]
- Cotta, C.; Fernández, A. Memetic Algorithms in Planning, Scheduling, and Timetabling; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Deb, K.; Agrawal, S. Understanding interactions among genetic algorithm parameters. Found. Genet. Algorithms 2002, 5, 265–286. [Google Scholar]
- Al-Sahaf, H.; Bi, Y.; Chen, Q.; Lensen, A.; Mei, Y.; Sun, Y.; Tran, B.; Xue, B.; Zhang, M. A survey on evolutionary machine learning. J. R. Soc. N. Z. 2019, 49, 205–228. [Google Scholar] [CrossRef]
- Yu, Y.; Chao, Q.; Zhou, Z. Towards analyzing recombination operators in evolutionary search. In International Conference on Parallel Problem Solving from Nature; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Li, K.; Chen, R.; Fu, G.; Yao, X. Two-archive evolutionary algorithm for constrained multi-objective optimization. IEEE Trans. Evol. Comput. 2018, 23, 303–315. [Google Scholar] [CrossRef]
- Wall, M. A Genetic Algorithm for Resource-Constrained Scheduling. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1996. [Google Scholar]
- Pinedo, M. Scheduling: Theory, Algorithms, and Systems; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Huang, G.; Huang, G.; Song, S.; You, K. Trends in extreme learning machines: A review. Neural Netw. 2015, 61, 32–48. [Google Scholar] [CrossRef] [PubMed]
- Ruiz, R.; Pan, Q.-K.; Naderi, B. Iterated Greedy methods for the distributed permutation flowshop scheduling problem. Omega 2019, 83, 213–222. [Google Scholar] [CrossRef]
- Tan, K.; Lee, L.; Zhu, Q.; Ou, K. Heuristic methods for vehicle routing problem with time windows. Artif. Intell. Eng. 2001, 15, 281–295. [Google Scholar] [CrossRef]
- Cordeau, J.; Desaulniers, G.; Desrosiers, J.; Solomon, M.; Soumis, F. The VRP with Time Windows; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Watson, J.-P.; Barbulescu, L.; Whitley, L.D.; Howe, A.E. Contrasting Structured and Random Permutation Flow-Shop Scheduling Problems: Search-Space Topology and Algorithm Performance. INFORMS J. Comput. 2002, 14, 98–123. [Google Scholar] [CrossRef]
- Fieldsend, J. Computationally efficient local optima network construction. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, New York, NY, USA, 15–19 July 2018. [Google Scholar]
- Zhou, Z.; Yu, Y. A new approach to estimating the expected first hitting time of evolutionary algorithms. In Proceedings of the 21st National Conference on Artificial Intelligence, Boston, MA, USA, 16–20 July 2006. [Google Scholar]
- Vérel, S.; Daolio, F.; Ochoa, G.; Tomassini, M. Local optima networks with escape edges. In International Conference on Artificial Evolution; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Bandaru, S.; Ng, A.; Deb, K. Data mining methods for knowledge discovery in multi-objective optimization. Expert Syst. Appl. 2017, 70, 139–159. [Google Scholar] [CrossRef]
- Liu, X.; Xie, Y.; Li, F.; Gui, W. Admissible Consensus for Homogenous Descriptor Multiagent Systems. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 965–974. [Google Scholar] [CrossRef]
- Gupta, A.; Ong, Y.-S.; Feng, L. Multifactorial Evolution: Toward Evolutionary Multitasking. IEEE Trans. Evol. Comput. 2015, 20, 343–357. [Google Scholar] [CrossRef]
- Park, J.; Mei, Y.; Nguyen, S.; Chen, G.; Zhang, M. An investigation of ensemble combination schemes for genetic programming based hyper-heuristic approaches to dynamic job shop scheduling. Appl. Soft Comput. 2018, 63, 72–86. [Google Scholar] [CrossRef]
- Miikkulainen, R.; Forrest, S. A biological perspective on evolutionary computation. Nat. Mach. Intell. 2021, 3, 9–15. [Google Scholar] [CrossRef]
- Pak, I. Random Walks on Groups: Strong Uniform Time Approach; Harvard University: Cambridge, MA, USA, 1997. [Google Scholar]
- Chen, W.; Ishibuchi, H.; Shang, K. Clustering-based subset selection in evolutionary multiobjective optimization. In Proceedings of the 2021 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Melbourne, Australia, 17–20 October 2021. [Google Scholar]
- Xu, W.; Wang, X. ETO Meets Scheduling: Learning Key Knowledge from Single-Objective Problems to Multi-Objective Problem. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021. [Google Scholar]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Pan, Y.; Li, X.; Yang, Y. A content-based neural reordering model for statistical machine translation. In Proceedings of the China Workshop on Machine Translation, Dalian, China, 27–29 September 2017; pp. 112–123. [Google Scholar]
- Sun, Y.; Chen, X.; Xie, Y.; Zeng, Z.; Gui, W. Knowledge-driven process industry smart manufacturing. Sci. Sin. Inf. 2020, 50, 1345. [Google Scholar]
- Bengio, Y. Deep learning of representations for unsupervised and transfer learning. Workshop Unsupervised Transf. Learn. 2011, 27, 17–36. [Google Scholar]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef]
- Zhou, Z.; Ma, X.; Liang, Z.; Zhu, Z. Multi-objective multi-factorial memetic algorithm based on bone route and large neighborhood local search for VRPTW. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).