The New Solution Concept to Ill-Posed Bilevel Programming: Non-Antagonistic Pessimistic Solution

Abstract

It is hardly realistic to assume that, under all decision circumstances, followers will always choose a solution that leads to the worst upper-level objective functional value. However, this generally accepted concept of the pessimistic solution to the ill-posed bilevel programming problems may lead to the leader’s attitude being more pessimistic vis à vis his anticipation of the follower’s decision being non-antagonistic. It will result in a wrong pessimistic solution and a greater potential of cooperation space between the leader and the followers. This paper presents a new concept of a non-antagonistic pessimistic solution with four numerical examples for bilevel programming problems from a non-antagonistic point of view. We prove that the objective function value of the non-antagonistic pessimistic solution generally dominates or is equal to the objective functional value of the pessimistic solution and the rewarding solution, and the maximum potential space for leader-follower cooperation can be overestimated in a generally applied pessimistic solution. Our research extends the concept of the pessimistic solution. It also sheds light on the insights that the non-antagonistic pessimistic solution can describe the practical potential of cooperation space between the leader and followers in non-antagonistic circumstances.

1. Introduction

The bilevel programming problem (BLPP) is a hierarchical non-cooperative optimization problem in which upper-level and lower-level players have their own criteria functions, each controlling corresponding decision variables. The upper-level player is often referred to as the leader who makes the decision first, while the lower-level player is the follower who acts accordingly. At the same time, the optimization result of the follower is the implicit constraint to the leader in attaining its optimality [1]. An ill-posed bilevel problem (IBPP) refers to the BLPP when multiple lower-level optimal solutions exist for certain upper-level decision variables. In this type of problem, the upper-level optimality is affected by the uncertain feedback of the lower-level solutions. The traditional optimal Stackelberg solution, usually defined in non-cooperative environments and for the case where the follower’s reaction set to the leader’s strategy is a singleton, seems inadequate for solving IBPPs. Furthermore, most solution methods in the current bilevel optimization literature are designed for well-posed problems [2,3,4,5] or the optimistic and pessimistic case of ill-posed problems [6,7,8,9,10]. However, assuming that followers will always choose a solution that leads to the best or worst upper-level objective functional value is hardly realistic. Therefore, a proper definition of the optimal solution is crucial for developing the solution method and approximating the best solution(s) for IBPPs.

In the pessimistic position of IBPP, the leader assumes that the follower can choose the solution that results in the worst value of the upper-level objective function. However, in practical problems, assuming that the follower will always choose a solution from the optimal reaction set that is worse for the leader is unrealistic. Consider, for instance, a bilevel reservoir operation problem during the flood season, where the flood control bureau and the power plant manager are the leader and the follower [11]. It is hard to imagine that the power plant manager would always choose the solution with the highest flood risk, unless he wanted the plant to be destroyed by the flood. This antagonistic assumption can lead to a wrong pessimistic solution and an enlarged potential for cooperation between the leader and the followers. Therefore, there is a gap between research studies and the application of the pessimistic solution in practice, and the leader’s attitude may be less pessimistic vis à vis his anticipation of the follower’s decision being fully antagonistic. While the pessimistic approach can be useful for identifying the worst-case scenario, it may not accurately reflect the actual behavior of the follower. To address this limitation, we need to develop new theories and methods that consider the possible positions that lower-level decisionmakers may take in hierarchical management scenarios.

This paper aims to bridge this gap by proposing a new concept of pessimistic solution to bilevel programming problems, called the non-antagonistic pessimistic solution, which considers the scenarios where followers may not always act antagonistically. It is shown that the objective function value of the non-antagonistic pessimistic solution generally dominates or is equal to that of the pessimistic and rewarding solutions. The non-antagonistic pessimistic solution can provide a more realistic estimate of the potential for cooperation in non-antagonistic circumstances.

The remainder of the paper is organized as follows. Section 2 reviews some recent definitions of BLPP solutions. Section 3 provides the previous definitions of the four extreme solutions and introduces the new definition for the IBPP solutions together with the associated properties and proof. It is followed by Section 4 with four examples to demonstrate the properties of the defined type of bilevel optimal solution. Section 5 is a discussion of the results. We close this paper with a conclusion in Section 6.

2. Literature Review of the Definitions of BLPPs

The past decades have witnessed a plethora of new definitions for BLPPs from varying perspectives, such as optimistic and pessimistic solutions, intermediate solutions [12,13], partial cooperation solutions [14], satisfactory solution(s) [15], viscosity solutions [16], deceiving/ rewarding solutions [17], pseudo-feasible solutions [18], etc. We classify these research efforts and definitions into two broad categories: (1) definitions for reducing lower-level decision uncertainties and (2) definitions for improving the feasibility and existence of the optimal solution. Most of the new definitions fall within the first classes, where lower-level decision uncertainties may be attributed to the presentence of variables uncertainty [19], nonunique solutions in single-objective BLPPs [20], preferential uncertainty in multi-objective BLPPs [21] and nonunique Nash equilibrium solutions in BLPPs with multi-followers [22].

For the first category of definitions, knowing what position the follower might take in solving the problem becomes important since it determines which solution(s) from the lower level should be considered at the upper level [23]. To deal with uncertainty related to lower-level nonunique solutions, we generally use the optimistic and pessimistic positions in single-objective bilevel optimization under the follower’s full cooperation or non-cooperation. Lucchetti et al. [24] presented two additional positions, which assume the follower makes a free choice or the leader is indifferent to the follower’s choice. For little justification to assume that the follower will only behave in the two extreme ways, Aboussoror and Loridan [12] first introduced the idea of the intermediate solution of the strong–weak Stackelberg problem, in which the leader’s optimal choice depends on the level of cooperation from the follower. Cao and Leung [14] further proposed the concept of partial cooperation solution(s) by introducing a cooperation index to describe the degree of follower cooperation. A deceiving solution is defined for multi-objective bilevel programming by Alves et al. [17] when the leader makes an optimistic decision, but the follower’s reaction is the least favorable to the leader. A rewarding solution is defined when the leader makes a pessimistic decision, but the follower’s reaction is the most favorable to the leader. In addition to the above solutions, considering the probabilities of the follower’s decision being in favor or against the interests of the leader, a mean optimal decision and a moderate solution have been defined by Nie [25] and Alves [17] for providing the highest expected value of the leader to hedge against preference uncertainty.

For the second category of definitions, the pessimistic solution is the most typical solution on which the cooperation space between the leader and the follower(s) could be reasonably specified [26]. The pessimistic problem may have no solution [24] and, in most cases, lacks lower semi-continuity [27] and is hard to solve [28]. This problem thus inspired great endeavors in researching the existence of optimal solutions and the stability of the optimal condition. Loridan and Morgan discussed the existence of solutions in their research [29,30] and contributions followed by other researchers to generate a stable and unique solution to the pessimistic bilevel problems [8,27,28,31,32,33]. Furthermore, to improve the feasibility and existence of an optimal solution, Shi [34] proposed a refined optimal solution definition by shifting the upper-level constraints involving the upper and lower level variables into the lower level. Marsha and Dempe [35] believe that the ideas based on shifting constraints between upper and lower-level problems violate the modeling procedure. Audet [36] further argues that this does not solve a wider class of problems, but rather relaxes the feasible region, allowing for infeasible points to be considered feasible. Mejia-de-Dios [18] recently defined and proved the existence of pseudo-feasible solutions in bilevel optimization to warn about the effect and issues related to misleading results in evolutionary bilevel optimization.

In summary, the pessimistic solution provides a valuable framework for hierarchical decision-making problems, but its practical application requires a deeper understanding of the follower’s behaviors. Less emphasis has been paid to the selection of the leader’s decision considering the non-antagonistic nature of the follower’s behaviors, particularly the traditional pessimistic solution’s definition results in an overestimated potential of cooperation space between the leader and the followers. Therefore, the novelty of the present study is to extend the concept of a pessimistic solution and to provide a more realistic assessment of the potential for cooperation in non-antagonistic circumstances.

3. The Non-Antagonistic Pessimistic Solution

We consider the following bilevel programming problem, a nested optimization problem with a hierarchical structure. It consists of two layers of optimization problems with independent objective functions and constraints, where the upper-level optimality relies on the optimal solution of the lower level. For both the upper and lower decision makers, striving for optimality cannot avoid being influenced by the other side’s decision.

$$\begin{array}{l}\underset{x}{\min }F(x,y)\\ s.t.\left\{\begin{array}{l}G(x,y)\le 0\\ \underset{y}{\min }f(x,y)\\ s.t.\hspace{0.17em}g(x,y)\le 0\end{array}\right.\end{array},$$

(1)

where $F:{\mathbb{R}}^m\times {\mathbb{R}}^n\to \mathbb{R}$ is the upper-level objective function, and $f:{\mathbb{R}}^m\times {\mathbb{R}}^n\to \mathbb{R}$ is the lower-level objective function. $\mathrm{x}\in \mathrm{X}\subset {\mathbb{R}}^m,$ $y\in Y\subset {\mathbb{R}}^n$ are the upper and lower level decision variables, where X = $\left\{x|x\in {\mathbb{R}}^m,G\left(x,y\right)\le 0\right\}$ and Y = $\left\{y|y\in {\mathbb{R}}^n,g\left(x,y\right)\le 0\right\}$ denote the upper and lower level decision space, and $G(x,y)\le 0$ and $g(x,y)\le 0$ represent the upper and lower constraints.

Some fundamental definitions and further descriptions are introduced as follows:

(a)

S is defined as the bilevel constraint region where the constraints of the upper and lower level are both satisfied:

$$S=\left\{(x,y)\right.\hspace{0.17em}\left|\hspace{0.17em}G(x,y)\right.\le 0,\left.\hspace{0.17em}g(x,y)\le 0\right\};$$

(2)

(b)

For each $\mathrm{x}\in \mathrm{X}$, the optimal solution set of the lower-level problem is defined as M(x). It is also referred to as the rational reaction set of the lower-level problem:

$$M(x)=\hspace{0.17em}\arg \underset{y}{\min }\left\{f(x,y)\hspace{0.17em}\left|\hspace{0.17em}g(x,y)\le 0\right.\right\};$$

(3)

(c)

The inducible region includes all points concerning $\mathrm{x}\in S(\mathrm{X})$ that are bi-level feasible and lead to the lower-level optimal:

$$IR=\left\{(x,y)\right.\hspace{0.17em}\left|\hspace{0.17em}(x,y)\right.\in S,\hspace{0.17em}y\in \left.M(x)\right\}.$$

(4)

If the follower’s reaction set $M\left(x\right)$ contains only one element, there would be only one optimal solution to the lower-level problem. When $M\left(x\right)$ is a set-valued mapping, the optimal solution to the lower problem is not unique. It is the type of IBPP we are discussing in this article where the existence of multiple optimal solutions might lead to an inappropriate formulation of the bilevel problem [10]. For the upper level, there is ambiguity about which lower-level optimal solution should be used in the presence of multiple lower-level optimal solutions according to this definition, in which the four extreme solutions developed are optimistic, pessimistic, deceptive, and rewarding solutions.

Definition 1. 

A pair of $(x_{opt},y_{opt})\in IR$ is the optimistic solution to the following optimistic bilevel problem (5). $F_{opt}=F(x_{opt},y_{opt})$, $f_{opt}=f(x_{opt},y_{opt})$.

$$\underset{x\in X}{\min }\underset{y\in M(x)}{\inf }F(x,y).$$

(5)

Problem (5) is the optimistic formulation of IBPP. The leader assumes that a most cooperative follower will always choose the solution from the reaction set that leads to the leader’s ideal outcome.

Definition 2. 

A pair of $(x_{pes},y_{pes})\in IR$ is called the pessimistic solution to the following pessimistic bilevel problem (6). $F_{pes}=F(x_{pes},y_{pes})$, $f_{pes}=f(x_{pes},y_{pes})$.

$$\underset{x\in X}{\min }\underset{y\in M(x)}{\sup }F(x,y).$$

(6)

Problem (6) is the pessimistic formulation of the IBPP, also known as the weak Stackelberg problem, in which the leader assumes that a most uncooperative follower will always choose a solution from the reaction set that leads to the leader’s “best-guaranteed result” [13].

Definition 3 

([17]). The rewarding solution $(x_{rew},y_{rew})$ is obtained when the leader makes a pessimistic decision ${x_{rew}=x}_{pes}$, while the follower’s reaction is most favorable to the leader, i.e., $(x_{rew},y_{rew})=(x_{pes},y_{rew})$, where $y_{rew}\in arg\underset{y}{min}\left\{F\left(x_{pes},y\right)\left|y\in M\left(x_{pes}\right)\right.\right\}$. $F_{rew}=F(x_{rew},y_{rew})$, $f_{rew}=f(x_{rew},y_{rew})$.

Definition 4 

([17]). The deceiving solution is obtained when the leader makes the optimistic decision ${x_{dec}=x}_{opt}$, but the follower’s reaction is the least favorable to the leader, i.e., $(x_{dec},y_{dec})=(x_{opt},y_{dec})$, where $y_{dec}\in arg\underset{y}{max}\left\{F(x_{opt},y)\left|y\in M\left(x_{opt}\right)\right.\right\}$. $F_{dec}=F{(x}_{dec},y_{dec})$, $f_{dec}=f(x_{dec},y_{dec})$.

In practice, the assumption of pessimistic problems that the follower always chooses a solution that yields the worst upper-level objective value under all decision circumstances is not realistic. Therefore, we propose the following concept of a non-antagonistic pessimistic solution.

Assumption 1. 

The set S is nonempty and compact, and $F(x,y)$, $f(x,y)$ are continuous on S.

Assumption 2. 

The optimal solution set of the lower-level problem $M\left(x\right)$ is nonempty and compact and is assumed to be the point-to-set mapping and lower semi-continuous with  $x\in X$.

Theorem 1 

([8]). Under Assumption 2, a global pessimistic optimal solution exists if the pessimistic formulation (6) has a feasible solution.

Definition 5. 

With Assumptions 1 and 2, the non-antagonistic pessimistic bilevel problem is expressed below. A pair of $(x_{nap},y_{nap})$ is called a non-antagonistic pessimistic solution to the following problem (7). $F_{nap}=F(x_{nap},y_{nap})$, $f_{nap}=f(x_{nap},y_{nap})$.

$$\begin{array}{l}\underset{x\in X}{\min }\underset{y\in M(x)}{\inf }F(x,y)\\ s.t.\hspace{0.17em}f(x,y)=f_{pes}\end{array}.$$

(7)

By making the lower-level objective equal to the value $f_{pes}$ of the lower level of the pessimistic model and by adding this as a constraint to optimize the upper-level goal, the leader allows the follower to achieve a specific goal within the nested optimization scheme. However, under this definition, the leader does not cede decision-making power to the followers but proactively relinquishes some interests to gain overall control.

Definition 6. 

$S_d$ is defined as the bilevel constraint region of the problem (7):

$$S_d=\left\{(x,y)\right.\left|G(x,y)\right.\le 0,\left.\hspace{0.17em}g(x,y)\le 0,\hspace{0.17em}f(x,y)=f_{pes}\right\}.$$

(8)

It is clear that $S_d\subseteq S$. For $x\in S_d$, the inducible region to problem (7) is defined as ${IR}_d$:

$$I{R}_d=\left\{(x,y)\right.\left|(x,y)\right.\in S_d,y\in \left.M(x)\right\}.$$

(9)

Therefore, the new problem could also be expressed as:

$$\underset{x\in S_d}{\min }\underset{y\in M(x)}{\inf }F(x,y).$$

(10)

The non-antagonistic pessimistic solution has the following properties:

Theorem 2. 

The objective function value of the non-antagonistic pessimistic solution $(F_{nap},f_{nap})$ dominates or is equal to the objective function value of the global pessimistic optimal solution $(F_{pes},f_{pes})$.

Proof of Theorem 2. 

According to the definition of the non-antagonistic pessimistic solution,

$$\begin{array}{cc}\hfill F(x_{nap},y_{nap})=& \underset{x\in S_d}{\min }\underset{y\in M(x)}{\inf }F(x,y)\hfill \\ & \le \underset{x\in S_d}{\min }\underset{y\in M(x)}{\sup }F(x,y).\hfill \\ & \le \underset{x\in X}{\min }\underset{y\in M(x)}{\sup }F(x,y)\hfill \end{array}$$

(11)

According to the definition of the pessimistic solution,

$$F(x_{pes},y_{pes})=\underset{x\in X}{\min }\underset{y\in M(x)}{\sup }F(x,y).$$

(12)

Thus, $F(x_{nap},y_{nap})\le F(x_{pes},y_{pes})$ can be proved, while by definition, $f(x_{nap},y_{nap})=f_{pes}$. Therefore, $(F_{nap},f_{nap})\succcurlyeq (F_{pes},f_{pes})$ can be proved. □

Theorem 3. 

The objective function value of the non-antagonistic pessimistic solution $(F_{nap},f_{nap})$ dominates or is equal to the objective function value of the rewarding solution $(F_{rew},f_{rew})$.

Proof of Theorem 3. 

With $f(x_{rew},y_{rew})=f_{pes}$ and $f(x_{nap},y_{nap})=f_{pes}$, $f(x_{rew},y_{rew})=f(x_{nap},y_{nap})$ can be derived. In addition, according to the definition of $S_d$, $x_{pes}\in S_d$ can be held. Then, we can prove that:

$$\begin{array}{cc}\hfill F(x_{nap},y_{nap})=& \underset{x\in S_d}{\min }\underset{y\in M(x)}{\inf }F(x,y)\hfill \\ & \le \underset{x\in S_d}{\min }\underset{y\in M(x)}{\inf }F(x_{pes},y)\hfill \\ & =\underset{y\in M(x_{pes})}{\inf }F(x_{pes},y)\hfill \\ & \le \underset{y\in M(x_{pes})}{\min }F(x_{pes},y)\hfill \end{array}.$$

(13)

According to the definition of the rewarding solution,

$$F(x_{rew},y_{rew})=\underset{y\in M(x_{pes})}{\min }F(x_{pes},y).$$

(14)

Therefore, $F(x_{nap},y_{nap})\le F(x_{rew},y_{rew})$, $(F_{nap},f_{nap})\succcurlyeq (F_{rew},f_{rew})$ can be proved. □

Definition 7. 

We define the maximum potential space for the leader to cooperate with the follower as ${PS}_{max}$:

$$P{S}_{\max }=\left|F_{pes}-F_{opt}\right|,$$

(15)

while the maximum potential space for the leader to cooperate with the follower in a non-antagonistic situation as ${PS}_{nap\text{-}max}$:

$$P{S}_{nap\text{-}\max }=\left|F_{nap}-F_{opt}\right|.$$

(16)

Supported by Theorem 2, the maximum potential space for leader–follower cooperation in the non-antagonistic situation ${PS}_{nap\text{-}max}$ is less than or equal to that in the antagonistic position assumed in the pessimistic solution ${PS}_{max}$.

Additionally, we prove that the rewarding solution has the following property:

Theorem 4. 

The objective function value of the rewarding solution $(F_{rew},f_{rew})$ dominates or equals the objective function value of the global pessimistic optimal solution $(F_{pes},f_{pes})$.

Proof of Theorem 4. 

According to the definition of reaction set mapping, ${x_{rew}=x}_{pes}$, $y_{rew}\in M(x_{pes})$, $f(x_{rew},y_{rew})=f(x_{pes},y_{pes})$ can be held. In addition,

$$\begin{array}{cc}\hfill F(x_{rew},y_{rew})=& \underset{y\in M(x_{pes})}{\min }F(x_{pes},y)\hfill \\ & \le \underset{y\in M(x_{pes})}{\sup }F(x_{pes},y)\hfill \\ & =F(x_{pes},y_{pes})\hfill \end{array}.$$

(17)

Therefore, $F(x_{rew},y_{rew})\succcurlyeq F(x_{pes},y_{pes})$ can be proved. □

4. Numerical Examples

In this section, we illustrate the solution properties of the non-antagonistic pessimistic solution using the four numerical examples. The results of optimistic, pessimistic, rewarding, and deceiving solutions are also listed below. First, we consider the following problem:

Example 1. 

$$\begin{array}{l}\underset{x}{\min }F(x,y)=x^2+y_1{}^2\\ s.t.\left\{\begin{array}{l}0\le x\le 4\\ \underset{y}{\min }f(x,y)=-(x^2+y_1+y_2).\\ s.t.\hspace{0.17em}x+y_1+y_2\le 4\\ \hspace{1em}{y}_1,y_2\ge 0\end{array}\right.\end{array}$$

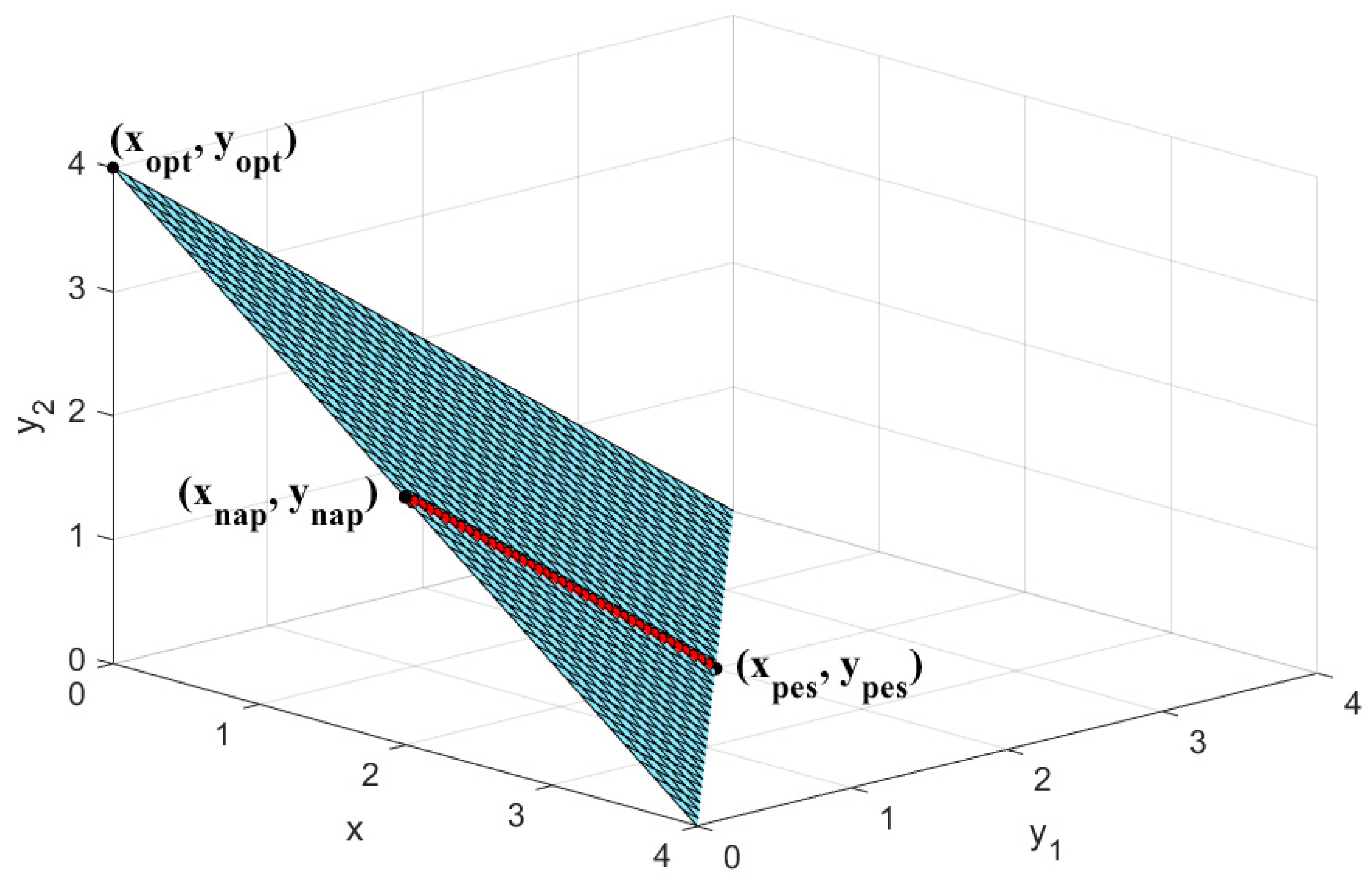
(18)

For $0\le x\le 4$ , the rational reaction set is expressed as below:

$$M(x)=\left\{(y_1,y_2)\left|{\displaystyle \sum _{i=1}^2{y}_i}\right.=4-x\right\}.$$

(19)

As presented in Figure 1, there exist multiple optimal solutions when adding the constraint $f_{pes}=-6$. All highlighted points represent ${IR}_d$, which have the same lower-level objective value equal to $f_{pes}$ but different upper-level objective values. Figure 2 describes the upper-level objective values of the optimistic, pessimistic and non-antagonistic solutions in ${IR}_d$. Although $F_{opt}=0$ and $F_{pes}=8$ can be useful in providing the lower and upper best-guaranteed result of the upper-level objective value, $F_{nap}=4$ has a better upper-level objective value compared to $F_{pes}$. ${PS}_{max}$ describes the potential for improvement of the upper-level objective value for the follower to transform their non-cooperative behavior into cooperative behavior. ${PS}_{nap\text{-}max}$ describes the potential improvement in the upper-level objective value for the follower to transform their limited antagonistic behavior into cooperative behavior. In this example, ${PS}_{max}=8$, ${PS}_{nap\text{-}max}=4$, ${PS}_{nap\text{-}max}<{PS}_{max}$ indicates that the traditional pessimistic solution overestimates the leader’s loss due to the follower’s non-antagonistic behavior, because when the followers reach the optimum, they are more likely to choose the non-antagonistic solution, which is reciprocal to the leader versus the pessimistic solution.

Table 1. The solutions and optimal values of Example 1.

Example 1	F	f	x	y1	y2
Optimistic solution	0	−4	0	0	4
Pessimistic solution	8	−6	2	2	0
Rewarding solution	4	−6	2	0	2
Deceiving solution	16	−4	0	4	0
Non-antagonistic pessimistic solution	4	−6	2	0	2

lists the five types of solutions of Example 1. In this example, $\left(F_{nap},f_{nap}\right)$ is not inferior to $\left(F_{opt},f_{opt}\right)$. It can also be interpreted that if a fully cooperative follower cannot be observed, the non-antagonistic solution would be the expected result of the leader’s practical goal. Furthermore, $\left(F_{rew},f_{rew}\right)$ has the same value as $\left(F_{nap},f_{nap}\right)$ due to $x_{rew}=x_{nap}$, while $(F_{dec},f_{dec})$ is dominated by the rest of the optimal solutions. More discussion about this will be included in the following example.

Example 2. 

$$\begin{array}{l}\underset{x}{\min }F(x,y)=x_1{}^2+x_2{}^2+y_1{}^2+y_2{}^2\\ s.t.\left\{\begin{array}{l}0\le x_1,x_2\le 4\\ \underset{y}{\min }f(x,y)=-(x_1{}^2+x_2{}^2+y_1+y_2+y_3).\\ s.t.\hspace{0.17em}{x}_1+x_2+y_1+y_2+y_3\le 4\\ \hspace{1em}{y}_1,y_2,y_3\ge 0\end{array}\right.\end{array}$$

(20)

For $0\le x_1,x_2\le 4$ , the rational reaction set is expressed as below:

$$M(x)=\left\{(y_1,y_2,y_3)\left|{\displaystyle \sum _{i=1}^3{y}_i}\right.=4-{\displaystyle \sum _{i=1}^2{x}_i}\right\}.$$

(21)

Table 2. The solutions and optimal values of Example 2.

Example 2	F	f	x1	x2	y1	y2	y3
Optimistic solution	0	−4	0	0	0	0	4
Pessimistic solution	5.333	−4.889	1.333	1.333	0	1.333	0
Rewarding solution	3.556	−4.889	1.333	1.333	0	0	1.333
Deceiving solution	16	−4	0	0	4	0	0
Non-antagonistic pessimistic solution	2.456	−4.889	1.567	0	0	0	2.433

lists the five types of solutions for Example 2. Same as in Example 1, $\left(F_{nap},f_{nap}\right)$ is not inferior to $\left(F_{opt},f_{opt}\right)$ and dominates $(F_{pes},f_{pes})$ , ${PS}_{nap\text{-}max}=2.456<{PS}_{max}=5.333$. However, $\left(F_{nap},f_{nap}\right)$ dominates $(F_{rew},f_{rew})$  with a better upper-level value in this example. This is because the rewarding solution fixes the decision of $x_{pes}$ to optimize the upper objective while the non-antagonistic solution does not constrain the given upper-level variable but to the solution space ${IR}_d$ , thus resulting in a larger scope for the leader’s decisions and greater possibilities of a better result.

In addition, $(F_{dec},f_{dec})$ is dominated by the objective function value of the remaining solutions. In practice, the follower is often not allowed to choose solutions that are fully opposed to the leader, which brings in the loss of both parties. Therefore, a deceiving solution indicates the loss of leadership for the leader and can never be an option in hierarchical management.

Example 3. 

$$\begin{array}{l}\underset{x}{\min }F(x,y)=x^2+y^2\\ s.t.\left\{\begin{array}{l}-1\le x\le 1\\ \underset{y}{\min }f(x,y)=xy\\ s.t.\hspace{0.17em}-1\le y\le 1\end{array}\right.\end{array}.$$

(22)

The reaction set of the problem (22) is expressed below:

$$M(x)=\left\{\begin{array}{l}1,\hspace{0.17em}-1\le x<0\\ [-1,1],\hspace{0.17em}x=0\\ -1,\hspace{0.17em}0<x\le 1\end{array}\right..$$

(23)

In

Table 3. The solutions and optimal values of Example 3.

Example 3	F	f	x	y
Optimistic solution	0	0	0	0
Pessimistic solution	1	0	0	−1 or 1
Rewarding solution	0	0	0	0
Deceiving solution	1	0	0	−1 or 1
Non-antagonistic pessimistic solution	0	0	0	0

, $\left(F_{nap},f_{nap}\right)$ and $\left(F_{opt},f_{opt}\right)$ are the same as $\left(F_{rew},f_{rew}\right)$ and dominate $(F_{pes},f_{pes})$. because $M(x_{nap})=M(x_{opt})=M(x_{rew})=M\left(0\right)$ and the non-antagonistic pessimistic, optimistic, and rewarding solutions have the same optimal upper-level objective value at $x=0$. In addition, $(F_{dec},f_{dec})$ is the same as $(F_{pes},f_{pes})$ in this example due to $M(x_{dec})=M(x_{pes})=M(0)$ and $\underset{y\in M\left(0\right)}{max}F(0,y)=\underset{y\in M\left(0\right)}{sup}F(0,y)=1$. However, $x_{dec}$ and $x_{pes}$ being the same is not often the case. Similarly, ${PS}_{nap\text{-}max}=0<{PS}_{max}=1$. When ${PS}_{nap\text{-}max}=0$, there is no potential space for the follower to cooperate with the leader. Therefore, the leader will not accept the pessimistic and deceiving solution.

Example 4 

([24]).

$$\begin{array}{l}\underset{x}{\min }F(x,y)=1/2(1-x)+xy\\ s.t.\hspace{0.17em}\left\{\begin{array}{l}0\le x\le 1\\ \underset{y}{\min }f(x,y)=(x-1)y\\ s.t.\hspace{0.17em}0\le y\le 1\end{array}\right.\end{array}.$$

(24)

The reaction set of problem (24) is expressed below:

$$M(x)=\left\{\begin{array}{l}1,\hspace{0.17em}0\le x<1\\ \left[0,1\right],\hspace{0.17em}x=1\end{array}\right..$$

(25)

As shown in

Table 4. The solutions and optimal values of Example 4.

Example 4	F	f	x	y
Optimistic solution	0	0	1	0
Pessimistic solution	0.5	−1	0	1
Rewarding solution	0.5	−1	0	1
Deceiving solution	1	0	1	1
Non-antagonistic pessimistic solution	0.5	−1	0	1

, $\left(F_{nap},f_{nap}\right)$ is not inferior to $\left(F_{opt},f_{opt}\right)$. However, the $\left(F_{nap},f_{nap}\right)$, $(F_{pes},f_{pes})$ and $\left(F_{rew},f_{rew}\right)$ in this example are the same due to $x_{nap}=x_{pes}=x_{rew}=0$, and $M\left(0\right)$ is a single point set. $F_{nap}=F_{pes}$ results in ${PS}_{nap\text{-}max}={PS}_{max}=0.5$. The leader’s practical expectation for the objective value should be $F_{nap}=$ 0.5 instead of $F_{opt}=$ 0, considering the non-antagonistic behavior of the follower.

From the above results: (1) if $x_{rew}=x_{nap}$, the rewarding solution and the non-antagonistic pessimistic solution are the same; (2) if $f_{nap}=f_{opt}$, the non-antagonistic pessimistic solution and the optimistic optimal solution share the same values; (3) if $x_{pes}=x_{nap}$ and $M\left(x_{pes}\right)=M\left(x_{nap}\right)$, the pessimistic solution and the non-antagonistic pessimistic solution are identical.

5. Discussion

Compared to the pessimistic solution, the non-antagonistic pessimistic solution obtains better upper-level objective values in three examples, except that the special case of Example 4 has the same upper value. It implies that the traditional pessimistic solution overestimates the leader’s loss due to the follower’s non-antagonistic behavior. For instance, in Example 1, ${PS}_{nap\text{-}max}=4,{PS}_{max}=8$. In the pessimistic assumption, the potential improvement of the leader’s goal when the follower cooperates with the leader is doubled. Similar to Example 1, the cooperation potential between the leader and follower is 1.17 times overestimated in Example 2.

Furthermore, compared to the rewarding solution, the non-antagonistic pessimistic solution can achieve a better upper-level objective value in Example 2 while being equal to the rewarding solution in the rest of the examples. In Example 2, $F_{nap}=2.456,$ $F_{rew}=3.556$ and $f_{nap}=f_{rew}=$ −4.889. By constraining the solution space ${IR}_d$ instead of the given upper-level variable $(1.333,1.333)$, it searches from a larger scope for the leader’s decisions and improves the optimization result with the upper-level decision $(1.567,0)$. This indicates that the non-antagonistic pessimistic solution is not one of the extreme solutions, like the rewarding solution.

In addition, the non-antagonistic pessimistic solution is non-inferior to the optimistic solution in Examples 1, 2, and 4 and is identical to the optimistic solution in Example 3. For instance, in Example 4, the $(F_{nap},f_{nap})=(0.5,-1)$ and the $(F_{opt},f_{opt})=(0,0)$. It also indicates that the non-antagonistic solution would be the best guaranteed result of the leader’s goal when the most obedient or rebellious follower cannot be expected in practice.

In general, the non-antagonistic pessimistic solution can be a better solution than the pessimistic and rewarding solution in terms of the upper-level objective value, while the deceiving solution can never become a good option considering the non-antagonistic decision-making process, for it overlooks the dominant position of the leader. We can also conclude that if a certain profit for the follower can be guaranteed, the leader may have the potential to adjust the strategy to receive cooperative feedback from the follower and achieve an overall optimized result versus an extremely pessimistic one. Moreover, this development of a non-antagonistic pessimistic solution definition corresponds to the behavioral characterization of the decisionmakers in realistic hierarchical management. Compared to the traditional optimistic and pessimistic solution, it can be more applicable to approach the optimal solutions in practice.

However, solving the non-antagonistic pessimistic solution relies on the pessimistic solution, which can be difficult to approximate for some complex engineering problems without continuous objectives and compact solution space. This will not be discussed here.

6. Conclusions

This paper proposes a new IBPP pessimistic solution concept that differs from the previous pessimistic solution with radical and non-practical assumptions. The non-antagonistic pessimistic solution does not aim to seek extreme solutions where the follower unconditionally complies with or goes against the leader. Instead, it provides a practical, management-oriented solution scope for decision making. It also validates the existence of a rational option for the leader to strive for maximum collaboration within a non-cooperative and non-antagonistic bilevel optimization scheme. Compared to the pessimistic optimal solutions, the non-antagonistic pessimistic solution could represent a more realistic loss of the leader, marred by uncertain follower feedback in the non-antagonistic bilevel games. In fairness to the non-antagonistic pessimistic solution, it was never intended as a surrogate definition for IBPP solutions but simply as a necessary definition under non-antagonistic bilevel games to avoid over/underestimating the largest potential space for the leader to cooperate with the follower.

A more nuanced understanding and description of the follower’s position is helpful to practically identify the worst-case scenario and to better understand the cooperation potential between the leader and follower. Future research could explore new solution definitions that arise from decision uncertainty considering followers’ preferences and non-preference-related factors. Future research could also develop new theories and methods that consider the possible positions that lower-level decisionmakers can take in hierarchical management scenarios. On the other hand, further investigation of the potential for stakeholder cooperation in practical situations is needed. For instance, during flood seasons, examining the potential for collaboration between the control bureau and the power plant manager can help provide insight into the gap between research studies and systematical applications in practice. However, approximating the non-antagonistic pessimistic solution requires a strong constraint, which can result in large computational efforts in practical management problems. Therefore, efficient algorithms are also expected to be developed in the future.