Ultimately Exponentially Bounded Estimates for a Class of Nonlinear Discrete−Time Stochastic Systems
Abstract
:1. Introduction
2. Model Description
- (1)
- (2)
- (3)
3. Main Results
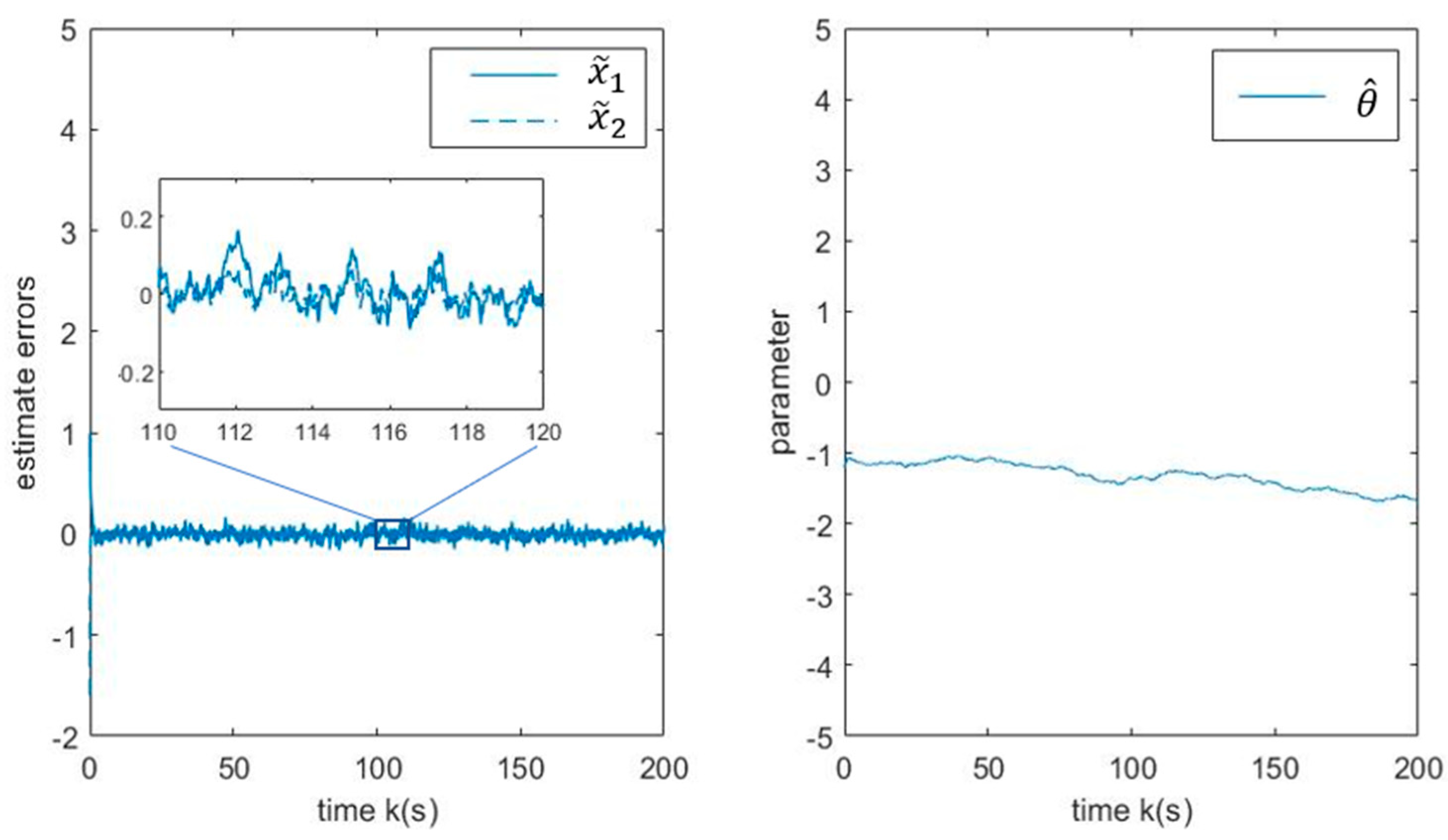
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, K.; Jiang, B. Adaptive observer−based fast fault estimation. Int. J. Control Autom. Syst. 2008, 6, 320–326. [Google Scholar]
- Yan, X.G.; Edwards, C. Fault estimation for single output nonlinear systems using an adaptive aliding mode estimator. IET Control Theory Appl. 2008, 2, 841–850. [Google Scholar] [CrossRef]
- Farza, M.; M’Saad, M.; Maatoug, T.; Kamoun, M. Adaptive observers for nonlinearly parameterized class of nonlinear systems. Automatica 2009, 45, 2292–2299. [Google Scholar] [CrossRef]
- Deng, H.; Krsti´c, M. Output−feedback stabilization of stochastic nonlinear systems driven by noise of unknown covariance. Syst. Control Lett. 2000, 39, 173–182. [Google Scholar] [CrossRef]
- Miao, X.; Li, L. Adaptive observer−based control for a class of nonlinear stochastic systems. Int. J. Comput. Math. 2015, 92, 2251–2260. [Google Scholar] [CrossRef]
- Haddad, W.M.; Lee, J. Lyapunov theorems for stability and semistability of discrete−time stochastic systems. Automatica 2022, 142, 110393. [Google Scholar] [CrossRef]
- Zong, X.; Lei, D.; Wu, F. Discrete Razumikhin−type stability theorems for stochastic discrete−time delay systems. J. Frankl. Inst. 2018, 355, 8245–8265. [Google Scholar] [CrossRef]
- Alaviani, S.S. Stability of Deterministic and Stochastic Nonlinear Discrete−Time Systems by Means of Fixed Point Theory. In Proceedings of the American Control Conference, Philadelphia, PA, USA, 10–12 July 2019; pp. 3051–3056. [Google Scholar]
- Jiang, X.; Tian, S.; Zhang, T.; Zhang, W. Stability and stabilization of nonlinear discrete-time stochastic systems. Int. J. Robust Nonlinear Control 2019, 29, 6419–6437. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, B.P.; Hu, W.S. Security tracking control for discrete−time stochastic systems subject to cyberattacks. ISA Trans. 2022, 127, 133–145. [Google Scholar] [CrossRef] [PubMed]
- Huang, F.; Li, J. Exponential Ultimate Boundedness and Stability of Impulsive Stochastic Functional Differential Equations. Int. J. Control 2021. [Google Scholar] [CrossRef]
- Zhang, T.L.; Deng, F.Q.; Zhang, W.H. Robust H−infinity filtering for nonlinear discrete−time stochastic systems. Automatica 2021, 123, 109343. [Google Scholar] [CrossRef]
- Song, T.; Liu, B. First−order and second−order necessary optimality conditions for discrete−time stochastic systems with delay. IMA J. Math. Control Inf. 2022, 39, 731–750. [Google Scholar] [CrossRef]
- Lui, D.G.; Petrillo, A.; Santini, S. Exponential bipartite tracking consensus in cooperative−antagonistic nonlinear Multi−Agent Systems with multiple communication time−varying delays. IFAC J. Syst. Control 2022, 22, 100209. [Google Scholar] [CrossRef]
- Song, Y.; He, L.; Wang, Y. Globally Exponentially Stable Tracking Control of Self−Restructuring Nonlinear Systems. IEEE Trans. Cybern. 2019, 51, 4755–4765. [Google Scholar] [CrossRef] [PubMed]
- Agniel, R.G.; Jury, E.I. Almost Sure Boundedness of Randomly Sampled Systems. SIAM J. Control 1971, 9, 372–384. [Google Scholar] [CrossRef]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; SIAM (Studies in Applied Mathematics): Philadelphia, PA, USA, 1994. [Google Scholar]
- Yi, K.; Hedrick, K. Observer−Based Identification of Nonlinear System Parameters. J. Dyn. Syst. Meas. Control 1995, 117, 175–182. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, X.; Xu, Y.; Yao, F. Ultimately Exponentially Bounded Estimates for a Class of Nonlinear Discrete−Time Stochastic Systems. Mathematics 2023, 11, 973. https://doi.org/10.3390/math11040973
Miao X, Xu Y, Yao F. Ultimately Exponentially Bounded Estimates for a Class of Nonlinear Discrete−Time Stochastic Systems. Mathematics. 2023; 11(4):973. https://doi.org/10.3390/math11040973
Chicago/Turabian StyleMiao, Xiufeng, Yaoqun Xu, and Fengge Yao. 2023. "Ultimately Exponentially Bounded Estimates for a Class of Nonlinear Discrete−Time Stochastic Systems" Mathematics 11, no. 4: 973. https://doi.org/10.3390/math11040973
APA StyleMiao, X., Xu, Y., & Yao, F. (2023). Ultimately Exponentially Bounded Estimates for a Class of Nonlinear Discrete−Time Stochastic Systems. Mathematics, 11(4), 973. https://doi.org/10.3390/math11040973





