Abstract
Finite Set Model Predictive Control (FS-MPC) is a widely used technique in power electronic converter applications. One challenge in FS-MPC implementation is selecting appropriate weighting factors, as there is currently no established methodology for finding the best values. An alternative approach is to consider cost functions without weighting factors, as used by the Sequential Model Predictive Control (SMPC). In this paper, the performance of SMPC applied to induction motors is analyzed. The SMPC strategy involves sequentially evaluating simple cost functions by considering a limited number of available switching states for the power electronic converter. This number is the control parameter of the SMPC. The parameter’s domains and a selection criteria based on THD were established in this investigation. The power converter topologies studied include the Voltage Source Inverter (VSI) and the Neutral Point Clamped three-level (3L-NPC). Simulations performed in PLECS software and Hardware-in-the-Loop (HIL) tests using an RT Box for valid parameters satisfy the characteristics of the classical predictive control, such as good control variables tracking and high dynamic response. For a VSI converter, increasing the control parameter results in reduced harmonic distortion, while for an NPC converter, optimal results are achieved with control parameter values within a specific range.
MSC:
93C10
1. Introduction
Finite Set Model Predictive Control (FS-MPC) is a technique widely used in power electronic converters for electrical energy flow control [1]. The main advantages of this control law are its simple structure and good dynamic response [2]. The fundamental principle of FS-MPC is to select the switching state of the power converter that minimizes the future error of the controlled variable [3]. In its implementation, a cost function is evaluated, which considers several terms depending on the controlled and operating variables. In order to relate these terms, weighting factors must be defined according to the desired performance features [4]. One of the challenges in FS-MPC is finding the right weighting factors to balance the control objectives [5,6]. Currently, the most common approach to do this is through simulation, where different combinations of weighting factors are tested to see their effect. While this method can be effective, it can be time-consuming and does not always guarantee that the optimal weighting factors will be found [7].
Motor drive is an application of growing interest, partly motivated by the development of electromobility. The induction motor (IM), specifically the squirrel cage type, is known for its robustness, reliability, and low cost [8].
In classical model predictive control applied to electrical machines, the electromagnetic torque and stator flux are typically included in the cost function [9]. These two variables are related through a weighting factor, which is typically obtained through an empirical process that requires significant effort.
A different perspective is to consider cost functions without weighting factors. An alternative presented in the literature to implement a predictive control of an IM without weighting factors is to evaluate cost functions for each control objective sequentially, based on priority. A generalized description of this strategy is presented in [10]. This variant of the classical MPC has been referred to as the Sequential Model Predictive Control [10,11] or the Cascade Model Predictive Control [12]. In this paper, the expression Sequential Model Predictive Control (SMPC) will be used. The SMPC algorithm produces a vector that contains implicit information about the switching states of the power converter that supplies the IM. Like classical predictive control, the switching state is applied in the next sampling period in order to minimize the predicted error in the control variables [13]. While SMPC does not require weighting factors, it does require a control parameter to be implemented. This control parameter is the number of switching states that are used to evaluate each cost function. In [11], two separate cost functions for torque and flux are considered. The two states that best minimize the torque cost function are selected to later evaluate the flux cost function. Finally, the state that minimizes the flux function is applied to the converter in the following sampling period. It is common in SMPC to evaluate torque first and then the flux cost function in order to achieve stable operation over the full speed range [14]. The sequential strategy presented in [11] is straightforward, but it does not specify how many states should be selected to evaluate the second cost function. While SMPC does offer a good trade-off between control objectives and good performance, the selection of the number of states to be evaluated is a significant issue [15]. This number is a necessary parameter of the SMPC strategy and must be carefully chosen to achieve good performance.
There are several variations of the SMPC algorithm that have been proposed in the literature for the case of two cost functions (torque and flux). For example, the Generalized SMPC (G-SMPC) offers good performance regardless of the order in which the cost functions are evaluated [16]. It can be inferred that the order in which the cost functions are evaluated sets a priority among the control objectives, with the first cost function being the most important and the second having the lowest priority. Previous strategies have a fixed priority, but there is also a strategy called the Even Handed SMPC (EH-SMPC) that does not have a fixed priority [17]. In EH-SMPC, all switching states are evaluated in both cost functions, and then a subset of states is selected to calculate the minimum cross-error, which not only determines the optimal state but also establishes the cost function with the highest priority. One limitation of the EH-SMPC strategy is its low adaptability due to the definition of the cross-error. In [18], a real-time reference value is used to update the error function, improving the controller’s adaptability to a variety of operating conditions. This strategy is referred to as the Enhanced EH-SMPC (EEH-SMPC).
Previous works have reported the use of a voltage source inverter (VSI) to supply the IM. These converters are suitable for low-power and low-voltage applications. However, when the power levels increase, multilevel voltage source converters (MVSCs) become the preferred solution [19]. Compared to two-level VSI converters, MVSCs can support higher voltages and have lower harmonic content in the output waveforms and lower losses [20,21]. Among the MVSCs, the Neutral Point Clamped (NPC) three-level converter is often used due to its simple structure and the benefits of the multilevel family. The 3L-NPC is a popular choice for high power medium voltage electrical motor drives [12]. SMPC applications in induction motors and 3L-NPC converters have been described in [12,22]. Implementing SMPC in 3L-NPC converters presents challenges due to multiple control objectives (torque, flux, and neutral point voltage) and a higher number of possible switching states, compared to VSI converters [14]. The complexity and difficulty in adjusting the controller also increase with the rise in motor drive power. To ease implementation and improve performance, various design criteria can be applied.
In the simplest case of SMPC applied to an induction motor (IM), there are two cost functions. In the first cost function, all possible states are evaluated, while in the second one, only a subset of states is evaluated. The number of states in this subset is the control parameter of the SMPC. The focus of this paper is to analyze the impact of this parameter on motor performance. The order of evaluation of the cost functions in this study is torque followed by flux. Both the VSI and 3L-NPC converters are considered. PLECS simulations in transient and steady-state are performed for different control parameters. Additionally, the simulation results have been validated through Hardware-in-the-Loop (HIL) testing using the RT Box tool. This paper provides important recommendations for the selection of the control parameter.
Although the case study presented in this research corresponds to energy conversion for motor drives, predictive control has been applied in a variety of applications such as grid-tied applications [23], wind turbine systems [24], and matrix converters [25]. In addition, sequential predictive control can provide new approaches in other applications where classical predictive control has been used. Therefore, obtaining mathematical models, tuning control parameters, and the possibility of applying the strategy in different areas are topics that can contribute to a variety of research. The main contributions of this paper are as follows:
- Study of the selection of the control parameter for the application of the SMPC strategy in electric motor control. The domain of the control parameter is established, and a selection criterion based on the THD is defined.
- The study addresses the VSI and 3L-NPC converters, which are common in low and medium-power motor drives. The objective is to highlight that as the power of the motor drive increases, the complexity of the converter increases, as well as the difficulty in adjusting the controller.
- The SMPC strategy is validated not only through simulation but also through HIL using two PLEXIM’s RT Boxes, one as a controller and the other one as a plant.
The structure of the paper is as follows: the methodological approach is outlined in Section 2, which primarily covers the mathematical modeling and the SMPC strategy description. Simulation and experimental results are presented in Section 3, while the discussion is included in Section 4. Finally, Section 5 presents the conclusions.
2. Methodological Approach
In this section, fundamental topics of the methodological structure are addressed, such as system modeling, prediction equations, and control strategy. Modeling is the first topic. It encompasses the mathematical representation of the physical system, including the converter and induction motor. Knowing the model is a prerequisite for applying predictive control, as it is necessary to obtain the prediction equations required by the SMPC strategy to evaluate cost functions and determine the best switching state for the converter according to control objectives.
The SMPC strategy methodology is based on the sequential evaluation of simple cost functions according to each control objective. In the case of two cost functions, all potential switching states are evaluated in the first cost function, while for the second cost function, only a determined number of them are evaluated. The selection of this number, known as the control parameter, is the main subject of study in this research.
A study of the performance of the SMPC for different values of the control parameter is presented in Section 3, both for the VSI converter and for the 3L-NPC.
2.1. Modeling
Figure 1 and Figure 2 show the typical power circuit used for motor drive applications. The main elements are the DC-bus, the power converter, and the electric motor. The converter shown in Figure 1 is the VSI, while the 3L-NPC converter is shown in Figure 2. The converter is the element that allows power transfer from the DC-bus to the electric motor according to a control law that is responsible for the motor operating under specific operation conditions. The control strategy proposed in this research is the SMPC, which requires the mathematical model of both the converter and the motor for its implementation. In this subsection, the power converters are described with a focus on the possible switching states, and the set of equations modeling the IM is included.
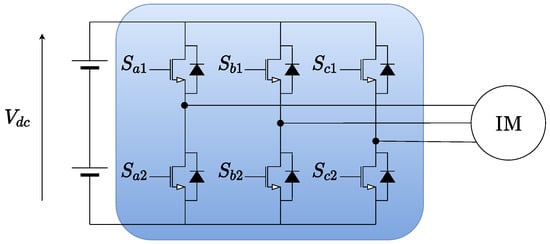
Figure 1.
Simplified circuit of VSI converter supplying an IM.
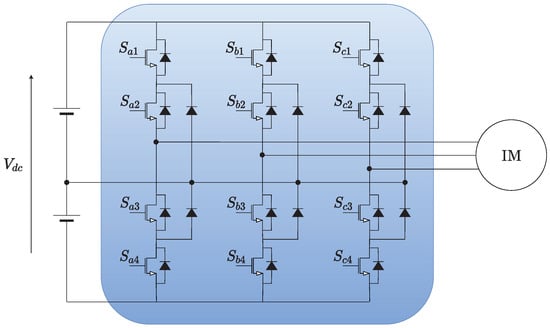
Figure 2.
Simplified circuit of 3L-NPC converter supplying an IM.
2.1.1. VSI Converter
The VSI is the power converter shown in Figure 1. VSI is the most commonly used converter in motor drive applications due to its simple structure and low number of switching devices. The main feature of this converter is the presence of three branches and two devices per branch, and each branch is connected to one of the motor phases. The upper power switch’s state of phase x is defined as , thus
where . P and N denote a phase connection with positive or negative DC-bus. Notice that . Now, VSI’s switching vector , where depicts a set of 8 elements which are the possible switching states.
For example, the second switching state (PNN) denotes that phase a of the motor is connected to the positive point of the DC-bus, while phases b and c are connected to the negative point. contains all the possible combinations that are obtained by ensuring connection of each of the motor phases to the positive or negative point.
2.1.2. 3L-NPC Converter
The 3L-NPC topology is shown in Figure 2. Compared to the VSI, the 3L-NPC converter is used in higher-power applications and can provide energy with lower harmonic content. However, it has a more complex circuit and a larger number of devices. Each of the branches that feeds the motor is composed of four switching devices and two diodes. In this power converter, the upper switches are and , and and are the lower power switches. The states of lower switches are defined in function of upper switches, thereby and . Then, for switches of the same branch,
P and N are the same definitions of VSI, and state O denotes connection with the middle point of the DC-bus. The 3L-NPC has 27 possible switching states.
contains all possible combinations obtained by connecting each of the motor phases to the positive, intermediate, or negative point of the DC-bus. For example, the second state (NNO) denotes that phases a and b of the motor are connected to the negative point, while phase c is connected to the middle point of the DC-bus. A detailed description of this converter can be found in [26].
2.1.3. Induction Motor
The most popular IM in industry is the squirrel-cage. Its main features are low cost and high reliability. The set of equations that model a squirrel-cage IM in a stator reference frame are [27]:
where , , and are the stator voltage, current, and flux respectively; and are the rotor current and flux; is the rotor angular frequency, p is the number of pole pairs, and T is the electromagnetic torque; and are the stator and rotor resistance, while , , and are the stator, rotor, and mutual inductance, respectively.
The equation to calculate the electromagnetic torque of the IM is,
where ⊗ denotes the cross product.
2.2. Prediction Equations
To assess the torque and flux cost functions, it is necessary to determine the predicted values of these variables for all potential switching states. The torque and stator flux are predicted according to discrete time equations of the IM. The flux prediction is obtained by the forward Euler discretization. Considering as sampling time, flux prediction equations are as follows:
The prediction equation of is obtained according to [28].
where is the rotor coupling factor, is the equivalent resistance referred to stator, is the transient time stator constant, is the leakage inductance, is the rotor time constant, and is the total leakage factor. The corresponding definitions are presented in Equations (13)–(18).
A torque prediction is given by:
Due to the delay caused by the sampling and calculation time of the control law, the optimal switching vector cannot be applied immediately. To compensate for this delay, it is necessary to use the values of torque, flux, and stator current at time . Using the values measured at time k and the predictions at , an optimal vector is obtained and subsequently applied at time . This method compensates for the inherent delay in the implementation of the controller, while still maintaining the principle of MPC that the applied vector minimizes the future value of the controlled variable as much as possible. The equations for required in the control law are shown below.
where is the predicted flux, given by
while is obtained from Equation (12),
2.3. Cost Functions
Equations (20) and (21) are finally the contributions of the mathematical model for the implementation of the SMPC strategy. Equations (20) and (21) predict the torque and flux for any of the converter switching states and are necessary to define the cost functions.
Actually, the torque cost function and flux cost function are future tracking errors of the torque or flux with respect to the torque reference or flux reference values. The torque and flux cost functions are shown below:
2.4. Sequential Model Predictive Control
The SMPC strategy is the fundamental component of the control law. Figure 3 shows the general scheme of the control law, where three blocks are clearly distinguished: the SMPC, the flux estimator, and the speed control. The SMPC strategy determines the switching state for the next sample period using measured currents , torque reference , and stator flux reference . Previously, the flux is estimated, and the reference torque is obtained. Flux is estimated by applying the methodology proposed in [28]. In this work, the equation for estimating stator flux is obtained by discretizing (7), while the estimation of rotor flux is obtained by solving for in (5) and substituting into (6). On the other hand, the speed control block consists of a PI controller that generates the reference torque value and whose input is the speed error.
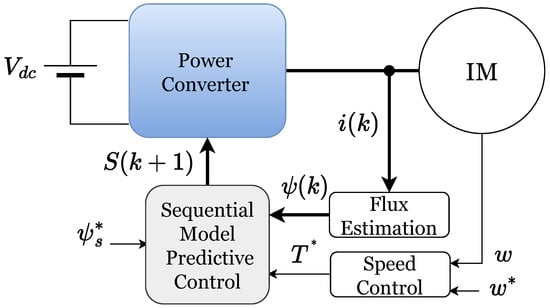
Figure 3.
General scheme of the proposed sequential model predictive control (SMPC) for motor drive applications.
Generally, the SMPC strategy evaluates simple cost functions for each control objective in a sequential manner. In this research, the electromagnetic torque is evaluated first, followed by the stator flux. The flow diagram of the proposed control is shown in Figure 4. Step 0 deals with the motor information necessary to execute the SMPC strategy (Steps 1 to 3), while Step 4 mentions the switching state selected by the controller to be applied to the converter. Each step of the SMPC strategy is described below:
- Step 0: Measure motor variables and estimate flux.
- Step 1: Evaluate the first cost function for all possible switching states (M). M value depends on the converter topology. M value is 8 in the VSI or 27 in the 3L-NPC converter.
- Step 2: Order the results of the first cost function evaluation in ascending order, and select the top N states. It is important to note that must be satisfied.
- Step 3: Evaluate the second cost function for the N states selected in the previous step.
- Step 4: Select the switching state that best minimizes the flux cost function, which will be applied to the converter in the next sampling period.
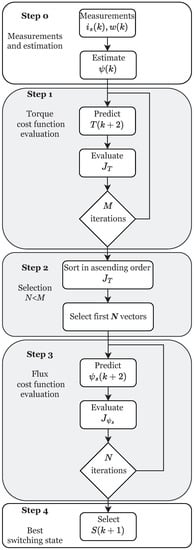
Figure 4.
Flow diagram of the sequential model predictive control (SMPC) with 2 cost funtions.
To carry out Step 2, the control parameter N must be defined. N represents the quantity of switching states to be evaluated in Step 3. The choice criteria for this parameter is based on the desired performance. Section 3 presents an analysis of the SMPC’s performance for various control parameter values, both for the VSI converter and for the 3L-NPC.
3. Results
This section presents simulation and experimental results based on Hardware-in-the-Loop tools.
3.1. Simulations
In this subsection, PLECS simulations of the proposed SMPC are presented to validate the control algorithm.
A contribution of this research is the comparison of the performance of the SMPC strategy for two reference converters: VSI for low powers and 3L-NPC for intermediate powers. For this reason, a motor with an intermediate nominal power (50 KW) was selected to make a comparison under equal conditions. The parameters of the equivalent circuit of the motor are shown in Table 1. Simulation and sampling time are 1 s and 20 μs, respectively. The references for the IM operation are a speed of 150 rad/s and load torque of 35.7 Nm.

Table 1.
System parameters.
Simulation results for VSI and 3L-NPC converters are presented in Figure 5, Figure 6, Figure 7 and Figure 8. The results show the IM’s performance in response to a step change in the speed reference. Due to the relationship between the mechanical variables of the motor, the speed reference imposes a torque reference, while an absolute stator flux reference of 0.85 has been defined to avoid saturation of the magnetic cores of the machine. Additionally, there are two very different situations in the results that are easily observable in all the figures. The first is the start-up or transient state where the IM has a high power consumption to reach the speed reference, and the second situation is where the motor operates at the reference speed known as the steady-state condition.
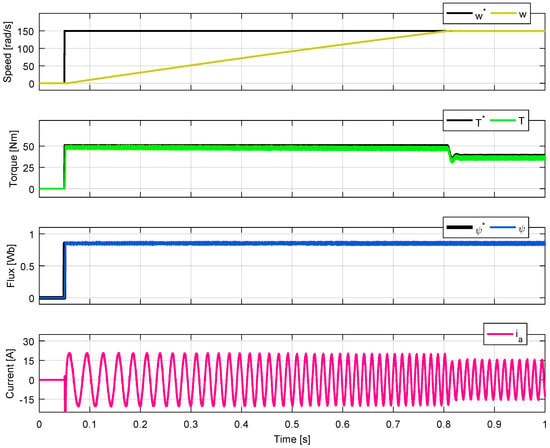
Figure 5.
Results for VSI with N = 2.
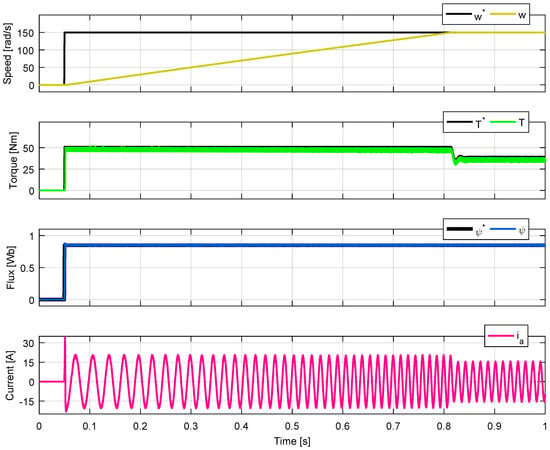
Figure 6.
Results for VSI with N = 3.
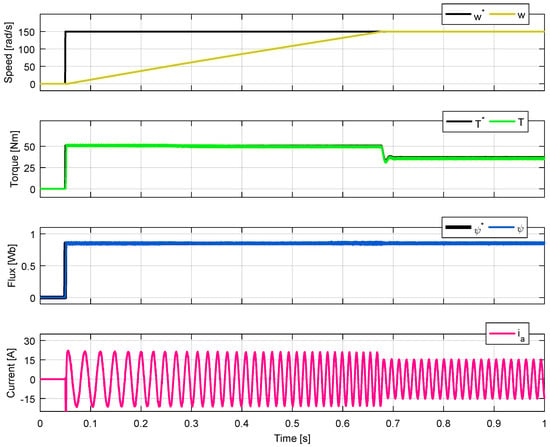
Figure 7.
Results for 3L-NPC with N = 4.
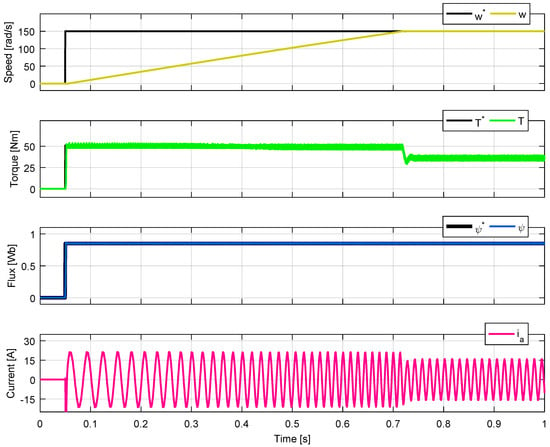
Figure 8.
Results for 3L-NPC with N = 12.
The same waveforms in the same positions have been presented both in the simulation and in the experimental results. The waveforms included from top to bottom in each figure are speed (ω), torque (T), absolute stator flux (), and phase a current (). The currents of phases b and c have the same waveform and amplitude but are phase shifted by 120 degrees. Figure 5, Figure 6, Figure 7 and Figure 8 show the simulation results for different N values which produce a good performance of the controller for both converters. The selected values of N are not arbitrary; they actually correspond to the minimum and maximum values that N can take for the IM to follow the speed reference. The results for the VSI for N = 2 (Figure 5) and N = 3 (Figure 6) are equivalent. This means that the motor reaches the speed reference by following the torque and flux references, consuming sinusoidal currents. Similarly, equivalent results are obtained for the NPC converter tests for N = 4 (Figure 7) and N = 12 (Figure 8). Additional analysis to examine the effect of selecting the N parameter on the IM response is provided in the next section.
3.2. Experimental Results
In this research, different Hardware-in-the-Loop (HIL) tests were carried out to validate the simulation results. The HIL test system used is shown in Figure 9 and consists mainly of: RT Box 1, RT Box 2, analog input peripheral module, and oscilloscope Keysight MSOX3104T. The RT Box is a Plexim HIL tool, specially designed for power electronics applications. A novelty of the application is the use of two RT Boxes, one of them emulates the plant which includes the power converter and the motor, while the other RT Box is responsible for acting as a controller, taking samples from the plant and sending switching signals. RT Box 2 is a newer hardware and also has better features compared to RT Box 1. The main difference is that RT Box 2 has multiple processing cores, which can perform multitasking.

Figure 9.
Experimental setup: (a) oscilloscope; (b) analog input board; (c) RT Box 1’ (d) RT Box 2; (e) laptop.
The study cases considered for the HIL tests are the same as in the simulation section, that is, tests for both converters and with control parameters N = 2 and N = 3 for the VSI and N = 4 and N = 12 for the NPC-3L. In each case, the results of speed, torque, flux, and the current of phase a are shown. The results are shown in Figure 10, Figure 11, Figure 12 and Figure 13.
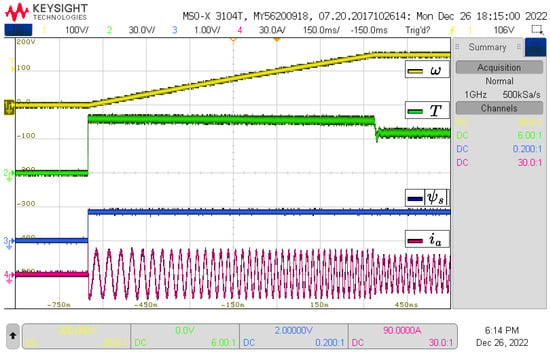
Figure 10.
HIL Results for VSI with N = 2.
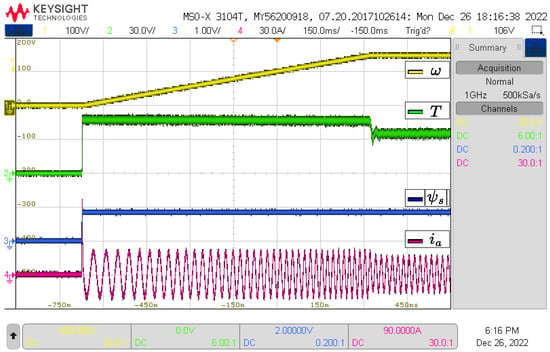
Figure 11.
HIL Results for VSI with N = 3.
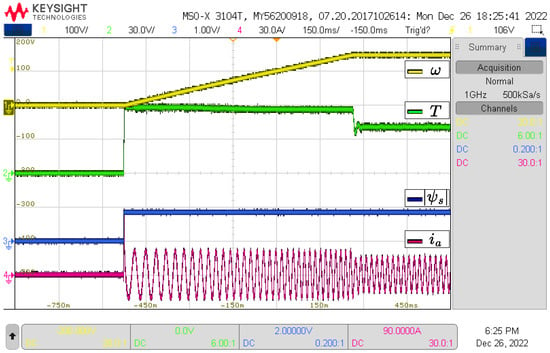
Figure 12.
HIL Results for 3L-NPC with N = 4.
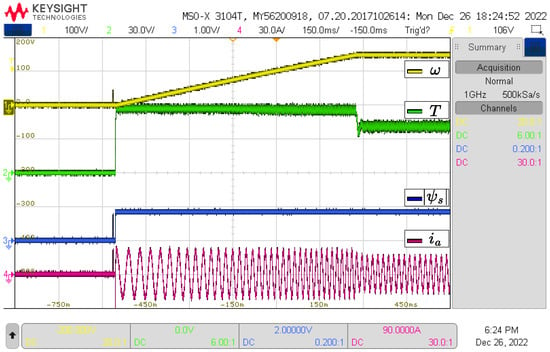
Figure 13.
HIL Results for 3L-NPC with N = 12.
4. Discussion
This section presents a discussion of the simulation and experimental results, as well as a comparison between the obtained results. Finally, the limitation of the proposed approach is presented.
4.1. Simulation
4.1.1. Cost Functions Evaluation Order
In this work, simple cost functions for torque and flux have been evaluated sequentially in order of priority. The first cost function to be evaluated must be the torque and secondly the flux; otherwise, the controller does not operate. This behavior can be explained because the torque is the main control objective, and it is also the measure variable, while the flux is the secondary objective, and it is an estimated variable.
4.1.2. Control Parameter Domain
N is an SMPC parameter, which defines the number of switching states that will be evaluated in the second cost function. The N values indicated in the previous results are not arbitrary. These values define the limits where the controller can operate. Then, it is possible to establish a selection interval for N parameter. N is an integer number that must be chosen in accordance with:
- VSI converters, .
- 3L-NPC converters, .
To obtain these selection intervals, simulations of all possible N values are performed. The interval summarizes the values of N where the controller exhibited good behavior. Notice that for the VSI converter, N can only take 2 values between 8 possible switching states, while for NPC converters, N parameter can take 9 values among 27 possible states.
4.1.3. SMPC Performance According to Selected Parameter
The controller performance for each parameter N is different. Figure 5 and Figure 6 show results for the VSI with N = 2 and N = 3. N = 2/N = 3 means that the states that best minimized the torque cost function are selected to evaluate the flux cost function. The waveforms have equivalent behaviors. The only significant difference is in the ripple of torque and flux. The minimum ripple for torque and flux is achieved for N = 2 and N = 3, respectively. Figure 7 and Figure 8 show results for a 3L-NPC with N = 4 and N = 12. In both cases, there is good tracking of the control objectives. However, there is a difference in the torque and flux ripples. For N = 4, torque ripple is minimal, and flux ripple increases. For N = 12, flux ripple is minimal, and torque ripple increases. It is clear that for N = 12, there are states that increase the torque error but decrease the flux error. However, if only four states are selected, these states decrease the torque error but are poorly evaluated in the flux cost function. It is concluded that a low value of parameter N reduces the tracking error of the first cost function and increases the error of the second one; while a high value of N reduces the tracking error of the second cost function and increases the error of the first function.
Although equivalent performances can be seen in Figure 5 and Figure 6 for the VSI, and in Figure 7 and Figure 8 for the 3L-NPC, it is necessary to analyze both the dynamic and the steady-state response to compare the results. A simple way to observe the control law behavior is to plot the error as a time function for the torque and flux, as these are the control objectives as shown in Figure 14 and Figure 15. The main finding obtained from these figures is that a lower value of the control parameter minimizes the first cost function (torque) and increases the second function (flux). Equivalently, a higher value of the control parameter penalizes the first cost function and favors the second. The implications of both ripple and tracking error analysis are the same. To minimize the ripple or tracking error of a control variable, the control parameter must be chosen smaller if the corresponding cost function is evaluated first, or larger if the associated cost function is evaluated second.
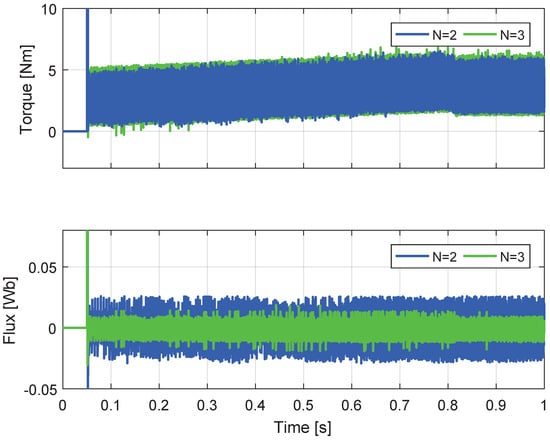
Figure 14.
Comparison of N values for VSI.
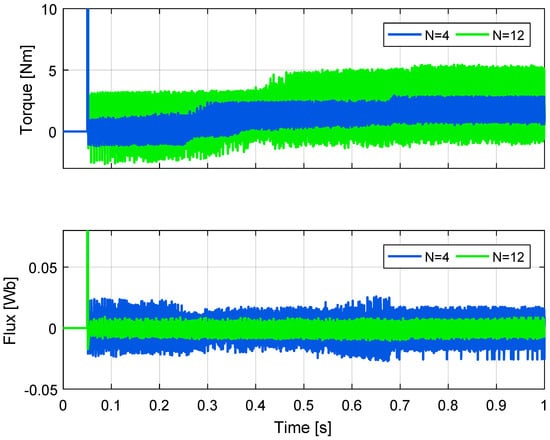
Figure 15.
Comparison of N values for 3L-NPC.
The harmonic content of the stator currents is another analysis that was considered. The first 20 harmonics of the phase a stator current are analyzed for each converter. The THD analysis is based on one signal cycle in steady-state condition at the end of the simulation interval. The results of the THD analysis of the current waveforms in Figure 5, Figure 6, Figure 7 and Figure 8 are shown in Table 2. In the VSI instance, there are only two valid values for N: N = 2 and N = 3. The THD for these values are and , respectively. The smallest THD is obtained for the highest value of N. In the 3L-NPC case, N has nine possible states (). Figure 7 and Figure 8 show the controller’s performance for the extreme values of the control parameter domain (N = 4 and N = 12). The corresponding THDs are and . THD values for all the nine possible values of the control parameter are shown in Figure 16.

Table 2.
Harmonic content analysis of the stator currents.
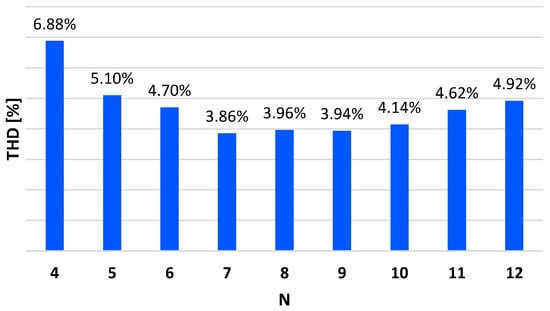
Figure 16.
Phase a stator current harmonic analysis, in 3L-NPC converter for each possible N value.
It can be seen in this figure that an intermediate value of N is preferred to reduce the THD. The smallest THD-index () is obtained for N = 7. In both cases, the trend is to increase the value of N in order to achieve a lower THD. The harmonic analysis also shows that multilevel topologies have lower harmonic distortion in their currents. The lowest THDs obtained are (VSI) and (3L-NPC).
In addition to the harmonic content information of the current in Figure 5, Figure 6, Figure 7 and Figure 8, Table 2 also shows the peak value of the current, frequency, and peak value of the fundamental component, as well as the three main harmonics of each case study. This information is useful for quantifying the controller’s performance in each case without actually providing relevant differences between them. The differentiating criterion is the THD, which was analyzed previously.
The results indicate that a lower THD can be achieved for higher values of N. This result is consistent with the proposed order for evaluating the cost functions (first torque and then flux). It was previously determined from the ripple analysis that higher N values prioritize the second cost function. The second cost function (flux) is directly related to the electrical variables. However, prioritizing the first cost function (torque) would have more significant impacts on the mechanical variables of the motor.
4.2. Experimental Results
Figure 10, Figure 11, Figure 12 and Figure 13 show the HIL results, which show good agreement with the simulation results. A noticeable difference between the HIL and the simulation results is a ripple increment in each variable. This is largely attributed to the interconnections between components and the delays present in the experimental setup. Both in the simulation and the experimental results, the IM reaches the speed reference, but with different settling times. A comparison of the settling times is shown in Table 3. In general, HIL tests show a longer settling time compared to simulation results. This is due to delays in sampling and updating in the control signal characteristic of digital controllers. In addition, it is observed that the NPC converter reaches the reference in less time than the VSI converter, both for simulation and for HIL.

Table 3.
Comparison of settling times in seconds.
4.3. Limitation of the Proposed Approach
This research is a first approach in the study of the SMPC strategy in motor drive applications. The typical case of two simple cost functions (torque and flux) was analyzed using both the VSI and the 3L-NPC converter. The objective was a fair comparison of the controller’s performance for the same cost functions. However, for the 3L-NPC topology case, three cost functions are usually considered: torque, flux, and voltage balance in the capacitors. In this research, voltage sources were used in the 3L-NPC converter’s DC-bus instead of capacitors, so the voltage is constant, and it is not necessary to include the voltage balance objective as one of the cost functions. The inclusion of a third cost function in the SMPC strategy algorithm is a pending task considering the future implementation of the application in a physical system.
5. Conclusions
Sequential Model Predictive Control (SMPC) is a strategy for controlling electrical machines that has gained widespread use in recent years. Unlike traditional predictive control, SMPC does not require weighting factors in the cost function. Instead, it evaluates simple cost functions in a predetermined order of priority. At each step, a subset of switching states is selected, and the cost functions are evaluated for each state. The size of this subset is a control parameter (N) that can be adjusted. After all of the cost functions have been evaluated, the switching state that results in the best final cost function value is applied to the power converter during the next sample period. SMPC can be applied in numerous fields, including electrical drive control and other areas where conventional predictive control has been used.
The purpose of this research was to fill the gap in the literature about the control parameter values for SMPC strategy. The typical case of two simple cost functions (torque and flux) was analyzed using both the VSI and the 3L-NPC converter. This work addressed two main issues: the control parameter domain and the performance of the SMPC strategy according to the selected control parameter. The study determined the values of the parameters through simulation and experiments based on HIL tools and suggested a choice criteria using harmonic content analysis. The control parameter can take integer values within the following intervals: [2, 3] for the VSI and [4, 12] for the 3L-NPC. For VSI systems, a larger value of the control parameter leads to lower harmonic distortion, while for NPC systems, intermediate values within the established domain are typically the best option. In addition, the findings revealed that the controller demonstrated excellent control variable tracking and rapid dynamic response, features typically associated with classical predictive control.
This study is a preliminary exploration of the use of an SMPC strategy in motor drive applications. Further research will explore additional control goals, alternative converters, and testing with real converters and motors.
Author Contributions
Conceptualization, D.M.-Y.; Methodology, D.M.-Y.; Software, B.A. and C.R.; Validation, B.A. and C.R.; Investigation, B.A.; Writing—original draft, D.M.-Y.; Writing—review & editing, M.R. and P.W.; Visualization, C.R.; Supervision, M.R.; Project administration, M.R.; Funding acquisition, P.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Chilean Government under Anillo Project ATE220023, CLIMAT AMSUD 210001, (ANID/FONDECYT/1220556), (ANID/FONDECYT/1191680), Millenium Institute on Green Ammonia as Energy Vector MIGA (ANID/Millennium Science Initiative Program/ICN2021_023), SERC Chile (ANID/FONDAP/15110019), (ANID/PFECHA/Doctorado-Nacional/2019-21191663), in part by Universidad de Talca and University of Nottingham.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| EH-SMPC | Even Handed Sequential Model Predictive Control. |
| EEH-SMPC | Enhanced Even Handed Sequential Model Predictive Control. |
| FS-MPC | Finite Set Model Predictive Control. |
| G-SMPC | Generalized Sequential Model Predictive Control. |
| HIL | Hardware-in-the-Loop. |
| IM | Induction Motor. |
| MPC | Model Predictive Control. |
| MVSCs | Multilevel Voltage Source Converters. |
| SMPC | Sequential Model Predictive Control. |
| VSI | Voltage Source Inverter. |
| 3L-NPC | Neutral Point Clamped converter of three levels. |
Nomenclature
| stator voltage. | |
| stator flux. | |
| rotor flux. | |
| stator current. | |
| rotor current. | |
| stator resistance. | |
| rotor resistance. | |
| stator inductance. | |
| rotor inductance. | |
| mutual inductance. | |
| w | electrical speed. |
| T | electromagnetic torque. |
| p | number of pole pairs. |
References
- Vazquez, S.; Leon, J.I.; Franquelo, L.G.; Rodriguez, J.; Young, H.A.; Marquez, A.; Zanchetta, P. Model Predictive Control: A Review of Its Applications in Power Electronics. IEEE Ind. Electron. Mag. 2014, 8, 16–31. [Google Scholar] [CrossRef]
- Rodriguez, J.; Garcia, C.; Mora, A.; Davari, S.A.; Rodas, J.; Valencia, D.F.; Elmorshedy, M.; Wang, F.; Zuo, K.; Tarisciotti, L.; et al. Latest Advances of Model Predictive Control in Electrical Drives-Part II: Applications and Benchmarking With Classical Control Methods. IEEE Trans. Power Electron. 2022, 37, 5047–5061. [Google Scholar] [CrossRef]
- Vazquez, S.; Rodriguez, J.; Rivera, M.; Franquelo, L.G.; Norambuena, M. Model Predictive Control for Power Converters and Drives: Advances and Trends. IEEE Trans. Ind. Electron. 2017, 64, 935–947. [Google Scholar] [CrossRef]
- Cortes, P.; Kouro, S.; La Rocca, B.; Vargas, R.; Rodriguez, J.; Leon, J.I.; Vazquez, S.; Franquelo, L.G. Guidelines for weighting factors design in Model Predictive Control of power converters and drives. In Proceedings of the 2009 IEEE International Conference on Industrial Technology, Churchill, VIC, Australia, 10–13 February 2009; pp. 1–7. [Google Scholar] [CrossRef]
- Zhang, K.; Fan, M.; Yang, Y.; He, L.; Li, X. Load Angle Limitation for PMSMs with Sequential Model Predictive Direct Torque Control. In Proceedings of the 2019 IEEE International Symposium on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Quanzhou, China, 31 May–2 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Z.; Liu, X.; Dan, H.; Xiong, W.; Ling, T.; Su, M. Weighting factor design based on SVR–MOPSO for finite set MPC operated power electronic converters. J. Power Electron. 2022, 22, 1085–1099. [Google Scholar] [CrossRef]
- Vargas, R.; Cortes, P.; Ammann, U.; Rodriguez, J.; Pontt, J. Predictive Control of a Three-Phase Neutral-Point-Clamped Inverter. IEEE Trans. Ind. Electron. 2007, 54, 2697–2705. [Google Scholar] [CrossRef]
- Vodola, V.; Odhano, S.; Norambuena, M.; Garcia, C.; Vaschetto, S.; Zanchetta, P.; Rodriguez, J.; Bojoi, R. Sequential MPC Strategy for High Performance Induction Motor Drives: A detailed analysis. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 6595–6600. [Google Scholar] [CrossRef]
- Osman, I.; Xiao, D.; Rahman, M.F. Two-Stage optimization based finite state predictive torque control for 3L-NPC inverter Fed IM drives. IET Electr. Power Appl. 2019, 13, 64–72. [Google Scholar] [CrossRef]
- Zhang, J.; Norambuena, M.; Li, L.; Dorrell, D.; Rodriguez, J. Sequential Model Predictive Control of Three-Phase Direct Matrix Converter. Energies 2019, 12, 214. [Google Scholar] [CrossRef]
- Norambuena, M.; Rodriguez, J.; Zhang, Z.; Wang, F.; Garcia, C.; Kennel, R. A Very Simple Strategy for High-Quality Performance of AC Machines Using Model Predictive Control. IEEE Trans. Power Electron. 2019, 34, 794–800. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Z.; Kamierkowski, M.P. Cascaded Predictive Control for Three-Level NPC Power Converter Fed Induction Machine Drives Without Weighting Factors. In Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Acuña, P.; Morán, L.; Rivera, M.; Aguilera, R.; Burgos, R.; Agelidis, V.G. A Single-Objective Predictive Control Method for a Multivariable Single-Phase Three-Level NPC Converter-Based Active Power Filter. IEEE Trans. Ind. Electron. 2015, 62, 4598–4607. [Google Scholar] [CrossRef]
- Xiao, D.; Akter, M.P.; Alam, K.; Dutta, R.; Mekhilef, S.; Rahman, M.F. Cascaded Predictive Flux Control for a 3-L Active NPC Fed IM Drives Without Weighting Factor. IEEE Trans. Energy Convers. 2021, 36, 1797–1807. [Google Scholar] [CrossRef]
- Zhang, K.; Fan, M.; Yang, Y.; Chen, R.; Zhu, Z.; Garcia, C.; Rodriguez, J. Tolerant Sequential Model Predictive Direct Torque Control of Permanent Magnet Synchronous Machine Drives. IEEE Trans. Transp. Electrif. 2020, 6, 1167–1176. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, B.; Yang, H.; Norambuena, M.; Rodriguez, J. Generalized Sequential Model Predictive Control of IM Drives With Field-Weakening Ability. IEEE Trans. Power Electron. 2019, 34, 8944–8955. [Google Scholar] [CrossRef]
- Davari, S.A.; Norambuena, M.; Nekoukar, V.; Garcia, C.; Rodriguez, J. Even-Handed Sequential Predictive Torque and Flux Control. IEEE Trans. Ind. Electron. 2020, 67, 7334–7342. [Google Scholar] [CrossRef]
- Wang, Z.; Guo, H.; Ping, Z.; Wang, Y.; Zhang, Z. Revised Sequential Predictive Torque Control with Adaptability under Multiple Operating Conditions for Induction Motors Drives. In Proceedings of the 2021 IEEE International Conference on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Jinan, China, 20–22 November 2021; pp. 502–506. [Google Scholar] [CrossRef]
- Wu, W.; Wang, D.; Liu, L. A Multi-Layer Sequential Model Predictive Control of Three-Phase Two-Leg Seven-Level T-Type Nested Neutral Point Clamped Converter Without Weighting Factors. IEEE Access 2019, 7, 162735–162746. [Google Scholar] [CrossRef]
- Aouichak, I.; Jacques, S.; Bissey, S.; Reymond, C.; Besson, T.; Le Bunetel, J.C. A Bidirectional Grid-Connected DC-AC Converter for Autonomous and Intelligent Electricity Storage in the Residential Sector. Energies 2022, 15, 1194. [Google Scholar] [CrossRef]
- Dekka, A.; Wu, B.; Fuentes, R.L.; Perez, M.; Zargari, N.R. Evolution of Topologies, Modeling, Control Schemes, and Applications of Modular Multilevel Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1631–1656. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z.; Huang, W.; Kennel, R.; Xie, W.; Wang, F. Encoderless Sequential Predictive Torque Control with SMO of 3L-NPC Converter-fed Induction Motor Drives for Electrical Car Applications. In Proceedings of the 2019 IEEE International Symposium on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Quanzhou, China, 31 May–2 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Z.; Gao, F.; Norambuena, M.; Rodríguez, J.; Yavas, O.; Kennel, R. Sequential direct model predictive control for gird-tied three-level NPC power converters. In Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; pp. 1–5. [Google Scholar]
- Cui, Z.; Zhang, Z.; Yang, Q.; Kennel, R. Cascaded model predictive control of three-level NPC back-to-back power converter PMSG wind turbine systems. In Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; pp. 1–6. [Google Scholar]
- Zhang, J.; Li, L.; Norambuena, M.; Rodriguez, J.; Dorrell, D.G. Sequential model predictive control of direct matrix converter without weighting factors. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 1477–1482. [Google Scholar]
- Donoso, F.; Mora, A.; Cárdenas, R.; Angulo, A.; Sáez, D.; Rivera, M. Finite-Set Model-Predictive Control Strategies for a 3L-NPC Inverter Operating With Fixed Switching Frequency. IEEE Trans. Ind. Electron. 2018, 65, 3954–3965. [Google Scholar] [CrossRef]
- Fitzgerald, A.E.; Kingsley, C.; Umans, S.D.; James, B. Electric Machinery; McGraw-Hill: New York, NY, USA, 2003; Volume 5. [Google Scholar]
- Rodriguez, J.; Cortes, P. Predictive Control of Power Converters and Electrical Drives; John Wiley & Sons: Hoboken, NJ, USA, 2012; Volume 40. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).