1. Introduction
Consensus has a long history in the distributed coordination of multi-agent systems [
1]. It has important applications in the formation control of mobile robots [
2,
3], sensor networks [
4,
5], group decision, opinion forming [
6,
7], etc, and has been studied widely from many viewpoints, such as interaction topology [
8,
9], updated method of control input [
10,
11], convergence rate [
12], dynamics of agents [
13,
14], and so on.
In the study of consensus, graphs are often applied to model the interactions among agents, where each node denotes one agent, and the weight associated with each edge represents the interaction intensity between two agents. In most existing works, such as [
8,
9,
10,
11,
12,
13,
14], it is assumed that each weight is non-negative, which means agents are cooperative. For consensus with non-negative graphs, a lot of results have been obtained. For example, consensus can be reached for single integrators if and only if the interaction topology has a spanning tree, or if the eigenvalues of the Lapalacian matrix have some special features [
15]. In addition to cooperative relationships, there are also antagonistic relationships in many contexts, such as economic systems, social networks, robot competitions, biology systems, and so on [
16,
17]. A negative weight can be applied to model these antagonistic relationships. A graph with a negative weight is called a signed graph [
18]. It is quite meaningful to study the consensus of multi-agent systems with a signed graph.
In [
19], consensus is discussed for first-order continuous-time multi-agent systems with signed graphs and bipartite consensus is first introduced. Some sufficient and necessary conditions are obtained in the case of fixed topology. If all agents eventually reach a state with the same magnitude but the opposite sign, then bipartite consensus is reached. Bipartite consensus is usually discussed for structurally balanced graphs, which can be converted into graphs with non-negative weights by applying a gauge transformation. Hence, the analysis for the consensus in the case of a signed graph is equivalent to that in the case of a non-negative graph. There has been some research into the bipartite consensus of multi-agent systems [
20,
21,
22,
23,
24,
25,
26]. It should be noted that gauge transformations cannot be applied to structurally unbalanced graphs. In [
20], bipartite consensus and trivial consensus were discussed for first-order discrete-time multi-agent systems in the case of structurally balanced signed graphs and structurally unbalanced signed graphs, respectively, where the control input was similar to that in [
19] and the topology graph is fixed. In [
21], some sufficient conditions for bipartite consensus were established for linear continuous-time multi-agent systems based on the event-triggered output feedback, where the topology graph was assumed to be fixed and structurally balanced. In [
22], some adaptive neural network distributed control algorithms were proposed by using conventional Nussbaum-type functions, and some sufficient conditions for bipartite consensus were provided for high-order nonlinear multi-agent systems with signed time-varying graphs. In [
23], the convergence behavior was analyzed for the discrete Altafini model, and some sufficient and necessary conditions were established for modulus consensus in the case of structurally balanced graphs and structurally unbalanced graphs, respectively, where module consensus includes consensus and bipartite consensus. In [
24], the stabilizability of continuous-time multi-agent systems was considered and some relations between network topology and stabilizability were revealed. In [
25], the bipartite consensus was discussed for continuous-time multi-agent systems with fixed topology, where an edge state is introduced. In [
26], the behavior of continuous-time multi-agent systems was analyzed in the case of fixed topology and switching topology. Note that the topology graph was structurally balanced at all times and the two groups with antagonistic relations were time-invariant in [
22,
26].
Theonvergence was analyzed for first-order continuous-time and discrete-time multi-agent systems with signed graphs by virtue of an eventually positive matrix in [
27], where the interaction graph was not assumed to be structurally balanced. The eventually positive matrix had a certain relation with a strongly connected graph. In [
28], two kinds of protocols were discussed for first-order discrete-time multi-agent systems in the case of asynchronous interactions, where the first protocol was similar to that in [
19] and the topology graph was fixed. The convergence behavior under two such protocols was analyzed by applying matrix theory and by reconstructing signed graphs.
In most work on consensus with signed graphs, such as that of [
19,
21,
22], it is often assumed the the signed graph is a structurally balanced graph or the Laplacian matrix of the graph is similar to that in [
19], then the convergence behavior of multi-agent systems, such as bipartite consensus, is further analyzed. This paper studies the consensus of first-order discrete-time multi-agent systems with signed graphs, which is different from the discrete-time model in [
20,
23]. The topology graph is not required to be a structurally balanced graph, and some sufficient conditions will be established for consensus in the case of fixed topology and switching topology, respectively, by applying matrix theory. In the case of switching topology, the topology does not need to have a spanning tree at each time to reach consensus.
This paper is organized as follows. Some concepts and models are introduced in
Section 2. The main results are presented in
Section 3. Simulations are provided to illustrate the effectiveness of the theoretical results in
Section 4, and the concluding remarks are made in
Section 5.
2. Preliminaries
2.1. Graph Theory
Some basic definitions in graph theory are introduced [
29].
For a directed graph , let and denote its vertex set and edge set, respectively, where and . For edge , is the parent vertex of and is the child vertex of . An edge is called a self-loop if its two ends are the same vertex. For , the set of its neighbors is denoted by or . A (directed) path from to is a sequence, , of distinct vertices such that . A directed graph is strongly connected if there exists a path from each vertex to each other vertex. A directed tree is a directed graph, where every vertex, except one special vertex, has exactly one parent vertex, and the special vertex, called a rooted vertex, has no parent vertices and can be connected to any other vertices by paths. A subgraph, , of is a graph such that and . is said to be a spanning subgraph if . For any if if and only if . Then is said to be an induced subgraph of , and is also said to be induced by . A spanning tree of is a directed tree which is a spanning subgraph of . is said to have a spanning tree if some edges form a spanning tree of . A subgraph is called a strongly connected component if it is the maximal strongly connected subgraph of . Furthermore, if there is no edge from any nodes except in to nodes in , then is called a rooted strongly connected component of .
A directed graph
with a matrix
is called a weighted directed graph
, where
if and only if
and
.
is called the weight of
.
is also called an undirected graph if
A is a symmetric matrix. Each element of the Laplacian matrix
is defined as
If each element of A is non-negative, then A (resp. ) is called a non-negative matrix (resp. non-negative graph); otherwise, A (resp. ) is called a signed matrix (signed graph).
Let denote the topology graph at time t, and let denote the union graph of at time , where the vertex set of is the same as that of . If there exists such that , then .
The following properties of the Laplacian matrix have been proven in [
15].
Lemma 1 ([
15]).
Assume A is a non-negative matrix; then,- (i)
L has an eigenvalue of zero and is the associated right eigenvector;
- (ii)
has a spanning tree if and only if L has an eigenvalue of zero and its other eigenvalues have positive real parts.
In Lemma 1, (i) still holds for a signed matrix, but (ii) does not always hold.
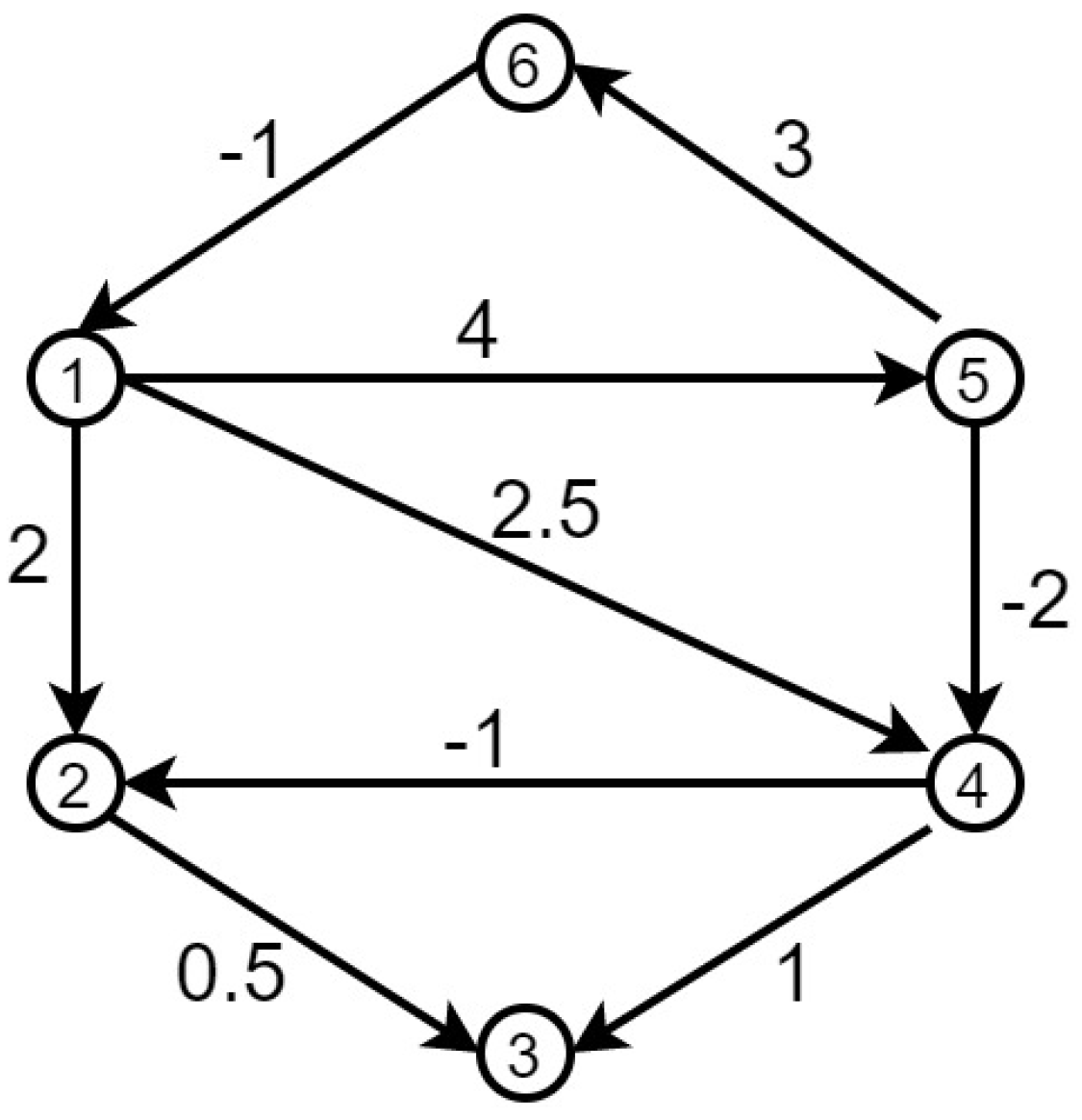
Example 1. Consider four agents with the topology shown in Figure 1. Although has a spanning tree, the eigenvalues of its Laplacian matrix are 0, 1.6727, −1.8424, and 5.1755.
2.2. Model
Consider a group of agents with first-order discrete-time dynamics,
where
and
are the state and conrol input (or protocol) of agent
i at time
k, respectively. Without loss of generality, assume
. The following control input is introduced,
where
h is the controller gain.
Let
, then the multi-agent system (
2) with protocol (
3) can be written as
where
is demonstrated by (
1).
For a signed graph, two kinds of consensus are mainly discussed: the traditional consensus and the bipartite consensus. The traditional consensus is considered in the following analysis.
Definition 1. For given protocol (3), multi-agent system (2) solves a consensus problem asymptotically if for any initial states . Based on the results in [
15], the following lemma is obtained.
Lemma 2. A consensus problem is solved asymptotically for the multi-agent system (2) with protocol (3) if and only if has an algebraically simple eigenvalue 1, and its other eigenvalues are located in a unit circle. Remark 1. Lemma 2 holds whether the topology graph is a non-negative graph or a signed graph. Note that the Laplacian matrix of a signed graph in some works, such as [19,20,21,23], iswhich is different from (1). For Lapalcian matrix (5), if the signed graph is structurally balanced, then it can be transformed into a non-negative graph by applying a gauge transformation, and the tools for analyzing a non-negative graph can consequently be used. However, a gauge transformation is not feasible for a Laplacian matrix (1). 3. Main Results
In this section, some sufficient conditions are provided for consensus in the case of fixed topology and switching topology, respectively.
3.1. Fixed Topology
For a directed graph
, let
denote its rooted strongly connected component, and let
denote the subgraph induced by the rest nodes. Thus,
where
and
are the Laplacian matrices of
and
, respectively. Let
.
First, some assumptions are made for :
- (A1)
has a spanning tree.
- (A2)
Zero is an algebraically simple eigenvalue of and all the other eigenvalues of have positive real parts.
It is known that (A2) is satisfied when
is non-negative. When
is not non-negative, some methods are provided to verify whether (A2) is satisfied. For example, zero is an algebraically simple eigenvalue of
and its other eigenvalues are with positive real parts if there exists a scalar
such that
is an eventually positive matrix [
27]. In addition, the verification of the eventually positive of matrix
B can lead to the result in [
30].
The following lemma is needed to establish the main result.
Lemma 3 ([
31]).
is nonsingular if the following three conditions all hold:- (1)
;
- (2)
There exists such that ;
- (3)
For any , there exists such that there exists a directed path from agent t to agent s, where
By Lemma 3, a sufficient condition is established for the fixed topology case.
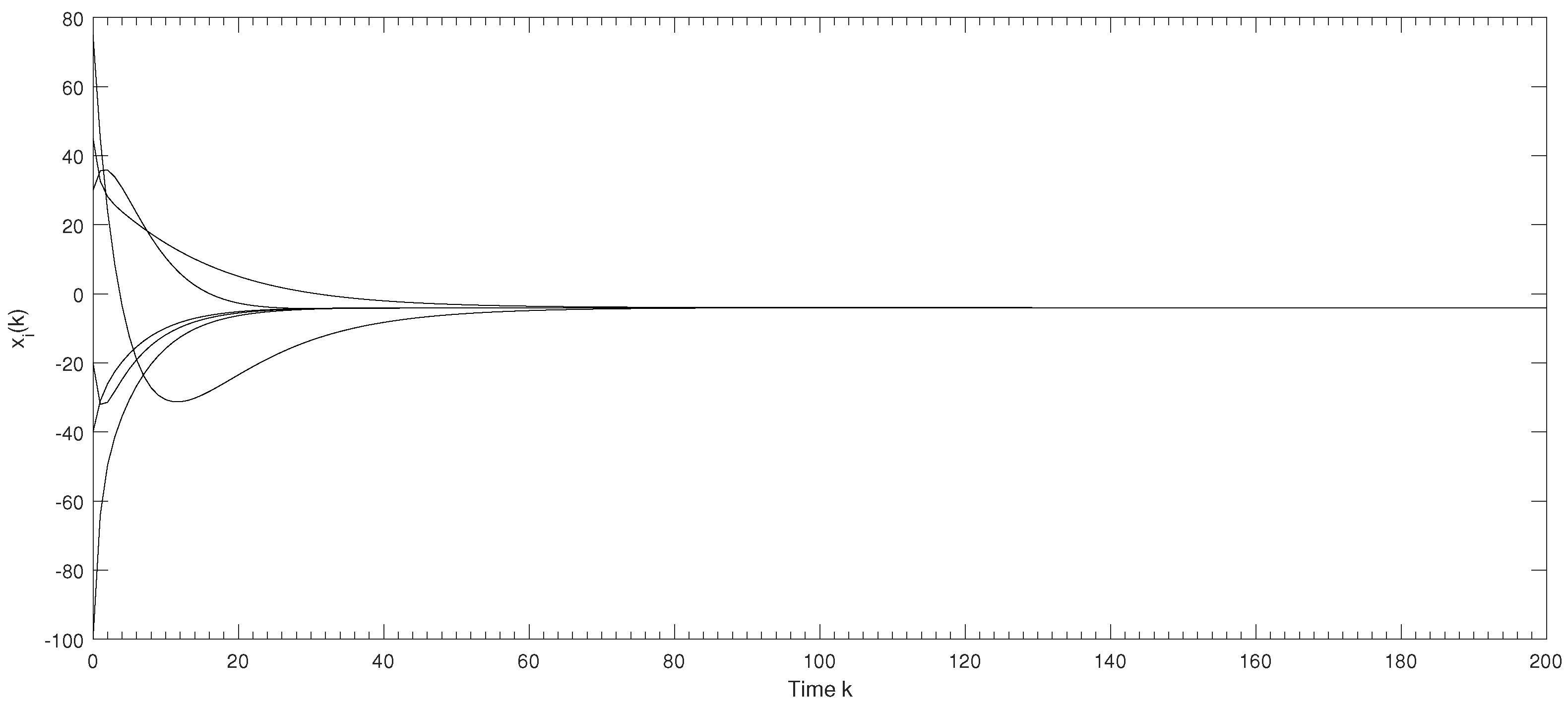
Theorem 1. Assume (A1) and (A2) hold. The multi-agent system (2) with protocol (3) solves a consensus problem asymptotically if the following conditions are all satisfied: - (1)
;
- (2)
There exists such that - (3)
For any , there exists such that a directed path from agent t to agent s exists, where , and ;
- (4)
, where denotes the set of all nonzero eigenvalues of a matrix.
Proof. By Lemma 2, a consensus problem can be solved asymptotically for the multi-agent system (
2) with protocol (
3) if and only if
has an algebraically simple eigenvalue 1 and its other eigenvalues are located in a unit circle, where
Next, the eigenvalues of and are analyzed, respectively.
By the first condition in Theorem 1,
is a diagonally dominant matrix. By Geršgorin’s Disk Theorem [
32], the eigenvalues of
are zero or have positive real parts. By Lemma 3,
is nonsingular under conditions (1–3); namely, zero is not its eigenvalue. Hence, all eigenvalues of
have positive real parts. Obviously,
means
and then all eigenvalues of
are located in a unit circle.
Based on (A2), has an algebraically simple eigenvalue 0 and its other eigenvalues are located in the right plane. By , 1 is an algebraically simple eigenvalue of , and its other eigenvalues are located in a unit circle.
Hence, 1 is an algebraically simple eigenvalue of , and its other eigenvalues are located in a unit circle. By Lemma 2, consensus can be reached asymptotically. □
In the multi-agent system with a leader, . In this case, has only one agent, denoted by agent 1. Then, the following result is obtained.
Corollary 1. Assume (A1) holds and agent 1 is a rooted vertex. The multi-agent system (2) with protocol (3) solves a consensus problem asymptotically if the following conditions are all satisfied: - (1)
;
- (2)
There exists such that - (3)
For any , there exists such that a directed path from agent t to agent s exists, where , and ;
- (4)
.
Especially, if is strongly connected, then condition (3) in Corollary 1 is obviously satisfied. Hence, the following corollary can be established.
Corollary 2. Assume agent 1 is a rooted vertex and is strongly connected. The multi-agent system (2) with protocol (3) solves a consensus problem asymptotically if the following conditions are all satisfied: - (1)
;
- (2)
There exists such that - (3)
.
In this section, some sufficient conditions are provided for consensus in the case of fixed topology. For multiple agents with cooperative and antagonistic interactions, the topology structure, the cooperative and antagonistic intensity (or edge weight), and the controller gain jointly determine whether consensus can be reached.
3.2. Switching Topology
For the case of switching topology, a leader is introduced and is labeled as agent 0 for the multi-agent system (
2). Assume the state of the leader is time-invariant; namely,
.
Consider the following protocol for the multi-agent system (
2),
where
, and
denote agent
i can receive the information from the leader.
Let
, then multi-agent system (
2) with protocol (
6) can be written as:
Obviously, consensus can be reached for multi-agent system (
2) with protocol (
6) if and only if system (
7) is asymptotically stable. Let
, then
where
.
Remark 2. In the works of consensus for discrete-time multi-agent systems, the Laplacian matrix is characterized by (1) or (5). Ref. [28] proposes two kinds of protocols for first-order discrete-time multi-agent systems with asynchronous interactions, where the Laplacian matrix in the second protocol is (1). Although the Laplacian matrix in protocol (6) is also (1), there is a difference between the second protocol in [28] and (6). In [28], it is assumed that the underlying interaction relationship is fixed, described by a fixed graph . That is, the topology graph at each time k, denoted by , is the subgraph of . Such an assumption is not made for (6). By analyzing the stability of system (
8), a sufficient condition is obtained for consensus of multi-agent system (
2) with protocol (
6) in the case of time-varying topology. Let
denote the topology formed by the leader and n agents. It is assumed that
is a finite set.
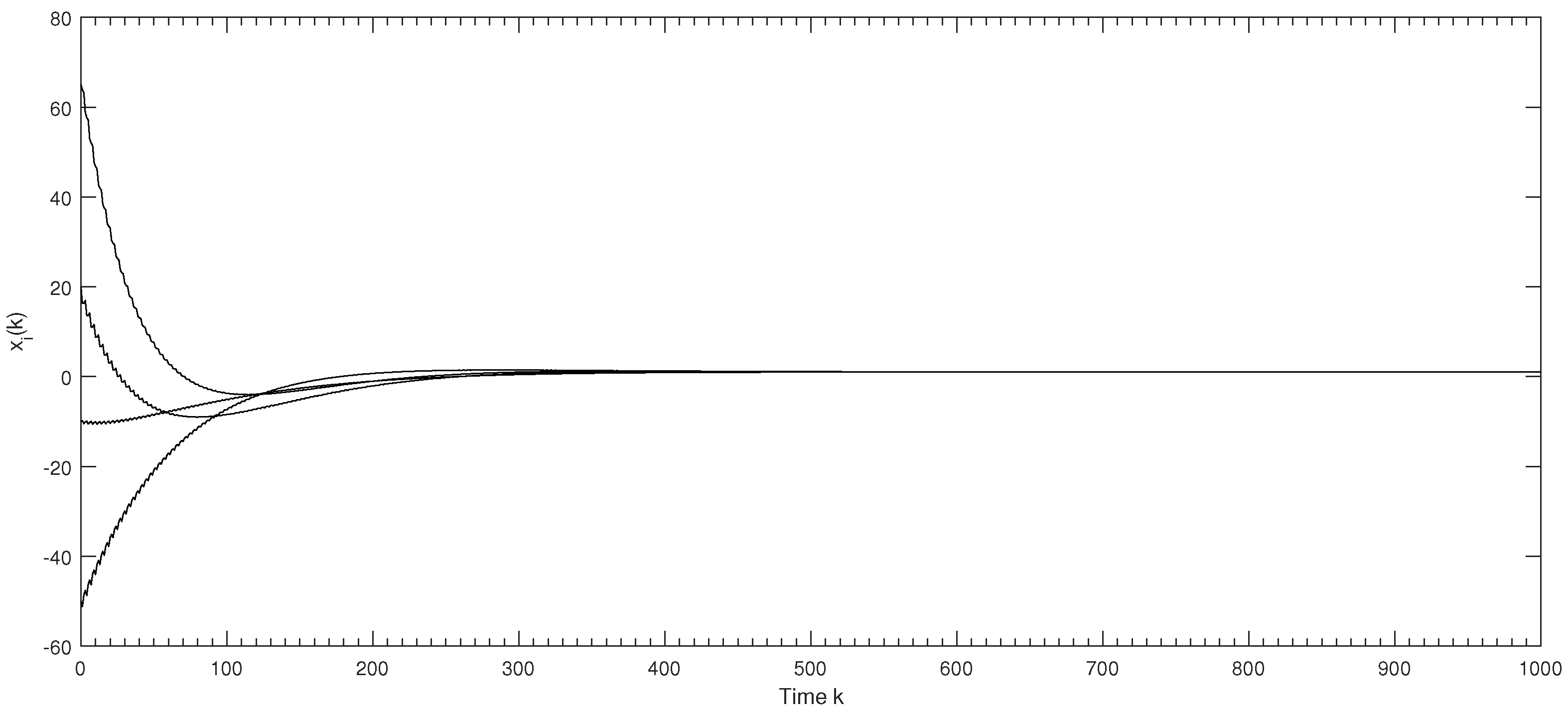
Theorem 2. Assume there exists discrete time instants , where and , such thatthen, there exists h such that multi-agent system (2) with protocol (6) solves a consensus problem asymptotically in the case of switching topology. Proof. Let
; then,
The asymptotical stability of system (
8) is equivalent to
Let
; then,
By calculation,
where
represents a matrix or a scalar, which is an infinitesimal of the same order of
, and
p is a positive integer.
By (
9),
. Hence,
h can be chosen small enough such that
. Let
h be small enough, then
where
denotes the infinite norm of
, and
By (
9),
. Hence,
if
h is small enough. There are finite different topologies among the leader and
n agents, and
. Hence,
is a finite set. Let
, then,
and
Thus,
; namely,
Hence,
and
, which means system (
8) is asymptotically stable. Consensus can be reached asymptotically. □
Remark 3. Some points should be noted. (9) implies that the union graph among the leader and n agents during each time interval has a spanning tree. Based on the assumption that is a finite set, there are finite inequalities in (9). In addition, the parameter d characterizes the convergence rate of multi-agent system (2) with protocol (6); namely, the smaller the parameter d, the faster the consensus is reached. The following theorem further provides a range of h which ensures consensus.
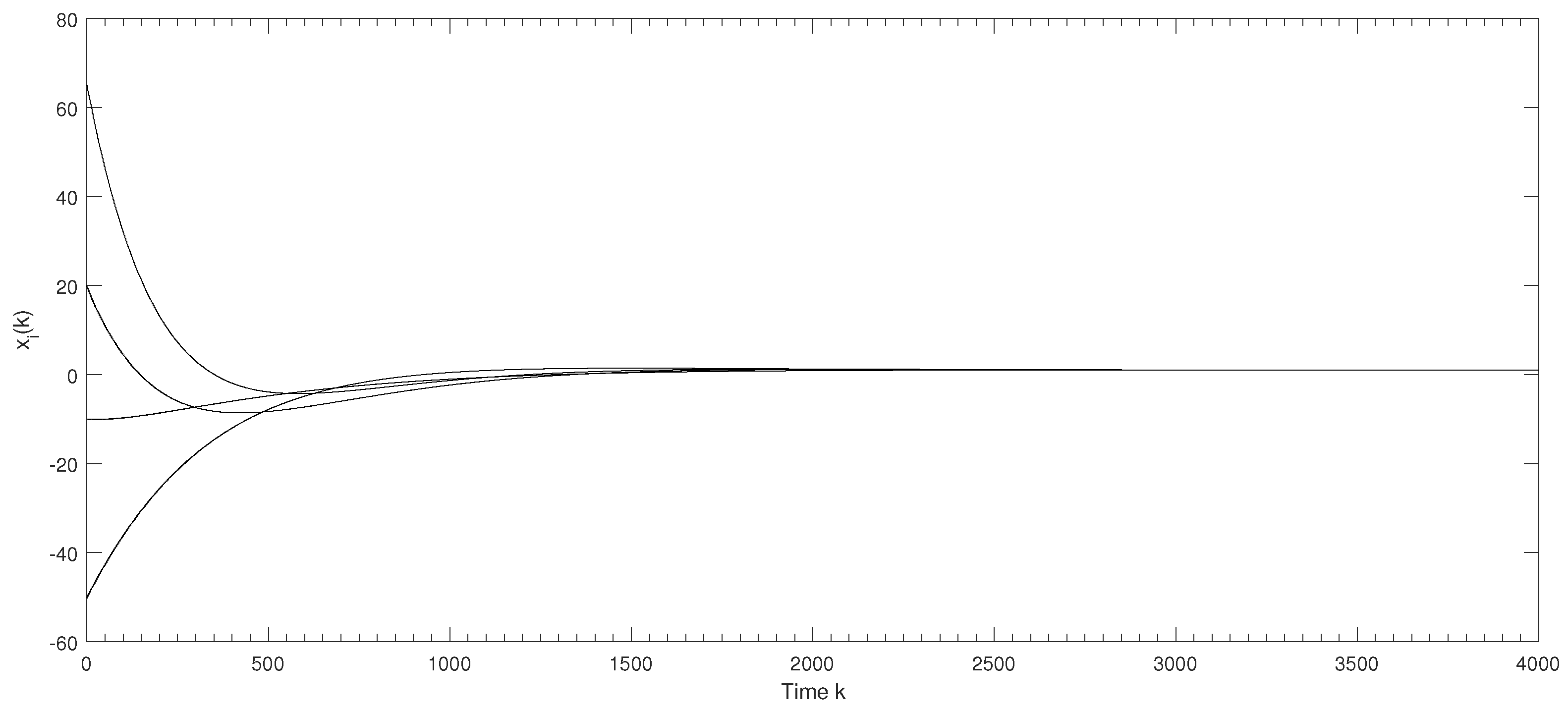
Theorem 3. Assume there exists discrete time instants , where and , such that If , then multi-agent system (2) with protocol (6) solves a consensus problems asymptotically in the case of switching topology, whereand Proof. Obviously,
. Then,
By (
11),
and
. If
, then
and
By (
11),
. Then,
and
If
h satisfies
then
. Hence,
which means
and system (
8) is asymptotically stable. Therefore, consensus can be reached asymptotically. □
Remark 4. It is assumed that is a finite set, and thus and σ can be obtained by finding the maximum or minimum from finite numbers. Although Theorem 3 is obtained based on the assumption , it still holds if there exists some by the proof of Theorem 3.
5. Conclusions
This paper has studied the consensus of first-order discrete-time multi-agent systems with cooperative and antagonistic interactions. By analyzing the eigenvalues of the Laplacian matrix, it is revealed that consensus is affected jointly by the interaction topology structure, the edge weights, and the controller gain in the case of fixed topology. For the case of switching topology, the results show that there exists controller gain such that consensus can be reached if the union graphs among some consecutive time intervals satisfy some quantity requirement, and the range for such a controller gain is further provided. It is shown that the topology graph at some time instants can be without a spanning tree, which is a relaxed requirement for the case of switching topology. However, the main results are obtained at the cost of restricting the range of the controller gain. The range may be relaxed by seeking other methods, which is our future focus point.
There are some other interesting problems for the consensus of agents with cooperative and antagonistic interactions. Several topics, such as the convergence rate, the robustness against uncertainties, and the consensus with predictive mechanism, require future research.