On the Solution of Dynamic Stability Problem of Functionally Graded Viscoelastic Plates with Different Initial Conditions in Viscoelastic Media
Abstract
1. Introduction
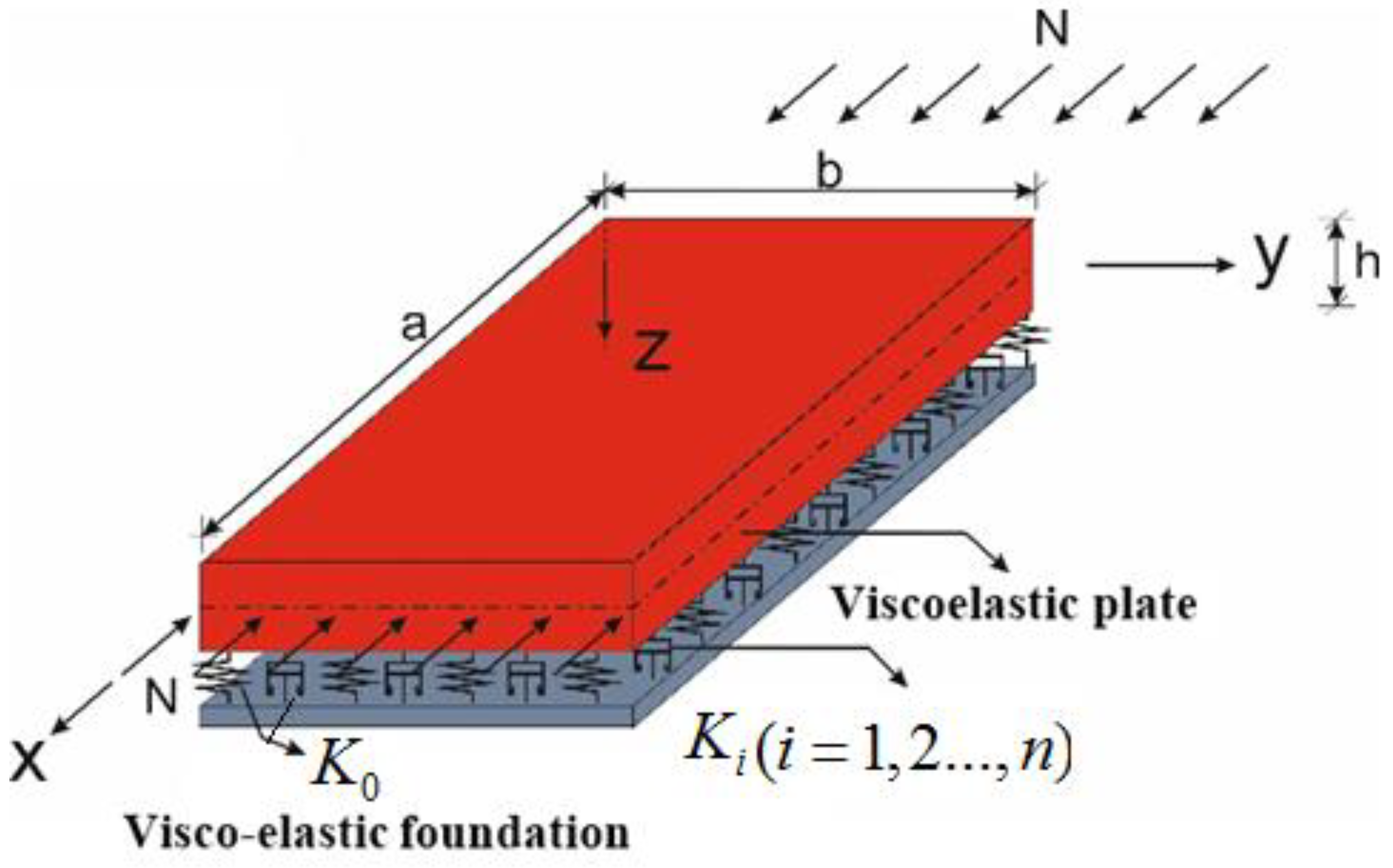
2. Mathematical Modeling of the Problem
2.1. Basic Relationships
2.2. Governing Equations
3. Solution Procedure
- (a)
- In the particular case, as or the first initial condition (FIC) and are satisfied, , (19) is transformed as:where
- (b)
- In the particular case, as or second initial conditions (SICs) and are satisfied, , Equation (19) turns into the following form:where
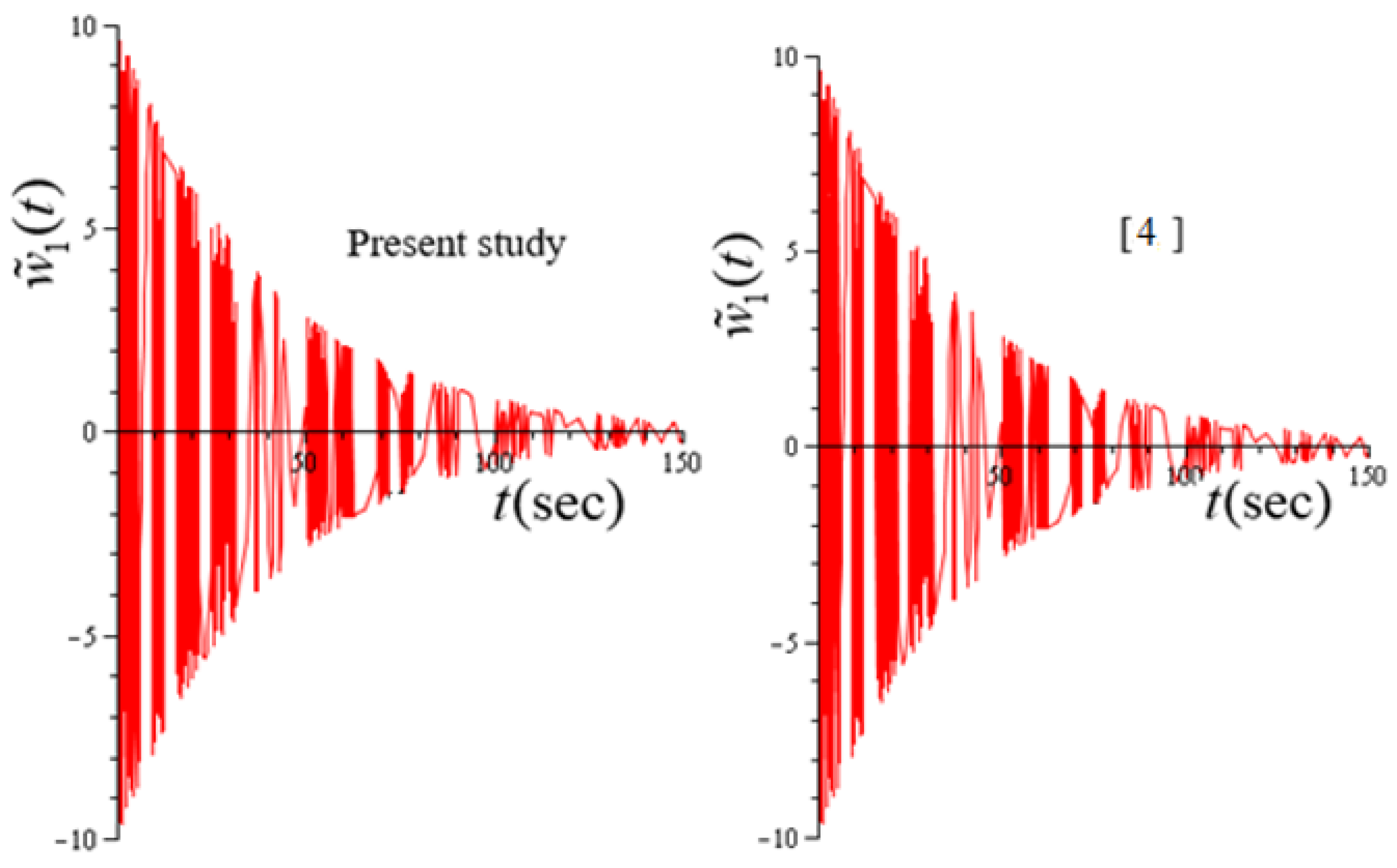
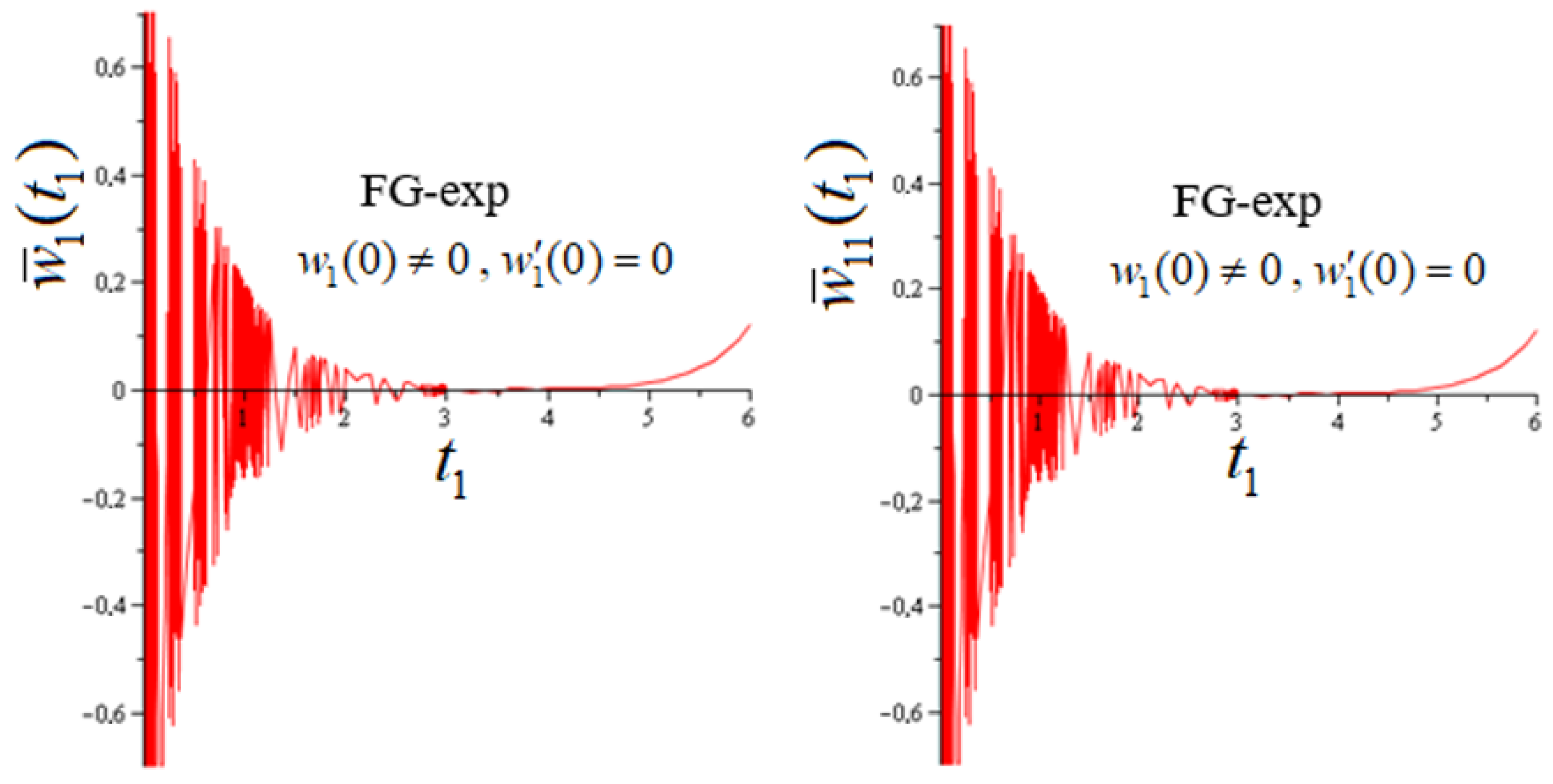
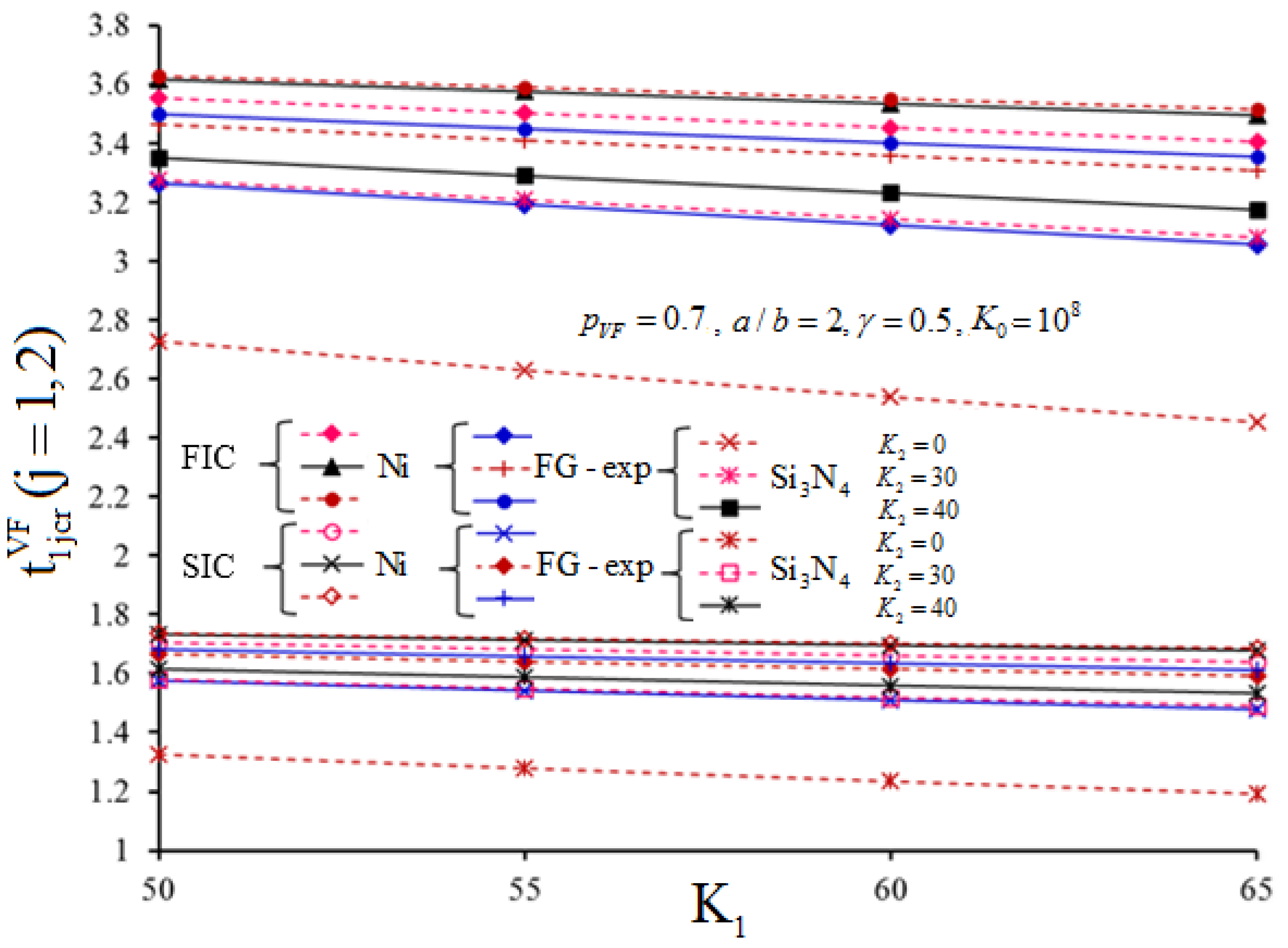
4. Numerical Analysis
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ogibalov, P.M.; Lomakin, V.A.; Kishkin, B.P. Mechanics of Polymers; Moscow State University: Moscow, Russia, 1975. (In Russian) [Google Scholar]
- Christensen, R.M. Theory of Viscoelasticity; Dover: New York, NY, USA, 1982. [Google Scholar]
- Drozdov, A.D.; Kolmanovskii, V.B. Stability in Viscoelasticity; Elsevier Science B.V.: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Matyash, V.I. Vibrations of isotropic viscoelastic shells. Polym. Mech. 1973, 7, 129–134. [Google Scholar] [CrossRef]
- Ding, R.; Zhu, Z.; Cheng, C. Some dynamical properties of a viscoelastic cylindrical shell. Appl. Math. Mech. Eng. Edit. 1999, 20, 233–240. [Google Scholar]
- Zenkour, A. Buckling of fiber-reinforced viscoelastic composite plates using various plate theories. J. Eng. Math. 2004, 50, 75–93. [Google Scholar] [CrossRef]
- Ilyasov, M. Dynamic stability of viscoelastic plates. Int. J. Eng. Sci. 2007, 45, 111–122. [Google Scholar] [CrossRef]
- Zhou, Y.F.; Wang, Z.M. Vibrations of axially moving viscoelastic plate with parabolically varying thickness. J. Sound. Vib. 2008, 316, 198–210. [Google Scholar]
- Ferreira, A.; Araújo, A.; Neves, A.; Rodrigues, J.; Carrera, E.; Cinefra, M.; Soares, C.M.M. A finite element model using a unified formulation for the analysis of viscoelastic sandwich laminates. Compos. Part B Eng. 2012, 45, 1258–1264. [Google Scholar] [CrossRef]
- Madeira, J.F.A.; Araujo, A.L.; Soares, C.M.M.; Soares, C.A.M.; Ferreira, A.J.M. Multi objective design of viscoelastic laminated composite sandwich panels. Compos. Part B Eng. 2015, 77, 391–401. [Google Scholar] [CrossRef]
- Alibeigloo, A. Effect of viscoelastic interface on three-dimensional static and vibration behavior of laminated composite plate. Compos. Part B Eng. 2015, 75, 17–28. [Google Scholar] [CrossRef]
- Zhou, X.; Yu, D.; Shao, X.; Zhang, S.; Wang, S. Research and applications of viscoelastic vibration damping materials: A review. Compos. Struct. 2016, 136, 460–480. [Google Scholar] [CrossRef]
- Luis, N.F.; Madeira, J.F.A.; Araujo, A.L.; Ferreira, A.J.M. Active vibration attenuation in viscoelastic laminated composite panels using multi objective optimization. Compos. Part B Eng. 2017, 28, 53–66. [Google Scholar] [CrossRef]
- Tekin, G.; Kadıoğlu, F. Viscoelastic behavior of shear-deformable plates. Int. J. Appl. Mech. 2017, 09, 1750085. [Google Scholar] [CrossRef]
- Bacciocchi, M.; Tarantino, A.M. Time-dependent behavior of viscoelastic three-phase composite plates reinforced by Carbon nanotubes. Compos. Struct. 2019, 216, 20–31. [Google Scholar] [CrossRef]
- Shen, H.S. Functionally Graded Materials, Nonlinear Analysis of Plates and Shells; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Tornabene, F.; Fantuzzi, N.; Viola, E.; Batra, R.C. Stress and strain recovery for functionally graded free-form and doubly-curved sandwich shells using higher-order equivalent single layer theory. Compos. Struct. 2015, 119, 67–89. [Google Scholar] [CrossRef]
- Mukherjee, S.; Paulino, G.H. The elastic-viscoelastic correspondence principle for functionally graded materials, revisited. J. Appl. Mech. 2003, 70, 359–363. [Google Scholar] [CrossRef]
- Ashrafi, H.; Shariyat, M.; Khalili, S.M.R.; Asemi, K. A boundary element formulation for the heterogeneous functionally graded viscoelastic structures. Appl. Math. Comput. 2013, 225, 246–262. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Elsibai, K.A.; Mashat, D.S. Elastic and viscoelastic solutions to rotating functionally graded hollow and solid cylinders. Appl. Math. Mech. Engl. Ed. 2008, 29, 1601–1616. [Google Scholar] [CrossRef]
- Shariyat, M.; Nasab, F.F. Low-velocity impact analysis of the hierarchical viscoelastic FGM plates, using an explicit shear-bending decomposition theory and the new DQ method. Compos. Struct. 2014, 113, 63–73. [Google Scholar] [CrossRef]
- Barretta, R.; Feo, L.; Luciano, R. Torsion of functionally graded nonlocal viscoelastic circular nanobeams. Compos. Part B Eng. 2015, 72, 217–222. [Google Scholar] [CrossRef]
- Deng, J.; Liu, Y.; Zhang, Z.; Liu, W. Stability analysis of multi-span viscoelastic functionally graded material pipes conveying fluid using a hybrid method. Eur. J. Mech.-A/Solids 2017, 65, 257–270. [Google Scholar] [CrossRef]
- Sofiyev, A. On the solution of the dynamic stability of heterogeneous orthotropic viscoelastic cylindrical shells. Compos. Struct. 2018, 206, 124–130. [Google Scholar] [CrossRef]
- Sofiyev, A. About an approach to the determination of the critical time of viscoelastic functionally graded cylindrical shells. Compos. Part B Eng. 2018, 156, 156–165. [Google Scholar] [CrossRef]
- Kerr, A.D. Elastic and viscoelastic foundation models. J. Appl. Mech. 1964, 31, 491–498. [Google Scholar] [CrossRef]
- Bajenov, V. The Bending of the Cylindrical Shells in an Elastic Medium; Visha Shkola: Kiev, Ukraine, 1975. (In Russian) [Google Scholar]
- Pouresmaeeli, S.; Ghavanloo, E.; Fazelzadeh, S.A. Vibration analysis of viscoelastic orthotropic nanoplates resting on viscoelastic medium. Compos. Struct. 2013, 96, 405–410. [Google Scholar] [CrossRef]
- Karličić, D.; Kozić, P.; Pavlović, R. Free transverse vibration of nonlocal viscoelastic orthotropic multi-nanoplate system (MNPS) embedded in a viscoelastic medium. Compos. Struct. 2014, 115, 89–99. [Google Scholar] [CrossRef]
- Zhang, D.-P.; Lei, Y.-J.; Wang, C.; Shen, Z.-B. Vibration analysis of viscoelastic single-walled carbon nanotubes resting on a viscoelastic foundation. J. Mech. Sci. Technol. 2017, 31, 87–98. [Google Scholar] [CrossRef]
- Zamani, H.A.; Aghdam, M.M.; Sadighi, M. Free vibration analysis of thick viscoelastic composite plates on vis-co-Pasternak foundation using higher-order theory. Compos. Struct. 2017, 182, 25–35. [Google Scholar] [CrossRef]
- Zeighampour, H.; Beni, Y.T.; Dehkordi, M.B. Wave propagation in viscoelastic thin cylindrical nanoshell resting on a visco-Pasternak foundation based on nonlocal strain gradient theory. Thin-Walled Struct. 2018, 122, 378–386. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Sobhy, M. Nonlocal piezo-hygrothermal analysis for vibration characteristics of a piezoelectric Kelvin-Voigt viscoelastic nanoplate embedded in a viscoelastic medium. Acta Mech. 2018, 229, 3–19. [Google Scholar] [CrossRef]
- Sophy, M.; Zenkour, A.M. The modified couple stress model for bending of normal deformable viscoelastic nanobeams resting on visco-Pasternak foundations. Mech. Adv. Matr. Struct. 2020, 27, 525–538. [Google Scholar]
- Sobhy, M.; Radwan, A.F. Influence of a 2D magnetic field on hygrothermal bending of sandwich CNTs-reinforced microplates with viscoelastic core embedded in a viscoelastic medium. Acta Mech. 2020, 231, 71–99. [Google Scholar] [CrossRef]
- Alazwari, M.A.; Zenkour, A.M.A. Quasi-3D refined theory for the vibration of functionally graded plates resting on vis-co-Winkler-Pasternak foundations. Mathematics 2022, 10, 716. [Google Scholar] [CrossRef]
- Frahlia, H.; Bennai, R.; Nebab, M.; Atmane, H.A.; Tounsi, A. Assessing effects of parameters of viscoelastic foundation on the dynamic response of functionally graded plates using a novel HSDT theory. Mech. Adv. Mater. Struct. 2022, 3, 1–15. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Allam, M.N.M.; Sobhy, M. Bending analysis of FG viscoelastic sandwich beams with elastic cores resting on Pasternak’s elastic foundations. Acta Mech. 2009, 212, 233–252. [Google Scholar] [CrossRef]
- Shariyat, M.; Alipour, M.M. A power series solution for vibration and complex modal stress analyses of variable thickness viscoelastic two-directional FGM circular plates on elastic foundations. Appl. Math. Model. 2013, 37, 3063–3076. [Google Scholar] [CrossRef]
- Liu, H.; Yang, J. Vibration of FG magneto-electro-viscoelastic porous nanobeams on visco-Pasternak foundation. Compos. Part B Eng. 2018, 155, 244–256. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Zerin, Z.; Kuruoglu, N. Dynamic behavior of FGM viscoelastic plates resting on elastic foundations. Acta Mech. 2019, 231, 1–17. [Google Scholar] [CrossRef]
- Zenkour, A.M.; El-Shahrany, H.D. Active control of a sandwich plate with reinforced magnetostrictive faces and viscoe-lastic core, resting on elastic foundation. J. Intel. Mater. Sys. Struct. 2021, 33, 1321–1337. [Google Scholar] [CrossRef]
- Li, H.; Gao, Z.; Zhao, J.; Ma, H.; Han, Q.; Liu, J. Vibration suppression effect of porous graphene platelet coating on fiber reinforced polymer composite plate with viscoelastic damping boundary conditions resting on viscoelastic foundation. Eng. Struct. 2021, 237, 112167. [Google Scholar] [CrossRef]
- Yuan, Y.; Niu, Z.; Smitt, J. Magneto-hygro-thermal vibration analysis of the viscoelastic nanobeams reinforcedwith carbon nanotubes resting on Kerr’s elastic foundation based on NSGT. Adv. Compos. Mater. 2022, 1–23. [Google Scholar] [CrossRef]



| Ni | FG-exp. | Si3N4 | Ni | FG-exp. | Si3N4 | |
|---|---|---|---|---|---|---|
| 0.1 | 4.236 | 4.434 | 4.669 | 2.031 | 2.13 | 2.248 |
| 0.3 | 3.686 | 3.884 | 4.12 | 1.757 | 1.856 | 1.973 |
| 0.5 | 3.431 | 3.629 | 3.864 | 1.629 | 1.728 | 1.845 |
| 0.7 | 3.263 | 3.461 | 3.696 | 1.545 | 1.644 | 1.761 |
| 0.1 | 4.6 | 4.742 | 4.93 | 2.207 | 2.279 | 2.374 |
| 0.3 | 4.011 | 4.16 | 4.354 | 1.912 | 1.988 | 2.086 |
| 0.5 | 3.737 | 3.889 | 4.086 | 1.775 | 1.853 | 1.952 |
| 0.7 | 3.556 | 3.711 | 3.91 | 1.685 | 1.764 | 1.864 |
| 0.1 | 3.971 | 3.705 | 3.136 | 1.918 | 1.797 | 1.529 |
| 0.3 | 3.807 | 3.8 | 3.648 | 1.821 | 1.825 | 1.762 |
| 0.5 | 3.62 | 3.679 | 3.659 | 1.724 | 1.759 | 1.758 |
| 0.7 | 3.476 | 3.565 | 3.607 | 1.65 | 1.699 | 1.728 |
| 0.1 | 3.987 | 3.759 | 3.313 | 1.925 | 1.822 | 1.613 |
| 0.3 | 3.803 | 3.806 | 3.71 | 1.819 | 1.827 | 1.789 |
| 0.5 | 3.611 | 3.673 | 3.68 | 1.719 | 1.755 | 1.766 |
| 0.7 | 3.465 | 3.553 | 3.609 | 1.644 | 1.692 | 1.727 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sofiyev, A. On the Solution of Dynamic Stability Problem of Functionally Graded Viscoelastic Plates with Different Initial Conditions in Viscoelastic Media. Mathematics 2023, 11, 823. https://doi.org/10.3390/math11040823
Sofiyev A. On the Solution of Dynamic Stability Problem of Functionally Graded Viscoelastic Plates with Different Initial Conditions in Viscoelastic Media. Mathematics. 2023; 11(4):823. https://doi.org/10.3390/math11040823
Chicago/Turabian StyleSofiyev, Abdullah. 2023. "On the Solution of Dynamic Stability Problem of Functionally Graded Viscoelastic Plates with Different Initial Conditions in Viscoelastic Media" Mathematics 11, no. 4: 823. https://doi.org/10.3390/math11040823
APA StyleSofiyev, A. (2023). On the Solution of Dynamic Stability Problem of Functionally Graded Viscoelastic Plates with Different Initial Conditions in Viscoelastic Media. Mathematics, 11(4), 823. https://doi.org/10.3390/math11040823






