Polynomial Chaos Expansion-Based Enhanced Gaussian Process Regression for Wind Velocity Field Estimation from Aircraft-Derived Data
Abstract
1. Introduction
1.1. Motivation
1.2. State of the Art
2. Methods
2.1. Data Derivation and Exploratory Analysis
2.1.1. Data Source
2.1.2. ADS-B and Mode S Systems
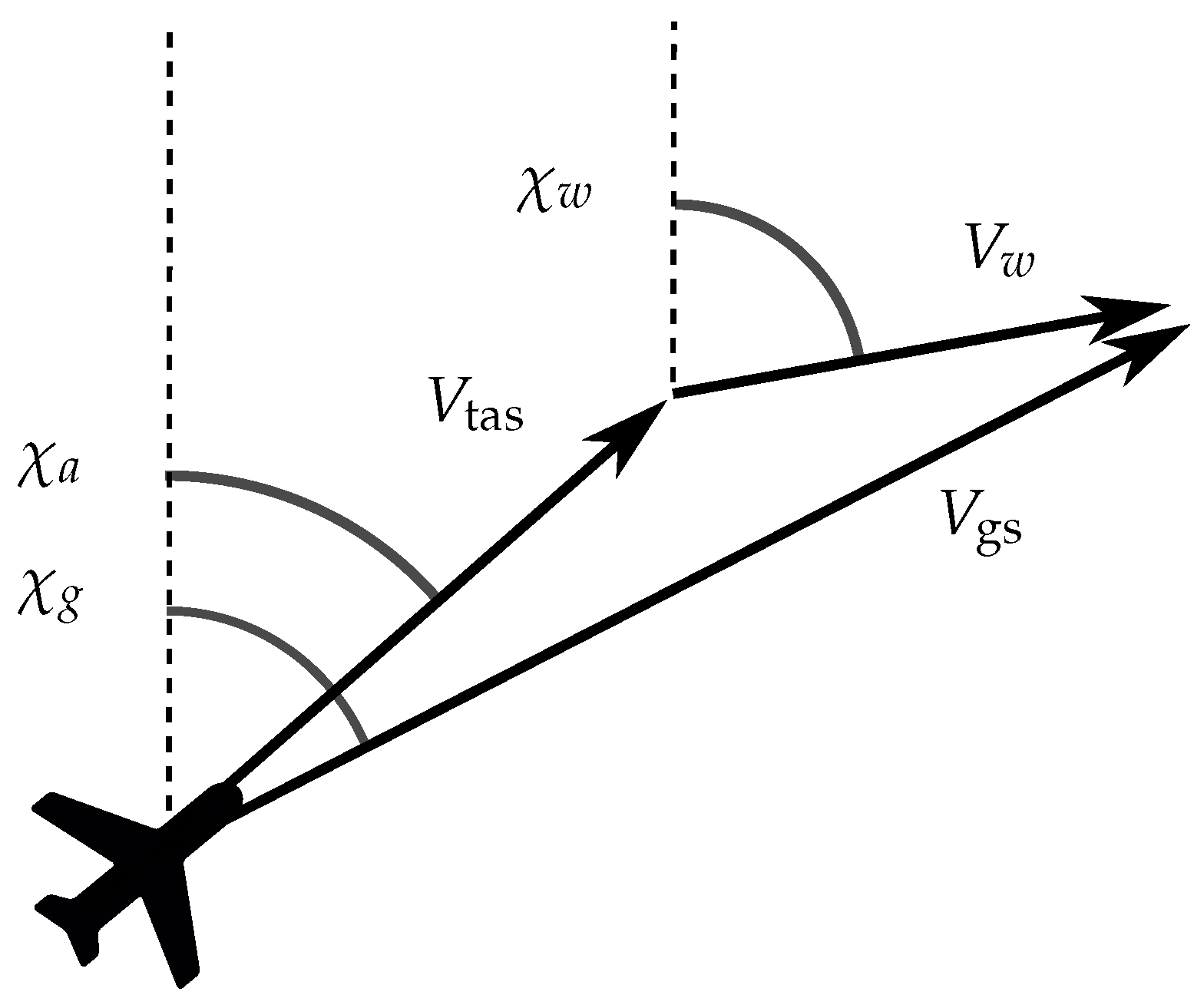
2.1.3. Wind Velocity Derivation from ADS-B and Mode S Data
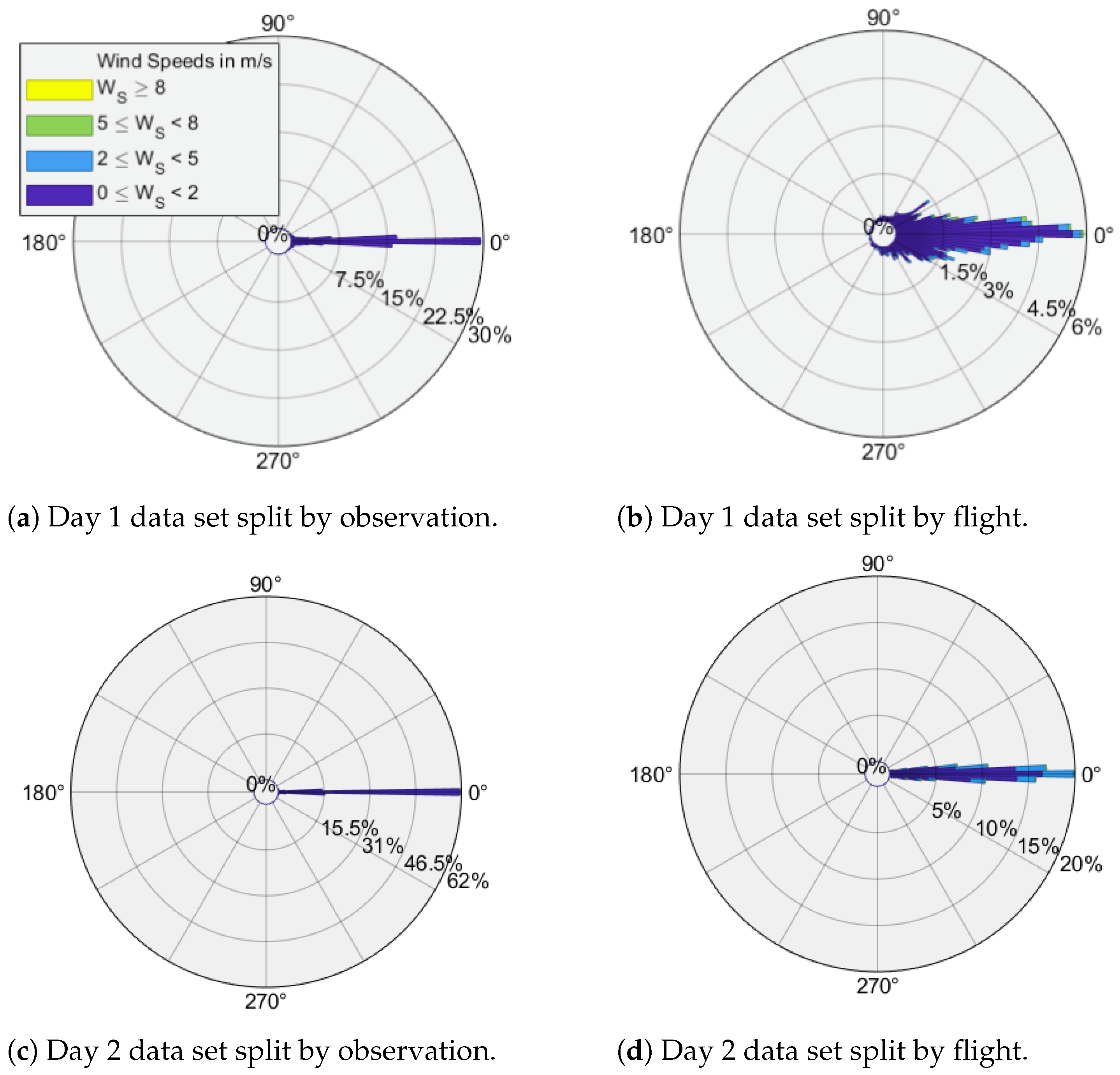
2.1.4. Exploratory Data Analysis
2.2. Gaussian Process Regression
2.3. Polynomial Chaos Expansion
2.4. Polynomial Chaos Expansion-Based Enhanced Gaussian Process Regression
2.5. Adaptation of PCE-GPR to the Wind Velocity Output
3. Results
3.1. Model Set Up
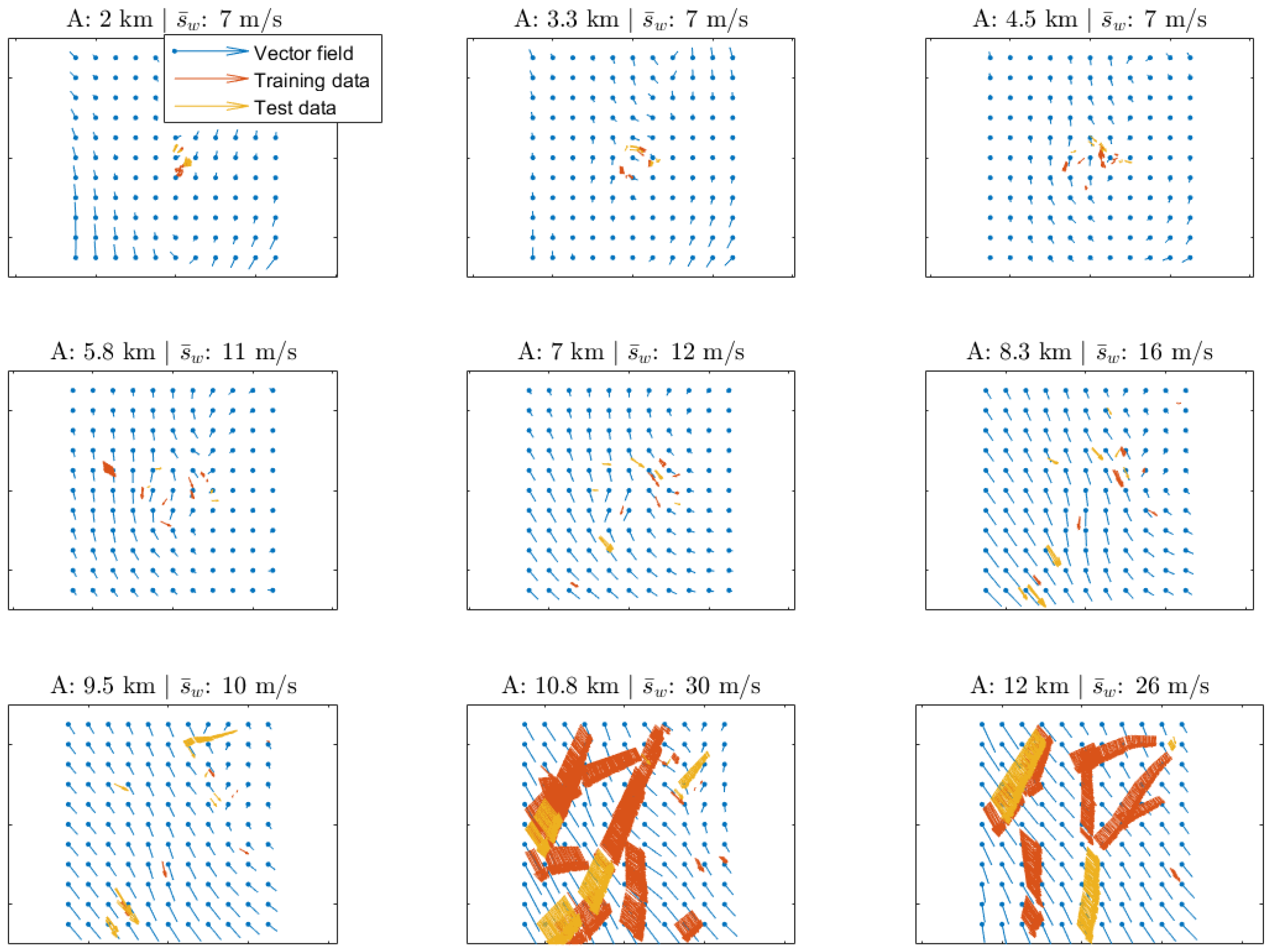
3.2. Wind Velocity Field Reconstruction
- By randomly choosing sets of individual observations, which will be referred to as data set randomly split by observation.
- By randomly selecting sets of flights, employing the individual observations gathered from them, which will be referred to as a data set randomly split by flight.
3.3. Wind Velocity Field Short-Term Prediction
3.4. Validation of the PCE-GPR Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hernández-Romero, E.; Valenzuela, A.; Rivas, D. Probabilistic multi-aircraft conflict detection and resolution considering wind forecast uncertainty. Aerosp. Sci. Technol. 2020, 105, 105973. [Google Scholar] [CrossRef]
- Dalmau, R.; Prats, X.; Baxley, B. Using broadcast wind observations to update the optimal descent trajectory in real-time. J. Air Transp. 2020, 28, 82–92. [Google Scholar] [CrossRef]
- Reynolds, T.G.; McPartland, M. Establishing wind information needs for four dimensional trajectory-based operations. In Proceedings of the 1st International Conference on Interdisciplinary Science for Innovative Air Traffic Management, Daytona Beach, FL, USA, 25–27 June 2012. [Google Scholar]
- Reynolds, T.G.; McPartland, M.; Teller, T.; Troxel, S. Exploring wind information requirements for four dimensional trajectory-based operations. In Proceedings of the 11th USA/Europe Air Traffic Management Research and Development Seminar, Lisbon, Portugal, 23–26 June 2015. [Google Scholar]
- de Haan, S. High-resolution wind and temperature observations from aircraft tracked by Mode-S air traffic control radar. J. Geophys. Res. Atmos. 2011, 116, D10111. [Google Scholar] [CrossRef]
- Sun, J.; Vû, H.; Ellerbroek, J.; Hoekstra, J.M. pyModeS: Decoding Mode-S surveillance data for open air transportation research. IEEE Trans. Intell. Transp. Syst. 2020, 21, 2777–2786. [Google Scholar] [CrossRef]
- Sun, J. The 1090 Megahertz Riddle: A Guide to Decoding Mode S and ADS-B Signals; TU Delft OPEN Publishing: Delft, The Netherlands, 2021. [Google Scholar]
- Guzzi, R. Data Assimilation: Mathematical Concepts and Instructive Examples; Springer: Cham, Switzerland, 2016. [Google Scholar]
- de Haan, S.; Stoffelen, A. Assimilation of high-resolution Mode-S wind and temperature observations in a regional NWP model for nowcasting applications. Weather Forecast. 2012, 27, 918–937. [Google Scholar] [CrossRef]
- Cardinali, C.; Isaksen, L.; Andersson, E. Use and impact of automated aircraft data in a global 4DVAR data assimilation system. Mon. Weather Rev. 2003, 131, 1865–1877. [Google Scholar] [CrossRef]
- Talagrand, O. Assimilation of observations, an introduction. J. Meteorol. Soc. Jpn. 1997, 75, 191–209. [Google Scholar] [CrossRef]
- de Jong, P.M.A.; van der Laan, J.J.; in ’t Veld, A.C.; van Paassen, M.M.; Mulder, M. Wind-profile estimation using airborne sensors. J. Aircr. 2014, 51, 1852–1863. [Google Scholar] [CrossRef]
- Liu, T.; Xiong, T.; Thomas, L.; Liang, Y. ADS-B based wind speed vector inversion algorithm. IEEE Access 2020, 8, 150186–150198. [Google Scholar] [CrossRef]
- Dalmau, R.; Pérez-Batlle, M.; Prats, X. Estimation and prediction of weather variables from surveillance data using spatio-temporal Kriging. In Proceedings of the 2017 IEEE/AIAA 36th Digital Avionics Systems Conference, St., Petersburg, FL, USA, 17–21 September 2017. [Google Scholar]
- Sun, J.; Vû, H.; Ellerbroek, J.; Hoekstra, J.M. Weather field reconstruction using aircraft surveillance data and a novel meteo-particle model. PLoS ONE 2018, 13, e0205029. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, H.; Li, J.; Xu, Z. Research and optimization of meteo-particle model for wind retrieval. Atmosphere 2021, 12, 1114. [Google Scholar] [CrossRef]
- Enea, G.; McPartland, M. Wind enhancements for trajectory based operations automation. In Proceedings of the AIAA Aviation 2022 Forum, Chicago, IL, USA, 27 June–1 July 2022. [Google Scholar]
- Marinescu, M.; Olivares, A.; Staffetti, E.; Sun, J. Wind profile estimation from aircraft derived data using Kalman filters and Gaussian process regression. In Proceedings of the 14th USA/Europe ATM Research and Development Seminar, Virtual Event, 20–23 September 2021. [Google Scholar]
- Marinescu, M.; Olivares, A.; Staffetti, E.; Sun, J. On the estimation of vector wind profiles using aircraft-derived data and Gaussian process regression. Aerospace 2022, 9, 377. [Google Scholar] [CrossRef]
- Marinescu, M.; Olivares, A.; Staffetti, E.; Sun, J. Wind field estimation from aircraft derived data using Gaussian process regression. PLoS ONE 2022, 17, e0276185. [Google Scholar] [CrossRef] [PubMed]
- Wiener, N. The homogeneous chaos. Am. J. Math. 1938, 60, 897–936. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G.E. The Wiener-Askey polynomial chaos for stochastic differential equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Oladyshkin, S.; Nowak, W. Data-driven uncertainty quantification using the arbitrary polynomial chaos expansion. Reliab. Eng. Syst. Saf. 2012, 106, 179–190. [Google Scholar] [CrossRef]
- Schöbi, R.; Sudret, B.; Wiart, J. Polynomial-chaos-based Kriging. Int. J. Uncertain. Quantif. 2015, 5, 171–193. [Google Scholar] [CrossRef]
- Schöbi, R.; Sudret, B.; Marelli, S. Rare event estimation using polynomial-chaos Kriging. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2017, 3, D4016002. [Google Scholar] [CrossRef]
- Martino, L.; Read, J. A joint introduction to Gaussian processes and relevance vector machines with connections to Kalman filtering and other kernel smoothers. Inf. Fusion 2021, 74, 17–38. [Google Scholar] [CrossRef]
- ASTERIX Official Web Page. Available online: https://www.eurocontrol.int/asterix (accessed on 15 November 2022).
- EUROCONTROL Technical Document Part12-CAT021. Available online: https://www.eurocontrol.int/publication/cat021-eurocontrol-specification-surveillance-data-exchange-asterix-part-12-category-21 (accessed on 15 November 2022).
- EUROCONTROL Technical Document Part04-CAT048. Available online: https://www.eurocontrol.int/publication/cat048-eurocontrol-specification-surveillance-data-exchange-asterix-part4 (accessed on 15 November 2022).
- Jammalamadaka, S.R.; Sengupta, A. Topics in Circular Statistics; World Scientific Publishing: Singapore, 2001. [Google Scholar]
- Rasmussen, C.E.; Williams, C. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Shi, J.Q.; Choi, T. Gaussian Process Regression Analysis for Functional Data; Chapman and Hall: London, UK, 2011. [Google Scholar]
- Torre, E.; Marelli, S.; Embrechts, P.; Sudret, B. Data-driven polynomial chaos expansion for machine learning regression. J. Comput. Phys. 2019, 388, 601–623. [Google Scholar] [CrossRef]
- Wan, X.; Karniadakis, G.E. Beyond Wiener-Askey expansions: Handling arbitrary PDFs. J. Sci. Comput. 2006, 27, 455–464. [Google Scholar] [CrossRef]
- Oladyshkin, S.; Nowak, W. Incomplete statistical information limits the utility of high-order polynomial chaos expansions. Reliab. Eng. Syst. Saf. 2018, 169, 137–148. [Google Scholar] [CrossRef]
- Gramacki, A. Nonparametric Kernel Density Estimation and Its Computational Aspects; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Chapman and Hall: London, UK, 1986. [Google Scholar]
- The Modified Rastrigin Function. Available online: https://uqworld.org/t/modified-rastrigin-function/126 (accessed on 15 November 2022).
- Wang, B.; Chen, T. Gaussian process regression with multiple response variables. Chemom. Intell. Lab. Syst. 2015, 142, 159–165. [Google Scholar] [CrossRef]
- Stein, M.L. The loss of efficiency in Kriging prediction caused by misspecifications of the covariance structure. Geostatistics 1989, 4, 273–282. [Google Scholar]
- Micchelli, C.A.; Xu, Y.; Zhang, H. Universal kernels. J. Mach. Learn. Res. 2006, 7, 2651–2667. [Google Scholar]
- Bo, L.; Sminchisescu, C. Greedy block coordinate descent for large scale Gaussian process regression. In Proceedings of the Proceedings of the Twenty-Fourth Conference on Uncertainty in Artificial Intelligence, Helsinki, Finland, 9–12 July 2008. [Google Scholar]
- Masutti, A. Single European sky—A possible regulatory framework for System Wide Information Management (SWIM). Air Space Law 2011, 36, 275–292. [Google Scholar] [CrossRef]
- SWIM Project. Available online: https://www.eurocontrol.int/concept/system-wide-information-management (accessed on 15 November 2022).
- AIRBUS: 4D-TBO. Available online: https://www.airbus.com/en/newsroom/stories/2020-12-4d-tbo-a-new-approach-to-aircraft-trajectory-prediction (accessed on 15 November 2022).

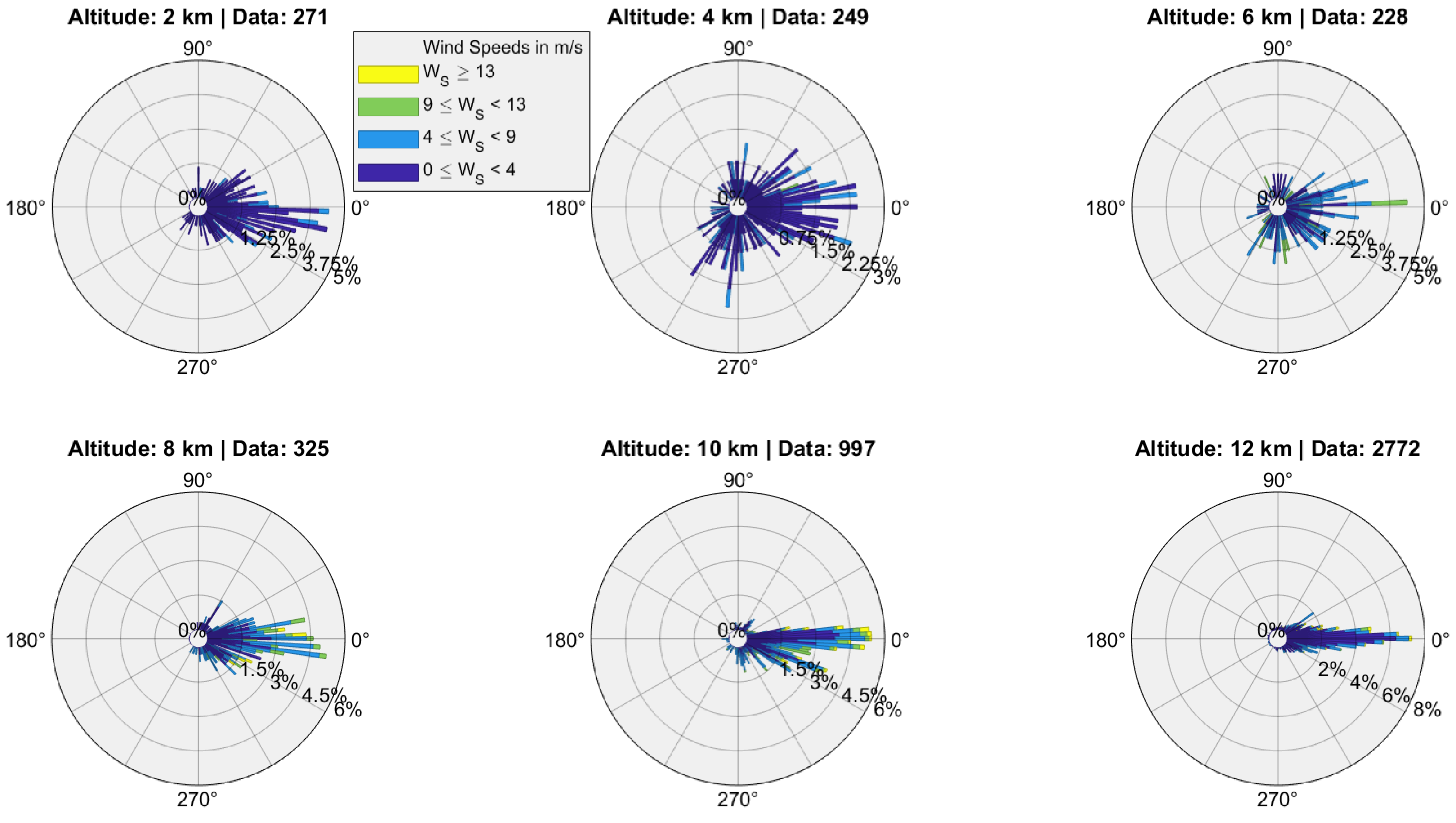
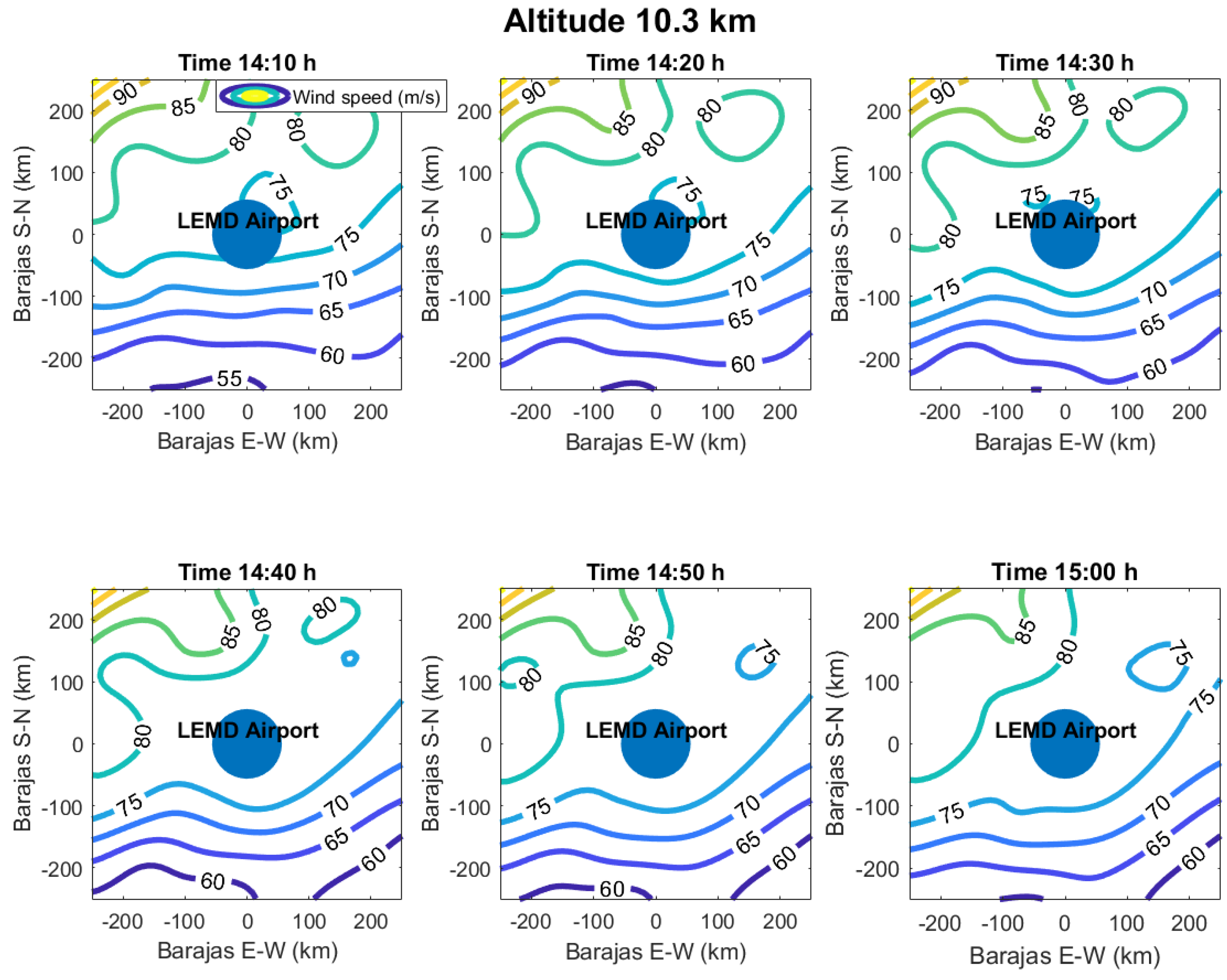
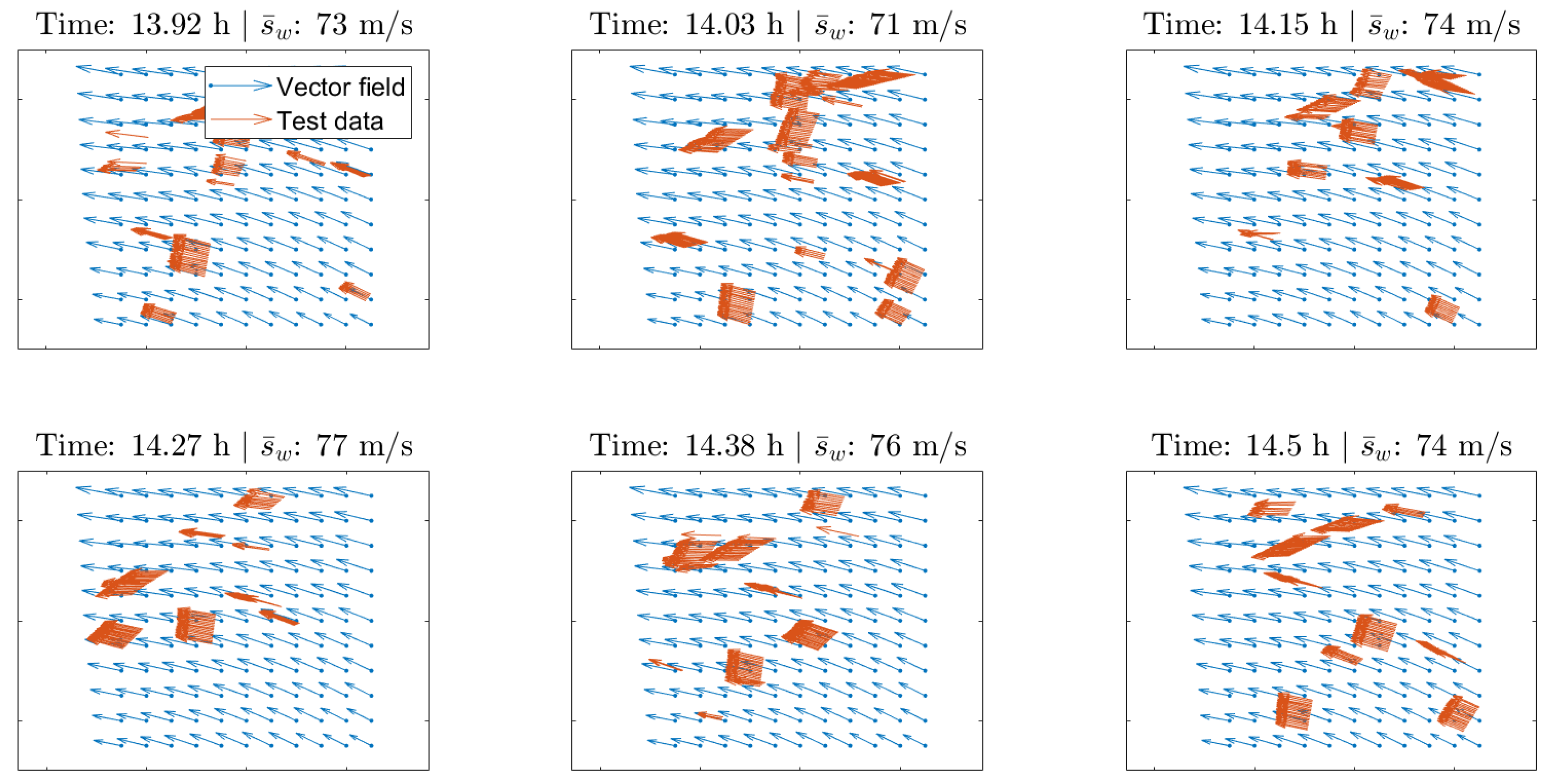
| Wind Speed (m/s) | Wind Direction (Deg) | |||
|---|---|---|---|---|
| Day 1 | Day 2 | Day 1 | Day 2 | |
| Min. | 0 | 0.013 | 0.01 | 163.79 |
| Max. | 56.04 | 100.75 | 359.99 | 351.55 |
| Mean | 17.80 | 60.56 | 307.16 | 166.66 |
| Dispersion | 11.30 | 16.67 | 19.40 (%) | 2.11 (%) |
| Data Set Split by Observation | Data Set Split by Flight | ||||
|---|---|---|---|---|---|
| Measure of Error | Component | Day 1 | Day 2 | Day 1 | Day 2 |
| RMSE (m/s) | u | 2.26 (18%) | 1.50 (21%) | 5.84 (1%) | 6.06 (−4%) |
| v | 1.46 (44%) | 1.45 (22%) | 4.79 (14%) | 4.84 (1%) | |
| MAE (m/s) | u | 1.17 (22%) | 0.99 (22%) | 4.46 (−1%) | 4.37 (−2%) |
| v | 0.83 (43%) | 1.05 (19%) | 3.45 (13%) | 3.59 (3%) | |
| MAD (m/s) | u | 0.53 (23%) | 0.64 (22%) | 3.60 (−6%) | 3.03 (−2%) |
| v | 0.49 (31%) | 0.80 (15%) | 2.44 (9%) | 2.70 (5%) | |
| Measure of Error | Component | Day 1 | Day 2 |
|---|---|---|---|
| RMSE (m/s) | u | 5.28 (6%) | 6.37 (13%) |
| v | 5.16 (6%) | 5.80 (8%) | |
| MAE (m/s) | u | 4.00 (12%) | 4.19 (29%) |
| v | 3.93 (12%) | 4.40 (15%) | |
| MAD (m/s) | u | 3.00 (4%) | 3.25 (12%) |
| v | 3.07 (3%) | 3.52 (4%) |
| Measure | Variable | Day 1 | Day 2 |
|---|---|---|---|
| Bias (m/s) | Wind speed | −2.75 | −0.24 |
| MAE (m/s) | Wind speed | 4.5 | 5.79 |
| Bias (deg) | Wind direction | 2.06 | −1.36 |
| Dispersion (%) | Wind direction | 8.5 | 0.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marinescu, M.; Olivares, A.; Staffetti, E.; Sun, J. Polynomial Chaos Expansion-Based Enhanced Gaussian Process Regression for Wind Velocity Field Estimation from Aircraft-Derived Data. Mathematics 2023, 11, 1018. https://doi.org/10.3390/math11041018
Marinescu M, Olivares A, Staffetti E, Sun J. Polynomial Chaos Expansion-Based Enhanced Gaussian Process Regression for Wind Velocity Field Estimation from Aircraft-Derived Data. Mathematics. 2023; 11(4):1018. https://doi.org/10.3390/math11041018
Chicago/Turabian StyleMarinescu, Marius, Alberto Olivares, Ernesto Staffetti, and Junzi Sun. 2023. "Polynomial Chaos Expansion-Based Enhanced Gaussian Process Regression for Wind Velocity Field Estimation from Aircraft-Derived Data" Mathematics 11, no. 4: 1018. https://doi.org/10.3390/math11041018
APA StyleMarinescu, M., Olivares, A., Staffetti, E., & Sun, J. (2023). Polynomial Chaos Expansion-Based Enhanced Gaussian Process Regression for Wind Velocity Field Estimation from Aircraft-Derived Data. Mathematics, 11(4), 1018. https://doi.org/10.3390/math11041018









