Collaborative Decision Model for Allocating Intensive Care Units Beds with Scarce Resources in Health Systems: A Portfolio Based Approach under Expected Utility Theory and Bayesian Decision Analysis

Abstract

The COVID-19 pandemic has brought health systems to the brink of collapse in several regions around the world, as the demand for health care has outstripped the capacity of their services, especially regarding intensive care. In this context, health system managers have faced a difficult question: who should be admitted to an intensive care unit (ICU), and who should not? This paper addresses this decision problem using Expected Utility Theory and Bayesian decision analysis. In order to estimate the chances of survival for patients, a structured protocol has been proposed conjointly with physicians, based on the Sequential Organ Failure Assessment (SOFA) score. A portfolio selection approach is proposed to support tackling the ICU allocation problem. A simulation study shows that the proposed approach is more advantageous than other approaches already presented in the literature, with respect to the number of lives saved. The patients’ probabilities of survival inside and outside the ICU are important parameters of the model. However, assessing such probabilities can be a difficult task for health professionals. In order to give due treatment to the imprecise information regarding these probabilities, a Monte Carlo simulation is used to estimate the probabilities of recommending a patient be admitted to the ICU is the most appropriate decision, given the conditions presented. The methodology was implemented in an Information and Decision System called SIDTriagem, which is available online for free. With regards to managerial implications, SIDTriagem has a great potential to help in the response to public health emergencies systems as it facilitates rational decision-making regarding allocating ICU beds when resources are scarce.

1. Introduction

In view of the excessive demands placed on health systems caused by the new coronavirus disease (COVID-19) outbreaks, many health professionals have faced a difficult, clinical and ethical question: who should receive life-supporting intensive care when there is a shortfall in the resources available, especially when the occupancy of beds in the Intensive Care Unit (ICU) and wards of hospitals is near capacity? This is the ICU allocation problem.

Despite some regions seeming to have already undergone the worst period of the COVID-19 outbreak, there is concern about the possible emergence of new waves of infections as a consequence of relaxing non-pharmacological measures and social distancing advice [1,2]. Given the potential for new public health emergencies, it is recognized that it is essential that health system managers make preparations to respond to these, and therefore that they must draw up structured protocols, with objective criteria, for admitting patients to and discharging them from hospital beds [3].

Hence, the main objective of this paper is to propose a structured protocol based on the clinical evaluation of the patients. This protocol has been proposed conjointly with physicians in order to estimate chances of survival based on important clinical variables of the patients, such as respiratory condition, cardiovascular condition, coagulation related aspects, creatinine, bilirubin, blood oxygen saturation, among other critical factors. Hence, this tool can be used to support health system managers to deal with the problem of allocating ICU beds in resource-limited circumstances, a current reality in many places due to the COVID-19 pandemic.

Previous studies have been developed concerning the triage problem and ICU allocation problem [4,5]. However, it should be highlighted here that the present study brings two main contributions compared to the model proposed by Frej et al. [5]. First, in Frej et al. [5], the chances of survival of a patient inside and outside ICU were stablished in an ad-hoc manner, without a structured protocol based on the clinical evaluation of the patients. Hence, in this sense, such interaction with doctors to build this model is one of the major contributions of this paper compared to the previous one since using the protocol it is possible to make such evaluation in an objective way, instead of considering physicians subjective judgment. Also, in this study the Sequential Organ Failure Assessment (SOFA) score [6] has been presented in order to aid such estimation. The use of SOFA is a novelty of the study. Second, in this work, a simulation study is performed to compare the efficiency of the proposed optimization model compared to three other approaches for tackling the ICU allocation process: admitting to the ICU patients with the highest probabilities of surviving their stay there (maximizing the ICU outcome); admitting to the ICU patients who have the lowest probabilities of survival outside the ICU; random selection. A simulation algorithm was developed to make such comparison, and the results obtained have shown that the proposed model outperforms these other approaches, leading to a higher number of lives saved.

In this study, the ICU allocation problem is investigated and structured as a portfolio selection problem [7], where the objective is to choose the set of patients for admission to the ICU such that the overall expected utility for the entire group of patients requiring intensive care at the same time is maximized [8]. A binary linear programming model based on the ideas of Frej et al. [5] is presented, which considers the probabilities of each patient surviving a stay in and outside the ICU. In order to compare the decision rule that we propose with other rules already presented in the literature, we defined the utilities of the model in such a way that the overall expected utility reflects the expected number of surviving patients, and obtained some results by conducting simulations.

Given that assessing the patients’ probabilities of survival can be a difficult task for health professionals, the main research question that motivates the development of this paper is how to address the ICU allocation problem through a utility-based portfolio optimization model considering imprecise information to estimate patients’ probabilities of survival in different scenarios? To deal with this problem, we propose a method that considers objective information, namely the Sequential Organ Failure Assessment (SOFA) score [6], from which the patient’s chances of survival are inferred.

The method was developed together with experts (doctors and researchers), and draws on the knowledge acquired from their experience and from papers published in scientific journals. Bayesian decision analysis is considered in the model in order to deal with the uncertainty inherently involved in the chances of survival of patients inside and outside ICU, according to the health conditions under which they arrive ate hospital. The chances of survival are defined as ranges of possible values for the patients’ probabilities of survival, in an approach that is appropriate for dealing with the uncertainties and variability inherent to this problem. In order to deal with imprecise information, a method based on Monte Carlo simulation [9] is proposed in order to calculate, for each patient, the robustness index of the recommendation for an ICU stay: this index indicates the probability that such a recommendation is the most appropriate in view of the presented conditions.

The proposed methodology was implemented in an Information and Decision System (IDS), called SIDTriagem, which is available online for free to users worldwide. The IDS was developed to be a tool that facilitates rational decision-making in the context of the ICU allocation problem, even under stressful conditions, thus ensuring decisions that are aligned with the policies defined by public health authorities. The development of the proposed methodology and the IDS was prompted by the critical situation experienced in many health systems during COVID-19 major outbreaks. However, the results of this study can be directly extended to other contexts, since the method for estimating a patient’s chances of survival is not restricted to COVID-19 patients.

This paper is structured as follows: Section 2 presents a brief background on the context of the COVID-19 pandemic, as well as previous approaches developed for dealing with the ICU allocation problem. In Section 3, a utility model based on a portfolio selection approach that is proposed to solve the ICU allocation problem is presented. Section 4 presents the materials and methods of this research, with the description of a method for estimating the patients’ chances of surviving a stay in and outside the ICU, which is based on the SOFA score, as well as the presentation of SIDTriagem, an IDS developed to operationalize the proposed methodology in order to support users who have to deal with the ICU allocation problem. The results and discussion of a simulation study performed to compare different approaches for solving this problem are presented in Section 5. Finally, Section 6 draws some conclusions and makes suggestions for future lines of research in this area.

2. Background

Deeply concerned by the alarming levels of the spread and severity of the new coronavirus disease (COVID-19), the World Health Organization (WHO) [10] declared on 11 March 2020 that it can be characterized as a pandemic [10]. This disease is caused by the Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2), an infectious agent with a high transmission efficiency that has facilitated its spread, and has led to major outbreaks of the disease in various regions around the world [11,12,13].

The clinical spectrum of SARS-CoV-2 infection has been shown to be wide. This ranges from patients having an asymptomatic infection to a mild respiratory illness and to severe acute respiratory syndrome [14]. Patients with a severe condition often require health treatment in an Intensive Care Unit (ICU), and to receive mechanical ventilation in the ICU [14]. Despite a relatively small proportion of infected people requiring hospitalization (this proportion ranges from 1.1% in the 20–29 year-old age group up to 18.4% in those aged 80 and older) [15], the high speed at which contagion by SARS-CoV-2 spreads has led to the near collapse of health systems in several regions around the world, thereby causing a demand for health care (especially intensive care) that can rapidly exceed the capacity of a health system’s services.

With regards to the treatment of ICU allocation, the literature presents several approaches for dealing with this problem. A systematic literature review of modeling tools to address inpatient bed management is presented by He et al. [16]. The authors highlight that this is a complex problem which involves distinct factors such as unexpected admissions, uncertainties related to length of stay of the patient and demand fluctuations.

In order to model the ICU allocation problem, in the literature it can be seen that several different approaches are addressed by authors, such as the use of big data and machine learning models [17]; regression models [18]; and discrete event simulation [19]. Another relevant topic related to ICU allocation problems that is well addressed in the literature is related to ethical issues that may arise in these situations, since human lives are involved [20,21,22]. Other authors still treat issues related to attitudes and perceptions of health professions related to such delicate decision situations such as ICU allocation [23,24].

As previously mentioned in the previous section, this paper aims to present a portfolio optimization model is proposed to address the ICU allocation problem based on the expected utility theory developed by Keeney & Raiffa [8]. If compared to other alternative approaches, an alternative way to deal with decision problems of this type with a simple ranking of the alternatives (and select patients until the restriction is not satisfied). However, the main motivation to use the portfolio optimization approach to deal with this problem instead of simply ranking patients is that, even with items (patients) being independent from each other—which is the case-, a ranking approach would not guarantee that the overall utility of the group selected would be maximized, whereas the portfolio optimization does that. Actually, in the literature, several portfolio optimization models are used for dealing with independent items [25,26].

In this sense, the contribution of this paper can be perceived in both methodological and practical terms: methodologically speaking, we develop a structured decision model to aid decision problems of ICU allocation; practically speaking, we develop an Information Decision System which operationalizes the proposed model and that can be used for doctors worldwide. In this sense, this research can be considered in a multidisciplinary way: the operations research (OR) model is presented as the basis to build the proposed Information Decision System, which doctors can use to solve their practical decision problems.

3. A Portfolio Selection Approach to Support the Allocation of Patients to ICU Beds

In order to introduce an approach for modelling the ICU allocation decision problem based on a portfolio selection problem, let us consider the following situation: in a generic health unit, ICU admission was requested for n patients who have previously undergone a triage process. Let us assume, however, that this health unit only has m available ICU beds and so m < n. Therefore, a decision must be made at this point: which of these n patients should occupy the m available ICU beds? This is a difficult decision since by defining who receives intensive care, the decision-maker (DM) also defines who does not receive it and remains in the ICU queue. This decision situation has an important stochastic factor: the patients’ probabilities of survival in and outside the ICU. For each patient being analyzed, four possible scenarios are possible: he/she survives the stay in the ICU, he/she survives outside the ICU, he/she dies in the ICU or he/she dies outside the ICU.

Let $y_i \left(i=1, \dots , n\right)$ be a binary decision variable in such a way that $y_i=1$ if the patient $i$ is selected to go to the ICU and $y_i=0$ otherwise. Let $p_i\left(S_{icu}\right)$ be the probability of survival of patient $i$ in the ICU and let $p_i\left(S_{out}\right)$ be the probability of survival of the patient $i$ outside the ICU. Taking these probabilities into consideration, an expected utility model [8] can be built in order to evaluate each alternative situation. For each patient $i$, the expected utility of his/her going to the ICU and not going to the ICU can be calculated as per Equations (1) and (2), respectively.

$$E{U}_i\left(y_i=1\right)=u_i\left(1\right)=p_i\left(S_{icu}\right).u\left(S_{icu}\right)+\left[1-p_i\left(S_{icu}\right)\right].u\left(D_{icu}\right)$$

(1)

$$E{U}_i\left(y_i=0\right)=u_i\left(0\right)=p_i\left(S_{out}\right).u\left(S_{out}\right)+\left[1-p_i\left(S_{out}\right)\right].u\left(D_{out}\right)$$

(2)

In (1) and (2), $u\left(S_{icu}\right)$, $u\left(S_{out}\right)$, $u\left(D_{icu}\right)$, and $u\left(D_{out}\right)$ are preference-related parameters and should reflect the conditions of the health system for which the model is adapted. They are defined as follows:

$u\left(S_{icu}\right)$: utility of survival inside the ICU;

$u\left(S_{out}\right)$: utility of survival outside the ICU;

$u\left(D_{icu}\right)$: utility of death inside the ICU;

$u\left(D_{out}\right)$: utility of death outside the ICU.

In this study, the utilities were set to $u=1$, $u=1$, $u=0$ and $u=0$, considering that survival has the highest possible utility, and death has the worst possible utility value in a 0–1 scale, regardless of whether the patient is referred to the ICU or not. These utilities indicate a value system that is based only on the number of lives saved, without considering the costs involved in the patients’ treatment. However, it is worth mentioning that other values can be considered, depending on the situation verified: in low-income settings, for example, the costs of ensuring intensive care for a large number of patients can have a great impact on public investment in other areas that are critical to society.

In order to clarify the mechanism of calculus of these expected utilities, let us consider, for instance, a scenario in which a patient has a probability of 90% of surviving in ICU ($p_i\left(S_{icu}\right)$ = 0.9) and a probability of 30% of surviving outside ICU ($p_i\left(S_{icu}\right)$ = 0.3). Hence, according to Equation (1), the expected utility for this patient if he/she goes to ICU is equal to $E{U}_i\left(y_i=1\right)=u_i\left(1\right)=0.9 \times 1+0.1 \times 0=0.9$; and, according to Equation (2), the expected utility for this patient if he/she does not go to ICU is equal to $E{U}_i\left(y_i=0\right)=u_i\left(0\right)=0.3 \times 1+0.7 \times 0=0.3$. Even though the calculations of such utility values may seem trivial, it should be highlighted that chances of survival inside and outside ICU are not easy to estimate in an exact manner. In this sense, the proposed model considers that ranges of possible values for the patients’ probabilities of survival are defined (instead of exact values), in an approach that is appropriate for dealing with the uncertainties and variability inherent to this problem; this topic is further explained in the next section. The exact value of the probability to calculate the expected utility is then stablished at each round of the simulation model, which is later described in this paper.

Given the calculations of the individual utilities, now the model should search for the best recommendation for each patient. What should be done now is to consider the overall expected utility for all patients being evaluated, and to try to maximize it in order to have the greatest possible gain. When the utilities of a patient surviving or dying in and outside the ICU are defined as presented above, the overall expected utility represents the expected number of surviving patients. Therefore, a binary linear programming model (Equations (3)–(5)) is used to find the best set of patients that should go to the ICU in order to maximize the global expected utility ($gEU$) of that group of patients for whom ICU admission was requested.

$$\mathrm{Maximize} gEU\left(y_1,\dots ,y_n\right)=\left[{\displaystyle \sum }_{i=1}^n{u}_i\left(1\right).y_i\right]+\left[{\displaystyle \sum }_{i=1}^n{u}_i\left(0\right).\left(1-y_i\right)\right]$$

(3)

Subject to:

$${\displaystyle \sum }_{i=1}^n{y}_i=m$$

(4)

$$y_i\in \left\{0,1\right\} \forall i=1,\dots ,n$$

(5)

The decision variables are $y_i$ $\left(i=1, \dots , n\right)$, which results in 1 if patient $i$ goes to the ICU and 0 otherwise. The objective function (3) aims to maximize the global expected utility, which is the sum of the expected utilities of all patients. The constraint in (4) guarantees that the number of patients allocated to the ICU is equal to the number of ICU beds available ($m$). Finally, the constraint in (5) is to ensure that $y_i$ $\left(i=1, \dots , n\right)$ is a binary variable which can only assume two possible values: 0 and 1.

As a result of this optimization model, the portfolio of patients that maximizes the number of lives saved is obtained. This is given as a recommendation to the DM, who should also consider other subjective factors that are inherent in this situation in order to make an appropriate decision.

The approach proposed in this section to tackle the ICU allocation problem differs from those proposed in previous literature. In order to compare this approach with others proposed previously, some results of a simulation study are presented in Section 5.

4. Materials and Methods

This section is divided into two main subtopics. First, a method for estimation of patients’ chances of survival based on the SOFA score is presented. This methodology was developed conjointly with physicians, considering their practical experience. The following subtopic presents the Information Decision System (IDS) developed to operationalize the proposed methodology.

4.1. A Method for Estimating the Patients’ Chances of Survival

In order to apply the binary linear programming model presented in Section 3 to solve the ICU allocation problem, the probability of patients surviving the stay in and outside the ICU has to be estimated. However, estimating such probabilities can be a difficult task even for experts. In order to support the assessment of these probabilities of survival, we have developed together with experts (doctors and researchers) a method for estimating the patients’ chances of survival. These were defined according to a verbal scale, where each class represents a range of possible values for the probability of patients surviving the stay in and outside the ICU: this approach is appropriate for dealing with the uncertainties and variability inherent in this problem.

The verbal scale used to define the patients’ chances of survival was translated into a numerical scale as represented in Figure 1.

The Sequential Organ Failure Assessment (SOFA) score is proposed to assess patients’ chances of survival. The SOFA score describes quantitatively the degree of organ failure/dysfunction of patients: it was initially developed for the assessment of sepsis-related organ failure, but its utility for assessing acute morbidity in a wide range of critical illnesses was quickly recognized [6,27,28]. Christian et al. [3] argued that the SOFA score is the most appropriate scoring system for use in a triage protocol, since it is based on physiological parameters and is easy to use. White et al. [29] also proposed its use in a protocol designed to support allocation decisions.

The SOFA score considers a set of criteria that reflects the function of six organ systems: respiratory, cardiovascular, neurological, renal, hepatic and hematological [6]. The tool allocates a score between 0 and 4 for each of the six organ systems, as described in

Table 1. The SOFA score. PaO₂—partial pressure of oxygen in the blood. FiO₂—fraction of inspired oxygen. MAP—mean arterial pressure.

Respiratory System
PaO2/FiO2 (mmHg)	SOFA score
≥400	0
<400	1
<30	2
<200 with respiratory support	3
<100 with respiratory support	4
Cardiovascular system
MAP (mmHg) or administration of vasopressors required (dosage in μg/kg/min)	SOFA score
MAP > 70	0
MAP < 70	1
Dopamine ≤ 5 or dobutamine (any dose)	2
Dopamine > 5 or epinephrine ≤ 0.1 or norepinephrine ≤ 0.1	3
Dopamine > 15 or epinephrine > 0.1 or norepinephrine > 0.1	4
Nervous system
Glasgow Coma Scale	SOFA score
15	0
13–14	1
10–12	2
6–9	3
<6	4
Kidneys
Creatinine (mm/dL) [μmol/L]; urine output (mL/day)	SOFA score
<1.2 [<110]	0
1.2–1.9 [110–170]	1
2.0–3.4 [171–299]	2
3.5–4.9 [300–440] or urine output < 500	3
>5.0 [>440] or urine output < 200	4
Liver
Bilirubin (mg/dL) [μmol/L]	SOFA score
<1.2 [<20]	0
1.2–1.9 [20–32]	1
2.0–5.9 [33–101]	2
6.0–11.9 [102–204]	3
>12.0 [>204]	4
Coagulation
Platelets (103/mL)	SOFA score
>150	0
<150	1
<100	2
<50	3
<20	4

Adapted from Vincent et al. [27].

, and the total score is calculated as the sum of the individual scores.

The SOFA score was designed to describe a sequence of complications of critically ill patients and not to predict outcome. However, the relationship between organ dysfunction and mortality has been demonstrated in the literature. Thus, some studies have investigated the utility of measuring the SOFA score for predicting the mortality rate of ICU patients [27,30].

Using univariate logistic analysis, Ferreira et al. [30] analyzed the correlation between several SOFA-related measures and the mortality rate of ICU patients. Regarding the initial SOFA score, which is measured for evaluating what patients to admit to an ICU, the authors verified that there is a good correlation with the mortality rate, the area under the receiver operating characteristic curve receiving a value of 0.79, with an 95% interval confidence between 0.75 to 0.83. Based on their results, the rule presented in

Table 2. Estimation of the patient’s chance of survival inside the ICU.

Initial SOFA Score	Chance of Survival Inside the ICU
0–5	Very high
6–9	High
10–11	Medium
12–24	Very low

was defined to estimate the patients’ chance of survival inside the ICU based on their initial SOFA score.

It can be seen that the levels of chances of survival inside the ICU are derived from the initial SOFA scores as a function with a non-linear scale. For this reason, the intervals of initial SOFA scores in Table 2, are not the same. Note that the score has a discrete scale combining by summing up partial scores in 6 objective criteria, as shown in Table 1. For the six first levels (between 0 and 5), the chance of survival is ‘very high’. For the four following levels (between 6 and 9), the chance of survival is ‘high’. After this level the chance decreases drastically. For the two following levels (between 10 and 11), the chance of survival is ‘medium’ and above score 11 the chance of survival severely decreases to ‘very low’. This non-linearity of this function for higher scores is related to the interactions among those 6 criteria in Table 1, when their partial scores increase.

In order to estimate patients’ chances of survival outside the ICU, other factors must be assessed, such as the need for specific equipment (e.g., mechanical ventilators). The rule presented in Figure 2 was developed together with experts (doctors and researchers) to estimate patients’ chances of survival outside the ICU.

The rule states the following: if the patient’s prognosis in the ICU is not good, the prognosis outside the ICU is poor. If the patient requires specific ICU equipment to sustain life, the chance of survival outside the ICU is very low: this is the case if the patient needs mechanical ventilation, or if he/she needs vasopressor therapy, which requires close monitoring of the patient’s condition [31]. Finally, the level of organ dysfunction influences the outcome: if the patient presents a more developed level of failure for a specific function, his/her chance of survival tends to be less.

4.2. An Information and Decision System to Support the Allocation of ICU Beds

In order to make the proposed methodology accessible for professionals involved in allocating patients to ICU beds, an IDS was developed. The IDS is called SIDTriagem and is available for free at the link www.insid.org.br/sidtriagem/app. The IDS was designed in order to be a useful tool to facilitate the decision process in the ICU allocation problem. The system can support decision-making even in stressful working conditions, such as those being faced by health professionals during the COVID-19 pandemic. To use the system, the user must make a registration and create his/her own password.

On the initial screen of the ICU module of the system, the user can indicate the number of patients requiring ICU beds and the number of ICU beds available. For each patient, the user has to indicate the chances of survival inside and outside the ICU: the verbal scale presented in Figure 1 is used. The user also has to enter how confident he/she is with regard to the information provided (very confident, confident, neutral, unconfident, very unconfident, or even N/A). Once the required information is included, by clicking on the button “Calculate”, the results are displayed.

By considering the ranges of possible values of the patients’ probabilities of survival, it is not possible to apply directly the binary linear programming model presented in Section 3, since it is possible that for different combinations of values within the indicated ranges, the recommendation about which patients should be admitted to the ICU may be different. In order to give due treatment to this imprecise information, a Monte Carlo simulation [9] was used to estimate the robustness index of the recommendation that a given patient be admitted to the ICU: the robustness index is the probability of such a recommendation being appropriate given the conditions presented. To apply the Monte Carlo simulation, the possible values of $p_i\left(S_{icu}\right)$ and $p_i\left(S_{out}\right)$ were considered to be uniformly distributed within the indicated ranges of values.

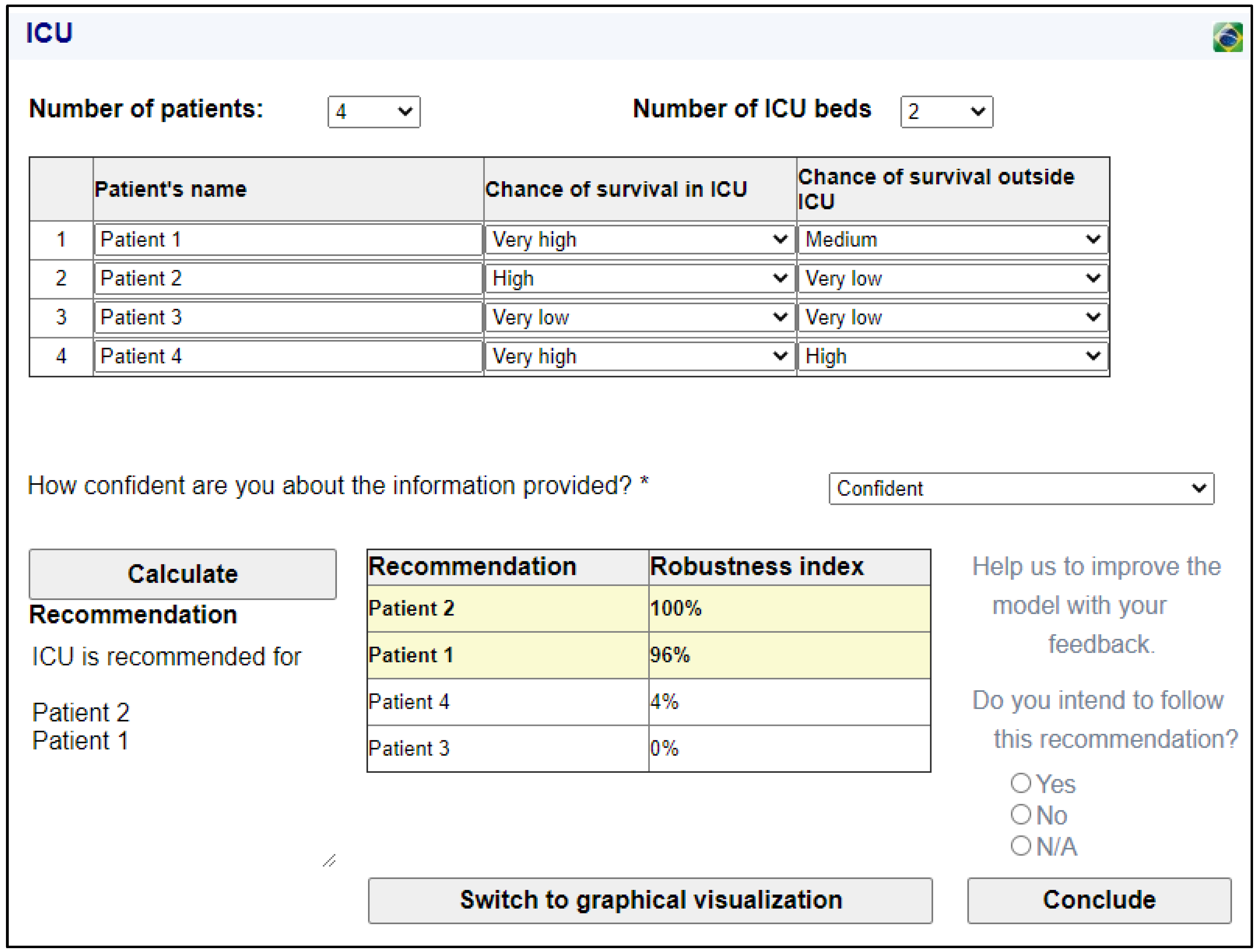
In order to illustrate how the proposed IDS works to obtain a recommendation for the ICU allocation problem, let us consider the following example: in a generic health unit, ICU admission was requested for four patients, but only two ICU beds are available. Patient 1 has a SOFA score of 5, with an individual score of 3 for the hepatic function. Thus, for patient 1, the chance of survival inside the ICU is very high, and the chance of survival outside the ICU is medium. Patient 2 has a SOFA score of 8, and requires mechanical ventilation. For patient 2, the chance of survival inside the ICU is high, but the chance of survival outside the ICU is very low. Patient 3 presents a very poor prognosis: his SOFA score is 12, and his chances of survival inside and outside the ICU are very low. Finally, patient 4 presents a good prognosis: her SOFA score is 4, and she has no individual score greater than 3. Her chance of survival inside the ICU is very high, and her chance of survival outside the ICU is high. The user enters the information in the system and is confident about the information provided. By clicking on the button “Calculate”, the results are displayed to the user as shown in Figure 3.

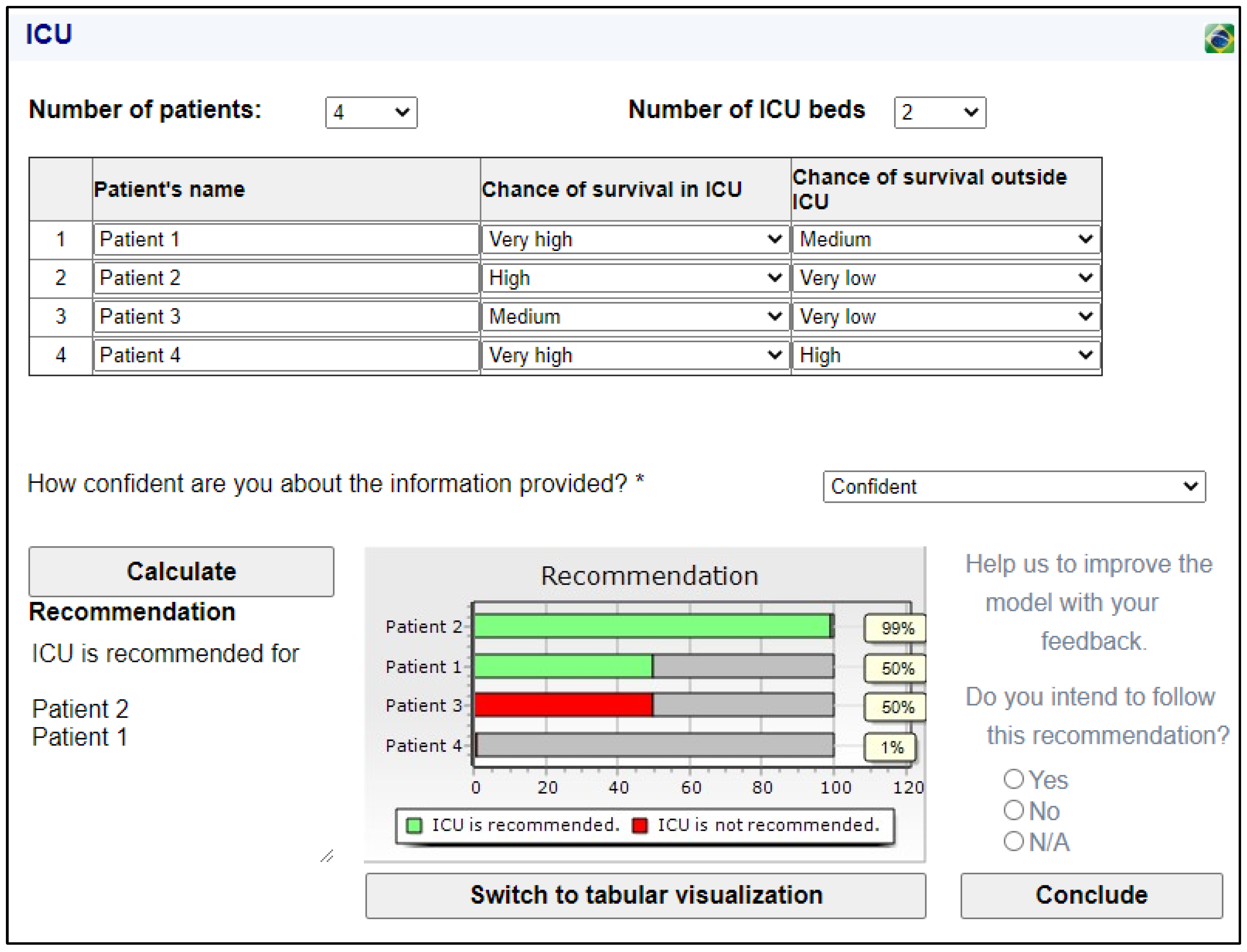
For the example presented, patients 1 and 2 can be admitted to the ICU with a good level of confidence that this is the most appropriate recommendation. The recommendation that patient 4 be admitted has a robustness index of 4%, and the recommendation that patient 3 should not be admitted is confirmed as its robustness index is zero. However, in some cases, the recommendation may present a tie (or near tie). For example, consider that the chance of survival of patient 3 during an ICU stay is medium instead of very low. The results obtained due to this change are shown in Figure 4. In Figure 4, an alternative type of visualization of the results (graphical visualization) was chosen.

In the example presented in Figure 4, patient 2 is highly recommended for ICU admission. Patients 1 and 3 presented the same robustness index for admission to the ICU, but only one of them can be chosen (patient 1 was randomly chosen for ICU admission). In this case, the DM has to evaluate other factors to define the best indication. The graphical visualization helps this situation, as it makes the ties clearer and ensures that the DM can visualize the complete information.

In the bottom right corner of Figure 4, we see that the system asks the user to help us to improve the model with his/her feedback, by selecting whether he/she intends to follow the recommendation provided by the system. By clicking on the button “Conclude”, another window is displayed and the user can write any additional comments.

It should be highlighted that SIDTriagem allows input parameters to be modified and the model can be run as many times as the user wants. In this sense, if the scenario changes (i.e., number of patients needing an ICU bed, number of ICU beds available or even the patients’ conditions and chances of survival), doctors are able to change parameters and run the model over and over again. In this sense, our model is perfectly capable to address dynamic scenarios.

5. Results and Discussion

In order to compare how efficient different approaches are at saving lives when tackling the ICU allocation problem, we developed a simulation algorithm to obtain some results and further discuss them. Four allocation rules were considered for comparison: (1) Maximizing the expected number of lives saved (the approach proposed in this paper); (2) Admitting to the ICU patients with the highest probabilities of surviving their stay there (maximizing the ICU outcome); (3) Admitting to the ICU patients who have the lowest probabilities of survival outside the ICU, (4) Random selection. The second rule is based on the LSF (Least Serious First) principle presented by [19], while the third and fourth rules are based on the MSF (Most Serious First) and RAN (Random) principles, respectively. In this study, the fourth rule is also suitable for simulating the FCFS (First Come-First Served) approach, since it is reasonable to assume that there is no relationship between the order of arrival and the probabilities of survival.

The simulation algorithm developed for this study has two input variables: the number of decision rounds (decision situations) (num_rounds), and the maximum number of patients considered in a decision situation (max_n). The algorithm presents as output the average number of surviving patients per decision round for the four rules presented above (A₁, A₂, A₃ and A₄). The following assumptions were considered:

a.

The decision made on a decision round does not affect the parameters of subsequent decision rounds.

b.

Once a patient is admitted to an ICU bed, he/she is discharged only if he/she recovers, dies or if it is clear that there is no chance of recovery (in which case, the patient is sent elsewhere for palliative treatment).

The assumption a, from a mathematical point of view, is reasonable since the probabilities of survival of a patient not admitted to an ICU bed in a decision round may change before the next one, and such a change may occur in different ways. The assumption b corresponds to a common practice in health units, given the ethical difficulty of discharging non-recovered patients without a clear signal that there is zero probability that they will recover. A pseudo-code of the simulation is shown in Algorithm 1.

Algorithm 1. Simulation algorithm developed to compare the approaches for tackling the ICU allocation problem.

1:  inputs: num_rounds, max_n

2:  for j = 1: 1: num_rounds

3:   generate n from the set {2, 3, …, max_n} by mcm_upd

4:   generate m from the set {1, 2, …, n−1} by mcm_upd

5:   for i = 1: 1: n

6:    generate $p_i\left(S_u\right)$ from the interval (0,1] by mcm_upd

7:    generate $p_i\left(S_f\right)$ from the interval [0, $p_i\left(S_u\right)$) by mcm_upd

8:   end for

9:   define the allocations of ICU beds according to approaches 1, 2, 3 and 4

10:   for i = 1: 1: n

11:    generate a random number $x_i$ from the interval [0, 1] by mcm_upd

12:    if $x_i\le p_i\left(S_f\right)$ patient i survives regardless of being admitted to the ICU

13:    if $p_i\left(S_f\right)<x_i\le p_i\left(S_u\right)$ patient i survives only if admitted to the ICU

14:    if $x_i>p_i\left(S_u\right)$ patient i dies regardless the admission to the ICU

15:   end for

16:   count the number of surviving patients after applying the four allocation rules

17:  end for

18:  output generation: calculate the average number of surviving patients per decision round for the four allocation rules (A1, A2, A3 and A4)

19:  mcm_upd–a Monte Carlo method considering a uniform probability distribution.

Note that the algorithm simulates decisions only where the number of patients requiring ICU beds is greater than the number of ICU beds available. We verified that when $num\_rounds\to \infty$, the average number of surviving patients per decision round converges to a value because of max_n and the allocation rule.

Some results obtained from the simulation are presented in

Table 3. Results obtained from simulation. num_rounds = 100,000. ${∆}_{1i}=\left[\frac{\left(A_1-A_i\right)}{A_i}\right].100$, for $i=\left\{2,3,4\right\}$.

	Average Numbers of Surviving Patients per Decision Round				Gain Obtained with Allocation Rule 1 Compared to Rules 2, 3 and 4
max_n	A1	A2	A3	A4	Δ12	Δ13	Δ14
2	0.869	0.832	0.758	0.750	4.49%	14.70%	15.81%
5	1.526	1.461	1.331	1.316	4.40%	14.65%	15.90%
10	2.616	2.506	2.285	2.256	4.41%	14.50%	15.95%
15	3.712	3.552	3.239	3.194	4.50%	14.62%	16.23%

. We defined num_rounds as 100,000 rounds, so that the algorithm can simulate the effects of decision-making in a systematic way according to an allocation rule.

The results presented in Table 3 evidence the advantage of adopting the approach proposed in this paper for solving the ICU allocation problem. When compared to approach 2, which is often favored in the literature [3,19], the approach that we propose leads to saving around 4.40% more lives. This difference was greater than 14% when the approach 1 is compared to the approach 3, and greater than 15% when approach 1 is compared to approach 4. When we consider a context where decisions are made in a systematic way during a public health emergency, these differences are quite significant because the number of severely ill patients is much higher than in normal circumstances.

With regards to managerial implications of the proposed approach, the developed Information Decision System and the proposed methodology have great potential to help in the response to public health systems emergencies, which is particularly important in the context of the COVID-19 pandemic. This tool can help to save more lives by facilitating rational decision-making regarding the allocation of a limited number of ICU beds, thus reducing the stress involved in this process. SIDTriagem has been applied in public hospitals in Pernambuco, Brazil, and doctors related to have benefits from its use for making better and structured decisions. The results of the systems’ use are being processed and shall be addressed in future studies. It should also be highlighted that the proposed model can be adapted for dealing with other different diseases, not limiting itself to the pandemic outbreak.

6. Conclusions

The COVID-19 outbreak has motivated the development of several research lines that aim to use mathematics and operations research techniques to address challenges that arise from the pandemic [32,33]. This paper addressed an important problem faced by many health system managers worldwide during the COVID-19 pandemic due to the very severe strain placed on many health systems: the definition of who should be admitted to intensive care when the number of ICU beds available is less than the demand. We have called this decision problem the ICU allocation problem.

To deal with the ICU allocation problem a structured protocol has been proposed based on the clinical evaluations of patients. This protocol has been built with doctors and considers important clinical variables in order to estimate chances of survival of the patients.

The model proposed to support the allocation problem considers the probabilities of the patients surviving a stay either in or outside the ICU. However, assessing such probabilities can be a difficult task for health professionals. Thus, addressing this issue, we proposed a method to estimate the patients’ chances of survival based on objective information, namely the SOFA score. The results from the method present the ranges of possible values for the patients’ probabilities of survival. In order to give due treatment to this imprecise information, a Monte Carlo simulation is used to calculate the robustness index of the recommendation that a patient be admitted to the ICU. The robustness index is the probability of such a recommendation being appropriate given the conditions presented

The ICU allocation problem presented here is based on the utilitarian principle, so that seeks to save as many lives as possible. A binary linear programming model based on a portfolio selection approach was presented, which seeks to maximize the expected number of patients who will survive in the hospital stay. A simulation study was performed to compare the proposed approach with others presented in the literature, and the results showed that the proposed approach is more advantageous when adopted in a systematic way, thus leading to more lives being saved.

The proposed methodology was implemented in an IDS called SIDTriagem, which is available online for free. The system was designed to improve the user’s experience and to make it easier for health system managers to make rational decisions regarding the ICU allocation problem. An illustration of how the system is used is presented, thereby showing how a recommendation can be obtained and how the results displayed can be interpreted.

As a limitation of the present methodology, it can be pointed out that the allocation rule followed an output-oriented view, in a sense of focusing only on the number of lives saved; i.e., the hospital services benefits. However other factors such as the costs involved, may also have influence of such decisions, especially in private health systems. In addition, the study proposed by Pereira et al. (2022) [34] discussed several aspects that have not been discussed in this paper, such as country population, GDP per capita and life expectancy at birth. In this sense, future research should explore how to incorporate other aspects in addition to the number of lives saved into the decision model, considering also a cost-oriented approach. In order to consider both costs and services benefits, a multiattribute decision model could be formulated in order to deal with it. Moreover, future research may also usefully focus on assessing how the IDS interface can be enhanced in order to improve the user’s experience.