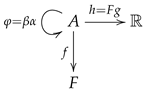
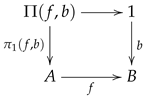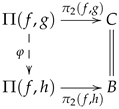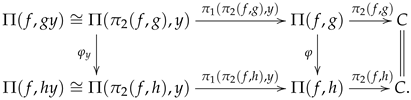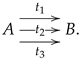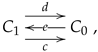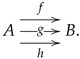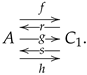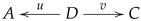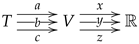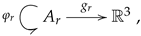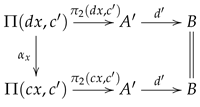1. Introduction
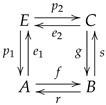
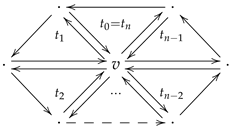
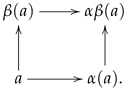
Every surface can be triangulated, thus giving rise to a triangulated surface consisting of a collection of vertices, i.e., points lying on the surface, together with a collection of triangles indexed over the selected vertices. Moreover, a start-neighbourhood is formed (see display (
2) below) every time we fix a vertex and consider the collection of triangles incident to it. If we denote by
V the set of vertices and by
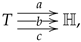
T the set of triangles, then a triangulation consists of three maps from
T to
V, say
satisfying the star-neighbourhood property. If the surface is embeddable in some
n-dimensional space
E, then we have a further mapping
, providing a geometrical realisation for the otherwise abstract vertices in
V. Furthermore, when the surface is orientable, we have the maps
given in a specific order, say
, and hence each element
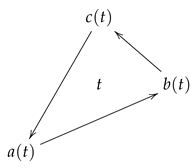
can be interpreted as an oriented triangle with vertices
, as illustrated.
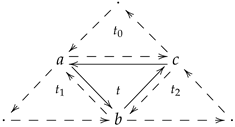
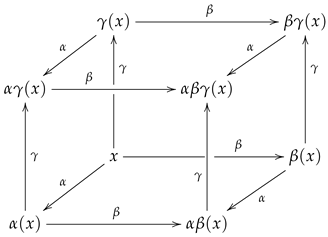
This means that the structure of a triangulation is a trigraph, displayed as
such that for every element
, the collection of all elements
that are incident to
v is finite, can be ordered as
, and forms a star-neighbourhood as illustrated in the following display.
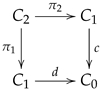
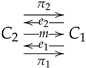
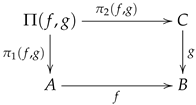
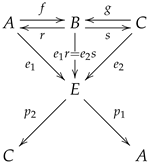
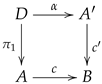
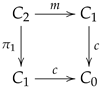
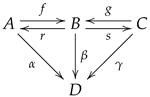
On the other hand, an internal groupoid is an internal category in which every arrow is invertible. An internal category is a particular instance of a multiplicative graph whose structure can be presented as a diagram of the form
in which
is a reflexive graph (see
Section 2.2), some squares derived from diagram (
3) are commutative squares, whereas some other squares are required to be pullback squares (see
Section 2.7 and
Section 4.5). In spite of the dissimilarity between an internal groupoid and a triangulation, there is one further type of categorical structure that can have both cases as particular instances.
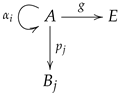
Multi-links have been introduced in the context of additive manufacturing and 3D-printing and are mathematical objects consisting of a set
A, called the set of indexes, a collection of endomaps
, called the transition maps, a geometric realization map
g from the set of indexes
A into some appropriate space
E. The endomaps may be subject to some conditions, which further specialize the structure into particular cases. The structure of a multi-link may thus be pictured as
with the collection of endomaps
ranging over some indexing set (see
Section 3.4).
At first glance, there is no obvious interactions between the three categorical structures just presented. Yet, a triangulation as well as an internal groupoid are two particular instances of a multi-link. This is somehow surprising; indeed, one of the most common presentations of an internal groupoid is as a reflexive graph together with a composition law , while being assumed that the object is obtained by taking the pullback of the domain morphism d along the codomain morphism c, hence being canonically equipped with the two canonical projections .
It turns out that a triangulation can be transformed into a multi-link
such that
and moreover, in order to have the
star-neighbourhood property displayed in (
2), one should add the requirement that
is an isomorphism (further details in
Section 3.5.3, see also [
1]).
Similarly, an internal groupoid with inversion morphism
(Definition 3) together with
extracted from diagram (
3) can be transformed into a multi-link as
such that
In this case, the object
A is precisely
, and
E is the same as
. The morphism
g is just
m, and the two morphisms
and
are uniquely determined by the following conditions:
The structure of a groupoid is recovered from the multi-link structure
by considering the trigraph
in which the two pairs of morphisms
and
are contractible in the sense of Beck (see [
2] p. 150). This topic will be further developed in a future work.
One point to be made in this paper is the importance of considering categorical structures that can be defined in any category, even without assuming the existence of any limits or colimits (this level of generality has also been considered in [
3,
4]).
We will be interested in a concrete particular example of a category to replace the category of sets and maps, which does not admit all products nor pullbacks and yet should be considered as an essential category from the point of view of the theory of computation (see, e.g., [
5]). It presents a model for finite mathematical high level computational systems such as Octave or Matlab. This category can thus be used in the development of new computational methods and algorithms at the level of abstract categorical structures. We will use the number 256 and denote by
the category whose objects are all sets, whereas the morphisms are those maps
that are bijections as soon as the cardinality of
A is greater than
. Of course, any other power of 2 or even any other finite number other than
would serve as well. The reason why we have chosen
is to have quaternions as 4-tuples of 64-bit floating point numbers [
6]. Clearly, this category does not have all pullbacks for in general a pullback diagram would require the existence of a set with cardinality greater than
together with the canonical projections which would not be necessarily bijections.
This paper is divided into three parts (table of contents at the end). In the first part, we briefly survey the well-know categories of morphisms, spans, reflexive graphs, internal categories and internal groupoids. We also consider the not so well-known categories of multiplicative graphs in the sense of G. Janelidze [
7], of pregroupoids in the sense of A. Kock [
8] and multiplicative kites in the sense of T. Van der Linden and the author [
9]. A new concept of split extension that can be defined in any category is suggested in
Section 2.1. The second part of the paper (
Section 3) surveys the notion of multi-link as well as its applications to 3D-printing. At the end (
Section 4), we extend the notion of centralizing relations from the context of equivalence relations to the more general context of digraphs and apply it in a new characterization of internal groupoids (see also [
10,
11]).
2. Elementary Internal Categorical Structures
It is usual while working with internal categorical structures to consider a category with pullbacks and equalizers and say that all the structures and diagrams are internal to . In this paper, we consider a category with no further assumptions. In particular, pullbacks may not exist for all pairs of morphisms. Instead, it is a property of a cospan, i.e., two morphisms sharing the same codomain, whether the pullback exists.
Most categorical structures are nothing but functor categories. However, we observe that most papers have the necessity to explicitly formulate the structures that they need. One purpose of this paper is to serve as a reference for terminology. For that reason, I have tried to make every choice as natural as possible.
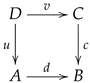
2.1. Morphisms, Pullbacks and Split-Extensions
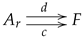
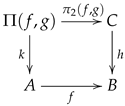
One of the most used yet most trivial categorical structures is the category
whose objects are morphisms in the category
and whose morphisms are the commutative squares. An object in
is simply denoted by the name of the arrow, say
, and if we need to specify its domain or codomain, we use the notation
or
, respectively. If
u and
v are two objects in
, then an arrow from
u to
v is represented as an ordered pair
, which may be displayed as
If needed, the in-line notation can be used as
and it will always mean that the square (
8) is commutative, that is,
. Examples will be provided along the rest of the paper.
When a commutative square is a pullback square, we will say that the square is Cartesian. Since we are not assuming the category
to have all pullbacks, it will be a property of a cospan
the existence of a span
such that the square
is commutative and Cartesian.
We may thus consider the class of Cartesian cospans. The category of cospans is obtained in a dual way as the category
and similarly we may consider a subcategory of it by specifying any class of cospans (see
Section 2.2).
In the category of abelian groups, there is an equivalence of categories between the category of internal groupoids and the category of morphisms. In general, for any pointed category with binary coproducts, its morphisms can be interpreted as internal categories of a special type as it is illustrated, for example, in [
12].
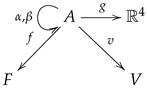
Before continuing, we would like to suggest a generalization of split extension, which can be defined in any category (see also [
13]). It is based on the new notions of joint and patch, which were used in [
14,
15] with slightly different meanings.
A
joint is a cospan that is Cartesian (let us say with Cartesian square as the one displayed below)
and has the property that for every morphism
with
there exists at most one morphism
such that
and
. In a joint
with a morphism
p as above, we will always denote by
when such
exists.
A patch is a joint together with a morphism p such that exists.
A
fine patch is a patch
in which the commutative square
is Cartesian. It is clear that a fine patch is a generalization for the notion of split extension in an arbitrary category
.
Most material in the following sections is from [
16].
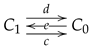
2.2. Reflexive Graphs and Spans
A reflexive graph is a diagram of the shape
in which the condition
holds true. It can be represented as a five-tuple
. A morphism between reflexive graphs, say form
to
, is a pair of morphisms
, displayed as
and such that
,
and
. The category of reflexive graphs is denoted
.
A span is a diagram of the shape
with no further conditions. It is represented as
, or as
when
and
are understood from the context, or even simply as a pair
. Even though the objects
and
may be omitted for simplicity, it is clear that a morphism of spans is a triple of morphisms, making the resulting squares commutative. The category of spans is denoted
. There is an obvious functor
assigning the span
to every reflexive graph
. Any class
of spans in
can be seen as a full subcategory
. For the sake of consistency, we will write
to denote the full subcategory of
determined by the spans in the class
. Similarly, we obtain
as the full subcategory of
whose span part is in
; in other words, it can be seen as a pullback in the category of categories and functors.
There are several reasons why one may be interested in taking a class of spans
instead of the category
itself and then take only those reflexive graphs whose span
is in
. Indeed, one is often forced to restrict the attention to a suitable class of well-behaved spans (or co-spans). Concrete applications can be found, for example, in [
16].
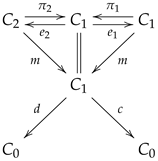
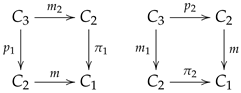
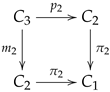
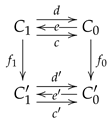
2.3. Multiplicative Graphs and Reflexive Graphs
The category of multiplicative graphs internal to
was introduced by G. Janelidze in [
7] and will be denoted as
. A multiplicative graph can be seen as a category in which multiplication (or composition) may not be associative and it has applications in categorical Galois theory [
17]. Its objects are the diagrams in
of the form
in which
is a reflexive graph,
the square
is a pullback square and the maps
,
are uniquely determined as
and
.
A multiplicative graph, displayed as in diagram (15), will be referred to as a six-tuple . Although the canonical morphisms from the pullback as well as the induced morphisms into the pullback are implicit, they are part of the structure since we are not assuming the category to have pullbacks. On the other hand, they are unique (up to an isomorphism) as soon as they exist.
Morphisms are triples in which is a morphism of reflexive graphs and is such that , and . When convenient, we refer to a morphism of multiplicative graphs as and it should be clear that , and .
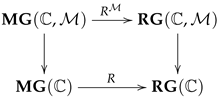
There is an obvious forgetful functor from the category of multiplicative graphs,
, to the category of reflexive graphs,
. This functor will be denoted by
R. Any class
of spans gives rise not only to a category
but also to a category
. This construction can be obtained as a pullback diagram in Cat
so that the functor
is nothing but the restriction of
R to the class
. The functor
R is to be interpreted as extracting from a multiplicative graph
its underlying reflexive graph
.
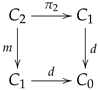
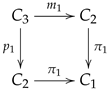
2.4. The Kernel Pair Construction
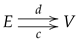
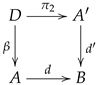
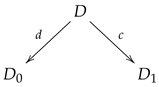
The following categorical transformation is useful in many situations and it is known as the kernel pair construction, providing a way of transforming a span into a reflexive graph.
Let
be a span. The kernel pair construction is obtained by combining the kernel pairs of the morphisms
d and
c with the pullback of its projections and induced injections as illustrated.
When
is the category of sets and maps, we may think of an element in
D as an arrow whose domain and codomain are drawn from different sets. In other words an element
is displayed as
In view of this interpretation, the elements in
are the pairs
,
, such that
and they may be pictured as
or in a simpler form as
Similarly, a pair
is pictured as
and it follows that the elements in
are the triples
such that
and
, which may be pictured as
In other words, when
is the category of sets and maps we have:
The kernel pair construction gives rise to a functor
with
. See [
9] for further information on the kernel pair construction.
2.5. Stability under Pullbacks
Under the assumption that the class
is stable under pullbacks, the functor
K restricts to
An alternative way of obtaining the kernel pair construction, if in the presence of binary products, is to take the following pullback
.
The requirement asking that
is pullback stable means precisely that for every span
in
and for every two morphisms
and
, the span
obtained by taking pullbacks as shown in the following picture,
is still in
.
The kernel pair construction for relations plays an important role in the theory of Mal’tsev categories, see for instance [
18], where it first appears in the form of the pullback (
20).
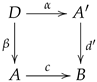
2.6. Pregroupoids
A pregroupid internal to a category
was introduced by A. Kock (see [
8] for its original definition and motivation where, in addition to the conditions stated below, associativity is also required) and consists of a span
together with a pregroupoid structure. A pregroupoid structure is a morphism
, such that
The object
is obtained together with the maps
by means of the kernel pair construction, as explained in the previous subsection. In set-theoretical terms, the object
consists on those triples
of arrows in
D for which
and
, so that the two conditions (21) are
while the two conditions (22) become
In this way, we form the category of pregroupoids with its span part drawn from the class . It is denoted as .
2.7. Internal Categories and Internal Groupoids
An internal category is a multiplicative graph in which the multiplication is associative (see
Section 4.5). The category of internal categories to
is denoted
. A groupoid is an internal category in which every morphism is invertible. Internally, it can be seen as an associative multiplicative graph in which the square
is a pullback (see [
19], see also
Section 4.5). The category of internal groupoids internal to
is denoted
. In a similar manner as before, we define the categories
and
of internal categories and internal groupoids in
with respect to a class
of spans.
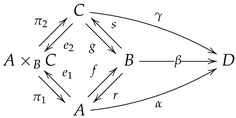
2.8. Multiplicative Kites
The notion of a kite was first considered in [
20] as an admissibility diagram. It was then considered in [
9] as a kite. Its main purpose is to generalize the structure of a groupoid and a pregroupoid so that it can be used as a setting where it is possible to transform a groupoid into a pregroupoid and vice versa.
A kite, internal to
, is a diagram of the form
with
,
.
A directed kite is a kite together with a span such that , .
Once again, if the span part of a kite is required to be in then it is an object in the category , where the morphisms are the natural transformations between such diagrams.
When pullbacks of split epimorphisms are available, each diagram such as (24) induces a diagram
in which the double diamond is a double split epimorphism (or a split square). The morphisms
are determined as
and
.
A multiplication on a kite is a morphism such that , , and .
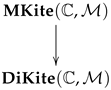
The forgetful functor from the category of multiplicative kites into the category of directed kites, with direction (i.e., the span part) drawn from the class
will be considered. This functor helps in understanding a directed kite as a structure with the property of having at least one multiplication, making it a multiplicative directed kite. This functor simply forgets the multiplicative structure.
2.9. Relevant Examples of Directed Kites
List of examples of directed kites as particular cases obtained from the structures that have been surveyed so far with remarks on the condition for it to be a multiplicative kite:
If
is a reflexive graph, then the following diagram is a directed kite:
This directed kite is multiplicative if and only if the reflexive graph is a multiplicative graph.
If
is a multiplicative graph, then the following diagram is a directed kite:
This directed kite has a unique multiplicative structure if and only if the multiplicative graph is associative (i.e., an internal category).
If
is an associative multiplicative graph (an internal category), then the following diagram is a directed kite:
This directed kite is multiplicative if and only if the internal category is an internal groupoid (see [
20]).
If
is a morphism of reflexive graphs, then the following diagram is a directed kite:
If the morphism of reflexive graphs can be extended to a morphism of multiplicative reflexive graphs, then the induced directed kite represented in the diagram above is multiplicative.
If
is a span, then the kernel pair construction gives a directed kite as follows:
This yields a reflection between the category of directed kites and the category of spans.
A directed kite goes to its direction span, a span goes to the directed kite displayed above. Moreover, the span is a pregroupoid if and only if its associated directed kite is multiplicative.
A split square is a diagram of the shape
such that
,
,
,
,
and
.
Any split square as (31) gives rise to a directed kite as illustrated.
In [
16], it is shown that the existence of a multiplicative structure on the directed kites such as (32) has an important classifying property for Mal’tsev-like categories which generalizes the concept of orthogonality between a span and a co-span as considered in [
21].
We will now see a different kind of mathematical structure which has been obtained as a result of investigations on 3D-printing and additive manufacturing.
3. The Categorical Structure of a Link and a Multi-Link
The notion of a multi-link was introduced in [
22] as a tool for the encoding and systematization of new and more efficient algorithms in the aim of 3D-printing.
3.1. Motivation from Computer Science and 3D-Printing
From the point of view of storage in a computer’s memory, the notion of a two-dimensional matrix, with lines and columns, does not make much sense. At least, it does not make much more sense than an arbitrary n-dimensional matrix. In practice, what is really stored in the computer’s memory disk is an array, and the most efficient arrays are the linear ones. In spite of everything that has been said during the last two or three decades about formal file systems, the non-structured ones are still the ones that are preferred. This explains, for example, why the STL file format is still so common nowadays.
The structure of a multi-link has been proposed as a structure, which on the one hand can be stored as a linear array of information, while, on the other hand, it can be used to encode highly non-trivial structures such as surfaces and their properties. These properties may be decomposed into logical, functional and geometrical information and they cover most of the whole spectrum of processes that are involved in 3D-printing (see [
22]).
Indeed, the mathematical structure of multi-link was motivated by a long series of experiments with mathematical structures and their properties, namely the ones that are related with efficiency and encoding of information. See for example [
23,
24,
25,
26] and the references therein. Here, we have also seen a new application for multi-links, namely the possibility of encoding not only a triangulation (or any surface discretized in non-triangular nor regular faces), but also the surprising capability of describing internal groupoids (see introduction).
First, we motivate the very special case of a link, which can be seen as an abstraction for the notion of a curve (appropriate for computational purposes) and then, by generalizing it in several different ways, we obtain the notion of multi-link. This basic notion was the result of a long period of maturation, and its main characteristic is the fact that it is suitable for the encoding of
n-dimensional matrices as simple linear arrays. The key ingredient is the observation that the transition maps from
to
and
can be seen as two permutable maps from the set of linearized indexes into itself. We give some details on this passage which are essentially repeated from [
22].
From
Section 3.4 onwards, we concentrate our attention on the abstract notion of a multi-link by observing that it has several useful and important particular cases. Indeed, as we will see, each one has its purpose and can be applied into a very specific situation for 3D-printing.
At the end of the section, we give a detailed description on the iso-slice algorithm, as well as an application to the generation of cooling and refrigerating channels in a mould. This will came later on; for the moment, let us concentrate our attention on links, first, and then on multi-links, as a mathematical abstract structure.
3.2. A Link as an Abstraction of a Planar Curve
A classical planar curve is usually defined as a continuous map from the unit interval into the field of complex numbers. From the point of view of analysis, this is a perfectly reasonable concept and it naturally extends to curves in the 3D-space. One simply substitutes the field of complex numbers by the euclidean three space, and it is then just one more step to move to the n-dimensional vector field . However, from the point of view of computation, this is not really a good definition and many attempts have been made to find a better alternative. Several variations can be considered and each one of them has its own advantages and disadvantages. Here, we consider one which seems to be good for the purposes of encoding contour level curves, the ones that are obtained from the slicing of triangulated surfaces, and their applications into the area of 3D-printing and direct digital manufacturing. The notion that we propose as an abstraction for a curve is called a link. It has arisen by observing that a curve, if approximated by a piecewise-linear sequence of directed edges, is a particular case of a directed graph. A directed graph is a mathematical object consisting of a set of vertices, a set of edges and two parallel maps that assign a vertex to an edge, namely its source and target. It turns out that some directed graphs, namely the ones that are obtained by taking an approximation to a curve, share the characteristic property of having a linking map. This linking map associates to each edge a successor edge along the direction of the curve. In this way, we have arrived at the abstract notion of a link. This notion is intended to be a computational model for a classical curve.
A link is a mathematical object which consists of a set, together with an endomap and a map into a geometrical algebra (the notion of a geometrical algebra has a precise meaning in mathematics; however, the reader not familiar with it may safely assume that it is simply a vector space, and for the purpose of this paper,
will be enough), as illustrated
This notion is thus interpreted as a generalized curve in
as follows. The curve is a piecewise linear sequence of segments; each segment in the curve is determined by an indexing element in the set of indexes
A, and it is geometrically realised as the vector in
whose endpoints are
This means that each segment in the curve is indexed by an element in
A, in fact we will sometimes picture the segment as a labelled edge in a directed graph
The set
A is called the set of indexes, the map
is called the successor, or transition map (it tells to each index, which is considered as the origin of the edge, what is its successor—the successor is at the same time the endpoint of its predecessor and the starting point of the edge of which it is the index of), this idea can be illustrated as follows:
For further examples, the reader is referred to [
27].
3.3. Moving from an Array to a Matrix While Keeping It Linear
If we would try to generalize the notion of a link as an abstraction for a curve as a new abstract entity which would serve as a good model for a surface, we would easily be led to a structure of the form
However, as soon as we try to interpret it as a surface, we soon realize that
should be of the form
In other words, it should consist of two independent maps
and
, together with the realization (or geometrical) map
The role of and is to determine the behaviour of the transitions along the x-direction and the y-direction. Note that these directions are only abstract and they should not be confused with the directions of .
Let us see a concrete example. Suppose we are interested in modelling the cylinder
so that we could make an approximation, say,
,
and define
,
and
as follows:
if
and
;
; and
As remarked before, the crucial point here is to observe that we may exchange the set
with another set, which is bijective to it, say
A, and the endomap
with two endomaps
that are permutable, i.e.,
. In this way, we form squares indexed by the elements of
A as illustrated
If the set X has elements, and the set Y has elements, then we can take the set A to be the set and the well known bijection which transforms pairs of indexes into linear indexes .
3.4. The Structure of a Multi-Link
The notion of a multi-link is a natural generalization of the notion of link and it is motivated by the concrete examples of a square-link (such as the one above), a double-link (which is a structure that models arbitrary surfaces) and several others that where designed for more specific purposes, such as contour filling algorithms or generating voxelized porous in 3-dimensional physical objects. A multi-link thus arises as the need to encode and organize a large amount of information in the form of data and algorithms that are relevant to the process of 3D-printing.
A multi-link is a mathematical object displayed as
in which
A is an arbitrary object,
E is some structured object such as a geometrical algebra and
and
are arbitrary indexing sets. The maps
are required to be surjections. Furthermore, some conditions may be required on the structure such as commutativity between the arrows involved. For example, if
then it is reasonable to assume
and think of the projections
as being the connected components for the orbits of the respective
.
The family of maps is considered to be the topological part of the multi-link, the map g is the geometrical part, while the family of projections is considered to be the logical or functional part of the structure. This is because in most of the examples the projection maps are simply assigning some functional behaviour to the edges, like colour properties or materials or other kinds of physical interpretation.
In the following subsections, we present some details on useful structures that can be seen as particular cases of multi-links.
3.5. Particular Cases as Examples of Multi-Links
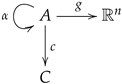
3.5.1. Coloured Link
A coloured link is a link with a surjective map into some set
C, of colours, in other words, it is of the form
such that
.
It is interpreted as a link in which every edge has a certain colour associated to it, and moreover, the edges in the same component (in the sense of orbits of ) have the same colour, but different components may have different colours.
3.5.2. A Square-Link
A square link was considered above, and it can be seen as a special case of a multi-link with two endomaps but without projection maps. The two endomaps, say
and
, are permutable, that is,
. If we take the example of the cylinder from above and use the bijection
from the Cartesian product of
and
into
, which is defined by
, then, in order to give the structure of a square-link it remains to specify the maps
and
. In this case, we put
,
and
in the other cases. For the map
we have
if
and
for all the other values of
. The map
g is now defined as
when
x is less or equal to 360 and
for the cases when
x is greater than 360.
3.5.3. A Triangulation
The structure of a triangulation has been studied in [
1] and it is an important example of a multi-link.
The structure of a triangulation generalizes the one of a directed graph. It consists of two sets (vertices and triangles) and three parallel maps between them, as displayed
An element
is interpreted as a triangle as illustrated in (
1).
In [
1], the observation that those triangulations which are obtained as the boundary of a physical object in 3D space are the ones with the property that every vertex has a start-neighbourhood (as illustrated in (
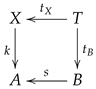
2)) has been used to transform a triangulation into a multi-link which at the time was merely a convenient way of encoding information.
The procedure works as follows. For practical reasons we substitute
with the Cayley algebra of quaternions
, see [
28]. In [
1], it is shown that the triangulations
in which every vertex has a star-neighbourhood, are equivalent (i.e., encode the same information) to a multi-link of the form
such that
Moreover, in order to have the star-neighbourhood property displayed in (
2),
has to be an isomorphism.
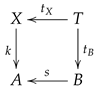
Having a structure such as (
34) with the star-neighbourhood property for each of its vertices, in order to obtain a structure such as (
35), we define:
and
with
,
as illustrated
and
given as
Conversely, if having a structure such as (
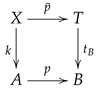
35) with its three conditions, then we define a triangulation as follows. The triangles
T are obtained by identifying the orbits of
, via the coequalizer of the pair of morphisms
. Observe that this particular coequalizer exists in the category
, even though its kernel relation may fail to exist. The vertices are obtained by identifying the orbits of
, via the coequalizer of the pair
. Let us denote the two coequalizers, respectively, as
and
. The complete structure, with
,
and
(where
s is any section for
p) is displayed as
with
the unique map such that
.
3.5.4. A Double-Link
The notion of a double-link serves to encode, in its most general form, the concept of a surface. Here, we will only give the definition and the simple example of the tetrahedron. Further examples and the study of its main properties are the matter of future work. All platonic solids can be found in [
29] as double-links.
A double-link is an instance of a multi-link which can be displayed as
such that
The example of a tetrahedron, due to its simplicity, can be used as an illustration. The following picture, which shows the planar graph representation of a tetrahedron (with the usual directed edges replaced by oriented squares that are build up from the labels
and
), is used to deduce a concrete example of a double-link, as follows.
Take A to be the set and let the endomaps and be defined by the labels indicated in the planar graph representation, that is , , etc. The projection map f is the quotient over the orbits of , thus giving the faces of the tetrahedron. The projection map v is the quotient over the orbits of , thus giving the set of vertices. The map g is any realization map from A to any space.
Note that a triangulation is a particular instance of a double-link. Indeed, we observe and .
3.5.5. A Cubic-Link
A cubic link is a straightforward generalization of a square-link and it is useful in modelling volumes with porous structures as illustrated in [
30].
A cubic link is a structure
such that
,
and
. It is interpreted as a collection of voxels of a cubic shape. In the same way as a square-link models a surface which is generated by a square patch along two abstract directions, a cubic link can be used to generate a 3D-manifold, which is generated by a collection of cubes attached along three different abstract directions, say
, as illustrated.
3.5.6. A N-Cube-Link
Once again, a straightforward generalization of a cubic-link is obtained if instead of three abstract directions we consider any finite number
n, thus obtaining
where
is any geometrical algebra (or more simply a vector space), and the
are permutable in the sense that
for any
in
. These structures arise, for example, in the construction of
n-dimensional volumes with porous structures in its interior and it has several applications in 3D-printing.
3.5.7. A Contour Filling Curve
The paper [
31] describes a procedure on how to generate sweep trajectories for planar regions that are encoded by its boundary and obtained by slicing a three-dimensional body.
The details that motivate this structure are referred to [
31]. Here, we simply recall the structure, which is an instance of a multi-link. It consists on a diagram of sets and maps, as illustrated,
such that
It is illustrated with appropriate pictures in [
22,
31] in which the role of the maps
is clear.
3.5.8. A Square Patch
A square patch is an intermediate level between a square-link and a double-link. It is the analogue to a triangulation except that it is made out of squares rather than triangles. The generalization from a triangulation is not difficult to obtain and we omit the details. As an instance of a multi-link, it is described as follows.
such that
The orbits of are interpreted as (square) faces while the orbits of are interpreted as vertices.
3.6. The Iso-Slice Algorithm
In this subsection, we give the necessary details for an implementation of an algorithm that efficiently computes level iso-contours. The contours are the ones obtained by slicing a triangulated surface in the euclidean 3D-space with respect to an iso-surface of a given level.
The algorithm may be decomposed in the following steps:
Consider a triangulation as input
Transform the triangulation into a double-link as explained before (see also [
1]). This gives a structure of the form
with the meaning that the orbits of
are the faces (elements in
F) and the orbits of
are the vertices (elements in
V).
Suppose there is given a family of iso-surfaces in 3D-space, let us say defined by a map
which intuitively may be thought of as assigning to every point in space a certain height; the main example is
, giving planar slices along the
z-direction, but
or
are also possible and give, respectively, cylinders and spheres; in general, we have arbitrary maps perhaps with a specific meaning. Nevertheless, the algorithm works the same way for every map.
Transform the structure of double link of item 2 in the structure of a coloured link by considering
,
and forgetting the projection map
v. This produces
and the map
h is intuitively the height of each point in
A relative to the iso-level-surface
F of item 3;
For each contour level do:
- (a)
Obtain the subset of
A in the coloured link of item 4 defined as:
- (b)
Consider the directed graph whose edges are the elements in
as well as the vertices; the domain map is the identity map and the codomain map is
, this will produce a picture which may be interpreted as
in which we suppose
a and
to be in
. This means that
is a height laying between
and
as well as between
and
. The idea is to connect
a and
and in order to do so it suffices to identify the orbits of
via
f. This procedure creates a directed graph.
- (c)
Construct the directed graph
from the subset
(item 5(a)) to the set of faces
F (item 4), with
and
. This graph is obtained by applying the quotient map
f to the graph considered in item 5(b).
- (d)
Link the digraph of item 5(c), that is, find
such that
. This is a general process, and it can be performed in a unique way, provided the faces are geometrically convex. Indeed, let
![Mathematics 11 00660 i108 Mathematics 11 00660 i108]()
be an arbitrary directed graph, it has a symmetry, that is, there exists a bijective map
such that
if and only if the incoming edges are in bijection with the out-coming ones for every vertex in
V. In our case, if the faces are convex then they will either not be intersected by the iso-surface level
r or they are intersected exactly in two different edges (in the picture displayed at item 5(b), this was assumed to happen at the edges starting at the indexes
a and
).
- (e)
Construct the link structure
with
where
recall that
and
, come from item 4.
Collect all the link structures for all the contours in which we may be interested in and return this information as output.
3.7. A Concrete Example of Application
An example of application for the iso-slicing algorithm is the following. Suppose it is given a solid body object of which we want to produce a mould with refrigeration channels as this is a recurrent problem in the mould industry. This means that if is the solid of our interest, then we consider the region of space . Moreover, suppose we wish to make some channels along the surface area of the boundary of , while keeping the channels on the interior of the region. Furthermore, in order to simplify the process, let us assume that these channels are generated by planar curves parallel to the xy-plane. To do so, we need to determine how the ratio distance between two consecutive layers should be defined so that the cooling temperature is isotropic along the surface metric. One way to do that is to use the previous procedure: the iso-slice algorithm. Its key aspect being the possibility to define the height function . In that case, the high function is interpreted as the distance measured along the surface between the points in a lower level and the corresponding ones in the upper level immediately above it. Below, we give some details on how this procedure can be implemented.
Suppose
is a triangulation such as the one given on item 1 of
Section 5, which is considered to be an approximation to a surface defined by the boundary of
. We are interested in generating contour levels along the iso-surfaces, which are geodesics along a direction perpendicular to the xy-plane. These contour paths will give us the generators for the cooling channels. In order to do that, we observe the following steps:
Obtain a square-link from the given triangulation:
- (a)
Find an appropriate set of contours equally spaced that can serve as a good approximation to the given triangulation;
- (b)
For each one of the contour levels identified on the previous item, execute the slicing algorithm with ;
- (c)
Re-sample the number of points obtained in each set of indexes from the final link (as in item 5(2) from the iso-slice algorithm) so that they all have the same number of points;
- (d)
Construct a square-link by letting A be the union of all , assuming that we have chosen say, and that each has, say, elements. This is done by letting the map to be given by the collection of and to be the identify on each point in the level with the closest one on the level . This does not necessarily give a structure for a surface which is homeomorphic to the initially given one, but it is equivalent from the point of view of the generation of the cooling channels.
Having a square link
as defined in Sub
Section 3.5.2, we now define the iso-surface family
iteratively as follows (consider the bijection
with the sets
and
). The base points, that is the ones in the level
, are all zero
; all the points at the same level will have the same value under
F; suppose we have
given, then we define
as the formula
Use the iso-slicing algorithm with the new height value F.
The end result of this procedure gives a family of contour levels parallel to the xy-direction which are isotropic along the geodesic paths measured on the surface.
Having the contour trajectories enveloping the original surface in a way which is isotropic concerning the refrigeration distribution of heat along the geodesic distances on the surface, we can then choose a cross-section for the channels and generate the final structure as a square-patch.
4. Internal Groupoids and a Centralization of Digraphs
In this section, the notion of centralization of equivalence relations is extended to digraphs and it is seen how to apply it in characterizing internal categories and groupoids. The concrete category
is analysed while illustrating the relevance for a centralization of digraphs as a generalization to the case of equivalence relations. Some techniques used here were inspired in the work on Mal’tsev categories [
32,
33,
34].
4.1. Generalizing the Centralization of Equivalence Relations
We are now going to extend the notion of centralizing relation (usually stated between two equivalence relations) to the more general case of two directed graphs (see also [
11]).
Let
be a category with no assumptions on the existence of any kind of limits or colimits. A directed graph is simply a structure with two ordered parallel arrows, displayed as
The first arrow is the domain and the second one the codomain (in a display such as (
44) the order is found from left to right following the direction of the arrows). This means, for example, that if we picture the same graph as above in a vertical display, it must necessarily be of the form
Given two directed graphs over the same object, say
with the first one displayed horizontally and the second one displayed vertically,
we consider the following conditions:
Following the particular case when
and
are relations, we will say that the two directed graphs
and
centralize each other when condition (G5) holds (see [
11] and its references).
Let us now investigate in more detail the example of the category . As remarked before, this category does not have pullbacks for all morphisms; however, it has other interesting categorical properties, such as coequalizers.
4.2. A Lemma on Pullbacks
Let
be a category with pullbacks and a terminal object (denoted by 1). Moreover, suppose that every morphism
, in
, induces a decomposition of its domain
as a coproduct of pullbacks of
f along
b, for every
, as displayed.
We will be interested in subcategories of with the following two properties:
(B1) If f is an isomorphism in , then it is a morphism in ;
(B2) If both and f are morphisms in , then h is also a morphism in .
The example that we have in mind is the following one, which is important in the study of algorithms and other data structures in programming languages such as Matlab.
The category
is the subcategory of
which has all sets as its objects while a map
is a morphism in
whenever the following property is satisfied:
Proposition 1. Let be a category with pullbacks, a terminal object and satisfying the property displayed in (51), with a subcategory of satisfying the two properties (B1) and (B2) above. Consider a diagram in of the form If the morphism is in , then the following conditions are equivalent:
- (a)
There exists , in , such that the squareis a pullback square; - (b)
For every in ,
Proof. Let us prove
. The existence of
k, in
, induces a morphism
, in
, such that the square
commutes and moreover
is an isomorphism (simply because (
53) is a pullback square). Hence, the isomorphism
restricts itself to an isomorphism
, for every
in
, as illustrated:
Conversely, having an isomorphism in
,
, for every morphism
, we observe that the diagram
commutes. Indeed, as illustrated in the diagram below, we observe that
The above diagram is of course a diagram in
, and now, by the property (
51), we have
and hence, the family of isomorphisms
induces an isomorphism
such that the square (
55) commutes. Finally, we obtain the desired morphism
by putting
, and this makes the square (
53) a commutative square. It is also a pullback square in
because
is an isomorphism. It remains to prove that it is a pullback square in
. First, we observe that, because of (B1),
is in
, hence
is in
, now (because of (B2)) we also have
in
. This means that
is in
, which also implies that the square (
53) is a pullback in
. □
4.3. Centralizing Relations in Sub256
In the concrete subcategory
of the category
, conditions
–
above can be expressed as a bijection between the sets of incoming and out-coming edges relative to the digraphs involved. An explicit formulation is given in the following proposition, in which we consider the more general case of a category
with a subcategory
as already considered in
Section 4.2.
Proposition 2. Let be a category with pullbacks, a terminal object and satisfying the property displayed in (51), with a subcategory of satisfying the two properties (B1) and (B2) above. Given two directed graphs over the same object displayed as (46) in , we have that – are equivalent, respectively, to: Proof. Obviously, implies , while its converse follows from the fact that has the property . The equivalence between and is an immediate consequence of Proposition 1, while the case is similarly obtained by swapping the horizontal and vertical directions, mutatis mutantis. □
The following picture is useful in interpreting the two diagrams displayed in
.
The conditions – are independent of each other, as we can see in the following examples.
Consider two directed graphs in
as displayed in (
46) and observe:
If
and
, then the property
does not hold since
, which has a cardinality greater than
, and hence only the bijections can have it as a domain (because of condition (
52)); in particular, the canonical projections
are not in
.
For the remaining items, consider the set
and the arrows labelled as
,
,
and
, which are pictured as
and where the maps
d and
will always be the first projection while the maps
c and
will always be the second projection.
Take and to see that we have only , but not neither .
Take and and observe that holds, but not .
Take and and observe that holds, but not .
Take and and observe that both and hold, but not .
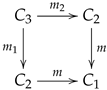
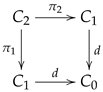
4.4. Trigraphs and Pre-Multiplicative Graphs
As we have seen, a trigraph is a generalization of a directed graph in the sense that it is a structure with three ordered parallel arrows, displayed as
Let us consider a pre-multiplicative graph as a diagram of the form
such that the square
is a pullback square. It is an underlying structure of a multiplicative graph (see
Section 2.3). We will say that the trigraph
is the multiplicative structure of the pre-multiplicative graph (
65). When the digraph
is reflexive, say with a reflexivity morphism
such that
, represented as
then we speak of a reflexive and pre-multiplicative graph whose multiplicative structure has splitings
, displayed as
such that
,
,
and
.
We will be interested in several specializations on the notion of a (reflexive and) pre-multiplicative graph.
Definition 1. A reflexive and pre-multiplicative graph, such as the one displayed above, is said to be unital when .
Definition 2. A pre-multiplicative graph, such as (65), is said to be - 1.
Transitive when and ;
- 2.
Pre-associative when the pair of digraphs and has the properties (G2) and (G3);
- 3
Associative when the pair of digraphs and has the property (G4);
- 4
Symmetric when the pair of digraphs and has the property (G5).
Observe that a reflexive, unital and transititve pre-multiplicative graph is the same as a multiplicative graph (
Section 2.3).
4.5. Internal Categories and Internal Groupoids Revisited
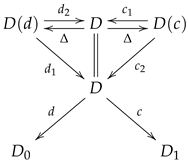
Let
be an arbitrary category and consider a diagram in
of the shape
satisfying the following conditions
Definition 3. An internal category in is a diagram such as (69), satisfying conditions (70) to (80), such that the two commutative squaresare pullback squares. Furthermore, it is an internal groupoid if there exists a morphism such that , , and . The morphisms and are uniquely determined by the properties and . We can easily prove the following well-known assertions (see [
19]).
Proposition 3. Let be a category. Given an internal category in , such as in Definition 3, we have:
- 1.
the two squaresare pullback squares. - 2.
The following conditions are equivalent:
- (a)
The category is an internal groupoid.
- (b)
The commutative squareis a pullback square; - (c)
The commutative squareis a pullback square; - (d)
The commutative squareis a pullback square; - (e)
The commutative squareis a pullback square. - (f)
The commutative squareis a pullback square.
Remark that when the category
has pullbacks of split epimorphisms along split epimorphisms, an internal category is completely determined by a diagram
together with an isomorphism
, from
into the pullback of the split epimorphism
d along the split spimorphism
c, which we will always denote by
.
Indeed, having
, in order to get a diagram such as (
69) we define:
while the rest of the structure is obtained by considering the two pullback squares of (
81), and hence we have
Note that we are consistently using the following notation for a pullback square whenever it is assumed to be obtained in a canonical way, for an arbitrary category.
We can now relate the notions on internal category and internal groupoid with the ones of pre-multiplicative graph and its variations.
Proposition 4. Every internal category is a reflexive and pre-multiplicative graph, which is unital, transitive and associative. The converse is also true.
Proposition 5. Every internal groupoid is a reflexive and pre-multiplicative graph which is unital, transitive and symmetric. The converse is also true.
We are now going to characterize a structure of a trigraph which can be obtained as the multiplicative structure of an internal category or internal groupoid. For the sake of completeness, we consider the intermediate notions of transitive, unital and reflexive pre-multiplicative graphs too.
Recall once more that a trigraph is simply an ordered triple of parallel morphisms
, displayed as
Our concern is to determine if the trigraph
is the multiplicative structure of an internal category or an internal groupoid. An obvious necessary condition is the existence of two splitings
such that
and
. We call such a structure a reflexive trigraph and represent it by a five-tuple
, displayed as
Before stating the results characterizing those reflexive trigraphs that are multiplicative structures, we need one more concept. A span
is said to be an
exact span if there exists a commutative square
which is at the same time a pushout square and a pullback square.
Theorem 1. Let be a category and a reflexive trigraph on it. The following conditions are equivalent:
- 1.
T is the multiplicative structure of a reflexive and pre-multiplicative graph.
- 2.
The span is an exact span.
Theorem 2. Let be a category and a reflexive trigraph on it. The following conditions are equivalent:
- 1.
T is the multiplicative structure of a unital, reflexive and pre-multiplicative graph.
- 2.
The span is an exact span and .
Theorem 3. Let be a category and a reflexive trigraph on it. The following conditions are equivalent:
- 1.
T is the multiplicative structure of a transitive, unital, reflexive and pre-multiplicative graph (i.e., a multiplicative graph).
- 2.
The span is an exact span, , and .
- 3.
The span is an exact span and ; moreover, the trigraph is pre-associative and the two conditions and are satisfied with α, β, and uniquely determined (up to a unique isomorphism) as in conditions (G1), (G2) and (G3).
Theorem 4. Let be a category and a reflexive trigraph on it. The following conditions are equivalent:
- 1.
T is the multiplicative structure of an internal category.
- 2.
The span is an exact span, , , and the triangulation has the property (G4).
In fact, we should better say that the pair of graphs and has the property (G4).
Theorem 5. Let be a category and a reflexive triangulation on it. The following conditions are equivalent:
- 1.
T is the multiplicative structure of an internal groupoid.
- 2.
The span is an exact span, , , and the triangulation has the property (G5).

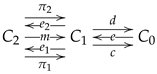
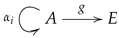
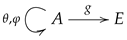

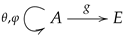
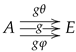
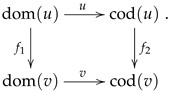
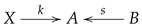


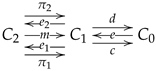

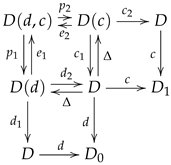



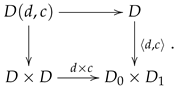


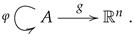
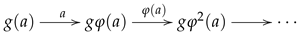
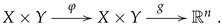

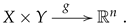


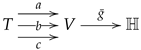


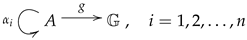

be an arbitrary directed graph, it has a symmetry, that is, there exists a bijective map such that if and only if the incoming edges are in bijection with the out-coming ones for every vertex in V. In our case, if the faces are convex then they will either not be intersected by the iso-surface level r or they are intersected exactly in two different edges (in the picture displayed at item 5(b), this was assumed to happen at the edges starting at the indexes a and ).
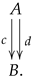
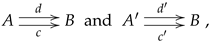
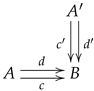
such that
is a pullback square;