On the Approximate Polar Curves of Foliations

Abstract

We present a decomposition theorem of the generic polar curves of a generalized curve foliation with only one separatrix and the Hamiltonian foliations defined by the approximate roots of the generatrix. This is a generalization to foliations of the decomposition theorem of approximate Jacobians given by García Barroso and Gwoździewicz for plane branches.

1. Introduction

Let $\mathbb{C}\left[\right[x,y\left]\right]$ be the ring of formal complex power series. A complex plane curve at the origin of ${\mathbb{C}}^2$ is given by the zeros of $f(x,y)\in \mathbb{C}\left[\right[x,y\left]\right]$, and we will denote it by ${\mathcal{C}}_f$. If f is irreducible, then we say that ${\mathcal{C}}_f$ is a branch. Since $\mathrm{ord}\left(f\right)=\mathrm{ord}\left(uf\right)$, for any unit $u\in \mathbb{C}\left[\right[x,y\left]\right]$, we define the multiplicity of ${\mathcal{C}}_f$, and we denote it by $\mathrm{mult}\left({\mathcal{C}}_f\right)$, as the order of f. We say that ${\mathcal{C}}_f$ is a singular curve if its multiplicity is greater than one; otherwise, ${\mathcal{C}}_f$ is a smooth curve.

In this work, we will consider a singular curve ${\mathcal{C}}_f$. Let $g(x,y)=ax+by$ with $(a,b)\ne (0,0)$. The polar curve of ${\mathcal{C}}_f$ with respect to the direction $g(x,y)$ is the curve ${\mathcal{P}}_g\left(f\right):J(f,g)=0$, where $J(f,g)$ denotes the Jacobian determinant of f and g. There exists a dense Zariski open set U of ${\mathbb{P}}^1\left(\mathbb{C}\right)$ such that for all $[-b:a]\in U$, the polar curves ${\mathcal{P}}_{-bx+ay}\left(f\right)$ are equisingular and in which case we will say that these polar curves are generic. In this article, when we say polar curve we always refer to a generic one. It is well-known that the equisingularity class of ${\mathcal{P}}_g\left(f\right)$ can vary in a family of equisingular curves as Pham showed [1] (Exemple 3): the curves ${\{f_a=y^3+x^{11}+a{x}^{8}y=0\}}_{a\in \mathbb{C}}$ have the same equisingularity class but the polar curves ${\mathcal{P}}_x\left(f_a\right)$ have two different smooth branches for $a\ne 0$ and it has a double smooth branch for $a=0$.

When f is irreducible, Merle [2] proved that the branches of the polar curve ${\mathcal{P}}_g\left(f\right)$ have characteristic contacts with ${\mathcal{C}}_f$, which means that their contacts with ${\mathcal{C}}_f$ are the characteristic exponents of ${\mathcal{C}}_f$ (these exponents codify the equisingularity class of ${\mathcal{C}}_f$). In particular, Merle gave a decomposition of the polar curve ${\mathcal{P}}_g\left(f\right)$ as the union of curves ${\left\{{\mathcal{C}}_{P_i}\right\}}_i$, which are not necessarily branches, but such that the multiplicity of ${\mathcal{C}}_{P_i}$ and the contact of every branch of ${\mathcal{C}}_{P_i}$ with ${\mathcal{C}}_f$ only depend on the equisingularity class of ${\mathcal{C}}_f$. More precisely, in the decomposition of Merle, any ${\mathcal{C}}_{P_i}$ is the union of all the branches of ${\mathcal{P}}_g\left(f\right)$ having the same contact with ${\mathcal{C}}_f$. Furthermore, Merle proved that his decomposition of the polar curve of the branch ${\mathcal{C}}_f$ not only depends on the equisingularity class of the branch, but determines it, that is, this decomposition is a complete equisingularity invariant of ${\mathcal{C}}_f$.

A singular foliation of codimension one over ${\mathbb{C}}^2$ is locally given by a 1-form $\omega =A(x,y)\mathrm{d}x+B(x,y)\mathrm{d}y$, where $A(x,y),B(x,y)\in \mathbb{C}\left[\right[x,y\left]\right]$ are not units, that is $A(0,0)=B(0,0)=0$. We will denote by ${\mathcal{F}}_{\omega }$ the foliation defined by $\omega$. We say that ${\mathcal{C}}_f:f(x,y)=0$ is invariant by ${\mathcal{F}}_{\omega }$ if $\omega \wedge \mathrm{d}f:=f.\eta ,$ where $\eta$ is a 2-form. If ${\mathcal{C}}_f$ is irreducible then the curve ${\mathcal{C}}_f$ is a separatrix of ${\mathcal{F}}_{\omega }$.

The polar curve of the foliations ${\mathcal{F}}_{{\omega }_1}$ and ${\mathcal{F}}_{{\omega }_2}$ is by definition the contact curve $w_1\wedge w_2$. This notion is a generalization of the polar curve ${\mathcal{P}}_g\left(f\right)$ since this one coincides with the polar curve of the foliations given by the 1-forms $\mathrm{d}f$ and $\mathrm{d}g$.

Rouillé (see [3,4]) generalised the decomposition theorem of Merle to the polar curves of foliations, where ${\mathcal{F}}_{{\omega }_2}=\mathrm{d}(-bx+ay)$ (for $(a,b)\ne (0,0)$) and ${\mathcal{F}}_{{\omega }_1}$ is a non-dicritical generalized curve foliation with only one separatrix or with non-resonant logarithmic model. This decomposition depends only on the equisingularity class of the separatrix. Rouillé’s proof is based on the comparison of the Newton polygon of the only separatrix of the foliation with the Newton polygon of the 1-form defining the foliation.

The polar curve ${\mathcal{P}}_g\left(f\right)$ of a reduced complex plane curve ${\mathcal{C}}_f$ and a non-singular curve ${\mathcal{C}}_g$ was studied, between other authors, by García Barroso (see [5,6]). García Barroso gave the decomposition of ${\mathcal{P}}_g\left(f\right)$ in terms of the Eggers tree of ${\mathcal{C}}_f$. The Eggers tree of ${\mathcal{C}}_f$ encodes the equisingularity class of ${\mathcal{C}}_f$ and it is equivalent to the dual resolution graph of ${\mathcal{C}}_f$ but the Eggers tree is better suited in order to relate the structure of ${\mathcal{C}}_f$ to that of its polar curve ${\mathcal{P}}_g\left(f\right)$. As in the irreducible case, the branches of the polar curve ${\mathcal{P}}_g\left(f\right)$, for reduced f, have characteristic contacts with ${\mathcal{C}}_f$, which means that their contacts with the branches of ${\mathcal{C}}_f$ are the characteristic exponents of the branches of ${\mathcal{C}}_f$ or the contact values of the branches of ${\mathcal{C}}_f$. But, in the case where f is reduced non-irreducible, the decomposition theorem of ${\mathcal{P}}_g\left(f\right)$ is not a complete equisingularity invariant as it happens when f is irreducible; nevertheless García Barroso proposed a new complete invariant of ${\mathcal{C}}_f$ built from the decomposition of its polar curves.

On the other hand, Corral (see [7,8]) generalized the decomposition theorem of the polar curve given by García Barroso to the case of non-dicritical generalized curve foliations which logarithmic model is not resonant, using the Eggers tree of the total union of separatrices. This decomposition depends only on the equisingularity class of this union.

In [9,10], Kuo and Parusiński gave a decomposition of ${\mathcal{P}}_g\left(f\right)$ when ${\mathcal{C}}_g$ is not necessarily smooth, generalizing the decomposition theorems of Merle and García Barroso. The main tool used by Kuo and Parusiński is the tree model of ${\mathcal{C}}_{fg}$ (a generalization of the Kuo-Lu tree introduced in [11], where ${\mathcal{C}}_{fg}$ is the union of ${\mathcal{C}}_f$ and ${\mathcal{C}}_g$), which encodes the contact values of the branches of ${\mathcal{C}}_{fg}$. Note that the Eggers tree of ${\mathcal{C}}_{fg}$ is a Galois quotient of its Kuo-Lu tree (see [12]). A new phenomenon appears when ${\mathcal{C}}_g$ is not smooth: the contact values of the branches of ${\mathcal{P}}_g\left(f\right)$ with the branches of ${\mathcal{C}}_{fg}$ are not necessarily contact values of the branches of ${\mathcal{C}}_{fg}$. Namely, it may not be possible anymore to determine all the contact values of branches of ${\mathcal{P}}_g\left(f\right)$ with the branches of ${\mathcal{C}}_{fg}$, using only the equisingularity class of ${\mathcal{C}}_{fg}$. This phenomenon appears when the tree model associated with ${\mathcal{C}}_{fg}$ have collinear points and bars (no such points or bars exist in the case when ${\mathcal{C}}_g$ is smooth).

In [13], García Barroso and Gwoździewicz gave a decomposition theorem for ${\mathcal{P}}_g\left(f\right)$, where ${\mathcal{C}}_f$ is a branch and ${\mathcal{C}}_g$ is a characteristic approximate root of ${\mathcal{C}}_f$ (this notion was introduced in [14] (page 48)). After a change of coordinates, if necessary, the first approximate root of ${\mathcal{C}}_f$ is given by $y=0$. The remaining characteristic approximate roots of ${\mathcal{C}}_f$ are singular curves whose equisingularity classes are determined by the equisingularity class of ${\mathcal{C}}_f$. In particular, in [13] it was proved that the set of decompositions of ${\mathcal{P}}_g\left(f\right)$, where g runs through the approximate roots of f is a complete equisingularity invariant of ${\mathcal{C}}_f$, generalizing the decomposition theorem of Merle. The case studied in [13] is a particular case of the results of Kuo and Parusinski, but the colineal phenomenon only appears in the first bunch of the decomposition and this allows to precise the information on the decomposition of the Jacobian curve in the framework of García Barroso and Gwoździewicz. On the other hand, in [13] the tree-model is not used, but rather Newton polygons and initial weighted forms associated with them. In this paper, we generalize to foliations, the results of [13] to the context of generalized curve foliations, again using the language of Newton polygons and initial weighted forms. Our main theorem gives a decomposition of the approximate polar curve ${\mathcal{P}}_{\omega }^{\left(k\right)}(x,y)=A(x,y)f_y^{\left(k\right)}(x,y)-B(x,y)f_x^{\left(k\right)}(x,y)=0$, where $\omega =A(x,y)\mathrm{d}x+B(x,y)\mathrm{d}y$ and $f^{\left(k\right)}=0$ is the kth approximate root of ${\mathcal{C}}_f$:

Theorem 1.

Let $\mathcal{F}:\omega =0$ and $\mathcal{G}:\mathrm{d}{f}^{\left(k\right)}=0$ be generalized curve foliations with separatrices ${\mathcal{C}}_f$ and ${\mathcal{C}}_{f^{\left(k\right)}}$ respectively. The approximate polar curve ${\mathcal{P}}_{\omega }^{\left(k\right)}$ has $\mathrm{mult}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\ge n+n_1\cdots n_k-2$ and admits a decomposition of the form

$${\mathcal{P}}_{\omega }^{\left(k\right)}={\mathsf{\Gamma }}^{(k+1)}\cdots {\mathsf{\Gamma }}^{\left(g\right)},$$

where the factors ${\mathsf{\Gamma }}^{\left(l\right)}$ are not necessarily irreducible and x is coprime with the product ${\mathsf{\Gamma }}^{(k+2)}\cdots {\mathsf{\Gamma }}^{\left(g\right)}$. Moreover,

(a)

$\mathrm{cont}({\mathcal{P}}_l,{\mathcal{C}}_f)=\frac{{\beta }_l}{n}$ for ${\mathcal{P}}_l$ irreducible component of ${\mathsf{\Gamma }}^{\left(l\right)},$ $k+2\le l\le g$.

(b)

$\mathrm{mult}\left({\mathsf{\Gamma }}^{\left(l\right)}\right)=n_1\cdots n_{l-1}(n_l-1)$, $k+2\le l\le g$.

(c)

$\mathrm{mult}\left({\mathsf{\Gamma }}^{(k+1)}\right)\ge n_1\cdots n_k(n_{k+1}+1)-2$ and $\mathrm{ord}\left(\gamma \right)\le \frac{{\beta }_{k+1}}{n}$ for any Newton–Puiseux root γ of ${\mathsf{\Gamma }}^{(k+1)}$,

where ${\left\{(m_l,n_l)\right\}}_l$ are the Newton–Puiseux pairs of ${\mathcal{C}}_f$.

The structure of this paper is as follows. In Section 2, we introduce all the notions and tools necessary in order to establish the difference between the orders of the Newton–Puiseux roots of ${\mathcal{C}}_f^{\left(k\right)}$ (characteristic approximate roots of the branch ${\mathcal{C}}_f$) and a truncation of a Newton–Puiseux root of ${\mathcal{C}}_f$. In Section 3, we present preliminary notions of foliations and some properties of the inverse image of a foliation. Moreover, we study the weighted initial forms associated with the Newton polygons of the foliations. In particular, we prove the following lemma which is a key tool for our purposes.

Lemma 1.

If $\nu \in {\mathbb{Q}}^{+}$ and ${\mathrm{In}}_{\nu }\left(\omega \right)\wedge {\mathrm{In}}_{\nu }\left(\eta \right)\ne 0$, then ${\mathrm{In}}_{\nu }(\omega \wedge \eta )={\mathrm{In}}_{\nu }\left(\omega \right)\wedge {\mathrm{In}}_{\nu }\left(\eta \right)$. Moreover, ${\mathrm{ord}}_{\nu }\left({\mathrm{In}}_{\nu }(\omega \wedge \eta )\right)={\mathrm{ord}}_{\nu }\left({\mathrm{In}}_{\nu }\omega \right)+{\mathrm{ord}}_{\nu }\left({\mathrm{In}}_{\nu }\eta \right)-1-\nu .$

Section 4 is the core of this paper. We study the approximate polar curves associated with a foliation having a single separatrix. In particular, we detail the weighted initial forms of the inverse images of these polar curves with respect to a ramification defined from the equisingularity class of the separatrix of the foliation. Moreover, we determine the properties of the Newton polygon of these inverse images, by relating them to the Newton polygon of the inverse images of the foliation.

Finally, in Section 5, we prove the main theorem on decomposition of the polar curve ${\mathcal{P}}_{\omega }^{\left(k\right)}(x,y)=A(x,y)f_y^{\left(k\right)}(x,y)-B(x,y)f_x^{\left(k\right)}(x,y)=0$, where $\omega =A(x,y)\mathrm{d}x+B(x,y)\mathrm{d}y$.

The results presented in this paper are part of Saravia-Molina’s PhD thesis (see [15]).

2. Preliminary Notions on Curves

Let $\mathbb{C}\left[\right[x,y\left]\right]$ be the ring of formal complex power series and $f(x,y)={\sum }_{ij}{a}_{ij}{x}^i{y}^j\in \mathbb{C}\left[[x,y]\right]$ be a non-zero power series without constant term. The order of f is $\mathrm{ord}\left(f\right)=min\{i+j:a_{ij}\ne 0\}$. The initial form of f is the sum of all terms of f of degree equals $\mathrm{ord}\left(f\right)$. The multiplicity of the plane curve ${\mathcal{C}}_f$ of equation $f(x,y)=0$, denoted by $m\left({\mathcal{C}}_f\right)$, is the order of f. We say that ${\mathcal{C}}_f$ is singular if $m\left({\mathcal{C}}_f\right)>1$.

Let $S\subseteq {\mathbb{N}}^2$. Denote by $D\left(S\right)$ the convex hull of $(S+{\mathbb{R}}_{\ge 0}^2)$, where + is the Minkowski sum, and by $\mathcal{N}\left(S\right)$ the polygonal boundary of $D\left(S\right)$, which we will call Newton polygon determined by S.

A support line of $\mathcal{N}\left(S\right)$ is any line $\mathcal{L}:x+\alpha y=c$ such that $\mathcal{L}\cap \mathcal{N}\left(S\right)\ne \varnothing$ y $\mathcal{N}\left(S\right)\subseteq {\mathcal{L}}^{+}=\{(x,y)\in {\mathbb{R}}^2:x+\alpha y\ge c\}$ (see Figure 1). We say that a line $\mathcal{L}$ has inclination $\alpha$ if its slope is $-\frac{1}{\alpha }$.

Figure 1. Support lines.

Let $f(x,y)={\sum }_{i,j}{a}_{ij}{x}^i{y}^j\in \mathbb{C}\left[[x,y]\right]$. The support of f is

$$\mathrm{supp}\left(f\right):=\{(i,j)\in {\mathbb{N}}^2:a_{ij}\ne 0\},$$

and the Newton polygon of f is by definition the Newton polygon $\mathcal{N}\left(\mathrm{supp}\right(f\left)\right)$.

Observe that $\mathcal{N}\left(f\right)=\mathcal{N}\left(uf\right)$ for all $u\in \mathbb{C}\{x,y\}$, as long as $u(0,0)\ne 0$.

Let $\tau \in {\mathbb{Q}}^{+}$ and ${\displaystyle f(x,y)=\sum _{i,j}{a}_{ij}{x}^i{y}^j\in \mathbb{C}\left[[x,y]\right].}$ Consider the variables x and y with the weights $w\left(x\right)=1$ and $w\left(y\right)=\tau$. The τ-weighted order of ${\mathcal{C}}_f$ is ${\mathrm{ord}}_{\tau }\left(f\right):=min\{i+\tau j:a_{ij}\ne 0\}$ and the τ-weighted initial part of f is ${\displaystyle i{n}_{\tau }\left(f\right):=\sum _{i+\tau j={\mathrm{ord}}_{\tau }\left(f\right)}{a}_{ij}{x}^i{y}^j}$.

By Weierstrass preparation theorem ([16] (Theorem 2.4)), for any $f\in \mathbb{C}\left[\right[x,y\left]\right]$ such that $\mathrm{ord}\left(f\right(0,y\left)\right)=n$ there are a unit $u(x,y)\in \mathbb{C}\left[\right[x,y\left]\right]$ and a polynomial $f^{*}(x,y)\in \mathbb{C}\left[\left[x\right]\right]\left[y\right]$ such that $f(x,y)=u(x,y)f^{*}(x,y)$ and $f^{*}(x,y)=y^n+a_1\left(x\right)y^{n-1}+a_2\left(x\right)y^{n-2}+\cdots +a_n\left(x\right)$ is a Weierstrass polynomial, that is, $a_i\left(x\right)\in \mathbb{C}\left[\left[x\right]\right]$ with $\mathrm{ord}\left(a_i\right)\ge i$ for $i=1,\dots ,n$.

Remark 1.

Let $f(x,y)=y^n+a_1\left(x\right)y^{n-1}+a_2\left(x\right)y^{n-2}+\cdots +a_n\left(x\right)\in \mathbb{C}\left[\left[x\right]\right]\left[y\right]$ be a Weierstrass polynomial and consider its partial derivatives $f_x$, $f_y$. Then,

• $f_x(x,y)=a_1^{\prime }\left(x\right)y^{n-1}+\cdots +a_{n-1}^{\prime }\left(x\right)y+a_n^{\prime }\left(x\right)$ and $\mathrm{ord}\left(f_x\right)\ge n-1$.
• $f_y(x,y)=n{y}^{n-1}+a_1\left(x\right)(n-1)y^{n-2}+\cdots +a_{n-1}\left(x\right)$, so $\mathrm{ord}\left(f_y\right)=n-1$.

Therefore, $\mathrm{ord}\left(f_x\right)\ge \mathrm{ord}\left(f_y\right)$.

The intersection multiplicity at the origin of the plane curves ${\mathcal{C}}_f$ and ${\mathcal{C}}_g$ is by definition ${({\mathcal{C}}_f,{\mathcal{C}}_g)}_0={dim}_{\mathbb{C}}\mathbb{C}\{x,y\}/(f,g),$ where $(f,g)$ denotes the ideal of $\mathbb{C}\{x,y\}$ generated by f and g. We can also denote ${({\mathcal{C}}_f,{\mathcal{C}}_g)}_0$ as ${(f,g)}_0$.

The following proposition is in the folklore but we give its proof since we can not precise a reference for it.

Proposition 1.

Let ${\mathcal{C}}_f$ and ${\mathcal{C}}_g$ be two formal plane curves. Then

$${(f(x^m,y+\alpha \left(x^m\right)),g(x^m,y+\alpha \left(x^m\right)))}_0=m·{(f(x,y),g(x,y))}_0,$$

for any $m\in \mathbb{N}$ and any power series $\alpha \left(x\right)\in \mathbb{C}\left[\right[x\left]\right]$,with $\alpha \left(0\right)=0$.

Proof. 

First we suppose that $\alpha \left(x\right)=0$. Let $f^{*}(x,y):=f(x^m,y)$ and $g^{*}(x,y):=g(x^m,y)$. By [16] (Theorem 4.17) we have

$$\begin{array}{ccc}\hfill {(f^{*},g^{*})}_0& =& {\mathrm{ord}}_y{\mathrm{Res}}_y(f^{*},g^{*})={\mathrm{ord}}_y{\mathrm{Res}}_y(f(x^m,y),g(x^m,y)))\hfill \\ & \underset{\left(a\right)}{=}& {\mathrm{ord}}_y\left({\mathrm{Res}}_y(f(x,y),g(x,y))\left(x^m\right)\right)=m·{\mathrm{ord}}_y{\mathrm{Res}}_y(f,g)=m·{(f,g)}_0,\hfill \end{array}$$

where ${\mathrm{Res}}_y(f,g)$ denotes the y-resultant of f and g and the equality $\left(a\right)$ holds since the resultant is invariant by change of basis (see [17]).

To prove the general case, we observe that $(x,y)\to (x^m,y+\alpha \left(x^m\right))$ is the composition of $E,F:\mathbb{C}\left[\right[x,y\left]\right]⟶\mathbb{C}\left[\right[x,y\left]\right]$ where $E(x,y)=(x^m,y)$ and $F(x,y)=(x,y+\alpha (x\left)\right)$, being F an automorphism. We conclude the proof of the proposition by [16] (Theorem 4.14 (iii)) and the particular case already proved. □

We denote by ${\displaystyle \mathbb{C}{\left[\left[x\right]\right]}^{*}=\bigcup _{n\in \mathbb{N}}\mathbb{C}\left[\left[x^{1/n}\right]\right]}$ the ring of fractional power series with coefficients in $\mathbb{C}$, also called ring of Puiseux series.

Let $y\left(x\right),z\left(x\right),w\left(x\right)\in \mathbb{C}{\left[\left[x\right]\right]}^{*}$. The triangular inequality (see [5] (Lemme 1.2.4)) says that

$$\mathrm{ord}\left(y\right(x)-z(x\left)\right)\ge min\left\{\mathrm{ord}\right(y\left(x\right)-w\left(x\right)),\mathrm{ord}(w\left(x\right)-z\left(x\right)\left)\right\}.$$

(1)

Moreover, if $\mathrm{ord}\left(y\right(x)-w(x\left)\right)\ne \mathrm{ord}\left(w\right(x)-z(x\left)\right)$ then the equality holds.

Let $f(x,y)\in \mathbb{C}\left[\right[x,y\left]\right]$ such that $f(0,0)=0$ and $f(0,y)\ne 0$. By Newton’s theorem ([16] (Theorem 3.8)) there is $\alpha \left(x\right)\in \mathbb{C}{\left[\left[x\right]\right]}^{*}$ with $\alpha \left(0\right)=0$ such that $f(x,\alpha \left(x\right))=0\in \mathbb{C}{\left[\left[x\right]\right]}^{*}.$ We say that $\alpha \left(x\right)\in \mathbb{C}{\left[\left[x\right]\right]}^{*}$ is a Newton–Puiseux root of ${\mathcal{C}}_f$. Let us denote by $\mathrm{Zer}\left(f\right)$ the set of the Newton–Puiseux roots of ${\mathcal{C}}_f$.

Suppose now that $f(x,y)$ is irreducible of order n.

Let $\alpha \left(x^{1/n}\right)\in \mathbb{C}{\left[\left[x\right]\right]}^{*}$ be a Newton–Puiseux root of ${\mathcal{C}}_f$. After Puiseux’s theorem ([18] (Théorème 8.6.1)), $\mathrm{Zer}\left(f\right)={\left\{\alpha \left({\epsilon }^j{x}^{1/n}\right)\right\}}_{j=1}^n$, where $\epsilon$ is a nth-primitive root of unity. Hence

$${\displaystyle f(x,y)=u(x,y)\prod _{j=1}^n\left(y-\left(\alpha \left({\epsilon }^j{x}^{1/n}\right)\right)\right),}$$

where $u\in \mathbb{C}\left[\right[x,y\left]\right]$ is a unit. If we put $x=t^n$, where t is a new variable, the Newton–Puiseux root ${\displaystyle \alpha \left(x\right)=\sum _{i\ge n}{a}_i{x}^{i/n}}$ of ${\mathcal{C}}_f$ can be written as

$$\left\{\begin{array}{ccc}\hfill x\left(t\right)& =\hfill & t^n\hfill \\ \hfill y\left(t\right)& =\hfill & {\displaystyle \sum _{i\ge n}{a}_i{t}^i,}\hfill \end{array}\right.$$

which we will call Puiseux parametrisation of ${\mathcal{C}}_f$.

Since ${\mathcal{C}}_f$ is a branch, its Newton polygon $\mathcal{N}\left(f\right)$ has only one compact face. Suppose that the inclination of this compact side is $\nu$ and let $i+\nu j=c$ be the line that contains it. By convexity of $\mathcal{N}\left(f\right)$, we can write

$${\displaystyle f(x,y)=\sum _{i+\nu j=c}{a}_{ij}{x}^i{y}^j+\sum _{i+\nu j>c}{a}_{ij}{x}^i{y}^j.}$$

There are $g\in \mathbb{N}$ and a sequence of natural numbers ${\beta }_0=n<\cdots <{\beta }_g$ such that $\{\mathrm{ord}({\alpha }_i-{\alpha }_j):{\alpha }_i,{\alpha }_j\in \mathrm{Zer}\left(f\right),i\ne j\}=\left\{\frac{{\beta }_l}{{\beta }_0}:1\le l\le g\right\}.$ The sequence $({\beta }_0,\dots ,{\beta }_g)$ is called the sequence of characteristic exponents of the branch ${\mathcal{C}}_f$.

Put $e_l:=gcd({\beta }_0,\dots ,{\beta }_l)$. The characteristic pairs of ${\mathcal{C}}_f$ is the set ${\left\{(m_l,n_l)\right\}}_{l=1}^g$ with $l=1,\dots ,g$ such that $gcd(m_l,n_l)=1$, $e_{l-1}=n_l{e}_l$ and ${\beta }_l=m_l{e}_l$. Observe that $n=n_1\cdots n_g$ and $\frac{{\beta }_l}{n}=\frac{m_l}{n_1\cdots n_l}$ for $l=1,\dots ,g$.

By [5] (Lemme 1.1.1, Corollaire 1.1.1) we have

(a)

${\mathrm{ord}}_x({\alpha }_j\left(x^{1/n}\right)-{\alpha }_j\left({\epsilon }^j{x}^{1/n}\right))\ge \frac{{\beta }_1}{{\beta }_0},$

(b)

If ${\alpha }_j\left(x^{1/n}\right)\ne {\alpha }_j\left({\epsilon }^j{x}^{1/n}\right)$ and ${\mathrm{ord}}_x({\alpha }_j\left(x^{1/n}\right)-{\alpha }_j\left({\epsilon }^j{x}^{1/n}\right))>\frac{{\beta }_i}{{\beta }_0}$ then ${\mathrm{ord}}_x({\alpha }_j\left(x^{1/n}\right)-{\alpha }_j\left({\epsilon }^j{x}^{1/n}\right))\ge \frac{{\beta }_{i+1}}{{\beta }_0}$ for $i\in \{1,\dots ,g-1\}$,

(c)

$$\begin{array}{ccc}\hfill ♯\left\{{\alpha }_j\left(x^{1/n}\right)\in \mathrm{Zer}\left(f\right):{\mathrm{ord}}_x\left({\alpha }_j\left(x^{1/n}\right)-{\alpha }_j\left({\epsilon }^j{x}^{1/n}\right)\right)=\frac{{\beta }_i}{{\beta }_0}\right\}& =& e_{i-1}-e_i\hfill \\ & =& (n_i-1)n_{i+1}\cdots n_g,\hfill \end{array}$$

where $\epsilon$ is a nth-primitive root of unity and $j\in \{1,\dots ,n\}$.

After a change of coordinates, if necessary, we can assume that $y=0$ verifies ${(f,y)}_0={\beta }_1$, that is, $y=0$ is not only the tangent of ${\mathcal{C}}_f$ but it has maximal contact with ${\mathcal{C}}_f$. So every Newton–Puiseux root of ${\mathcal{C}}_f:f(x,y)=0$ is given by

$${\displaystyle y_{{\mathcal{C}}_f}\left(x\right)=a_{{\beta }_1}{x}^{\frac{{\beta }_1}{n}}+\sum _{\begin{array}{c}j\in \left(e_1\right)\\ {\beta }_1<j<{\beta }_2\end{array}}{a}_j{x}^{\frac{j}{n}}+a_{{\beta }_2}{x}^{\frac{{\beta }_2}{n}}+\cdots +\sum _{\begin{array}{c}j\ge {\beta }_g\end{array}}{a}_j{x}^{\frac{j}{n}},}$$

(2)

where $a_{{\beta }_j}\in \mathbb{C}\backslash \left\{0\right\}$ for $1\le j\le g$.

The curve ${\mathcal{C}}_f$ has a Newton–Puiseux root of the form (2) is equivalent to the Weierstrass polynomial associated with f does not have a term of $n-1$ (Tschirnhausen transformation), where n is the order of f.

Let ${\mathcal{C}}_f$ and ${\mathcal{C}}_g$ be two branches, with multiplicities n and m, respectively. Put $\mathrm{Zer}\left(f\right)={\left\{y_i\left(x^{1/n}\right)\right\}}_{i=1}^n$ and $\mathrm{Zer}\left(g\right)={\left\{z_j\left(x^{1/m}\right)\right\}}_{j=1}^m$. The contact between ${\mathcal{C}}_f$ and ${\mathcal{C}}_g$ is

$$\mathrm{cont}({\mathcal{C}}_f,{\mathcal{C}}_g)=\underset{{\displaystyle \begin{array}{c}1\le i\le n\\ 1\le j\le m\end{array}}}{max}\left\{{\mathrm{ord}}_x\left(y_i\left(x\right)-z_j\left(x\right)\right)\right\}\in \mathbb{Q}\cup \{\infty \}.$$

Let $y\left(x^{1/n}\right)$ be a fixed Newton–Puiseux root of the branch ${\mathcal{C}}_f:f(x,y)=0$. By [5] (Lemme 1.2.3) we obtain

$${\displaystyle \mathrm{cont}({\mathcal{C}}_f,{\mathcal{C}}_g)=\underset{1\le j\le m}{max}\left\{{\mathrm{ord}}_x(y\left(x^{1/n}\right)-z_j\left(x^{1/m}\right))\right\},}$$

(3)

where $\mathrm{Zer}\left(g\right)={\left\{z_j\left(x^{1/m}\right)\right\}}_{j=1}^m$. The rational number ${max}_{1\le j\le m}\left\{{\mathrm{ord}}_x(y\left(x^{1/n}\right)-z_j\left(x^{1/m}\right))\right\}$ is called the contact of the Newton–Puiseux root $y\left(x^{1/n}\right)$ of ${\mathcal{C}}_f$ with the branch ${\mathcal{C}}_g$.

Approximate Root of a Branch

The notion of approximate root was introduce by Abhyankar and Moh in order to prove the Embedding line theorem which states that the affine line can be embedded in a unique way, up to ambient automorphisms, in the affine plane. Let A be an integral domain (a unitary commutative ring without zero divisors). Let $f\left(y\right)\in A\left[y\right]$ be a monic polynomial of degree d and consider p a divisor of d. In general, there is not $g\left(y\right)\in A\left[y\right]$ such that $f\left(y\right)=g{\left(y\right)}^p$. One can ask for an approximation of this equality and it was proved that if p is an invertible element of A which divides d, then by [14] there is a unique monic polynomial $g\left(y\right)\in A\left[y\right]$ such that the degree of $f-g^p$ is less than $d-\frac{d}{p}$. The polynomial $g\left(y\right)$ is called the pth approximate root of f.

Notice that if $f\left(y\right)=y^n+a_1\left(x\right)y^{n-1}+\cdots +a_n\left(x\right)\in A\left[y\right]$ and n is invertible in A then the Tschirnhausen transformation $y+\frac{a_1\left(x\right)}{n}$ is the nth approximate root of $f\left(y\right)$. Observe that in the case $A=\mathbb{C}\left[\right[x\left]\right]$, any divisor p of n is invertible in A. In this paper we will use the notion of approximate root taken the domain $A=\mathbb{C}\left[\right[x\left]\right]$.

Let $f\in \mathbb{C}\left[\right[x\left]\right]\left[y\right]$ be an irreducible Weierstrass polynomial such that the curve ${\mathcal{C}}_f:f(x,y)=0$ has characteristic exponents $({\beta }_0,\dots ,{\beta }_g)$. The kth characteristic approximate root of f, denoted by $f^{\left(k\right)}$, is the $e_k$th aproximate root of f, where $e_k=gcd({\beta }_0,\dots ,{\beta }_k)$.

Proposition 2

([14] (Proposition 4.6)). Let $f(x,y)\in \mathbb{C}\left[\right[x\left]\right]\left[y\right]$ be an irreducible Weierstrass polynomial such that the characteristic exponents of ${\mathcal{C}}_f$ are $({\beta }_0,\dots ,{\beta }_g).$ The kth characteristic approximate root $f^{\left(k\right)}$ of f verifies:

(i)

The polynomial $f^{\left(k\right)}$ is irreducible and the characteristic exponents of ${\mathcal{C}}^{\left(k\right)}:f^{\left(k\right)}(x,y)=0$ are $\left(\frac{{\beta }_0}{e_k},\dots ,\frac{{\beta }_k}{e_k}\right)$.

(ii)

The y-degree of $f^{\left(k\right)}$ is equal to $\frac{{\beta }_0}{e_k}$ and $\mathrm{cont}(f,f^{\left(k\right)})=\frac{{\beta }_{k+1}}{{\beta }_0}$.

Since $f(x,y)\in \mathbb{C}\left[\right[x\left]\right]\left[y\right]$ is irreducible and admits a Newton–Puiseux root of the form (2), that is, f does not have a term of degree $n-1$, then the degree of $f-y^n=n-2<n-1$ and we conclude that $f^{\left(0\right)}=y$.

Put $m:={\displaystyle \frac{{\beta }_0}{e_k}}=n_1\cdots n_k$ and $Zer\left(f^{\left(k\right)}\right)={\left\{{\delta }_j\left(x^{1/m}\right)\right\}}_{j=1}^m$. We can write

$${\displaystyle f^{\left(k\right)}(x,y)=\prod _{j=1}^m(y-{\delta }_j\left(x\right)),}$$

(4)

Let ${\displaystyle \gamma \left(x\right)=\sum _i{b}_i{x}^{\frac{i}{n}}\in \mathbb{C}{\left[\left[x\right]\right]}^{*}}$ be a Puiseux series. The support of $\gamma \left(x\right)$ is

$$\mathrm{supp}\left(\gamma \right):=\left\{\frac{i}{n}:b_i\ne 0\right\}.$$

By [19] (Property 4.5) the exponent $\frac{{\beta }_{k+1}}{{\beta }_0}$ does not appear in any Newton–Puiseux root of ${\mathcal{C}}_f^{\left(k\right)}:f^{\left(k\right)}(x,y)=0$, otherwise, it should be a characteristic exponent of ${\mathcal{C}}_f^{\left(k\right)}$ which is a contradiction with Proposition 2. Therefore, every Newton–Puiseux root of ${\mathcal{C}}_f^{\left(k\right)}$, with $k\ge 1$, is expressed by

$${\displaystyle {\delta }_{{\mathcal{C}}_f^{\left(k\right)}}\left(x\right)=\sum _{j\in \left(\frac{{\beta }_0}{e_k}\right)}{b}_j{x}^{\frac{j}{\frac{{\beta }_0}{e_k}}}+b_{\frac{{\beta }_1}{e_k}}{x}^{\frac{{\beta }_1}{{\beta }_0}}+\sum _{\begin{array}{c}j\in \left(\frac{e_1}{e_k}\right)\\ \frac{{\beta }_1}{e_k}<j<\frac{{\beta }_2}{e_k}\end{array}}{b}_j{x}^{\frac{j}{\frac{{\beta }_0}{e_k}}}+\cdots +b_{\frac{{\beta }_k}{e_k}}{x}^{\frac{{\beta }_k}{{\beta }_0}}+\sum _{\begin{array}{c}\frac{{\beta }_k}{e_k}<j<\frac{{\beta }_{k+1}}{e_k}\end{array}}{b}_j{x}^{\frac{j}{\frac{{\beta }_0}{e_k}}}+\sum _{\begin{array}{c}j>\frac{{\beta }_{k+1}}{e_k}\end{array}}{b}_j{x}^{\frac{j}{\frac{{\beta }_0}{e_k}}}.}$$

(5)

Without lost of generality we can assume that the Newton–Puiseux root ${\delta }_1\left(x\right)$ of ${\mathcal{C}}_f^{\left(k\right)}$ verifies

$${\mathrm{ord}}_x({\delta }_1\left(x\right)-y_{{\mathcal{C}}_f}\left(x\right))=\frac{{\beta }_{k+1}}{{\beta }_0},$$

(6)

where $y_{{\mathcal{C}}_f}\left(x\right)$ is as in (2). So

$${\displaystyle {\delta }_1\left(x\right)=a_{{\beta }_1}{x}^{\frac{{\beta }_1}{n}}+\sum _{\begin{array}{c}j\in \left(e_1\right)\\ {\beta }_1<j<{\beta }_2\end{array}}{a}_j{x}^{\frac{j}{n}}+\cdots +a_{{\beta }_k}{x}^{\frac{{\beta }_k}{n}}+\sum _{\begin{array}{c}j\in \left(e_k\right)\\ {\beta }_k<j<{\beta }_{k+1}\end{array}}{a}_j{x}^{\frac{j}{n}}+\sum _{\begin{array}{c}j>\frac{{\beta }_{k+1}}{e_k}\end{array}}{b}_j{x}^{\frac{j{e}_k}{n}}.}$$

(7)

Let ${\displaystyle z\left(x\right)=\sum _{i\ge n}{a}_i{x}^{i/n}\in \mathbb{C}{\left[\left[x\right]\right]}^{*}}$, and $q\in {\mathbb{Q}}^{+}$. The q-truncation of $z\left(x\right)$ is

$$T_q\left(z\left(x\right)\right)=\sum _{i/n<q}{a}_i{x}^{i/n}.$$

For abuse of notation, a $\frac{{\beta }_l}{{\beta }_0}$-truncation of $y_{{\mathcal{C}}_f}\left(x\right)$ given in (2) is denoted by

$${\displaystyle T_l\left(x\right):=T_{\frac{{\beta }_l}{{\beta }_0}}\left(y_{{\mathcal{C}}_f}\left(x\right)\right)=a_{{\beta }_1}{x}^{\frac{{\beta }_1}{n}}+\sum _{\begin{array}{c}j\in \left(e_1\right)\\ {\beta }_1<j<{\beta }_2\end{array}}{a}_j{x}^{\frac{j}{n}}+a_{{\beta }_2}{x}^{\frac{{\beta }_2}{n}}+\cdots +\sum _{\begin{array}{c}j\in \left(e_{l-1}\right)\\ {\beta }_{l-1}<j<{\beta }_l\end{array}}{a}_j{x}^{\frac{j}{n}},}$$

(8)

that is, we consider the sum of the terms of $y_{{\mathcal{C}}_f}\left(x\right)$ whose exponents are strictly less than $\frac{{\beta }_l}{{\beta }_0}$.

Remark 2.

We denote $T_l\left(x\right)$ but it is not independent of $y_{{\mathcal{C}}_f}\left(x\right)$. If we change $y_{{\mathcal{C}}_f}\left(x\right)$ by another Newton–Puiseux root of ${\mathcal{C}}_f$, its truncation is different.

By construction, we obtain

$$\mathrm{ord}(y_{{\mathcal{C}}_f}\left(x\right)-T_l\left(x\right))=\frac{{\beta }_l}{{\beta }_0}.$$

(9)

Hence $T_{k+1}\left(x\right)=T_{k+1}\left(y_{\mathcal{C}}\left(x\right)\right)=T_{\frac{{\beta }_{k+1}}{{\beta }_0}}\left({\delta }_1\left(x\right)\right)$. For abuse of notation we will write $T_{k+1}\left({\delta }_1\left(x\right)\right):=T_{\frac{{\beta }_{k+1}}{{\beta }_0}}\left({\delta }_1\left(x\right)\right).$

Since ${\mathcal{C}}_f^{\left(k\right)}:f^{\left(k\right)}=0$ is a branch, by Proposition 2 we obtain, for $k\ge 1$,

$$\left\{{\mathrm{ord}}_x({\delta }_1\left(x\right)-{\delta }_j\left(x\right)),2\le j\le \frac{{\beta }_0}{e_k}\right\}={\left\{\frac{{\beta }_i}{{\beta }_0}\right\}}_{i=1}^k.$$

(10)

Observe that given $y_{{\mathcal{C}}_f}\left(x\right)\in Zer\left(f\right)$ then ${\delta }_1\left(x\right)$ is unique. Indeed if there is another Newton–Puiseux root ${\delta }_i\left(x\right)$ of ${\mathcal{C}}_f^{\left(k\right)}$ verifying (6), using triangular inequality, $\mathrm{ord}({\delta }_1\left(x\right)-{\delta }_i\left(x\right))\ge \frac{{\beta }_{k+1}}{{\beta }_0}$, which contradicts the equality (10).

We will denote

$$Z_i^{\left(k\right)}:=\left\{{\delta }_j\left(x\right)\in Zer\left(f^{\left(k\right)}\right):{\mathrm{ord}}_x({\delta }_j\left(x\right)-y_{{\mathcal{C}}_f}\left(x\right))=\frac{{\beta }_i}{{\beta }_0}\right\},$$

for $1\le i\le k$. Using (10), we have

$$\begin{array}{ccc}{Z}_i^{\left(k\right)}\hfill & :=\hfill & \left\{{\delta }_j\left(x\right)\in Zer\left(f^{\left(k\right)}\right):{\mathrm{ord}}_x({\delta }_j\left(x\right)-{\delta }_1\left(x\right))=\frac{{\beta }_i}{{\beta }_0}\right\}.\hfill \end{array}$$

(11)

In the following lemmas we will assume that $1\le k<g$, $i\in \{1,\dots ,k\}$ and ${\delta }_j\left(x\right)\in Z_i^{\left(k\right)}$.

Lemma 2.

If $l\in \{1,\dots ,k\}$ then

$${\mathrm{ord}}_x\left({\delta }_j\left(x\right)-T_l\left(x\right)\right)=\left\{\begin{array}{cc}\frac{{\beta }_i}{{\beta }_0},\hfill & i<l\hfill \\ \hfill & \hfill & \\ \frac{{\beta }_l}{{\beta }_0},\hfill & i\ge l,\hfill \end{array}\right.$$

where $T_l\left(x\right)$ is as in (8).

Proof. 

Applying (11) and (9)

$$\begin{array}{ccc}{\mathrm{ord}}_x({\delta }_j\left(x\right)-T_l\left(x\right))\hfill & \ge \hfill & min\{{\mathrm{ord}}_x({\delta }_j\left(x\right)-y_{\mathcal{C}}\left(x\right)),{\mathrm{ord}}_x(y_{\mathcal{C}}\left(x\right)-T_l\left(x\right))\}\hfill \\ \hfill & =\hfill & min\left\{\frac{{\beta }_i}{{\beta }_0},\frac{{\beta }_l}{{\beta }_0}\right\}=\frac{{\beta }_{min\{i,l\}}}{{\beta }_0}.\hfill \end{array}$$

(12)

Note that $i,l\in \{1,\dots ,k\}$. Hence if $i\ne l$ then ${\mathrm{ord}}_x({\delta }_j\left(x\right)-T_l\left(x\right))=\frac{{\beta }_{min\{i,l\}}}{{\beta }_0}$.

Now, if $i=l$, then we have ${\mathrm{ord}}_x({\delta }_j\left(x\right)-y_{\mathcal{C}}\left(x\right))=\frac{{\beta }_l}{{\beta }_0}={\mathrm{ord}}_x(y_{\mathcal{C}}\left(x\right)-T_l\left(x\right))$. We can write

$$\begin{array}{ccc}{y}_{\mathcal{C}}\left(x\right)\hfill & =\hfill & {\displaystyle a_{{\beta }_1}{x}^{\frac{{\beta }_1}{{\beta }_0}}+\cdots +a_{{\beta }_l}{x}^{\frac{{\beta }_l}{{\beta }_0}}+\cdots +\sum _{j\ge {\beta }_g}{a}_j{x}^{\frac{j}{n}}=T_l\left(x\right)+\sum _{j\ge {\beta }_l}{a}_j{x}^{\frac{j}{n}},where}\hfill \\ T_l\left(x\right)\hfill & =\hfill & {\displaystyle a_{{\beta }_1}{x}^{\frac{{\beta }_1}{{\beta }_0}}+\cdots +\sum _{\begin{array}{c}j\in \left(e_{l-1}\right)\\ {\beta }_{l-1}<j<{\beta }_l\end{array}}{a}_j{x}^{\frac{j}{n}}and{\delta }_j\left(x\right)=T_l\left(x\right)+\sum _{j\ge \frac{{\beta }_l}{e_k}}{b}_j{x}^{\frac{j{e}_k}{n}}.}\hfill \end{array}$$

Moreover $a_{{\beta }_l}\ne b_{{\beta }_l}$, and $b_{{\beta }_l}\ne 0$ since $\frac{{\beta }_l}{{\beta }_0}$ is a characteristic exponent of ${\delta }_j\left(x\right)$. Therefore, we conclude that ${\mathrm{ord}}_x({\delta }_j\left(x\right)-T_l\left(x\right))=\frac{{\beta }_l}{{\beta }_0}$.

On the other hand, using (6) and (9) we have

$${\mathrm{ord}}_x({\delta }_1\left(x\right)-T_l\left(x\right))\ge min\left\{\frac{{\beta }_l}{{\beta }_0},\frac{{\beta }_{k+1}}{{\beta }_0}\right\}=\frac{{\beta }_l}{{\beta }_0},$$

so ${\mathrm{ord}}_x({\delta }_1\left(x\right)-T_l\left(x\right))=\frac{{\beta }_l}{{\beta }_0}$ then $l<k+1$. □

Lemma 3.

If $l=k+1$ then

$${\mathrm{ord}}_x\left({\delta }_j\left(x\right)-T_l\left(x\right)\right)=\left\{\begin{array}{cc}\frac{{\beta }_i}{{\beta }_0},\hfill & j\in \{2,\dots ,m\}\hfill \\ \tau ,\hfill & \tau >\frac{{\beta }_{k+1}}{{\beta }_0},j=1,\hfill \end{array}\right.$$

where $\tau \in {\mathbb{Q}}^{+}$.

Proof. 

Let $i\in \{1,\dots ,k\}$ and $j\in \{2,\dots ,m\}$. From (11) we have ${\mathrm{ord}}_x({\delta }_j\left(x\right)-y_{\mathcal{C}}\left(x\right))=\frac{{\beta }_i}{{\beta }_0}$. By (9), ${\mathrm{ord}}_x(y_{\mathcal{C}}\left(x\right)-T_{k+1}\left(x\right))=\frac{{\beta }_{k+1}}{{\beta }_0}$, and applying the triangular inequality we have ${\mathrm{ord}}_x({\delta }_j\left(x\right)-T_{k+1}\left(x\right))=\frac{{\beta }_i}{{\beta }_0}$. Again by (6) and (9) we have

$${\mathrm{ord}}_x({\delta }_1\left(x\right)-T_{k+1}\left(x\right))\ge min\left\{\frac{{\beta }_{k+1}}{{\beta }_0},\frac{{\beta }_{k+1}}{{\beta }_0}\right\}.$$

Since ${\delta }_1\left(x\right)$ and $T_{k+1}\left(x\right)$ do not have a term of exponent $\frac{{\beta }_{k+1}}{{\beta }_0}$ then we conclude that ${\mathrm{ord}}_x({\delta }_1\left(x\right)-T_l\left(x\right))=\tau >\frac{{\beta }_{k+1}}{{\beta }_0}$ for some $\tau \in {\mathbb{Q}}^{+}$. □

Lemma 4.

If $l>k+1$ then

$${\mathrm{ord}}_x\left({\delta }_j\left(x\right)-T_l\left(x\right)\right)=\left\{\begin{array}{cc}\frac{{\beta }_i}{{\beta }_0}\hfill & sij\in \{2,\dots ,m\}\hfill \\ \frac{{\beta }_{k+1}}{{\beta }_0}\hfill & sij=1.\hfill \end{array}\right.$$

Proof. 

We have chosen ${\delta }_1\left(x\right)$ such that ${\mathrm{ord}}_x({\delta }_1\left(x\right)-y_{\mathcal{C}}\left(x\right))=\frac{{\beta }_{k+1}}{{\beta }_0}$ and we know that ${\mathrm{ord}}_x(y_{\mathcal{C}}\left(x\right)-T_l\left(x\right))=\frac{{\beta }_l}{{\beta }_0}$. Applying the triangular inequality we have ${\mathrm{ord}}_x({\delta }_1\left(x\right)-T_l\left(x\right))=\frac{{\beta }_{k+1}}{{\beta }_0}$. Using the same arguments as in Lemma 3 we conclude ${\mathrm{ord}}_x({\delta }_j\left(x\right)-T_l\left(x\right))=\frac{{\beta }_i}{{\beta }_0}$. □

3. Preliminary Notions on Foliations

Let ${\mathcal{F}}_{\omega }:\omega =0$ be a foliation given by the 1-form $\omega =A(x,y)\mathrm{d}x+B(x,y)\mathrm{d}y$, where $A(x,y),B(x,y)\in \mathbb{C}\left[\right[x,y\left]\right]$. The multiplicity of ${\mathcal{F}}_{\omega }$ is $\mathrm{mult}\left(\omega \right)=min\left\{\mathrm{ord}\right(A),\mathrm{ord}(B\left)\right\}$. Let $f(x,y)\in \mathbb{C}\left[\right[x,y\left]\right]$, we say that ${\mathcal{C}}_f:f(x,y)=0$ is invariant by ${\mathcal{F}}_{\omega }$ if $\omega \wedge \mathrm{d}f:=f.\eta ,$ where $\eta$ is a 2-form (that is $\eta =g\mathrm{d}x\wedge \mathrm{d}y$, with $g\in \mathbb{C}\left[\right[x,y\left]\right]$). If ${\mathcal{C}}_f$ is irreducible then it is called separatrix of ${\mathcal{F}}_{\omega }:\omega =0$.

We will consider non-dicritical foliations, that is, foliations having a finite set of separatrices (see [20], pp. 158, 165). Let ${\left({\mathcal{C}}_{f_j}\right)}_{j=1}^r$ be the set of all separatrices of the non-dicritical foliation ${\mathcal{F}}_{\omega }:\omega =0$. Denote by $\mathcal{C}\left({\mathcal{F}}_{\omega }\right)$ the union $\bigcup {\mathcal{C}}_{f_j}$, which we will call union of separatrices of ${\mathcal{F}}_{\omega }$.

The dual vector field associated with ${\mathcal{F}}_{\omega }$ is $X=B(x,y)\frac{\partial }{\partial x}-A(x,y)\frac{\partial }{\partial y}$. We say that the origin $(x,y)=(0,0)$ is a simple or reduced singularity of ${\mathcal{F}}_{\omega }$ if the matrix associated with the linear part of the field

$$\left(\begin{array}{cc}\frac{\partial B(0,0)}{\partial x}& \frac{\partial B(0,0)}{\partial y}\\ & & \\ -\frac{\partial A(0,0)}{\partial x}& -\frac{\partial A(0,0)}{\partial y}\end{array}\right)$$

(13)

has two eigenvalues $\lambda \ne \mu$, $\mu \ne 0$ and such that $\frac{\lambda }{\mu }\notin {\mathbb{Q}}^{+}$. In [21] (page 40) it was proved that if the origin is a simple singularity of ${\mathcal{F}}_{\omega }$ then there are local coordinates $(x,y)$ such that $\omega =(\lambda x\mathrm{d}y-\mu y\mathrm{d}x)+{\omega }_1,$ where $\mathrm{mult}\left({\omega }_1\right)$ is greater than or equal to 2. It could happen that

(a)

$\lambda \mu \ne 0$ and $\frac{\lambda }{\mu }\notin {\mathbb{Q}}^{+}$ in which case we will say that the singularity is not degenerate or

(a)

$\lambda \mu =0$ and $(\lambda ,\mu )\ne (0,0)$ in which case we will say that the singularity is a saddle-node.

The strong separatrix of a foliation with a saddle-node singularity P is an analytic invariant curve whose tangent line at the singular point P is the eigenspace associated with the non-zero eigenvalue of the matrix given in (13). Otherwise we will say that the analytic invariant curve is a weak separatrix.

From now on $\pi :M\to ({\mathbb{C}}^2,0)$ represents the process of singularity reduction of ${\mathcal{F}}_{\omega }$[22] (pp. 248–269), obtained by a finite sequence of point blows-up, where ${\displaystyle \mathcal{D}:={\pi }^{-1}\left(0\right)=\bigcup _{j=1}^n{D}_j}$ is the exceptional divisor, which is a finite union of projective lines with normal crossing (that is, they are locally described by one or two regular and transversal curves). In this process, any separatrix of ${\mathcal{F}}_{\omega }$ is smooth, disjoint and transverse to some $D_j\subset \mathcal{D}$, and it does not pass through a corner (intersection of two components of the divisor $\mathcal{D}$).

A foliation ${\mathcal{F}}_{\omega }$ is a generalized curve foliation if it has no saddle-nodes in its reduction process of singularities.

Let ${\mathcal{F}}_{\omega }$ be a non-dicritical generalized curve foliation and let $\mathcal{C}\left({\mathcal{F}}_{\omega }\right)$ be its union of separatrices. By [20] (Theorem 3) we have $\mathrm{mult}\left(\omega \right)=\mathrm{mult}\left(\mathcal{C}\left({\mathcal{F}}_{\omega }\right)\right)-1$.

The Milnor’s number of a foliation ${\mathcal{F}}_{\omega }:\omega =A(x,y)\mathrm{d}x+B(x,y)\mathrm{d}y=0$ with isolated singularity at the origin is $\mu \left(\omega \right)={(A,B)}_0$.

By [20] (Theorem 4), if ${\mathcal{F}}_{\omega }:\omega =0$ is a non-dicritical foliation then $\mu \left(\omega \right)\ge \mu \left(\mathrm{d}f\right)$ and the equality is fulfilled if and only if ${\mathcal{F}}_{\omega }$ is a generalized curve foliation.

The support of $\omega$ is $\mathrm{supp}\left(\omega \right)=\mathrm{supp}\left(xA\right)\cup \mathrm{supp}\left(yB\right).$ If we write ${\displaystyle \omega =\sum _{i,j}{\omega }_{ij},}$ where ${\omega }_{ij}=A_{ij}{x}^{i-1}{y}^j\mathrm{d}x+B_{ij}{x}^i{y}^{j-1}\mathrm{d}y$, then $\mathrm{supp}\left(\omega \right)=\{(i,j):(A_{ij},B_{ij})\ne (0,0)\}.$ The Newton polygon of ${\mathcal{F}}_{\omega }$, denoted by $\mathcal{N}\left({\mathcal{F}}_{\omega }\right)$ or $\mathcal{N}\left(\omega \right)$ is the Newton polygon $\mathcal{N}\left(\mathrm{supp}\right(\omega \left)\right)$. We say that a point $(i,j)\in \mathrm{supp}\left(\omega \right)$ is contribution of B (respectively of A) if $(i,j)\in \mathrm{supp}\left(yB\right)$ (respectively $(i,j)\in \mathrm{supp}\left(xA\right)$).

Remark 3.

(i)

The Newton polygon depends on coordinates, so we have to keep in mind what coordinates we are working on.

(ii)

For ${\mathcal{C}}_f:f=0$ and $\mathcal{F}:\mathrm{d}f=0$, we obtain $\mathrm{supp}\left(\mathrm{d}f\right)=\mathrm{supp}\left(f\right)$, hence $\mathcal{N}\left(\mathrm{d}f\right)=\mathcal{N}\left(f\right)$.

(iii)

Let ${\omega }_1$ and ${\omega }_2$ be two non-dicritical generalized curve foliations with the same set of separatrices. Then, after [4] (Proposition 3.8), we obtain $\mathcal{N}\left({\omega }_1\right)=\mathcal{N}\left({\omega }_2\right)$. In particular, if ${\mathcal{F}}_{\omega }$ is a non-dicritical generalized curve foliation and ${\mathcal{C}}_f$ is a reduced equation of its union of separatrices, then $\mathcal{N}\left(\omega \right)=\mathcal{N}\left(\mathrm{d}f\right)$. Hence, after the previous item, we conclude the equality $\mathcal{N}\left(\omega \right)=\mathcal{N}\left(\mathrm{d}f\right)=\mathcal{N}\left(f\right)$, for any non-dicritical generalized curve foliation ω with union of separatrices $f=0$.

(iv)

If the curve ${\mathcal{C}}_f$ is irreducible, its Newton polygon $\mathcal{N}\left(f\right)$ has a single compact side. If the foliation ω has a single irreducible separatrix ${\mathcal{C}}_f$ then the Newton polygon $\mathcal{N}\left(\omega \right)$ also has a single compact side.

Given a rational number $\nu \in {\mathbb{Q}}^{{+}^{}}$, we define the ν-weighted initial form of $\omega$, as

$${\displaystyle {\mathrm{In}}_{\nu }\left(\omega \right):=\sum _{i+\nu j={\mathrm{ord}}_{\nu }\left(\omega \right)}{\omega }_{ij},}$$

(14)

where ${\mathrm{ord}}_{\nu }\left(\omega \right)=min\{i+\nu j:{\omega }_{ij}\ne 0\}$ is the weighted ν-order of $\omega$.

Lemma 5.

Let $f(x,y)\in \mathbb{C}\left[\right[x,y\left]\right]$. Then ${\mathrm{In}}_{\nu }\left(\mathrm{d}f(x,y)\right)=\mathrm{d}\left({\mathrm{In}}_{\nu }f(x,y)\right).$

Proof. 

Put ${\displaystyle f(x,y)=\sum _{i+\nu j=c}{a}_{ij}{x}^i{y}^j+\sum _{i+\nu j>c}{a}_{ij}{x}^i{y}^j}$, where $c={\mathrm{ord}}_{\nu }\left(f\right)$. Hence ${\displaystyle {\mathrm{In}}_{\nu }f(x,y)=\sum _{i+\nu j=c}{a}_{ij}{x}^i{y}^j}$ and

$${\displaystyle \mathrm{d}\left({\mathrm{In}}_{\nu }f(x,y)\right)=\sum _{i+\nu j=c}i{a}_{ij}{x}^{i-1}{y}^j\mathrm{d}x+\sum _{i+\nu j=c}j{a}_{ij}{x}^i{y}^{j-1}\mathrm{d}y.}$$

(15)

On the other hand

$$\begin{array}{ccc}\hfill \mathrm{d}f(x,y)& =& \left({\displaystyle \sum _{i+\nu j=c}i{a}_{ij}{x}^{i-1}{y}^j+\sum _{i+\nu j>c}i{a}_{ij}{x}^{i-1}{y}^j}\right)\mathrm{d}x+\hfill \\ & & \left({\displaystyle \sum _{i+\nu j=c}j{a}_{ij}{x}^i{y}^{j-1}+\sum _{i+\nu j>c}j{a}_{ij}{x}^i{y}^{j-1}}\right)\mathrm{d}y,\hfill \end{array}$$

where

$${\displaystyle {\mathrm{In}}_{\nu }\mathrm{d}f(x,y)=\sum _{i+\nu j=c}i{a}_{ij}{x}^{i-1}{y}^j\mathrm{d}x+\sum _{i+\nu j=c}j{a}_{ij}{x}^i{y}^{j-1}\mathrm{d}y.}$$

(16)

The lemma follows from (15) and (16). □

Let L be a compact side of $\mathcal{N}\left(\omega \right)$ of inclination $\nu$, with vertices $({\alpha }_1,{\beta }_1)$ and $({\alpha }_2,{\beta }_2)$ where ${\beta }_1\ge {\beta }_2$. After [23] (Corollary 1) we say that L is a good side if the following conditions hold:

• $B_{{\alpha }_1{\beta }_1}\ne 0$ and $-{\displaystyle \frac{A_{{\alpha }_1{\beta }_1}}{B_{{\alpha }_1{\beta }_1}}}\notin {\mathbb{Q}}_{\ge \nu }=\{r\in \mathbb{Q}:r\ge \nu \}$,
• $A_{{\alpha }_2{\beta }_2}+\nu B_{{\alpha }_2{\beta }_2}\ne 0$.

If $\{y=0\}$ is not a separatrix of $\omega$ and L is the good side of greater inclination of $\mathcal{N}\left(\omega \right)$ then L is called the main side of $\omega$.

Properties of the Inverse Image of a Foliation

Let $E:{\mathbb{C}}^2⟶{\mathbb{C}}^2$ a map defined by $E(\overline{x},\overline{y}):=(E_1(\overline{x},\overline{y}),E_2(\overline{x},\overline{y}))$. The inverse image of $A\in \mathbb{C}\left[\right[x,y\left]\right]$ with respect to E is $E^{*}\left(A\right)(\overline{x},\overline{y}):=(A\circ E)(\overline{x},\overline{y})$. Moreover, the inverse image of the foliation ${\mathcal{F}}_{\omega }:\omega =A(x,y)\mathrm{d}x+B(x,y)\mathrm{d}y=0$ with respect to E is $E^{*}\left(\omega \right):=E^{*}\left(A\right)(\overline{x},\overline{y})\mathrm{d}\left(E_1(\overline{x},\overline{y})\right)+E^{*}\left(B\right)(\overline{x},\overline{y})\mathrm{d}\left(E_2(\overline{x},\overline{y})\right)$.

Consider the branch ${\mathcal{C}}_f:f=0$ with characteristic exponents $({\beta }_0,\dots ,{\beta }_g)$, and $n_i={\displaystyle \frac{gcd({\beta }_0,\dots ,{\beta }_{i-1})}{gcd({\beta }_0,\dots ,{\beta }_i)}}$. Let $l\in \{1,\dots ,g\}$. We borrow, from [4] (page 306), the application $F_l:{\mathbb{C}}^2\to {\mathbb{C}}^2$ defined as

$$F_l(\overline{x},\overline{y})=({\overline{x}}^{n_1{n}_2\cdots n_{l-1}},\overline{y}+{\overline{T}}_l\left(\overline{x}\right)),$$

(17)

where ${\overline{T}}_l\left(\overline{x}\right):=T_{\frac{{\beta }_l}{{\beta }_0}}\left(y_{\mathcal{C}}\left({\overline{x}}^{n_1{n}_2\cdots n_{l-1}}\right)\right)$ as Equation (8). Given a foliation $\omega =A(x,y)\mathrm{d}x+B(x,y)\mathrm{d}y$, an important tool in this paper is the inverse image of $\omega$ with respect to $F_l$, which is

$$F_l^{*}\left(\omega \right)=\mathcal{A}(\overline{x},\overline{y})\mathrm{d}\overline{x}+\mathcal{B}(\overline{x},\overline{y})\mathrm{d}\overline{y},$$

(18)

where $\mathcal{A}(\overline{x},\overline{y})=\left(n_1\cdots n_{l-1}{\overline{x}}^{n_1\cdots n_{l-1}-1}{A}^{*}(\overline{x},\overline{y})+B^{*}(\overline{x},\overline{y}){\overline{T}}_l^{\prime }\left(\overline{x}\right)\right)$ and $\mathcal{B}(\overline{x},\overline{y})=B^{*}(\overline{x},\overline{y})$ (being $A^{*}$ (respectively $B^{*}$) the inverse image of A (respectively of B) with respect to $F_l$).

Lemma 6.

Let $\omega =A(x,y)\mathrm{d}x+B(x,y)\mathrm{d}y$ be a generalized curve foliation, where the union of separatrices of the foliation ${\mathcal{F}}_{\omega }$ is ${\mathcal{C}}_h:h=0$ and $x=0$ is not in the tangent cone of $h=0$. Then the curve $F_l^{*}\left(h\right)=0$ is the union of separatrices of the foliation $F_l^{*}\left(\omega \right)$.

Proof. 

Since $h=0$ is the union of separatrices of $\omega$, then $\mathrm{d}h\wedge \omega =h{\eta }_1$, where ${\eta }_1=g(x,y)\mathrm{d}x\wedge \mathrm{d}y$ is a 2-form, for certain $g(x,y)\in \mathbb{C}\left[\right[x,y\left]\right]$. In particular

$$B{h}_x-A{h}_y=hg.$$

(19)

From [24] (Proposition 5) and (18), we obtain

$$\begin{array}{ccc}\hfill \mathrm{d}\left(F_l^{*}\left(h\right)\right)& =& F_l^{*}\left(\mathrm{d}h\right)\hfill \\ \hfill & =& \left(n_1\cdots n_{l-1}{\overline{x}}^{n_1\cdots n_{l-1}-1}{\left(h_x\right)}^{*}(\overline{x},\overline{y})+{\left(h_y\right)}^{*}(\overline{x},\overline{y}){\overline{T}}_l^{\prime }\left(\overline{x}\right)\right)\mathrm{d}\overline{x}+{\left(h_y\right)}^{*}(\overline{x},\overline{y})\mathrm{d}\overline{y}.\hfill \end{array}$$

(20)

Using (20) and (18), the definition of the inverse image of a series with respect to $F_l^{*}$ and (19), we have

$$\begin{array}{ccc}\mathrm{d}\left(F_l^{*}\left(h\right)\right)\wedge F_l^{*}\left(\omega \right)\hfill & =\hfill & n_1\cdots n_{l-1}{\overline{x}}^{n_1\cdots n_{l-1}-1}{F}_l^{*}\left(h\right)F_l^{*}\left(g\right)\mathrm{d}\overline{x}\wedge \mathrm{d}\overline{y}.\hfill \end{array}$$

(21)

We claim that $F_l^{*}\left(h\right)=0$ is the union of separatrices of $F_l^{*}\left(\omega \right)$. Indeed, suppose that $\mathcal{S}={\mathcal{C}}_{g_1}\cup {\mathcal{C}}_{F_l^{*}\left(h\right)}$ is the union of separatrices of $F_l^{*}\left(\omega \right)$, for some non-unit $g_1\in \mathbb{C}\left[[x,y]\right]\backslash \left\{0\right\}$, which is not a factor of $F_l^{*}\left(h\right)$. We conclude that ${\mathcal{C}}_{F_l\left(g_1\right)}\cup {\mathcal{C}}_h$ is the union of separatrices of $\omega$ which is a contradiction. □

In the following two lemmas we consider a generalized curve foliation $\mathcal{F}:\omega =0$, where $\omega =A(x,y)\mathrm{d}x+B(x,y)\mathrm{d}y$ and the branch ${\mathcal{C}}_f:f=0$ with characteristic exponents $({\beta }_0,\dots ,{\beta }_g)$, and $n_i={\displaystyle \frac{gcd({\beta }_0,\dots ,{\beta }_{i-1})}{gcd({\beta }_0,\dots ,{\beta }_i)}}$ is its only separatrix. Let $l\in \{1,\dots ,g\}$. The following lemma generalizes [4] (Lemme 3.9). Rouillé proved it in the particular case of ${\overline{T}}_l\left(\overline{x}\right)=0$.

Lemma 7.

If $x=0$ is not in the tangent cone of $f(x,y)=0$, then $F_l^{*}\left(\omega \right)$ is a generalized curve foliation.

Proof. 

From (18) we have

$$F_l^{*}\left(\mathrm{d}f\right)=\left(n_1\cdots n_{l-1}{\overline{x}}^{n_1\cdots n_{l-1}-1}{\left(f_x\right)}^{*}(\overline{x},\overline{y})+{\left(f_y\right)}^{*}(\overline{x},\overline{y}){\overline{T}}_l^{\prime }\left(\overline{x}\right)\right)\mathrm{d}\overline{x}+{\left(f_y\right)}^{*}(\overline{x},\overline{y})\mathrm{d}\overline{y}.$$

Applying the definition of Milnor number and [16] (Theorem 4.14 (vi), (iv)), we have

$$\begin{array}{ccc}\mu \left(F_l^{*}\left(\mathrm{d}f\right)\right)\hfill & =\hfill & {\left(n_1\cdots n_{l-1}{\overline{x}}^{n_1\cdots n_{l-1}-1}{\left(f_x\right)}^{*}(\overline{x},\overline{y})+{\left(f_y\right)}^{*}(\overline{x},\overline{y}){\overline{T}}_l^{\prime }\left(\overline{x}\right),{\left(f_y\right)}^{*}(\overline{x},\overline{y})\right)}_0\hfill \\ \hfill & =\hfill & (n_1\cdots n_{l-1}-1){\left(\overline{x},{\left(f_y\right)}^{*}(\overline{x},\overline{y})\right)}_0+{\left({\left(f_x\right)}^{*}(\overline{x},\overline{y}),{\left(f_y\right)}^{*}(\overline{x},\overline{y})\right)}_0.\hfill \end{array}$$

(22)

Since $x=0$ is not in the tangent cone of $\mathrm{d}f$, then x does not divide the initial form of $f_y$, so ${\mathrm{ord}}_y\left(f_y(0,y)\right)={\mathrm{ord}}_y\left(f_y(x,y)\right)$. By Remark 1, we obtain $\mathrm{mult}\left(df\right)={\mathrm{ord}}_y\left(f_y(x,y)\right)$ and,

$${\left(\overline{x},{\left(f_y\right)}^{*}(\overline{x},\overline{y})\right)}_0={\mathrm{ord}}_{\overline{y}}{\left(f_y\right)}^{*}(0,\overline{y})={\mathrm{ord}}_{\overline{y}}{f}_y(0,\overline{y})={\mathrm{ord}}_y{f}_y(0,y)=\mathrm{mult}\left(\mathrm{d}f\right),$$

(23)

where ${\left(f_y\right)}^{*}=F_l^{*}\left(f_y\right)$. Applying Proposition 1, we have

$${\left({\left(f_x\right)}^{*}(\overline{x},\overline{y}),{\left(f_y\right)}^{*}(\overline{x},\overline{y})\right)}_0=(n_1\cdots n_{l-1}){\left(f_x,f_y\right)}_0=(n_1\cdots n_{l-1})\mu \left(\mathrm{d}f\right).$$

(24)

Replacing (23) and (24) in (22), we obtain

$$\mu \left(F_l^{*}\left(\mathrm{d}f\right)\right)=(n_1\cdots n_{l-1}-1)\mathrm{mult}\left(\mathrm{d}f\right)+(n_1\cdots n_{l-1})\mu \left(\mathrm{d}f\right).$$

(25)

Similarly for $F_l^{*}\left(\omega \right)$ we have

$$\mu \left(F_l^{*}\left(\omega \right)\right)=(n_1\cdots n_{l-1}-1)\mathrm{mult}\left(\omega \right)+(n_1\cdots n_{l-1})\mu \left(\omega \right).$$

(26)

Since $\omega$ is a generalized curve foliation, then $\mathrm{mult}\left(\omega \right)=\mathrm{mult}\left(\mathrm{d}f\right)$ and $\mu \left(\omega \right)=\mu \left(\mathrm{d}f\right)$. The lemma follows from (25) and (26). □

In [4] (Lemme 4.3) Rouillé stated that the side of the highest inclination of $\mathcal{N}\left(F_l^{*}\left(\omega \right)\right)$ is the main side and he explicitly determined its inclination, however he did not compute its height. We determine this height in the following lemma.

Lemma 8.

The Newton polygon $\mathcal{N}\left(F_l^{*}\left(\omega \right)\right)$ has a compact side of inclination $\frac{m_l}{n_l}$ and height $e_{l-1}$. Moreover this side is the highest inclination side, between all the compact sides, of $\mathcal{N}\left(F_l^{*}\left(\omega \right)\right)$ and it is the main side.

Proof. 

After [4] (Lemme 4.3), the Newton polygon $\mathcal{N}\left(F_l^{*}\left(\omega \right)\right)$ has a compact side L of inclination $\frac{m_l}{n_l}$ and this is its main side. We will prove that the height of L is $e_{l-1}$. We will assume without loss of generality that $f\in \mathbb{C}\left[\right[x\left]\right]\left[y\right]$ is a Weierstrass polynomial. Put ${\displaystyle f(x,y)=\prod _{i=1}^n(y-y_i\left(x\right))}$, where $y_i\left(x\right)$ are the roots of f. The inverse image of f with respect to $F_l$ (as in (17)) is

$${\displaystyle F_l^{*}f(\overline{x},\overline{y})=\prod _{i=1}^n\left(\overline{y}-(\overline{y_i}\left(\overline{x}\right)-{\overline{T}}_l\left(\overline{x}\right)\right),}$$

(27)

where $\overline{y_i}\left(\overline{x}\right)=y_i\left({\overline{x}}^{n_1\cdots n_{l-1}}\right)$. From (9) and Lemma Section 2, we have

$$\mathrm{ord}(y_{\mathcal{C}}\left(x\right)-T_l\left(x\right))=\frac{{\beta }_l}{{\beta }_0}and\mathrm{ord}(y_i\left(x\right)-y_{\mathcal{C}}\left(x\right))=\frac{{\beta }_s}{n},forcertains\in \{1,\dots ,g\}.$$

(28)

If $s<l$, using the triangular inequality, then $\mathrm{ord}(y_i\left(x\right)-T_l\left(x\right))=\frac{{\beta }_s}{n}$. If $s=l$ then $\mathrm{ord}(y_{\mathcal{C}}\left(x\right)-T_l\left(x\right))=\mathrm{ord}(y_i\left(x\right)-y_{\mathcal{C}}\left(x\right))=\frac{{\beta }_l}{n}$. Applying the triangular inequality, we obtain $\mathrm{ord}(y_i\left(x\right)-T_l\left(x\right))=\frac{{\beta }_l}{n}$, hence the coefficients of the term $x^{\frac{{\beta }_l}{n}}$ in the power series $y_i$ and $y_{\mathcal{C}}$ are different. For $s>l$, we have $\mathrm{ord}(y_{\mathcal{C}}\left(x\right)-T_l\left(x\right))=\frac{{\beta }_l}{n}<\frac{{\beta }_s}{n}=\mathrm{ord}(y_i\left(x\right)-y_{\mathcal{C}}\left(x\right))$, and again by the triangular inequality, we obtain $\mathrm{ord}(y_i\left(x\right)-T_l\left(x\right))=\frac{{\beta }_l}{n}$. Therefore, $\mathrm{ord}(y_i\left(x\right)-T_l\left(x\right))\le \frac{{\beta }_l}{n}$, so $\mathrm{ord}\left(\overline{y_i}\left(\overline{x}\right)-{\overline{T}}_l\left(\overline{x}\right)\right)\le \frac{m_l}{n_l}.$ Observe that the height of L is the cardinality of the set

$$S:=\left\{\overline{y_i}\left(\overline{x}\right):\mathrm{ord}\left(\overline{y_i}\left(\overline{x}\right)-{\overline{T}}_l\left(\overline{x}\right)\right)<\frac{m_l}{n_l}\right\}.$$

We claim that the cardinality of S equals the cardinality of

$$R:=\left\{y_j\left(x\right):\mathrm{ord}\left(y_{\mathcal{C}}\left(x\right)-y_j\left(x\right)\right)<\frac{{\beta }_l}{n}\right\},$$

where $y_{\mathcal{C}}\left(x\right)$ is the fixed root of ${\mathcal{C}}_f$ such that $\mathrm{ord}(y_{\mathcal{C}}\left(x\right)-T_l\left(x\right))=\frac{{\beta }_l}{n}$.

In fact, if $y_j\left(x\right)\in R$ then $\mathrm{ord}\left({\overline{y}}_{\mathcal{C}}\left(\overline{x}\right)-\overline{y_j}\left(\overline{x}\right)\right)<\frac{m_l}{n_l}$. On the other hand $\mathrm{ord}({\overline{y}}_{\mathcal{C}}\left(\overline{x}\right)-{\overline{T}}_l\left(\overline{x}\right))=\frac{m_l}{n_l}$, and using the triangular inequality, we obtain $\mathrm{ord}(\overline{y_j}\left(\overline{x}\right)-{\overline{T}}_l\left(\overline{x}\right))<\frac{m_l}{n_l}$, so $\overline{y_j}\left(\overline{x}\right)\in S$ and $♯R\le ♯S$. Similarly, we prove that $♯S\le ♯R$. Let us compute the cardinality of R. After (a), (b) and (c) of page, we obtain

$$♯S=♯R=\sum _{i=1}^{l-1}♯\left\{y_j\left(x\right):\mathrm{ord}(y_j\left(x\right)-y_{\mathcal{C}}\left(x\right))=\frac{{\beta }_i}{{\beta }_0}\right\}=e_0-e_{l-1}.$$

Since the number of roots of $F_l^{*}\left(f\right)$ is $n=e_0$, then the number of roots of $F_l^{*}\left(f\right)$ with order greater than or equal to $\frac{m_l}{n_l}$ is $e_{l-1}$.

Note that $e_{l-1}$ is the height of the compact side of the Newton polygon $\mathcal{N}\left(F_l^{*}\left(f\right)\right)$ which inclination is $\frac{m_l}{n_l}$. As $F_l^{*}\left(f\right)$ is the union of separatrices of the generalized curve foliation $F_l^{*}\left(\omega \right)$, after the third part of Remark 3, we obtain $\mathcal{N}\left(F_l^{*}\left(f\right)\right)=\mathcal{N}\left(F_l^{*}\left(\omega \right)\right)$ and the lemma follows. □

Let $\mathcal{F}$ and $\mathcal{G}$ be singular foliations defined by the 1-forms $\omega =A(x,y)\mathrm{d}x+B(x,y)\mathrm{d}y$ and $\eta =P(x,y)\mathrm{d}x+Q(x,y)\mathrm{d}y$ respectively. We are interested in describing the curve given by the contact between these two foliations, that is, the curve defined by $\omega \wedge \eta$, which admits the equation

$$A(x,y)Q(x,y)-B(x,y)P(x,y)=0.$$

Proof of Lemma 1.

Consider ${\displaystyle \omega =\sum _{ij}{\omega }_{ij}}$, ${\displaystyle \eta =\sum _{rs}{\eta }_{rs}}$, where ${\omega }_{ij}=A_{ij}{x}^{i-1}{y}^j\mathrm{d}x+B_{ij}{x}^i{y}^{j-1}\mathrm{d}y$ and ${\eta }_{rs}=P_{rs}{x}^{r-1}{y}^s\mathrm{d}x+Q_{rs}{x}^r{y}^{s-1}\mathrm{d}y$, for $i,j,r,s\in \mathbb{N}$ and $A_{ij},B_{ij},P_{rs},Q_{rs}\in \mathbb{C}$.

We have $\begin{array}{ccc}\hfill {\omega }_{ij}\wedge {\eta }_{rs}& =\hfill & \left(A_{ij}{Q}_{rs}-B_{ij}{P}_{rs}\right)x^{i+r-1}{y}^{j+s-1}\mathrm{d}x\wedge \mathrm{d}y.\hfill \end{array}$ If $A_{ij}{Q}_{rs}-B_{ij}{P}_{rs}\ne 0$ then

$${\mathrm{ord}}_{\nu }\left({\omega }_{ij}\wedge {\eta }_{rs}\right)=(i+\nu j)+(r+\nu s)-1-\nu ={\mathrm{ord}}_{\nu }\left({\omega }_{ij}\right)+{\mathrm{ord}}_{\nu }\left({\eta }_{rs}\right)-1-\nu .$$

Hence from (14) and since ${\mathrm{In}}_{\nu }\left(\omega \right)\wedge {\mathrm{In}}_{\nu }\left(\eta \right)\ne 0$, we obtain ${\mathrm{In}}_{\nu }\left(\omega \wedge \eta \right)=\left({\mathrm{In}}_{\nu }\left(\omega \right)\wedge {\mathrm{In}}_{\nu }\left(\eta \right)\right)$ and ${\mathrm{ord}}_{\nu }\left({\mathrm{In}}_{\nu }(\omega \wedge \eta )\right)={\mathrm{ord}}_{\nu }\left({\mathrm{In}}_{\nu }\omega \right)+{\mathrm{ord}}_{\nu }\left({\mathrm{In}}_{\nu }\eta \right)-1-\nu ;$ and the Lemma 1 follows.

Consider a generalized curve foliation $\mathcal{F}:\omega =0$ whose only separatrix is $\mathcal{C}:f=0$. Then $\mathcal{G}:\mathrm{d}\left(f^{\left(k\right)}\right)=0$ is a generalized curve foliation having as the only separatrix the k-th approximate root characteristic $f^{\left(k\right)}$ of f with $0\le k\le g-1$. □

Example 1.

Let us consider the curve ${\mathcal{C}}_f:f={(y^2-x^3)}^2-x^{6}y$ with characteristic exponents $(4,6,9)$ and approximate roots $f^{\left(0\right)}=y$ and $f^{\left(1\right)}=y^2-x^3$. The branch ${\mathcal{C}}_f$ is the only separatrix of the generalized curve foliation given by

$$\begin{array}{ccc}\omega \hfill & =\hfill & (-x^{7}y+x^7-6x^{5}y-2x^4{y}^2+6x^5+x{y}^4-6x^2{y}^2)\mathrm{d}x\hfill \\ & +\hfill & (-x^6{y}^2+x^{6}y-x^6-2x^3{y}^3+y^5-4x^{3}y+4y^3)\mathrm{d}y.\hfill \end{array}$$

Moreover $\mathrm{d}{f}^{\left(0\right)}=\mathrm{d}y$ and $\mathrm{d}{f}^{\left(1\right)}=-3x^2\mathrm{d}x+2y\mathrm{d}y$. For $\frac{{\beta }_2}{{\beta }_0}=\frac{9}{4}$, we have ${\mathrm{In}}_{\frac{9}{4}}\left(\omega \right)=6x^5\mathrm{d}x,{\mathrm{In}}_{\frac{9}{4}}\left(\mathrm{d}{f}^{\left(0\right)}\right)=\mathrm{d}yand{\mathrm{In}}_{\frac{9}{4}}\left(\mathrm{d}{f}^{\left(1\right)}\right)=-3x^2\mathrm{d}x,$ so ${\mathrm{In}}_{\frac{9}{4}}\left(\omega \right)\wedge {\mathrm{In}}_{\frac{9}{4}}\left(\mathrm{d}{f}^{\left(0\right)}\right)=6x^5\mathrm{d}x\wedge \mathrm{d}y,$ but ${\mathrm{In}}_{\frac{9}{4}}\left(\omega \right)\wedge {\mathrm{In}}_{\frac{9}{4}}\left(\mathrm{d}{f}^{\left(1\right)}\right)=0.$ In this last case we can not apply Lemma 1. However, we can apply it to their respective inverse images with respect to $F_2(\overline{x},\overline{y}):=({\overline{x}}^2,\overline{y}+{\overline{x}}^3)$ and $\nu =\frac{{\beta }_2}{e_1}=\frac{9}{2}$:

$$\begin{array}{ccc}{F}_2^{*}\left(\omega \right)\hfill & =\hfill & (8{\overline{x}}^9{\overline{y}}^2+2{\overline{x}}^3{\overline{y}}^4+3{\overline{x}}^2{\overline{y}}^5+8{\overline{x}}^6{\overline{y}}^3+12{\overline{x}}^{11}{\overline{y}}^2-12{\overline{x}}^{11}\overline{y}-2{\overline{x}}^{15}\overline{y}-2{\overline{x}}^{18}-15{\overline{x}}^{14}\hfill \\ & +\hfill & 24{\overline{x}}^5{\overline{y}}^2-30{\overline{x}}^{20}-3{\overline{x}}^{14}{\overline{y}}^2+15{\overline{x}}^5{\overline{y}}^4-6{\overline{x}}^{17}\overline{y}+12{\overline{x}}^2{\overline{y}}^3+24{\overline{x}}^8{\overline{y}}^3)\mathrm{d}\overline{x}\hfill \\ & +\hfill & (-{\overline{x}}^{12}{\overline{y}}^2-2{\overline{x}}^{15}\overline{y}-{\overline{x}}^{18}-{\overline{x}}^{12}+8{\overline{x}}^6{\overline{y}}^3+4{\overline{x}}^9{\overline{y}}^2+{\overline{y}}^5+5{\overline{x}}^3{\overline{y}}^4+8{\overline{x}}^6\overline{y}+4{\overline{y}}^3\hfill \\ & +\hfill & 12{\overline{x}}^3{\overline{y}}^2)\mathrm{d}\overline{y},\hfill \end{array}$$

$F_2^{*}\left(\mathrm{d}{f}^{\left(0\right)}\right)=3{\overline{x}}^2\mathrm{d}\overline{x}+\mathrm{d}\overline{y}$ and $F_2^{*}\left(\mathrm{d}{f}^{\left(1\right)}\right)=6{\overline{x}}^2\overline{y}\mathrm{d}\overline{x}+2(\overline{y}+{\overline{x}}^3)\mathrm{d}\overline{y}$.

Hence $I{n}_{\nu }\left(F_2^{*}\left(\omega \right)\right)=(-15{\overline{x}}^{14}+24{\overline{x}}^5{\overline{y}}^2)\mathrm{d}\overline{x}+8{\overline{x}}^6\overline{y}\mathrm{d}\overline{y}$, $I{n}_{\nu }\left(F_2^{*}\left(\mathrm{d}{f}^{\left(0\right)}\right)\right)=3{\overline{x}}^2\mathrm{d}\overline{x}$, and $I{n}_{\nu }\left(F_2^{*}\left(\mathrm{d}{f}^{\left(1\right)}\right)\right)=6{\overline{x}}^2\overline{y}\mathrm{d}\overline{x}+2{\overline{x}}^3\mathrm{d}\overline{y}$. Then $I{n}_{\nu }\left(F_2^{*}\left(\omega \right)\right)\wedge I{n}_{\nu }\left(F_2^{*}\left(\mathrm{d}{f}^{\left(0\right)}\right)\right)=-48{\overline{x}}^8\overline{y}\mathrm{d}\overline{x}\wedge \mathrm{d}\overline{y}$ and $I{n}_{\nu }\left(F_2^{*}\left(\omega \right)\right)\wedge I{n}_{\nu }\left(F_2^{*}\left(\mathrm{d}{f}^{\left(1\right)}\right)\right)=-30{\overline{x}}^{17}\mathrm{d}\overline{x}\wedge \mathrm{d}\overline{y}.$

Therefore, when we are not in the hypothesis of Lemma 1, we will apply it to the inverse images of ω and $\mathrm{d}{f}^{\left(1\right)}$ with respect to some $F_l$.

4. Approximate Polar Curves of a Foliation

Consider the branch ${\mathcal{C}}_f:f(x,y)=0$ with characteristic exponents $({\beta }_0,\dots ,{\beta }_g)$. Remember that $n_i={\displaystyle \frac{gcd({\beta }_0,\dots ,{\beta }_{i-1})}{gcd({\beta }_0,\dots ,{\beta }_i)}}$. Suppose, without loss of generality, that f is a Weierstrass polynomial. Let $f^{\left(k\right)}$ be the kth approximate root of f, where $0\le k\le g-1$.

Let $\omega =A(x,y)\mathrm{d}x+B(x,y)\mathrm{d}y$ be a 1-form defining a generalized curve foliation $\mathcal{F}:\omega =0$ which only separatrix is ${\mathcal{C}}_f$. The approximate polar curve (or just polar curve) of ω with respect to the characteristic approximate root $f^{\left(k\right)}$ of f is the curve of equation

$${\mathcal{P}}_{\omega }^{\left(k\right)}(x,y):=A(x,y)f_y^{\left(k\right)}(x,y)-B(x,y)f_x^{\left(k\right)}(x,y)=0.$$

(29)

Its inverse image with respect to $F_l$ (defined as in (17)) is

$$F_l^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)(\overline{x},\overline{y})=A^{*}(\overline{x},\overline{y}){\left(f_y^{\left(k\right)}\right)}^{*}(\overline{x},\overline{y})-B^{*}(\overline{x},\overline{y}){\left(f_x^{\left(k\right)}\right)}^{*}(\overline{x},\overline{y}).$$

(30)

Lemma 9.

With the above notations we have

$$F_l^{*}\left(\omega \right)\wedge F_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)=n_1\cdots n_{l-1}{\overline{x}}^{n_1{n}_2\cdots n_{l-1}-1}\left(F_l^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\right)\mathrm{d}\overline{x}\wedge \mathrm{d}\overline{y}.$$

Proof. 

Applying (18) to the foliations $\omega$ and $\mathrm{d}{f}^{\left(k\right)}$ and after (29) and (30), we have

$$\begin{array}{ccc}\hfill F_l^{*}\left(\omega \right)\wedge F_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)& =\hfill & \left(n_1\cdots n_{l-1}{\overline{x}}^{n_1\cdots n_{l-1}-1}{A}^{*}+B^{*}{\overline{T}}_l^{\prime }\right){\left(f_y^{\left(k\right)}\right)}^{*}\hfill \\ & -\hfill & \left(n_1\cdots n_{l-1}{\overline{x}}^{n_1\cdots n_{l-1}-1}{\left(f_x^{\left(k\right)}\right)}^{*}+{\left(f_y^{\left(k\right)}\right)}^{*}{\overline{T}}_l^{\prime }\right)B^{*}\mathrm{d}\overline{x}\wedge \mathrm{d}\overline{y}\hfill \\ & =\hfill & n_1\cdots n_{l-1}{\overline{x}}^{n_1{n}_2\cdots n_{l-1}-1}\left(A^{*}{\left(f_y^{\left(k\right)}\right)}^{*}-B^{*}{\left(f_x^{\left(k\right)}\right)}^{*}\right)\mathrm{d}\overline{x}\wedge \mathrm{d}\overline{y}\hfill \\ & =\hfill & n_1\cdots n_{l-1}{\overline{x}}^{n_1{n}_2\cdots n_{l-1}-1}\left(F_l^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\right)\mathrm{d}\overline{x}\wedge \mathrm{d}\overline{y}.\hfill \end{array}$$

□

Let $\nu =\frac{m_l}{n_l}$, with $l\in \{1,\dots ,g\}$ where $m_l=\frac{{\beta }_l}{e_l}$ and $n_l=\frac{e_{l-1}}{e_l}$. We are interested in finding ${\mathrm{In}}_{\nu }\left(F_l^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\right)$. The strategy will be to apply Lemma 9. For this we need to know ${\mathrm{In}}_{\nu }{F}_l^{*}\left(\omega \right)$ and ${\mathrm{In}}_{\nu }\left(F_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)\right)$. We can write

$${\mathrm{In}}_{\nu }{F}_l^{*}\left(\omega \right)=\sum _{i+\nu j=c_l}{\mathcal{A}}_{ij}{\overline{x}}^{i-1}{\overline{y}}^j\mathrm{d}\overline{x}+\sum _{i+\nu j=c_l}{\mathcal{B}}_{ij}{\overline{x}}^i{\overline{y}}^{j-1}\mathrm{d}\overline{y},$$

(31)

where $c_l={\mathrm{ord}}_{\nu }\left({\mathrm{In}}_{\nu }{F}_l^{*}\left(\omega \right)\right)$ and ${\mathcal{A}}_{ij},{\mathcal{B}}_{ij}\in \mathbb{C}$. We will denote by ${\mathcal{L}}_l$ the support line of inclination $\nu$ of the Newton polygon of $F_l^{*}\left(\omega \right)$, that is

$${\mathcal{L}}_l:i+\nu j=c_l.$$

(32)

On the other hand, in order to calculate ${\mathrm{In}}_{\nu }\left(F_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)\right)$, we will analyze what happens with ${\mathrm{In}}_{\nu }\left(F_l^{*}\left(f^{\left(k\right)}\right)\right)$ and then we will apply Lemma 5.

Recall that $\mathrm{cont}\left(f,f^{\left(k\right)}\right)=\frac{{\beta }_{k+1}}{n}={\mathrm{ord}}_x(y_{\mathcal{C}}\left(x\right)-{\delta }_1\left(x\right))$ (see equality (6)).

First, consider the case $k=0$. As $f^{\left(0\right)}(x,y)=y$, then $\mathrm{d}{f}^{\left(0\right)}(x,y)=\mathrm{d}y$. Then $F_l^{*}\left(f^{\left(0\right)}\right)=F_l^{*}\left(y\right)=\overline{y}+{\overline{T}}_l\left(\overline{x}\right)$ and

$$F_l^{*}\left(\mathrm{d}{f}^{\left(0\right)}\right)=\mathrm{d}(\overline{y}+{\overline{T}}_l\left(\overline{x}\right))={\overline{T}}_l^{\prime }\left(\overline{x}\right)\mathrm{d}\overline{x}+\mathrm{d}\overline{y},$$

(33)

where ${\overline{T}}_l\left(\overline{x}\right)=T_{\frac{{\beta }_l}{{\beta }_0}}\left(y_{\mathcal{C}}\left({\overline{x}}^{n_1{n}_2\cdots n_{l-1}}\right)\right)$.

Now, we will study the case $k\ge 1$. After (4), we obtain

$$\begin{array}{ccc}{F}_l^{*}\left(f^{\left(k\right)}\right)\hfill & =\hfill & {\displaystyle \prod _{j=1}^m\left(\overline{y}-({\overline{\delta }}_j\left(\overline{x}\right)-{\overline{T}}_l\left(\overline{x}\right))\right)}\hfill \\ \hfill & =\hfill & {\displaystyle \left(\overline{y}-({\overline{\delta }}_1\left(\overline{x}\right)-{\overline{T}}_l\left(\overline{x}\right))\right)\prod _{i=1}^k\left({\displaystyle \prod _{{\delta }_j\in Z_i^{\left(k\right)}}\left(\overline{y}-({\overline{\delta }}_j\left(\overline{x}\right)-{\overline{T}}_l\left(\overline{x}\right))\right)}\right),}\hfill \end{array}$$

(34)

where ${\overline{\delta }}_j\left(\overline{x}\right)={\delta }_j\left({\overline{x}}^{n_1\cdots n_{l-1}}\right)$, $Z_i^{\left(k\right)}=\left\{{\delta }_j\in Zer{f}^{\left(k\right)}:{\mathrm{ord}}_x({\delta }_j\left(x\right)-y_{\mathcal{C}}\left(x\right))=\frac{{\beta }_i}{{\beta }_0}\right\}$ for $i\in \{1,\dots ,k\}$ and $j\in \{2,\dots ,m\}$.

After (7) we have

$$\begin{array}{ccc}\hfill {\overline{\delta }}_1\left(\overline{x}\right)& =& {\displaystyle a_{{\beta }_1}{\overline{x}}^{\frac{{\beta }_1}{n}(n_1\cdots n_{l-1})}+\sum _{\begin{array}{c}j\in \left(e_1\right)\\ {\beta }_1<j<{\beta }_2\end{array}}{a}_j{\overline{x}}^{\frac{j}{n}(n_1\cdots n_{l-1})}+\cdots +a_{{\beta }_k}{\overline{x}}^{\frac{{\beta }_k}{n}(n_1\cdots n_{l-1})}+}\hfill \\ & +& {\displaystyle \sum _{\begin{array}{c}j\in \left(e_k\right)\\ {\beta }_k<j<{\beta }_{k+1}\end{array}}{a}_j{\overline{x}}^{\frac{j}{n}(n_1\cdots n_{l-1})}+\sum _{\begin{array}{c}j>\frac{{\beta }_{k+1}}{e_k}\end{array}}{b}_j{\overline{x}}^{\frac{j{e}_k}{n}(n_1\cdots n_{l-1})},}\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\overline{T}}_l\left(\overline{x}\right)& =& {\displaystyle a_{{\beta }_1}{\overline{x}}^{\frac{{\beta }_1}{n}(n_1\cdots n_{l-1})}+\sum _{\begin{array}{c}j\in \left(e_1\right)\\ {\beta }_1<j<{\beta }_2\end{array}}{a}_j{\overline{x}}^{\frac{j}{n}(n_1\cdots n_{l-1})}+a_{{\beta }_2}{\overline{x}}^{\frac{{\beta }_2}{n}(n_1\cdots n_{l-1})}+\cdots +}\hfill \\ & +& {\displaystyle \sum _{\begin{array}{c}j\in \left(e_{l-1}\right)\\ {\beta }_{l-1}<j<{\beta }_l\end{array}}{a}_j{\overline{x}}^{\frac{j}{n}(n_1\cdots n_{l-1})}.}\hfill \end{array}$$

Now from [5] (Corollaire 1.1.1) and the equality (11), we obtain $♯Z_i^{\left(k\right)}=(n_i-1)n_{i+1}\cdots n_k,$ for $i\in \{1,\dots ,k\}$. Let us denote by

$${\rho }_l^{\left(k\right)}:=\left({\displaystyle \sum _{i=1}^k\left(♯Z_i^{\left(k\right)}\frac{{\beta }_i}{{\beta }_0}\right)}\right)(n_1\cdots n_{l-1})=\left({\displaystyle \sum _{i=1}^k(n_i-1)n_{i+1}\cdots n_k\frac{{\beta }_i}{{\beta }_0}}\right)(n_1\cdots n_{l-1}),$$

(35)

where $l\in \{k+1,\dots ,g\}$. Since the empty sum is zero, we have ${\rho }_l^{\left(0\right)}=0$.

Lemma 10.

If $\nu =\frac{m_l}{n_l}$ with $l\ge k+2$, then

$$I{n}_{\nu }\left(F_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)\right)=a_{{\beta }_{k+1}}{\theta }^{\left(k\right)}{c}_l^{\left(k\right)}{\overline{x}}^{c_l^{\left(k\right)}-1}\mathrm{d}\overline{x},$$

where $c_l^{\left(k\right)}={\rho }_l^{\left(k\right)}+\frac{{\beta }_{k+1}}{{\beta }_0}(n_1\cdots n_{l-1})$, being ${\rho }_l^{\left(k\right)}$ as in (35), ${\theta }^{\left(0\right)}=1$ and ${\theta }^{\left(k\right)}\in \mathbb{C}\backslash \left\{0\right\}$ for $1\le k\le g-1$. In particular ${\mathrm{ord}}_{\nu }\left(I{n}_{\nu }\left(F_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)\right)\right)=c_l^{\left(k\right)}$.

Proof. 

Suppose first of all that $1\le k\le g-1$. After Lemma 4, $\mathrm{ord}\left({\overline{\delta }}_j\left(\overline{x}\right)-{\overline{T}}_l\left(\overline{x}\right)\right)=\frac{{\beta }_i}{{\beta }_0}(n_1\cdots n_{l-1})$ for $2\le j\le m$ and $\mathrm{ord}\left({\overline{\delta }}_1\left(\overline{x}\right)-{\overline{T}}_l\left(\overline{x}\right)\right)=\frac{{\beta }_{k+1}}{{\beta }_0}(n_1\cdots n_{l-1})$. Replacing in (34), we obtain

$$\begin{array}{ccc}I{n}_{\nu }\left(F_l^{*}\left(f^{\left(k\right)}\right)\right)\hfill & =\hfill & I{n}_{\nu }\left(\left(\overline{y}-({\overline{\delta }}_1\left(\overline{x}\right)-{\overline{T}}_l\left(\overline{x}\right))\right)\right)I{n}_{\nu }\left({\displaystyle \prod _{i=1}^k\left({\displaystyle \prod _{{\delta }_j\in Z_i^{\left(k\right)}}\left(\overline{y}-({\overline{\delta }}_j\left(\overline{x}\right)-{\overline{T}}_l\left(\overline{x}\right))\right)}\right)}\right)\hfill \\ & =\hfill & a_{{\beta }_{k+1}}{\overline{x}}^{\frac{{\beta }_{k+1}}{{\beta }_0}(n_1\cdots n_{l-1})}{\theta }^{\left(k\right)}{\overline{x}}^{{\rho }_l^{\left(k\right)}},\hfill \end{array}$$

where ${\rho }_l^{\left(k\right)}=\left({\displaystyle \sum _{i=1}^k\left(♯Z_i^{\left(k\right)}\frac{{\beta }_i}{{\beta }_0}\right)}\right)(n_1\cdots n_{l-1})$ and ${\theta }^{\left(k\right)}\in \mathbb{C}\backslash \left\{0\right\}$.

Therefore $I{n}_{\nu }\left(F_l^{*}\left(f^{\left(k\right)}\right)\right)=a_{{\beta }_{k+1}}{\theta }^{\left(k\right)}{\overline{x}}^{c_l^{\left(k\right)}}$, with $c_l^{\left(k\right)}={\rho }_l^{\left(k\right)}+\frac{{\beta }_{k+1}}{{\beta }_0}(n_1\cdots n_{l-1})$. So $\mathrm{d}\left({\mathrm{In}}_{\nu }{F}_l^{*}\left(f^{\left(k\right)}\right)\right)=a_{{\beta }_{k+1}}{\theta }^{\left(k\right)}{c}_l^{\left(k\right)}{\overline{x}}^{c_l^{\left(k\right)}-1}\mathrm{d}\overline{x}$. Applying Lemma 5 we have

$${\mathrm{In}}_{\nu }{F}_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)=\mathrm{d}\left({\mathrm{In}}_{\nu }\left(F_l^{*}\left(f^{\left(k\right)}\right)\right)\right)=a_{{\beta }_{k+1}}{\theta }^{\left(k\right)}{c}_l^{\left(k\right)}{\overline{x}}^{c_l^{\left(k\right)}-1}\mathrm{d}\overline{x},$$

(36)

and ${\mathrm{ord}}_{\nu }\left({\mathrm{In}}_{\nu }{F}^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)\right)=c_l^{\left(k\right)}$.

Let us study the case $k=0$. From Equation (33), we have

$$F_l^{*}\left(\mathrm{d}{f}^{\left(0\right)}\right)=\left(a_{{\beta }_1}\frac{{\beta }_1}{n}(n_1\cdots n_{l-1}){\overline{x}}^{\frac{{\beta }_1}{n}(n_1\cdots n_{l-1})-1}+\cdots \right)\mathrm{d}\overline{x}+\mathrm{d}\overline{y},$$

so $\mathrm{supp}\left(F_l^{*}\mathrm{d}{f}^{\left(0\right)}\right)=\left\{\left(\frac{{\beta }_1}{n}(n_1\cdots n_{l-1}),0\right),(0,1)\right\}$. Since ${\displaystyle \frac{{\beta }_l}{n}}={\displaystyle \frac{m_l}{n_1\cdots n_l}}>{\displaystyle \frac{{\beta }_1}{n}}$ then ${\displaystyle \frac{m_l}{n_l}}>{\displaystyle \frac{{\beta }_1}{n}}(n_1\cdots n_{l-1})$. Consequently ${\mathrm{In}}_{\nu }\left(F_l^{*}\left(\mathrm{d}{f}^{\left(0\right)}\right)\right)=\left(a_{{\beta }_1}\frac{{\beta }_1}{n}(n_1\cdots n_{l-1}){\overline{x}}^{\frac{{\beta }_1}{n}(n_1\cdots n_{l-1})-1}\right)\mathrm{d}\overline{x},$ and ${\mathrm{ord}}_{\nu }\left({\mathrm{In}}_{\nu }{F}_l^{*}\left(\mathrm{d}{f}^{\left(0\right)}\right)\right)=\frac{{\beta }_1}{n}(n_1\cdots n_{l-1})$. □

Lemma 11.

If $\nu =\frac{m_l}{n_l}$ with $l\ge k+2$, then

$$I{n}_{\nu }\left(F_l^{*}\left(\omega \right)\wedge F_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)\right)=\left({\displaystyle \sum _{i+\nu j=c_l}\overline{\theta }{\mathcal{B}}_{ij}{\overline{x}}^{c_l^{\left(k\right)}-1+i}{\overline{y}}^{j-1}}\right)\mathrm{d}\overline{x}\wedge \mathrm{d}\overline{y},$$

where $\overline{\theta }=-a_{{\beta }_{k+1}}{\theta }^{\left(k\right)}{c}_l^{\left(k\right)}\in \mathbb{C}\backslash \left\{0\right\}$ and $c_l^{\left(k\right)}={\rho }_l^{\left(k\right)}+\frac{{\beta }_{k+1}}{{\beta }_0}(n_1\cdots n_{l-1})$, being ${\rho }_l^{\left(k\right)}$ as in (35). Moreover

$${\mathrm{ord}}_{\nu }\left({\mathrm{In}}_{\nu }\left(F_l^{*}\left(\omega \right)\wedge F_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)\right)\right)=c_l+c_l^{\left(k\right)}-1-\nu ,$$

where $c_l={\mathrm{ord}}_{\nu }\left({\mathrm{In}}_{\nu }{F}_l^{*}\left(\omega \right)\right)$.

Proof. 

After Lemma 10, we have

$$I{n}_{\nu }\left(F_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)\right)=a_{{\beta }_{k+1}}{\theta }^{\left(k\right)}{c}_l^{\left(k\right)}{\overline{x}}^{c_l^{\left(k\right)}-1}\mathrm{d}\overline{x},$$

(37)

where ${\theta }^{\left(k\right)}\in \mathbb{C}\backslash \left\{0\right\}$. From (31) and (37), we obtain

$${\mathrm{In}}_{\nu }{F}_l^{*}\left(\omega \right)\wedge {\mathrm{In}}_{\nu }\left(F_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)\right)=\left({\displaystyle \sum _{i+\nu j=c_l}\overline{\theta }{\mathcal{B}}_{ij}{\overline{x}}^{c_l^{\left(k\right)}-1+i}{\overline{y}}^{j-1}}\right)\mathrm{d}\overline{x}\wedge \mathrm{d}\overline{y},$$

where $\overline{\theta }:=-a_{{\beta }_{k+1}}{\theta }^{\left(k\right)}{c}_l^{\left(k\right)}\ne 0$ and ${\mathcal{B}}_{ij}\ne 0$ for some $i,j$ since by definition of main side, $F_l^{*}\left(\omega \right)$ has contribution of $\mathcal{B}$ (see Lemma 8).

Therefore ${\mathrm{In}}_{\nu }{F}_l^{*}\left(\omega \right)\wedge {\mathrm{In}}_{\nu }\left(F_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)\right)\ne 0$, and applying Lemma 1, we obtain

$$I{n}_{\nu }\left(F_l^{*}\left(\omega \right)\wedge F_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)\right)=\left({\displaystyle \sum _{i+\nu j=c_l}\overline{\theta }{\mathcal{B}}_{ij}{\overline{x}}^{c_l^{\left(k\right)}-1+i}{\overline{y}}^{j-1}}\right)\mathrm{d}\overline{x}\wedge \mathrm{d}\overline{y},$$

and

$$\begin{array}{ccc}{\mathrm{ord}}_{\nu }\left({\mathrm{In}}_{\nu }\left(F_l^{*}\left(\omega \right)\wedge F_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)\right)\right)\hfill & =\hfill & {\mathrm{ord}}_{\nu }\left({\mathrm{In}}_{\nu }{F}_l^{*}\left(\omega \right)\right)+{\mathrm{ord}}_{\nu }\left({\mathrm{In}}_{\nu }{F}_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)\right)-1-\nu \hfill \\ & =\hfill & c_l+c_l^{\left(k\right)}-1-\nu .\hfill \end{array}$$

□

Lemma 12.

For $\nu =\frac{m_l}{n_l}$ with $l=k+1$, we have

$$I{n}_{\nu }{F}_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)=a^{\left(k\right)}{\rho }_l^{\left(k\right)}{\overline{x}}^{{\rho }_l^{\left(k\right)}-1}\overline{y}\mathrm{d}\overline{x}+a^{\left(k\right)}{\overline{x}}^{{\rho }_l^{\left(k\right)}}\mathrm{d}\overline{y},$$

where ${\rho }_l^{\left(k\right)}=\left({\displaystyle \sum _{i=1}^k\left(♯Z_i^{\left(k\right)}\frac{{\beta }_i}{{\beta }_0}\right)}\right)(n_1\cdots n_{l-1})$, $a^{\left(0\right)}=1$ and $a^{\left(k\right)}\in \mathbb{C}\backslash \left\{0\right\}$ for $1\le k\le g-1$. In particular ${\mathrm{ord}}_{\nu }\left(I{n}_{\nu }{F}_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)\right)={\rho }_l^{\left(k\right)}+\nu$.

Proof. 

Suppose first of all that $1\le k\le g-1$. By Lemma 3, $\mathrm{ord}\left({\overline{\delta }}_j\left(\overline{x}\right)-{\overline{T}}_l\left(\overline{x}\right)\right)=\frac{{\beta }_i}{{\beta }_0}(n_1\cdots n_{l-1})$ for $2\le j\le m$, $1\le i\le k$ and $\mathrm{ord}\left({\overline{\delta }}_1\left(\overline{x}\right)-{\overline{T}}_l\left(\overline{x}\right)\right)=\tau (n_1\cdots n_{l-1})$, with $\tau >\frac{{\beta }_{k+1}}{{\beta }_0}$. Replacing in (34), we obtain

$$\begin{array}{ccc}I{n}_{\nu }\left(F_l^{*}\left(f^{\left(k\right)}\right)\right)\hfill & =\hfill & I{n}_{\nu }\left(\left(\overline{y}-({\overline{\delta }}_1\left(\overline{x}\right)-{\overline{T}}_l\left(\overline{x}\right))\right)\right)I{n}_{\nu }\left({\displaystyle \prod _{i=1}^k\left({\displaystyle \prod _{{\delta }_j\in Z_i^{\left(k\right)}}\left(\overline{y}-({\overline{\delta }}_j\left(\overline{x}\right)-{\overline{T}}_l\left(\overline{x}\right))\right)}\right)}\right)\hfill \\ & =\hfill & a^{\left(k\right)}{\overline{x}}^{{\rho }_l^{\left(k\right)}}\overline{y},\hfill \end{array}$$

where ${\rho }_l^{\left(k\right)}=\left({\displaystyle \sum _{i=1}^k\left(♯Z_i^{\left(k\right)}\frac{{\beta }_i}{{\beta }_0}\right)}\right)(n_1\cdots n_{l-1})$ and $a^{\left(k\right)}\in \mathbb{C}\backslash \left\{0\right\}$.

Therefore $\mathrm{d}\left({\mathrm{In}}_{\nu }\left(F_l^{*}\left(f^{\left(k\right)}\right)\right)\right)=a^{\left(k\right)}{\rho }_l^{\left(k\right)}{\overline{x}}^{{\rho }_l^{\left(k\right)}-1}\overline{y}\mathrm{d}\overline{x}+a^{\left(k\right)}{\overline{x}}^{{\rho }_l^{\left(k\right)}}\mathrm{d}\overline{y}$. Applying Lemma 5, we obtain

$${\mathrm{In}}_{\nu }{F}_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)=\mathrm{d}\left({\mathrm{In}}_{\nu }\left(F_l^{*}\left(f^{\left(k\right)}\right)\right)\right)=\left(a^{\left(k\right)}{\rho }_l^{\left(k\right)}{\overline{x}}^{{\rho }_l^{\left(k\right)}-1}\overline{y}\mathrm{d}\overline{x}+a^{\left(k\right)}{\overline{x}}^{{\rho }_l^{\left(k\right)}}\mathrm{d}\overline{y}\right)$$

(38)

and ${\mathrm{ord}}_{\nu }\left({\mathrm{In}}_{\nu }\left(F_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)\right)\right)={\rho }_l^{\left(k\right)}+\nu$.

Now we study the case $k=0$. From Equation (33) and for $l=1$, we observe that ${\overline{T}}_l\left(\overline{x}\right)=0$ and $F_1^{*}\left(\mathrm{d}{f}^{\left(0\right)}\right)=\mathrm{d}\left(\overline{y}\right)$. Therefore $I{n}_{\nu }{F}_1^{*}\left(\mathrm{d}{f}^{\left(0\right)}\right)=\mathrm{d}\overline{y}$ and ${\mathrm{ord}}_{\nu }\left(I{n}_{\nu }{F}_1^{*}\left(\mathrm{d}{f}^{\left(0\right)}\right)\right)=\nu$. We finish the proof because ${\rho }_l^{\left(0\right)}=0$ and $a^{\left(0\right)}=1$. □

Lemma 13.

For $\nu =\frac{m_l}{n_l}$ with $l=k+1$, we have

$$I{n}_{\nu }\left(F_l^{*}\left(\omega \right)\wedge F_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)\right)=\left({\displaystyle \sum _{i+\nu j=c_l}{a}^{\left(k\right)}({\mathcal{A}}_{ij}-{\rho }_l^{\left(k\right)}{\mathcal{B}}_{ij}){\overline{x}}^{i+{\rho }_l^{\left(k\right)}-1}{\overline{y}}^j}\right)\mathrm{d}\overline{x}\wedge \mathrm{d}\overline{y},$$

where ${\rho }_l^{\left(k\right)}=\left({\displaystyle \sum _{i=1}^k\left(♯Z_i^{\left(k\right)}\frac{{\beta }_i}{{\beta }_0}\right)}\right)(n_1\cdots n_{l-1})$, $a^{\left(0\right)}=1$ and $a^{\left(k\right)}\in \mathbb{C}\backslash \left\{0\right\}$ for $1\le k\le g-1$. Moreover

$${\mathrm{ord}}_{\nu }\left({\mathrm{In}}_{\nu }\left(F_l^{*}\left(\omega \right)\wedge F_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)\right)\right)=c_l+{\rho }_l^{\left(k\right)}-1,$$

with $c_l={\mathrm{ord}}_{\nu }\left({\mathrm{In}}_{\nu }{F}_l^{*}\left(\omega \right)\right)$.

Proof. 

By (31), the support line of inclination $\nu$ of the Newton polygon of $F_l^{*}\left(\omega \right)$ has equation ${\mathcal{L}}_l:i+\nu j=c_l$, being $c_l={\mathrm{ord}}_{\overline{x}}\left(\mathcal{A}(\overline{x},0)\right)$. Therefore, there is $(i_0,j_0)\in {\mathcal{L}}_l\cap \mathrm{supp}\left(F_l^{*}\left(\omega \right)\right)$ such that ${\mathcal{A}}_{i_0{j}_0}\ne 0$ and ${\mathcal{B}}_{i_0{j}_0}=0$. On the other hand, using Lemma 12, we have

$$I{n}_{\nu }\left(F_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)\right)=a^{\left(k\right)}{\rho }_l^{\left(k\right)}{\overline{x}}^{{\rho }_l^{\left(k\right)}-1}\overline{y}\mathrm{d}\overline{x}+a^{\left(k\right)}{\overline{x}}^{{\rho }_l^{\left(k\right)}}\mathrm{d}\overline{y},$$

(39)

where $a^{\left(k\right)}\in \mathbb{C}\backslash \left\{0\right\}$ and ${\rho }_l^{\left(k\right)}$ as in (35). From (31) and (39), we obtain

$$I{n}_{\nu }\left(F_l^{*}\left(\omega \right)\right)\wedge I{n}_{\nu }\left(F_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)\right)=\left({\displaystyle \sum _{i+\nu j=c_l}{a}^{\left(k\right)}({\mathcal{A}}_{ij}-{\rho }_l^{\left(k\right)}{\mathcal{B}}_{ij}){\overline{x}}^{i+{\rho }_l^{\left(k\right)}-1}{\overline{y}}^j}\right)\mathrm{d}\overline{x}\wedge \mathrm{d}\overline{y}.$$

Hence ${\mathrm{In}}_{\nu }{F}_l^{*}\left(\omega \right)\wedge {\mathrm{In}}_{\nu }{F}_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)\ne 0$ (since ${\mathcal{A}}_{i_0{j}_0}\ne 0$ and ${\mathcal{B}}_{i_0{j}_0}=0$). Applying Lemma 1, we obtain

$$I{n}_{\nu }\left(F_l^{*}\left(\omega \right)\wedge F_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)\right)=\left({\displaystyle \sum _{i+\nu j=c_l}{a}^{\left(k\right)}({\mathcal{A}}_{ij}-{\rho }_l^{\left(k\right)}{\mathcal{B}}_{ij}){\overline{x}}^{i+{\rho }_l^{\left(k\right)}-1}{\overline{y}}^j}\right)\mathrm{d}\overline{x}\wedge \mathrm{d}\overline{y},$$

and

$$\begin{array}{ccc}{\mathrm{ord}}_{\nu }\left({\mathrm{In}}_{\nu }\left(F_l^{*}\left(\omega \right)\wedge F_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)\right)\right)\hfill & =\hfill & {\mathrm{ord}}_{\nu }\left({\mathrm{In}}_{\nu }{F}_l^{*}\left(\omega \right)\right)+{\mathrm{ord}}_{\nu }\left({\mathrm{In}}_{\nu }{F}_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)\right)-1-\nu \hfill \\ & =\hfill & c_l+{\rho }_l^{\left(k\right)}-1.\hfill \end{array}$$

□

As a consequence of Lemmas 11 and 13, we have the following corollary:

Corollary 1.

Let $\nu =\frac{m_l}{n_l}$ with $l\ge k+1$. The support line of inclination ν of the Newton polygon of ${\mathrm{In}}_{\nu }\left(F_l^{*}\left(\omega \right)\wedge F_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)\right)$ is

$${\mathcal{L}}_1:i+\nu j=c_l+c_l^{\left(k\right)}-1-\nu ,\mathrm{for}l\ge k+2,$$

and

$${\mathcal{L}}_2:i+\nu j=c_l+{\rho }_l^{\left(k\right)}-1,\mathrm{for}l=k+1,$$

where $c_l={\mathrm{ord}}_{\nu }\left({\mathrm{In}}_{\nu }{F}_l^{*}\left(\omega \right)\right)$ and $c_l^{\left(k\right)}={\rho }_l^{\left(k\right)}+\frac{{\beta }_{k+1}}{{\beta }_0}(n_1\cdots n_{l-1})$, being ${\rho }_l^{\left(k\right)}$ as in (35).

Proposition 3.

Let $\nu =\frac{m_l}{n_l}$ with $l\ge k+1$. If

$${\mathrm{In}}_{\nu }{F}_l^{*}\left(\omega \right)=\sum _{i+\nu j=c_l}{\mathcal{A}}_{ij}{\overline{x}}^{i-1}{\overline{y}}^j\mathrm{d}\overline{x}+\sum _{i+\nu j=c_l}{\mathcal{B}}_{ij}{\overline{x}}^i{\overline{y}}^{j-1}\mathrm{d}\overline{y}$$

then

$${\displaystyle {\mathrm{In}}_{\nu }\left(F_l^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\right)=\sum _{i+j\nu =c_l}\overline{\theta }{\mathcal{B}}_{ij}{\overline{x}}^{c_l^{\left(k\right)}+i-(n_1\cdots n_{l-1})}{\overline{y}}^{j-1},\mathrm{for}l\ge k+2}$$

(40)

and

$${\mathrm{In}}_{\nu }\left(F_l^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\right)=\left({\displaystyle \sum _{i+\nu j=c_l}{a}^{\left(k\right)}({\mathcal{A}}_{ij}-{\rho }_l^{\left(k\right)}{\mathcal{B}}_{ij}){\overline{x}}^{i+{\rho }_l^{\left(k\right)}-n_1\cdots n_k}{\overline{y}}^j}\right),\mathrm{for}l=k+1;$$

(41)

where $a^{\left(0\right)}=1$, $a^{\left(k\right)},\overline{\theta }\in \mathbb{C}\backslash \left\{0\right\}$ for $1\le k\le g-1$, $c_l={\mathrm{ord}}_{\nu }\left({\mathrm{In}}_{\nu }{F}_l^{*}\left(\omega \right)\right)$ and $c_l^{\left(k\right)}={\rho }_l^{\left(k\right)}+\frac{{\beta }_{k+1}}{{\beta }_0}(n_1\cdots n_{l-1})$, being ${\rho }_l^{\left(k\right)}$ as in (35).

Proof. 

From Lemma 9, we obtain

$${\mathrm{In}}_{\nu }(F_l^{*}\left(\omega \right)\wedge F_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right))={\mathrm{In}}_{\nu }\left(n_1\cdots n_{l-1}{\overline{x}}^{n_1\cdots n_{l-1}-1}\left(F_l^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\right)\mathrm{d}\overline{x}\wedge \mathrm{d}\overline{y}\right).$$

(42)

If $l\ge k+2$ then by Lemma 11 and replacing in (42) we have equality (40). The equality (41) follows from Lemma 13 and again equality (42). □

As a consequence of Proposition 3 we determine, in the following corollary, the points of the Newton polygon of $F_l^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)$ from the points of the Newton polygon of $F_l^{*}\left(\omega \right)$.

Corollary 2.

1 

If $l\ge k+2$ and $(i,j)$ is a point of $\mathcal{N}\left(F_l^{*}\left(\omega \right)\right)$ with ${\mathcal{B}}_{ij}\ne 0$ then $(c_l^{\left(k\right)}+i-(n_1\cdots n_{l-1}),j-1)$ is a point of $\mathcal{N}\left(F_l^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\right)$.

2 

If $l=k+1$ and $(i,j)$ is a point of $\mathcal{N}\left(F_l^{*}\left(\omega \right)\right)$ with ${\mathcal{A}}_{ij}-{\rho }_l^{\left(k\right)}{\mathcal{B}}_{ij}\ne 0$ then $(i+{\rho }_l^{\left(k\right)}-n_1\cdots n_k,j)$ is a point of $\mathcal{N}\left(F_l^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\right)$.

In the following proposition we will need information about the Newton polygon $\mathcal{N}\left(F_l^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\right)$.

Proposition 4.

Let $\nu =\frac{m_l}{n_l}$ with $l\ge k+1$. The support line of inclination ν of the Newton polygon of ${\mathrm{In}}_{\nu }\left(F_l^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\right)$ is

$${\mathcal{L}}_l^{\left(k\right)}:i+\nu j=c_{k,l}-\nu ,\mathrm{for}l\ge k+2$$

(43)

and

$${\mathcal{L}}_l^{\left(k\right)}:i+\nu j=c_l+{\rho }_l^{\left(k\right)}-n_1\cdots n_k,\mathrm{for}l=k+1$$

(44)

where $c_{k,l}:=c_l+c_l^{\left(k\right)}-n_1\cdots n_{l-1}$, being $c_l={\mathrm{ord}}_{\nu }\left({\mathrm{In}}_{\nu }{F}_l^{*}\left(\omega \right)\right)$, $c_l^{\left(k\right)}={\mathrm{ord}}_{\nu }\left({\mathrm{In}}_{\nu }{F}_l^{*}\left(\mathrm{d}{f}^{\left(k\right)}\right)\right)$ and ${\rho }_l^{\left(k\right)}$ as in (35).

Proof. 

Suppose first of all that $l\ge k+2$. Let $(a,b)$ be a point of the support of ${\mathrm{In}}_{\nu }\left(F_l^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\right)$. From the equality (40), there exists a point $(i_a,j_b)$ of the support of $\mathcal{N}\left(F_l^{*}\left(\omega \right)\right)$, such that $a=c_l^{\left(k\right)}+i_a-n_1\cdots n_{l-1}$ and $b=j_b-1.$ Hence $a+\nu b=c_{k,l}-\nu ,$ where $c_{k,l}:=c_l+c_l^{\left(k\right)}-n_1\cdots n_{l-1}$ and the support line of inclination $\nu$ of the Newton polygon of ${\mathrm{In}}_{\nu }\left(F_l^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\right)$ is ${\mathcal{L}}_l^{\left(k\right)}:i+\nu j=c_{k,l}-\nu .$ Similarly if $l=k+1$, then from the equality (41) there is a point $(i_a,j_b)$ in the support of $\mathcal{N}\left(F_l^{*}\left(\omega \right)\right)$ with ${\mathcal{A}}_{i_a{j}_b}-{\rho }_{k+1}^{\left(k\right)}{\mathcal{B}}_{i_a{j}_b}\ne 0$. So $a+\nu b=c_{k+1}+{\rho }_{k+1}^{\left(k\right)}-n_1\cdots n_k$ and ${\mathcal{L}}_l^{\left(k\right)}:i+\nu j=c_{k+1}+{\rho }_{k+1}^{\left(k\right)}-n_1\cdots n_k$ is the support line of inclination $\nu$ of the Newton polygon of ${\mathrm{In}}_{\nu }\left(F_l^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\right)$. □

As a consequence of Proposition 4, we have the following corollaries.

Corollary 3.

Let $\nu =\frac{m_{k+1}}{n_{k+1}}$ and L (respectively ${\mathcal{L}}_{k+1}$) be the compact side (respectively the support line) of inclination ν of the Newton polygon of $F_{k+1}^{*}\left(\omega \right)$. Then the line ${\mathcal{L}}_{k+1}^{\left(k\right)}$ as in (44) is the support line of inclination ν of $\mathcal{N}\left(F_{k+1}^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\right)$. Moreover if the Newton polygon of $F_{k+1}^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)$ admits a compact side of inclination ν then it is the one with the greatest inclination.

Proof. 

By Proposition 4 and the convexity of the Newton polygon, it only remains to prove that if $\mathcal{N}\left(F_{k+1}^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\right)$ admits a compact side of inclination $\nu$, then it is the one with the greatest inclination. From (32) we know that the support line of inclination $\nu$ of the Newton polygon of $F_{k+1}^{*}\left(\omega \right)$ is ${\mathcal{L}}_{k+1}:i+j\nu =c_{k+1}$ and this line contains the main side of $\mathcal{N}\left(F_{k+1}^{*}\left(\omega \right)\right)$ (see Lemma 8). In particular the compact side of greater inclination of $\mathcal{N}\left(F_{k+1}^{*}\left(\omega \right)\right)$ has inclination $\nu$ and it intersects the horizontal axis. So there is $i_0\in \mathbb{N}$ such that ${\mathcal{B}}_{i_{0}0}=0$ and ${\mathcal{A}}_{i_{0}0}\ne 0$. From this last inequality, we obtain $(i_0,0)\in \mathrm{supp}\left({\mathrm{In}}_{\nu }\left(F_{k+1}^{*}\left(\omega \right)\right)\right)$, so $i_0=c_{k+1}$. By (41), $(i_0,0)\in \mathrm{supp}\left({\mathrm{In}}_{\nu }\left(F_{k+1}^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\right)\right)$ for $i_0=c_{k+1}+{\rho }_{k+1}^{\left(k\right)}-n_1\cdots n_k$ since ${\mathcal{A}}_{i_{0}0}-{\rho }_{k+1}^{\left(k\right)}{\mathcal{B}}_{i_{0}0}\ne 0$. Hence the line ${\mathcal{L}}_{k+1}^{\left(k\right)}$ intersects the horizontal axis and it is the support line of inclination $\nu$ of $\mathcal{N}\left(F_{k+1}^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\right)$ and the corollary follows. □

Remark 4.

Note that the Newton polygon of $F_{k+1}^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)$ does not necessarily have a compact side of inclination $\nu =\frac{m_{k+1}}{n_{k+1}}$ as the following example illustrates: if $f(x,y)=y^2-x^3$ then $f^{\left(0\right)}(x,y)=y$ and ${\mathcal{P}}_{\mathrm{d}f}^{\left(0\right)}=-3x^2$. Therefore the Newton polygon of $\mathrm{d}f$ has a single compact side and it is of inclination $\nu =\frac{3}{2}$ and is contained on the line ${\mathcal{L}}_1:i+\nu j=3$ but nevertheless the Newton polygon of $F_1^{*}\left({\mathcal{P}}_{\mathrm{d}f}^{\left(0\right)}\right)$ has a single vertex that is $(2,0)$ and its support line of inclination ν is ${\mathcal{L}}_1^{\left(0\right)}:i+\nu j=2$.

Corollary 4.

Let $\nu =\frac{m_l}{n_l}$, for $k+2\le l\le g$ and L (respectively ${\mathcal{L}}_l$) be the compact side (respectively the support line) of inclination ν of the Newton polygon of $F_l^{*}\left(\omega \right)$. Then the line ${\mathcal{L}}_l^{\left(k\right)}$ as in (43) is the support line of inclination ν of $\mathcal{N}\left(F_l^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\right)$. Moreover if the Newton polygon of $F_l^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)$ admits a compact side of inclination ν then it is the one with the greatest inclination.

Proof. 

It is similar to the proof of Corollary 3. □

Remember that $\mathcal{N}\left(F_l^{*}\left(\omega \right)\right)$ has a main side and it is contained on the support line of this Newton polygon of inclination $\nu =\frac{m_l}{n_l}$ (see Lemma 8).

Lemma 14.

Let $(a_1,b_1)$ be the vertex of the main side of $\mathcal{N}\left(F_l^{*}\left(\omega \right)\right)$ with the smallest y-coordinate and having a contribution of $\mathcal{B}(\overline{x},\overline{y})$. Then $b_1\ge n_l$.

Proof. 

By hypothesis $b_1\ne 0$. After (32), the support line of $\mathcal{N}\left(F_l^{*}\left(\omega \right)\right)$ of inclination $\nu$ is $i+\nu j=c_l$ for certain $c_l\ne 0$. In particular $b_1=\frac{(c_l-a_1)}{\nu }=\frac{(c_l-a_1)}{m_l}{n}_l\in \mathbb{N}$, and therefore $\frac{(c_l-a_1)}{m_l}$ is positive. Since $n_l$ and $m_l$ are coprime then $\frac{(c_l-a_1)}{m_l}$ is a positive natural and the lemma follows. □

If $\mathcal{N}$ is a Newton polygon and $q\in {\mathbb{Q}}^{+}$, we will denote ${\mathcal{N}}_{\ge q}$ (respectively ${\mathcal{N}}_{>q}$) the Newton polygon which results from eliminating in $\mathcal{N}$ the sides of inclination strictly less than (respectively less than or equal to) q.

Proposition 5.

Put $\nu =\frac{m_l}{n_l}$ with $k+2\le l\le g$. Let $(a_0,b_0)$ be the vertex of the main side of $\mathcal{N}\left(F_l^{*}\left(\omega \right)\right)$ with the highest y-coordinate and having a contribution of $\mathcal{B}(\overline{x},\overline{y})$. Then the highest y-coordinate of the vertices of $\mathcal{N}{\left(F_l^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\right)}_{\ge \nu }$ is $b_0-1$.

Proof. 

It is a consequence of Corollary 4 and the first part of Corollary 2. □

5. Decomposition of the Approximate Polar Curve of a Foliation: Proof of Theorem 1

Remember that $f\in \mathbb{C}\left\{x\right\}\left[y\right]$ is an irreducible Weierstrass polynomial with characteristic exponents $({\beta }_0,\dots ,{\beta }_g)$. Put $n_i=\frac{gcd({\beta }_0,\dots ,{\beta }_{i-1})}{gcd({\beta }_0,\dots ,{\beta }_i)}$ for $1\le i\le g$. Denote by $f^{\left(k\right)}$, $0\le k\le g-1$ the characteristic approximate roots of f. Let us prove Theorem 1, which generalizes [13] (Theorem 1).

Let $k+2\le l\le g$ and $\nu =\frac{m_l}{n_l}$. Let ${\nu }_1<{\nu }_2<\cdots <{\nu }_q$ be the inclinations of $\mathcal{N}{\left(F_l^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\right)}_{\ge \nu }$, which are strictly greater than $\nu$. Denote by $L_i$ the compact side of $\mathcal{N}{\left(F_l^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\right)}_{\ge \nu }$ of inclination ${\nu }_i$. Let $r\in \{1,\dots ,q\}$. The Newton–Puiseux roots of the curve $F_l^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)$ corresponding to the compact side of $\mathcal{N}\left(F_l^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\right)$ of inclination ${\nu }_r$ are of the form ${\overline{\gamma }}_{rs}\left(\overline{x}\right)=d_{rs}{\overline{x}}^{{\nu }_r}+{\epsilon }_{rs}\left(\overline{x}\right),$ with $d_{rs}\ne 0$ and $or{d}_{\overline{x}}{\epsilon }_{rs}\left(\overline{x}\right)>{\nu }_r$, where $s=1,\dots ,s_r$, being $s_r$ the height of the side $L_r$. For $l\ge k+2$ we define ${\displaystyle {\overline{\mathsf{\Gamma }}}^{\left(l\right)}:=\prod _{r=1}^q\prod _{s=1}^{s_r}(\overline{y}-{\overline{\gamma }}_{rs}\left(\overline{x}\right))}$. After Lemma 6, the reduced equation of the union of separatrices of $F_l^{*}\left(\omega \right)$ is $F_l^{*}\left(f\right)=0.$ By Lemma 8 the support line containing the main side of $\mathcal{N}\left(F_l^{*}\left(\omega \right)\right)$ has inclination $\frac{m_l}{n_l}$. Since $\omega =0$ is a generalized curve foliation then $F_l^{*}\left(\omega \right)$ is also (see Lemma 7) and applying the third part of Remark 3 we have the equality $\mathcal{N}\left(F_l^{*}\left(\omega \right)\right)=\mathcal{N}\left(F_l^{*}\left(f\right)\right)$. Hence, from [18] (Lemme 8.4.2), the order of any Newton–Puiseux root of $F_l^{*}\left(f\right)$ is less than or equal to $\frac{m_l}{n_l}$ and by Lemma 8, $F_l^{*}\left(f\right)$ has Newton–Puiseux roots of order $\frac{m_l}{n_l}$. Let $\overline{\mathcal{D}}$ be an irreducible component of $F_l^{*}\left(f\right)$ whose Newton–Puiseux roots have order equals $\frac{m_l}{n_l}$. Since ${\nu }_r>\nu =\frac{m_l}{n_l}$, for all $r=1,\dots ,q;$ any irreducible component ${\overline{\mathcal{P}}}_l$ of ${\overline{\mathsf{\Gamma }}}^{\left(l\right)}$ verifies $\mathrm{cont}(\overline{\mathcal{D}},{\overline{\mathcal{P}}}_l)=\frac{m_l}{n_l}$. So, going back to the coordinates $(x,y)$, we obtain

$$\mathrm{cont}({\mathcal{C}}_f,{\mathcal{P}}_l)=\frac{m_l}{n_1\cdots n_{l-1}·n_l}=\frac{{\beta }_l}{n},\mathrm{con}k+2\le l\le g,$$

where ${\mathcal{P}}_l$ and ${\mathsf{\Gamma }}^{\left(l\right)}$ are such that ${\overline{\mathcal{P}}}_l=F_l^{-1}\left({\mathcal{P}}_l\right)$ and ${\overline{\mathsf{\Gamma }}}^{\left(l\right)}=F_l^{-1}\left({\mathsf{\Gamma }}^{\left(l\right)}\right)$.

Let $k+2\le l\le g$. The Newton–Puiseux roots of the polar ${\mathcal{P}}_{\omega }^{\left(k\right)}$ which contact with ${\mathcal{C}}_f$ is greater than or equal to $\frac{{\beta }_l}{n}$ coincide with the Newton–Puiseux roots of ${\mathsf{\Gamma }}^{(k+2)}\cdots {\mathsf{\Gamma }}^{\left(g\right)}$. By Lemma 8 and Proposition 5, the height of $\mathcal{N}{\left(F_l^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\right)}_{\ge \nu }$ is $e_{l-1}-1$. Hence the number of Newton–Puiseux roots of ${\mathcal{C}}_f$ having contact, with the polar curve ${\mathcal{P}}_{\omega }^{\left(k\right)}$, greater than or equal to $\frac{{\beta }_l}{n}$ is

$$n_1\cdots n_{l-1}(e_{l-1}-1).$$

(45)

Reasoning in a similar way, the number of Newton–Puiseux roots of the separatrix ${\mathcal{C}}_f$ having contact, with the polar curve ${\mathcal{P}}_{\omega }^{\left(k\right)}$, greater or equal to $\frac{{\beta }_{l+1}}{n}$ is

$$n_1\cdots n_l(e_l-1).$$

(46)

From Equations (45) and (46) we conclude that the number of Newton–Puiseux roots of the separatrix ${\mathcal{C}}_f$ that have contact, with the polar curve ${\mathcal{P}}_{\omega }^{\left(k\right)}$, equal to $\frac{{\beta }_l}{n}$ is

$$n_1\cdots n_{l-1}(e_{l-1}-1)-n_1\cdots n_l(e_l-1)=n_1\cdots n_l-n_1\cdots n_{l-1}=n_1\cdots n_{l-1}(n_l-1).$$

(47)

Therefore

$$\mathrm{mult}\left({\mathsf{\Gamma }}^{\left(l\right)}\right)=n_1\cdots n_{l-1}(n_l-1).$$

(48)

On the other hand

$$\begin{array}{ccc}\mathrm{mult}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\hfill & =\hfill & \mathrm{mult}\left(A{f}_y^{\left(k\right)}-B{f}_x^{\left(k\right)}\right)\hfill \\ \hfill & \ge \hfill & min\left\{\mathrm{mult}\left(A{f}_y^{\left(k\right)}\right),\mathrm{mult}\left(B{f}_x^{\left(k\right)}\right)\right\}\hfill \\ \hfill & =\hfill & min\left\{\mathrm{mult}\left(A\right)+\mathrm{mult}\left(f_y^{\left(k\right)}\right),\mathrm{mult}\left(B\right)+\mathrm{mult}\left(f_x^{\left(k\right)}\right)\right\}.\hfill \end{array}$$

(49)

Since $\mathrm{ord}\left(f_x^{\left(k\right)}\right)\ge \mathrm{ord}\left(f_y^{\left(k\right)}\right)=n_1\cdots n_k-1$ (see Remark 1) and

$$\mathrm{mult}\left(\omega \right)=min\left\{\mathrm{ord}\right(A),\mathrm{ord}(B\left)\right\}=n-1,$$

we obtain from (49)

$$\mathrm{mult}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\ge n+n_1\cdots n_k-2.$$

(50)

We define ${\mathsf{\Gamma }}^{(k+1)}:=\frac{{\mathcal{P}}_{\omega }^{\left(k\right)}}{{\mathsf{\Gamma }}^{(k+2)}\cdots {\mathsf{\Gamma }}^{\left(g\right)}}$. Using Equations (48) and (50) we have

$$\begin{array}{ccc}\mathrm{mult}\left({\mathsf{\Gamma }}^{(k+1)}\right)\hfill & =\hfill & \mathrm{mult}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)-\mathrm{mult}\left({\mathsf{\Gamma }}^{(k+2)}\cdots {\mathsf{\Gamma }}^{\left(g\right)}\right)\hfill \\ & \ge \hfill & n+n_1\cdots n_k-2-(n-n_1\cdots n_{k+1})\hfill \\ & =\hfill & n_1\cdots n_k(n_{k+1}+1)-2.\hfill \end{array}$$

Since $n_i\ge 2$ for any $i=1,\dots ,g$, then $\mathrm{mult}\left({\mathsf{\Gamma }}^{(k+1)}\right)\ge 1$, so ${\mathsf{\Gamma }}^{(k+1)}$ it is not a unit. The Newton–Puiseux roots of ${\overline{\mathsf{\Gamma }}}^{(k+1)}$ correspond to the sides of $\mathcal{N}\left(F_l^{*}\left({\mathcal{P}}_{\omega }^{\left(k\right)}\right)\right)$ whose inclinations are strictly less than $\frac{m_{k+2}}{n_{k+2}}$. Using the Corollary 3 we have $\mathrm{ord}\left(\overline{\gamma }\right)\le \frac{m_{k+1}}{n_{k+1}}$ for every Newton–Puiseux root $\overline{\gamma }$ of ${\overline{\mathsf{\Gamma }}}^{(k+1)}$, hence $\mathrm{ord}\left(\gamma \right)\le \frac{{\beta }_{k+1}}{n}$ for any Newton–Puiseux root $\gamma$ of the factor ${\mathsf{\Gamma }}^{(k+1)}$. This finishes the proof.

The following example illustrates that the multiplicity of the polar curve ${\mathcal{P}}_{\omega }^{\left(k\right)}$ cannot be determined exclusively with the equisingularity class of the branch $f(x,y)=0$, since in general, we cannot determine the multiplicity of the factor ${\mathsf{\Gamma }}^{(k+1)}$.

Example 2.

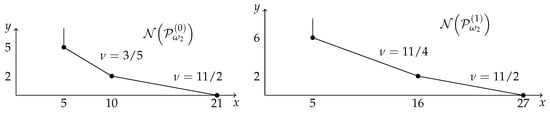
Let ${\mathcal{C}}_f:{(y^2-x^{11})}^2-x^{17}y=0$ be an irreducible curve with characteristic exponents (4,22,23). Let us consider the foliations defined by the 1-forms

$$\begin{array}{ccc}\hfill {\omega }_1& =& (x^{23}+x^{22}y+22x^{21}-x^{18}y-x^{17}{y}^2-17x^{16}y-2x^{12}{y}^2-2x^{11}{y}^3-22x^{10}{y}^2+x{y}^4\hfill \\ & & +y^5)\mathrm{d}x+(x^{23}-x^{18}y-x^{17}-2x^{12}{y}^2-4x^{11}y+x{y}^4+4y^3)\mathrm{d}y,\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\omega }_2& =& (x^{27}y-x^{22}{y}^2+22x^{21}-2x^{16}{y}^3-17x^{16}y-22x^{10}{y}^2+x^5{y}^5)\mathrm{d}x\hfill \\ & +& (x^{22}{y}^5-x^{17}{y}^6-2x^{11}{y}^7-x^{17}-4x^{11}y+y^9+4y^3)\mathrm{d}y,\hfill \end{array}$$

having ${\mathcal{C}}_f$ as separatrix. The approximate roots of ${\mathcal{C}}_f$ are $f^{\left(0\right)}=y$ and $f^{\left(1\right)}=y^2-x^{11}$, so

$$\begin{array}{ccc}{\mathcal{P}}_{{\omega }_1}^{\left(0\right)}\hfill & =\hfill & x^{23}+x^{22}y+22x^{21}-x^{18}y-x^{17}{y}^2-17x^{16}y-2x^{12}{y}^2-2x^{11}{y}^3\hfill \\ & -\hfill & 22x^{10}{y}^2+x{y}^4+y^5,\hfill \end{array}$$

and

$$\begin{array}{ccc}{\mathcal{P}}_{{\omega }_1}^{\left(1\right)}\hfill & =\hfill & 11x^{33}-11x^{28}y-11x^{27}+2x^{23}y-20x^{22}{y}^2-2x^{18}{y}^2-2x^{17}{y}^3-34x^{16}{y}^2\hfill \\ & -\hfill & 4x^{12}{y}^3+7x^{11}{y}^4+2x{y}^5+2y^6,\hfill \end{array}$$

where $\mathrm{mult}\left({\mathcal{P}}_{{\omega }_1}^{\left(0\right)}\right)=5$ and $\mathrm{mult}\left({\mathcal{P}}_{{\omega }_1}^{\left(1\right)}\right)=6$. In Figure 2 we present the Newton polygons of ${\mathcal{P}}_{{\omega }_1}^{\left(0\right)}$ and ${\mathcal{P}}_{{\omega }_1}^{\left(1\right)}$.

Figure 2. Newton polygons of ${\mathcal{P}}_{{\omega }_1}^{\left(0\right)}$ and ${\mathcal{P}}_{{\omega }_1}^{\left(1\right)}$.

On the other hand, we obtain

$${\mathcal{P}}_{{\omega }_2}^{\left(0\right)}=x^{27}y-x^{22}{y}^2+22x^{21}-2x^{16}{y}^3-17x^{16}y-22x^{10}{y}^2+x^5{y}^5,$$

and

$$\begin{array}{ccc}{\mathcal{P}}_{{\omega }_2}^{\left(1\right)}\hfill & =\hfill & 11x^{32}{y}^5-11x^{27}{y}^6+2x^{27}{y}^2-22x^{21}{y}^7-11x^{27}-2x^{22}{y}^3\hfill \\ & -\hfill & 4x^{16}{y}^4+11x^{10}{y}^9-34x^{16}{y}^2+2x^5{y}^6,\hfill \end{array}$$

where $\mathrm{mult}\left({\mathcal{P}}_{{\omega }_2}^{\left(0\right)}\right)=10$ and $\mathrm{mult}\left({\mathcal{P}}_{{\omega }_2}^{\left(1\right)}\right)=11$. See Figure 3 for the Newton polygons of ${\mathcal{P}}_{{\omega }_2}^{\left(0\right)}$ and ${\mathcal{P}}_{{\omega }_2}^{\left(1\right)}$.

Figure 3. Newton polygons of ${\mathcal{P}}_{{\omega }_2}^{\left(0\right)}$ and ${\mathcal{P}}_{{\omega }_2}^{\left(1\right)}$.