Abstract
The computation of the time-varying matrix pseudoinverse has become crucial in recent years for solving time-varying problems in engineering and science domains. This paper investigates the issue of calculating the time-varying pseudoinverse based on full-rank decomposition (FRD) using the zeroing neural network (ZNN) method, which is currently considered to be a cutting edge method for calculating the time-varying matrix pseudoinverse. As a consequence, for the first time in the literature, a new ZNN model called ZNNFRDP is introduced for time-varying pseudoinversion and it is based on FRD. Five numerical experiments investigate and confirm that the ZNNFRDP model performs as well as, if not better than, other well-performing ZNN models in the calculation of the time-varying pseudoinverse. Additionally, theoretical analysis and numerical findings have both supported the effectiveness of the proposed model.
MSC:
65F20; 15A24; 68T05
1. Introduction
The real-time solution to the matrix pseudoinverse (or Moore-Penrose inverse), which commonly occurs in robotics [1], nonlinear systems [2], game theory [3], and other engineering and science domains [4,5,6], has garnered a great deal of attention in recent decades. When a matrix A is taken into consideration, the pseudoinverse is the generalization of the inverse matrix . For any matrix with entries that are real or complex numbers, the unique pseudoinverse is defined, and it is typically calculated using decomposition techniques, including the singular value decomposition, the QR decomposition, and the full-rank decomposition (FRD) [7,8]. To the best of our knowledge, these techniques typically targeted constant (or time-invariant) matrices. Nevertheless, real-time matrix pseudoinversion issues are frequently encountered. For instance, inverse kinematic issues for online control of redundant robot manipulators can be resolved through the online solution of the time-varying pseudoinverse [9,10]. It is significant to note that the zeroing neural network (ZNN) method effectively enables the real-time solution of the time-varying pseudoinverse using both direct and indirect methods, such as matrix decomposition. For instance, when computing the time-varying pseudoinverse, a ZNN model based on singular value decomposition performs better than a direct ZNN model [11], so it is beneficial to look into ZNN models based on various matrix decomposition techniques. Therefore, the subject of this paper is the calculation of the time-varying pseudoinverse of a given time-varying matrix, based on the FRD method and the ZNN method. Our approach, in particular, complies with the concepts of Propositions 1 and 2, where Proposition 1 is based on [12] (Theorem D.4 (Full rank decomposition)) and Proposition 2 is restated from [12] [Theorem D.5] (Full rank decomposition and pseudoinversion). It is worth mentioning that, for , the calculation and representation of several generalized inverses is closely related to the next Penrose equations:
while the pseudoinverse is the matrix X that satisfies all four Penrose equations. Additionally, the following basic symbols from the paper are noteworthy: implies the identity matrix; and imply the zero and all-ones matrices, respectively; implies the vectorization process; ⊗ implies the Kronecker product; implies the time derivative; implies the matrix Frobenius norm. Last, the notations sum(.), zeros(.), eye(.), reshape(.), mod(.) and floor(.) in the algorithms of this paper follow the standard MATLAB function concept [13].
Proposition 1.
Let be an arbitrary matrix of rank r, be the reduced row echelon form of A, and be a vector that indicates the pivot columns of A. A unique FRD is created from reduced row echelon form by setting the pivot columns of A in C, i.e., , and the non-zero rows of B in F, i.e., .
Proposition 2.
Let be an arbitrary matrix of rank r, and is the FRD of A, then:
Many different approaches for computing the pseudoinverse have been developed over the past few decades, including fast calculation algorithms [14] and error bounds techniques [15]. However, when used for large-scale scenarios, these serial computational techniques (such as iterative algorithms) are ineffective. As matrix size rises, the computing workload increases significantly [16,17]. Thus, to decrease computational complexity and boost computational efficiency, a model with parallel computing capabilities is recommended. As effective parallel computing tools, recurrent neural networks (RNNs) have recently been thoroughly studied and used to address a variety of problems, such as mobile object localization [18], robotic motion tracking [19] and portfolio selection [20,21]. Gradient (or Hopfield) neural networks (GNNs), which are typical RNNs, have been heavily used to solve the constant matrix pseudoinversion problem in real time [22,23]. However, because it is difficult or perhaps impossible for GNNs and these serial methods to take into account the derivative information of the relevant matrices, neither serial methods nor GNNs are useful in calculating the time-varying matrix pseudoinverse.
The ZNN, a unique RNN with strong parallel processing capabilities, was introduced by Zhang et al. [24] to address the aforementioned problems. When it comes to computing the time-varying pseudoinverse, the ZNN approach is currently thought to be state-of-the-art. In particular, ZNNs were initially created to trace the time-varying inverse of a matrix [24]. Nevertheless, later versions of them were dynamic models for computing the time-varying pseudoinverse of full-row/column rank matrices [25,26,27,28]. Subsequent evolution has led to the evolvent of a great number of models for computing various generalized inverses [11], including the Drazin inverse [29], the ML-weighted pseudoinverse [30], and outer inverses [31]. Along these, the ZNN method has been thoroughly investigated and employed to a broad variety of time-varying issues, with its main applications being the approximation of numerous matrix functions [32,33], problems involving quadratic optimization [10], and problems involving linear matrix equation systems [34,35]. To create ZNN dynamics, one must first define an error matrix, , for the subjacent issue. The dynamical evolution is applied in the following phase:
It is important to note that in (3) a design parameter is used to scale the convergence, and indicates the elementwise application of an increasing and odd activation function on the error matrix. In this work, we examine the ZNN evolution (3) by the linear activation function, leading to the next formula:
This paper proposes a ZNN model, dubbed ZNNFRDP, for the calculation of the time-varying pseudoinverse based on FRD.
These are the main contributions of this investigation:
- A new ZNN model, called ZNNFRDP, for the calculation of the time-varying pseudoinverse based on FRD is introduced and investigated. Keep in mind that ZNNFRDP stands for ZNN model based on FRD for the calculation of pseudoinverse.
- Theoretical analysis supported by five numerical experiments show that the ZNNFRDP model performs as well as, if not better than, other well-performing ZNN models in the computation of the time-varying pseudoinverse.
The remainder of the paper’s layout is comprised of Section 2, Section 3, Section 4 and Section 5. In particular, Section 2 defines and analyzes the ZNNFRDP model for computing the time-varying pseudoinverse, while Section 3 demonstrates and investigates the model’s computational effectiveness. The concluding observations and inferences are given in Section 5.
2. Materials and Methods
In this section, the ZNN model, termed ZNNFRDP, that computes the time-varying pseudoinverse based on FRD is introduced and analyzed. Assume that is a differentiable time-varying matrix of constant rank r. In order to guarantee that the ZNNFRDP model applies FRD, the unique FRD presented in Proposition 1 is employed. In particular, consider that is a vector that indicates the pivot columns of . Then, creating and as indicating in Proposition 1, and setting , and as indicating in proposition 2, the equations of the next group are satisfied in the case of pseudoinverse based on FRD:
The ZNNFRDP model takes into account determining the four unknowns and of (5). Notice that the elements below the major diagonal of are zeros since it is a partitioned matrix of the reduced row echelon form of . Additionally, and are symmetric invertible matrices because and are full rank matrices. It is significant to note that when is differentiable, and are also differentiable.
For zeroing (5), we set the next error matrix equations group (EMEG):
Furthermore, the first derivative of EMEG (6) is:
When from (4) is replaced with defined in (7) and the equation is solved in terms of , the result below is obtained:
As shown below, the techniques of Kronecker product and vectorization are used to simplify the dynamic model of (8):
To create a straightforward dynamical model that can quickly calculate the , , , and , (9) must be simplified even more. As a consequence, the Lemma 1 based on [36] regarding vectorization is presented.
Lemma 1.
For , let denote the matrix F vectorization. What follows holds:
where be a fixed permutation matrix depended solely by the number of rows r and columns n of matrix F.
The next Algorithm 1 shows an algorithmic process for computing the permutation matrix Q in (10) that refers to a matrix.
| Algorithm 1. Matrix Q calculation. |
Require: The number of columns n and rows r of matrix .
Ensure: The matrix Q. |
Moreover, since all the elements below the major diagonal of are zeros, just the elements of located in the major diagonal and above must be obtained. Therefore, it is significant to use a vector denoted to replace , by stacking these elements of into . The dimension of (9) is lessened in this way, while is forced to have all of its elements below the major diagonal zeros. Therefore, by using the elements on and above the major diagonal of , it is possible to obtain the following equation that replaces in (9):
where is an operational matrix which can be calculated applying the algorithmic procedure shown Algorithm 2. Further, the elements on and above the major diagonal of are piled to create the column vector .
| Algorithm 2. Matrix G calculation. |
Require: The number of columns n and rows r of matrix .
Ensure: The matrix G. |
Additionally, because and are symmetric matrices, we only have to obtain their elements that are placed on and above its major diagonal. Thus, it is significant to use vectors denoted by and in place of and , respectively, by stacking these elements of and into the vectors and , respectively. The dimension of (9) is lessened in this way, while and are forced to be symmetric matrices. Therefore, using the elements on and above the major diagonals of and , it is possible to obtain the following equations that replace and in (9):
where is an operational matrix which can be calculated applying the algorithmic procedure shown Algorithm 3. Further, the elements on and above the major diagonal of and are piled to create the column vectors .
Using the permutation matrix Q and the operational matrices G and R, (9) can be rewritten as follows:
Then, by setting
the ZNN model below, termed ZNNFRDP, is proposed for calculating the time-varying pseudoinverse based on FRD of an arbitrary input matrix :
which can be solved successfully in MATLAB using an ode solver. Note that , and , while is a non-singular mass matrix. In accordance with Theorem 1, the ZNNFRDP model (15) converges to the theoretical solution (TSol) of the time-varying pseudoinverse.
| Algorithm 3. Matrix R calculation. |
Require: A real symmetric matrix’s column or row number r.
Ensure: The matrix R. |
Theorem 1.
Let be a differentiable matrix of rank r and be a vector that contains the numbers of all pivot columns of . Starting from any initial price , the ZNNFRDP model (15) exponentially converges to the TSol at each time . Furthermore, the TSol of the time-varying pseudoinverse is the last elements of .
Proof.
The EMEG is declared as in (6) in order to determine the TSol of the time-varying pseudoinverse. The model (8) is developed using the linear ZNN design (4) for zeroing (6). When , every equation in the EMEG (8) converges to the TSol starting from any initial price, according to [24] [Theorem 1]. As a result, the ZNNFRDP model (15) also converges to the TSol starting from any initial price when since it is really an alternate version of (8). In accordance with (14), the TSol of the time-varying pseudoinverse is the last elements of . Therefore, the proof is finished. □
Additionally, diagram presentation can be used to describe the above-mentioned ZNNFRDP model process for real-time solution of the time-varying pseudoinverse of matrix . For the block diagram presentation, the dynamical Equation (15) can be transformed as follows:
and the corresponding block diagram of the ZNNFRDP model (16) is shown in Figure 1.
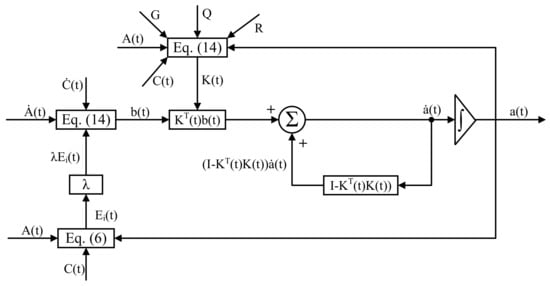
Figure 1.
Block diagram of the ZNNFRDP model for real-time solution of the time-varying pseudoinverse of matrix .
Lastly, the complexity of producing and solving (16) contributes to the ZNNFRDP model’s overall computational complexity. The computational complexity of producing (16) is operations since each iteration of the equation has multiplication and addition operations. Considering that a linear system of equations is solved at each step by an implicit solver such as ode15s, the complexity of solving (16) is because it involves a matrix. Therefore, the ZNNFRDP model’s overall computational complexity is .
3. Results
The performance of the ZNNFRDP (15) model in five numerical experiments (NEs), which involve calculating time-varying pseudoinverses of rank deficient matrices, is examined in this section. Furthermore, the ZNNFRDP model is compared to two additional ZNN models, namely ZNNP and ZNNSVDP, which are presented in [11]. It is worth mentioning that both the ZNNP and ZNNSVDP models calculate the pseudoinverse of an arbitrary matrix, with the ZNNSVDP model employing singular value decomposition to do so. With the exception of , where all-ones matrices have been set, the initial prices have been set to matrices with ones on the major diagonal and elsewhere zeros for and in all NEs. Furthermore, in the denotation of the input matrix, the functions and have been used. Last, the MATLAB solver ode15s is employed for the computations in all NEs within the time range and with the parameter . Because of this, all ZNN models find the real-time solution of the time-varying pseudoinverse of a given matrix starting at and ending at .
3.1. Experiment 1
Assume the following input matrix of rank 2 with :
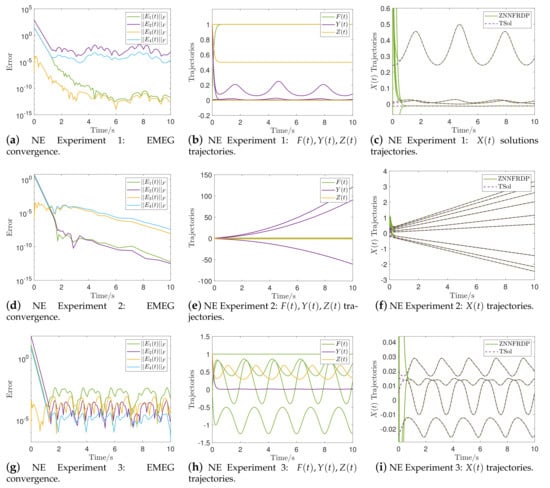
Figure 2.
EMEG convergence and solutions’ trajectories of the ZNNFRDMP model in NEs in Section 3.1–Section 3.3.
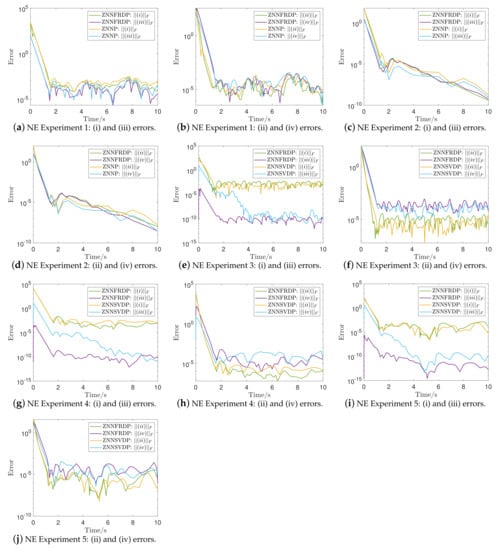
Figure 3.
MP equations (i)–(iv) errors of the ZNNFRDMP, ZNNSVDMP and ZNNP models solutions in NEs in Section 3.1–Section 3.5.
3.2. Experiment 2
Assume the following input matrix of rank 3 with :
3.3. Experiment 3
Assume the following input matrix of rank 1 with :
3.4. Experiment 4
Assume the following input matrix of rank 1 with , and :
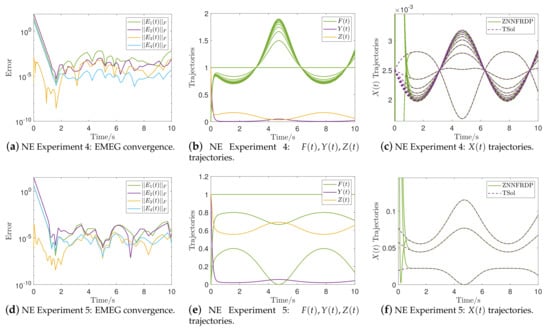
Figure 4.
EMEG convergence and solutions’ trajectories of the ZNNFRDMP model in NEs in Section 3.4–Section 3.5.
3.5. Experiment 5
Assume the following input matrix of rank 2 with :
4. Discussion
This section first presents the performance of the ZNNFRDP model for computing time-varying pseudoinverses before comparing it to the performance of the ZNNP and ZNNSVDP models.
The performance of the ZNNFRDP model for computing time-varying pseudoinverses is investigated through NEs in Section 3.1–Section 3.5, with the results shown in Figure 2 and Figure 4. Particularly, the EMEG convergence in NEs in Section 3.1–Section 3.5 is measured by the Frobenius norm in Figure 2a,d,g and Figure 4a,d, respectively. These figures demonstrate how the EMEG’s begin at with a high error value above and converge before in a low error value in the range of . As opposed to this, the EMEG’s always begins at with a low error value under and converges before in an even lower error value in the range of . That is, the EMEG starts from a non-optimal initial price and converges to the zero matrix finally. The trajectories of and in NEs in Section 3.1–Section 3.5 are shown in Figure 2b,e,h and Figure 4b,e, respectively, while the trajectories of are shown in Figure 2c,f,i and Figure 4c,f, respectively. All of these images show that while the trajectories of match those of the TSol, a certain pattern appears in the trajectories of and before .
In general, employing the FRD to compute the pseudoinverse as suggested in (2) will increase rounding errors and result in a loss of precision when using conventional computational methods. However, our study uses the ZNN method, which is considerably different from the conventional computational methods. In fact, for example, we are not calculating the inverse of any matrix by using conventional textbook methods. Numerous papers and books (written in the last two decades) on the ZNN method demonstrate how effective the ZNN design is in attempting to zero out rounding errors by defining an appropriate EMEG (see (6)). It is important to mention that a rounding error is the difference between a rounded-off numerical value and the actual value. Considering that the EMEG’s actual solution is the zero matrix, any EMEG’s element that is not zero during the computations is regarded as a rounding error. As a result, the actual task of the ZNN method is to zero the rounding errors.
It is important to note that the steady-state errors in Figure 2 and Figure 3 are of order in the majority of situations because double precision arithmetic () is used by default in MATLAB. Keep in mind that the symbol stands for the machine epsilon, an upper bound on the relative approximation error brought on by rounding in floating point arithmetic. Therefore, in order to achieve lower steady-state errors, a higher error tolerance in ode15s must be chosen. Furthermore, the time of convergence, which in the NEs is close to , and the value of are correlated. To decrease the time of convergence, a larger value of must be chosen [24]. Therefore, the major factor used to rate the ZNN models’ overall performance is the their convergence performance under the same value of .
The performance of the ZNNFRDP, ZNNP and ZNNSVDP models is compared by measuring the errors caused in the Moore-Penrose equations (i)–(iv) from (1) through NEs in Section 3.1–Section 3.5, with the results shown in Figure 3. Particularly, the performance of the ZNNFRDP and ZNNP models is compared through NEs in Section 3.1 and Section 3.2. The results of the ZNNFRDP and ZNNP models are shown in Figure 3a,b, where we observe that in NE in Section 3.1, the errors caused in the Moore-Penrose equations (i)–(iii) and (ii)–(iv), respectively, are shown in Figure 3a,b. These figures demonstrate how these errors begin at with a high value above and converge before in a low error value in the range of . The overall performance of the ZNNFRDP model in NE in Section 3.1 is almost identical to that of the ZNNP. In NE in Section 3.2, the errors caused in the Moore-Penrose equations (i)–(iii) and (ii)–(iv), respectively, are shown in Figure 3c,d. These figures demonstrate how these errors begin at with a high value above and converge before in a low error value in the range of . The convergence performance of the ZNNFRDP model in NE in Section 3.2 is slightly better than that of the ZNNP, while their overall performances are almost identical. As a result, the ZNNFRDP model performed slightly better than the ZNNP in NEs in Section 3.1 and Section 3.2.
Additionally, the performance of the ZNNFRDP and ZNNSVDP models is compared through NEs in Section 3.3–Section 3.5. It is important to note that NE in Section 3.4 compares the performances of these models in a high-dimensional input matrix with dimensions , whereas NE in Section 3.5 compares their performance in an ill-conditioned input matrix. In NE in Section 3.3, the errors caused in the Moore-Penrose equations (i)–(iii) and (ii)–(iv), respectively, are shown in Figure 3e,f. These figures demonstrate how the errors caused in the Moore-Penrose equations (i), (ii) and (iv) begin at with a high value above and converge before in a low error value in the range of , whereas the error caused in the Moore-Penrose Equation (i) begins at with a lower value and converges before in a lower error value in the range of . The convergence performance of the ZNNFRDP model in NE in Section 3.3 is slightly better than that of the ZNNSVDP, while their overall performances are close. In NEs in Section 3.4 and Section 3.5, the errors caused in the Moore-Penrose equations (i)–(iii), respectively, are shown in Figure 3a,b, while the errors caused in the Moore-Penrose equations (ii)–(iv), respectively, are shown in Figure 3a,b. These figures demonstrate how the errors caused in the Moore-Penrose equations (ii) and (iv) begin at with a high value above and converge before in a low error value in the range of , where the convergence performance of the ZNNFRDP model is slightly worse than that of the ZNNSVDP, while the overall performance of the ZNNFRDP model is slightly better than that of the ZNNSVDP. The error caused in the Moore-Penrose Equation (i) begin at with a lower value and converge before in a lower error value in the range of . The convergence and the overall performance of the ZNNFRDP models are almost identical. The error caused in the Moore-Penrose Equation (iii) begin at with a lower value and converge before in a lower error value in the range of . The convergence and the overall performance of the ZNNFRDP model are much better than that of the ZNNSVDP. As a result, the ZNNFRDP model performed better than the ZNNSVDP in NEs in Section 3.3–Section 3.5.
Finally, it was demonstrated in Section 2 that the ZNNFRDP model has an overall computational complexity of , whereas [11] claims that the ZNNP model has an overall computational complexity of and the ZNNSVDP model has an overall computational complexity of . Therefore, the ZNNFRDP model has a lower overall computational complexity than the ZNNSVDP model, which is an advantage, but a higher overall computational complexity than the ZNNP model, which is a disadvantage.
To summarize, the following can be deduced from this section’s NEs:
- The convergence of the ZNNFRDP model starts from a non-optimal initial price and converge in a small period of time to the zero matrix.
- The errors caused in the Moore-Penrose equations (i)–(iv) and the and solutions trajectories act consistently due to the EMEGs’ proclivity toward convergence.
- The EMEGs will converge more quickly when the price of the design parameter is greater.
- The ZNNFRDP model performs as well as, if not better than, the ZNNP and ZNNSVDP models.
- In essence, the time-varying pseudoinverses are calculated with exceptional and efficient performance by the ZNNFRDP model.
5. Conclusions
In this paper, the issue of calculating the time-varying pseudoinverse based on FRD using the ZNN method was examined. Therefore, a novel ZNN model called ZNNFRDP that uses the FRD to compute the time-varying pseudoinverse was proposed and explored in this research. Five NEs show that the ZNNFRDP model’s EMEG has a tendency to converge exponentially to the zero matrix after beginning from a non-optimal initial price. Additionally, they show that the ZNNFRDP model performs as well as, if not better than, other well-performing ZNN models in the computation of the time-varying pseudoinverse. Thus, theoretical analysis and numerical results both supported the effectiveness of the proposed model.
The list below includes some possible research topics.
- To hasten the convergence of the ZNN dynamics, nonlinear activation functions [37,38] may be used.
- It may be possible to use ZNN designs with terminal convergence [39,40] to produce new improved ZNNFRDP models.
Author Contributions
All authors (H.A., H.J., M.K., R.A., T.E.S., S.D.M. and V.N.K.) contributed equally. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Research Deanship of Hail University-KSA Project Number (RG -21 127).
Data Availability Statement
Not applicable.
Acknowledgments
Authors acknowledge the Research Deanship of Hail University-KSA for the administrative, financial, and technical support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, S.; Dong, Y.; Ouyang, Y.; Yin, Z.; Peng, K. Adaptive neural control for robotic manipulators with output constraints and uncertainties. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5554–5564. [Google Scholar] [CrossRef] [PubMed]
- Mourtas, S.; Katsikis, V.; Kasimis, C. Feedback control systems stabilization using a bio-inspired neural network. EAI Endorsed Trans. AI Robot. 2022, 1, 1–13. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, Z.; Guo, L. Event-triggered strategy design for discrete-time nonlinear quadratic games with disturbance compensations: The noncooperative case. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 1885–1896. [Google Scholar] [CrossRef]
- Yang, X.; He, H. Self-learning robust optimal control for continuous-time nonlinear systems with mismatched disturbances. Neural Netw. 2018, 99, 19–30. [Google Scholar] [CrossRef] [PubMed]
- Mourtas, S.D. A weights direct determination neuronet for time-series with applications in the industrial indices of the federal reserve bank of St. Louis. J. Forecast. 2022, 14, 1512–1524. [Google Scholar] [CrossRef]
- Li, S.; He, J.; Li, Y.; Rafique, M.U. Distributed recurrent neural networks for cooperative control of manipulators: A game-theoretic perspective. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 415–426. [Google Scholar] [CrossRef]
- Ben-Israel, A.; Greville, T.N.E. Generalized Inverses: Theory and Applications, 2nd ed.; CMS Books in Mathematics; Springer: New York, NY, USA, 2003. [Google Scholar] [CrossRef]
- Wang, G.; Wei, Y.; Qiao, S.; Lin, P.; Chen, Y. Generalized Inverses: Theory and Computations; Springer: Singapore, 2018; Volume 53. [Google Scholar]
- Tan, N.; Yu, P.; Ni, F. New varying-parameter recursive neural networks for model-free kinematic control of redundant manipulators with limited measurements. IEEE Trans. Instrum. Meas. 2022, 71, 3161713. [Google Scholar] [CrossRef]
- Zhong, N.; Huang, Q.; Yang, S.; Ouyang, F.; Zhang, Z. A varying-parameter recurrent neural network combined with penalty function for solving constrained multi-criteria optimization scheme for redundant robot manipulators. IEEE Access 2021, 9, 50810–50818. [Google Scholar] [CrossRef]
- Kornilova, M.; Kovalnogov, V.; Fedorov, R.; Zamaleev, M.; Katsikis, V.N.; Mourtas, S.D.; Simos, T.E. Zeroing neural network for pseudoinversion of an arbitrary time-varying matrix based on singular value decomposition. Mathematics 2022, 10, 1208. [Google Scholar] [CrossRef]
- Aleskerov, F.; Ersel, H.; Piontkovski, D. Linear Algebra for Economists; Springer Texts in Business and Economics; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Gupta, A.K. Numerical Methods Using MATLAB; MATLAB solutions series; Apress: Berkeley, CA, USA, 2014. [Google Scholar]
- Katsikis, V.N.; Pappas, D.; Petralias, A. An improved method for the computation of the Moore–Penrose inverse matrix. Appl. Math. Comput. 2011, 217, 9828–9834. [Google Scholar] [CrossRef]
- Stanimirović, P.S.; Roy, F.; Gupta, D.K.; Srivastava, S. Computing the Moore-Penrose inverse using its error bounds. Appl. Math. Comput. 2020, 371, 124957. [Google Scholar] [CrossRef]
- Leithead, W.E.; Zhang, Y. O(N2)-operation approximation of covariance matrix inverse in Gaussian process regression based on quasi-Newton BFGS method. Commun. Stat. Simul. Comput. 2007, 36, 367–380. [Google Scholar] [CrossRef]
- Zhang, Z.; Lu, Y.; Zheng, L.; Li, S.; Yu, Z.; Li, Y. A new varying-parameter convergent-differential neural-network for solving time-varying convex QP problem constrained by linear-equality. IEEE Trans. Autom. Control 2018, 63, 4110–4125. [Google Scholar] [CrossRef]
- Simos, T.E.; Katsikis, V.N.; Mourtas, S.D.; Stanimirović, P.S.; Gerontitis, D. A higher-order zeroing neural network for pseudoinversion of an arbitrary time-varying matrix with applications to mobile object localization. Inf. Sci. 2022, 600, 226–238. [Google Scholar] [CrossRef]
- Zhang, Z.; Zheng, L.; Yu, J.; Li, Y.; Yu, Z. Three recurrent neural networks and three numerical methods for solving a repetitive motion planning scheme of redundant robot manipulators. IEEE/ASME Trans. Mechatron. 2017, 22, 1423–1434. [Google Scholar] [CrossRef]
- Katsikis, V.N.; Mourtas, S.D.; Stanimirović, P.S.; Li, S.; Cao, X. Time-varying mean-variance portfolio selection problem solving via LVI-PDNN. Comput. Oper. Res. 2022, 138, 105582. [Google Scholar] [CrossRef]
- Bai, L.; Zheng, K.; Wang, Z.; Liu, J. Service provider portfolio selection for project management using a BP neural network. Ann. Oper. Res. 2022, 308, 41–62. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, D.; Li, Z. Common nature of learning between back-propagation and Hopfield-type neural networks for generalized matrix inversion with simplified models. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 579–592. [Google Scholar] [CrossRef]
- Lv, X.; Xiao, L.; Tan, Z.; Yang, Z.; Yuan, J. Improved gradient neural networks for solving Moore–Penrose inverse of full-rank matrix. Neural Process. Lett. 2019, 50, 1993–2005. [Google Scholar] [CrossRef]
- Zhang, Y.; Ge, S.S. Design and analysis of a general recurrent neural network model for time-varying matrix inversion. IEEE Trans. Neural Netw. 2005, 16, 1477–1490. [Google Scholar] [CrossRef]
- Chai, Y.; Li, H.; Qiao, D.; Qin, S.; Feng, J. A neural network for Moore-Penrose inverse of time-varying complex-valued matrices. Int. J. Comput. Intell. Syst. 2020, 13, 663–671. [Google Scholar] [CrossRef]
- Sun, Z.; Li, F.; Jin, L.; Shi, T.; Liu, K. Noise-tolerant neural algorithm for online solving time-varying full-rank matrix Moore-Penrose inverse problems: A control-theoretic approach. Neurocomputing 2020, 413, 158–172. [Google Scholar] [CrossRef]
- Wu, W.; Zheng, B. Improved recurrent neural networks for solving Moore-Penrose inverse of real-time full-rank matrix. Neurocomputing 2020, 418, 221–231. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Y.; Tan, N.; Cai, B. Zhang neural network solving for time-varying full-rank matrix Moore-Penrose inverse. Computing 2011, 92, 97–121. [Google Scholar] [CrossRef]
- Qiao, S.; Wang, X.Z.; Wei, Y. Two finite-time convergent Zhang neural network models for time-varying complex matrix Drazin inverse. Linear Algebra Its Appl. 2018, 542, 101–117. [Google Scholar] [CrossRef]
- Qiao, S.; Wei, Y.; Zhang, X. Computing time-varying ML-weighted pseudoinverse by the Zhang neural networks. Numer. Funct. Anal. Optim. 2020, 41, 1672–1693. [Google Scholar] [CrossRef]
- Wang, X.; Stanimirovic, P.S.; Wei, Y. Complex ZFs for computing time-varying complex outer inverses. Neurocomputing 2018, 275, 983–1001. [Google Scholar] [CrossRef]
- Zhang, H.; Wan, L. Zeroing neural network methods for solving the Yang-Baxter-like matrix equation. Neurocomputing 2020, 383, 409–418. [Google Scholar] [CrossRef]
- Dai, J.; Yang, X.; Xiao, L.; Jia, L.; Liu, X.; Wang, Y. Design and analysis of a self-adaptive zeroing neural network for solving time-varying quadratic programming. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–10. [Google Scholar] [CrossRef]
- Dai, J.; Tan, P.; Yang, X.; Xiao, L.; Jia, L.; He, Y. A fuzzy adaptive zeroing neural network with superior finite-time convergence for solving time-variant linear matrix equations. Knowl.-Based Syst. 2022, 242, 108405. [Google Scholar] [CrossRef]
- Xiao, L.; Tan, H.; Dai, J.; Jia, L.; Tang, W. High-order error function designs to compute time-varying linear matrix equations. Inf. Sci. 2021, 576, 173–186. [Google Scholar] [CrossRef]
- Graham, A. Kronecker Products and Matrix Calculus with Applications; Courier Dover Publications: Mineola, NY, USA, 2018. [Google Scholar]
- Liao, B.; Zhang, Y. From different ZFs to different ZNN models accelerated via Li activation functions to finite-time convergence for time-varying matrix pseudoinversion. Neurocomputing 2014, 133, 512–522. [Google Scholar] [CrossRef]
- Wang, X.Z.; Ma, H.; Stanimirović, P.S. Nonlinearly activated recurrent neural network for computing the Drazin inverse. Neural Process. Lett. 2017, 46, 195. [Google Scholar] [CrossRef]
- Xiao, L. A finite-time convergent neural dynamics for online solution of time-varying linear complex matrix equation. Neurocomputing 2015, 167, 254–259. [Google Scholar] [CrossRef]
- Xiao, L. A nonlinearly-activated neurodynamic model and its finite-time solution to equality-constrained quadratic optimization with nonstationary coefficients. Appl. Soft Comput. 2016, 40, 252–259. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).