Subgradient Extra-Gradient Algorithm for Pseudomonotone Equilibrium Problems and Fixed-Point Problems of Bregman Relatively Nonexpansive Mappings
Abstract
1. Introduction
- (i)
- and
- (ii)
- or
2. Materials and Methods
- (i)
- is empty when ,
- (ii)
- is not in general empty when ,
- (iii)
- is nonempty when ; precisely, .
- (L1) and subdifferential is single valued on its domain,
- (L2) and is single valued on its domain.
- (i)
- The vector is the Bregman projection of x onto C concerning
- (ii)
- The vector is the unique solution of the variational inequality
- (iii)
- The vector is the unique solution of the inequality
- (i)
- f is uniformly smooth on boundedsubsets of X and bounded on bounded subsets.
- (ii)
- f is Fréchet differentiable and is uniformlynorm-to-norm continuous on bounded subsets of X.
- (iii)
- is super coercive and uniformly convex on bounded subsets of .
- (i)
- f is super coercive and uniformly convex on bounded subsets of X.
- (ii)
- is bounded on bounded subsets anduniformly smooth on bounded subsets of .
- (iii)
- is Fréchet differentiable and is uniformly norm-to-norm continuous on bounded subsets of .
- g is monotone on C, that is
- g is Pseudomonotone on C; that is,
- g is Bregman - strongly Pseudomonotone on C if there exists a constant such that
- g is Bregman–Lipschitz-type continuous on C; that is, there exist two positive constants such that
- (i)
- S is called Bregman quasinonexpansive if for all .
- (ii)
- S is called Bregman relatively nonexpansive if S is Bregman quasinonexpansive and .
- g is Pseudomonotone on C.
- g is Bregman–Lipschitz-type continuous on C.
- is convex, lower semicontinuous and subdifferentiable on X for every fixed .
- g is jointly weakly continuous on in the sense that, if and converge weakly to , respectively, then as .
- (i)
- and
- (ii)
- or
3. Main Results
| Algorithm 1 Subgradient extra-gradient algorithm |
|
4. Application
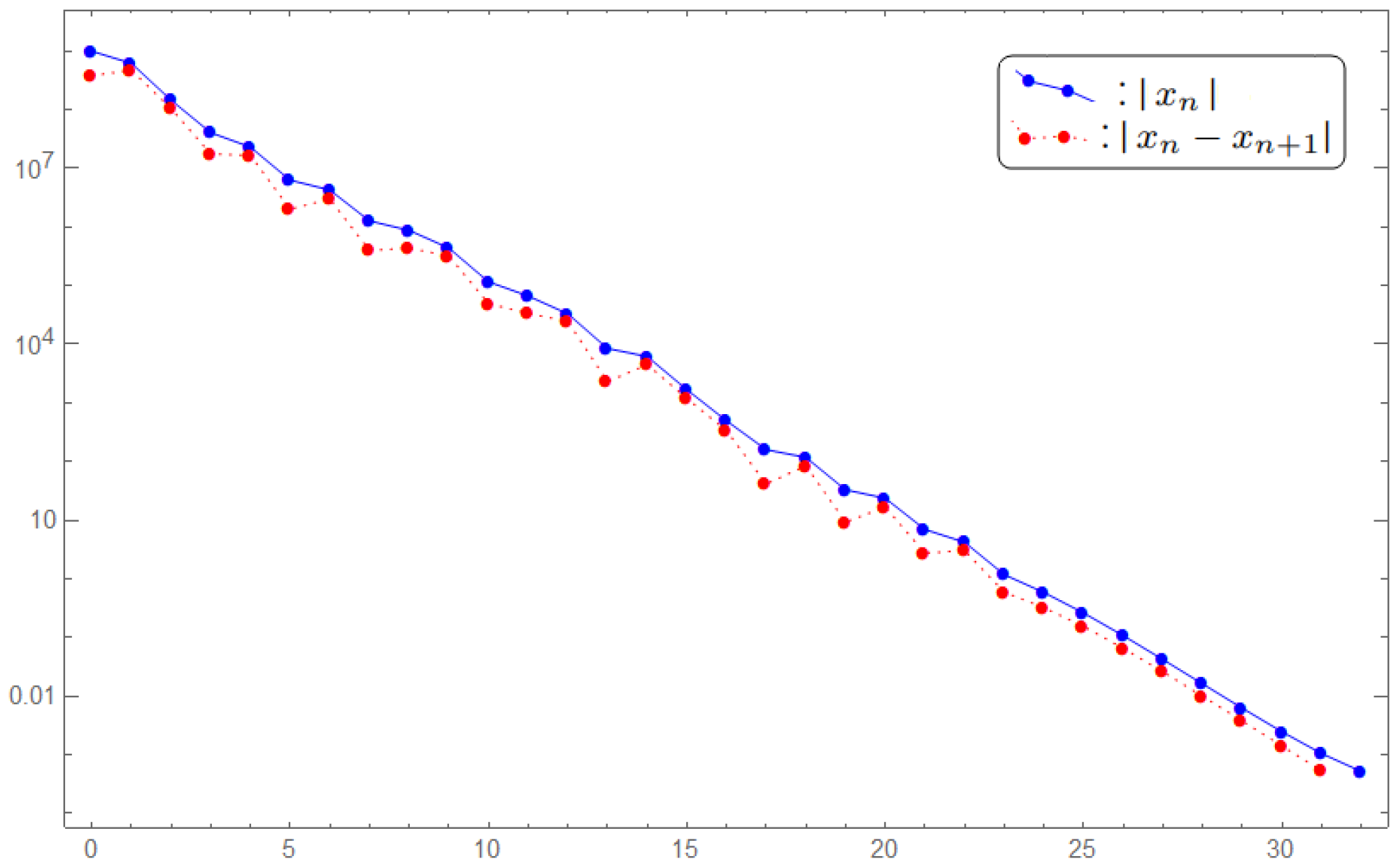
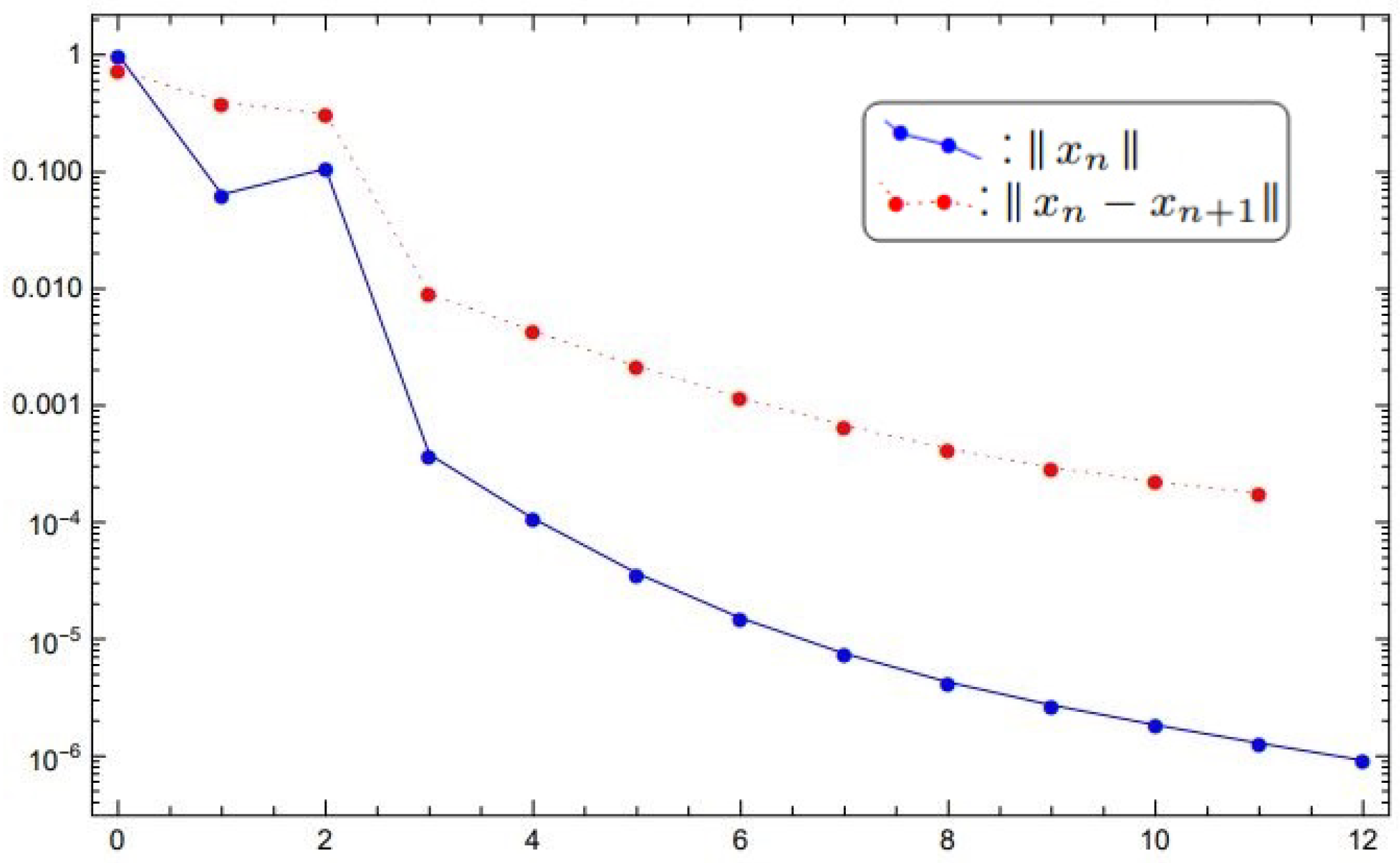
5. Numerical Experiment
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Blum, E.; Oettli, W. From optimization and variational inequalities to equilibrium problems. Math. Stud. 1994, 63, 123–145. [Google Scholar]
- Kim, J.K.; Majee, P. Modified Krasnoselski Mann iterative method for hierarchical fixed point problem and split mixed equilibrium problem. J. Ineq. Appl. 2020, 2020, 227. [Google Scholar] [CrossRef]
- Kim, J.K.; Salahuddin. Existence of solutions for multi-valued equilibrium problems. Nonlinear Funct. Anal. Appl. 2018, 23, 779–795. [Google Scholar]
- Muangchoo, K. A new explicit extragradient method for solving equilibrium problems with convex constraints. Nonlinear Funct. Anal. Appl. 2022, 27, 1–22. [Google Scholar]
- Iusem, A.N.; Sosa, W. Iterative algorithms for equilibrium problems. Optimization 2003, 52, 301–316. [Google Scholar] [CrossRef]
- Kassay, G.; Reich, S.; Sabach, S. Iterative methods for solving systems of variational inequalities in reflexive Banach spaces. SIAM J. Optim. 2011, 21, 1319–1344. [Google Scholar] [CrossRef]
- Reich, S.; Sabach, S. Two strong convergence theorems for Bregman strongly nonexpansive operators in reflexive Banach spaces. Nonlinear Anal. 2010, 73, 122–135. [Google Scholar] [CrossRef]
- Reich, S.; Sabach, S. A projection method for solving nonlinear problems in reflexive Banach spaces. J. Fixed Point Theory Appl. 2011, 9, 101–116. [Google Scholar] [CrossRef]
- Takahashi, W.; Zembayashi, K. Strong convergence theorem by a new hybrid method for equilibrium problems and relatively nonexpansive mappings. Fixed Point Theory Appl. 2008, 2008, 528476. [Google Scholar] [CrossRef]
- Takahashi, W.; Zembayashi, K. Strong and weak convergence theorems for equilibrium problems and relatively nonexpansive mappings in Banach spaces. Nonlinear Anal. 2009, 70, 45–57. [Google Scholar] [CrossRef]
- Dadashi, V.; Iyiola, O.S.; Shehu, Y. The subgradient extragradient method for pseudomonotone equilibrium problems. Optimization 2020, 69, 901–923. [Google Scholar] [CrossRef]
- Anh, P.N. A hybrid extragradient method extended to fixed point problems and equilibrium problems. Optimization 2013, 62, 271–283. [Google Scholar] [CrossRef]
- Joshi, M.; Tomar, A. On unique and nonunique fixed points in metric spaces and application to chemical sciences. J. Funct. Spaces 2021, 2021, 5525472. [Google Scholar] [CrossRef]
- Ozgur, N.Y.; Tas, N. Some fixed-circle theorems on metric spaces. Bull. Malays. Math. Sci. Soc. 2019, 42, 1433–1449. [Google Scholar] [CrossRef]
- Tomar, A.; Joshi, M.; Padaliya, S.K. Fixed point to fixed circle and activation function in partial metric space. J. Appl. Anal. 2022, 28, 57–66. [Google Scholar] [CrossRef]
- Anh, P.N. Strong convergence theorems for nonexpansive mappings and Ky Fan inequalities. J. Optim. Theory Appl. 2012, 154, 303–320. [Google Scholar] [CrossRef]
- Anh, P.N.; Kim, J.K.; Hien, N.D.; Hong, N.V. Strong convergence of inertial hybrid subgradient methods for solving equilibrium problems in Hilbert spaces. J. Nonlinear Convex Anal. 2023, 24, 499–514. [Google Scholar]
- Anh, P.N.; Thach, H.T.C.; Kim, J.K. Proximal-like subgradient methods for solving multi-valued variational inequalities. Nonlinear Funct. Anal. Appl. 2020, 25, 437–451. [Google Scholar]
- Eskandani, G.Z.; Raeisi, M.; Rassias, T.M. A Hybrid extragradient method for pseudomonotone equilibrium problems by using Bregman distance. Fixed Point Theory Appl. 2018, 27, 120–132. [Google Scholar] [CrossRef]
- Wairojjana, N.; Pakkaranang, N. Halpern Tseng’s Extragradient Methods for Solving Variational Inequalities Involving Semistrictly Quasimonotone Operator. Nonlinear Funct. Anal. Appl. 2022, 27, 121–140. [Google Scholar]
- Wairojjana, N.; Pholasa, N.; Pakkaranang, N. On Strong Convergence Theorems for a Viscosity-type Tseng’s Extragradient Methods Solving Quasimonotone Variational Inequalities. Nonlinear Funct. Anal. Appl. 2022, 27, 381–403. [Google Scholar]
- Yang, J.; Liu, H. The subgradient extragradient method extended to pseudomonotone equilibrium problems and fixed point problems in Hilbert space. Optimi. Lett. 2020, 14, 1803–1816. [Google Scholar] [CrossRef]
- Bonnans, J.F.; Shapiro, A. Perturbation Analysis of Optimization Problems; Springer: New York, NY, USA, 2000. [Google Scholar]
- Bauschke, H.H.; Borwein, J.M.; Combettes, P.L. Essential smoothness, essential strict convexity, and Legendre functions in Banach spaces. Commun. Contemp. Math. 2001, 3, 615–647. [Google Scholar] [CrossRef]
- Abass, H.A.; Narain, O.K.; Onifade, O.M. Inertial extrapolation method for solving systems of monotone variational inclusion and fixed point problems using Bregman distance approach. Nonlinear Funct. Anal. Appl. 2023, 28, 497–520. [Google Scholar]
- Bauschke, H.H.; Borwein, J.M.; Combettes, P.L. Bregman monotone optimization algorithms. SIAM J. Control Optim. 2003, 42, 596–636. [Google Scholar] [CrossRef]
- Butnariu, D.; Censor, Y.; Reich, S. Iterative averaging of entropic projections for solving stochastic convex feasibility problems. Comput. Optim. Appl. 1997, 8, 21–39. [Google Scholar] [CrossRef]
- Butnariu, D.; Iusem, A.N. Totally Convex Functions for Fixed Points Computation and Infinite Dimensional Optimization; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Kim, J.K.; Tuyen, T.M. A parallel iterative method for a finite family of Bregman strongly nonexpansive mappings in reflexive Banach spaces. J. Korean Math. Soc. 2020, 57, 617–640. [Google Scholar]
- Lotfikar, R.; Zamani Eskandani, G.; Kim, J.K. The subgradient extragradient method for solving monotone bilevel equilibrium problems using Bregman distance. Nonlinear Funct. Anal. Appl. 2023, 28, 337–363. [Google Scholar]
- Reem, D.; Reich, S.; De Pierro, A. Re-examination of Bregman functions and new properties of their divergences. Optimization 2019, 68, 279–348. [Google Scholar] [CrossRef]
- Reich, S.; Sabach, S. A strong convergence theorem for a proximal-type algorithm in reflexive Banach spaces. J. Nonlinear Convex Anal. 2009, 10, 471–485. [Google Scholar]
- Butnariu, D.; Resmerita, E. Bregman distances, totally convex functions and a method for solving operator equations in Banach spaces. Abstr. Appl. Anal. 2006, 2006, 084919. [Google Scholar] [CrossRef]
- Sabach, S. Products of finitely many resolvents of maximal monotone mappings in reflexive banach spaces. SIAM J. Optim. 2011, 21, 1289–1308. [Google Scholar] [CrossRef]
- Bregman, L.M. A relaxation method for finding the common point of convex sets and its application to the solution of problems in convex programming. USSR Comput. Math. Math. Phys. 1967, 7, 200–217. [Google Scholar] [CrossRef]
- Alber, Y.I. Metric and generalized projection operators in Banach spaces: Properties and applications. In Theory and Applications of Nonlinear Operators of Accretive and Monotone Type; Kartsatos, A.G., Ed.; Lecture notes in pure and applied mathematics; Dekker: New York, NY, USA, 1996; Volume 178, pp. 15–50. [Google Scholar]
- Censor, Y.; Lent, A. An iterative row-action method for interval convex programming. J. Optim. Theory Appl. 1981, 34, 321–353. [Google Scholar] [CrossRef]
- Kohsaka, F.; Takahashi, W. Proximal point algorithm with Bregman functions in Banach spaces. J. Nonlinear Convex Anal. 2005, 6, 505–523. [Google Scholar]
- Phelps, R.P. Convex Functions, Monotone Operators and Differentiability, 2nd ed.; Lecture Notes in Mathematics; Springer: Berlin, Germany, 1993; Volume 1364. [Google Scholar]
- Zălinescu, C. Convex Analysis in General Vector Spaces; World Scientific Publishing: Singapore, 2002. [Google Scholar]
- Naraghirad, E.; Yao, J.C. Bregman weak relatively nonexpansive mappings in Banach spaces. Fixed Point Theory Appl. 2013, 2013, 141. [Google Scholar] [CrossRef]
- Butnariu, D.; Iusem, A.N.; Zălinescu, C. On uniform convexity, total convexity and convergence of the proximal point and outer Bregman projection algorithms in Banach spaces. J. Convex Anal. 2003, 10, 35–61. [Google Scholar]
- Tiel, J.V. Convex Analysis: An Introductory Text; Wiley: Chichester, UK; New York, NY, USA, 1984. [Google Scholar]
- Cioranescu, I. Geometry of Banach Spaces, Duality Mappings and Nonlinear Problems; Kluwer Academic: Dordrecht, The Netherlands, 1990. [Google Scholar]
- Reich, S. A weak convergence theorem for the alternating method with Bregman distances. In Theory and Applications of Nonlinear Operators; Marcel Dekker: New York, NY, USA, 1996; pp. 313–318. [Google Scholar]
- Butnariu, D.; Reich, S.; Zaslavski, A.J. Asymptotic behavior of relatively nonexpansive operators in Banach spaces. J. Appl. Anal. 2001, 7, 151–174. [Google Scholar] [CrossRef]
- Shahzad, N.; Zegeye, H. Convergence theorem for common fixed points of a finite family of multi-valued Bregman relatively nonexpansive mappings. Fixed Point Theory Appl. 2014, 2014, 152. [Google Scholar] [CrossRef][Green Version]
- Xu, H.K. Another control condition in an iterative method for nonexpansive mappings. Bullet. Austral. Math. Soc. 2002, 65, 109–113. [Google Scholar] [CrossRef]
- Maingé, P.E. Strong convergence of projected subgradient methods for nonsmooth and nonstrictly convex minimization. Set-Valued Anal. 2008, 16, 899–912. [Google Scholar] [CrossRef]
- Ambrosetti, A.; Prodi, G. A Primer of Nonlinear Analysis; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Schöpfer, F.; Schuster, T.; Louis, A.K. An iterative regularization method for the solution of the split feasibility problem in Banach spaces. Inverse Probl. 2008, 24, 055008. [Google Scholar] [CrossRef]
- Shehu, Y.; Dong, Q.; Jiang, D. Single projection method for pseudo-monotone variational inequality in Hilbert spaces. Optimization 2018, 68, 385–409. [Google Scholar] [CrossRef]
- Hieu, D.V.; Muu, L.D.; Anh, P.K. Parallel hybrid extragradient methods for pseudmonotone equilibrium problems and nonexpansive mappings. Numer. Algor. 2016, 73, 197–217. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lotfikar, R.; Eskandani, G.Z.; Kim, J.-K.; Rassias, M.T. Subgradient Extra-Gradient Algorithm for Pseudomonotone Equilibrium Problems and Fixed-Point Problems of Bregman Relatively Nonexpansive Mappings. Mathematics 2023, 11, 4821. https://doi.org/10.3390/math11234821
Lotfikar R, Eskandani GZ, Kim J-K, Rassias MT. Subgradient Extra-Gradient Algorithm for Pseudomonotone Equilibrium Problems and Fixed-Point Problems of Bregman Relatively Nonexpansive Mappings. Mathematics. 2023; 11(23):4821. https://doi.org/10.3390/math11234821
Chicago/Turabian StyleLotfikar, Roushanak, Gholamreza Zamani Eskandani, Jong-Kyu Kim, and Michael Th. Rassias. 2023. "Subgradient Extra-Gradient Algorithm for Pseudomonotone Equilibrium Problems and Fixed-Point Problems of Bregman Relatively Nonexpansive Mappings" Mathematics 11, no. 23: 4821. https://doi.org/10.3390/math11234821
APA StyleLotfikar, R., Eskandani, G. Z., Kim, J.-K., & Rassias, M. T. (2023). Subgradient Extra-Gradient Algorithm for Pseudomonotone Equilibrium Problems and Fixed-Point Problems of Bregman Relatively Nonexpansive Mappings. Mathematics, 11(23), 4821. https://doi.org/10.3390/math11234821




