Torsion Elements and Torsionable Hypermodules

Abstract

This article is motivated by the recently published studies on divisible hypermodules and falls in the area of hypercompositional algebra. In particular, it focuses on the torsion elements in Krasner hypermodules. First, we define the concept of a torsion element over a hypermodule, and based on it, we introduce a new class of hypermodules, namely the torsionable hypermodule. After investigating some of their fundamental properties, we will show that the class of torsionable hypermodules is a subclass of the class of divisible hypermodules. Finally, we present the relationships between divisible, torsionable, and normal injective hypermodules.

1. Introduction

In this article, we have aimed to see how the result of normal injective hypermodules may be used in the context of hypercompositional algebra by means of special elements called torsion and torsionable elements. The possibility of the use of normal injective and projective hypermodules in this way was opened up by the fundamental works of [1,2,3]. It is extremely tempting these days to do everything in an Abelian category instead of the category of hypermodules, and indeed, most of the results done in this article fit in the Abelian category. We have tried to use categorical methods where we could.

Our subject is torsion elements and torsionable hypermodule and their relationships with divisible and injective hypermodules. Therefore, we must assume the reader to be familiar already with the notion of a hypermodule. Krasner in [4] introduced the notion of hyperring and hypermodule over a hyperring, which is known as Krasner hyperrings and Krasner hypermodules in 1956. Unless we state explicitly, we shall assume that our hypermodules are Krasner hypermodules. There are also other types of hyperrings and hypermodules, such as multiplicative hyperrings defined by Rota [5] or generalized hyperrings defined by Vougiouklis [6]. For more details about the Krasner hypermodule and its properties in connection with the categorical approach, please refer to [7,8,9,10,11,12,13,14].

This article goes in the same direction and provides some results of normal injective hypermodules with category aspects. Injectivity has a significant role in the category theory. In [15], the injective objects in the category of posets are Dedekind–MacNeille completions. The injective object in the category of Boolean algebras is complete Boolean algebra [16].

Inspired by the characterization of injective modules in category theory, in this article, we aim to obtain some new results in hypercompositional algebra. Zero-divisor elements have an important role in a commutative unitary ring in classical algebra, where we have two binary operations for a ring. If we consider hyperrings as an extension of a ring, where the classical operations are substituted by hyperoperations, then zero divisors are still important elements in studying the properties of hyperrings, especially Krasner hyperrings (see [17]). Moreover, if we consider an R-hypermodule M, where R is a Krasner hyperring, then we can extend the definition of a zero-divisor element of R to zero-divisor element of R over M as an element r of R if there exists a nonzero element $m\in M$ such that $r·m=0_M$. By notation $Z_R\left(M\right)$, we denote the set of all zero-divisor elements of R over M. Using the definition of zero-divisor element of R over R-hypermodule M, the definition of divisible R-hypermodule was introduced in [17]. There is a difference between the definition of a divisible element of a hypermodule in hypercompositional algebra and the divisible element of a module in classical algebra. In the definition of a divisible element of an R-hypermodule M, the concept of a nonzero divisor of R over the hypermodule M is used, while in the definition of classical algebra for a divisible element, the definition of nonzero divisor of a ring is used. Therefore, our definition of a divisible element of a hypermodule is more general than the classical definition. The same motivation for the torsion element in an R-hypermodule holds for us in this article. In homological algebra, an element m of a R-module M is said to be a torsion element of M if there exists a nonzero element r of R such that $rm=0$, where R is an integral domain [18]. We will use the same idea to define a torsion element and torsionable hypermodule, but since the structure of a hypermodule is different from a module, the definitions of a torsion element will be different, and torsionable hypermodule will be introduced. We will illustrate these differences by investigating the relationships of $To{r}_R\left(M\right)$, i.e., the set of all torsion elements of the R-hypermodule M, with $Z_R\left(M\right)$. Some fundamental properties of $To{r}_R\left(M\right)$ will be presented. Furthermore, using $To{r}_R\left(M\right)$, the definition of a torsionable element will be given. This definition will help us to state and prove one of the main results of this paper. In particular, we show that every torsionable R-hypermodule M is a normal injective, where R is a commutative hyperring. Moreover, if R is a commutative hyperring, then every torsionable R-hypermodule is divisible, too.

2. Preliminaries

Throughout this paper, unless we state explicitly, R denotes a Krasner hyperring that we will call, for short, hyperring.

Definition 1

([4]). A hypercompositional structure $(R,+,·)$ is called a hyperring when

 1. 

$(R,+)$ is a canonical hypergroup, i.e.,

 (a) 

$a,b\in R\Rightarrow a+b\subseteq R,$

 (b) 

$\forall a,b,c\in R,a+(b+c)=(a+b)+c,$

 (c) 

$\forall a,b\in R,a+b=b+a,$

 (d) 

$\exists 0\in R,\forall a\in R,a+0=\left\{a\right\},$

 (e) 

$\forall a\in R,\exists -a\in R\mathrm{such}\mathrm{that}0\in a+x\iff x=-a,$

 (f) 

$\forall a,b,c\in R,c\in a+b\Rightarrow a\in c+(-b).$

 2. 

$(R,·)$ is a semigroup with a bilaterally absorbing element 0, i.e.,

 (a) 

$a,b\in R\Rightarrow a·b\in R,$

 (b) 

$\forall a,b,c\in R,a·(b·c)=(a·b)·c,$

 (c) 

$\forall a\in R,0·a=a·0=0.$

 3. 

The product distributes from both sides over the hyperaddition, i.e.,

 (a) 

$\forall a,b,c\in R,a·(b+c)=a·b+a·c\mathrm{and}(b+c)·a=b·a+c·a.$

Definition 2.

A hyperring R is called commutative, if $(R,·)$ is commutative, i.e., for each $a,b\in R$,

$$a·b=b·a.$$

Moreover, if $(R,·)$ is a monoid, then we say that R is a hyperring with a unit element, or a unitary hyperring.

The concept of hypermodule over a hyperring R was introduced by Krasner and studied later in detail for its algebraic properties in [2,7,9].

Definition 3.

Let R be a unitary hyperring with the unit element $1_R$. A canonical hypergroup $(M,+)$ together with a left external map $R\times M⟶M$ defined by

$$(a,m)\mapsto a·m\in M$$

(1)

such that for all $a,b\in R$ and $m_1,m_2\in M$ we have

 1. 

$(a+b)·m_1=a·m_1+b·m_1,$

 2. 

$a·(m_1+m_2)=a·m_1+a·m_2,$

 3. 

$\left(ab\right)·m_1=a·(b·m_1),$

 4. 

$a·0_M=0_R·m_1=0_M,$

 5. 

$1_R·m_1=m_1$

is called a left Krasner hypermodule over R, or in short, a left R-hypermodule. Similarly, one may define a right R-hypermodule. Obviously, when R is a commutative hyperring, then the left and the right R-hypermodule coincide.

The next proposition shows that every hyperring can be a hypermodule over itself.

Proposition 1

([7]). Let R be a unitary hyperring. Then R is an R-hypermodule.

Definition 4.

Let R be a hyperring, M be an R-hypermodule, and $(N,+)$ be a subhypergroup of $(M,+)$, which is also closed under multiplication by elements of R. Then, N is a subhypermodule of M.

Different types of homomorphism between R-hypermodules are explained in [3,17]. In what follows, we review some definitions of homomorphisms.

Definition 5.

Let M and N be two R-hypermodules. A multivalued function $f:M⟶{\mathcal{P}}^{\ast }\left(N\right)$ is called an R-homomorphism if:

 (i) 

$\forall m_1,m_2\in M,f\left(m_1{+}_M{m}_2\right)\subseteq f\left(m_1\right){+}_{N}f\left(m_2\right),$

 (ii) 

($\forall m\in M)(\forall r\in R),f\left(r{·}_{M}m\right)=r{·}_{N}f\left(m\right),$

while f is called strong homomorphism if instead of $\left(i\right)$ we have

 (i′) 

$\forall m_1,m_2\in M,f\left(m_1{+}_M{m}_2\right)=f\left(m_1\right){+}_{N}f\left(m_2\right).$

A single-valued function $f:M⟶N$ is called a strict R-homomorphism if axioms $\left(i\right)$ and $\left(ii\right)$ are valid and it is called a normal R-homomorphism if $\left(i^{\prime }\right)$ and $\left(ii\right)$ are valid.

The family of all normal R-homomorphisms from M to N is denoted by $Ho{m}_R^n(M,N)$. In the following, we will recall some types of R-homomorphisms.

Definition 6

([3]). Let $f\in Ho{m}_R^n(M,N)$. Then f is called

 (i) 

a surjective normal R-homomorphism if $Im\left(f\right)=N$.

 (ii) 

an injective normal R-homomorphism if for all $m_1,m_2\in M$, $f\left(m_1\right)=f\left(m_2\right)$ implies $m_1=m_2$.

 (iii) 

normal R-isomorphism if it is a bijective normal R-homomorphism.

In [3], the characterizations of a normal injective R-hypermodule were studied using hyperideals, exact chains of R-hypermodules, and normal R-homomorphisms. We recall these characterizations.

Theorem 1.

Let R be a hyperring and N be an R-hypermodule. Then the following statements are equivalent:

 (1)

N is a normal injective R-hypermodule.

 (2)

For any hyperideal I of R, an inclusion hyperring homomorphism $i:I⟶R$ and a normal R-homomorphism $k:I⟶N$, there exists a normal R-homomorphism $h:R⟶N$ such that the diagram in Figure 1 has the composition structure, i.e., $hi=k$.

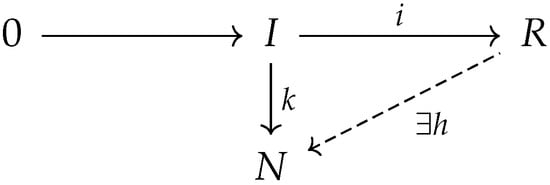
Figure 1. Composition structure of a diagram for a normal injective R-hypermodule, using hyperideals.

Theorem 2.

An R-hypermodule N is normal injective if it satisfies the following equivalent conditions.

 (i) 

For any exact chain

$$0⟶M_1\stackrel{\gamma }{⟶}{M}_2\stackrel{\delta }{⟶}{M}_3⟶0$$

(2)

of R-hypermodules and normal R-homomorphisms, the chain

$$0⟶Ho{m}_R^n(M_3,N)\stackrel{\Delta }{⟶}Ho{m}_R^n(M_2,N)\stackrel{\Gamma }{⟶}Ho{m}_R^n(M_1,N)⟶0$$

(3)

is exact, too.

 (ii) 

For any R-hypermodules $M_1,M_2,N$ and normal R-homomorphisms $\gamma :M_1⟶M_2$ and $k:M_1⟶N$ such that the chain $0⟶M_1\stackrel{\gamma }{⟶}{M}_2$ is exact, there exists a normal R-homomorphism $h:M_2⟶N$ such that $h\gamma =k$.

 (iii) 

For any hyperideal I of R, any inclusion hyperring homomorphism $i:I⟶R$, and normal R-homomorphism $k:I⟶N$, there exists a normal R-homomorphism $h:R⟶N$ such that $hi=k$.

A zero-divisor element in a hyperring R was described in the following definition. For more detail regarding these elements, refer to [17].

Definition 7.

Let R be a hyperring. An element r of R is said to be a right zero divisor if there exists a nonzero element $r^{\prime }\in R$ such that $r^{\prime }r=0$. Similarly, a left zero-divisor element is defined as an element of R such that $r{r}^{\prime }=0$ for an element $r^{\prime }\in R\setminus \left\{0\right\}$. If R is a commutative hyperring, then the right and the left zero divisors coincide, and we refer to them as zero divisors of R. We denote by $Z\left(R\right)$ the set of all zero divisors of the hyperring R, i.e.,

$$Z\left(R\right)=\{r\in R\mid \exists r^{\prime }\in R,r^{\prime }\ne 0,r{r}^{\prime }=0\}$$

(4)

3. Torsion Elements of an $\mathit{R}$-Hypermodule $\mathit{M}$

In this article, for simplicity, we consider left R-hypermodules, which we call R-hypermodules. Moreover, in the following lemma, the sum of the family of subhypermodules is constructed.

Lemma 1.

Let R be a hyperring, M be an R-hypermodule and ${\left\{M_i\right\}}_{i\in I}$ be a family of subhypermodules of M. Then the sum of this family is denoted by ${\sum }_{i\in I}{M}_i$, and it is the union of the sets ${\sum }_{i\in I}{m}_i$, where for every $i\in I$, $m_i\in M_i$. More specifically,

$$\sum _{i\in I}{M}_i=\bigcup _{m_i\in M_i}\left(\sum _{i\in I}{m}_i\right).$$

(5)

Therefore, for subhypermodules $M_1$ and $M_2$, we have:

$$M_1+M_2=\bigcup _{m_1\in M_1,m_2\in M_2}\left(m_1+m_2\right)=\{m\in M\mid \exists m_1\in M_1,\exists m_2\in M_{2}suchthatm\in m_1+m_2\}$$

(6)

where $m_1+m_2$ is a set (in particular a subset of M) and not only an element, while

$$M_1+M_2+M_3=\bigcup _{m\in m_1+m_2,m_3\in M_3}\left(m+m_3\right),$$

where $m_1\in M_1$ and $m_2\in M_2$ are arbitrary elements.

The structure ${\sum }_{i\in I}{M}_i$ is a subhypermodule of M and the smallest subhypermodule of M containing every $M_i$.

Definition 8.

Let R be a hyperring and M be an R-hypermodule. An element $r\in R$ is said to be a zero divisor over M if there exists a nonzero element $m\in M$ such that $r·m=0_M$. By notation $Z_R\left(M\right)$, we denote the set of all zero-divisor elements over M, i.e.,

$$Z_R\left(M\right)=\{r\in R\mid \exists m\in M,m\ne 0,r{·}_{M}m=0_M\}.$$

(7)

For a nonzero R-hypermodule M, $Z_R\left(M\right)\ne Ø$ since $0_R\in Z_R\left(M\right)$.

Definition 9.

Let M be an R-hypermodule. A nonzero element m of M is said to be divisible if for every nonzero divisor $r\in R$ over M ($r\notin Z_R\left(M\right)$), there exists $m^{\prime }\in M$ such that $m=r·m^{\prime }$. Moreover, if each element of M is a divisible element, then M is said to be a divisible R-hypermodule.

In [9], Ch. G. Massouros defined a torsion-free element of an R-hypermodule M and a torsion-free R-hypermodule followed by some results. Using that definition, we introduce the subset $To{r}_R\left(M\right)$ and investigate its properties.

Definition 10.

Let R be a hyperring and M be an R-hypermodule. An element m of M is said to be a torsion element of M if there exists a nonzero element $r\in R$ such that $r·m=0_M$. We denote by $To{r}_R\left(M\right)$ the set of all torsion elements of the R-hypermodule M i.e.,

$$To{r}_R\left(M\right)=\{m\in M\mid \exists r\in R,r\ne 0,r·m=0_M\}.$$

(8)

Clearly, $0_M\in To{r}_R\left(M\right)$. Moreover, if M has not nonzero torsion element, i.e.,

$$To{r}_R\left(M\right)=\left\{0_M\right\},$$

then we called M a torsion-free R-hypermodule.

If an element $m\in M$ is not a torsion element, i.e., $m\notin To{r}_R\left(M\right)$, then we call m a torsion-free element of M. Therefore, based on Definition 10, a torsion-free element is defined as follows, which is the same as the definition of Ch. G. Massouros in [9].

Definition 11.

An element m of a R-hypermodule M is called torsion-free if and only if $r·m=0_m$ implies $r=0_R$.

Proposition 2.

Let R be a hyperring and M be an R-hypermodule. Then $Z_R\left(M\right)=\left\{0\right\}$ if and only if $To{r}_R\left(M\right)=\left\{0\right\}$.

Proof. 

Suppose that $Z_R\left(M\right)=\left\{0\right\}$ and $m\in To{r}_R\left(M\right)$ be a nonzero element. Then there exists a nonzero element $r\in R$ such that $r·m=0_M$. Therefore, $r\in Z_R\left(M\right)$ and this is a contradiction. Therefore, $m=0$ and $To{r}_R\left(M\right)=\left\{0\right\}$. The other side of the proposition is the same. □

Example 1

([19]). Let $R=\{0,1,2\}$. Define the hyperaddition “+” and multiplication “·” by the following:

+	0	1	2
0	{0}	{1}	{2}
1	{1}	R	{1}
2	{2}	{1}	{0,2}

and

·	0	1	2
0	0	0	0
1	0	1	2
2	0	2	0

Then R is a hyperring and $A=\{0,2\}$ is the only maximal hyperideal of R. Consider $\frac{R}{A}=\{A,1+A,2+A\}$, then based on Example 4.6 of [19], $\frac{R}{A}$ is an R-hypermodule with the following hyperaddition “⊎”

⊎	A	1+A	2+A
A	A	1+A	2+A
1+A	1+A	1+A	1+A
2+A	2+A	1+A	{A, 2+A }

and the external operation $\odot :R\times \frac{R}{A}⟶\frac{R}{A}$ which define

$$r\odot (a+A)=r{·}_{R}a+A,$$

for all $r\in R$ and $a+A\in \frac{R}{A}$. Then clearly $Z\left(R\right)=\left\{2\right\}$. Moreover, since

$$2\odot (2+A)=2{·}_{R}2+A=A=0_{\frac{R}{A}},$$

we conclude that $Z_R\left(M\right)=\{0,2\}$ and $2+A\in To{r}_R\left(\frac{R}{A}\right)$, while $1+A\notin To{r}_R\left(\frac{R}{A}\right)$. Therefore,

$$To{r}_R\left(\frac{R}{A}\right)=\{A,2+A\},$$

and the only torsion-free element of R-hypermodule $\frac{R}{A}$ is $1+A$. Moreover, we can verify that the Proposition 2 is true in this example.

Theorem 3.

Let R be a commutative hyperring such that $Z\left(R\right)=Ø$ and M be an R-hypermodule. Then $To{r}_R\left(M\right)$ is a subhypermodule of M.

Proof. 

Clearly $To{r}_R\left(M\right)$ is not an empty set since $0_M\in To{r}_R\left(M\right)$. Suppose that $m,n\in To{r}_R\left(M\right)$. Then there exist nonzero elements $r_1,r_2\in R$ such that $r_1·m=0_M$ and $r_2·n=0_M$. Put $r=r_1{·}_R{r}_2$. Since $Z\left(R\right)=Ø$, $r\ne 0_R$ and

$$r·(m+n)=\left(r_1{·}_R{r}_2\right)·(m+n)=\left(r_1{·}_R{r}_2\right)·m+\left(r_1{·}_R{r}_2\right)·n=$$

$$r_2·(r_1·m)+r_1·(r_2·n)=0_M+0_M=0_M.$$

Therefore, $m+n\subseteq To{r}_R\left(M\right)$ and $To{r}_R\left(M\right)$ is a subhypermodule of M. □

Corollary 1.

Let R be a commutative hyperdomain and M be an R-hypermodule. Then $To{r}_R\left(M\right)$ is a subhypermodule of M.

Proposition 3.

Let $M_1$ and $M_2$ be two R-hypermodules where R is a commutative hyperring. Then

$$To{r}_R\left(M_1\right)+To{r}_R\left(M_2\right)\subseteq To{r}_R(M_1+M_2)$$

(9)

Proof. 

Suppose that $m\in To{r}_R\left(M_1\right)+To{r}_2\left(M_2\right)$. Then, based on Lemma 1, there exist $n_1\in To{r}_R\left(M_1\right)$ and $n_2\in To{r}_R\left(M_2\right)$ such that $m\in n_1+n_2$. Thus, there exist nonzero elements $r_1,r_2\in R$ such that $r_1·n_1=0_{M_1}$ and $r_2·n_2=0_{M_2}$. Put $r=r_1{·}_R{r}_2$. Then clearly $r\ne 0_R$, and we have

$$r·m\in r·(n_1+n_2)=r·n_1+r·n_2=\left(r_1{·}_R{r}_2\right)·n_1+\left(r_1{·}_R{r}_2\right)·n_2=$$

$$r_2·(r_1·n_1)+r_1·(r_2·n_2)=0_{M_1}+0_{M_2}=0_{M_1+M_2}.$$

Therefore, there exists a nonzero element $r\in R$, such that $r·m=0_{M_1+M_2}$. Therefore, using (8), $m\in To{r}_R(M_1+M_2)$ and $To{r}_R\left(M_1\right)+To{r}_2\left(M_2\right)\subseteq To{r}_R(M_1+M_2)$. □

Proposition 4.

Let M be an R-hypermodule and N be an R-subhypermodule of M. Then

$$To{r}_R\left(\frac{M}{N}\right)=\frac{To{r}_R\left(M\right)}{N}$$

(10)

Proof. 

Suppose that $m+N\in \frac{To{r}_R\left(M\right)}{N}$ is an arbitrary element. Then $m\in To{r}_R\left(M\right)$. Therefore, a nonzero element $r\in R$ exists such that $r·m=0_M$. Then we have

$$r·(m+N)=r·m+N=0_M+N=N=0_{\frac{M}{N}}.$$

This means that there exists $r\in R$ such that $r·(m+N)=0_{\frac{M}{N}}$. Therefore, $m+N\in To{r}_R\left(\frac{M}{N}\right)$ and $\frac{To{r}_R\left(M\right)}{N}\subseteq To{r}_R\left(\frac{M}{N}\right)$.

Now let $m+N\in To{r}_R\left(\frac{M}{N}\right)$. Then a nonzero element $r\in R$ exists such that $r·(m+N)=N$. Therefore,

$$r·(m+N)=r·m+N=N⟹r·m=0_M.$$

Therefore, $m\in To{r}_R\left(M\right)$ and $m+N\in \frac{To{r}_R\left(M\right)}{N}$. Therefore, $To{r}_R\left(\frac{M}{N}\right)\subseteq \frac{To{r}_R\left(M\right)}{N}$ and we conclude that

$$To{r}_R\left(\frac{M}{N}\right)=\frac{To{r}_R\left(M\right)}{N}$$

□

Definition 12.

Let M be an R-hypermodule. A nonzero element m of M is said to be torsionable if for every torsion-free element $m^{\prime }$ of M ($m^{\prime }\notin To{r}_R\left(M\right)$), there exists $r\in R$ such that $m=r·m^{\prime }$. Moreover, if each nonzero element of M is a torsionable element, then M is said to be a torsionable R-hypermodule.

Example 2.

In Example 1, consider nonzero elements of R-hypermodule $\frac{R}{A}$, i.e., $1+A$ and $2+A$. Then for the only torsion-free element of $\frac{R}{A}$ which is $1+A$, we have:

$$1+A=1\odot (1+A),2+A=2\odot (1+A).$$

Therefore, $1+A$ and $2+A$ are torsionable elements of $\frac{R}{A}$ and therefore $\frac{R}{A}$ is a torsionable R-hypermodule.

Proposition 5.

Let M be an R-hypermodule where R is a commutative hyperring. Then, every torsionable element of M is a divisible element.

Proof. 

Suppose that $0\ne m\in M$ is a torsionable element and $r\in R$ is a nonzero-divisor element over M. Then, for each $n\in M$, $r·n\ne 0_M$. Therefore, for element m, we have $r·m\ne 0_M$. Put $m^{\prime }=r·m$. Then $m^{\prime }\ne 0$, and we claim that $m^{\prime }$ is a torsion-free element of M. Because if $m^{\prime }\in To{r}_R\left(M\right)$, then there exists nonzero element $r^{\prime }\in R$ such that $r^{\prime }·m^{\prime }=0_M$. Therefore,

$$r^{\prime }·m^{\prime }=r^{\prime }·(r·m)=\left(r^{\prime }{·}_{R}r\right)·m=\left(r{·}_R{r}^{\prime }\right)·m=r·(r^{\prime }·m)=0_M$$

which is a contradiction since $r\notin Z_R\left(M\right)$. Therefore, $m^{\prime }\notin To{r}_R\left(M\right)$. Since m is a torsionable element, using Definition 12, there exists a nonzero element $s\in R$ such that $m=s·m^{\prime }$. Therefore,

$$m=s·m^{\prime }=s·(r·m)=r·(s·m)=r·m_1,$$

where $m_1$ is an element of M. This means that m is a divisible element. □

Example 3.

In Example 1, $Z_R\left(\frac{R}{A}\right)=\{0,2\}$ and $1+A$ and $2+A$ are torsionable elements of $\frac{R}{A}$. Since for nonzero-divisor element of R over $\frac{R}{A}$, (i.e., $1\notin Z_R\left(\frac{R}{A}\right)),$ we have

$$1+A=1\odot (1+A),2+A=1\odot (2+A),$$

thus $1+A$ and $2+A$ are divisible elements.

Corollary 2.

Let R be a commutative hyperring and M be a torsionable R-hypermodule. Then M is a divisible R-hypermodule.

Example 4.

Using Example 3 and routine verification, we can show that the torsionable R-hypermodule $\frac{R}{A}$ in Example 2 is a divisible R-hypermodule too.

Proposition 6.

Let M and N be R-hypermodules and $f\in Ho{m}_R^n(M,N)$ be a surjective normal R-homomorphism. If M is a torsionable R-hypermodule, then N is a torsionable, too.

Proof. 

Suppose that M is a torsionable R-hypermodules and $f:M⟶N$ is a surjective normal R-homomorphism. Let $n\in N$ be an arbitrary element and $n^{\prime }\notin To{r}_R\left(N\right)$. Since f is surjective, there exist elements $m,m^{\prime }\in M$ such that $f\left(m\right)=n$ and $f\left(m^{\prime }\right)=n^{\prime }$. First, we claim that $m^{\prime }\notin To{r}_R\left(M\right)$. To show it, suppose that $m^{\prime }\in To{r}_R\left(M\right)$. Then, there exists a nonzero element $r\in R$ such that $r·m^{\prime }=0_M$. Therefore,

$$f(r·m^{\prime })=r·f\left(m^{\prime }\right)=r·n^{\prime }=0_N.$$

This means that $n^{\prime }\in To{r}_R\left(N\right)$ and this is a contradiction. Therefore, $m^{\prime }\notin To{r}_R\left(M\right)$. Since M is a torsionable R-hypermodule and $m\in M$, a nonzero element $r\in R$ exists such that $m=r·m^{\prime }$. Therefore

$$n=f\left(m\right)=f(r·m^{\prime })=r·f\left(m^{\prime }\right)=r·n^{\prime }.$$

Therefore, N is a torsionable R-hypermodule. □

Proposition 7.

Let M and N be R-hypermodules and $f\in Ho{m}_R^n(M,N)$ be an injective normal R-homomorphism. If N is a torsionable R-hypermodule, then M is torsionable, too.

Proof. 

Suppose that N is a torsionable R-hypermodules and $f:M⟶N$ is an injective normal R-homomorphism. Let $m\in M$ be an arbitrary element and $m^{\prime }\notin To{r}_R\left(M\right)$. Then $f\left(m\right)=n$ and $f\left(m^{\prime }\right)=n^{\prime }$ are elements of N and we claim that $n^{\prime }\notin To{r}_R\left(N\right)$. To show it, suppose that $n^{\prime }\in To{r}_R\left(N\right)$. Then there exists a nonzero element $r\in R$ such that $r·n^{\prime }=0_N$. Therefore,

$$r·n^{\prime }=r·f\left(m^{\prime }\right)=f(r·m^{\prime })=0_N.$$

Since f is an injective normal R-homomorphism, $r·m^{\prime }=0_M$, and this means that $m^{\prime }\in To{r}_R\left(M\right)$ and this is a contradiction. Therefore, $n^{\prime }\notin To{r}_R\left(N\right)$. Moreover, N is a torsionable R-hypermodule and $n\in N$. Therefore, there exists a nonzero element $r\in R$ such that $n=r·n^{\prime }$. Therefore

$$f\left(m\right)=r·f\left(m^{\prime }\right)=f(r·m^{\prime }).$$

Using the injectivity of f, we conclude that $m=r·m^{\prime }$. Therefore, M is a torsionable R-hypermodule. □

Theorem 4.

Let M be a torsionable R-hypermodule and N be an R-subhypermodule of M. Then, the quotient R-hypermodule $\frac{M}{N}$ is a torsionable hypermodule, too.

Proof. 

Let $m+N\in \frac{M}{N}$ be a nonzero arbitrary element and $m^{\prime }+N\notin To{r}_R\left(\frac{M}{N}\right)$. Using Proposition 4, we conclude that $m^{\prime }+N\notin \frac{To{r}_R\left(M\right)}{N}$. Therefore, $m^{\prime }\notin To{r}_R\left(M\right)$. Since M is a torsionable R-hypermodule, $r\in R$ exists such that $m=r·m^{\prime }$. Therefore,

$$m+N=r·m^{\prime }+N=r·(m^{\prime }+N).$$

This means that $m+N$ is a torsionable element and $\frac{M}{N}$ is a torsionable R-hypermodule. □

Theorem 5.

Let R be a hyperring and M be a R-hypermodule. If M is torsion-free and divisible, then M is a normal injective.

Proof. 

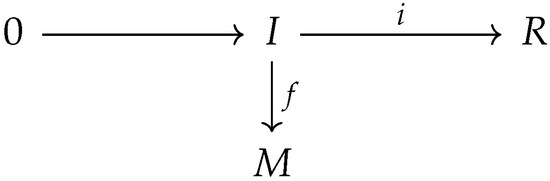
Suppose that M is a torsion-free divisible R-hypermodule. To show that M is a normal injective, we consider the following diagram where I is a hyperideal of R, $i:I⟶R$ is an inclusion hyperring homomorphism and $f:I⟶M$ is a normal R-homomorphism.

If $I=0$, then the conclusion is clear. Therefore, assume that $I\ne 0$ and consider a nonzero element $a\in I$. Since M is a torsion-free R-hypermodule, for every $m\in M$ such as $m\ne 0_M$, $a·m\ne 0$. Therefore, using Definition 8, we conclude that $a\in I$ is a nonzero-divisor element over M, i.e., $a\notin Z_R\left(M\right)$. Moreover, M is a divisible hypermodule and $f\left(a\right)\in M$. Therefore, $f\left(a\right)$ is a divisible element, and for nonzero divisor $a\in R$ over M, there exists $n\in M$ such that $f\left(a\right)=a·n$. Let $b\in I$ be an arbitrary element. Then for the element a, we have

$$a·f\left(b\right)=f\left(a{·}_{R}b\right)=f\left(b{·}_{R}a\right)=b·f\left(a\right)=b·a·n=a·b·n,$$

thus,

$$a·f\left(b\right)=a·b·n,$$

which means that

$$0\in a·f\left(b\right)-a·b·n=a·\left(f\right(b)-(b·n\left)\right).$$

Since $a\ne 0$ and M is a torsion-free R-hypermodule, we conclude that

$$0\in f\left(b\right)-b·n.$$

Therefore, $f\left(b\right)=b·n$. Now define the normal R-homomorphism $g:R⟶M$ such that for each $r\in R$, $g\left(r\right)=r·n$. Then, for each $b\in I$,

$$f\left(b\right)=b·n=gi\left(b\right),$$

which means that the diagram in Figure 2 has the composition structure, i.e., $gi=f$. □

Figure 2. Composition structure of a diagram for R-hypermodule M, using hyperideals.

Theorem 6.

Let R be a commutative hyperring and M be an R-hypermodule. If M is torsionable, then M is a normal injective.

Proof. 

Suppose that M is a torsionable R-hypermodule. Then using Corollary 2, M is a divisible R-hypermodule. Therefore, M is a normal injective by Theorem 5. □

Remark 1.

Using Proposition 2 and Theorem 4.5 of [17], we have another proof for Theorem 5.

Theorem 7.

Let R be a hyperring and M be a torsion-free normal injective R-hypermodule. Then M is a divisible R-hypermodule.

Proof. 

Since M is a torsion-free normal injective R-hypermodule, $To{r}_R\left(M\right)=Ø$ and by Proposition 2, $Z_R\left(M\right)=Ø$. Using Theorem 4.4 of [17], we conclude that M is a divisible R-hypermodule. □

Corollary 3.

Let R be a hyperring and M be a torsion-free R-hypermodule. Then M is normal injective if and only if M is divisible R-hypermodule.

4. Conclusions and Future Work

In this article, we have studied the torsion and torsionable elements in an R-hypermodule M and introduced a torsionable R-hypermodule, where R is a Krasner hyperring. After investigating the main properties of torsion and torsionable elements, we studied the relationship between these elements and divisible elements in an R-hypermodule. Moreover, we investigated the relationship between torsionable and divisible R-hypermodule. Finally, we proved that if R is a commutative hyperring and M is a torsionable R-hypermodule, then M is a normal injective too.

In future work, we intend to apply these results to obtain new properties of normal injective and normal projective R-hypermodule. We believe that these results will be useful in obtaining some important results in the category point of view of hypercompositional structures.