Abstract
In this work, it is shown that the geometry of a gravity field generated by a spheroid with low eccentricity can be described with the help of a newly modified Helmholtz equation. To distinguish this equation from the modified Helmholtz equation, we refer to it as the G-modified Helmholtz equation. The use of this new equation to study the spheroid’s gravity field is advantageous in expressing the gravity vector as a vector series of spherical harmonics. The solution of the G-modified Helmholtz equation involves both the gravity intensity g (or simply gravity g) and the intensity E of an electrostatic field as shown in sequel. An electrostatic field generated by an oblate spheroid charged with l electrons (uniform ellipsoidal charge distribution) is demonstrated to be a special case. Both gravity intensity g and intensity E are governed by the same law and can be expressed as a series of spherical harmonics, and thus the G-modified Helmholtz equation is useful for describing the gravity and electrostatic fields.
MSC:
35A09; 35C10; 35J25; 33C5; 33C75
1. Introduction
Spheroids are widely used in many applications that involve gravity. For example, a simplified model of the geoid in [1] (equipotential surface of the Earth’s gravity field, which approximates the mean sea level and serves as a reference surface for heights) is a spheroid with specific semimajor and semiminor axes. The spheroid has a significant advantage in that it can be mathematically described far more easily than other closed surfaces.
The case of the geoid is referred to because the Earth’s gravity field is quite complicated due to the irregular distribution of masses and their density. As a consequence, the gravity vector’s magnitude and direction vary from point to point. Therefore, the shape of the geoid is quite irregular. The geoid can be approximated globally or locally through the use of a chosen spheroid.
The gravity potential, gravity vector, and gravity intensity g from [2,3] are used in geophysics and geodesy. The gradient of the gravity potential is equal to the gravity vector, and the magnitude of the gravity vector is gravity g. A finite series of spherical harmonics can offer a representation of the gravity potential. The G-modified Helmholtz equation is a partial differential equation that is directly related to gravity g. As shown in [4], it can be represented as a series of spherical harmonics and there is no need to involve the gravity potential to determine it.
Here, an “inverse problem” will be solved, i.e., if gravity g is known, then the first-order partial derivatives of gravity potential are also known. This fact enables us to express the gravity vector as a vector series of spherical harmonics. Furthermore, it has been demonstrated that it is feasible to reconstruct the gradient of the gravity potential without relying on the gravity potential itself.
The G-modified Helmholtz equation is also useful for studying electrostatic fields. It will be shown that the electrostatic intensity E can be represented as a series of spherical harmonics. This series is identical to that of gravity g. The determination of electrostatic intensity E outside of an oblate spheroid can be accomplished by solving a boundary value problem of a Dirichlet type, which is a typical example. It is mentioned in this study that a MacLaurin spheroid is a flattened spheroid that occurs when a self-gravitating fluid object, with a uniform density, rotates at a constant angular velocity around a fixed axis, passing through its center of mass. The spheroid that is used for the determination of the gravity vector and the electrostatic intensity E is a non-rotating spheroid, i.e., it is not a MacLaurin spheroid.
The decision to select the surface of a spheroid from [5,6,7] is primarily based on the widespread utilization of spherical and ellipsoidal forms in diverse electromagnetism-related scenarios. In addition, some relative subjects in electromagnetics can also be found in [8,9,10]. Oblate spheroids are advantageous in various applications, for instance, electrostatic interactions between spheroidal dielectric particles in [11,12], and hybrid explicit/implicit solvent biomolecular simulations.
When taking the traditional approach, to determine the gravity g or the intensity E, we have to determine the first-order partial derivatives of the gravity potential, and then the square root of the square sum of these derivatives. Unfortunately, this procedure requires numerous manipulations, and the final form of the gravity g or intensity E is not related to any form of expression that involves a series of eigenfunctions.
Therefore, the novelty of this work is the direct determination of the gravity vector g and the electrostatic intensity E as a series of spherical harmonics. In such a way, it is proven that the intensity E is also a solution of a partial differential equation, which is the G-modified Helmholtz equation.
2. Alternative Expressions for the First-Order Partial Derivatives of the Gravity Potential and the Geometry of a Spheroid’s Gravity Field
It is feasible to represent the gravity vector at a specific point Q outside the spheroid by employing a vector series of spherical harmonics, bypassing the need for gravitational potential. In addition, if point Q is in close proximity to the spheroid’s surface, then the gravity vector is strongly related to the gravitational flattening of the spheroid. In [4], it was proven that the intensity g of the external gravity field, generated by an oblate spheroid containing mass m, was a solution to the following boundary value problem:
The determination of the intensity g was independent of the gravity potential. Equation (1) is the G-modified Helmholtz equation, and its classical solution is
and
In Equations (2)–(4), θ′ is the spherical latitude measured from the z-axis, and in [13],
is a parameterization of the spheroid S (a is the semimajor axis and e is the first eccentricity of the spheroid S). The pair (φ, λ) is referred to as spheroidal (or geodetic) latitude and longitude, respectively. The solution is given by the following formula (which contains only the Legendre polynomials) due to the symmetry of this gravity field:
Let S2 be the unit sphere. A parameterization of this sphere is
Let P be an arbitrary point on the surface of the spheroid. Since the spheroid is a smooth oriented surface, the unit normal vector is defined at this point. The spheroid’s Gauss map is shown in the following function:
The image of the unit normal vector at point P is a pair (ΦP, ΛP). This pair represents the spherical coordinates of the unit normal vector. Now, let γ be a plumbline of the spheroid’s gravity field that passes from point P. On the plumbline γ, we choose a point Q that is not far away from point P. Let V be the gravity potential, V0 be the value of the gravity potential on the spheroid’s surface, and VQ be the value of the gravity potential of the equipotential surface passing through point Q.
The equipotential surfaces are smooth closed surfaces of revolution. Let
be a parameterization of the equipotential surface that passes at point Q. The surface coordinates of point Q are (φQ, λQ). In addition, let ε be a line that is normal to the spheroid S passing through point Q. If Q′ is the intersection point between line ε and the spheroid, then we define a spheroidal height hQ of point Q using the following quantity:
The triplet (φQ, λQ, hQ) is defined as the spheroidal (or geodetic) coordinates of point Q. It was mentioned that the spheroidal coordinates of point P are the triplet (φP, λP, 0). For the unit normal vector at point Q, we have that
The pair (ΦQ, ΛQ) differ from (φQ, λQ), but since points P and Q belong to the plumbline γ, it holds that
Figure 1 depicts point P, point Q, and the angle δΦ, which represents the angular difference between the tangent lines formed at these specific points. It is proven in [14] that δΛ = 0 and the quantity δΦ is equal to
where R is the radius of a sphere that has the same volume as the spheroid. Its value [15] is equal to
where b is the semiminor axis of the spheroid.
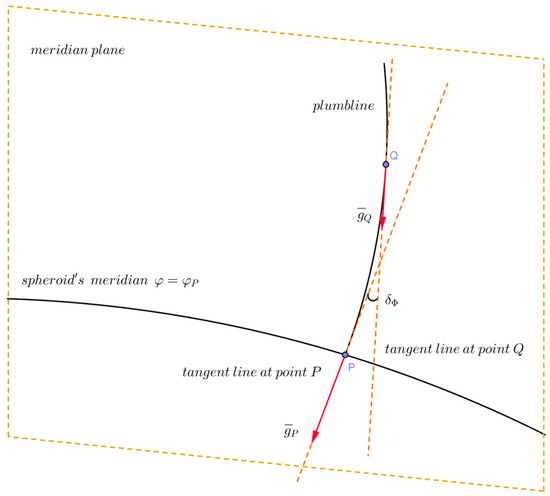
Figure 1.
The angle δΦ between gravity vectors at point P and point Q.
The quantity f* is the gravitational flattening of the spheroid S, and it is given as
Therefore, the angle δΦ is related to the gravitational flattening f*. The gravity vectors at points P and Q are tangents to the plumbline γ. The gravity vector at point P aligns with the spheroid’s unit normal vector at the same point. Similarly, the gravity vector at point Q aligns with the unit normal vector of the equipotential surface V = VQ at the same point. The gravity vector at point Q is related to the angle δΦ and it is equal to
where
The expression presented in Equation (17) serves as an alternative expression of the gradient of the gravity potential V. We will use this property to show that it is possible to determine the partial derivatives of the gravity potential V for points close to the spheroid, even if the function V is unknown. All quantities on the right-hand side of Equation (17) are known (gQ is known from the solution of the G-modified Helmholtz equation). Point Q is assumed to be situated on the spheroid’s first quadrant, without any loss of generality. It is shown (see Appendix A) that the gravity vector at point Q can be expressed as
The value of these constants depends on the spheroidal coordinates of point Q and the spheroid’s gravitational flattening. The gravity vector (gradient of the gravity potential) is determined by Equation (19). This equation establishes the feasibility of reconstructing the gradient of the gravity potential using solely the information of gravity on the surface of the spheroid and its gravitational flattening. The gravity g depends on the mass m of the spheroid; hence, when two identical spheroids encompass dissimilar masses, the unit vector in Equation (19) undergoes variation.
The function δΦ for points on the plumbline γ passing through a fixed point P on the spheroid’s surface theoretically determines the coordinates of the direction vector, represented as functions C1, C2, and C3 of θ′ and r in the equations
and
Therefore, along the plumbline, the gravity vector can be expressed as a vector series of spherical harmonics, i.e.,
3. The Gravity Vector on a Spherical Coordinate Basis
In the previous section, the gravity vector, which represents the gradient of the gravity potential, was described using a Cartesian coordinate basis. In this section, we will express the gravity vector using a spherical coordinate basis. The transformation between Cartesian and spherical coordinates is
Let
be the Cartesian basis and the orthonormal basis of the spherical coordinates, respectively. The transformation matrix between the two bases is
Thus,
The above relations become (see Equations (A14)–(A16) and λQ =λP)
Hence, the gradient of the gravity potential V in the spherical coordinates in [16] is equal to
The above represents the sought-after equation for the gradient of gravity potential, which depends upon the gravity intensity g. Equation (31) offers a simpler form [17] compared to alternative expressions that occur from the gradient of the gravity potential.
4. The Intensity of an Electrostatic Field Generated by an Oblate Spheroid
The G-modified Helmholtz equation proves valuable not just for examining the gravity fields but also for investigating the electrostatic fields.
Let U be the electrostatic potential of a uniformly charged sphere with a radius of R. The external electrostatic field of the sphere demonstrates equipotential surfaces, which share the same spherical form as the spherical gravity field. The examination of the electrostatic field’s equipotential surfaces can be conducted by following the methodology outlined in Section 2 of [4]. This leads to the conclusion that the electrostatic intensity is a solution of the G-modified Helmholtz equation:
Hence, intensity E can also be expressed as a series of spherical harmonics:
The electrostatic field’s intensity E, derived from an ellipsoidal charge with l electrons, is determined by using an exterior boundary value problem. The confining surface is the spheroid S, and the mathematical representation of this problem is as follows (for some information related to the boundary condition, see [5]):
ε0 is the permittivity of the vacuum and
The letter “q” stands for the electron’s charge and Mz is a form factor for the spheroid (for further information, see [5]). By replacing φ with θ′, the boundary condition becomes
Since the spheroid’s first eccentricity is close to zero, the form factor Mz can be written as
In addition,
Hence, the boundary condition becomes
It is worth mentioning that for e = 0 (for example a = b = R) and l = 1, the intensity is equal to
The above relation describes the intensity of the electrostatic field on the surface of a uniformly charged sphere with the radius R. Hence, the boundary value problem in question for the intensity E is
Due to the symmetry of the electrostatic field in [4], the solution of the partial differential equation is
where the prime on the Legendre polynomials indicates the first derivative. On the surface of the spheroid S, we have that
and
To determine the coefficients a2n (up to a degree N) and the integrals of the above relation, as well as the formation of the algebraic system (A + k2B)X = C),we refer to [4]. As a result, the electrical intensity E outside the spheroid S is given by
The above formula is identical to that of gravity g (see Equation (6)). Equation (47) is important [18] since it describes the intensity E in a simple and elegant way.
For l = 1, e = 0 (b = a), a00 = q/4πε0, and a2n = 0 (n = 1, 2, …, N), the intensity is equal to that of a charged sphere with the radius a:
5. Conclusions
The spheroid’s gravity field exhibits an intriguing geometry, and the G-modified Helmholtz equation allows us to delve deeper into its intricacies. The magnitude of the gravity vector, denoted as g, can be represented as a series of spherical harmonics. To explore this further, we selected a point P on the spheroid and a point Q on the plumbline passing through P. By leveraging the spheroid’s gravity field symmetry, we were able to express the coordinates of the gravity vector at point Q using a basis comprising the unit normal vector at point P and the tangent vector along the spheroid’s meridian at the same point. Along the selected plumbline, it was demonstrated that the gravitational vector can be represented as a vector series of spherical harmonics. Therefore, two equivalent expressions exist for the gradient of the gravity potential: a vector series of spherical harmonics derived from the Laplace equation, and a vector series of spherical harmonics derived from the G-Helmholtz equation. The latter series depends on the gravity intensity g, and for points near the surface of the spheroid is strongly related to the gravitational flattening of the spheroid.
The series expansion of the gradient of gravity potential through the G-modified Helmholtz equation highlights the potential to determine the gravity intensity g through boundary value problems. Consequently, future research could involve exploring the different types of boundary value problems associated with the gravity intensity g and the spheroid.
In the third section of the article, we showed that the electrostatic intensity E is also a classical solution of the G-modified Helmholtz equation. As a special case, we studied the intensity E outside of an oblate spheroid charged with l electrons. By solving a suitable boundary value problem of a Dirichlet type, we obtained the expression for the intensity E. Remarkably we discovered that the intensity E can also be expressed as a series of spherical harmonics, mirroring the identical representation found for the gravity g. Hence, in addition to the gravity g (and the gravity vector), the electrostatic intensity E also gains an efficient and noteworthy representation. In the future, for the electrostatic intensity E, it is possible to explore similar boundary value problems to those associated with the gravity intensity g. This line of study can provide an opportunity for further investigation into the properties of the intensity E.
Funding
This research received no funding.
Data Availability Statement
No data were used.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
The relations between spheroidal latitude φ and spherical latitude θ′ [4] are as follows:
Hence, Equation (18) can be a function of θ′ and λ. In addition,
The unit normal vector at point P is
Equations (18), (A3) and (A4) become (see Equations (A1) and (A2))
and
Hence, Equation (17) becomes
with
From Equation (17), we have that
The first-order partial derivatives of the gravity potential V in Cartesian coordinates are given by the following relations:
It is possible to simplify the above expressions into
In the context of a spherical gravity field, the coordinates of the gravity vector can be obtained using the above relations in the limited case (e = 0). Let
The constants c1, c2, and c3 are the coordinates of a unit vector that defines the direction of the gravity vector, i.e., gradVQ, which is
or
References
- Ghazal, N.K.; Saray, N.S. A comparison of Orthometric Heights Calculated from (GPS/Levelling) and (EGM08) Methods Based-GIS. J. Phys. Conf. Ser. 2021, 1879, 032072. Available online: https://iopscience.iop.org/article/10.1088/1742-6596/1879/3/032072/pdf (accessed on 2 October 2023). [CrossRef]
- Van Camp, M.; De Viron, O.; Watlet, A.; Francis, O.; Caudron, C. Geophysics From Terrestrial Time—Variable Gravity Measurements. Rev. Geophys. 2017, 55, 938–992. Available online: https://agupubs.onlinelibrary.wiley.com/doi/full/10.1002/2017RG000566 (accessed on 15 September 2023). [CrossRef]
- Sampietro, D.; Capponi, M. Seismic Constrained Gravity Inversion: A Reliable Tool to Improve Geophysical Models, Away From Seismic Information. Geosciences 2021, 11, 467. Available online: https://www.mdpi.com/2076-3263/11/11/467 (accessed on 14 September 2023). [CrossRef]
- Manoussakis, G. The Gravity Force Generated by a Non-Rotated Level Ellipsoid of Revolution with Low Eccentricity as a Series of Spherical Harmonics. Mathematics 2023, 11, 1974. Available online: https://www.mdpi.com/2227-7390/11/9/1974 (accessed on 12 September 2023). [CrossRef]
- Luiten, O.J.; van der Geer, S.B.; de Loos, S.J.; Kiewiet, F.B.; van der Wiel, M.J. How to Realize Uniform Three–Dimensional Ellipsoidal Electron Bunches. Phys. Rev. Lett. 2004, 93, 1–4. Available online: https://research.tue.nl/en/publications/how-to-realize-uniform-three-dimensional-ellipsoidal-electron-bun (accessed on 12 September 2023). [CrossRef] [PubMed]
- Sten, J.C.-E.; Fragoyiannis, G.; Vafeas, P.; Koivisto, P.K.; Dassios, G. Theoritical development of theoritical cross—Sectional hyperboloidal harmonics and their applications to electrostatics. J. Math. Phys. 2017, 58, 1–19. Available online: https://helda.helsinki.fi/server/api/core/bitstreams/a9bf3294-c601-4fc5-88cf-e88c57b212cf/content (accessed on 15 September 2023). [CrossRef]
- Vafeas, P.; Papadopoulos, P.Κ.; Lesselier, D. Electromagnetic low-frequency dipolar excitation of two metal spheres in a conductive medium. J. Appl. Math. 2012, 2012, 628261. Available online: https://downloads.hindawi.com/journals/jam/2012/628261.pdf?_gl=1*8jk5r0*_ga*MTk5NzM3MDg2MS4xNjk1MTMzMjAz*_ga_NF5QFMJT5V*MTY5NTEzMzIwMy4xLjEuMTY5NTEzMzU2Ny42MC4wLjA.&_ga=2.132599182.1206054273.1695133203-1997370861.1695133203 (accessed on 15 September 2023). [CrossRef]
- Vafeas, P.; Sten, J.C.-E.; Chatjigeorgiou, I.K. On the electrostatic potential for the two-hyperboloid and double-cone of a single sheet with elliptic cross-section. Q. J. Mech. Appl. Math. 2021, 74, 117–135. Available online: https://academic.oup.com/qjmam/article-abstract/74/1/117/6150373 (accessed on 16 September 2023). [CrossRef]
- Vafeas, P.; Perrusson, G.; Lesselier, D. Low-frequency scattering from perfectly conducting spheroidal bodies in a conductive medium with magnetic dipole excitation. Int. J. Eng. Sci. 2009, 47, 372–390. Available online: https://www.researchgate.net/publication/222923079_Low-frequency_scattering_from_perfectly_conducting_spheroidal_bodies_in_a_conductive_medium_with_magnetic_dipole_excitation (accessed on 16 September 2023). [CrossRef]
- Perrusson, G.; Vafeas, P.; Chatjigeorgiou, I.Κ.; Lesselier, D. Low-frequency on-site identification of a highly conductive body buried in Earth from a model ellipsoid. IMA J. Appl. Math. 2015, 80, 963–980. Available online: https://www.researchgate.net/publication/274162167_Low-frequency_on-site_identification_of_a_highly_conductive_body_buried_in_Earth_from_a_model_ellipsoid (accessed on 16 September 2023). [CrossRef]
- Derbenev, I.N.; Filippov, A.V.; Stace, A.J.; Besley, E. Electrostatic interactions between spheroidal dielectric particles. J. Chem. Phys. 2020, 152, 024121. Available online: https://pubmed.ncbi.nlm.nih.gov/31941309/ (accessed on 16 September 2023). [CrossRef] [PubMed]
- Shaozhong, D. Electrostatic potential of point charges inside dielectric oblate spheroids. J. Electrost. 2009, 67, 807–814. Available online: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2764543/pdf/nihms132122.pdf (accessed on 16 September 2023).
- Deakin, R.E.; Hunter, M.N. Geometric Geodesy, Part A; School of Mathematical and Geospatial Sciences, RMIT University: Melbourne, Australia, 2013; p. 52. Available online: http://www.mygeodesy.id.au/documents/Geometric%20Geodesy%20A(2013).pdf (accessed on 12 September 2023).
- Heiskanen, W.; Moritz, H. Physical Geodesy; W. H. Freeman and Company: San Francisco, CA, USA; London, UK, 1967; pp. 69, 73, 196. Available online: https://archive.org/details/HeiskanenMoritz1967PhysicalGeodesy (accessed on 12 September 2023).
- Jekeli, C. Geometric Reference Systems in Geodesy; Division of Geodetic Science, School of Earth Sciences, Ohio State University: Columbus, OH, USA, 2016; pp. 2–23. Available online: https://kb.osu.edu/bitstream/handle/1811/77986/Geom_Ref_Sys_Geodesy_2016.pdf (accessed on 2 September 2023).
- Arfken, G. Mathematical Methods for Physicists, 2nd ed.; Academic Press: New York, NY, USA, 1970; pp. 80–81. Available online: https://www.math.lsu.edu/~shipman/courses/11B-2057/Arfken1970.pdf (accessed on 12 September 2023).
- Miloh, T. A note on the potential of an homogeneous ellipsoid in ellipsoidal coordinates. J. Phys. A Math. Gen. 1990, 23, 581–584. Available online: https://www.academia.edu/20738928/A_note_on_the_potential_of_a_homogeneous_ellipsoid_in_ellipsoidal_coordinates (accessed on 15 September 2023). [CrossRef]
- Yakovlev, B.A.; Federyaeva, V.S. Analytical Solution for the Electric Field Response Generated by a non Conductive Ellispoid (Prolate Sphereoid) in a Conductiong Fluid Subject to an External Electric Field, Brain and Human Body Modeling; Makarov, S.N., Noetscher, G.M., Nummenmaa, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; pp. 383–389. Available online: https://www.researchgate.net/publication/343482185_Analytical_Solution_for_the_Electric_Field_Response_Generated_by_a_Nonconducting_Ellipsoid_Prolate_Spheroid_in_a_Conducting_Fluid_Subject_to_an_External_Electric_Field/link/5f46e9b9458515a88b6e28f4/download (accessed on 2 October 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).