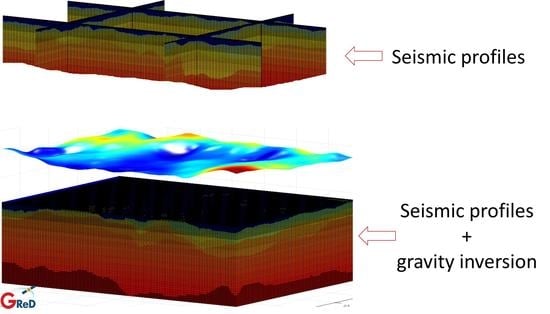
Seismic Constrained Gravity Inversion: A Reliable Tool to Improve Geophysical Models Away from Seismic Information
Abstract
:1. Introduction
- a local (smaller than m × m) area to be investigated;
- a good geological knowledge of the area available from previous studies;
- several seismic profiles or even 3D seismic available, properly constraining the shallowest geological structures and units;
- well logs to constrain density distribution in the shallowest layers;
- Moho and basement depths known with poor spatial resolution and accuracy.
- a large (greater than m × m) area to be investigated;
- a general geological knowledge of the area available from literature;
- few seismic profiles available, giving sparse information on the shallowest geological structures and units;
- few, or even no, constraints for the density distribution;
- Moho and basement depths known only from global models (such as the CRUST1.0 model [5]) but with poor spatial resolution and accuracy.
2. Methods
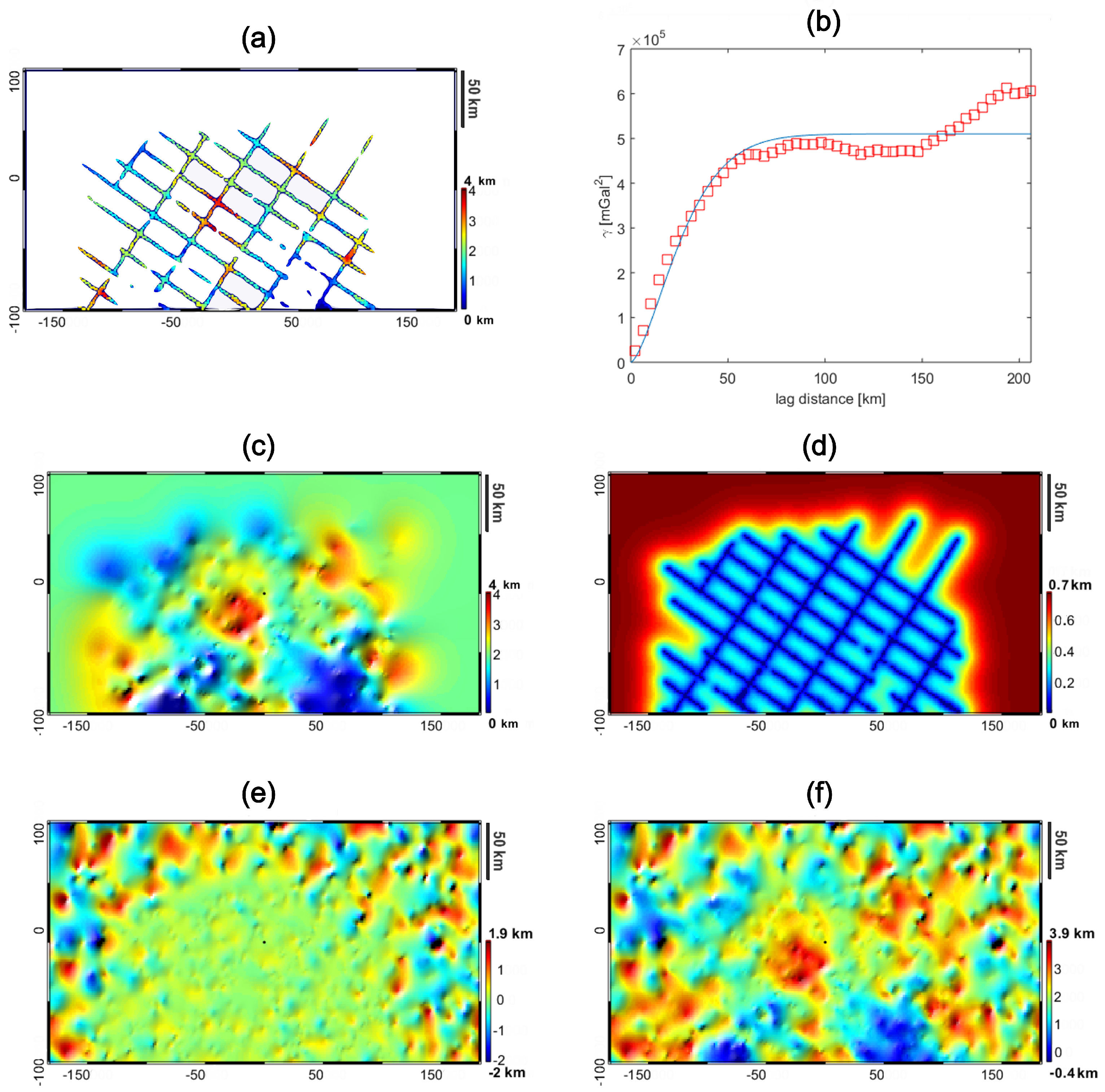
3. The Synthetic Case Study
- 1.
- we compute a thickness of each geological unit;
- 2.
- we estimate an empirical covariance of the thickness of each layer and interpolate it by means of Gaussian theoretical covariance function;
- 3.
- for each layer, we compute a new random thickness with the same stochastic characteristics of the original dataset by classical triangular decomposition of the covariance matrix [13];
- 4.
- we apply the same procedure to the first layer, namely the bathymetry;
- 5.
- finally, starting from the new bathymetry and thicknesses, we build a set of simulated seismic profiles with the same stochastic characteristics as the initial one.
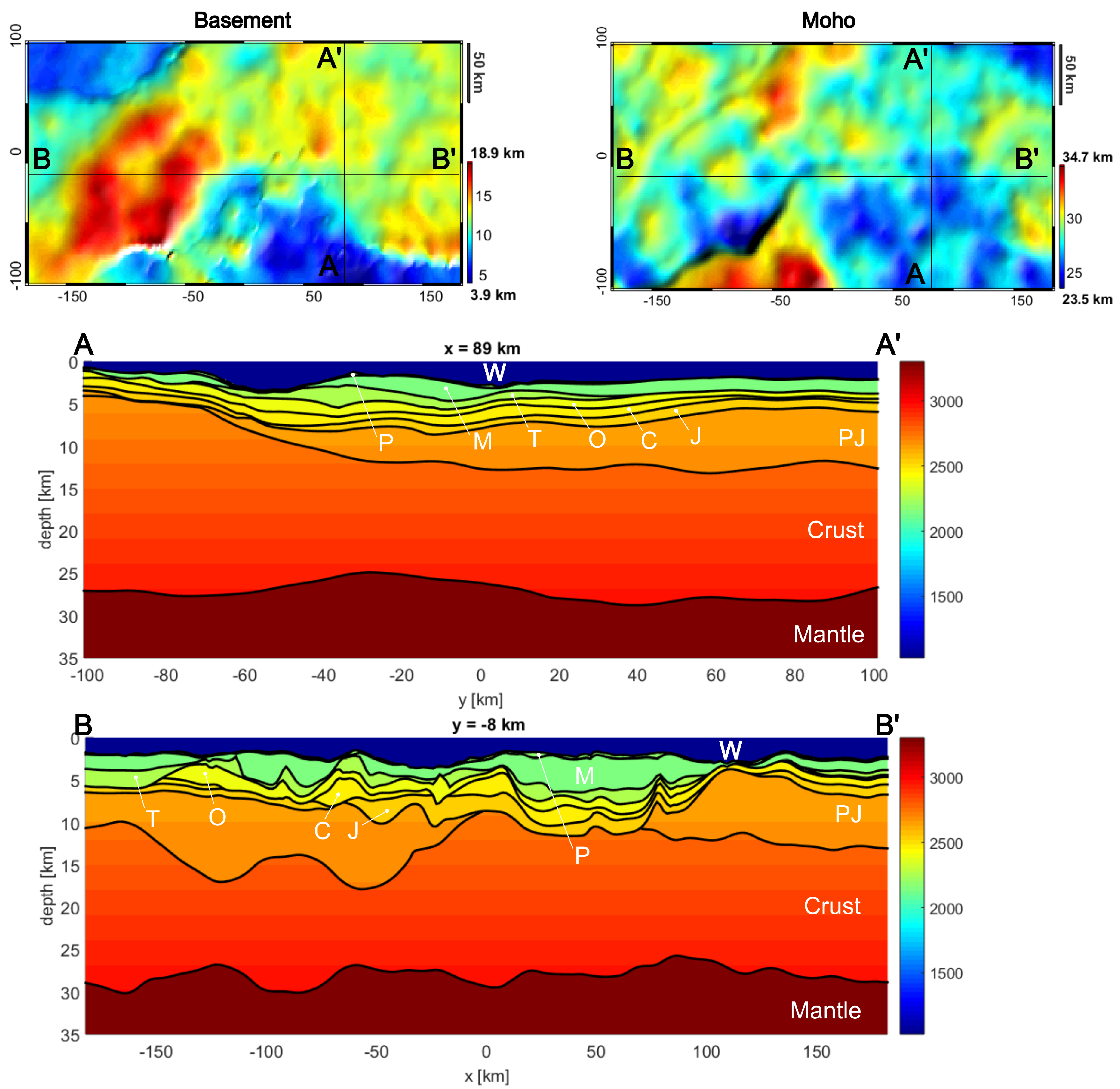
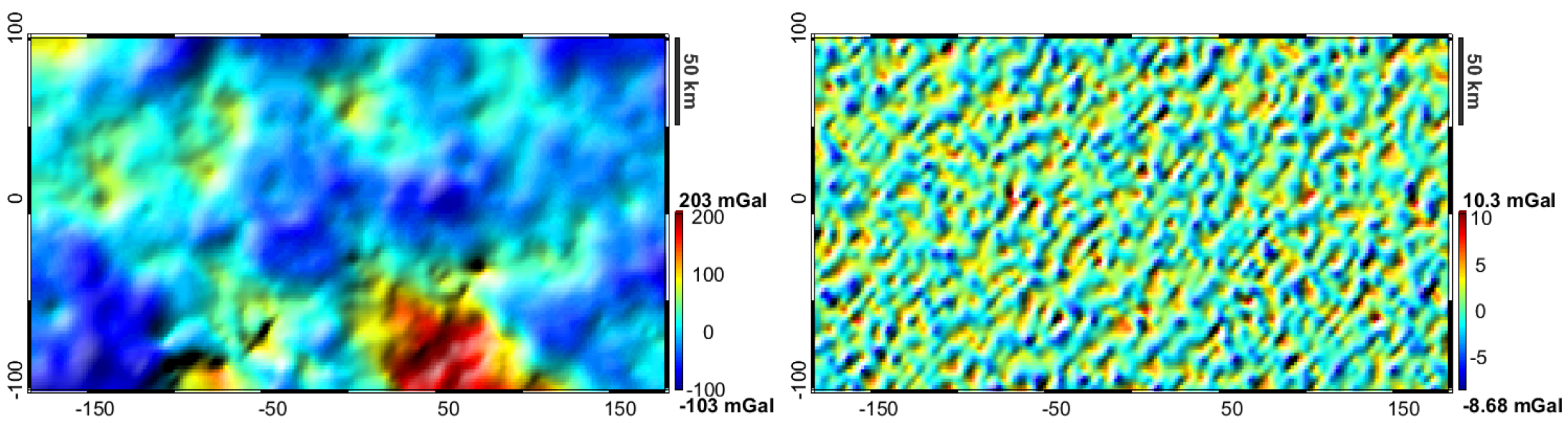
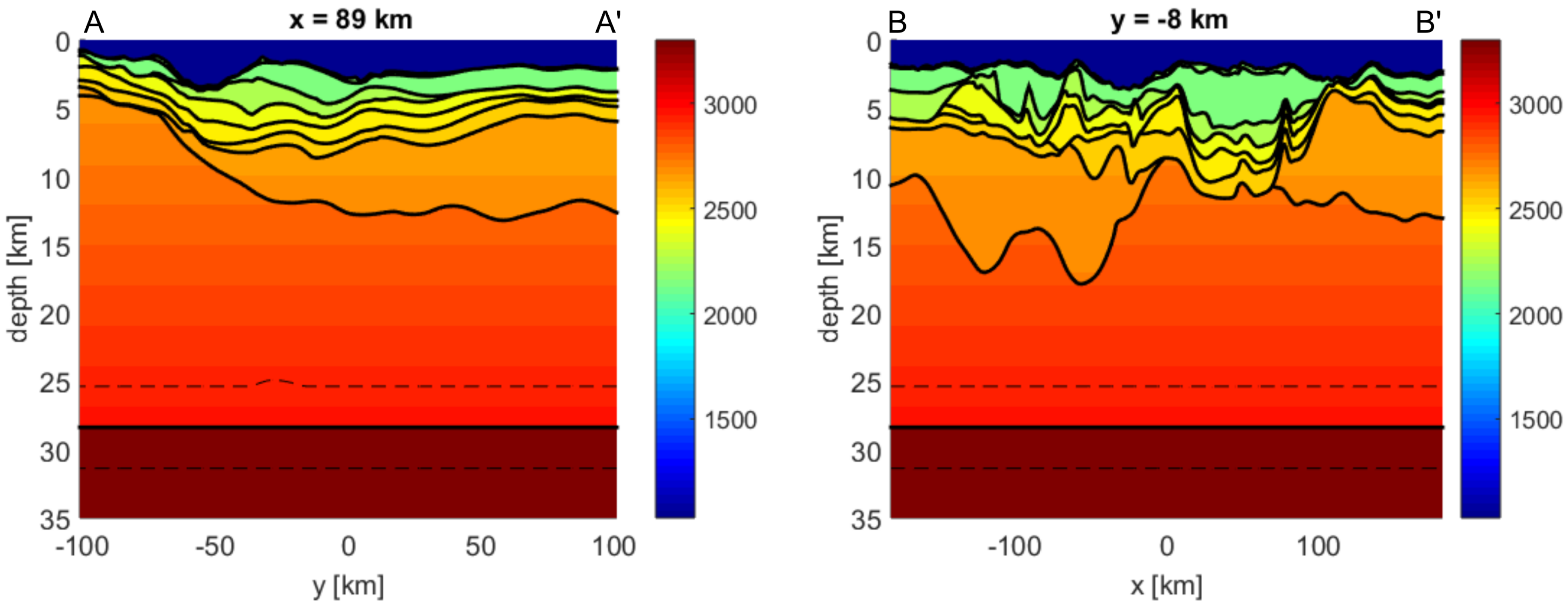
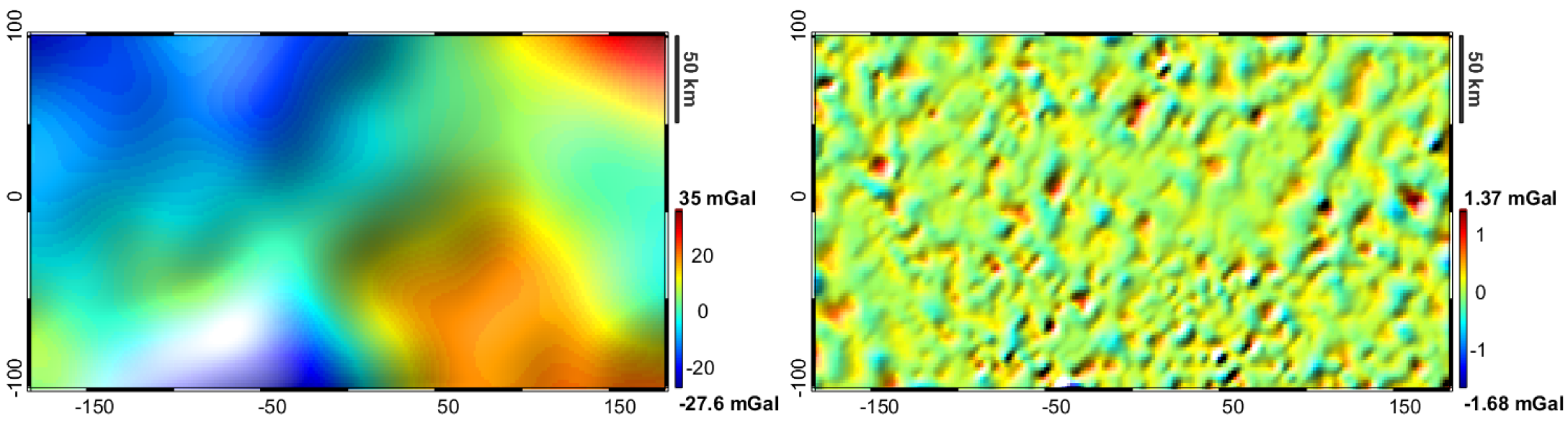
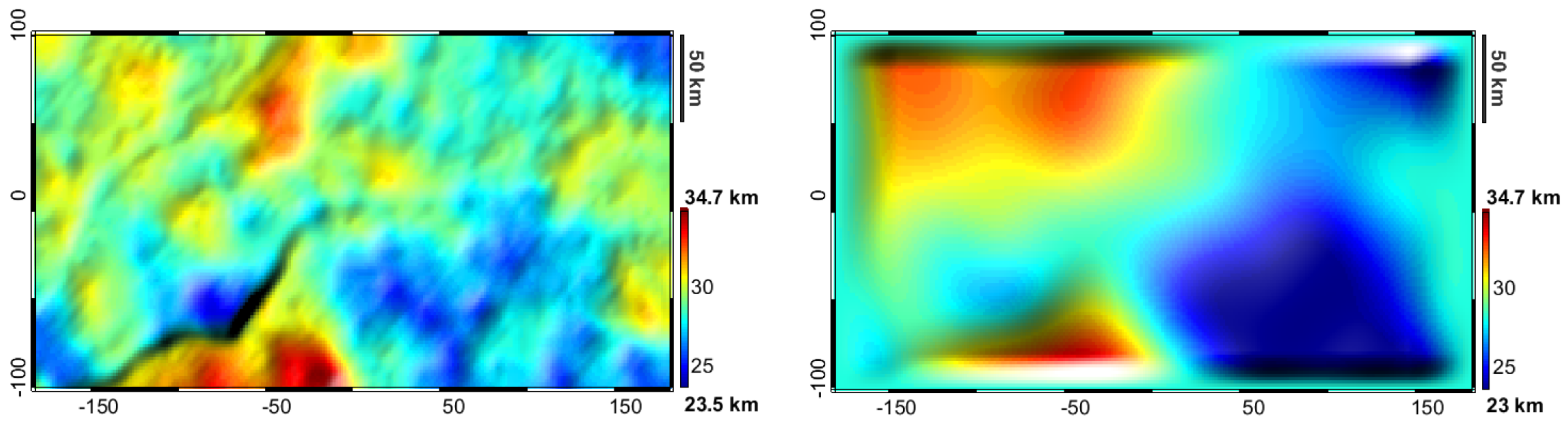
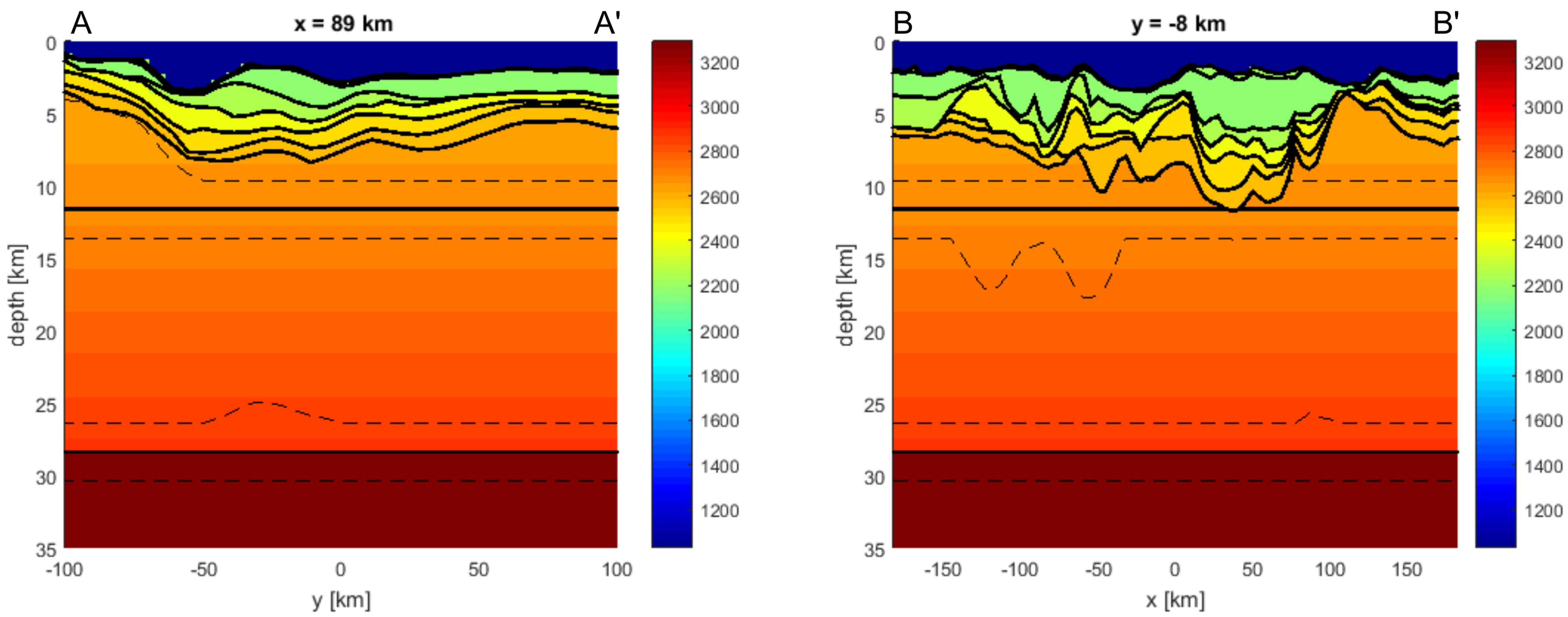
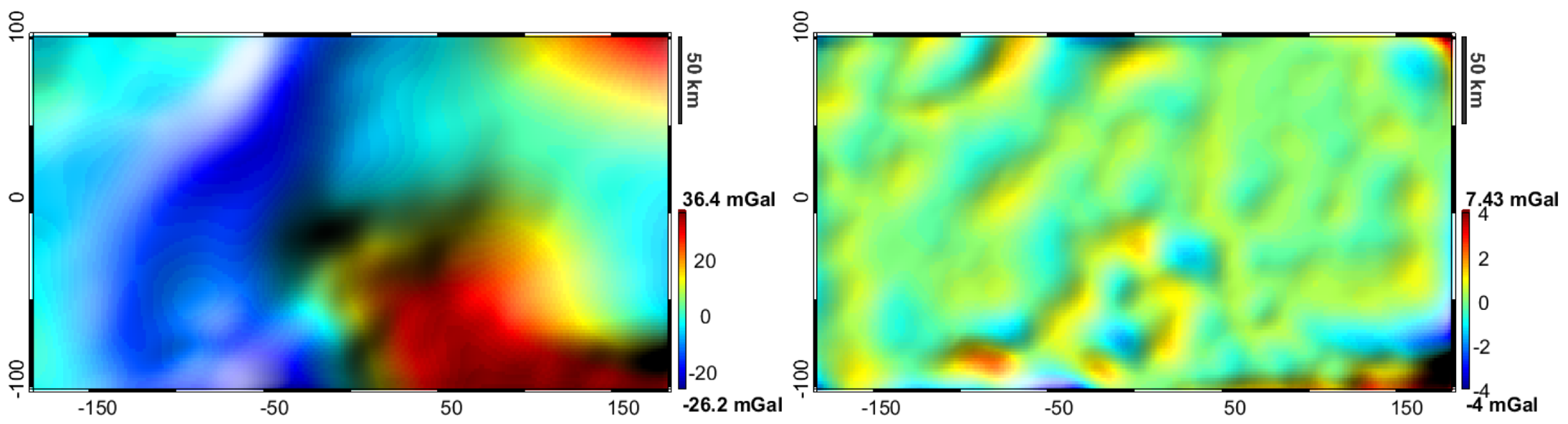
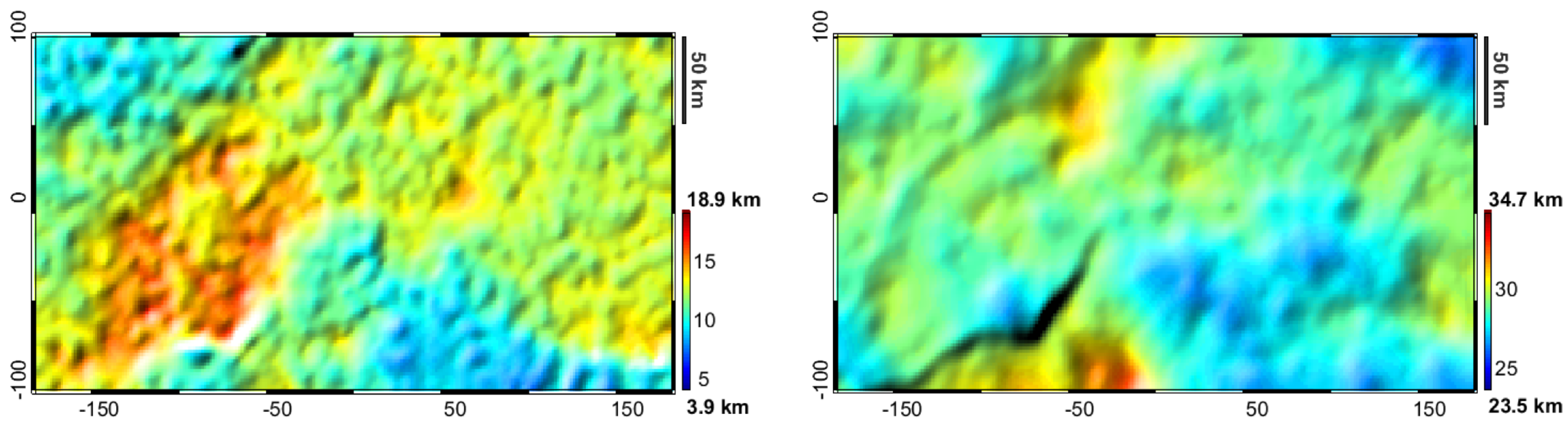
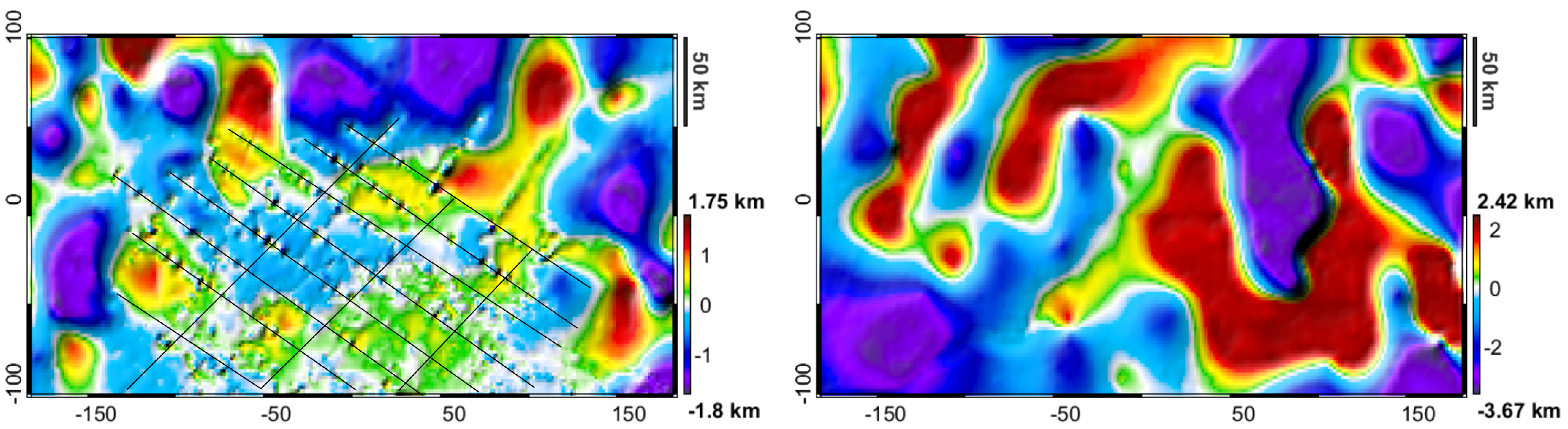
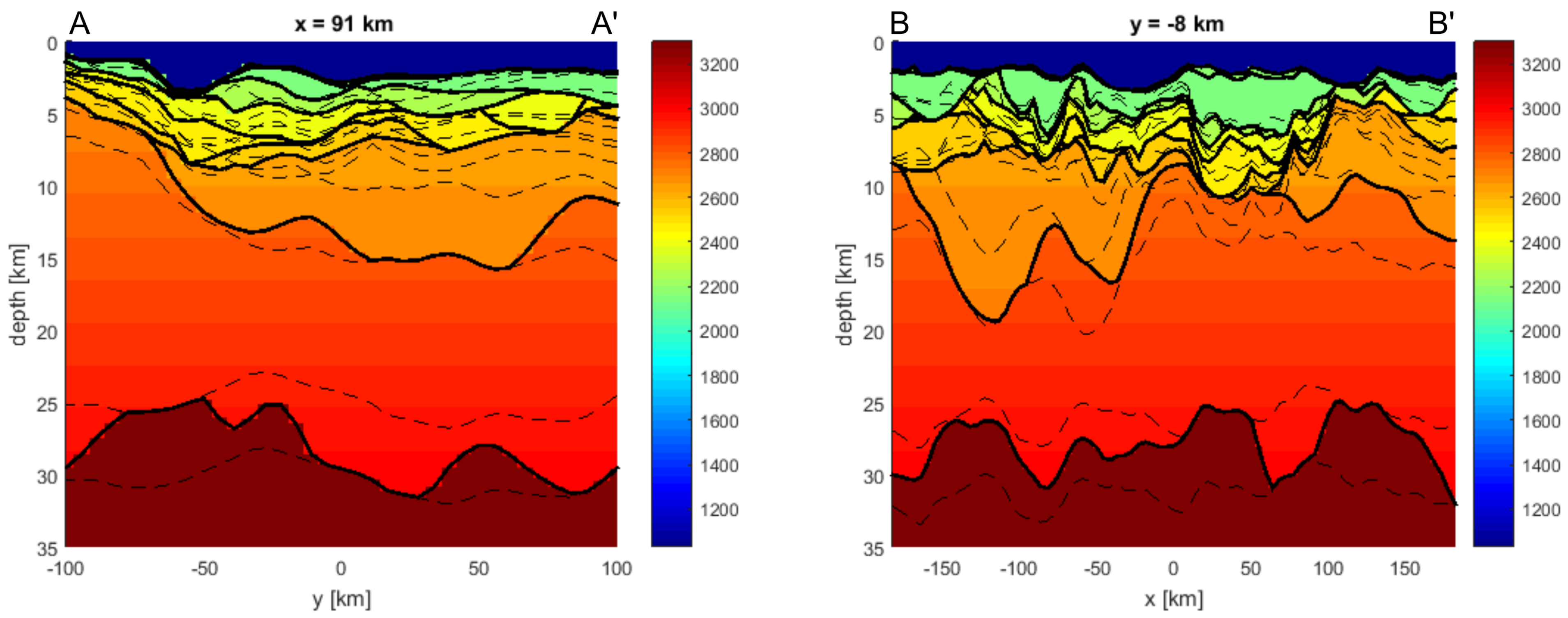
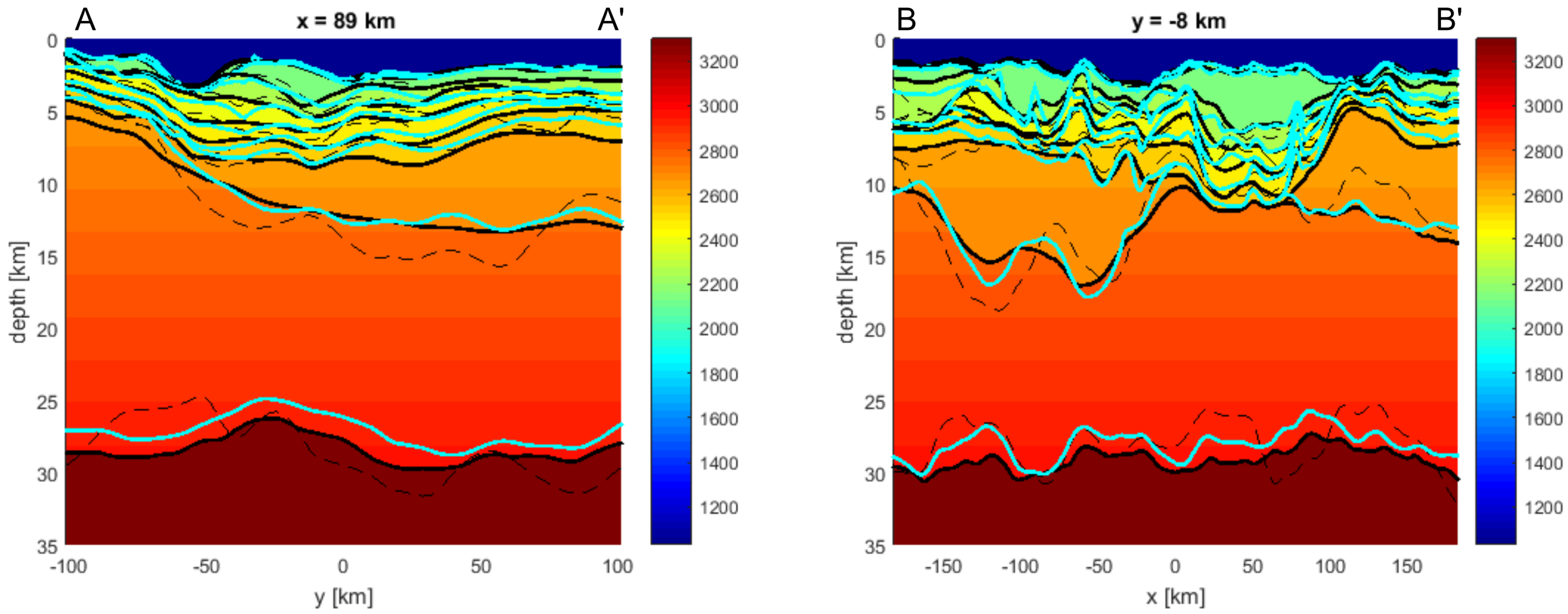
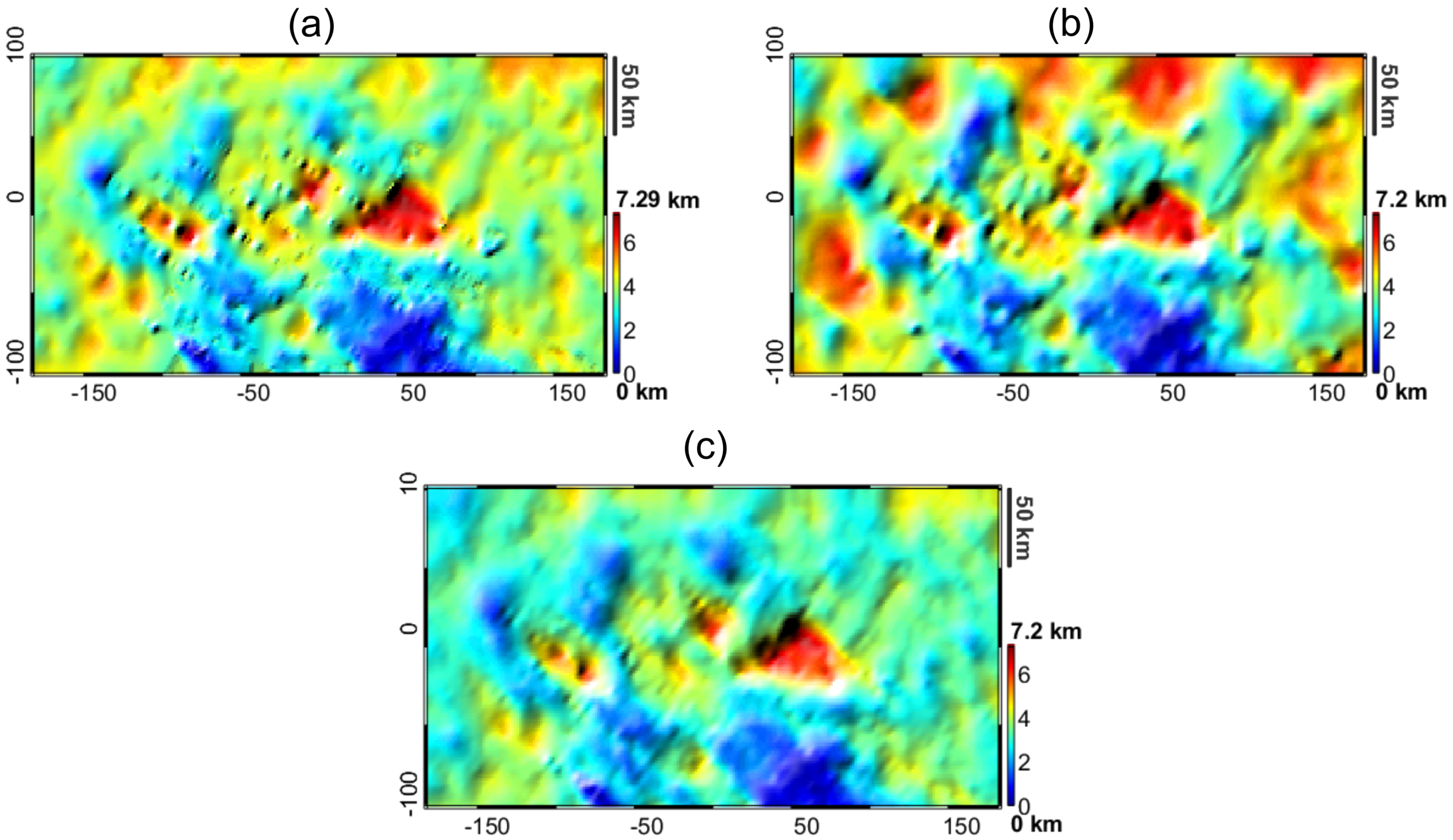
4. Results
4.1. Test 1: The Two-Layer Problem (Moho Estimate)
4.2. Scenario 1: Advanced Modelling of Deepest Layers (Basement and Moho Estimate)
4.3. Scenario 2: Exploration in Frontier Areas (Shallowest Layers Fixed in Few Points)
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Simulation of Non-Stationary Random Fields
- 1
- we compute the empirical variogram, using the available interpreted seismic profiles data as observations;
- 2
- we fit the empirical variogram by means of a proper theoretic variogram function;
- 3
- knowing the theoretical variogram, we can estimate a map of the depth of the considered geological unit and its predicted accuracy by means of a kriging solution;
- 4
- we randomly select on the obtained map a set of points;
- 5
- we extract a random value on each of the points obtained at step 4 from a Gaussian probability function with a STD equal to the one predicted by the kriging map on that specific location;
- 6
- we spatially correlate the extracted sample by applying a kriging procedure on the random points with the same variogram function estimated at step 2.
References
- Reguzzoni, M.; Sampietro, D. GEMMA: An Earth crustal model based on GOCE satellite data. Int. J. Appl. Earth Obs. Geoinf. 2015, 35, 31–43. [Google Scholar] [CrossRef]
- Sampietro, D.; Capponi, M. Gravity for lIthosphere Architecture Determination and Analysis: The Central Eastern Mediterranean Case Study. Geophys. Prospect. 2021. [Google Scholar] [CrossRef]
- Ebbing, J.; Braitenberg, C.; Götze, H.J. Forward and inverse modelling of gravity revealing insight into crustal structures of the Eastern Alps. Tectonophysics 2001, 337, 191–208. [Google Scholar] [CrossRef]
- Zingerle, P.; Pail, R.; Gruber, T.; Oikonomidou, X. The combined global gravity field model XGM2019e. J. Geod. 2020, 94, 66. [Google Scholar] [CrossRef]
- Laske, G.; Masters, G.; Ma, Z.; Pasyanos, M. Update on CRUST1. 0—A 1-degree global model of Earth’s crust. Geophys. Res. Abstr. 2013, 15, 20132658abstrEGU. [Google Scholar]
- Sampietro, D.; Sanso, F. Uniqueness theorems for inverse gravimetric problems. In VII Hotine-Marussi Symposium on Mathematical Geodesy; Springer: Berlin/Heidelberg, Germany, 2012; pp. 111–115. [Google Scholar]
- Marchetti, P.; Sampietro, D.; Capponi, M.; Rossi, L.; Reguzzoni, M.; Porzio, F.; Sansò, F. Lithological constrained gravity inversion. A Bayesian approach. In Proceedings of the 81st EAGE Conference and Exhibition 2019, London, UK, 3–6 June 2019; pp. 1–5. [Google Scholar]
- Sansó, F.; Sampietro, D. Analysis of the Gravity Field: Direct and Inverse Problems; Birkhäuser: Basel, Switzerland, 2021. [Google Scholar]
- Robert, C.; Casella, G. Monte Carlo Statistical Methods; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Geman, S.; Geman, D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans. Pattern Anal. Mach. Intell. 1984, PAMI-6, 721–741. [Google Scholar] [CrossRef] [PubMed]
- Wackernagel, H. Multivariate Geostatistics: An Introduction with Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Sampietro, D.; Capponi, M.; Mansi, A.; Gatti, A.; Marchetti, P.; Sansò, F. Space-Wise approach for airborne gravity data modelling. J. Geod. 2017, 91, 535–545. [Google Scholar] [CrossRef] [Green Version]
- Davis, M.W. Production of conditional simulations via the LU triangular decomposition of the covariance matrix. Math. Geol. 1987, 19, 91–98. [Google Scholar]
- Nagy, D. The gravitational attraction of a right rectangular prism. Geophysics 1966, 31, 362–371. [Google Scholar] [CrossRef]
- Sampietro, D.; Capponi, M. Practical tips for 3D regional gravity inversion. Geosciences 2019, 9, 351. [Google Scholar] [CrossRef] [Green Version]
- Oldenburg, D.W. The inversion and interpretation of gravity anomalies. Geophysics 1974, 39, 526–536. [Google Scholar] [CrossRef]
- Ebadi, S.; Barzaghi, R.; Safari, A.; Bahroudi, A. Evaluation of different gravimetric methods to Moho recovery in Iran. Ann. Geophys. 2019, 62, GD561. [Google Scholar] [CrossRef]
- Reguzzoni, M.; Sampietro, D.; Rossi, L. The gravimetric contribution to the Moho estimation in the presence of vertical density variations. Rend. Lincei Sci. Fis. E Nat. 2020, 31, 69–81. [Google Scholar] [CrossRef]


| Layer | Average Depth [m] | Depth STD [m] | Correlation Length [m] |
|---|---|---|---|
| Bathymetry | 2010 | 730 | 24,000 |
| Base Plio-Quaternary | 2220 | 710 | 23,000 |
| Base Mess. Salt | 3550 | 970 | 26,000 |
| Base Tortonian | 4210 | 1460 | 29,000 |
| Base Oligocene | 4990 | 1550 | 26,000 |
| Base Creataceous | 5800 | 1480 | 28,000 |
| Base Jurassic | 6920 | 1680 | 26,000 |
| Basement | 11,610 | 2960 | 46,000 |
| Moho | 28,360 | 1730 | 31,000 |
| Layer | Average Density [kg/m] | Density Gradient [kg/m] |
|---|---|---|
| Water | 1030 | 0 |
| Plio-Quaternary | 2220 | 0 |
| Mess. Salt | 2160 | 0 |
| Tortonian | 2260 | 0 |
| Oligocene | 2400 | 0 |
| Creataceous | 2480 | 0 |
| Jurassic | 2550 | 0 |
| Pre-Jurassic | 2620 | 0.005 |
| Continental Crust | 2670 | 0.012 |
| Mantle | 3300 | 0 |
| Layer | Average Density [kg/m] | Density STD [kg/m] |
|---|---|---|
| Water | 1030 | 0 |
| Plio-Quaternary | 2206 | 10 |
| Mess. Salt | 2172 | 10 |
| Tortonian | 2251 | 10 |
| Oligocene | 2411 | 10 |
| Creataceous | 2473 | 10 |
| Jurassic | 2549 | 10 |
| Pre-Jurassic | 2614 | 22 |
| Continental Crust | 2680 | 31 |
| Mantle | 3321 | 31 |
| Layer | A-PRIORI vs. True Model | A-POSTERIORI vs. True Model | ||
|---|---|---|---|---|
| Mean [m] | STD [m] | Mean [m] | STD [m] | |
| Water | 0 | 0 | 0 | 0 |
| Base Plio-Quaternary | 0 | 100 | 0 | 85 |
| Base Mess. Salt | 150 | 659 | 47 | 378 |
| Base Tortonian | 323 | 742 | 94 | 393 |
| Base Oligocene | 316 | 883 | 168 | 409 |
| Base Cretaceous | 370 | 861 | 309 | 418 |
| Base Jurassic | 250 | 930 | 707 | 517 |
| Basement | 80 | 1718 | 267 | 818 |
| Moho | 361 | 1736 | 837 | 825 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sampietro, D.; Capponi, M. Seismic Constrained Gravity Inversion: A Reliable Tool to Improve Geophysical Models Away from Seismic Information. Geosciences 2021, 11, 467. https://doi.org/10.3390/geosciences11110467
Sampietro D, Capponi M. Seismic Constrained Gravity Inversion: A Reliable Tool to Improve Geophysical Models Away from Seismic Information. Geosciences. 2021; 11(11):467. https://doi.org/10.3390/geosciences11110467
Chicago/Turabian StyleSampietro, Daniele, and Martina Capponi. 2021. "Seismic Constrained Gravity Inversion: A Reliable Tool to Improve Geophysical Models Away from Seismic Information" Geosciences 11, no. 11: 467. https://doi.org/10.3390/geosciences11110467
APA StyleSampietro, D., & Capponi, M. (2021). Seismic Constrained Gravity Inversion: A Reliable Tool to Improve Geophysical Models Away from Seismic Information. Geosciences, 11(11), 467. https://doi.org/10.3390/geosciences11110467