Abstract
In this paper, the solution to the Dirichlet problem for the wave equation on the star graph is constructed. To begin, we solve the boundary value problem on the interval (on one edge of the graph). We use the generalized functions method to obtain the wave equation with a singular right-hand side. The solution to the Dirichlet problem is determined through the convolution of the fundamental solution with the singular right-hand side of the wave equation. Thus, the solution found on the interval is determined by the initial functions, boundary functions, and their derivatives (the unknown boundary functions). A resolving system of two linear algebraic equations in the space of the Fourier transform in time is constructed to determine the unknown boundary functions. Following inverse Fourier transforms, the solution to the Dirichlet problem of the wave equation on the interval is constructed. After determining all the solutions on all edges and taking the continuity condition and Kirchhoff joint condition into account, we obtain the solution to the wave equation on the star graph.
Keywords:
star graph; boundary vertices; internal vertex; Dirichlet problem; Kirchhoff joint condition; wave equation; Fourier transform; generalized functions MSC:
35R02; 35L05; 35L20
1. Introduction
Some mathematical physics problems of complex systems consisting of elements with different physical properties can be conveniently modeled by boundary value problems on graphs. The study of differential equations on graphs (or networks) was derived from various scientific sources. For the scattering problem of the free electrons, differential equations on graphs were investigated in the works of B.S. Pavlov [1,2] using extensional theory methods. Since then, there have been many papers studying the properties of differential equations on geometric graphs. By applying the method of the separation of variables to partial differential equations on a graph, we obtain a spectral problem of the Sturm–Liouville type on a graph, which has been studied by many authors (we refer the reader to the works of G. Lumer [3], J. von Below [4,5], S. Nicaise [6,7], and other authors [8,9,10,11]. In particular, we note the work of V.V. Provotorov [12], in which a good example of the application of the results of the Sturm–Liouville problem is given to model the oscillatory processes of an elastic mast with supporting elastic braces.
The wave equation is a very general mathematical model for a large number of physical processes that describe mechanical oscillations of various structures, electromagnetic field oscillations, and the propagation of acoustic waves in liquids and gases. The study of the wave equation on a geometric graph is relatively recent. One of the first works in this direction was the monograph by F. Ali-Mehmeti “Nonlinear waves in networks” [13]. In this work, the solution to the wave equation in a d’Alembert-type form was obtained for a graph with the structure of a cross composed of four identical edges. C. Cattaneo and L. Fontana [14] applied the idea of the d’Alembert formula and found the solution to the Cauchy problem for the wave equation on finite-weighted networks. These works differ from ours in that they used spectral theory, considered Cauchy problems, and obtained solutions in the form of a series of sines and cosines. J. Friedman and J-P. Tillich [15] studied the wave equation whose Laplacian is based on the edge on metric graphs. In this case, the values of the solution were given in terms of the Chebyshev polynomials of the normalized adjacency matrix. The difference between this paper and [16] is that in [16], a solution that depends on the initial values was obtained by introducing a set of oriented broken lines into the initial boundary value problem for the wave equation on a geometric graph. Our solution differs in that it has an integral representation and is expressed using the given initial and boundary values.
In the past few decades, most works have been devoted to the controllability, observability, and stabilization of elastic systems (we refer the reader to the works of Cox and Zuazua [17] and other authors [18,19,20]). In applications, there are problems associated with the generation of a certain mode of vibration in the system or with the damping of existing unwanted vibrations in various structures. One of the most frequently used methods for solving these problems is boundary control, in which through some mechanisms, the state of the system is controlled at the boundary or some part of it. In [21,22], the exact and approximate boundary controllability of the wave equation on a graph was studied and sufficient conditions were established on the spectrum of the Laplace operator on the graph. K. Ammari and coauthors proved that the solution to the wave equation on a tree graph decreases with time [23,24] if an absorbing boundary condition is imposed at one of the ends, additionally requiring the mutual irrationality of the signal propagation times through different sections (results of this kind in the literature are called solution stabilization). Schmidt [25] introduced a graphical rule (a rule for the arrangement of signs) that allows the solvability of the control problem for a linearized equation of plane oscillations of a two-dimensional network of strings to be established. We especially mention the works of S. Avdonin. A large number of works are devoted to control, observation, identification, and inverse problems of the wave equation on metric graphs (also on star graphs) (see [26,27,28,29]). The boundary control method, the leaf-peeling method, and the distributed-parameter system have been used to investigate problems of controllability, observability, and stability for the wave equation, but the method of generalized functions has not been used. As we mentioned before, different ODE and PDE problems on star graphs were considered in [12,13,29,30,31]. Now, let us explain how our work differs from the works mentioned above.
We consider the Dirichlet problem for a non-homogeneous wave equation with non-zero initial conditions on a star graph. The basic element for a wave equation on a graph is a finite-length edge; therefore, Dirichlet problems are considered on each edge. The novelty of this work is that a method of generalized functions has been developed to solve these problems [32,33,34]. This method transforms the Dirichlet boundary value problems on each edge into wave equations with a singular right-hand side in the space of generalized functions. In this case, the initial and boundary conditions are included in the wave equation as a density of simple and double layers on the right side. The fundamental solution to this equation, which satisfies certain damping and radiation conditions, is used to construct the solution to the original Dirichlet boundary value problem in the form of a convolution with a singular right-hand side of the wave equation. The regular integral representation of this convolution provides a solution to the Dirichlet problem. It allows us to construct resolving singular boundary integral equations to determine the unknown boundary functions as we approach the domain’s boundary. To solve these integral equations, we use the generalized Fourier transform in time and then solve algebraic equations to determine the Fourier transforms of the boundary functions. Following inverse Fourier transforms, solutions to the Dirichlet problems of the wave equations on each edge are constructed. After finding all solutions on all edges and taking into account the continuity and Kirchhoff joint conditions, we obtain the solution to the wave equation on the star graph with one nodal point.
The previous research conducted by the first author of this paper was related to potential theory [35,36,37,38,39]. Due to its theoretical and practical importance, the authors of this paper present the first joint study of the problem of partial differential equations in graph theory.
2. Statement of the Dirichlet Problem on the Star Graph
Let be a star graph with n edges, where is a set of vertices, is a set of edges, and each edge is identified with an interval (see Figure 1). The set of boundary vertices (the vertices of degree one) is denoted by , and the set of an internal vertex is . On each edge, we use the following notations: , , , etc.
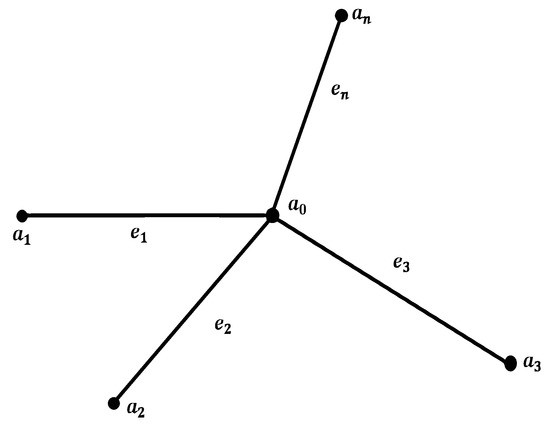
Figure 1.
A star graph G.
Now, we associate the following initial boundary value problem (IBVP) for the 1D wave equation on the graph G:
with the initial conditions:
and the Dirichlet boundary conditions:
and the continuity condition at the interior vertex
that is,
and the Kirchhoff joint condition at the interior vertex
that is,
To solve the Dirichlet problem on a star graph G with n edges, we introduce the concepts of shock waves, classical solutions, and generalized solutions. Then, we consider a boundary problem on any one edge .
3. Generalized Solutions to the Wave Equation, Shock Waves
We consider the 1D wave equation:
where is a local integrable function. Equation (9) is strictly hyperbolic and the class of its solutions contains discontinuous functions in the derivatives and . The discontinuity surfaces in Equation (9) are characteristic surfaces that satisfy the characteristic equation in :
Here, is the normal vector to . It corresponds to the following characteristics: . Thus, the wave fronts move at speed c in . Such wave fronts satisfy Hadamard’s conditions:
where we denote the jump of f on by :
The class of similar hyperbolic equation solutions is known as shock waves because functions and derivatives of functions have a jump on their fronts.
We consider functions that are continuous with derivatives up to the second order almost everywhere, with the exception of a finite or countable number of discontinuity surfaces, sufficiently smooth almost everywhere, and satisfy Hadamard’s conditions. We call such solutions classic solutions. It can be shown that these classic solutions are generalized solutions to (9) (see [32]).
4. Statement of the Dirichlet Problem on One Edge
We consider the 1D wave equation in the domain :
with the initial conditions:
and Dirichlet boundary conditions (IBVP1):
Let us move on to the space of generalized functions of slow growth to solve the Dirichlet problem on the interval . For this purpose, we introduce the characteristic function of the domain of the solution:
where
is a set characteristic function and
is the Heaviside function.
We also introduce regular generalized functions
where is a classic solution to the problem.
To solve this Dirichlet problem, we use the method of generalized functions [32,33,34]. For a regular function in the space of generalized functions of slow growth , we obtain a wave equation with a singular right-hand side:
where
and is a singular delta function.
The solution to the wave Equation (19) is determined using a convolution of the fundamental solution and the right-hand side . As a fundamental solution, we use the function , which satisfies the following equation:
and also satisfies the radiation conditions:
The solution to Equation (21) is the Riemann function:
A generalized solution to the given BVP is obtained using a convolution of the Riemann function with the right-hand side of the equation:
Using the property of convolutions with a delta function, we obtain the following integral results:
Due to the DuBois–Reymond lemma, we obtain the following theorem.
By analogy with the representation of solutions to the Laplace equation, this formula can be called the dynamic analog of Green’s formula.
As a result, the solution found depends on the initial functions, the boundary functions, and their derivatives (the unknown boundary functions). Now, we use the Fourier transform in time to determine the unknown boundary functions and .
5. Fourier Transform of the Solution with Respect to Time
It is convenient to use the direct Fourier transform in time and the inverse Fourier transform to solve the boundary equations, which have the following forms for :
where is the Fourier variable with respect to time. Using the properties of the Fourier transform of convolutions and derivatives, we obtain the Fourier transform of from (24):
Here, is the Fourier transform of the Riemann function in time.
For the 1D wave equation
the Fourier transform with respect to t yields
Consequently, we obtain the following solution in Fourier space:
If x in this formula tends to the left and right boundaries of the interval , we obtain linear algebraic equations to determine the unknown boundary functions and .
For , we obtain:
or
For , we obtain:
or
We can determine the unknown functions directly using Equations (39) and (41):
or Equations (39) and (41) can be rewritten in matrix form
where
are known as right-hand sides.
Equation (43) connects four boundary functions and allows us to determine two unknown boundary functions if any two are given. We substitute the inverse Fourier transforms of the boundary functions and into Formula (32) after determining their inverse Fourier transforms. As a result, we find the solution on the interval .
6. Determination of the Unknown Boundary Functions on the Graph with n Edges
For each edge , we obtain linear algebraic equations to determine the unknown boundary functions:
We also have continuity conditions at the interior vertex :
and the Kirchhoff joint condition at the interior vertex :
Theorem 2.
The resolving system of equations for the transformants of the Dirichlet problem on a star graph G with n edges has the form
where
and
Here, , , .
And the solution to System (47) is determined using the formula
Here, is the determinant of matrix A, and is the determinant of a matrix determined by the simple Cramer rule for each .
After determining all the boundary functions, we can determine the solutions of the graph G on each edge, as shown above for the solution on the interval. As a result, we have determined the solution of the wave equation on the star graph G.
7. An Example
In this section, we show how to determine the unknown boundary functions and ensure the satisfaction of continuity and the Kirchhoff conditions for a graph with two edges.
For edge , we obtain two linear algebraic equations to determine the unknown boundary functions and :
and to determine the unknown boundary functions and of the edge :
We also have a continuity condition at the interior vertex :
and the Kirchhoff joint condition at the interior vertex :
Theorem 3.
The resolving system of equations for the transformants of the Dirichlet problem on a star graph G with two edges has the form
where
and
We obtained the following results:
We use the inverse Fourier transforms to find the solutions for each edge. Then, we obtain the solution to the wave equation on the graph G with two edges.
8. Conclusions
In this work, we obtained the resolving system of equations using the generalized functions method and Fourier transforms for the solutions on each edge. This system connects four boundary values—the values of the function and its derivatives at the boundary points of each edge—and allows us to find a solution on each edge. Thus, the solution to the Dirichlet problem for the wave equation is constructed on the star graph with one nodal point where the continuity and Kirchhoff joint conditions are satisfied.
The constructed solutions in the space of Fourier transforms provide a solution to boundary value problems for stationary oscillations of a specific frequency, so they can be used to study the dynamics of structures under periodic impacts, which is also common in practice. It is also possible to study resonance phenomena in rod structures, which are associated with an increase in the amplitude of vibrations at certain frequencies, potentially leading to a loss of strength and the destruction of structures containing such rod elements. Simply find the control system’s determinant by frequency to accomplish this.
Author Contributions
Introduction and original problem, G.A. and L.A.; proof theorem, G.A., L.A., and D.A.; writing—review and editing, G.A.; project administration, G.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by the Ministry of High Education and Science of the Republic of Kazakhstan (Project AP09261033).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledge the financial support provided by the Ministry of High Education and Science of the Republic of Kazakhstan.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pavlov, B.S.; Faddeev, M.D. Model of free electrons and the scattering problem. Theor. Math. Phys. 1983, 55, 485–492. [Google Scholar] [CrossRef]
- Gerasimenko, N.I.; Pavlov, B.S. The scattering problem on noncompact graphs. Theor. Math. Phys. 1988, 74, 230–240. [Google Scholar] [CrossRef]
- Lumer, G. Connecting of local operators and evolution equations on networks. Lect. Notes Math. 1980, 787, 219–234. [Google Scholar] [CrossRef]
- Von Below, J. A characteristic equation accosiated to an eigenvalue problem on C2 networks. Linear Algebra Its Appl. 1985, 71, 309–325. [Google Scholar] [CrossRef]
- Von Below, J. Sturm-Liouville eigenvalue problems on networks. Math. Methods Appl. Sci. 1988, 10, 383–395. [Google Scholar] [CrossRef]
- Nicaise, S. Some results on spectral theory over networks, applied to nerve impuls transmission. Lect. Notes Math. 1985, 1771, 532–541. [Google Scholar] [CrossRef]
- Nicaise, S.; Penkin, O. Relationship between the lower frequency spectrum of plates and networks of beams. Math. Methods Appl. Sci. 2000, 23, 1389–1399. [Google Scholar] [CrossRef]
- Ali Mehmeti, F. A characteristion of generalized C∞- notion on nets. Int. Equ. Oper. Theory 1986, 9, 753–766. [Google Scholar] [CrossRef]
- Borovskikh, A.V.; Lazarev, K.P. Fourth-order differential equations on geometric graphs. J. Math. Sci. 2004, 119, 719–738. [Google Scholar] [CrossRef]
- Provotorov, V.V. Expansion in eigenfunctions of the Sturm–Liouville problem on a bundle graph. Russ. Math. 2008, 52, 45–57. [Google Scholar] [CrossRef]
- Freiling, G.; Ignatiev, M.Y.; Yurko, V.A. An inverse spectral problem for Sturm-Liouville operators with singular potentials on star-type graph. Proc. Symp. Pure Math. 2008, 77, 397–408. [Google Scholar]
- Provotorov, V.V. Eigenfunctions of the Sturm-Liouville problem on a star graph. Sb. Math. 2008, 199, 1523–1545. [Google Scholar] [CrossRef]
- Ali Mehmeti, F. Nonlinear Waves in Networks; Mathematical Research; Akademie-Verlag: Berlin, Germany, 1996. [Google Scholar]
- Cattaneo, C.; Fontana, L. D’Alembert formula on finite one dimensional networks. J. Math. Anal. Appl. 2003, 284, 403–424. [Google Scholar] [CrossRef]
- Friedman, J.; Tillich, J.-P. Wave equations for graphs and the edge-based Laplacian. Pac. J. Math. 2004, 216, 229–266. [Google Scholar] [CrossRef]
- Korovina, O.V.; Pryadiev, V.L. Structure of mixed problem solution for wave equation on compact geometrical graph in nonzero initial velocity case. Izv. Saratov Univ. Math. Mech. Inform. 2009, 9, 37–46. [Google Scholar] [CrossRef]
- Cox, S.; Zuazua, E. The rate at which energy decays in a damped string. Commun. in Partial Diff. Equ. 1994, 19, 213–243. [Google Scholar] [CrossRef]
- Komornik, V.; Zuazua, E. A direct method for the boundary stabilization of the wave equation. J. Math. Pures Appl. 1990, 69, 33–54. [Google Scholar]
- Xu, G.Q.; Guo, B.Z. Riesz basis property of evolution equations in Hilbert spaces and application to a coupled string equation. SIAM J. Control Optim. 2003, 42, 966–984. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, L.Q. Vibration control of an axially moving string system: Wave cancellation method. Appl. Math. Comput. 2006, 175, 851–863. [Google Scholar] [CrossRef]
- Dager, R.; Zuazua, E. Spectral boundary controllability of networks of strings. Comptes Rendus Math. 2002, 334, 545–550. [Google Scholar] [CrossRef]
- Zuazua, E. Control and stabilization of waves on 1-d networks. Lect. Notes Math. 2013, 2062, 463–493. [Google Scholar]
- Ammari, K.; Jellouli, M. Remark on stabilization of tree-shaped networks of strings. Appl. Math 2007, 52, 327–343. [Google Scholar] [CrossRef]
- Ammari, K.; Jellouli, M.; Khenissi, M. Stabilization of generic trees of strings. J. Dyn. Control Syst. 2005, 11, 177–193. [Google Scholar] [CrossRef]
- Schmidt, E.J.P.G. On the modelling and exact controllability of networks of vibrating strings. SIAM J. Control Optim. 1992, 30, 229–245. [Google Scholar] [CrossRef]
- Avdonin, S.A.; Zhao, Y. Exact controllability of the 1-D wave equation on finite metric tree graphs. Appl. Math. Optim. 2021, 83, 2303–2326. [Google Scholar] [CrossRef]
- Avdonin, S.A.; Nicaise, S. Source identification problems for the wave equation on graphs. Inverse Probl. 2015, 31, 095007. [Google Scholar] [CrossRef]
- Avdonin, S.A. Control, observation and identification problems for the wave equation on metric graphs. IFAC-PapersOnLine 2019, 52, 52–57. [Google Scholar] [CrossRef]
- Avdonin, S.A.; Avdonina, N.; Zhao, Y. Exact controllability for the wave equation on star graphs. IFAC-PapersOnLine 2019, 52, 30–35. [Google Scholar] [CrossRef]
- Kanguzhin, B.; Auzerkhan, G. Conjugation conditions for systems of differential equations of different orders on a star graph. Symmetry 2022, 14, 1761. [Google Scholar] [CrossRef]
- Band, R.; Gnutzmann, S.; Krueger, A.J. On the nodal structure of nonlinear stationary waves on star graphs. Symmetry 2019, 11, 185. [Google Scholar] [CrossRef]
- Alexeyeva, L.A. The method of generalized functions in non-stationary boundary value problems for the wave equation. Math. J. 2006, 6, 16–32. [Google Scholar]
- Alexeyeva, L.A.; Arepova, G.D. Generalized solutions of boundary value problems for the d’Alembert equation with local and associated boundary conditions. Bull. L.N. Gumilyov ENU. Math. Comput. Sci. Mech. Ser. 2022, 138, 23–35. (In Russian) [Google Scholar] [CrossRef]
- Alexeyeva, L.A.; Akhmetzhanova, M.M. Spatially one-dimensional boundary value problems of coupled thermoelasticity: Generalized functions method. Mech. Solids 2022, 57, 2151–2165. [Google Scholar] [CrossRef]
- Kal’menov, T.S.; Otelbaev, M.; Arepova, G.D. Bitsadze-Samarskii boundary conditions for an elliptic-parabolic volume potential with smooth matching. Differ. Equ. 2020, 56, 740–755. [Google Scholar] [CrossRef]
- Kal’menov, T.S.; Arepova, G.D. Representation of solution of the Dirichlet problem for the Laplace equation in the form of a generalized convolution. Complex Var. Elliptic Equ. 2018, 64, 816–824. [Google Scholar] [CrossRef]
- Kal’menov, T.S.; Otelbaev, M.; Arepova, G.D. Bitsadze-Samarskii boundary condition for elliptic-parabolic volume potential. Dokl. Math. 2018, 97, 223–226. [Google Scholar] [CrossRef]
- Kal’menov, T.S.; Arepova, G.D.; Arepova, D.D. Bitsadze-Samarskii boundary condition of the volume potential for an elliptic-parabolic equation with a scalar parameter. Electron. J. Differ. Equ. 2018, 2018, 1–14. Available online: https://hdl.handle.net/10877/15329 (accessed on 15 September 2023).
- Kal’menov, T.S.; Arepova, G.D. Quasi-Spectral decomposition of the heat potential. Electron. J. Differ. Equ. 2016, 2016, 1–4. Available online: https://hdl.handle.net/10877/16948 (accessed on 15 September 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).