A Many-Objective Evolutionary Algorithm Based on Indicator and Decomposition
Abstract
1. Introduction
- 1.
- We use the indicator to achieve population convergence in the early stage so that the population can obtain the approximate PF. The maintenance of diversity is made for the obtained population through uniformly generated reference points, which make the final population possess good diversity.
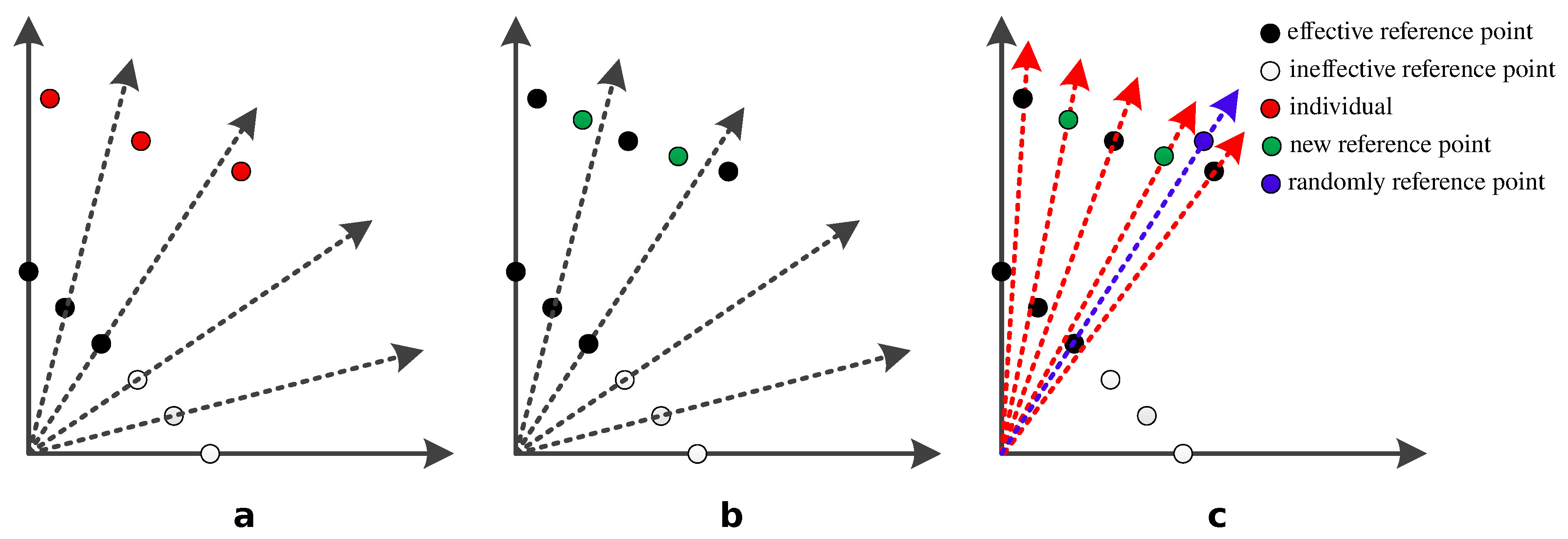
- 2.
- We propose an adaptive reference-point adjustment strategy based on the learning population for irregular PFs. A new reference-point set is generated through learning the population selected by the environment, and then the newly generated reference point set is used to select individuals for the next evolution.
- 3.
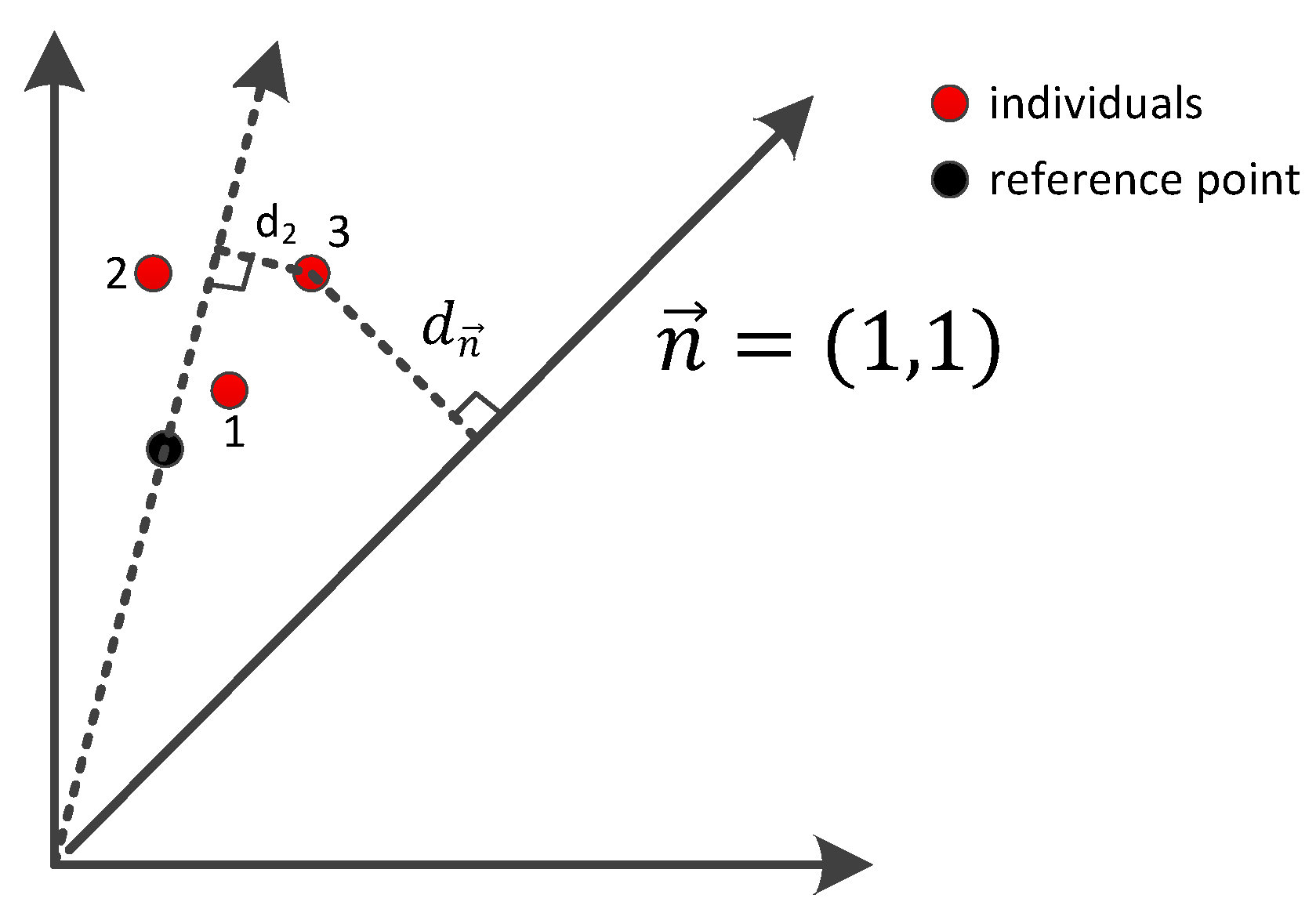
- In order to maintain the diversity of the final solutions, we introduce a diversity-maintenance mechanism based on the vertical distance to the normal vector. Compared with other methods, this method is good at sharp tail PF shapes. Simulation experiments are carried out to verify the effectiveness of the proposed algorithm.
2. Preliminaries
2.1. Indicator
2.2. Penalty Boundary Intersection (PBI) Method
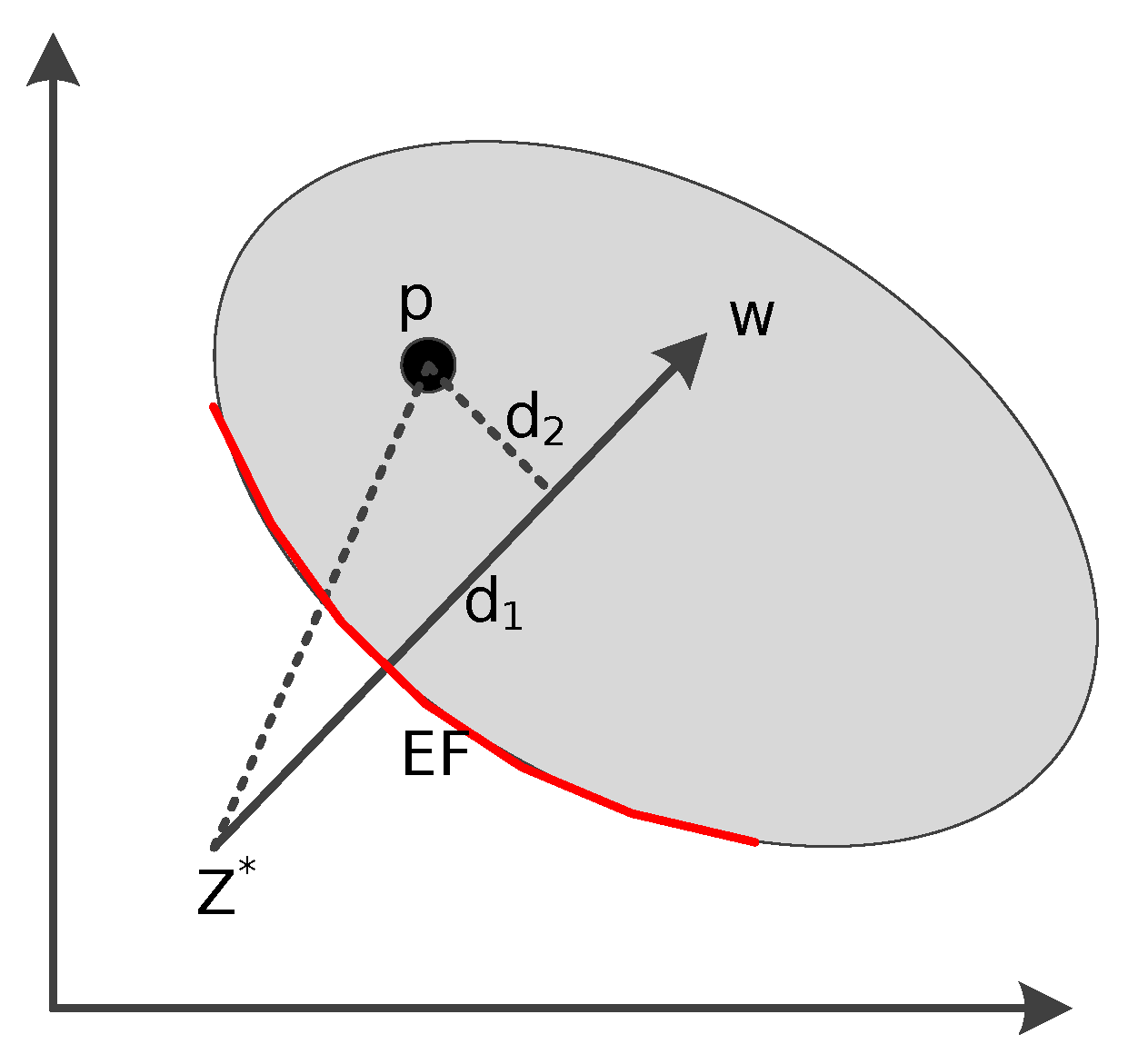
2.3. Motivation
3. Proposed Algorithm
3.1. Framework
| Algorithm 1 The framework of IDEA. |
|
3.2. Learning Population
| Algorithm 2 Learning Population. |
|
3.3. Environmental Selection
| Algorithm 3 Environmental selection. |
|
3.4. Handling Irregular Problem
3.5. Computational Complexity of One Generation of IDEA
| Algorithm 4 The procedure of handling irregular PFs. |
|
4. Experimental Design and Analysis
4.1. Experimental Settings
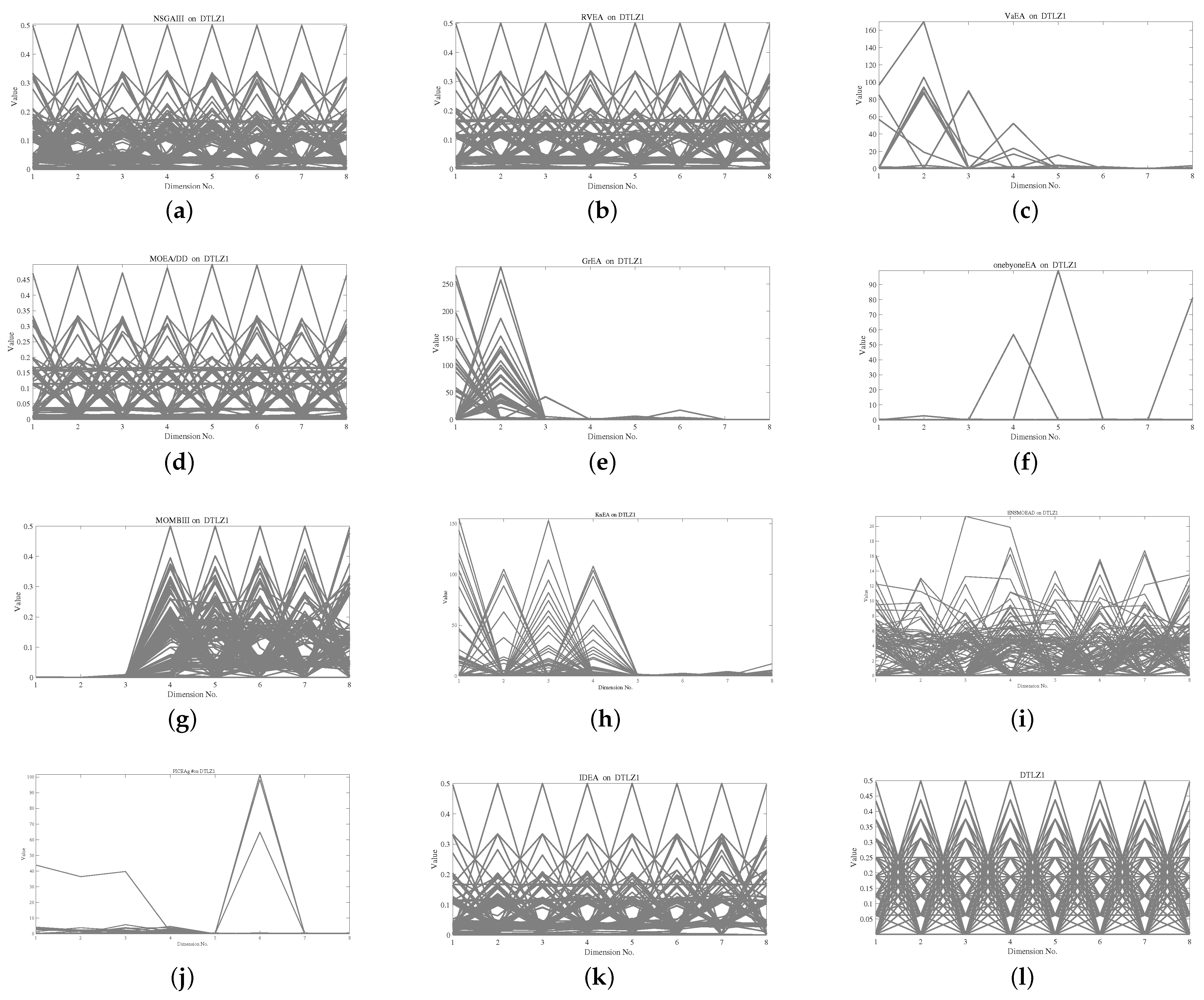
4.2. Comparisons between IDEA and Existing MOEAs
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Giagkiozis, I.; Purshouse, R.C.; Fleming, P.J. An overview of population-based algorithms for multi-objective optimisation. Int. J. Syst. Sci. 2015, 46, 1572–1599. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the strength Pareto evolutionary algorithm. TIK-Report 2001, 103. [Google Scholar]
- Corne, D.W.; Jerram, N.R.; Knowles, J.D.; Oates, M.J. PESA-II: Region-based selection in evolutionary multiobjective optimization. In Proceedings of the 3rd Annual Conference on Genetic and Evolutionary Computation, San Francisco, CA, USA, 7–11 July 2001; pp. 283–290. [Google Scholar]
- Li, M.; Yang, S.; Liu, X. Diversity comparison of Pareto front approximations in many-objective optimization. IEEE Trans. Cybern. 2014, 44, 2568–2584. [Google Scholar] [CrossRef]
- Li, B.; Li, J.; Tang, K.; Yao, X. Many-objective evolutionary algorithms: A survey. ACM Comput. Surv. (CSUR) 2015, 48, 13. [Google Scholar] [CrossRef]
- Liang, Z.; Hu, K.; Ma, X.; Zhu, Z. A many-objective evolutionary algorithm based on a two-round selection strategy. IEEE Trans. Cybern. 2019, 51, 1417–1429. [Google Scholar] [CrossRef] [PubMed]
- Cui, Z.; Chang, Y.; Zhang, J.; Cai, X.; Zhang, W. Improved NSGA-III with selection-and-elimination operator. Swarm Evol. Comput. 2019, 49, 23–33. [Google Scholar] [CrossRef]
- Hadka, D.; Reed, P. Borg: An auto-adaptive many-objective evolutionary computing framework. Evol. Comput. 2013, 21, 231–259. [Google Scholar] [CrossRef]
- Yang, S.; Li, M.; Liu, X.; Zheng, J. A grid-based evolutionary algorithm for many-objective optimization. IEEE Trans. Evol. Comput. 2013, 17, 721–736. [Google Scholar] [CrossRef]
- Zou, J.; Fu, L.; Zheng, J.; Yang, S.; Yu, G.; Hu, Y. A many-objective evolutionary algorithm based on rotated grid. Appl. Soft Comput. 2018, 67, 596–609. [Google Scholar] [CrossRef]
- Elarbi, M.; Bechikh, S.; Gupta, A.; Said, L.B.; Ong, Y.S. A new decomposition-based NSGA-II for many-objective optimization. IEEE Trans. Syst. Man Cybern. Syst. 2017, 48, 1191–1210. [Google Scholar] [CrossRef]
- Yuan, Y.; Xu, H.; Wang, B.; Yao, X. A new dominance relation-based evolutionary algorithm for many-objective optimization. IEEE Trans. Evol. Comput. 2015, 20, 16–37. [Google Scholar] [CrossRef]
- He, Z.; Yen, G.G.; Zhang, J. Fuzzy-based Pareto optimality for many-objective evolutionary algorithms. IEEE Trans. Evol. Comput. 2013, 18, 269–285. [Google Scholar] [CrossRef]
- Kukkonen, S.; Lampinen, J. Ranking-dominance and many-objective optimization. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 3983–3990. [Google Scholar]
- While, L.; Hingston, P.; Barone, L.; Huband, S. A faster algorithm for calculating hypervolume. IEEE Trans. Evol. Comput. 2006, 10, 29–38. [Google Scholar] [CrossRef]
- Zhou, A.; Jin, Y.; Zhang, Q.; Sendhoff, B.; Tsang, E. Combining model-based and genetics-based offspring generation for multi-objective optimization using a convergence criterion. In Proceedings of the 2006 IEEE International Conference on Evolutionary Computation, Vancouver, BC, Canada, 16–21 July 2006; pp. 892–899. [Google Scholar]
- Yuan, J.; Liu, H.L.; Gu, F.; Zhang, Q.; He, Z. Investigating the Properties of Indicators and an Evolutionary Many-objective Algorithm Based on a Promising Region. IEEE Trans. Evol. Comput. 2020, 25, 75–86. [Google Scholar] [CrossRef]
- Liang, Z.; Luo, T.; Hu, K.; Ma, X.; Zhu, Z. An indicator-based many-objective evolutionary algorithm with boundary protection. IEEE Trans. Cybern. 2020, 51, 4553–4566. [Google Scholar] [CrossRef]
- Bader, J.; Zitzler, E. HypE: An algorithm for fast hypervolume-based many-objective optimization. Evol. Comput. 2011, 19, 45–76. [Google Scholar] [CrossRef] [PubMed]
- Igel, C.; Hansen, N.; Roth, S. Covariance matrix adaptation for multi-objective optimization. Evol. Comput. 2007, 15, 1–28. [Google Scholar] [CrossRef]
- Tian, Y.; Cheng, R.; Zhang, X.; Cheng, F.; Jin, Y. An indicator-based multiobjective evolutionary algorithm with reference point adaptation for better versatility. IEEE Trans. Evol. Comput. 2017, 22, 609–622. [Google Scholar] [CrossRef]
- Zitzler, E.; Künzli, S. Indicator-based selection in multiobjective search. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Birmingham, UK, 18–22 September 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 832–842. [Google Scholar]
- Zhang, Q.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2013, 18, 577–601. [Google Scholar] [CrossRef]
- Li, K.; Deb, K.; Zhang, Q.; Kwong, S. An evolutionary many-objective optimization algorithm based on dominance and decomposition. IEEE Trans. Evol. Comput. 2014, 19, 694–716. [Google Scholar] [CrossRef]
- Cheng, R.; Jin, Y.; Olhofer, M.; Sendhoff, B. A reference vector guided evolutionary algorithm for many-objective optimization. IEEE Trans. Evol. Comput. 2016, 20, 773–791. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Sakane, Y.; Tsukamoto, N.; Nojima, Y. Evolutionary many-objective optimization by NSGA-II and MOEA/D with large populations. In Proceedings of the 2009 IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009; pp. 1758–1763. [Google Scholar]
- Liu, H.L.; Gu, F.; Zhang, Q. Decomposition of a multiobjective optimization problem into a number of simple multiobjective subproblems. IEEE Trans. Evol. Comput. 2013, 18, 450–455. [Google Scholar] [CrossRef]
- Li, K.; Zhang, Q.; Kwong, S.; Li, M.; Wang, R. Stable matching-based selection in evolutionary multiobjective optimization. IEEE Trans. Evol. Comput. 2013, 18, 909–923. [Google Scholar]
- Wu, M.; Li, K.; Kwong, S.; Zhang, Q. Evolutionary many-objective optimization based on adversarial decomposition. IEEE Trans. Cybern. 2018, 50, 753–764. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Setoguchi, Y.; Masuda, H.; Nojima, Y. Performance of decomposition-based many-objective algorithms strongly depends on Pareto front shapes. IEEE Trans. Evol. Comput. 2016, 21, 169–190. [Google Scholar] [CrossRef]
- Li, M.; Yang, S.; Liu, X. Pareto or Non-Pareto: Bi-Criterion Evolution in Multiobjective Optimization. IEEE Trans. Evol. Comput. 2016, 20, 645–665. [Google Scholar] [CrossRef]
- Qi, Y.; Ma, X.; Liu, F.; Jiao, L.; Sun, J.; Wu, J. MOEA/D with adaptive weight adjustment. Evol. Comput. 2014, 22, 231–264. [Google Scholar] [CrossRef]
- Jain, H.; Deb, K. An evolutionary many-objective optimization algorithm using reference-point based nondominated sorting approach, part II: Handling constraints and extending to an adaptive approach. IEEE Trans. Evol. Comput. 2013, 18, 602–622. [Google Scholar] [CrossRef]
- Das, S.S.; Islam, M.M.; Arafat, N.A. Evolutionary algorithm using adaptive fuzzy dominance and reference point for many-objective optimization. Swarm Evol. Comput. 2019, 44, 1092–1107. [Google Scholar] [CrossRef]
- Asafuddoula, M.; Singh, H.K.; Ray, T. An enhanced decomposition-based evolutionary algorithm with adaptive reference vectors. IEEE Trans. Cybern. 2017, 48, 2321–2334. [Google Scholar]
- Cai, X.; Mei, Z.; Fan, Z. A decomposition-based many-objective evolutionary algorithm with two types of adjustments for direction vectors. IEEE Trans. Cybern. 2017, 48, 2335–2348. [Google Scholar] [PubMed]
- Zou, J.; Liu, J.; Yang, S.; Zheng, J. A many-objective evolutionary algorithm based on rotation and decomposition. Swarm Evol. Comput. 2021, 60, 100775. [Google Scholar] [CrossRef]
- Wansasueb, K.; Pholdee, N.; Panagant, N.; Bureerat, S. Multiobjective meta-heuristic with iterative parameter distribution estimation for aeroelastic design of an aircraft wing. Eng. Comput. 2022, 38, 695–713. [Google Scholar] [CrossRef]
- Duman, S.; Akbel, M.; Kahraman, H.T. Development of the multi-objective adaptive guided differential evolution and optimization of the MO-ACOPF for wind/PV/tidal energy sources. Appl. Soft Comput. 2021, 112, 107814. [Google Scholar] [CrossRef]
- Das, I.; Dennis, J.E. Normal-boundary intersection: A new method for generating the Pareto surface in nonlinear multicriteria optimization problems. SIAM J. Optim. 1998, 8, 631–657. [Google Scholar] [CrossRef]
- Liu, Y.; Gong, D.; Sun, J.; Jin, Y. A many-objective evolutionary algorithm using a one-by-one selection strategy. IEEE Trans. Cybern. 2017, 47, 2689–2702. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhou, Y.; Li, M.; Chen, Z. A vector angle-based evolutionary algorithm for unconstrained many-objective optimization. IEEE Trans. Evol. Comput. 2016, 21, 131–152. [Google Scholar] [CrossRef]
- Wang, R.; Purshouse, R.C.; Fleming, P.J. Preference-inspired coevolutionary algorithms for many-objective optimization. IEEE Trans. Evol. Comput. 2012, 17, 474–494. [Google Scholar] [CrossRef]
- Zhang, X.; Tian, Y.; Jin, Y. A knee point-driven evolutionary algorithm for many-objective optimization. IEEE Trans. Evol. Comput. 2014, 19, 761–776. [Google Scholar] [CrossRef]
- Zhao, S.Z.; Suganthan, P.N.; Zhang, Q. Decomposition-based multiobjective evolutionary algorithm with an ensemble of neighborhood sizes. IEEE Trans. Evol. Comput. 2012, 16, 442–446. [Google Scholar] [CrossRef]
- Deb, K.; Thiele, L.; Laumanns, M.; Zitzler, E. Scalable test problems for evolutionary multiobjective optimization. In Evolutionary Multiobjective Optimization; Springer: Berlin/Heidelberg, Germany, 2005; pp. 105–145. [Google Scholar]
- Cheng, R.; Li, M.; Tian, Y.; Zhang, X.; Yang, S.; Jin, Y.; Yao, X. A benchmark test suite for evolutionary many-objective optimization. Complex Intell. Syst. 2017, 3, 67–81. [Google Scholar] [CrossRef]
- Huband, S.; Hingston, P.; Barone, L.; While, L. A review of multiobjective test problems and a scalable test problem toolkit. IEEE Trans. Evol. Comput. 2006, 10, 477–506. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, R.B. Simulated binary crossover for continuous search space. Complex Syst. 1995, 9, 115–148. [Google Scholar]
- Deb, K.; Goyal, M. A combined genetic adaptive search (GeneAS) for engineering design. Comput. Sci. Inform. 1996, 26, 30–45. [Google Scholar]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Inselberg, A. Parallel Coordinates: Visual Multidimensional Geometry and Its Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009; Volume 20. [Google Scholar]


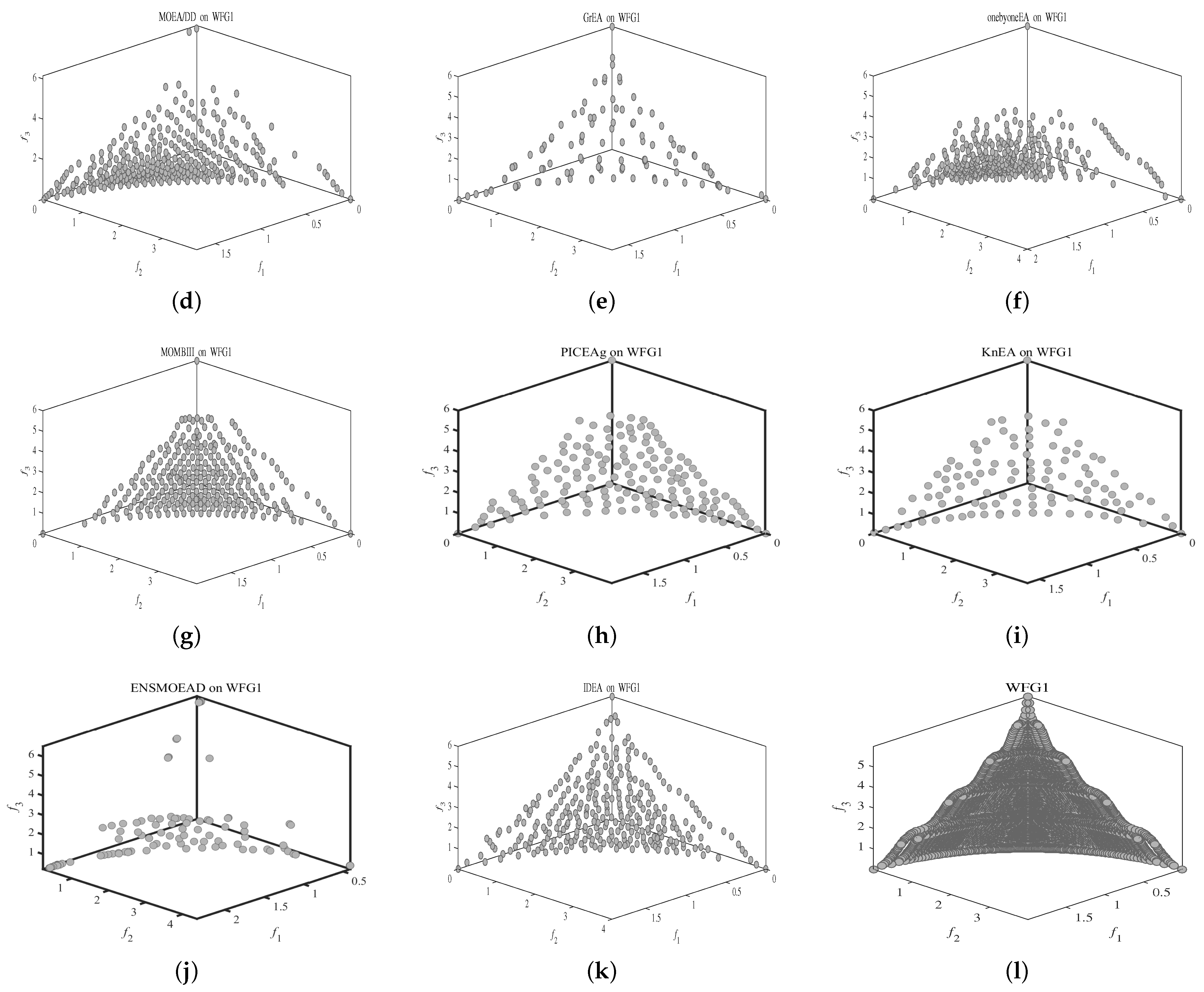
| Problem | Number of Objectives (M) | Number of Variables (D) | Number of Generations () | Pareto Front |
|---|---|---|---|---|
| Regular Pareto front | ||||
| DTLZ1 | 5, 8, 10, 15 | M-1 + 5 | 500 | Linear |
| DTLZ2, 3, 4 | 5, 8, 10, 15 | M-1 + 10 | 500 | Concave |
| WFG4–9 | 5, 8, 10, 15 | M-1 + 10 | 1000 | Concave |
| Irregular Pareto front | ||||
| IDTLZ1 | 5, 8, 10, 15 | M-1 + 5 | 500 | Inverted, Linear |
| IDTLZ2 | 5, 8, 10, 15 | M-1 + 10 | 500 | Inverted, Concave |
| MaF6 | 5, 8, 10, 15 | M-1 + 10 | 500 | Degenerate |
| MaF7 | 5, 8, 10, 15 | M-1 + 20 | 500 | Disconnected |
| WFG1 | 5, 8, 10, 15 | M-1 + 10 | 1000 | Sharp tails |
| WFG2 | 5, 8, 10, 15 | M-1 + 10 | 1000 | Disconnected, Sharp tails |
| WFG3 | 5, 8, 10, 15 | M-1 + 10 | 1000 | Mostly degenerate |
| Number of Objectives (M) | Parameter (, ) | Number of Reference Points |
|---|---|---|
| 5 | 5, 0 | 126 |
| 8 | 3, 2 | 156 |
| 10 | 2, 2 | 110 |
| 15 | 2, 1 | 135 |
| Problem | M | NSGA-III | RVEA | MOEA/DD | GrEA | VaEA | onebyoneEA | MOMBI-II | PICEAg | KnEA | ENSMOEAD | IDEA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DTLZ1 | 5 | 6.3579e-2 (3.85e-4) = | 6.3294e-2 (1.15e-4) = | 6.3401e-2 (8.52e-5) = | 1.6229e-1 (9.18e-2) - | 1.2004e-1 (3.17e-2) - | 6.8153e-2 (1.64e-3) - | 6.3953e-2 (6.33e-4) = | 1.2236e-1 (1.59e-2) - | 1.7083e-1 (6.03e-2) - | 3.1108e-1 (1.90e-1) - | 6.3303e-2 (5.15e-4) |
| 8 | 1.2970e-1 (3.44e-2) = | 9.7347e-2 (1.06e-3) = | 9.5979e-2 (4.47e-4) = | 3.3146e-1 (7.39e-2) - | 2.7398e-1 (1.60e-1) - | 1.1343e-1 (1.35e-3) = | 2.1015e-1 (5.20e-2) - | 2.3577e-1 (2.64e-2) - | 1.3277e+0 (1.39e+0) - | 1.7338e-1 (7.83e-2) = | 1.0871e-1 (1.21e-2) | |
| 10 | 2.3492e-1 (1.64e-1) = | 1.2014e-1 (1.47e-2) = | 1.1358e-1 (7.29e-4) = | 1.2515e+0 (3.79e+0) - | 4.1036e-1 (1.95e-1) - | 1.2826e-1 (1.45e-3) = | 2.7082e-1 (1.55e-2) = | 3.1488e-1 (1.99e-2) - | 8.2622e+0 (5.80e+0) - | 3.0006e-1 (3.21e-1) = | 1.4973e-1 (2.56e-2) | |
| 15 | 2.3085e-1 (8.85e-2) = | 1.5755e-1 (7.94e-3) + | 1.4322e-1 (6.16e-3) = | 8.6720e+0 (1.35e+1) - | 3.7561e-1 (1.46e-1) - | 1.4197e-1 (9.94e-4) = | 2.9004e-1 (4.07e-2) = | 3.4474e-1 (2.27e-2) - | 1.1018e+1 (1.18e+1) - | 3.4853e-1 (2.17e-1) - | 1.6428e-1 (2.86e-2) | |
| DTLZ2 | 5 | 1.9490e-1 (1.90e-5) = | 1.9489e-1 (1.30e-5) = | 1.9489e-1 (4.15e-6) = | 1.9783e-1 (1.14e-3) - | 1.9372e-1 (1.21e-3) = | 1.9012e-1 (1.66e-3) = | 1.9612e-1 (7.66e-4) - | 1.9555e-1 (1.28e-3) = | 2.1219e-1 (4.55e-3) - | 3.2430e-1 (1.63e-3) - | 1.9488e-1 (9.50e-6) |
| 8 | 3.1627e-1 (7.14e-4) = | 3.1545e-1 (1.06e-4) = | 3.1507e-1 (4.20e-5) = | 3.5079e-1 (1.19e-3) = | 3.6360e-1 (2.22e-3) - | 3.5058e-1 (2.68e-3) = | 3.3129e-1 (1.65e-2) = | 3.6333e-1 (1.81e-2) - | 3.8349e-1 (6.64e-3) - | 5.8962e-1 (1.01e-2) - | 3.1652e-1 (3.99e-4) | |
| 10 | 4.8207e-1 (5.61e-2) - | 4.3697e-1 (3.08e-4) = | 4.4032e-1 (1.85e-3) = | 5.0437e-1 (4.30e-2) - | 4.8172e-1 (2.29e-3) - | 4.5902e-1 (2.55e-3) - | 6.8130e-1 (1.29e-1) - | 6.0955e-1 (7.07e-2) - | 5.1013e-1 (1.11e-2) - | 7.0965e-1 (3.70e-2) - | 4.3528e-1 (1.12e-3) | |
| 15 | 6.4932e-1 (1.56e-2) = | 6.2480e-1 (1.76e-3) = | 6.2372e-1 (1.36e-3) = | 5.9445e-1 (3.01e-2) = | 6.0788e-1 (1.43e-2) = | 5.5700e-1 (2.97e-3) + | 8.5524e-1 (7.99e-2) - | 8.3260e-1 (6.06e-2) = | 6.1970e-1 (2.23e-2) = | 8.8875e-1 (5.53e-2) - | 6.2637e-1 (2.11e-3) | |
| DTLZ3 | 5 | 1.9490e-1 (1.90e-5) = | 1.9489e-1 (1.30e-5) = | 1.9489e-1 (4.15e-6) = | 1.9783e-1 (1.14e-3) - | 1.9372e-1 (1.21e-3) = | 1.9012e-1 (1.66e-3) = | 1.9612e-1 (7.66e-4) - | 1.9555e-1 (1.28e-3) = | 2.1219e-1 (4.55e-3) - | 3.2430e-1 (1.63e-3) - | 1.9488e-1 (9.50e-6) |
| 8 | 1.9608e+0 (1.94e+0) = | 3.3151e-1 (1.10e-2) + | 3.2659e-1 (1.99e-2) + | 4.0806e+0 (2.26e+0) = | 8.6398e+0 (4.63e+0) = | 3.5423e-1 (3.45e-3) + | 4.2977e-1 (1.19e-1) + | 8.1213e-1 (4.77e-2) = | 9.3434e+1 (2.44e+1) - | 2.2638e+0 (3.15e+0) = | 2.8971e+0 (2.57e+0) | |
| 10 | 4.6146e+0 (3.53e+0) = | 6.8382e-1 (4.15e-1) + | 5.6509e-1 (2.48e-1) + | 9.2386e+0 (7.11e+0) = | 1.8796e+1 (1.39e+1) = | 4.6564e-1 (5.15e-3) + | 9.9538e-1 (3.58e-2) + | 1.0152e+0 (6.17e-2) = | 3.3320e+2 (6.58e+1) = | 8.1495e+0 (2.37e+1) = | 5.8166e+0 (3.01e+0) | |
| 15 | 6.0731e+0 (3.14e+0) = | 8.4420e-1 (3.28e-1) + | 6.9215e-1 (2.23e-1) + | 1.6914e+2 (6.44e+1) = | 1.8080e+1 (7.81e+0) = | 5.6388e-1 (5.63e-3) + | 1.1035e+0 (9.91e-3) = | 1.1634e+0 (3.86e-2) = | 5.6540e+2 (1.47e+2) - | 1.2181e+1 (3.32e+1) = | 7.6826e+0 (1.25e+1) | |
| DTLZ4 | 5 | 2.5650e-1 (1.10e-1) = | 2.0620e-1 (5.05e-2) + | 1.9490e-1 (1.56e-5) + | 2.2107e-1 (6.74e-2) = | 1.9648e-1 (1.24e-3) = | 2.2626e-1 (7.90e-2) + | 2.0972e-1 (5.00e-2) = | 2.9342e-1 (1.48e-1) = | 2.0989e-1 (4.41e-3) + | 3.8789e-1 (2.73e-2) = | 4.6090e-1 (2.24e-1) |
| 8 | 3.6745e-1 (9.41e-2) = | 3.2211e-1 (2.49e-2) + | 3.2752e-1 (3.64e-2) + | 3.5110e-1 (1.30e-3) = | 3.6562e-1 (4.41e-3) = | 3.6388e-1 (3.11e-2) + | 3.6858e-1 (4.53e-2) = | 4.2356e-1 (6.31e-2) = | 3.7331e-1 (3.71e-3) = | 6.5963e-1 (3.73e-2) - | 3.9988e-1 (1.11e-1) | |
| 10 | 4.9913e-1 (7.82e-2) = | 4.5270e-1 (2.76e-2) + | 4.4793e-1 (2.71e-2) + | 4.8914e-1 (1.71e-2) = | 4.8594e-1 (3.67e-3) = | 4.9508e-1 (5.79e-2) = | 5.6311e-1 (6.31e-2) = | 6.0235e-1 (5.33e-2) = | 5.0342e-1 (7.96e-3) = | 8.3599e-1 (5.70e-2) - | 5.1001e-1 (5.53e-2) | |
| 15 | 6.4779e-1 (1.99e-2) = | 6.3015e-1 (4.32e-3) = | 6.4057e-1 (1.65e-2) = | 5.8066e-1 (5.86e-3) + | 6.0096e-1 (4.75e-3) + | 5.8340e-1 (1.92e-2) + | 6.5943e-1 (1.79e-2) = | 6.9469e-1 (3.12e-2) = | 6.1132e-1 (3.13e-3) = | 9.5200e-1 (3.77e-2) - | 6.3722e-1 (1.07e-2) | |
| WFG4 | 5 | 1.1776e+0 (7.09e-4) = | 1.1783e+0 (7.23e-4) = | 1.2413e+0 (4.71e-3) = | 1.1219e+0 (8.71e-3) = | 1.1078e+0 (8.19e-3) + | 1.7681e+0 (1.45e-1) - | 1.1891e+0 (2.24e-2) = | 1.0771e+0 (8.48e-3) + | 1.2237e+0 (1.69e-2) = | 2.9708e+0 (2.80e-1) - | 1.1797e+0 (9.17e-4) |
| 8 | 2.9601e+0 (2.83e-3) + | 2.9641e+0 (7.53e-3) + | 4.1537e+0 (1.44e-1) = | 2.8928e+0 (1.18e-2) + | 3.0197e+0 (3.82e-2) = | 4.3998e+0 (1.78e-1) = | 3.3146e+0 (4.04e-1) = | 3.4721e+0 (3.76e-1) = | 3.3876e+0 (4.15e-2) = | 4.6295e+0 (4.73e-1) = | 3.6083e+0 (7.19e-2) | |
| 10 | 5.1162e+0 (5.68e-2) = | 4.8764e+0 (3.79e-2) + | 6.9056e+0 (2.30e-1) = | 5.9090e+0 (3.34e-1) = | 4.8985e+0 (3.79e-2) + | 6.7965e+0 (2.32e-1) = | 8.8996e+0 (1.17e+0) - | 7.4339e+0 (5.58e-1) = | 5.4820e+0 (5.95e-2) = | 7.6371e+0 (5.04e-1) - | 6.2367e+0 (2.62e-1) | |
| 15 | 9.3505e+0 (6.06e-2) = | 9.2657e+0 (9.13e-2) = | 1.3658e+1 (2.95e-1) = | 9.8444e+0 (4.03e-1) = | 8.2096e+0 (1.07e-1) + | 1.1598e+1 (3.42e-1) = | 1.8664e+1 (1.44e+0) - | 1.5959e+1 (1.15e+0) - | 9.0052e+0 (1.50e-1) + | 1.3051e+1 (9.38e-1) = | 1.0986e+1 (6.17e-1) | |
| WFG5 | 5 | 1.1650e+0 (2.21e-4) = | 1.1659e+0 (3.25e-4) = | 1.2127e+0 (1.69e-3) = | 1.1133e+0 (8.64e-3) = | 1.1069e+0 (7.42e-3) = | 1.6716e+0 (1.15e-1) - | 1.2755e+0 (2.21e-2) - | 1.0693e+0 (5.96e-3) + | 1.2110e+0 (1.74e-2) = | 2.9120e+0 (1.54e-1) - | 1.1658e+0 (5.57e-4) |
| 8 | 2.9413e+0 (1.83e-3) + | 2.9496e+0 (7.27e-3) + | 3.9169e+0 (7.34e-2) = | 2.8884e+0 (2.00e-2) + | 3.0307e+0 (3.74e-2) = | 4.2639e+0 (1.90e-1) = | 3.5204e+0 (7.06e-2) = | 2.9082e+0 (1.73e-2) + | 3.3420e+0 (2.50e-2) = | 4.8479e+0 (1.27e-1) = | 3.6124e+0 (7.47e-2) | |
| 10 | 5.0775e+0 (7.09e-3) + | 4.8100e+0 (2.73e-2) + | 6.0792e+0 (1.33e-1) = | 6.0173e+0 (6.14e-1) = | 4.9262e+0 (4.02e-2) + | 6.7113e+0 (1.45e-1) = | 1.0592e+1 (4.42e+0) = | 6.2535e+0 (2.78e-1) = | 5.4942e+0 (5.02e-2) = | 7.3569e+0 (2.32e-1) = | 6.3355e+0 (8.78e-2) | |
| 15 | 9.2827e+0 (1.22e-2) = | 9.1763e+0 (5.79e-2) + | 1.2946e+1 (2.39e-1) = | 1.0056e+1 (3.01e-1) = | 8.0298e+0 (7.27e-2) + | 1.1416e+1 (1.97e-1) = | 2.4739e+1 (2.15e+0) - | 1.3123e+1 (6.29e-1) = | 8.9083e+0 (1.09e-1) + | 1.3049e+1 (1.03e+0) = | 1.2106e+1 (8.28e-1) | |
| WFG6 | 5 | 1.1626e+0 (1.22e-3) = | 1.1648e+0 (2.73e-3) + | 1.2146e+0 (6.05e-3) = | 1.1259e+0 (7.55e-3) = | 1.1241e+0 (7.24e-3) = | 2.0860e+0 (1.15e-1) - | 1.2307e+0 (1.04e-1) = | 1.0853e+0 (6.18e-3) + | 1.2409e+0 (3.27e-2) = | 2.5458e+0 (4.10e-1) - | 1.1651e+0 (3.03e-3) |
| 8 | 2.9460e+0 (3.14e-3) + | 2.9745e+0 (1.33e-2) = | 4.0810e+0 (6.91e-2) = | 2.9173e+0 (2.24e-2) + | 3.1392e+0 (5.51e-2) = | 4.9472e+0 (1.21e-1) = | 3.0881e+0 (1.91e-1) = | 2.9572e+0 (2.51e-2) + | 3.4861e+0 (6.04e-2) = | 5.5914e+0 (4.23e-1) - | 3.4471e+0 (1.34e-1) | |
| 10 | 5.0931e+0 (8.70e-3) + | 5.1861e+0 (1.96e-1) + | 6.4001e+0 (3.37e-1) = | 5.4470e+0 (3.92e-1) + | 4.9780e+0 (5.20e-2) + | 7.3785e+0 (1.33e-1) = | 6.4436e+0 (1.25e+0) = | 5.8329e+0 (3.57e-1) = | 5.9158e+0 (3.07e-1) = | 8.1136e+0 (4.51e-1) = | 6.4897e+0 (2.79e-1) | |
| 15 | 9.5190e+0 (6.29e-1) + | 9.5031e+0 (3.10e-1) = | 1.2851e+1 (3.43e-1) = | 8.9668e+0 (2.97e-1) + | 7.9192e+0 (6.76e-2) + | 1.2162e+1 (2.58e-1) = | 1.7353e+1 (1.61e+0) - | 1.2942e+1 (1.01e+0) = | 9.7071e+0 (6.34e-1) = | 1.3978e+1 (5.99e-1) = | 1.2311e+1 (4.41e-1) | |
| WFG7 | 5 | 1.1779e+0 (3.81e-4) = | 1.1786e+0 (1.09e-3) = | 1.2379e+0 (3.51e-3) = | 1.1359e+0 (9.07e-3) = | 1.1131e+0 (8.75e-3) + | 2.2694e+0 (1.21e-1) - | 1.2245e+0 (7.45e-2) = | 1.0844e+0 (6.80e-3) + | 1.2254e+0 (1.88e-2) = | 2.5592e+0 (2.61e-1) - | 1.1790e+0 (8.96e-4) |
| 8 | 2.9852e+0 (9.46e-2) + | 2.9885e+0 (1.73e-2) + | 3.6798e+0 (1.36e-1) = | 2.9043e+0 (1.41e-2) + | 3.0784e+0 (6.18e-2) = | 4.7805e+0 (1.97e-1) = | 3.0601e+0 (9.20e-2) + | 2.9893e+0 (1.36e-1) + | 3.3033e+0 (3.71e-2) = | 4.8939e+0 (2.67e-1) = | 3.6564e+0 (1.02e-1) | |
| 10 | 5.2801e+0 (2.80e-1) = | 4.9728e+0 (8.57e-2) + | 6.1055e+0 (1.52e-1) = | 5.3889e+0 (3.53e-1) = | 4.8913e+0 (4.64e-2) + | 7.0929e+0 (2.82e-1) = | 7.0331e+0 (1.26e+0) = | 5.8424e+0 (6.40e-1) = | 5.3193e+0 (1.14e-1) = | 7.8188e+0 (1.82e-1) - | 6.1075e+0 (2.30e-1) | |
| 15 | 9.2938e+0 (1.68e-1) = | 9.3590e+0 (8.87e-2) = | 1.3230e+1 (3.87e-1) = | 9.2634e+0 (4.00e-1) = | 8.0336e+0 (6.99e-2) + | 1.1447e+1 (5.49e-1) = | 1.6107e+1 (2.10e+0) - | 1.2709e+1 (1.49e+0) = | 8.6518e+0 (2.79e-1) + | 1.4471e+1 (1.06e+0) - | 1.0748e+1 (6.52e-1) | |
| WFG8 | 5 | 1.1472e+0 (1.02e-3) = | 1.1661e+0 (1.10e-3) = | 1.2162e+0 (5.84e-3) = | 1.1400e+0 (1.09e-2) = | 1.2054e+0 (1.74e-2) = | 1.8335e+0 (8.53e-2) - | 2.9663e+0 (2.33e-2) - | 1.1592e+0 (9.69e-3) = | 1.2972e+0 (1.82e-2) - | 3.3784e+0 (1.37e-1) - | 1.1650e+0 (7.49e-3) |
| 8 | 3.3276e+0 (2.49e-1) = | 3.0507e+0 (2.76e-2) = | 3.7669e+0 (2.90e-1) - | 3.0518e+0 (5.11e-2) = | 3.2510e+0 (3.13e-2) = | 4.5738e+0 (2.91e-1) - | 3.9781e+0 (2.19e-1) - | 3.6896e+0 (1.75e-1) - | 3.5565e+0 (5.96e-2) = | 5.5816e+0 (1.52e-1) - | 3.1320e+0 (4.87e-2) | |
| 10 | 5.2787e+0 (2.05e-1) = | 5.4241e+0 (1.50e-1) = | 6.2102e+0 (3.92e-1) = | 6.1006e+0 (5.27e-2) = | 5.1295e+0 (3.59e-2) = | 6.9828e+0 (3.19e-1) - | 9.8525e+0 (8.61e-1) - | 6.5333e+0 (3.65e-1) - | 5.6690e+0 (3.30e-1) = | 7.7547e+0 (3.17e-1) - | 5.4545e+0 (1.98e-1) | |
| 15 | 9.2269e+0 (3.50e-1) = | 9.3722e+0 (4.12e-1) = | 1.0130e+1 (1.41e+0) = | 1.0471e+1 (9.74e-2) = | 8.5626e+0 (1.43e-1) = | 1.1563e+1 (6.16e-1) = | 2.0496e+1 (1.31e+0) - | 1.3563e+1 (7.97e-1) - | 9.9974e+0 (6.57e-1) = | 1.6032e+1 (1.23e+0) - | 9.6539e+0 (4.88e-1) | |
| WFG9 | 5 | 1.1341e+0 (4.81e-3) = | 1.1516e+0 (2.23e-3) = | 1.2059e+0 (7.03e-3) = | 1.0822e+0 (7.74e-3) + | 1.0869e+0 (1.39e-2) = | 1.6886e+0 (1.23e-1) = | 2.3146e+0 (2.54e-1) - | 1.0572e+0 (8.93e-3) + | 1.1729e+0 (1.62e-2) = | 2.9145e+0 (1.98e-1) - | 1.1538e+0 (2.79e-3) |
| 8 | 2.9247e+0 (7.03e-3) + | 2.9414e+0 (1.35e-2) + | 3.9840e+0 (1.80e-1) = | 2.9086e+0 (1.09e-2) + | 3.0113e+0 (3.37e-2) = | 4.2097e+0 (1.56e-1) = | 3.7008e+0 (2.65e-2) = | 2.9851e+0 (1.68e-1) + | 3.2511e+0 (1.97e-2) = | 5.1840e+0 (3.02e-1) - | 3.7019e+0 (1.40e-1) | |
| 10 | 5.0369e+0 (6.00e-2) + | 4.8586e+0 (4.37e-2) + | 5.8592e+0 (1.71e-1) = | 5.8720e+0 (3.64e-1) = | 4.8288e+0 (4.52e-2) + | 6.2180e+0 (2.16e-1) = | 9.4215e+0 (4.85e+0) - | 6.0315e+0 (4.38e-1) = | 5.2228e+0 (6.75e-2) + | 7.3969e+0 (5.36e-1) - | 6.1223e+0 (2.84e-1) | |
| 15 | 8.8033e+0 (1.31e-1) + | 9.1527e+0 (1.13e-1) = | 1.1313e+1 (2.56e-1) = | 9.4323e+0 (3.35e-1) = | 7.7558e+0 (6.43e-2) + | 1.0228e+1 (3.92e-1) = | 2.5788e+1 (2.36e+0) - | 1.3614e+1 (5.47e-1) = | 8.2391e+0 (1.93e-1) + | 1.3847e+1 (1.03e+0) = | 1.1519e+1 (1.06e+0) | |
| +/−/= | 10/1/29 | 18/0/22 | 6/1/33 | 9/7/24 | 13/7/20 | 6/9/23 | 3/17/20 | 9/10/21 | 6/10/24 | 0/25/15 | ||
| Problem | M | NSGA-III | RVEA | MOEA/DD | GrEA | VaEA | onebyoneEA | MOMBI-II | PICEAg | KnEA | ENSMOEAD | IDEA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DTLZ1 | 5 | 9.7445e-1 (6.83e-4) = | 9.7474e-1 (1.99e-4) = | 9.7480e-1 (1.78e-4) = | 7.2922e-1 (1.94e-1) - | 8.7340e-1 (5.27e-2) - | 9.1956e-1 (6.91e-3) - | 9.7386e-1 (1.41e-3) = | 9.2996e-1 (2.24e-2) - | 6.8276e-1 (1.34e-1) - | 4.4217e-1 (3.72e-1) - | 9.7449e-1 (1.06e-3) |
| 8 | 9.7859e-1 (3.44e-2) = | 9.9749e-1 (1.30e-4) = | 9.9723e-1 (1.64e-4) = | 5.3977e-1 (2.04e-1) - | 7.2531e-1 (3.36e-1) - | 9.7544e-1 (4.21e-3) = | 9.1470e-1 (6.96e-2) - | 9.0165e-1 (4.62e-2) - | 1.5301e-1 (3.15e-1) - | 8.8629e-1 (2.08e-1) - | 9.9651e-1 (1.42e-3) | |
| 10 | 7.9573e-1 (3.40e-1) = | 9.9041e-1 (9.60e-3) - | 9.5904e-1 (1.28e-2) = | 3.6111e-1 (2.14e-1) - | 4.5272e-1 (3.88e-1) - | 9.7933e-1 (4.65e-3) = | 8.1983e-1 (5.88e-2) - | 7.7192e-1 (8.24e-2) - | 0.0000e+0 (0.00e+0) - | 7.2894e-1 (3.40e-1) - | 9.9135e-1 (5.89e-3) | |
| 15 | 8.9601e-1 (2.27e-1) = | 9.9864e-1 (8.66e-4) = | 9.8946e-1 (8.74e-3) = | 1.9429e-1 (2.46e-1) - | 5.1852e-1 (3.52e-1) - | 9.8989e-1 (2.84e-3) = | 7.8704e-1 (1.19e-1) - | 7.4953e-1 (8.65e-2) - | 0.0000e+0 (0.00e+0) - | 5.4963e-1 (3.59e-1) - | 9.7005e-1 (1.01e-1) | |
| DTLZ2 | 5 | 7.9452e-1 (4.77e-4) = | 7.9475e-1 (4.11e-4) = | 7.9477e-1 (4.59e-4) = | 7.9196e-1 (1.10e-3) - | 7.7502e-1 (2.98e-3) - | 7.7772e-1 (4.05e-3) - | 7.9364e-1 (4.30e-4) = | 7.7787e-1 (2.61e-3) - | 7.7067e-1 (5.90e-3) - | 6.9113e-1 (8.31e-3) - | 7.9494e-1 (4.32e-4) |
| 8 | 9.2286e-1 (5.93e-4) = | 9.2373e-1 (2.45e-4) = | 9.2381e-1 (1.95e-4) = | 9.0219e-1 (1.77e-3) - | 9.0306e-1 (3.26e-3) - | 9.0561e-1 (3.79e-3) - | 9.2462e-1 (4.94e-3) = | 9.0145e-1 (1.63e-2) - | 8.8595e-1 (8.16e-3) - | 5.4370e-1 (1.93e-2) - | 9.2430e-1 (3.58e-4) | |
| 10 | 9.1759e-1 (3.01e-2) - | 9.4299e-1 (5.86e-4) = | 8.9676e-1 (3.32e-2) - | 9.4257e-1 (1.92e-2) = | 9.1212e-1 (4.04e-3) - | 9.2510e-1 (3.60e-3) = | 7.9448e-1 (9.91e-2) - | 8.1240e-1 (5.25e-2) - | 9.3591e-1 (1.38e-2) = | 3.7185e-1 (2.28e-2) - | 9.4411e-1 (2.74e-4) | |
| 15 | 9.7239e-1 (1.07e-2) - | 9.9001e-1 (1.66e-3) = | 9.9036e-1 (1.01e-4) = | 9.7722e-1 (9.02e-3) = | 9.0601e-1 (3.17e-2) - | 9.6215e-1 (2.51e-3) - | 8.1797e-1 (9.12e-2) - | 8.1531e-1 (6.11e-2) - | 9.7122e-1 (2.44e-2) = | 3.3299e-1 (2.04e-2) - | 9.8909e-1 (3.21e-3) | |
| DTLZ3 | 5 | 6.7969e-1 (2.16e-1) = | 6.9463e-1 (2.38e-1) = | 7.7565e-1 (9.61e-3) = | 2.5930e-1 (1.28e-1) - | 4.0105e-1 (2.12e-1) - | 7.3334e-1 (1.73e-1) = | 7.7908e-1 (6.79e-3) = | 5.6362e-1 (3.88e-2) = | 5.8856e-1 (1.53e-1) = | 8.1682e-2 (1.31e-1) - | 7.2889e-1 (1.68e-1) |
| 8 | 1.9320e-1 (3.21e-1) = | 9.0302e-1 (1.62e-2) + | 9.0340e-1 (2.66e-2) + | 2.4037e-3 (1.07e-2) = | 0.0000e+0 (0.00e+0) = | 8.9914e-1 (3.49e-3) + | 8.8245e-1 (6.73e-2) + | 3.7344e-1 (5.45e-2) = | 0.0000e+0 (0.00e+0) = | 3.0866e-1 (2.38e-1) = | 1.5318e-1 (2.86e-1) | |
| 10 | 6.1488e-2 (1.89e-1) = | 6.6707e-1 (3.95e-1) + | 5.9787e-1 (2.85e-1) + | 0.0000e+0 (0.00e+0) = | 0.0000e+0 (0.00e+0) = | 9.0792e-1 (1.71e-2) + | 4.0882e-1 (6.39e-2) + | 2.4789e-1 (5.09e-2) + | 0.0000e+0 (0.00e+0) = | 1.6483e-1 (1.71e-1) = | 8.3074e-3 (3.72e-2) | |
| 15 | 2.6072e-2 (1.17e-1) - | 7.1219e-1 (4.32e-1) + | 8.8444e-1 (3.03e-1) + | 0.0000e+0 (0.00e+0) = | 0.0000e+0 (0.00e+0) = | 9.5603e-1 (7.09e-3) + | 4.1409e-1 (1.40e-2) + | 2.0381e-1 (5.24e-2) + | 0.0000e+0 (0.00e+0) = | 1.6375e-1 (1.61e-1) = | 3.3290e-2 (1.49e-1) | |
| DTLZ4 | 5 | 7.5819e-1 (6.72e-2) + | 7.9009e-1 (2.05e-2) + | 7.9489e-1 (3.71e-4) + | 7.8263e-1 (2.93e-2) = | 7.7286e-1 (2.72e-3) = | 7.7485e-1 (3.20e-2) = | 7.8840e-1 (1.99e-2) = | 7.3467e-1 (7.13e-2) = | 7.7713e-1 (4.36e-3) = | 6.5731e-1 (2.34e-2) = | 6.5151e-1 (1.40e-1) |
| 8 | 9.0144e-1 (4.70e-2) = | 9.2273e-1 (5.05e-3) = | 9.2005e-1 (1.23e-2) = | 9.0529e-1 (2.44e-3) = | 8.9471e-1 (7.63e-3) - | 9.1400e-1 (8.62e-3) = | 9.2243e-1 (1.35e-2) = | 8.8648e-1 (2.37e-2) = | 9.0248e-1 (4.71e-3) = | 6.2783e-1 (1.50e-2) - | 8.9543e-1 (4.67e-2) | |
| 10 | 9.1619e-1 (3.44e-2) = | 9.3739e-1 (1.04e-2) = | 9.3990e-1 (8.71e-3) + | 9.5028e-1 (6.66e-3) + | 9.1340e-1 (5.26e-3) = | 9.2854e-1 (2.45e-2) = | 9.0488e-1 (4.29e-2) = | 8.7536e-1 (2.80e-2) = | 9.3980e-1 (7.57e-3) = | 5.0318e-1 (1.71e-2) - | 9.0367e-1 (3.34e-2) | |
| 15 | 9.7878e-1 (1.38e-2) = | 9.9006e-1 (1.58e-3) = | 9.8737e-1 (5.21e-3) = | 9.8316e-1 (1.53e-3) = | 9.4736e-1 (6.36e-3) - | 9.7632e-1 (3.98e-3) - | 9.8177e-1 (6.27e-3) = | 9.3833e-1 (1.61e-2) - | 9.8405e-1 (1.37e-3) = | 4.6594e-1 (2.54e-2) - | 9.8540e-1 (6.36e-3) | |
| WFG4 | 5 | 7.9181e-1 (9.28e-4) = | 7.9117e-1 (7.27e-4) = | 7.5901e-1 (3.01e-3) - | 7.7689e-1 (2.19e-3) - | 7.5984e-1 (3.45e-3) - | 6.4131e-1 (1.67e-2) - | 7.9177e-1 (4.54e-3) = | 7.6781e-1 (3.65e-3) - | 7.7018e-1 (2.76e-3) - | 5.1390e-1 (3.59e-2) - | 7.9441e-1 (3.99e-4) |
| 8 | 9.1731e-1 (1.18e-3) = | 9.1490e-1 (1.57e-3) = | 8.0047e-1 (1.82e-2) - | 8.6480e-1 (3.28e-3) = | 8.8394e-1 (6.74e-3) = | 7.4214e-1 (1.48e-2) - | 8.8688e-1 (5.35e-2) = | 8.2498e-1 (4.13e-2) = | 9.0910e-1 (2.06e-3) = | 6.5714e-1 (4.93e-2) - | 8.9440e-1 (4.02e-3) | |
| 10 | 9.2661e-1 (1.43e-2) + | 9.2341e-1 (6.36e-3) = | 7.8139e-1 (2.12e-2) = | 8.5246e-1 (1.86e-2) = | 8.9702e-1 (5.20e-3) = | 7.5910e-1 (1.44e-2) = | 6.1392e-1 (6.58e-2) - | 7.1772e-1 (4.83e-2) = | 9.4481e-1 (2.19e-3) + | 5.0636e-1 (5.61e-2) - | 8.2188e-1 (3.36e-2) | |
| 15 | 9.8426e-1 (3.06e-3) + | 9.8066e-1 (2.29e-3) = | 6.3829e-1 (3.53e-2) - | 9.2764e-1 (9.45e-3) = | 9.2742e-1 (6.45e-3) = | 8.3187e-1 (9.58e-3) = | 5.7310e-1 (7.35e-2) - | 7.1063e-1 (5.61e-2) = | 9.8284e-1 (1.19e-3) + | 5.8568e-1 (9.44e-2) - | 8.8006e-1 (1.96e-2) | |
| WFG5 | 5 | 7.4401e-1 (2.81e-4) = | 7.4369e-1 (4.97e-4) = | 7.1779e-1 (9.38e-4) - | 7.3684e-1 (2.15e-3) = | 7.1999e-1 (3.92e-3) - | 6.0838e-1 (1.53e-2) - | 7.1703e-1 (7.74e-3) - | 7.2217e-1 (2.24e-3) - | 7.2455e-1 (4.38e-3) - | 4.6665e-1 (3.40e-2) - | 7.4382e-1 (4.31e-4) |
| 8 | 8.6286e-1 (4.22e-4) + | 8.6201e-1 (5.63e-4) = | 7.7454e-1 (7.56e-3) = | 8.2472e-1 (4.21e-3) = | 8.3507e-1 (3.56e-3) = | 7.0016e-1 (1.95e-2) - | 7.7164e-1 (1.48e-2) = | 8.3767e-1 (2.27e-3) = | 8.4466e-1 (2.75e-3) = | 5.8823e-1 (3.12e-2) - | 8.3371e-1 (6.76e-3) | |
| 10 | 8.7483e-1 (1.11e-3) = | 8.7858e-1 (7.04e-4) = | 7.6553e-1 (1.54e-2) = | 7.9456e-1 (5.63e-2) = | 8.3937e-1 (3.76e-3) = | 7.0823e-1 (1.10e-2) = | 4.5913e-1 (2.33e-1) - | 6.8096e-1 (1.96e-2) - | 8.8309e-1 (1.84e-3) + | 5.1575e-1 (3.29e-2) - | 7.8965e-1 (4.23e-3) | |
| 15 | 9.1576e-1 (2.29e-3) + | 9.1693e-1 (1.97e-4) + | 6.0793e-1 (1.82e-2) = | 8.3840e-1 (7.57e-3) = | 8.6302e-1 (3.57e-3) = | 7.7648e-1 (8.71e-3) = | 2.6015e-1 (8.40e-2) - | 6.7442e-1 (3.35e-2) = | 9.1170e-1 (9.17e-4) = | 5.5500e-1 (2.57e-2) - | 8.1591e-1 (1.44e-2) | |
| WFG6 | 5 | 7.2318e-1 (1.10e-2) = | 7.2920e-1 (1.97e-2) = | 6.8940e-1 (1.97e-2) - | 7.2182e-1 (1.23e-2) = | 7.0264e-1 (1.23e-2) - | 5.3602e-1 (2.83e-2) - | 7.2550e-1 (1.81e-2) = | 7.0845e-1 (1.03e-2) = | 7.0327e-1 (1.40e-2) - | 4.6102e-1 (6.92e-2) - | 7.3274e-1 (1.76e-2) |
| 8 | 8.3760e-1 (1.30e-2) = | 8.3307e-1 (1.55e-2) = | 7.2865e-1 (2.67e-2) = | 8.1120e-1 (1.75e-2) = | 8.2292e-1 (1.23e-2) = | 6.0933e-1 (2.77e-2) - | 8.3858e-1 (2.35e-2) = | 8.2080e-1 (1.38e-2) = | 8.1567e-1 (2.53e-2) = | 5.1901e-1 (8.42e-2) - | 8.1384e-1 (2.19e-2) | |
| 10 | 8.4862e-1 (2.08e-2) + | 7.1195e-1 (7.33e-2) = | 6.8971e-1 (7.31e-2) = | 8.1882e-1 (3.61e-2) = | 8.3499e-1 (1.90e-2) + | 6.0902e-1 (3.15e-2) = | 6.6231e-1 (8.72e-2) = | 7.1181e-1 (3.15e-2) = | 8.5282e-1 (2.58e-2) + | 3.7456e-1 (7.60e-2) - | 7.2360e-1 (3.88e-2) | |
| 15 | 8.7959e-1 (2.04e-2) + | 7.6000e-1 (6.03e-2) = | 5.8484e-1 (3.85e-2) = | 8.5613e-1 (3.25e-2) + | 8.7018e-1 (2.34e-2) + | 6.8213e-1 (3.13e-2) = | 4.8279e-1 (9.63e-2) - | 7.0208e-1 (6.24e-2) = | 8.7608e-1 (3.07e-2) + | 3.8271e-1 (1.50e-1) - | 7.1964e-1 (3.65e-2) | |
| WFG7 | 5 | 7.9232e-1 (5.58e-4) = | 7.9020e-1 (5.84e-4) = | 7.6258e-1 (3.26e-3) - | 7.9198e-1 (1.23e-3) = | 7.7048e-1 (3.26e-3) - | 5.7933e-1 (1.57e-2) - | 7.8755e-1 (1.14e-2) = | 7.7235e-1 (2.39e-3) - | 7.7682e-1 (3.92e-3) - | 5.5536e-1 (5.85e-2) - | 7.9267e-1 (7.07e-4) |
| 8 | 9.1731e-1 (8.91e-3) + | 9.0906e-1 (2.65e-3) + | 8.5204e-1 (1.46e-2) = | 8.8829e-1 (3.16e-3) = | 9.0314e-1 (2.47e-3) = | 6.9558e-1 (1.44e-2) - | 9.1987e-1 (8.57e-3) + | 8.8851e-1 (2.54e-2) = | 8.9282e-1 (6.59e-3) = | 6.5626e-1 (3.85e-2) - | 8.8981e-1 (7.83e-3) | |
| 10 | 9.1643e-1 (2.66e-2) + | 9.1581e-1 (1.48e-2) + | 8.4180e-1 (1.91e-2) = | 9.0144e-1 (3.72e-2) + | 9.1959e-1 (2.29e-3) + | 7.1700e-1 (1.20e-2) = | 7.0793e-1 (9.88e-2) = | 7.9733e-1 (5.99e-2) = | 9.4092e-1 (6.13e-3) + | 4.9267e-1 (4.28e-2) = | 7.8561e-1 (5.93e-2) | |
| 15 | 9.7867e-1 (8.20e-3) + | 9.6776e-1 (1.64e-2) = | 7.2921e-1 (2.71e-2) - | 9.4505e-1 (1.02e-2) = | 9.5253e-1 (3.55e-3) = | 8.3546e-1 (1.05e-2) = | 6.5207e-1 (1.37e-1) - | 8.0399e-1 (7.26e-2) = | 9.7224e-1 (2.25e-2) + | 5.1957e-1 (4.19e-2) - | 9.1922e-1 (2.21e-2) | |
| WFG8 | 5 | 6.8384e-1 (1.74e-3) = | 6.7482e-1 (1.90e-3) = | 6.6150e-1 (5.30e-3) = | 6.7519e-1 (3.51e-3) = | 6.3141e-1 (1.02e-2) - | 4.9476e-1 (2.52e-2) - | 3.1729e-1 (5.04e-3) - | 6.3802e-1 (7.53e-3) - | 6.4122e-1 (3.73e-3) - | 2.5469e-1 (2.45e-2) - | 6.8862e-1 (1.84e-2) |
| 8 | 7.8235e-1 (1.58e-2) = | 7.5333e-1 (5.05e-2) = | 7.0989e-1 (5.57e-2) - | 7.4690e-1 (2.93e-2) - | 7.1925e-1 (1.32e-2) - | 4.9836e-1 (4.64e-2) - | 5.9695e-1 (1.62e-2) - | 7.5766e-1 (5.69e-3) = | 7.6525e-1 (2.14e-2) = | 3.3579e-1 (3.54e-2) - | 7.9681e-1 (1.82e-2) | |
| 10 | 7.7140e-1 (2.08e-2) - | 6.7892e-1 (1.03e-1) = | 5.4606e-1 (9.19e-2) - | 8.3029e-1 (3.51e-3) = | 7.6167e-1 (1.31e-2) = | 4.4671e-1 (1.05e-1) - | 5.0403e-1 (5.99e-2) - | 7.4356e-1 (3.18e-2) = | 8.3607e-1 (1.61e-2) = | 3.3122e-1 (6.65e-2) - | 7.8217e-1 (4.05e-2) | |
| 15 | 8.9846e-1 (3.27e-2) = | 6.2231e-1 (1.51e-1) = | 7.8402e-1 (1.61e-1) = | 8.9771e-1 (3.46e-3) = | 8.3930e-1 (1.18e-2) = | 4.9365e-1 (1.21e-1) = | 3.5405e-1 (2.93e-2) - | 7.5496e-1 (4.13e-2) = | 9.0642e-1 (3.28e-2) = | 3.5295e-1 (4.79e-2) - | 7.7807e-1 (9.72e-2) | |
| WFG9 | 5 | 7.4945e-1 (3.96e-3) = | 7.5331e-1 (2.64e-3) = | 7.0773e-1 (1.05e-2) - | 7.4748e-1 (4.00e-3) = | 7.1279e-1 (3.10e-2) - | 6.0632e-1 (2.27e-2) - | 5.4358e-1 (6.03e-2) - | 7.4085e-1 (1.04e-2) = | 7.4861e-1 (4.56e-3) = | 4.7813e-1 (7.60e-2) - | 7.5359e-1 (6.59e-3) |
| 8 | 8.5651e-1 (1.02e-2) = | 8.4512e-1 (2.11e-2) = | 7.3318e-1 (3.11e-2) - | 8.1055e-1 (6.25e-3) = | 8.0206e-1 (4.38e-2) = | 6.9038e-1 (1.70e-2) - | 7.3246e-1 (4.16e-2) = | 8.3368e-1 (4.61e-2) = | 8.6422e-1 (5.93e-3) + | 5.0669e-1 (5.87e-2) - | 8.2049e-1 (1.04e-2) | |
| 10 | 8.1980e-1 (4.00e-2) + | 8.3437e-1 (4.86e-2) + | 6.8055e-1 (4.60e-2) = | 8.0898e-1 (2.22e-2) + | 7.2545e-1 (7.49e-2) = | 6.9802e-1 (3.01e-2) = | 5.4897e-1 (2.51e-1) - | 7.2526e-1 (3.28e-2) = | 8.4307e-1 (7.94e-2) + | 4.7902e-1 (7.68e-2) - | 7.3618e-1 (4.35e-2) | |
| 15 | 8.7522e-1 (6.70e-2) = | 8.0448e-1 (8.41e-2) = | 5.3211e-1 (6.45e-2) = | 8.7297e-1 (7.29e-3) = | 7.7153e-1 (7.07e-2) = | 7.2418e-1 (3.96e-2) = | 2.3669e-1 (8.53e-2) - | 7.0360e-1 (2.14e-2) = | 8.7984e-1 (6.84e-2) + | 3.7213e-1 (5.37e-2) - | 7.5320e-1 (6.12e-2) | |
| +/−/= | 11/4/25 | 8/1/31 | 5/12/23 | 4/9/27 | 3/18/19 | 3/18/19 | 4/19/17 | 2/14/24 | 10/11/19 | 0/35/5 | ||
| Problem | M | NSGA-III | RVEA | MOEA/DD | GrEA | VaEA | onebyoneEA | MOMBI-II | PICEAg | KnEA | ENSMOEAD | IDEA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| WFG1 | 5 | 4.3763e-1 (2.48e-3) = | 4.2703e-1 (7.27e-3) = | 5.7320e-1 (2.76e-2) - | 5.2792e-1 (1.65e-2) - | 4.3439e-1 (5.09e-3) = | 7.7381e-1 (4.11e-2) - | 4.8710e-1 (5.33e-2) = | 6.3240e-1 (2.74e-1) - | 4.7835e-1 (8.50e-3) = | 1.3799e+0 (7.74e-2) - | 4.3896e-1 (1.35e-2) |
| 8 | 8.5684e-1 (1.70e-2) + | 9.9409e-1 (2.61e-2) = | 1.2687e+0 (3.09e-2) = | 1.2958e+0 (1.05e-1) = | 8.5863e-1 (1.80e-2) + | 1.6551e+0 (5.31e-2) - | 1.0137e+0 (4.70e-2) = | 1.2428e+0 (1.67e-1) = | 9.1226e-1 (2.05e-2) = | 1.9021e+0 (9.12e-2) - | 1.0714e+0 (6.72e-2) | |
| 10 | 1.1045e+0 (4.14e-2) + | 1.1803e+0 (5.01e-2) = | 1.3073e+0 (4.98e-2) = | 1.2322e+0 (3.73e-2) = | 1.1649e+0 (3.77e-2) = | 1.8378e+0 (4.75e-2) - | 1.6505e+0 (2.87e-1) = | 1.7124e+0 (1.10e-1) = | 1.2300e+0 (5.48e-2) = | 2.2529e+0 (1.35e-1) - | 1.2659e+0 (7.63e-2) | |
| 15 | 1.7627e+0 (1.73e-1) = | 1.7656e+0 (8.18e-2) = | 2.0243e+0 (4.21e-2) - | 2.1833e+0 (8.03e-2) = | 1.6914e+0 (4.07e-2) + | 2.4310e+0 (2.93e-2) - | 2.3159e+0 (3.44e-1) = | 2.3973e+0 (1.71e-1) - | 1.7580e+0 (8.89e-2) = | 2.4192e+0 (1.12e-1) - | 2.0205e+0 (1.38e-1) | |
| WFG2 | 5 | 4.7258e-1 (1.61e-3) = | 4.4635e-1 (7.97e-3) + | 5.9445e-1 (1.75e-2) - | 5.1884e-1 (1.93e-2) = | 4.5852e-1 (1.06e-2) = | 7.5509e-1 (6.80e-2) - | 4.9571e-1 (5.82e-2) = | 5.1193e-1 (1.41e-2) = | 5.3244e-1 (2.11e-2) = | 1.2339e+0 (1.61e-1) - | 4.9566e-1 (1.20e-2) |
| 8 | 1.0251e+0 (1.49e-1) + | 9.8987e-1 (3.76e-2) + | 1.3887e+0 (7.41e-3) = | 9.9952e-1 (4.00e-2) + | 9.3494e-1 (1.36e-2) + | 1.7585e+0 (5.83e-2) = | 1.1633e+0 (8.18e-2) = | 1.1219e+0 (6.75e-2) = | 1.0754e+0 (2.65e-2) = | 1.6155e+0 (1.45e-1) = | 1.2565e+0 (7.91e-2) | |
| 10 | 1.2731e+0 (1.10e-1) + | 1.3391e+0 (5.43e-2) = | 1.3921e+0 (2.79e-2) = | 1.2425e+0 (3.07e-2) + | 1.2704e+0 (2.75e-2) + | 1.9548e+0 (3.12e-2) = | 3.6023e+0 (1.31e+0) - | 1.7745e+0 (1.24e-1) = | 1.3538e+0 (5.68e-2) = | 1.9002e+0 (1.18e-1) = | 1.4900e+0 (7.45e-2) | |
| 15 | 1.7568e+0 (7.68e-2) + | 1.8593e+0 (7.82e-2) = | 2.1867e+0 (1.28e-2) = | 1.9310e+0 (7.96e-2) = | 1.7408e+0 (4.06e-2) + | 2.5204e+0 (3.41e-2) = | 6.6940e+0 (2.93e+0) - | 3.4687e+0 (8.07e-1) - | 2.1834e+0 (6.70e-1) = | 2.4038e+0 (1.86e-1) = | 2.0867e+0 (6.94e-2) | |
| WFG3 | 5 | 5.7985e-1 (5.75e-2) = | 5.3607e-1 (2.44e-2) = | 6.5151e-1 (1.60e-2) - | 3.9129e-1 (5.46e-2) = | 6.4405e-1 (5.43e-2) - | 1.3522e+0 (1.38e-1) - | 1.6372e+0 (1.05e-1) - | 1.8622e-1 (1.89e-2) = | 5.1336e-1 (1.12e-1) = | 1.9841e+0 (1.67e-1) - | 4.2348e-1 (4.38e-2) |
| 8 | 1.8370e+0 (1.69e-1) = | 2.1256e+0 (2.26e-1) - | 1.9315e+0 (4.52e-2) = | 8.7246e-1 (1.54e-1) = | 1.4043e+0 (1.42e-1) = | 3.5082e+0 (2.44e-1) - | 8.1822e+0 (5.24e-1) - | 4.2602e-1 (5.06e-2) = | 1.0357e+0 (1.28e-1) = | 2.5689e+0 (1.38e-1) - | 1.2569e+0 (2.44e-1) | |
| 10 | 2.4770e+0 (6.82e-1) = | 3.7778e+0 (8.33e-1) = | 3.5789e+0 (8.03e-2) - | 1.2130e+0 (3.20e-1) = | 2.2790e+0 (1.41e-1) = | 5.2499e+0 (3.85e-1) - | 1.0781e+1 (1.63e-2) - | 7.6424e-1 (6.15e-2) + | 1.6473e+0 (4.32e-1) = | 3.0888e+0 (2.33e-1) = | 2.2771e+0 (2.47e-1) | |
| 15 | 3.2573e+0 (1.56e+0) = | 6.4004e+0 (6.13e-1) = | 7.0248e+0 (7.97e-2) = | 2.9457e+0 (4.56e-1) = | 3.9182e+0 (2.58e-1) = | 9.0113e+0 (6.27e-1) - | 1.6367e+1 (1.22e-1) - | 1.2029e+0 (1.30e-1) + | 3.1922e+0 (1.13e+0) = | 3.8134e+0 (3.61e-1) = | 4.6338e+0 (1.83e+0) | |
| IDTLZ1 | 5 | 1.3877e-1 (1.20e-2) = | 1.6943e-1 (3.10e-2) = | 1.4976e-1 (4.18e-2) = | 9.2744e-2 (5.24e-2) + | 7.5948e-2 (2.50e-2) + | 6.3014e-2 (7.09e-3) + | 1.1349e-1 (4.48e-4) = | 1.0173e-1 (1.52e-2) = | 6.9447e-2 (9.59e-3) + | 9.3350e-2 (2.02e-3) + | 1.2815e-1 (1.07e-2) |
| 8 | 1.3904e-1 (2.55e-3) = | 2.5503e-1 (2.12e-2) - | 2.1694e-1 (1.26e-2) - | 1.4064e-1 (5.80e-2) = | 1.0844e-1 (9.80e-3) = | 1.4418e-1 (2.55e-2) = | 1.7282e-1 (6.49e-3) - | 1.1508e-1 (4.10e-3) = | 1.0695e-1 (8.29e-3) = | 1.2410e-1 (2.63e-3) = | 1.1773e-1 (8.75e-3) | |
| 10 | 1.5184e-1 (3.83e-3) = | 3.3838e-1 (2.79e-1) - | 2.3764e-1 (1.67e-2) - | 1.4594e-1 (3.58e-3) = | 1.2986e-1 (2.16e-3) = | 2.1874e-1 (2.69e-2) - | 1.9732e-1 (9.01e-3) - | 1.4482e-1 (2.72e-3) = | 1.6989e-1 (2.82e-2) = | 1.9992e-1 (1.17e-2) - | 1.5090e-1 (2.51e-2) | |
| 15 | 1.7344e-1 (5.50e-3) = | 3.5878e-1 (3.79e-2) - | 3.2455e-1 (2.24e-2) - | 1.6182e-1 (4.32e-3) + | 1.5011e-1 (2.07e-3) + | 2.4553e-1 (1.52e-2) = | 2.0895e-1 (1.05e-2) = | 1.7398e-1 (4.15e-3) = | 2.1355e-1 (1.87e-2) = | 1.9532e-1 (1.11e-2) = | 2.1245e-1 (3.56e-2) | |
| IDTLZ2 | 5 | 2.4190e-1 (5.44e-3) - | 2.9419e-1 (3.95e-3) - | 2.8127e-1 (4.30e-3) - | 2.1326e-1 (4.75e-3) = | 2.0440e-1 (1.67e-3) = | 2.5915e-1 (9.82e-3) - | 3.1766e-1 (1.14e-3) - | 2.0289e-1 (2.91e-3) = | 2.1082e-1 (1.01e-2) = | 2.1807e-1 (2.45e-3) - | 2.0018e-1 (2.34e-3) |
| 8 | 5.0621e-1 (1.72e-2) = | 6.1261e-1 (9.08e-3) - | 6.4034e-1 (1.50e-2) - | 4.1458e-1 (8.78e-3) = | 3.7173e-1 (2.22e-3) + | 4.6632e-1 (8.31e-3) = | 5.8693e-1 (4.95e-3) - | 3.9305e-1 (3.81e-3) = | 3.7462e-1 (9.16e-3) + | 4.0326e-1 (5.43e-3) = | 4.1513e-1 (6.97e-3) | |
| 10 | 6.6693e-1 (1.08e-2) - | 7.4191e-1 (2.92e-2) - | 7.4320e-1 (7.47e-3) - | 7.1634e-1 (6.87e-3) - | 4.8555e-1 (2.52e-3) = | 5.4783e-1 (9.96e-3) = | 7.3122e-1 (4.32e-3) - | 4.9761e-1 (8.15e-3) = | 5.0793e-1 (1.00e-2) = | 6.7932e-1 (2.46e-2) - | 5.0341e-1 (3.00e-2) | |
| 15 | 7.5765e-1 (1.05e-2) = | 8.6127e-1 (1.61e-2) - | 9.4808e-1 (2.24e-2) - | 8.1442e-1 (2.82e-3) = | 5.9595e-1 (2.91e-3) = | 6.7362e-1 (1.05e-2) = | 8.4968e-1 (5.02e-3) - | 6.3880e-1 (6.51e-3) = | 6.0566e-1 (7.51e-2) = | 7.8799e-1 (3.68e-2) = | 7.3338e-1 (2.61e-2) | |
| MaF6 | 5 | 4.9209e-2 (6.12e-3) - | 1.4546e-1 (1.31e-1) - | 7.2132e-2 (9.06e-3) - | 3.5135e-2 (2.16e-3) = | 4.2317e-3 (1.44e-4) = | 3.5988e-3 (1.13e-4) = | 1.8971e-1 (5.01e-3) - | 8.1507e-3 (5.30e-3) = | 7.8461e-3 (3.97e-3) = | 3.8586e-2 (4.04e-5) - | 6.1167e-3 (2.59e-3) |
| 8 | 2.0372e-1 (3.12e-1) = | 9.4023e-2 (2.31e-2) - | 1.1045e-1 (8.81e-3) - | 2.3535e-1 (1.59e-1) - | 1.9749e-1 (3.36e-1) = | 2.8668e-3 (4.66e-5) = | 6.5428e-1 (1.14e-1) - | 1.1790e-2 (1.12e-2) = | 4.5226e-1 (5.92e-1) = | 2.2094e-2 (6.17e-5) = | 2.0848e-2 (6.50e-2) | |
| 10 | 4.5421e-1 (2.70e-1) = | 4.7214e-1 (2.48e-1) = | 1.1834e-1 (7.92e-3) + | 3.7700e+0 (3.12e+0) - | 4.2887e-1 (1.74e-1) = | 4.0812e-3 (8.43e-5) + | 7.2602e-1 (3.76e-2) - | 1.3724e-1 (2.74e-1) = | 6.6445e+0 (8.50e+0) - | 2.2695e-2 (1.14e-4) = | 2.3084e-1 (1.96e-1) | |
| 15 | 7.7284e-1 (3.76e-1) = | 2.1311e-1 (1.20e-1) = | 1.4040e-1 (2.16e-2) = | 7.9855e+0 (4.61e+0) - | 5.5530e-1 (1.57e-1) = | 3.3259e-3 (6.97e-5) + | 6.6196e-1 (1.45e-1) = | 8.8412e-1 (3.80e-1) = | 3.8003e+1 (2.19e+1) - | 2.7151e-2 (7.61e-4) = | 3.2864e-1 (2.21e-1) | |
| MaF7 | 5 | 3.3473e-1 (1.97e-2) = | 5.6398e-1 (1.21e-2) - | 3.0005e+0 (1.21e-6) - | 2.6696e-1 (9.27e-3) = | 3.3410e-1 (7.69e-3) = | 3.9662e-1 (3.01e-2) - | 5.1937e-1 (1.30e-1) - | 1.1444e+0 (4.81e-1) - | 3.0591e-1 (9.36e-3) = | 1.3205e+0 (3.57e-1) - | 2.9835e-1 (6.16e-2) |
| 8 | 7.9127e-1 (3.08e-2) = | 1.5450e+0 (3.72e-1) = | 1.7534e+0 (5.71e-1) - | 8.0542e-1 (3.94e-2) = | 7.1434e-1 (1.18e-2) = | 1.1871e+0 (8.97e-2) = | 3.2650e+0 (9.64e-1) - | 4.0721e+0 (5.54e-2) - | 6.5912e-1 (9.45e-2) + | 1.3085e+0 (1.77e-1) = | 9.5358e-1 (8.11e-2) | |
| 10 | 1.5092e+0 (3.79e-1) = | 1.8784e+0 (3.89e-1) = | 2.5362e+0 (2.28e-1) - | 3.4870e+0 (7.43e-1) - | 1.1072e+0 (1.73e-2) = | 2.4877e+0 (3.53e-1) = | 5.5595e+0 (7.33e-2) - | 5.5731e+0 (9.47e-2) - | 1.1574e+0 (3.98e-2) = | 1.6219e+0 (1.44e-1) = | 1.5823e+0 (5.09e-1) | |
| 15 | 7.6141e+0 (1.11e+0) = | 2.4102e+0 (1.46e-1) = | 3.4812e+0 (9.98e-2) = | 9.5308e+0 (1.15e+0) - | 2.6545e+0 (1.68e-1) = | 3.0238e+0 (2.36e-1) + | 1.0955e+1 (1.27e-1) - | 1.1075e+1 (1.46e-1) - | 2.6701e+0 (3.78e-1) = | 1.9906e+0 (4.25e-2) + | 3.6462e+0 (1.58e+0) | |
| +/−/= | 5/3/20 | 2/11/15 | 1/17/10 | 4/7/17 | 8/1/19 | 4/12/12 | 0/19/9 | 2/7/19 | 3/2/23 | 2/12/14 | ||
| Problem | M | NSGA-III | RVEA | MOEA/DD | GrEA | VaEA | onebyoneEA | MOMBI-II | PICEAg | KnEA | ENSMOEAD | IDEA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| WFG1 | 5 | 9.9818e-1 (8.37e-5) + | 9.9726e-1 (2.92e-4) = | 9.7249e-1 (1.08e-2) - | 9.6878e-1 (6.47e-3) - | 9.9653e-1 (5.19e-4) = | 9.8482e-1 (3.68e-3) = | 9.9517e-1 (3.20e-3) = | 9.9686e-1 (8.52e-4) = | 9.9015e-1 (1.62e-3) = | 9.3906e-1 (1.77e-2) - | 9.9589e-1 (1.35e-3) |
| 8 | 9.9956e-1 (1.41e-4) = | 9.9660e-1 (1.19e-3) = | 9.8806e-1 (6.81e-3) - | 9.8069e-1 (5.34e-3) - | 9.9951e-1 (2.50e-4) = | 9.9480e-1 (1.29e-3) = | 9.9955e-1 (2.89e-4) = | 9.9985e-1 (4.95e-5) + | 9.9560e-1 (1.23e-3) = | 9.8159e-1 (1.77e-2) - | 9.9805e-1 (1.56e-3) | |
| 10 | 9.9946e-1 (1.92e-4) = | 9.9290e-1 (1.87e-2) = | 9.9056e-1 (1.54e-3) - | 9.8273e-1 (4.86e-3) - | 9.9839e-1 (5.22e-3) = | 9.9493e-1 (2.95e-3) = | 9.8018e-1 (2.85e-2) - | 9.9900e-1 (2.78e-4) = | 9.9321e-1 (2.84e-3) = | 6.9429e-1 (1.02e-1) - | 9.9794e-1 (1.90e-3) | |
| 15 | 9.9987e-1 (8.13e-5) + | 9.9781e-1 (5.67e-4) = | 9.9471e-1 (1.23e-3) = | 9.7960e-1 (7.87e-3) - | 9.9980e-1 (1.81e-4) + | 9.9837e-1 (7.03e-4) = | 9.9197e-1 (2.90e-2) = | 9.9926e-1 (3.00e-4) = | 9.9487e-1 (2.50e-3) = | 9.9907e-1 (8.82e-4) = | 9.9823e-1 (6.81e-4) | |
| WFG2 | 5 | 9.9606e-1 (5.34e-4) + | 9.9377e-1 (1.24e-3) + | 9.7369e-1 (3.57e-3) = | 9.6773e-1 (5.39e-3) = | 9.8968e-1 (1.56e-3) = | 9.7357e-1 (8.38e-3) = | 9.9504e-1 (1.46e-3) + | 9.9104e-1 (2.43e-3) + | 9.9148e-1 (8.40e-4) + | 9.4712e-1 (2.41e-2) = | 9.7663e-1 (5.73e-3) |
| 8 | 9.9670e-1 (2.02e-3) + | 9.8631e-1 (3.95e-3) = | 9.5920e-1 (6.10e-3) = | 9.8288e-1 (3.00e-3) = | 9.9448e-1 (1.42e-3) + | 9.8936e-1 (3.67e-3) = | 9.9021e-1 (8.43e-3) + | 9.9782e-1 (6.66e-4) + | 9.9484e-1 (1.00e-3) + | 9.9286e-1 (4.22e-3) + | 9.8073e-1 (9.26e-3) | |
| 10 | 9.9543e-1 (2.89e-3) + | 9.5962e-1 (7.32e-3) = | 9.5709e-1 (1.51e-2) = | 9.7365e-1 (6.35e-3) = | 9.9454e-1 (1.11e-3) + | 9.9038e-1 (4.10e-3) = | 9.3027e-1 (4.38e-2) = | 9.9215e-1 (2.99e-3) = | 9.9388e-1 (1.31e-3) + | 9.8394e-1 (8.65e-3) = | 9.7762e-1 (1.10e-2) | |
| 15 | 9.9533e-1 (2.40e-3) + | 9.7186e-1 (6.44e-3) = | 9.4984e-1 (7.76e-3) - | 9.7330e-1 (4.20e-3) = | 9.9435e-1 (1.43e-3) = | 9.9379e-1 (1.80e-3) = | 9.1210e-1 (9.92e-2) = | 9.9310e-1 (3.03e-3) = | 9.8116e-1 (1.77e-2) = | 9.9805e-1 (1.37e-3) + | 9.8044e-1 (1.17e-2) | |
| WFG3 | 5 | 1.4415e-1 (1.21e-2) = | 1.5086e-1 (2.42e-2) = | 1.3853e-1 (1.04e-2) = | 2.2197e-1 (6.94e-3) = | 1.1825e-1 (1.42e-2) - | 7.5251e-2 (9.70e-3) - | 9.1522e-2 (1.28e-3) - | 2.5815e-1 (3.53e-3) = | 1.3382e-1 (3.35e-2) = | 9.1321e-2 (1.78e-3) - | 1.8951e-1 (1.89e-2) |
| 8 | 3.0692e-2 (2.17e-2) = | 0.0000e+0 (0.00e+0) - | 1.2629e-2 (2.01e-2) = | 6.1026e-2 (3.43e-2) = | 7.4054e-2 (1.16e-2) = | 1.8164e-3 (5.71e-3) - | 1.0959e-1 (1.15e-2) + | 1.7058e-1 (9.62e-3) + | 1.4500e-2 (1.81e-2) = | 8.8931e-2 (1.11e-3) = | 4.9728e-2 (2.35e-2) | |
| 10 | 3.3450e-4 (1.50e-3) = | 0.0000e+0 (0.00e+0) = | 0.0000e+0 (0.00e+0) = | 0.0000e+0 (0.00e+0) = | 4.0702e-2 (1.34e-2) + | 0.0000e+0 (0.00e+0) = | 6.6617e-2 (1.20e-2) + | 1.0830e-1 (2.57e-2) + | 0.0000e+0 (0.00e+0) = | 6.8982e-2 (1.21e-2) + | 0.0000e+0 (0.00e+0) | |
| 15 | 0.0000e+0 (0.00e+0) = | 0.0000e+0 (0.00e+0) = | 0.0000e+0 (0.00e+0) = | 0.0000e+0 (0.00e+0) = | 0.0000e+0 (0.00e+0) = | 0.0000e+0 (0.00e+0) = | 0.0000e+0 (0.00e+0) = | 0.0000e+0 (0.00e+0) = | 0.0000e+0 (0.00e+0) = | 8.0927e-2 (3.03e-2) + | 0.0000e+0 (0.00e+0) | |
| IDTLZ1 | 5 | 4.0580e-3 (4.82e-4) = | 2.1929e-3 (8.90e-4) = | 3.4664e-3 (1.52e-3) = | 8.4108e-3 (2.72e-3) + | 9.5217e-3 (2.24e-3) + | 1.1215e-2 (6.20e-4) + | 5.4766e-3 (1.64e-4) = | 6.0996e-3 (1.10e-3) = | 1.0326e-2 (6.70e-4) + | 5.6683e-3 (4.84e-4) = | 4.4935e-3 (5.78e-4) |
| 8 | 2.8381e-5 (1.62e-6) = | 1.6134e-6 (8.18e-7) - | 4.6963e-6 (1.25e-6) - | 1.7708e-5 (9.13e-6) = | 2.5929e-5 (5.19e-6) = | 2.1458e-5 (8.64e-6) = | 1.2294e-5 (2.25e-6) - | 1.5408e-5 (3.71e-6) = | 2.7932e-5 (3.30e-6) = | 6.2207e-6 (3.10e-6) - | 2.5223e-5 (5.26e-6) | |
| 10 | 3.2493e-7 (6.00e-8) + | 6.9530e-9 (3.94e-9) = | 3.3081e-8 (1.04e-8) = | 4.3696e-7 (3.63e-8) + | 4.3673e-7 (6.15e-7) = | 6.9543e-8 (4.76e-8) = | 9.0415e-8 (1.72e-8) = | 1.2929e-7 (3.65e-7) = | 1.3217e-7 (9.40e-8) = | 3.9739e-9 (1.26e-8) = | 1.2519e-7 (1.61e-7) | |
| 15 | 2.7453e-12 (8.09e-13) + | 2.8542e-14 (2.37e-14) = | 3.9124e-14 (1.62e-14) + | 7.7987e-12 (1.98e-12) + | 0.0000e+0 (0.00e+0) = | 5.0748e-13 (2.39e-13) + | 1.0568e-12 (2.67e-13) + | 0.0000e+0 (0.00e+0) = | 7.1252e-13 (8.34e-13) + | 0.0000e+0 (0.00e+0) = | 0.0000e+0 (0.00e+0) | |
| IDTLZ2 | 5 | 6.9370e-2 (7.98e-3) = | 6.1728e-2 (1.77e-3) - | 7.6538e-2 (2.85e-3) = | 1.1600e-1 (8.42e-4) + | 1.0137e-1 (1.34e-3) = | 1.2134e-1 (1.15e-3) + | 4.7511e-2 (7.64e-4) - | 1.1436e-1 (1.74e-3) = | 1.0548e-1 (4.45e-3) = | 6.8911e-2 (3.73e-3) = | 8.4106e-2 (4.11e-3) |
| 8 | 2.1018e-3 (3.07e-4) = | 1.1730e-3 (2.14e-4) - | 1.3470e-3 (1.67e-4) - | 3.7350e-3 (1.96e-4) = | 1.6345e-3 (5.82e-5) = | 5.1117e-3 (1.41e-4) = | 1.6626e-3 (2.01e-4) = | 3.8368e-3 (1.98e-4) = | 2.0429e-3 (3.24e-4) = | 9.9444e-5 (3.36e-5) - | 3.0682e-3 (1.80e-4) | |
| 10 | 1.7634e-4 (7.13e-6) = | 9.9335e-5 (2.87e-5) = | 7.4267e-5 (1.07e-5) - | 2.8547e-4 (1.63e-5) = | 1.0371e-4 (6.44e-6) = | 3.3639e-4 (1.79e-5) + | 1.1688e-4 (1.56e-5) = | 2.0759e-4 (2.47e-5) = | 5.3821e-5 (2.32e-5) - | 1.4641e-7 (1.56e-7) - | 1.7590e-4 (3.54e-5) | |
| 15 | 2.4123e-7 (1.66e-8) + | 7.5540e-8 (3.00e-8) = | 8.2080e-9 (5.67e-9) = | 3.4590e-7 (1.21e-8) + | 1.0588e-7 (9.61e-8) = | 2.5855e-7 (3.20e-8) + | 1.0340e-7 (1.47e-8) = | 9.9552e-8 (1.92e-8) = | 6.5181e-10 (2.91e-9) = | 4.2998e-14 (1.87e-13) = | 2.1697e-8 (1.27e-8) | |
| MaF6 | 5 | 1.2298e-1 (1.60e-3) = | 1.1362e-1 (5.57e-3) - | 1.1368e-1 (7.08e-4) - | 1.1888e-1 (4.54e-4) - | 1.2977e-1 (3.44e-4) = | 1.2944e-1 (3.68e-4) = | 9.7000e-2 (2.93e-3) - | 1.2884e-1 (6.27e-4) = | 1.2807e-1 (8.90e-4) = | 1.1619e-1 (2.82e-4) - | 1.2878e-1 (7.28e-4) |
| 8 | 7.2254e-2 (4.85e-2) - | 9.7184e-2 (1.84e-3) - | 9.5904e-2 (1.03e-3) - | 4.9611e-2 (4.19e-2) - | 7.5733e-2 (4.82e-2) = | 1.0607e-1 (3.12e-4) = | 9.3289e-2 (3.11e-3) - | 1.0606e-1 (2.62e-4) = | 5.8245e-2 (5.41e-2) - | 1.0258e-1 (2.29e-4) = | 1.0536e-1 (2.87e-3) | |
| 10 | 2.2044e-2 (4.03e-2) = | 9.2990e-2 (1.82e-3) = | 9.4330e-2 (5.07e-4) = | 0.0000e+0 (0.00e+0) - | 1.0676e-2 (3.09e-2) = | 1.0039e-1 (2.13e-4) + | 9.1234e-2 (8.85e-4) = | 9.2962e-2 (2.46e-2) = | 1.0036e-2 (3.09e-2) - | 9.8186e-2 (2.36e-4) = | 8.8737e-2 (1.08e-2) | |
| 15 | 0.0000e+0 (0.00e+0) = | 9.1645e-2 (3.11e-4) = | 9.2185e-2 (5.71e-4) = | 0.0000e+0 (0.00e+0) = | 0.0000e+0 (0.00e+0) = | 9.5091e-2 (2.84e-4) + | 9.1285e-2 (4.78e-4) = | 2.2443e-2 (4.01e-2) = | 0.0000e+0 (0.00e+0) = | 9.3860e-2 (2.85e-4) + | 6.3303e-2 (2.81e-2) | |
| MaF7 | 5 | 2.3889e-1 (5.83e-3) = | 2.0312e-1 (2.80e-3) - | 9.0909e-2 (5.92e-9) - | 2.6012e-1 (2.15e-3) = | 2.3473e-1 (3.36e-3) = | 1.5331e-1 (2.32e-2) - | 2.4252e-1 (7.43e-3) = | 2.1650e-1 (2.01e-2) - | 2.5189e-1 (5.18e-3) = | 5.0859e-3 (7.33e-3) - | 2.5179e-1 (3.41e-3) |
| 8 | 1.9458e-1 (2.30e-3) = | 1.4604e-1 (1.80e-2) - | 1.7565e-2 (2.62e-2) - | 2.1953e-1 (2.86e-3) = | 1.6205e-1 (4.98e-3) = | 7.8797e-2 (1.40e-2) - | 1.7408e-1 (1.31e-2) = | 1.5861e-1 (2.29e-3) - | 1.3909e-1 (2.52e-2) - | 4.4794e-4 (1.20e-3) - | 1.9700e-1 (2.81e-3) | |
| 10 | 1.2892e-1 (3.39e-2) = | 1.3759e-1 (2.34e-2) = | 6.0881e-5 (1.38e-5) - | 1.6623e-1 (1.57e-2) = | 1.3421e-1 (6.77e-3) - | 1.7277e-2 (9.01e-3) - | 1.3304e-1 (1.92e-3) - | 1.3264e-1 (2.98e-3) - | 1.5896e-2 (2.70e-2) - | 9.9228e-6 (2.90e-5) - | 1.6693e-1 (7.84e-3) | |
| 15 | 1.4224e-1 (1.36e-2) = | 1.1502e-1 (1.02e-2) = | 3.2214e-7 (1.88e-8) - | 1.3670e-1 (1.12e-2) = | 9.2981e-2 (4.40e-3) - | 2.7661e-5 (3.76e-5) - | 1.2198e-1 (2.16e-3) = | 1.1877e-1 (2.47e-3) = | 2.0586e-4 (6.28e-4) - | 1.0347e-8 (4.19e-8) - | 1.3472e-1 (4.32e-3) | |
| +/−/= | 9/1/18 | 1/8/19 | 1/13/14 | 5/7/16 | 5/3/20 | 7/6/15 | 5/7/16 | 5/3/20 | 5/6/17 | 5/12/11 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, Y.; Huang, J.; Li, X.; Liu, Y.; Zheng, J.; Zou, J. A Many-Objective Evolutionary Algorithm Based on Indicator and Decomposition. Mathematics 2023, 11, 413. https://doi.org/10.3390/math11020413
Xia Y, Huang J, Li X, Liu Y, Zheng J, Zou J. A Many-Objective Evolutionary Algorithm Based on Indicator and Decomposition. Mathematics. 2023; 11(2):413. https://doi.org/10.3390/math11020413
Chicago/Turabian StyleXia, Yizhang, Jianzun Huang, Xijun Li, Yuan Liu, Jinhua Zheng, and Juan Zou. 2023. "A Many-Objective Evolutionary Algorithm Based on Indicator and Decomposition" Mathematics 11, no. 2: 413. https://doi.org/10.3390/math11020413
APA StyleXia, Y., Huang, J., Li, X., Liu, Y., Zheng, J., & Zou, J. (2023). A Many-Objective Evolutionary Algorithm Based on Indicator and Decomposition. Mathematics, 11(2), 413. https://doi.org/10.3390/math11020413






