Efficient Graph Network Using Total Magic Labeling and Its Applications

Abstract

Cryptography is a pivotal application of graph theory in ensuring secure communication systems. Modern cryptography is deeply rooted in mathematical theory and computer science practices. It is widely recognized that encryption and decryption processes are primarily outcomes of mathematical research. Given the increasing importance of safeguarding secret information or messages from potential intruders, it is imperative to develop effective technical tools for this purpose. These intruders are often well-versed in the latest technological advancements that could breach security. To address this, our study focuses on the efficacious combinatorial technique of graph networks using efficient domination and total magic labeling. The introduction of a graph network based on total magic labeling can significantly influence the network’s performance. This research introduces a novel combinatorial method for encrypting and decrypting confidential numbers by leveraging an efficient dominant notion and labeled graph.

1. Introduction

Let  $H_{GN}\left(V_{GN}, E_{Gn}\right)$ represent an undirected connected graph with  $p_{GN}$ vertices and  $q_{GN}$ edges. The degree, neighborhood and closed neighborhood of a vertex  $v_{GN}$ in the graph  $H_{GN}$ are denoted by  $deg\left(v_{GN}\right), N_{GN}\left(v_{GN}\right)$ and  $N_{GN}\left[v_{GN}\right]=N_{GN}\left(v_{GN}\right)\cup \left\{v_{GN}\right\}$, respectively. Ore [1] was the pioneer in introducing the terms “dominating set” and “dominating number” in his research. For a comprehensive understanding of domination theory-related terms, readers can refer to [2]. Numerous types of domination parameters have been introduced and explored over time. Teresa et al. [3] delved into various forms of dominations and their associated constraints. Cockayne et al. [4] delved into total dominance, a study further expanded in [5,6]. Harary and others explored double domination in [7], while studies on paired domination are documented in [8,9]. Chellali et al. [10] explored the relationship between total and paired domination in trees. Further insights on paired domination are available in [11,12,13]. Dunbar and Haynes [14] examined domination in inflated graphs, with their research continuing in [15,16,17,18]. Sampath Kumar initiated the study of equitable domination, which was later expanded upon by Swaminathan and Dharmalingam [19]. Meenakshi delved into the equitable domination of the complements of inflated graphs in [20,21].

Rosa [22] was the first to introduce graph labeling in 1967 and continued his studies on tree labeling [23]. Yeh embarked on a survey of labeling results for graphs with a distance of two. Grannell et al. [24] introduced modular gracious labeling of trees, a concept that bridges α-labeling and graceful labeling. Further studies on graceful labeling can be found in [25,26,27]. Prime labeling was initially explored by Tout, Dabboucy and Howalla [28] in 1982. Vertex equitable labeling was pioneered by Jeyanthi et al. [29], and various types of labeling were subsequently studied, as documented in [30,31,32,33,34,35,36]. It is important to note that our focus is solely on finite, simple and connected graphs.

The primary motivation behind this research is to devise novel algorithms impervious to intruders. It is essential for potential adversaries to understand the graphical network development statistics and the parameters used to decipher concealed sensitive data represented as numerical values [37,38,39]. This research introduces an encryption system comprising (i) Plain text, (ii) Encryption algorithm, (iii) Secret key, (iv) Cypher text and a decryption system consisting of (i) Cypher text, (ii) Secret Key, (iii) Decryption algorithm, (iv) Plain text. Initially, the general graph network (with modulo t) is constructed using the encryption algorithm, which leverages parameters (secret key), efficient domination and total magic labeling. The resulting graph (Cypher text) embeds hidden messages or information in the form of numerical values located in the incident links of the efficient dominating set members. To access this secret information, one must decrypt the provided algorithm. Examples are provided for the construction of graph networks with modulo 5 and modulo 7. Additionally, an adversary model has been established for this research, with discussions centered on various facets of the attacker [40,41].

Utilizing the aforementioned methodology, one can establish three distinct networks [42,43,44]: a graph network with a minimum number of edges, a graph network with a moderate number of edges and a graph network with a maximum number of edges [45,46,47]. Opting for the first network, characterized by the fewest edges, exposes the system to vulnerabilities, as adversaries can easily discern the concealed secret information, highlighting a significant system flaw [48,49,50]. In the subsequent discussion section, we will delve deeper into the proposed method, analyzing its strengths and weaknesses in comparison to existing approaches. This will provide readers with a comprehensive understanding of the method’s efficacy and potential areas of improvement. By juxtaposing our method with established techniques, we aim to elucidate its unique advantages and potential challenges, offering a holistic perspective on its applicability in real-world scenarios.

2. Preliminaries

Definition 1 

([1]). Let  $H_{GN}\left(V_{GN}, E_{Gn}\right)$ be a finite, simple and connected graph. A set  $S_{GN}*\subseteq V_{GN}\left(H_{GN}\right)$ is a dominating set if, for every vertex  $v_{gn}$ in  $V_{GN}$ but not in  $S_{GN}*$, there exists at least one vertex  $u_{GN}$ in  $S_{GN}*$ such that  $v_{gn}$ is adjacent to  $u_{GN}$. The cardinality of the smallest dominating set in  $H_{GN}$ is termed the domination number of  $H_{GN}$ and is denoted by  ${\gamma }_{GN}\left(H_{GN}\right).$

Definition 2 

([33]). A set  $S_{GN}*\subseteq V_{GN}\left(H_{GN}\right)$ is a total dominating set if every vertex  $v_{GN}$ in  $V_{GN}$ is adjacent to a vertex of  $S_{GN}$. The cardinality of the smallest total dominating set is termed the total domination number and is denoted by  ${\gamma }_t\left(H_{GN}\right).$

Definition 3 

([34]). A dominating set  $S_{GN}*\subseteq V_{GN}\left(H_{GN}\right)$ is a paired dominating set if the induced subgraph  $\langle S_{NG}*\rangle$ has a perfect matching. The smallest cardinality of a paired dominating set in  $H_{GN}$ is termed the paired domination number of  $H_{GN}$ and is denoted by  ${\gamma }_{pr}\left(H_{GN}\right).$

Definition 4 

([34]). A dominating set  $S_{GN}*\subseteq V_{GN}\left(H_{GN}\right)$ is termed an efficient dominating set ( $E_{eff}DS$) if, for every vertex  $u_{GN}\in V_{GN},\hspace{0.33em}\left|N_{GN}\left[u_{GN}\right]\cap S_{GN}*\right|=1.$ Equivalently, a dominating set  $S_{GN}*$ is efficient if the distance between any two vertices in $S_{GN}*$ is at least three.

Definition 5 

([24]). Let  $G_{GN}{}^{*}=\left(V_{GN}{}^{*}, E_{GN}{}^{*}\right)$ be a finite simple connected graph. Labeling of  $G_{GN}{}^{*}$ is a mapping from a set of vertices, edges or both to a set of labels. Typically, labels are positive (or non-negative), but real numbers can also be employed.

Definition 6 

([24]). A function of  $V_{GN}{}^{*}\left(G_{GN}{}^{*}\right)$ to a set of labels is vertex labeling. A graph having such a function is called a vertex-labeled graph.

Definition 7 

([29]). A function of  $E_{GN}{}^{*}\left(G_{GN}{}^{*}\right)$ to a set of labels is edge labeling. A graph having such a function is called an edge-labeled graph.

Definition 8 

([29]).  $G_{GN}{}^{*}=\left(V_{GN}\left(G_{GN}{}^{*}\right), E_{GN}\left(G_{GN}{}^{*}\right)\right)$ finite undirected graphs without loops and many edges with vertex set  $V_{GN}\left(G_{GN}{}^{*}\right)$ and edge set  $E_{GN}\left(G_{GN}{}^{*}\right)$, where  $l=\left|V_{GN}\left(G_{GN}{}^{*}\right)\right|$,  $m=\left|E_{GN}\left(G_{GN}{}^{*}\right)\right|$. A graph labeling  $G_{GN}{}^{*}$ is any mapping that translates a certain set of graph elements to a specific set of positive integers. If the domain is a vertex (or edge) set, the labeling is referred to as vertex (or edge) labeling. When the domain contains both vertices and edges, the labeling is referred to as total labeling.

Definition 9 

([29]). Graph labelings can assign weights to each edge and/or vertex. If every vertex weight (or edge weight, as appropriate) has the same value, the labeling is termed magic.

Definition 10 

([27]). Let  $G_{GN}{}^{*}=\left(V_{GN}{}^{*}\left(G_{GN}{}^{*}\right), E_{GN}{}^{*}\left(G_{GN}{}^{*}\right)\right)$ denote a graph with the vertex set  $V_{GN}{}^{*}\left(G_{GN}{}^{*}\right)$ and the edge set  $E_{GN}{}^{*}\left(G_{GN}{}^{*}\right)$. A vertex magic total labeling of  $G_{GN}{}^{*}$ is a one-to-one mapping  $g :V_{GN}{}^{*}\left(G_{GN}{}^{*}\right)\cup E_{GN}{}^{*}\left(G_{GN}{}^{*}\right)\to \left\{1, 2, . . ., v+e\right\}$ if there exists a constant c such that for every vertex x of  $G_{GN}{}^{*}$. f $\left(a\right)+\sum _{b\in N\left(a\right)}f\left(ab\right)=c$. The magic constant for f is the constant c.

Definition 11 

([27]). If there is a bijection  $g_{GN}{}^{*} :V_{GN}{}^{*}\left(G_{GN}{}^{*}\right)\cup E_{GN}{}^{*}\left(G_{GN}{}^{*}\right)\to \left\{1, 2, . . ., p+q\right\}$ such that there exists a constant “c” for any (l, m) in  $E_{GN}{}^{*}\left(G_{GN}{}^{*}\right)$ satisfying  $g_{GN}{}^{*}\left(l\right)+g_{GN}{}^{*}\left(l.m\right)+g_{GN}{}^{*}\left(m\right)=c$, then the graph with  $p_{GN}{}^{*}$ vertices and  $q_{GN}{}^{*}$ edges are said to be total edge magic.

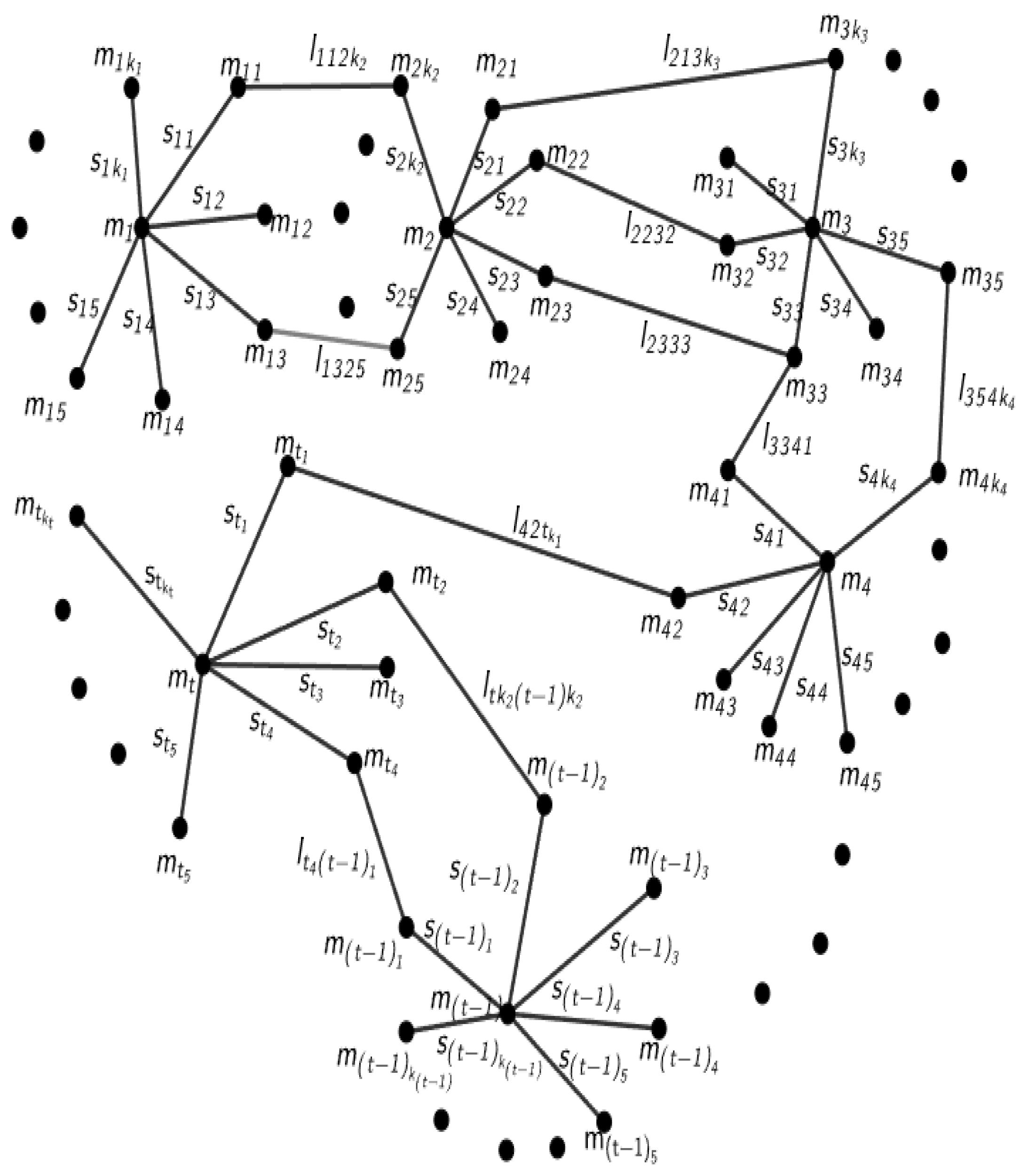
3. Graph Network Construction

Let H_GN = (V_GN, E_GN) be a graph that has  $\left|V_{GN}\left(H_{GN}\right)\right|={\nu }_{GN} \mathrm{and} \left|E_{GN}\left(H_{GN}\right)\right|=e_{GN}.$

Let  $S{\prime }_{GN}=\left\{m_1,m_2,\dots .,m_t\right\}$ be the E_effDS members with degrees say  $\mathrm{deg}(m_1)=k_1$,  $\mathrm{deg}(m_2)=k_2,\mathrm{deg}(m_3)=k_3,\dots .$ and  $\mathrm{deg}(m_t)=k_t$, where  $k_1,k_2,k_3,\dots .,k_t\ge 1$.

Let  $m_{11},m_{12},\dots ,m_{1k_1}$; $m_{21},m_{22},\dots ,m_{2k_2};$ $m_{31},m_{32},\dots ,m_{3k_3};\mathrm{and} m_{t_1},m_{t_2},\dots ,m_{t{k}_t}$ be the neighboring nodes of  $m_1,m_2,m_3,\dots ,m_t,$ respectively,  $d\left(m_1,m_{1k_1}\right)=d\left(m_2,m_{2k_2}\right)=d\left(m_3,m_{3k_3}\right)=\dots .=d\left(m_t,m_{t{k}_t}\right)=1, 1\le k_1\le j_1{}^{*}; 1\le k_2\le j_2*;$…;$1\le k_t\le j_t{.}^{*}$ Define $V_{GN}\left(H_{GN}\right)=\left\{m_1,m_2,\dots ,m_t\right\}\cup {\left\{m_{1k_1}\right\}}_{k_1=1}^{j_1{}^{*}}\cup {\left\{m_{2k}{}_2\right\}}_{k_2=1}^{j_2{}^{*}}\cup \dots .\cup {\left\{m_{t{k}_t}\right\}}_{k_t=1}^{j_r{}^{*}}$and  $\left|V_{GN}\left(H_{GN}\right)\right|=j_1{}^{*}+j_2{}^{*}+j_3{}^{*}+\dots .+j_t{}^{*}+t={\nu }_{GN}.$

Let  ${E^{\prime }}_{GN1}=\left\{m_{1k_1}{m}_{2k_2},m_{2k_2}{m}_{3k_3},\dots ,m_{\left(t-1\right)k_{t-1}}{m}_{t{k}_t}\right\}$ for only one  $k_1,k_2,\dots .,k_t,$ where  $1\le k_1\le j_1{}^{*},1\le k_2\le j_2{}^{*},1\le k_3\le j_3{}^{*},\dots ,1\le k_t\le j_t{}^{*}.$

Let  ${E^{\prime }}_{GN-\min }=\left\{m_1{m}_{1k_1},m_2{m}_{2k_2},\dots ,m_t{m}_{t{k}_t}/1\le k_1\le j_1{}^{*}, 1\le k_2\le {\mathrm{j}}_2{}^{*} \dots , 1\le k_{\mathrm{t}}\le j_t{}^{*}\right\}$ $\cup {E^{\prime }}_{GN1}$. Then  $\left|{E^{\prime }}_{GN-\min }\right|=j_1{}^{*}+j_2{}^{*}+\dots +j_t{}^{*}+t={v^{\prime }}_{GN}(say).$

Define  ${E^{\prime }}_{GN-\max }=\left\{(i^{\ast },j^{\ast }); 1\le i^{\ast },j\le j_1{}^{*}+j_2{}^{*}+\dots .+j_t{}^{*}+t; i^{\ast }\ne j^{\ast }\right\}$ $-\left\{\begin{array}{l} m_1{m}_2,m_2{m}_3,m_3{m}_4,\dots ,m_{t-1}{m}_t, m_1{m}_{2k_2},m_1{m}_{3k}{}_3,\dots ,m_1{m}_{t{k}_t},m_2{m}_{3k_3},\dots ,m_2{m}_{t{k}_t},\dots ,\\ m_t{m}_{1k_1},m_r{m}_{2k_2},\dots ,m_2{m}_{(t-1)k_{(t-1)}}, 1\le k_1\le j_1{}^{*}, 1\le k_2\le j_2{}^{*},\dots . 1\le k_t\le j_t{}^{*}.\end{array}\right.$

Then  $\begin{array}{l}\left|E_{GN-\max }\right|={\beta }^{\prime }(let)=\frac{1}{2}\left[{{\nu }^{\prime }}_{GN}{}^2+{{\nu }^{\prime }}_{GN}-2t(1+{v^{\prime }}_{GN})\right], \\ where {{\nu }^{\prime }}_{GN}=j_1{}^{\ast }+j_2{}^{\ast }+\dots +j_t{}^{\ast }+t.\end{array}$. H′_GN satisfies,  ${\alpha }^{\prime }\le \left|{E^{\prime }}_{GN}\left(H^{\prime }\right)\right|\le {\beta }^{\prime }.$

4. Encryption System of Graph Network

It consists of (i) Plain text, (ii) Encryption Algorithm, (iii) Secret Key, (iv) Cypher Text.

4.1. Plain Text

Plain text of the graph network is the secret information or secret messages in the form of numerical value using modulo t; t is a positive integer. Let the secret number be L_SN ≡ a_sn (mod t), where a_sn = 0.

4.2. Encryption Algorithm: L_SN ≡ a_sn (mod t), Where a_sn = 0

Input:  $L_{SN}\ge t_{sn}$,  $L_{SN}\equiv a_{sn}\left(mod t_{sn}\right)$, where a_sn = 0.

Output: Encrypted Labeled Graph (ELG), H′_GN

Start

Step 1: Divide L_SN into t separations, say  $L_0,L_1,L_2,\dots ,L_{t-1}$, where  $L_0\equiv 0\left(mod r_{cn}\right),L_1\equiv 1\left(mod r_{cn}\right),L_2\equiv 2\left(mod r_{cn}\right),\dots ,L_{t-1}\equiv \left(t-1\right)\left(mod t_{cn}\right)$.

Step 2: Fix  $deg(m_1)=k_1,\mathrm{deg}(m_2)=k_2,\dots .,deg(m_t)=k_t, \mathrm{where} k_1,k_2,\dots ,k_t\ge 1$. Let  $m_{11},m_{12},\dots ,m_{1s_1}$;  $m_{21},m_{22},\dots ,m_{2s_2};$ $m_{31},m_{32},\dots ,m_{3s_3};\mathrm{and} m_{t_1},m_{t_2},\dots ,m_{t{s}_t}$ be the neighboring nodes of  $m_1,m_2,m_3,\dots ,m_t,$ respectively,  $d\left(m_1,m_{1k_1}\right)=d\left(m_2,m_{1k_2}\right)=$  $d\left(m_3,m_{3k_3}\right)=\dots ..=d\left(m_t,m_{t{k}_t}\right)=1,1\le k_1\le j_1{}^{*};1\le k_2\le j_2*;$ …;  $1\le k_t\le {j_t}^{*}.$

Step 3: Define $V_{GN}\left(H_{GN}\right)=\left\{m_1,m_2,\dots ,m_r\right\}\cup {\left\{m_{1k_1}\right\}}_{k_1=1}^{j_1{}^{*}}\cup {\left\{m_{2k}{}_2\right\}}_{k_2=1}^{j_2{}^{*}}\cup \dots .\cup {\left\{m_{t{k}_t}\right\}}_{k_t=1}^{j_t{}^{*}}$ and  $\left|V_{GN}\left(H_{GN}\right)\right|=j_1{}^{*}+j_2{}^{*}+j_3{}^{*}+\dots .+j_t{}^{*}+t=\nu {\prime }_{GN}.$

Let  $E{\prime }_{GN1}=\left\{m_{1k_1}{m}_{2k_2},m_{2k_2}{m}_{3k_3},\dots ,m_{\left(t-1\right)k_{t-1}}{m}_{t{k}_t}\right\}$ for only one  $k_1,k_2,\dots .,k_t$ where  $1\le k_1\le j_1{}^{*},1\le k_2\le j_2{}^{*},1\le k_3\le j_3{}^{*},\dots ,1\le k_t\le j_t{}^{*}.$ Let  $E{\prime }_{GN-min}$  $\left\{m_1{m}_{1k_1},m_2{m}_{2k_2},\dots ,m_t{m}_{t{k}_t}/1\le k_1\le j_1{}^{*}, 1\le k_2\le j_2{}^{*} \dots , 1\le k_t\le j_t{}^{*}\right\}\cup E{\prime }_{GN1}.$

Now let

 ${E^{\prime }}_{GN-\max }=\left\{(i^{\ast },j^{\ast }); 1\le i^{\ast },j^{\ast }\le j_1{}^{\ast }+j_2{}^{\ast }+\dots .+j_t{}^{\ast }+t; i^{\ast }\ne j^{\ast }\right\}$ $-\left\{\begin{array}{l} m_1{m}_2,m_2{m}_3,m_3{m}_4,\dots ,m_{t-1}{m}_t, m_1{m}_{2k_2},m_1{m}_{3k}{}_3,\dots ,m_1{m}_{t{k}_t},m_2{m}_{3k_3},\dots ,m_2{m}_{t{k}_t},\dots ,\\ m_t{m}_{1k_1},m_r{m}_{2k_2},\dots ,m_2{m}_{(t-1)k_{(t-1)}}, 1\le k_1\le j_1{}^{*}, 1\le k_2\le j_2{}^{*},\dots . 1\le k_t\le j_t{}^{*}.\end{array}\right.$Then  $\left|E_{GN-\max }\right|={\beta }^{\prime }(let)=\frac{1}{2}\left[\nu {\prime }_{GN}{}^2+\nu {\prime }_{GN}-2t(1+{v^{\prime }}_{GN})\right], where {{\nu }^{\prime }}_{GN}=j_1{}^{\ast }+j_2{}^{\ast }+\dots +j_t{}^{\ast }+t.$H′_GN satisfies,  $\alpha \prime \le \left|E{\prime }_{GN}\left(H\prime \right)\right|\le \beta \prime .$

Step 4:  $z_0=\left[\frac{L_0}{t}\right],$  $z_1=\left[\frac{L_1}{t}\right],$  $z_2=\left[\frac{L_2}{t}\right],$ …,  $z_{t-1}=\left[\frac{L_{t-1}}{t}\right]$.

Step 5: Split  $z_0=s_{11}+s_{12}+\dots +s_{1k_1}$;  $z_1=s_{21}+s_{22}+\dots +s_{2k_2};\dots ,$  $z_{t-1}=s_{t1}+s_{t2}+\dots +s_{t{k}_t}$ where k₁, k₂, …, k_t  $\ge 0.$

Step 6: Let  $f{\prime }_{GN}:V_{GN};\to \left\{{\alpha }_{i^{*}}\in Z^{+}\right\}$ defined as  $f{\prime }_{GN}\left(v\right)={\alpha }_{i^{*}}$ being a many-to-one function. Let  $g{\prime }_{GN}:E_{GN}\to {\alpha }_{j^{*}},{\alpha }_{j^{*}}\in N^{*},$ where N* = {$s_{11},s_{12},\dots ,s_{1k_1}$;

$s_{31},s_{32},\dots ,s_{3j_3};\dots ;s_{t1},s_{t2},\dots ,s_{t{j}_t}$ and  $t_{i^{*}}\in Z^{+}\}$ such that $g{\prime }_{GN}\left(m_1{m}_{1j_1{}^{*}}\right)=s_1{}_{k_1};g{\prime }_{GN}\left(x_2{x}_{2j_2{}^{*}}\right)=s_2{}_{k_2};\dots ;g{\prime }_{GN}\left(m_t{m}_{t{k}_t}\right)=s_t{}_{k_t}$ for $1\le k_1\le j_1{}^{*},1\le k_2\le j_2{}^{*},\dots ,1\le k_t\le j_t{}^{*}$ be a many-to-one function such that  $f\left({\alpha }_{i^{*}}\right)+f\left({\alpha }_{j^{*}}\right)+f\left({\alpha }_{i^{*}}{\alpha }_{j^{*}}\right)={\alpha }_k,$ every edge  ${\alpha }_{i^{*}}{\alpha }_{j^{*}}\in E{\prime }_{GN},{\alpha }_k$ is a constant. The constructed graph network preserves total magic labeling.

Step 7: Define

$$g{\prime }_{GN}\left(m_1{m}_{1k_1}\right)=s_{1_{k_1}}={\alpha }_k-f\left(m_1\right)-f\left(m_{1k_1}\right),1\le k_1\le j_1{}^{*};$$

$$g{\prime }_{GN}\left(m_2{m}_{2k_2}\right)=s_{2_{k_2}}={\alpha }_k-f\left(m_2\right)-f\left(m_{2k_2}\right),1\le k_2\le j_2{}^{*};$$

$$g{\prime }_{GN}\left(m_3{m}_{3k_3}\right)=s_{3_{k_3}}={\alpha }_k-f\left(m_3\right)-f\left(m_{3k_3}\right),1\le k_3\le j_3{}^{*}; \dots ;$$

$$g{\prime }_{GN}\left(m_{i^{*}}{m}_{i^{*}{k}_i}\right)=s_{i^{*}{}_{k_i}}={\alpha }_k-f\left(m_{i^{*}}\right)-f\left(m_{i^{*}{k}_{i^{*}}}\right),1\le k_{i^{*}}\le j_{i^{*}};i^{*}=1,2,\dots ,t$$

$$g{\prime }_{GN}\left(m_{1i^{*}}{m}_{1k}{}_1\right)={\alpha }_k-f\left(m_{1i^{*}}\right)-f\left(m_{1k_1}\right),1\le i^{*}\le t,1\le k_1\le j_1{}^{*};$$

$$g{\prime }_{GN}\left(m_{2i^{*}}{m}_{2k}{}_2\right)={\alpha }_k-f\left(m_{2i^{*}}\right)-f\left(m_{2k_2}\right),1\le i^{*}\le t,1\le k_2\le j_2{}^{*};$$

$$g{\prime }_{GN}\left(m_{3i^{*}}{m}_{3k}{}_3\right)={\alpha }_k-f\left(m_{3i^{*}}\right)-f\left(m_{3k_3}\right),1\le i^{*}\le t,1\le k_3\le j_3{}^{*}; \dots ;$$

$$g{\prime }_{GN}\left(m_{t{i}^{*}}{m}_{tk}{}_t\right)={\alpha }_k-f\left(m_{t{i}^{*}}\right)-f\left(m_{t{k}_t}\right),1\le i^{*}\le t,1\le k_t\le j_t;$$

and

$$i^{*}\ne j_{i^{*}}{}^{*},i^{*}=1,2,\dots ,t$$

$$g{\prime }_{GN}\left(m_{1i^{*}}{m}_{2k}\right)={\alpha }_k-f\left(m_{1i^{*}}\right)-f\left(m_{2k}\right),1\le i^{*}\le t,1\le k\le j_2{}^{*};$$

$$g{\prime }_{GN}\left(m_{2i^{*}}{m}_{3k}\right)={\alpha }_k-f\left(m_{2i^{*}}\right)-f\left(m_{3k}\right),1\le i^{*}\le t,1\le k\le j_3{}^{*};$$

$$g{\prime }_{GN}\left(m_{3i^{*}}{m}_{4k}\right)={\alpha }_k-f\left(m_{3i^{*}}\right)-f\left(m_{4k}\right),1\le i^{*}\le t,1\le k\le j_4{}^{*}; \dots ;$$

$$g{\prime }_{GN}(m_{(t-1)i^{\ast }}{m}_{tk})={\alpha }_k-f(m_{(t-1)i^{\ast }})-f(m_{tk}),1\le i^{\ast }\le t, 1\le k\le j_t{}^{\ast };$$

$$i^{*}\ne j_{i^{*}}{}^{*},i^{*}=1,2,\dots ,t.$$

Define

$$g{\prime }_{GN}\left(m_{1i^{*}}{m}_{1k_1}\right)={\alpha }_k-f\left(m_{1i^{*}}\right)-f\left(m_{1k_1}\right),1\le i^{*}\le t,1\le k_1\le j_1{}^{*};$$

$$g{\prime }_{GN}\left(m_{2i^{*}}{m}_{2k}{}_2\right)={\alpha }_k-f\left(m_{2i^{*}}\right)-f\left(m_{2k_2}\right),1\le i^{*}\le t,1\le k_2\le j_2{}^{*};\dots .;$$

$$\begin{array}{c}g{\prime }_{GN}\left(m_{j^{*}{i}^{*}}{m}_{i^{*}{k}_t}\right)={\alpha }_k-f\left(m_{j^{*}{i}^{*}}\right)-f\left(m_{j^{*}{k}_j}\right)1\le i^{*},j^{*}\le t,1\le k_t\le j_t{}^{*};\\ i^{*}\ne j_t{}^{*} \mathrm{and} i^{*}\ne k_t;\end{array}$$

$$g{\prime }_{GN}\left(m_{1i^{*}}{m}_{2k}\right)={\alpha }_k-f\left(m_{1i^{*}}\right)-f\left(m_{2k}\right),1\le i^{*}\le t,1\le k\le j_2{}^{*};$$

$$g{\prime }_{GN}\left(m_{2i^{*}}{m}_{3k}\right)={\alpha }_k-f\left(m_{2i^{*}}\right)-f\left(m_{3k}\right),1\le i^{*}\le t,1\le k\le j_3{}^{*};\dots ;$$

$$g{\prime }_{GN}\left(m_{\left(t-1\right)i^{*}}{m}_{t{k}_t}\right)={\alpha }_k-f\left(m_{\left(t-1\right)i^{*}}\right)-f\left(m_{tk}{}_t\right),1\le i^{*}\le t,1\le k_t\le j_t{}^{*};$$

$$i^{*}\ne j_{i^{*}}{}^{*},j^{*}=1,2,\dots ,t$$

End.

4.3. Secret Key

Find the E_eff DS of the graph network, which is  $S{\prime }_{GN}=\left\{m_1,m_2,\dots .,m_t\right\}$.

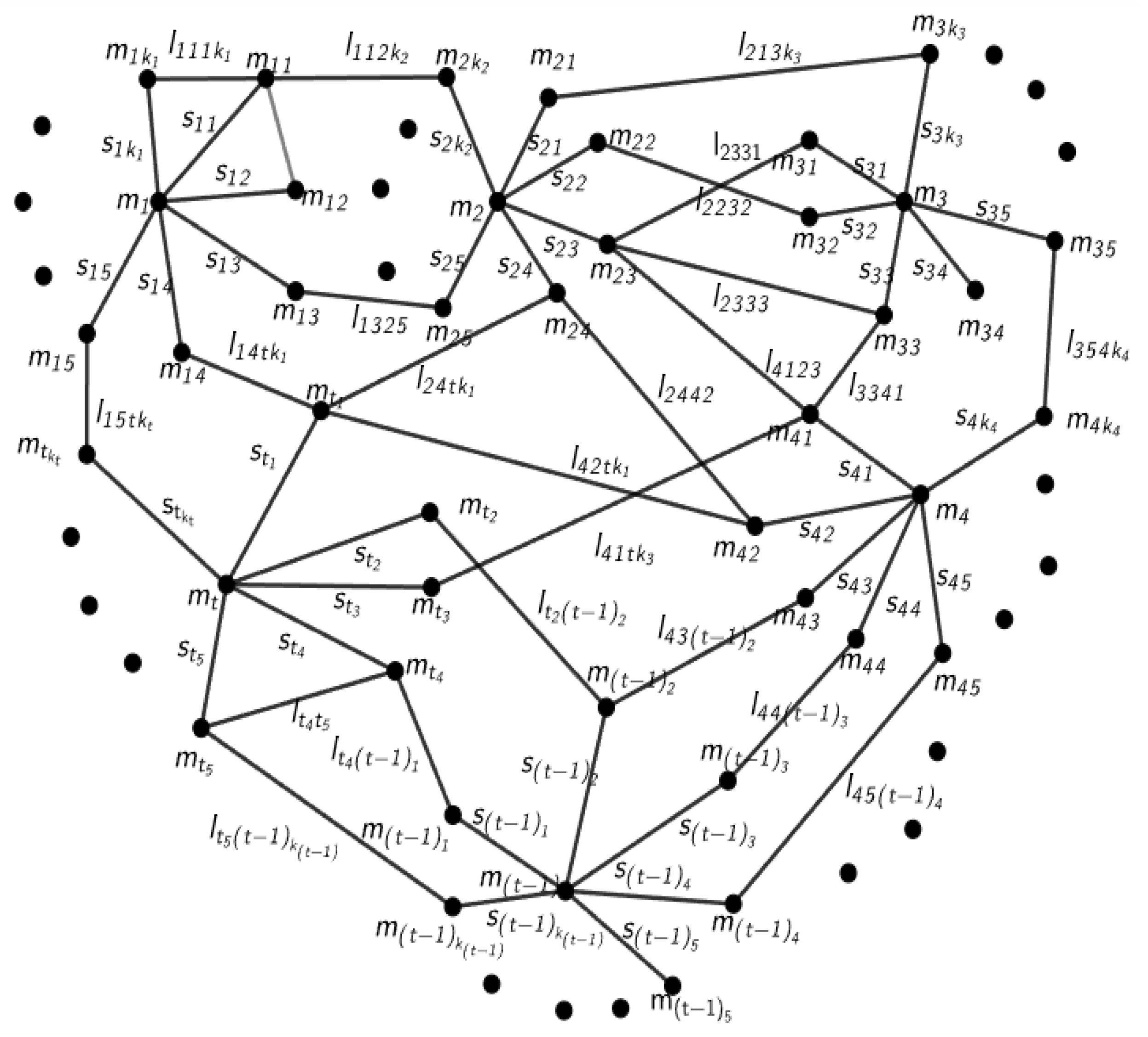
4.4. Cypher Text

Using an encryption algorithm and secret key, we have constructed the sub-graph network GN₁, GN₂, GN₃, …, GN_t , which makes the labeled graph network. There are three possible instances considered here, according to the construction. (i) Labeled graph network with a minimum number of edges say H′_{GN min-(t)}, shown in Figure 1. (It is a labeled graph network tree.) (ii) Labeled graph network with a moderate number of edges say H′_{GN mod-(t)}, shown in Figure 2. (iii) Labeled graph network with more number of edges say H′_{GN more-(t)}, shown in Figure 3.

5. Decryption System of Graph Network

(i) Cypher text, (ii) Secret key, (iii) Decryption algorithm, (iv) Plain text.

Cypher text is the labeled graph network. Using a secret key, we decrypt it, and we get back the plain text.

Decryption Algorithm

Input: ELG, H′_GN

Output: L_GN, the plain text.

Begin

Step 1: Find the

$${\mathrm{E}}_{eff}\mathrm{DS} S{\prime }_{GN}=\left\{m_1,m_2,\dots .,m_t\right\}$$

such that

$$N_{GN}\left[m_1\right]\cap N_{GN}\left[m_2\right]\cap \dots N_{GN}\left[m_t\right]=\phi .$$

Step 2:

$$L_0=a_0+t{\displaystyle \sum }_{n=1}^{j_1{}^{*}}g{\prime }_{GN}(m_1{m}_{1n})\hspace{0.33em},$$

where

$$a_{i^{*}}\equiv i^{*}\left(mod t\right)$$

$$L_1=a_1+t{\displaystyle \sum _{n=1}^{j_2{}^{\ast }}g{\prime }_{GN}(m_2{m}_{2n}}),\dots ,$$

$$L_{t-1}=a_{n-1}+t{\displaystyle \sum }_{n=1}^{j_t{}^{*}}g{\prime }_{GN}(m_t{m}_{tn})$$

Step 3:

$$L={\displaystyle \sum }_{n=0}^{t-1}{L}_n$$

End.

6. Illustration: Secret Number L_SN ≡ a_sn (mod t), Where a_sn = 0 and t = 5

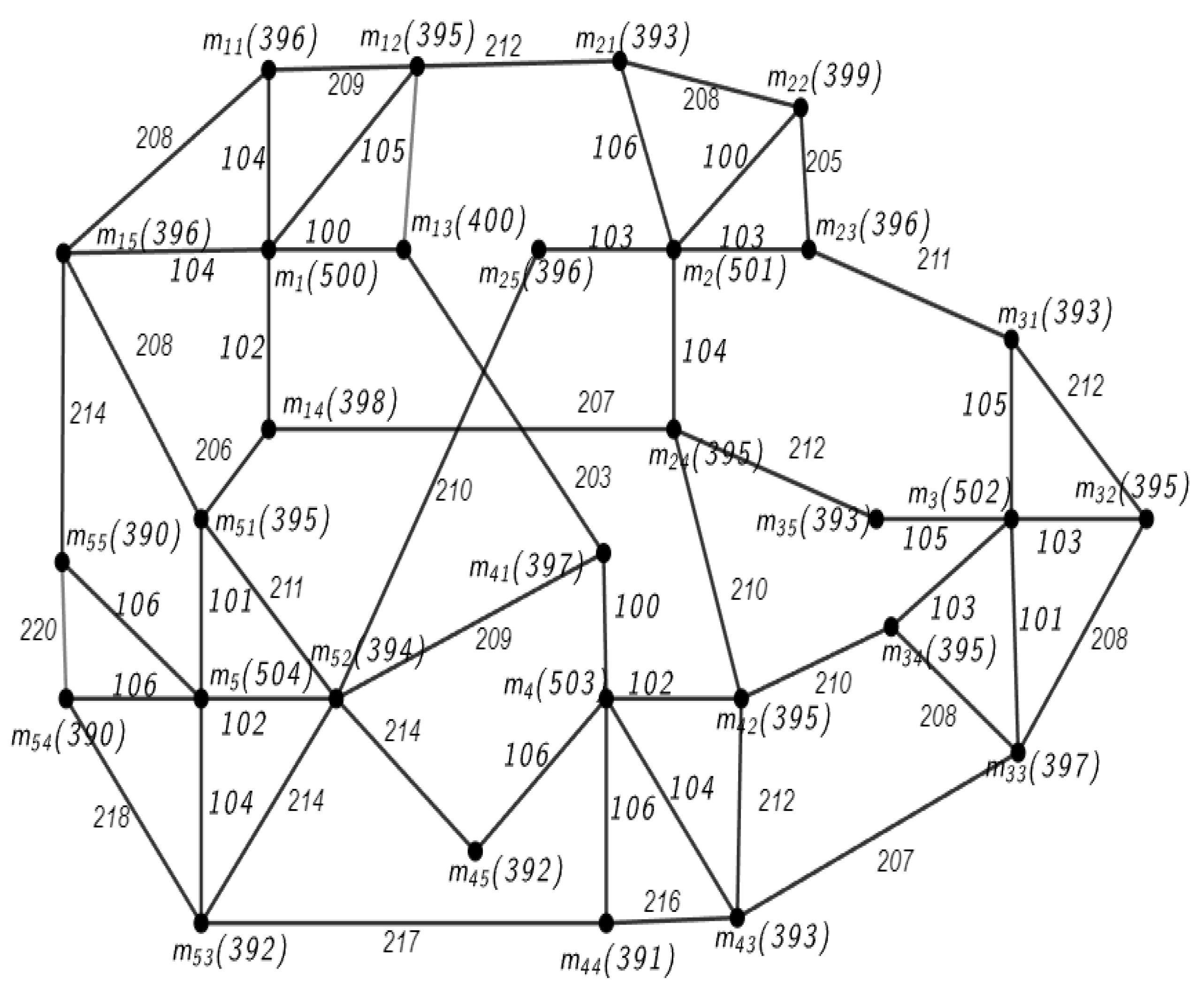
6.1. Graph Network for L_SN ≡ a_sn (mod t), Where a_sn = 0 and t = 5

Let H_GN = (V_GN, E_GN) be a graph that has  $\left|V_{GN}\left(H_{GN}\right)\right|={\nu }_{GN} \mathrm{and}$  $\left|E_{GN}\left(H_{GN}\right)\right|=e_{GN}.$ Let X = $\left\{m_1,m_2,m_3,m_4,m_5\right\}$be E_eff DS members with degrees say  $\mathrm{deg}(m_1)=k_1,\mathrm{deg}(m_2)=k_2, \mathrm{deg}(m_3)=k_3,$  $\mathrm{deg}(m_4)=k_4$ and  $\mathrm{deg}(m_5)=k_5$ where  $k_1,k_2,k_3,k_4,k_5\ge 1.$

Let  $m_{11},m_{12},\dots ,m_{1k_1}$;  $m_{21},m_{22},\dots ,m_{2k_2};$  $m_{31},m_{32},\dots ,m_{3k_3};$  $m_{41},m_{42},\dots ,m_{4k_4};$ and  $m_{51},m_{52},\dots ,m_{5k_5}$ be the neighboring nodes of  $m_1,m_2,m_3,m_4,m_5$ respectively, $d\left(m_1,m_{1k_1}\right)=d\left(m_2,m_{1k_2}\right)=d\left(m_3,m_{3k_3}\right)=d\left(m_4,m_{4k_4}\right)=d\left(m_5,m_{5k_5}\right)=1$.  $1\le k_1\le j_1{}^{*},1\le k_2\le j_2{}^{*},1\le k_3\le j_3{}^{*},1\le k_4\le j_4{}^{*},1\le k_5\le j_5{}^{*}.$

$$\begin{gathered} \begin{array}{c}Define V_{GN}(H_{GN})=\left\{m_1,m_2,m_3,m_4,m_5\right\}\cup {\left\{m_{1k_1}\right\}}_{k_1=1}^{j_1{}^{\ast }}\cup {\left\{m_{2k}{}_2\right\}}_{k_2=1}^{j_2{}^{\ast }}\cup {\left\{m_{3k}{}_3\right\}}_{k_3=1}^{j_3{}^{\ast }}\\ \cup {\left\{m_{4k}{}_4\right\}}_{k_4=1}^{j_4{}^{\ast }}\cup {\left\{m_{5k_5}\right\}}_{k_5=1}^{j_5{}^{\ast }}\end{array} \\ \left|V_{GN}\left(H_{GN}\right)\right|=j_1{}^{*}+j_2{}^{*}+j_3{}^{*}+\dots .+j_t{}^{*}+5={\nu }_{GN}. \end{gathered}$$

Let  ${E^{\prime }}_{GN1}=\left\{m_{1k_1}{m}_{2k_2},m_{2k_2}{m}_{3k_3},m_{3k_3}{m}_{4k_4},m_{4k_4}{m}_{5k_5}\right\}$ for only one  $k_1,k_2,\dots .,k_5$ where  $1\le k_1\le j_1{}^{*},1\le k_2\le j_2{}^{*},1\le k_3\le j_3{}^{*},1\le k_4\le j_4{}^{*},1\le k_5\le j_5{}^{*}.$

Let ${E^{\prime }}_{GN-\min }=\left\{m_1{m}_{1k_1},m_2{m}_{2k_2},\dots ,m_5{m}_{5k_5}/1\le k_1\le j_1{}^{\ast }, 1\le k_2\le {\mathrm{j}}_2{}^{\ast } \dots , 1\le k_5\le j_5{}^{\ast }\right\}$ $\cup {E^{\prime }}_{GN1}.$ Then  $\left|{E^{\prime }}_{GN-\min }\right|=j_1{}^{\ast }+j_2{}^{\ast }+\dots +j_5{}^{\ast }+5={v^{\prime }}_{GN}(let).$

Let ${E^{\prime }}_{GN-\max }=\left\{(i^{\ast },j^{\ast }); 1\le i^{\ast }, j^{\ast }\le j_1{}^{\ast }+j_2{}^{\ast }+\dots .+j_5{}^{\ast }+5; i^{\ast }\ne j^{\ast }\right\}$  $E$, where  $1\le k_1\le j_1,1\le k_2\le j_2,1\le k_3\le j_3,1\le k_4\le j_4,1\le k_5\le j_5.$  ${E^{\prime }}_{GN-\max }=\left\{(i^{\ast },j^{\ast }); 1\le i^{\ast }, j^{\ast }\le j_1{}^{\ast }+j_2{}^{\ast }+\dots .+j_5{}^{\ast }+5; i^{\ast }\ne j^{\ast }\right\}$. H’_GN satisfies  $\alpha {\prime }_{GN}\le \left|E{\prime }_{GN}\left(H\prime \right)\right|\le {{\beta }^{\prime }}_{GN}$.

6.2. Encryption Algorithm

L_SN ≡ a_sn (mod t), where a_sn = 0 and t = 5.

Input:  $L_{SN}\ge t$,  $L_{SN}\equiv a_{sn}\left(mod 5\right)$, where a_sn = 0

Output: ELG, H′_GN

Start

Step 1: Divide L_SN into t divisions say  $L_0,L_1,L_2,L_3 \mathrm{and} L_4$, where  $L_0\equiv 0\left(mod t\right),L_1\equiv 1\left(mod t\right),L_2\equiv 2\left(mod t\right),L_3\equiv 3\left(mod t\right),L_4\equiv 4\left(mod t\right).$

Step 2: Fix  $deg(m_1)=k_1,deg(m_2)=k_2,deg(m_3)=k_3,deg(m_4)=k_4,deg(m_5)=k_5,$ where  $k_1,k_2,k_3,k_4,k_5\ge 1.$ Let  $m_{11},m_{12},\dots ,m_{1k_1}$; $m_{21},m_{22},\dots ,m_{2_{k2}};$ $m_{31},m_{32},\dots ,m_{3k_3};$  $m_{41},m_{42},\dots ,m_{4k_4};$  $m_{51},m_{52},\dots ,m_{5k_5}$ be the neighboring nodes of  $m_1,m_2,m_3,m_4,m_5$, respectively, and  $d\left(m_1,m_{1k_1}\right)=d\left(m_2,m_{1k_2}\right)=d\left(m_3,m_{3k_3}\right)=$  $d\left(m_4,m_{4k_4}\right)=d\left(m_5,m_{5k_5}\right)=11\le k_1\le j_1{}^{*},1\le k_2\le j_2{}^{*},1\le k_3\le j_3{}^{*},1\le k_4\le j_4{}^{*},1\le k_5\le j_5{}^{*}.$

Step 3: $\mathrm{Define} V_{GN}\left(H_{GN}\right)=\left\{m_1,m_2,m_3,m_4,m_5\right\}\cup {\left\{m_{1k_1}\right\}}_{k_1=1}^{j_1{}^{*}}\cup {\left\{m_{2k}{}_2\right\}}_{k_2=1}^{j_2{}^{*}}\cup {\left\{m_{3k}{}_3\right\}}_{k_3=1}^{j_3{}^{*}}\cup {\left\{m_{4k}{}_4\right\}}_{k_4=1}^{j_4{}^{*}}\cup {\left\{m_{5k_5}\right\}}_{k_5=1}^{j_5{}^{*}}$ and  $\left|V_{GN}\left(H_{GN}\right)\right|=j_1{}^{*}+j_2{}^{*}+j_3{}^{*}+\dots .+j_t{}^{*}+5=\nu {\prime }_{GN}.$

Let  ${E^{\prime }}_{GN1}=\left\{m_{1k_1}{m}_{2k_2},m_{2k_2}{m}_{3k_3},m_{3k_3}{m}_{4k_4},m_{4k_4}{m}_{5k_5}\right\}$ for only one  $k_1,k_2,\dots .,k_5$ where  $1\le k_1\le j_1{}^{*},1\le k_2\le j_2{}^{*},1\le k_3\le j_3{}^{*},1\le k_4\le j_4{}^{*},1\le k_5\le j_5{}^{*}.$

Let

${E^{\prime }}_{GN-\min }=\left\{\begin{array}{l}{m}_{1k_1}{m}_{2k_2}, m_{2k_2}{m}_{3k_3},m_{3k_3}{m}_{4k_4},m_{4k_4}{m}_{5k_5}/\\ 1\le k_1\le j_1{}^{\ast }, 1\le k_2\le {\mathrm{j}}_2{}^{\ast },1\le k_3\le {\mathrm{j}}_3{}^{\ast },1\le k_4\le {\mathrm{j}}_4{}^{\ast }, 1\le k_5\le j_5{}^{\ast }\end{array}\right\}$ $\cup {E^{\prime }}_{GN1}.$

Then $\left|{E^{\prime }}_{GN-\min }\right|=j_1{}^{\ast }+j_2{}^{\ast }+\dots +j_t{}^{\ast }+5={v^{\prime }}_{GN}(say).$

Let ${E^{\prime }}_{GN-\max }=\left\{(i^{\ast },j^{\ast }); 1\le i^{\ast },j^{\ast }\le j_1{}^{\ast }+j_2{}^{\ast }+j_3{}^{\ast }+j_4{}^{\ast }+j_5{}^{\ast }+5; i^{\ast }\ne j^{\ast }\right\}$ $-\left\{\begin{array}{l} m_1{m}_2,m_2{m}_3,m_3{m}_4,.m_4{m}_5, m_1{m}_{2k_2},m_1{m}_{3k}{}_3,m_1{m}_{4k}{}_4, m_1{m}_{5k}{}_5,\dots ,m_1{m}_{t{k}_t},\\ m_2{m}_{3k_3},\dots ,m_2{m}_{5k_5},\dots ,m_5{m}_{1k_1},m_5{m}_{2k_2},\dots ,m_5{m}_{4k_4}\end{array}\right.$

where $1\le k_1\le j_1,1\le k_2\le j_2,1\le k_3\le j_3,1\le k_4\le j_4,1\le k_5\le j_5.$

Then  $\left|E_{GN-\max }\right|={{\beta }^{\prime }}_{GN}(let)=\frac{1}{2}\left[\nu {\prime }_{GN}{}^2+\nu {\prime }_{GN}-10(1+v{\prime }_{GN})\right],$

where ${{\nu }^{\prime }}_{GN}=j_1{}^{\ast }+j_2{}^{\ast }+\dots +j_t{}^{\ast }+5.$

H′_GN satisfies  $\alpha {\prime }_{GN}\le \left|E{\prime }_{GN}\left(H{\prime }_{GN}\right)\right|\le \beta {\prime }_{GN}.$

Step 4:  $\alpha {\prime }_{GN}\le \left|E{\prime }_{GN}\left(H{\prime }_{GN}\right)\right|\le \beta {\prime }_{GN}.$  $z_1=\left[\frac{L_1}{5}\right],$  $z_2=\left[\frac{L_2}{5}\right],$  $z_3=\left[\frac{L_3}{5}\right],$  $z_4=\left[\frac{L_4}{5}\right].$

Step 5: Split

$$\begin{array}{c}{z}_0=s_{11}+s_{12}+\dots +s_{1k_1};\\ z_1=s_{21}+s_{22}+\dots +s_{2j_{k2}};\\ z_2=s_{31}+s_{32}+\dots +s_{3k_3};.\\ z_3=s_{41}+s_{42}+\dots +s_{4k_4};\\ z_4=s_{51}+s_{52}+\dots +s_{5k_5}.\end{array}$$

where k₁, k₂, k₃, k₄, k₅  $\ge 0.$

Step 6: Let  $f{\prime }_{GN}:V_{GN};\to \left\{{\alpha }_{i^{*}}\in Z^{+}\right\}$ defined as  $f{\prime }_{GN}\left(v\right)={\alpha }_{i^{*}}$ being a many-to-one function. Let  $g{\prime }_{GN}:E_{GN}\to {\alpha }_{j^{*}},{\alpha }_{j^{*}}\in N{\prime }_{GN}$ be a many-to-one function where  $N{\prime }_{GN}=\{s_{11},s_{12},\dots ,s_{1k_1}$;  $s_{21},s_{22},\dots ,s_{2k_2};$ $s_{31},s_{32},\dots ,s_{3k_3};$  $s_{41},s_{42},\dots ,s_{4k_4};$ $s_{51},s_{52},\dots ,s_{5k_5}$} and $\mathrm{such} \mathrm{that} g{\prime }_{GN}\left(m_1{m}_{1j_1{}^{*}}\right)=s_1{}_{j_1{}^{*}};g{\prime }_{GN}\left(m_3{m}_{3k_3}\right)=s_3{}_{j_3{}^{*}};g{\prime }_{GN}\left(m_4{m}_{4k_4}\right)=s_4{}_{k_4};g{\prime }_{GN}\left(m_5{m}_{5k_5}\right)=s_5{}_{k_5}$ for  $1\le k_1\le j_1{}^{*},1\le k_2\le j_2{}^{*},1\le k_3\le j_3{}^{*},$  $1\le k_4\le j_4{}^{*},1\le k_5\le j_5{}^{*}$ such that  $f\left({\alpha }_{i^{*}}\right)+f\left({\alpha }_{j^{*}}\right)+f\left({\alpha }_{i^{*}}{\alpha }_{j^{*}}\right)={\alpha }_k,$ every edge  ${\alpha }_{i^{*}}{\alpha }_{j^{*}}\in E{\prime }_{GN},{\alpha }_k$ is a constant. The constructed graph network preserves total magic labeling.

Step 7: Define

$$g{\prime }_{GN}\left(m_1{m}_{1k_1}\right)=s_1{}_{k_1}={\alpha }_k-f\left(m_1\right)-f\left(m_{1k_1}\right)1\le k_1\le j_1{}^{*};$$

$$g{\prime }_{GN}\left(m_2{m}_{2k_2}\right)=s_{2k_2}={\alpha }_k-f\left(m_2\right)-f\left(m_{2k_2}\right),1\le k_2\le j_1{}^{*};$$

$$g{\prime }_{GN}\left(m_3{m}_{3k_3}\right)=s_{3k_3}={\alpha }_k-f\left(m_3\right)-f\left(m_{3k_3}\right)$$

$$g{\prime }_{GN}\left(m_4{m}_{4k_4}\right)=s_{4k_4}={\alpha }_k-f\left(m_1\right)-f\left(m_{4k_4}\right),1\le k_4\le j_4{}^{*};$$

$$g{\prime }_{GN}\left(m_5{m}_{5k_5}\right)=s_{5k_5}={\alpha }_k-f\left(m_5\right)-f\left(m_{5k_5}\right),1\le k_5\le j_5{}^{*};$$

$$g{\prime }_{GN}\left(m_{1i^{*}}{m}_{1k}{}_1\right)={\alpha }_k-f\left(m_{1i^{*}}\right)-f\left(m_{1k_1}\right),1\le i^{*}\le t,1\le k_1\le j_1{}^{*};$$

$$g{\prime }_{GN}\left(m_{2i^{*}}{m}_{2k}{}_2\right)={\alpha }_k-f\left(m_{2i^{*}}\right)-f\left(m_{2k_2}\right),1\le i^{*}\le t,1\le k_2\le j_2{}^{*};$$

$$g{\prime }_{GN}\left(m_{3i^{*}}{m}_{3k}{}_3\right)={\alpha }_k-f\left(m_{3i^{*}}\right)-f\left(m_{3k_3}\right),1\le i^{*}\le t,1\le k_3\le j_3;$$

$$g{\prime }_{GN}\left(m_{4i^{*}}{m}_{4k}{}_4\right)={\alpha }_k-f\left(m_{4i^{*}}\right)-f\left(m_{4k_4}\right),1\le i^{*}\le t,1\le k_4\le j_4{}^{*};$$

$$\begin{array}{c}g{\prime }_{GN}\left(m_{5i^{*}}{m}_{5k_5}\right)={\alpha }_k-f\left(m_{5i^{*}}\right)-f\left(m_{5k_5}\right), 1\le i\le t, 1\le k_5\le j_5;\\ \mathrm{and} i\ne j_i{}^{*},i^{*}=1,2,\dots ,t.\end{array}$$

$$g{\prime }_{GN}\left(m_{1i^{*}}{m}_{2k}\right)={\alpha }_k-f\left(m_{1i^{*}}\right)-f\left(m_{2k}\right),1\le i^{*}\le t,1\le k\le j_2{}^{*};$$

$$g{\prime }_{GN}\left(m_{2i^{*}}{m}_{3k}\right)={\alpha }_k-f\left(m_{2i^{*}}\right)-f\left(m_{3k}\right),1\le i^{*}\le t,1\le k\le j_3{}^{*};$$

$$g{\prime }_{GN}\left(m_{3i^{*}}{m}_{4k}\right)={\alpha }_k-f\left(m_{3i^{*}}\right)-f\left(m_{4k}\right),1\le i^{*}\le t,1\le k\le j_4{}^{*};$$

$$\begin{array}{c}g{\prime }_{GN}\left(m_{4i^{*}}{m}_{5k}\right)={\alpha }_k-f\left(m_{4i^{*}}\right)-f\left(m_{5k}\right),1\le i^{\ast }\le t, 1\le k\le j_5{}^{\ast };\\ i^{*}\ne j_i{}^{*},i^{*}=1,2,\dots ,t.\end{array}$$

End.

6.3. Decryption Algorithm

Input: ELG, H′_GN

Output: L_GN.

Begin

Step 1: Find the E_effDS,  $S{\prime }_{GN}=\left\{m_1,m_2,m_3,m_4,m_5\right\}$ such that  $N_{GN}\left[m_1\right]\cap N_{GN}\left[m_2\right]\cap N_{GN}\left[m_3\right]\cap N_{GN}\left[m_4\right]\cap N_{GN}\left[m_5\right]=\phi$.

Step 2:

$$L_0=a_0+t{\displaystyle \sum }_{n=1}^{j_1{}^{*}}g(m_1{m}_{1n}), \mathrm{where} a_{i^{*}}\equiv i^{*}\left(mod 5\right).$$

$$L_1=a_1+t{\displaystyle \sum _{n=1}^{j_2{}^{\ast }}g{\prime }_{GN}(m_2{m}_{2n}}),$$

$$L_2=a_2+t{\displaystyle \sum }_{n=1}^{j_2{}^{*}}g{\prime }_{GN}(m_2{m}_{2n}),$$

$$L_3=a_3+t{\displaystyle \sum _{n=1}^{j_2{}^{\ast }}g{\prime }_{GN}(m_3{m}_{3n}}),$$

$$L_4=a_4+t{\displaystyle \sum }_{n=1}^{j_2{}^{*}}g{\prime }_{GN}(m_4{m}_{4n}).$$

Step 3:

$$L={\displaystyle \sum }_{n=0}^{t-1}{L}_n$$

End.

6.4. Secret Number L_SN = 12,935 (mod t), Where  $a_{sn}$ = 0 and t = 5

In this illustration, we split the L_SN into seven parts and assign each to the E_effDS members and the connections arising on them, so that  $L={{\displaystyle \sum }}_{n=0}^{t-1}{L}_n$ where  $L_{j^{*}}=t_{i^{*}}+t{{\displaystyle \sum }}_{\begin{array}{l}j=1\\ l=1tot\end{array}}^{k_{i^{*}}}g{\prime }_{GN}(m_l{m}_{l{j}^{*}})$ and  $where t_{i^{*}}=L_{i^{*}}\equiv i^{*}\left(mod 5\right)$.

6.4.1. Encrypting L_SN, 12,935

Step 1: Split L_SN = 12,935 into five partitions say L₀, L₁, L₂, L₃ and L_4, namely L₀ = 2575 ≡ 0 (mod 5), L₁ = 2581 ≡ 1 (mod 5), L₂ = 2587 ≡ 2 (mod 5), L₃ = 2593 ≡ 3 (mod 5) and L₄ = 2599 ≡ 4 (mod 5).

Step 2: Construct the graph H′_GN with  $\left|V{\prime }_{GN}\left(H{\prime }_{GN}\right)\right|=30$,  $\left|E{\prime }_{GN}\left(H{\prime }_{GN}\right)\right|$= 69 and its E_effDS, S’_GN = $\left\{m_1,m_2,m_3,m_4,m_5\right\}$.

Step 3: Arbitrarily choose  $\mathrm{deg}(m_1)=\mathrm{deg}(m_2)=k_2,\dots .,\mathrm{deg}(m_5)=5.$

Let  $m_{11},m_{12},m_{13}.m_{14},m_{15}$; $m_{21},m_{22},m_{23},m_{24},m_{25};$ $m_{31},m_{32},m_{33}.m_{34},m_{35};$  $m_{41},m_{42},m_{43},m_{44},m_{45};$ $m_{51},m_{52},m_{53}.m_{54},m_{55}$ be the neighboring nodes of  $m_1,m_2,m_3,m_4,m_5$, respectively.

Step 4: Choose  $z_0=\left[\frac{L_0}{5}\right]=515,$  $z_1=\left[\frac{L_1}{5}\right]=516,$  $z_2=\left[\frac{L_2}{5}\right]=517.$  $z_3=\left[\frac{L_3}{5}\right]=518,$  $z_4=\left[\frac{L_4}{5}\right]=519.$

Step 5: Split  $z_0$ = 515 = 104 + 105 + 100 + 102 + 104 (where  $s_{11}=104,s_{12}=105,s_{13}=100,$  $s_{14}=102,s_{15}=104).$ Split  $z_1$ = 516 = 106 + 100 + 103 + 104 + 103 (where  $s_{21}=106,s_{22}=100,s_{23}=103,s_{24}=104,s_{25}=103).$ Split  $z_2$ = 517 = 105 + 103 + 101 + 103 + 105 (where $s_{31}=105,s_{32}=103,s_{33}=101,s_{34}=103,s_{25}=105).$ Split  $z_3$ = 518 = 100 + 102 + 104 + 106 + 106 (where $s_{41}=100,s_{42}=102,s_{413}=104,s_{44}=106,s_{45}=106).$ Split  $z_4$ = 519 = 101 + 102 + 104 + 106 + 106 (where  $s_{51}=101,s_{52}=102,s_{53}=104,$  $s_{54}=106,s_{25}=106).$

Step 6: Let  $f{\prime }_{GN}:V_{GN};\to \left\{{\alpha }_{i^{*}}\in Z^{+}\right\}$ defined it as  $f{\prime }_{GN}\left(v_{GN}\right)={\alpha }_{i^{*}}$ a many-to-one function. Let $g{\prime }_{GN}:E_{GN}\to {\alpha }_{j^{*}},{\alpha }_{j^{*}}\in N{\prime }_{GN}$ be a many-to-one function where  $N{\prime }_{GN}=\{m_{11},m_{12},m_{13},m_{14},m_{15};m_{21},m_{22},m_{213},m_{24},m_{25};m_{31},m_{32},m_{33},m_{34},m_{35};$  $m_{41},m_{42},m_{43},m_{44},m_{45};$  $m_{51},m_{52},m_{53},m_{54},m_{55}$} and such that $g{\prime }_{GN}\left(m_1{m}_{1k_1}\right)=s_1{}_{k_1};g{\prime }_{GN}\left(m_2{m}_{2k_2}\right)=s_2{}_{k2};g{\prime }_{GN}\left(m_3{m}_{3k_3}\right)=s_3{}_{k_3};g{\prime }_{GN}\left(m_4{m}_{4k_4}\right)=s_4{}_{k_4};g{\prime }_{GN}\left(m_5{m}_{5k_5}\right)=s_5{}_{k_5}$for  $1\le k_1\le 5,1\le k_2\le 5,1\le k_3\le 5,1\le k_4\le 5,1\le k_5\le 5$ such that  $f\left({\alpha }_{i^{*}}\right)+f\left({\alpha }_{j^{*}}\right)+f\left({\alpha }_{i^{*}}{\alpha }_{j^{*}}\right)={\alpha }_k,$ for every edge  ${\alpha }_{i^{*}}{\alpha }_{j^{*}}\in E{\prime }_{GN},{\alpha }_k$is a constant. The constructed graph network preserves magic labeling.

Step 7: Define

$$g{\prime }_{GN}\left(m_1{m}_{15}\right)={\alpha }_k-f\left(m_1\right)-f\left(m_{15}\right)=104,\mathrm{where} {\alpha }_k=1000.$$

$$g{\prime }_{GN}\left(m_1{m}_{14}\right)={\alpha }_k-f\left(m_1\right)-f\left(m_{15}\right)=102;$$

$$g{\prime }_{GN}\left(m_1{m}_{13}\right)={\alpha }_k-f\left(m_1\right)-f\left(m_{13}\right)=100;$$

$$g{\prime }_{GN}\left(m_1{m}_{12}\right)={\alpha }_k-f\left(m_1\right)-f\left(m_{12}\right)=105;$$

$$g{\prime }_{GN}\left(m_1{m}_{11}\right)={\alpha }_k-f\left(m_1\right)-f\left(m_{11}\right)=104.$$

Define

$$g{\prime }_{GN}\left(m_2{m}_{25}\right)={\alpha }_k-f\left(m_2\right)-f\left(m_{25}\right)=103;$$

$$g{\prime }_{GN}\left(m_2{m}_{24}\right)={\alpha }_k-f\left(m_2\right)-f\left(m_{24}\right)=104;$$

$$g{\prime }_{GN}\left(m_2{m}_{23}\right)={\alpha }_k-f\left(m_2\right)-f\left(m_{23}\right)=103;$$

$$g{\prime }_{GN}\left(m_2{m}_{22}\right)={\alpha }_k-f\left(m_2\right)-f\left(m_{22}\right)=100;$$

$$g{\prime }_{GN}\left(m_2{m}_{21}\right)={\alpha }_k-f\left(m_2\right)-f\left(m_{21}\right)=100.$$

Define

$$g{\prime }_{GN}\left(m_3{m}_{35}\right)={\alpha }_k-f\left(m_3\right)-f\left(m_{35}\right)=105;$$

$$g{\prime }_{GN}\left(m_3{m}_{34}\right)={\alpha }_k-f\left(m_3\right)-f\left(m_{34}\right)=103;$$

$$g{\prime }_{GN}\left(m_3{m}_{33}\right)={\alpha }_k-f\left(m_3\right)-f\left(m_{33}\right)=101;$$

$$g{\prime }_{GN}\left(m_3{m}_{32}\right)={\alpha }_k-f\left(m_3\right)-f\left(m_{32}\right)=103;$$

$$g{\prime }_{GN}\left(m_3{m}_{31}\right)={\alpha }_k-f\left(m_3\right)-f\left(m_{31}\right)=105.$$

Define

$$g{\prime }_{GN}\left(m_4{m}_{45}\right)={\alpha }_k-f\left(m_4\right)-f\left(m_{45}\right)=105;$$

$$g{\prime }_{GN}\left(m_4{m}_{44}\right)={\alpha }_k-f\left(m_4\right)-f\left(m_{44}\right)=103;$$

$$g{\prime }_{GN}\left(m_4{m}_{43}\right)={\alpha }_k-f\left(m_4\right)-f\left(m_{43}\right)=101;$$

$$g{\prime }_{GN}\left(m_4{m}_{42}\right)={\alpha }_k-f\left(m_4\right)-f\left(m_{42}\right)=102;$$

$$g{\prime }_{GN}\left(m_4{m}_{41}\right)={\alpha }_k-f\left(m_4\right)-f\left(m_{41}\right)=100.$$

Define

$$g{\prime }_{GN}\left(m_5{m}_{55}\right)={\alpha }_k-f\left(m_5\right)-f\left(m_{55}\right)=106;$$

$$g{\prime }_{GN}\left(m_5{m}_{54}\right)={\alpha }_k-f\left(m_5\right)-f\left(m_{54}\right)=106;$$

$$g{\prime }_{GN}\left(m_5{m}_{53}\right)={\alpha }_k-f\left(m_5\right)-f\left(m_{53}\right)=104;$$

$$g{\prime }_{GN}\left(m_5{m}_{52}\right)={\alpha }_k-f\left(m_5\right)-f\left(m_{52}\right)=102;$$

$$g{\prime }_{GN}\left(m_5{m}_{51}\right)={\alpha }_k-f\left(m_5\right)-f\left(m_{51}\right)=100.$$

$$g{\prime }_{GN}\left(m_{1i^{*}}{m}_{2k}\right)={\alpha }_k-f\left(m_{1i^{*}}\right)-f\left(m_{2k}\right), 1\le i^{*}\le t,1\le k\le j_3{}^{*};$$

$$g{\prime }_{GN}\left(m_{2i^{*}}{m}_{3k}\right)={\alpha }_k-f\left(m_{2i^{*}}\right)-f\left(m_{3k}\right),1\le i^{*}\le t,1\le k\le j_3{}^{*};$$

$$g{\prime }_{GN}\left(m_{3i^{*}}{m}_{4k}\right)={\alpha }_k-f\left(m_{3i^{*}}\right)-f\left(m_{4k}\right),1\le i^{*}\le t,1\le k\le j_4{}^{*};$$

$$g{\prime }_{GN}\left(m_{4i^{*}}{m}_{5k}\right)={\alpha }_k-f\left(m_{4i^{*}}\right)-f\left(m_{5k}\right)1\le i^{*}\le t,1\le k\le j_5{}^{*}.$$

The encrypted labeled graph network for L_SN ≡ a_sn (mod t), where a_sn = 0 and t = 5. Say H′_GN-(5) is shown in Figure 4.

6.4.2. DECRYPTING L_SN, 12,935

Step 1: Find the E_effDS,  $S{\prime }_{GN}=\left\{m_1,m_2,m_3,m_4,m_5\right\}$ such that  $N_{GN}\left[m_1\right]\cap N_{GN}\left[m_2\right]\cap N_{GN}\left[m_3\right]\cap N_{GN}\left[m_4\right]\cap N_{GN}\left[m_5\right]=\phi$.

Step 2:  $L_0=a_0+t{{\displaystyle \sum }}_{n=1}^{j_1{}^{*}}g(m_1{m}_{1n}), \mathrm{where} a_{i^{*}}\equiv i^{*}\left(\mathrm{mod}5\right)$ = 5 (104 + 105 + 100 + 102 + 104) = 2575  $L_1=a_1+t{{\displaystyle \sum }}_{n=1}^{j_2{}^{*}}g{\prime }_{GN}(m_2{m}_{2n})$ = 1 + 5(106 + 100 + 103 + 104 + 103) = 2581  $L_2=a_2+t{{\displaystyle \sum }}_{n=1}^{j_3{}^{*}}g{\prime }_{GN}(m_3{m}_{3n})$ = 2 + 5(105 + 103 + 101 + 103 + 105) = 2587  $L_3=a_3+t{{\displaystyle \sum }}_{n=1}^{j_4{}^{*}}g{\prime }_{GN}(m_4{m}_{4n})$ = 3 + 5(100 + 102 + 104 + 106 + 106) = 2593  $L_4=a_4+t{{\displaystyle \sum }}_{n=1}^{j_5{}^{*}}g{\prime }_{GN}(m_5{m}_{5n})$ = 4 + 5(101 + 102 + 104 + 106 + 106) = 2599

Step 3:  $L={{\displaystyle \sum }}_{n=0}^{t-1}{L}_n$ = 2575 + 2581 + 2587 + 2593 + 2599 = 12,935.

7. Illustration: Secret Number L_SN ≡ a_sn (mod t), Where a_sn = 0 and t = 7

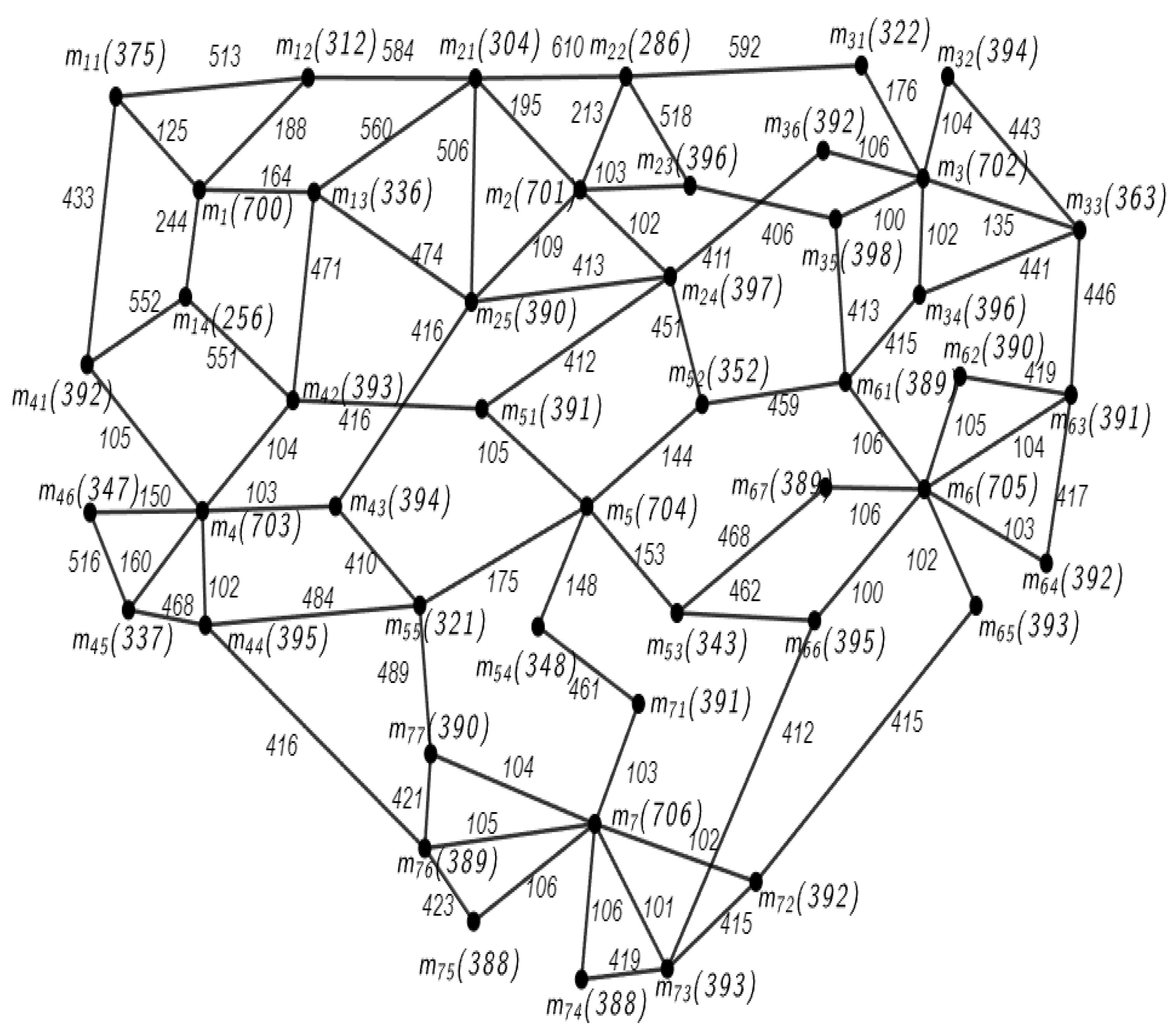
7.1. Graph Network Construction L_SN ≡ a_sn (mod t), Where a_sn = 0 and t = 7

Let H_GN = (V_GN, E_GN) be a simple graph with  $\left|V_{GN}\left(H_{GN}\right)\right|={\nu }_{GN} \mathrm{and} \left|E_{GN}\left(H_{GN}\right)\right|=e_{GN}.$ Let  $S{\prime }_{GN}=\left\{m_1,m_2,\dots .,m_7\right\}$ be the set of nodes, which are the members of E_eff DS with degrees say  $\mathrm{deg}(m_1)=k_1,\mathrm{deg}(m_2)=k_2, \mathrm{deg}(m_3)=k_3,$  $deg(m_4)=k_4$,  $deg(m_5)=k_5$,  $deg(m_6)=k_6$ and  $deg(m_7)=k_7$ where  $k_1,k_2,k_3,k_4,k_5,k_6,k_7\ge 1.$ Let  $m_{11},m_{12},\dots ,m_{1k_1}$;  $m_{21},m_{22},\dots ,m_{2k_2};$  $m_{31},m_{32},\dots ,m_{3k_3};$ $m_{41},m_{42},\dots ,m_{4k_4};$ $m_{51},m_{52},\dots ,m_{5k_5}$; $m_{61},m_{62},\dots ,m_{6k_6}$ and $m_{71},m_{72},\dots ,m_{7k_7}$ be the neighboring nodes of $m_1,m_2,m_3,m_4,m_5,m_6,m_7,$respectively,  $d\left(m_1,m_{1k_1}\right)=d\left(m_2,m_{1k_2}\right)=d\left(m_3,m_{3k_3}\right)$ $=d\left(m_4,m_{4k_4}\right)=d\left(m_5,m_{5k_5}\right)=d\left(m_6,m_{6k_6}\right)=d\left(m_7,m_{7k_7}\right)=1$. $1\le k_1\le j_1{}^{*},1\le k_2\le j_2{}^{*},1\le k_3\le j_3{}^{*},1\le k_4\le j_4{}^{*},1\le k_5\le j_5{}^{*},1\le k_6\le j_6{}^{*},1\le k_7\le j_7{}^{*}.$

$$\begin{array}{r}Define V_{GN}(H_{GN})=\left\{m_1,m_2,m_3,m_4,m_5\right\}\cup {\left\{m_{1k_1}\right\}}_{k_1=1}^{j_1{}^{\ast }}\cup {\left\{m_{2k}{}_2\right\}}_{k_2=1}^{j_2{}^{\ast }}\cup {\left\{m_{3k}{}_3\right\}}_{k_3=1}^{j_3{}^{\ast }}\\ \cup {\left\{m_{4k}{}_4\right\}}_{k_4=1}^{j_4{}^{\ast }}\cup {\left\{m_{5k_5}\right\}}_{k_5=1}^{j_5{}^{\ast }}\cup {\left\{m_{6k}{}_6\right\}}_{k_6=1}^{j_6{}^{\ast }}\cup {\left\{m_{7k_7}\right\}}_{k_7=1}^{j_7{}^{\ast }}\end{array}$$

$$\left|V_{GN}\left(H_{GN}\right)\right|=j_1+j_2+j_3+\dots .+j_7+7={\nu }_{GN}.$$

Let  ${E^{\prime }}_{GN1}=\left\{m_{1k_1}{m}_{2k_2},m_{2k_2}{m}_{3k_3},m_{3k_3}{m}_{4k_4},m_{4k_4}{m}_{5k_5},m_{6k_6}{m}_{7k_7}\right\}$ for only one  $k_1,k_2,\dots .,k_7$ where  $1\le k_1\le j_1{}^{*},1\le k_2\le j_2{}^{*},1\le k_3\le j_3{}^{*},1\le k_4\le j_4{}^{*},1\le k_5\le j_5{}^{*},1\le k_6\le j_6,1\le k_7\le j_7.$ Define  ${E^{\prime }}_{GN-\min }=\left\{m_1{m}_{1k_1},m_2{m}_{2k_2},\dots ,m_7{m}_{7k_7}/1\le k_1\le j_1, 1\le k_2\le {\mathrm{j}}_2 ,\dots , 1\le k_7\le j_7\right\}$ $\cup {E^{\prime }}_{GN1}.$

Then  $\left|{E^{\prime }}_{GN-\min }\right|=j_1{}^{\ast }+j_2{}^{\ast }+\dots +j_7{}^{\ast }+7={v^{\prime }}_{GN}=(say).$

Define  ${E^{\prime }}_{GN-\max }=\left\{(i^{\ast },j^{\ast }); 1\le i^{\ast },j^{\ast }\le j_1{}^{\ast }+j_2{}^{\ast }+\dots .+j_7{}^{\ast }+7; i^{\ast }\ne j^{\ast }\right\}$, where  $1\le k_1\le j_1{}^{*},1\le k_2\le j_2{}^{*},1\le k_3\le j_3{}^{*},1\le k_4\le j_4{}^{*},1\le k_5\le j_5{}^{*},1\le k_6\le j_6,1\le k_7\le j_7.$ Then  $\begin{array}{l}\left|{\mathrm{E}}_{\mathrm{GN}-\max }\right|={{\beta }^{\prime }}_{\mathrm{GN}}(\mathrm{say})=\frac{1}{2}\left[\nu {\prime }_{\mathrm{GN}}{}^2+\nu {\prime }_{\mathrm{GN}}-14(1+\mathrm{v}{\prime }_{\mathrm{GN}})\right],\\ \end{array}$ $\mathrm{where} {{\nu }^{\prime }}_{\mathrm{GN}}={\mathrm{j}}_1{}^{\ast }+{\mathrm{j}}_2{}^{\ast }+\dots +{\mathrm{j}}_7{}^{\ast }+7.$

The edge set’s cardinality for the set of H′_GN satisfies $\alpha {\prime }_{GN}\le \left|E{\prime }_{GN}\left(H\prime \right)\right|\le \beta {\prime }_{GN.}$

We have presented the algorithm for creating a network and labeling its nodes and edges to encrypt the secret number L_SN.

7.2. Encryption Algorithm

L_SN ≡ a_sn (mod t), where a_sn = 0 and t =7.

Input:  $L_{SN}\ge t$,  $L_{SN}\equiv a_{sn}\left(mod 5\right)$, where a_sn = 0.

Output: ELG, H′_GN

Begin

Step 1: Divide L_SN into t divisions say  $L_0,L_1,L_2,L_3,L_4,L_5 \mathrm{and} L_6,$ where  $L_0\equiv 0(\mathrm{mod} t),L_1\equiv 1(\mathrm{mod} t),L_2 \equiv 2(\mathrm{mod} t), L_3 \equiv 3(\mathrm{mod} t),L_4 \equiv 4(\mathrm{mod} t),$ $L_5\equiv 5\left(modt\right),L_6\equiv 6\left(modt\right).$

Step 2: Fix  $\mathrm{deg}(m_1)=k_1,\mathrm{deg}(m_2)=k_2, \mathrm{deg}(m_3)=k_3,\mathrm{deg}(m_4)=k_4,\mathrm{deg}(m_5)=k_5,$ $deg(m_5)=k_5,deg(m_6)=k_{6,}$where  $k_1,k_2,k_3,k_4,k_5,k_5,k_6\ge 1.$

Let  $m_{11},m_{12},\dots ,m_{1k_1}$;  $m_{21},m_{22},\dots ,m_{2_{k2}};$  $m_{31},m_{32},\dots ,m_{3k_3};$  $m_{41},m_{42},\dots ,m_{4k_4};$  $m_{51},m_{52},\dots ,m_{5k_5};$  $m_{61},m_{62},\dots ,m_{6k_6};$ … $; m_{71},m_{72},\dots ,m_{7k_7}$ be the neighboring nodes of  $m_1,m_2,m_3,m_4,m_5,m_6,m_7,$ respectively, and  $d\left(m_1,m_{1k_1}\right)=d\left(m_2,m_{1k_2}\right)=d\left(m_3,m_{3k_3}\right)=d\left(m_4,m_{4k_4}\right)=d\left(m_5,m_{5k_5}\right)=1=d\left(m_6,m_{6k_6}\right)=d\left(m_7,m_{7k_7}\right)=1$. $1\le k_1\le j_1{}^{*},1\le k_2\le j_2{}^{*},1\le k_3\le j_3{}^{*},1\le k_4\le j_4{}^{*},1\le k_5\le j_5{}^{*},1\le k_6\le j_6{}^{*},1\le k_7\le j_7{}^{*}.$

Step 3: Define $V_{GN}\left(H_{GN}\right)=\left\{m_1,m_2,m_3,m_4,m_5\right\}\cup {\left\{m_{1k_1}\right\}}_{k_1=1}^{j_1{}^{*}}$$\cup {\left\{m_{2k}{}_2\right\}}_{k_2=1}^{j_2{}^{*}}\cup$${\left\{m_{3k}{}_3\right\}}_{k_3=1}^{j_3{}^{*}}\cup$${\left\{m_{4k}{}_4\right\}}_{k_4=1}^{j_4{}^{*}}\cup$${\left\{m_{5k_5}\right\}}_{k_5=1}^{j_5{}^{*}}\cup$${\left\{m_{6k}{}_6\right\}}_{k_6=1}^{j_6{}^{*}}\cup$${\left\{m_{7k_7}\right\}}_{k_7=1}^{j_7{}^{*}}.$ and  $\left|V_{GN}\left(H_{GN}\right)\right|=j_1{}^{*}+j_2{}^{*}+j_3{}^{*}+\dots .+j_7{}^{*}+7=\nu {\prime }_{GN}.$

Let  ${E^{\prime }}_{GN1}=\left\{m_{1k_1}{m}_{2k_2},m_{2k_2}{m}_{3k_3},m_{3k_3}{m}_{4k_4},m_{4k_4}{m}_{5k_5},m_{5k_5}{m}_{6k_6},m_{6k_6}{m}_{7k_7}\right\}$ for only one  $k_1,k_2,\dots .,k_7,$ where  $1\le k_1\le j_1{}^{*},1\le k_2\le j_2{}^{*},1\le k_3\le j_3{}^{*},$  $1\le k_4\le j_4{}^{*},1\le k_5\le j_5{}^{*},1\le k_6\le j_6{}^{*},1\le k_7\le j_7{}^{*}.$

Let  ${E^{\prime }}_{GN-\min }=\left\{\begin{array}{l}{m}_{1k_1}{m}_{2k_2}, m_{2k_2}{m}_{3k_3},m_{3k_3}{m}_{4k_4},m_{4k_4}{m}_{5k_5},m_{5k_5}{m}_{6k_6},m_{6k_6}{m}_{7k_7}/\\ 1\le k_1\le j_1{}^{\ast }, 1\le k_2\le {\mathrm{j}}_2{}^{\ast },1\le k_3\le {\mathrm{j}}_3{}^{\ast },1\le k_4\le {\mathrm{j}}_4{}^{\ast }, 1\le k_5\le j_5{}^{\ast },1\le k_6\le {\mathrm{j}}_6{}^{\ast }, 1\le k_7\le j_7{}^{\ast }\end{array}\right\}$ $\cup {E^{\prime }}_{GN1}.$

Then  $\left|{E^{\prime }}_{GN-\min }\right|=j_1{}^{\ast }+j_2{}^{\ast }+\dots +j_7{}^{\ast }+7={v^{\prime }}_{GN}.$

Let  ${E^{\prime }}_{GN-\max }=\left\{(i^{\ast },j^{\ast }); 1\le i^{\ast },j^{\ast }\le j_1{}^{\ast }+j_2{}^{\ast }+j_3{}^{\ast }+j_4{}^{\ast }+j_5{}^{\ast }+j_6{}^{\ast }+j_7{}^{\ast }+7; i^{\ast }\ne j^{\ast }\right\}$  $-\left\{\begin{array}{l}{m}_1{m}_2,m_2{m}_3,m_3{m}_4,m_4{m}_5, m_5{m}_6,m_6{m}_7, m_1{m}_{2k_2},m_1{m}_{3k}{}_3,m_1{m}_{4k}{}_4, m_1{m}_{5k}{}_5,\dots ,m_1{m}_{7k_7},\\ m_2{m}_{3k_3},\dots ,m_2{m}_{7k_7},\dots ,m_7{m}_{1k_1},m_7{m}_{2k_2},\dots ,m_7{m}_{6k_6}\end{array}\right\}$ where  $1 \le k_1 \le j_1^{*}, 1 \le k_2 \le j_2^{*}, 1 \le k_3 \le j_3^{*}, 1 \le k_4 \le j_4^{*}, 1 \le k_5 \le j_5^{*}, 1 \le k_6 \le j_6^{*}, 1 \le k_7 \le j_7^{*}.$ Then  $\left|E_{GN-max}|{|}_{GN}\frac{.}{.}\left[\nu {\prime }_{GN}{}^{.}+\nu {\prime }_{GN}-14\left(.+v{\prime }_{GN}\right)\right]\right|$, where  $\nu {\prime }_{GN}=j_1{}^{*}+j_2{}^{*}+\dots +j_7{}^{*}+7.$

H’_GN satisfies  $\alpha {\prime }_{GN}\le \left|E{\prime }_{GN}\left(H{\prime }_{GN}\right)\right|\le \beta {\prime }_{GN}.$

Step 4:  $z_0=\left[\frac{L_0}{7}\right],$  $z_1=\left[\frac{L_1}{7}\right], z_2=\left[\frac{L_2}{7}\right], z_3=\left[\frac{L_3}{7}\right],$  $z_4=\left[\frac{L_4}{7}\right],$  $z_5=\left[\frac{L_5}{7}\right],$  $z_6=\left[\frac{L_6}{7}\right].$

Step 5: Split

$$z_0=s_{11}+s_{12}+\dots +s_{1k_1};$$

$$z_1=s_{21}+s_{22}+\dots +s_{2j^{*}{}_{k2}};$$

$$z_2=s_{31}+s_{32}+\dots +s_{3k_3};$$

$$z_3=s_{41}+s_{42}+\dots +s_{4k_4};$$

$$z_4=s_{51}+s_{52}+\dots +s_{5k_5};$$

$$z_5=s_{61}+s_{62}+\dots +s_{6k_6};$$

$$z_6=s_{71}+s_{72}+\dots +s_{7k_7}.$$

where k₁, k₂, k₃, k₄, k₅, k₆, k₇  $\ge 0.$

Step 6: Let  $f{\prime }_{GN}:V_{GN};$$\to \left\{{\alpha }_{i^{*}}\in Z^{+}\right\}$ defined as  $f{\prime }_{GN}\left(v\right)={\alpha }_{i^{*}}$ being a many-to-one function. Let  $g{\prime }_{GN}:E_{GN}\to {\alpha }_{j^{*}},{\alpha }_{j^{*}}\in N{\prime }_{GN}$ be a many-to-one function where $N{\prime }_{GN}=\{s_{11},s_{12},\dots ,s_{1k_1}$;  $s_{21},s_{22},\dots ,s_{2k_2};$  $s_{31},s_{32},\dots ,s_{3k_3};$  $s_{41},s_{42},\dots ,s_{4k_4};$  $s_{51},s_{52},\dots ,s_{5k_5},$  $s_{61},s_{62},\dots ,s_{6k_6};$  $s_{71},s_{72},\dots ,s_{7k_7}$} and such that $g{\prime }_{GN}\left(m_1{m}_{1j_1{}^{*}}\right)=s_1{}_{j_1{}^{*}};$$g{\prime }_{GN}\left(m_3{m}_{3k_3}\right)=s_3{}_{j_3{}^{*}};$$g{\prime }_{GN}\left(m_4{m}_{4k_4}\right)=s_4{}_{k_4};$$g{\prime }_{GN}\left(m_5{m}_{5k_5}\right)=s_5{}_{k_5};$$g{\prime }_{GN}\left(m_6{m}_{6k_6}\right)=s_6{}_{k_{64}};$$g{\prime }_{GN}\left(m_7{m}_{7k_7}\right)=s_7{}_{k_7}$ for  $1\le k_1\le$$j_1{}^{*},$$1\le k_2\le j_2{}^{*},$$1\le k_3\le j_3{}^{*},$$1\le k_4\le j_4{}^{*},$$1\le k_5\le j_5{}^{*},$$1\le k_6\le j_6{}^{*},$$1\le k_7\le j_7{}^{*}$ such that  $f\left({\alpha }_{i^{*}}\right)+f\left({\alpha }_{j^{*}}\right)+f\left({\alpha }_{i^{*}}{\alpha }_{j^{*}}\right)={\alpha }_k$ for every edge  ${\alpha }_{i^{*}}{\alpha }_{j^{*}}\in E{\prime }_{GN},{\alpha }_k$ is a constant. The constructed graph network preserves total magic labeling.

Step 7: Define

$$g{\prime }_{GN}\left(m_1{m}_{1k_1}\right)=s_{1k_1}={\alpha }_k-f\left(m_1\right)-f\left(m_{1k_1}\right),1\le k_1\le j_1{}^{*};$$

$$g{\prime }_{GN}\left(m_2{m}_{2k_2}\right)=s_{2k_2}={\alpha }_k-f\left(m_2\right)-f\left(m_{2k_2}\right),1\le k_2\le j_2{}^{*};$$

$$g{\prime }_{GN}\left(m_3{m}_{3k_3}\right)=s_{3k_3}={\alpha }_k-f\left(m_3\right)-f\left(m_{3k_3}\right),1\le k_3\le j_3{}^{*};$$

$$g{\prime }_{GN}\left(m_4{m}_{4k_4}\right)=s_{4k_4}={\alpha }_k-f\left(m_1\right)-f\left(m_{4k_4}\right),1\le k_4\le j_4{}^{*};$$

$$g{\prime }_{GN}\left(m_5{m}_{5k_5}\right)=s_{5k_5}={\alpha }_k-f\left(m_5\right)-f\left(m_{5k_5}\right),1\le k_5\le j_5{}^{*};$$

$$g{\prime }_{GN}\left(m_{1i^{*}}{m}_{1k}{}_1\right)={\alpha }_k-f\left(m_{1i^{*}}\right)-f\left(m_{1k_1}\right),1\le i^{*}\le t,1\le k_1\le j_1{}^{*};$$

$$g{\prime }_{GN}\left(m_{2i^{*}}{m}_{2k}{}_2\right)={\alpha }_k-f\left(m_{2i^{*}}\right)-f\left(m_{2k_2}\right),1\le i^{*}\le t,1\le k_2\le j_2{}^{*};$$

$$g{\prime }_{GN}\left(m_{3i^{*}}{m}_{3k}{}_3\right)={\alpha }_k-f\left(m_{3i^{*}}\right)-f\left(m_{3k_3}\right),1\le i^{*}\le t,1\le k_3\le j_3{}^{*};$$

$$g{\prime }_{GN}\left(m_{4i^{*}}{m}_{4k}{}_4\right)={\alpha }_k-f\left(m_{4i^{*}}\right)-f\left(m_{4k_4}\right),1\le i^{*}\le t,1\le k_4\le j_4{}^{*};$$

$$g{\prime }_{GN}\left(m_{5i^{*}}{m}_{5k_5}\right)={\alpha }_k-f\left(m_{5i^{*}}\right)-f\left(m_{5k_5}\right),1\le i^{*}\le t,1\le k_5\le j_5{}^{*};$$

$$g{\prime }_{GN}\left(m_{6i^{*}}{m}_{6k}{}_6\right)={\alpha }_k-f\left(m_{6i^{*}}\right)-f\left(m_{6k_6}\right),1\le i^{*}\le t,1\le k_6\le j_6{}^{*};$$

$$\begin{array}{c}g{\prime }_{GN}\left(m_{7i^{*}}{m}_{7k_7}\right)={\alpha }_k-f\left(m_{7i^{*}}\right)-f\left(m_{7k_7}\right),1\le i^{*}\le t,1\le k_7\le j_7{}^{*},\\ \mathrm{and} i^{*}\ne j_i{}^{*},i^{*}=1,2,\dots ,t\end{array}$$

$$g{\prime }_{GN}\left(m_{1i^{*}}{m}_{2k}\right)={\alpha }_k-f\left(m_{1i^{*}}\right)-f\left(m_{2k}\right),1\le i^{*}\le t,1\le k\le j_2{}^{*};$$

$$g{\prime }_{GN}\left(m_{2i^{*}}{m}_{3k}\right)={\alpha }_k-f\left(m_{2i^{*}}\right)-f\left(m_{3k}\right),1\le i^{*}\le t,1\le k\le j_3{}^{*};$$

$$g{\prime }_{GN}\left(m_{3i^{*}}{m}_{4k}\right)={\alpha }_k-f\left(m_{3i^{*}}\right)-f\left(m_{4k}\right),1\le i^{*}\le t,1\le k\le j_4{}^{*};$$

$$\begin{array}{c}g{\prime }_{GN}\left(m_{4i^{*}}{m}_{5k}\right)={\alpha }_k-f\left(m_{4i^{*}}\right)-f\left(m_{5k}\right),1\le i^{\ast }\le t, 1\le k\le j_5{}^{\ast };\\ i^{*}\ne j_i{}^{*},i^{*}=1,2,\dots ,t.\end{array}$$

$$g{\prime }_{GN}\left(m_{5i^{*}}{m}_{6k}\right)={\alpha }_k-f\left(m_{5i^{*}}\right)-f\left(m_{6k}\right),1\le i^{*}\le t,1\le k\le j_6{}^{*};$$

$$g{\prime }_{GN}\left(m_{6i^{*}}{m}_{7k}\right)={\alpha }_k-f\left(m_{6i^{*}}\right)-f\left(m_{7k}\right),1\le i^{\ast }\le t, 1\le k\le j_7{}^{\ast };$$

$$i^{*}\ne j_{i^{*}}{}^{*},i^{*}=1,2,\dots ,t$$

End.

7.3. Decryption Algorithm

Input: ELG, H′_GN

Output: L_GN

Begin

Step 1: Find the E_eff DS $S{\prime }_{GN}=\left\{m_1,m_2,m_3,m_4,m_5,m_6,m_7\right\}$ such that $N_{GN}\left[m_1\right]\cap N_{GN}\left[m_2\right]\cap N_{GN}\left[m_3\right]\cap N_{GN}\left[m_4\right]\cap N_{GN}\left[m_5\right]\cap N_{GN}\left[m_6\right]\cap N_{GN}\left[m_7\right]=\phi$.

Step 2:  $L_0=a_0+t{{\displaystyle \sum }}_{n=1}^{j_1{}^{*}}g(m_1{m}_{1n}) \mathrm{where} a_{i^{*}}\equiv i^{*}\left(\mathrm{mod} 7\right)$

$$L_1=a_1+t{\displaystyle \sum _{n=1}^{j_2{}^{\ast }}g{\prime }_{GN}(m_2{m}_{2n}}),$$

$$L_2=a_2+t{\displaystyle \sum }_{n=1}^{j_3{}^{*}}g{\prime }_{GN}(m_3{m}_{3n}),$$

$$L_3=a_3+t{\displaystyle \sum _{n=1}^{j_4{}^{\ast }}g{\prime }_{GN}(m_4{m}_{4n}}),$$

$$L_4=a_4+t{\displaystyle \sum }_{n=1}^{j_5{}^{*}}g{\prime }_{GN}(m_5{m}_{5n}),$$

$$L_5=a_5+t{\displaystyle \sum _{n=1}^{j_6{}^{\ast }}g{\prime }_{GN}(m_6{m}_{6n}}),$$

$$L_6=a_6+t{\displaystyle \sum }_{n=1}^{j_7{}^{*}}g{\prime }_{GN}(m_7{m}_{7n}).$$

Step 3:

$$L={\displaystyle \sum }_{n=0}^{t-1}{L}_n$$

End.

7.4. ILLUSTRATION: Secret Number L_SN = 35497 ≡ a_sn (mod t), Where a_sn = 0 and t = 7

7.4.1. Graph Network Construction for L_SN ≡ a_sn (mod t), Where a_sn = 0 and t = 7

In this example, we divide L_SN into seven parts and allocate each to the E_eff DS members and the connections arising on them, so that  $L={{\displaystyle \sum }}_{n=0}^{t-1}{L}_n$ where  $L_{j^{*}}=t_{i^{*}}+t{{\displaystyle \sum }}_{\begin{array}{l}j=1\\ l=1tot\end{array}}^{k_{i^{*}}}g{\prime }_{GN}(m_l{m}_{l{j}^{*}})$ and $\mathrm{where} t_{i^{*}}=L_{i^{*}}\equiv i^{*}\left(mod 7\right)$.

7.4.2. ENCRYPTING L_SN, 35,497

To encrypt the confidential number 35,497 which is a multiple of 7, let L_SN = 35,497 ≡ a_sn (mod t), where a_sn = 0 and t = 7.

Step 1: Split L_SN = 35,497 into seven partitions say L₀, L₁, L₂, L₃, L₄, L₅ and L₆ namely L₀ = 5047 ≡ 0 (mod 7), L₁ = 5055 ≡ 1 (mod 7), L₂ = 5063 ≡ 2 (mod 7), L₃ = 5071 ≡ 3 (mod 7) and L₄ = 5079 ≡ 4 (mod 7), L₅ = 5087 ≡ 5(mod 7), L₆ = 5095 ≡ 6 (mod 7).

Step 2: Arbitrarily choose deg(m₁) = 4, deg(m₂) = 5, deg(m₃) = 6, deg(m₄) = 6, deg(m₅) = 5, deg(m₄) = 7 and deg(m₅) = 7. Let  $m_{11},m_{12},m_{13}.m_{14},m_{15}$;  $m_{21},m_{22},m_{23},m_{24},m_{25};$  $m_{31},m_{32},m_{33}.m_{34},m_{35};$  $m_{41},m_{42},m_{43}.m_{44},m_{45};$  $m_{51},m_{52},m_{53}.m_{54},m_{55}$;  $m_{61},m_{62},\dots ,m_{6k_6};$ … $;m_{71},m_{72},\dots ,m_{7k_7}$ be the neighboring nodes of  $m_1,m_2,m_3,m_4,m_5,m_6,m_7$, respectively.

Step 3: Construct the graph H′_GN with  $\left|V{\prime }_{GN}\left(H{\prime }_{GN}\right)\right|=47$ and  $\left|E{\prime }_{GN}\left(H{\prime }_{GN}\right)\right|$= 81 and its E_eff DS, S’_GN = {m₁, m₂, m₃, m₄, m₅, m₆, m₇}.

Step 4:  $z_0=\left[\frac{L_0}{7}\right]=721, z_1=\left[\frac{L_1}{7}\right]=722,$  $z_2=\left[\frac{L_2}{7}\right]=723,$  $z_3=\left[\frac{L_3}{7}\right]=724,$  $z_4=\left[\frac{L_4}{7}\right]=725$,  $z_5=\left[\frac{L_5}{7}\right]=726,$  $z_6=\left[\frac{L_6}{7}\right]=727.$

Step 5: Split  $z_0$ = 721 = 125 + 188 + 164 + 244 (where  $s_{11}=125,s_{12}=188,s_{13}=164,s_{14}=244).$ Split  $z_1$ = 722 = 195 + 213 + 103 + 102 + 109 (where  $s_{21}=195,s_{22}=213,s_{23}=103,s_{24}=102,s_{25}=109).$

Split  $z_2$ = 723 = 176 + 104 + 135 + 102 + 100 + 106 (where  $s_{31}=176,s_{32}=104,s_{33}=135,s_{34}=102,s_{25}=100,s_{25}=106).$

Split  $z_3$ = 724 = 105 + 104 + 103 + 102 + 160 + 150 (where  $s_{41}=105,s_{42}=104,s_{43}=103,s_{44}=102,s_{45}=160;s_{46}=150).$

Split  $z_4$ = 725 = 105 + 144 + 153 + 148 + 175 (where  $s_{51}=105,s_{52}=144,s_{53}=153,s_{54}=148,s_{25}=175).$

 $z_5$ = 726 = 106 + 105 + 104 + 103 + 102 + 100 + 106 (where  $s_{61}=106,s_{62}=105,s_{63}=104,s_{64}=103,s_{65}=102,s_{66}=100,s_{67}=106).$

 $z_6$ = 727 = 103 + 102 + 101 + 106 + 106 + 105 + 104 (where  $s_{71}=103,s_{72}=102,s_{73}=101,s_{74}=106,s_{75}=106,s_{76}=105,s_{77}=104).$

Step 6: Let  $f{\prime }_{GN}:V_{GN};\to \left\{{\alpha }_{i^{*}}\in Z^{+}\right\}$ defined as  $f{\prime }_{GN}\left(v_{GN}\right)={\alpha }_{i^{*}}$being a many-to-one function. Let  $g{\prime }_{GN}:E_{GN}\to {\alpha }_{j^{*}},{\alpha }_{j^{*}}\in N{\prime }_{GN}$ be a many-to-one function where  $N{\prime }_{GN}=\{m_{11},m_{12},\dots ,m_{14}$;  $m_{21},m_{22},\dots ,m_{25};$  $m_{31},m_{32},\dots ,m_{36};$  $m_{41},m_{42},\dots ,m_{46};$  $m_{51},m_{52},\dots ,m_{55}$; $m_{61},m_{62},\dots ,m_{67}$ and  $m_{71},m_{72},\dots ,m_{77}\}$ such that  $g{\prime }_{GN}$$\left(m_1{m}_{1k_1}\right)=$$s_1{}_{k_1};$$g{\prime }_{GN}$$\left(m_2{m}_{2k_2}\right)=$$s_2{}_{k2};$$g{\prime }_{GN}$$\left(m_3{m}_{3k_3}\right)=$$s_3{}_{k_3};$$g{\prime }_{GN}$$\left(m_4{m}_{4k_4}\right)=$$s_4{}_{k_4};$$g{\prime }_{GN}$$\left(m_5{m}_{5k_5}\right)=$$s_5{}_{k_5};$$g{\prime }_{GN}$$\left(m_6{m}_{6k_6}\right)=$$s_6{}_{k_{64}};$$g{\prime }_{GN}\left(m_7{m}_{7k_7}\right)=$$s_7{}_{k_7}$for  $1\le k_1\le j_1,$$1\le k_2\le j_2,$$1\le k_3\le j_3,$$1\le k_4\le j_4,$$1\le k_5\le j_5,$$1\le k_6\le j_6{}^{*},$$1\le k_7\le j_7{}^{*}$ such that  $f\left({\alpha }_{i^{*}}\right)+f\left({\alpha }_{j^{*}}\right)+f\left({\alpha }_{i^{*}}{\alpha }_{j^{*}}\right)={\alpha }_k$, for every edge  ${\alpha }_{i^{*}}{\alpha }_{j^{*}}\in E{\prime }_{GN},{\alpha }_k$ is a constant. The constructed graph network preserves total magic labeling.

Step 7: Define

$$g{\prime }_{GN}\left(m_1{m}_{14}\right)={\alpha }_k-f\left(m_1\right)-f\left(m_{14}\right)=244 \mathrm{where} {\alpha }_k=1200;$$

$$g{\prime }_{GN}\left(m_1{m}_{13}\right)={\alpha }_k-f\left(m_1\right)-f\left(m_{13}\right)=164;$$

$$g{\prime }_{GN}\left(m_1{m}_{12}\right)={\alpha }_k-f\left(m_1\right)-f\left(m_{12}\right)=188;$$

$$g{\prime }_{GN}\left(m_1{m}_{11}\right)={\alpha }_k-f\left(m_1\right)-f\left(m_{11}\right)=125.$$

Define

$$g{\prime }_{GN}\left(m_2{m}_{25}\right)={\alpha }_k-f\left(m_2\right)-f\left(m_{25}\right)=109;$$

$$g{\prime }_{GN}\left(m_2{m}_{24}\right)={\alpha }_k-f\left(m_2\right)-f\left(m_{24}\right)=102;$$

$$g{\prime }_{GN}\left(m_2{m}_{23}\right)={\alpha }_k-f\left(m_2\right)-f\left(m_{23}\right)=103;$$

$$g{\prime }_{GN}\left(m_2{m}_{22}\right)={\alpha }_k-f\left(m_2\right)-f\left(m_{22}\right)=213;$$

$$g{\prime }_{GN}\left(m_2{m}_{21}\right)={\alpha }_k-f\left(m_2\right)-f\left(m_{21}\right)=195.$$

Define

$$g{\prime }_{GN}\left(m_3{m}_{36}\right)={\alpha }_k-f\left(m_3\right)-f\left(m_{36}\right)=106;$$

$$g{\prime }_{GN}\left(m_3{m}_{35}\right)={\alpha }_k-f\left(m_3\right)-f\left(m_{35}\right)=100;$$

$$g{\prime }_{GN}\left(m_3{m}_{34}\right)={\alpha }_k-f\left(m_3\right)-f\left(m_{34}\right)=102;$$

$$g{\prime }_{GN}\left(m_3{m}_{33}\right)={\alpha }_k-f\left(m_3\right)-f\left(m_{33}\right)=135;$$

$$g{\prime }_{GN}\left(m_3{m}_{32}\right)={\alpha }_k-f\left(m_3\right)-f\left(m_{32}\right)=104;$$

$$g{\prime }_{GN}\left(m_3{m}_{31}\right)={\alpha }_k-f\left(m_3\right)-f\left(m_{31}\right)=176.$$

Define

$$g{\prime }_{GN}\left(m_4{m}_{46}\right)={\alpha }_k-f\left(m_4\right)-f\left(m_{46}\right)=150;$$

$$g{\prime }_{GN}\left(m_4{m}_{45}\right)={\alpha }_k-f\left(m_4\right)-f\left(m_{45}\right)=160;$$

$$g{\prime }_{GN}\left(m_4{m}_{44}\right)={\alpha }_k-f\left(m_4\right)-f\left(m_{44}\right)=102;$$

$$g{\prime }_{GN}\left(m_4{m}_{43}\right)={\alpha }_k-f\left(m_4\right)-f\left(m_{43}\right)=103;$$

$$g{\prime }_{GN}\left(m_4{m}_{42}\right)={\alpha }_k-f\left(m_4\right)-f\left(m_{42}\right)=104;$$

$$g{\prime }_{GN}\left(m_4{m}_{41}\right)={\alpha }_k-f\left(m_4\right)-f\left(m_{41}\right)=105.$$

Define

$$g{\prime }_{GN}\left(m_5{m}_{55}\right)={\alpha }_k-f\left(m_5\right)-f\left(m_{55}\right)=175;$$

$$g{\prime }_{GN}\left(m_5{m}_{54}\right)={\alpha }_k-f\left(m_5\right)-f\left(m_{54}\right)=148;$$

$$g{\prime }_{GN}\left(m_5{m}_{53}\right)={\alpha }_k-f\left(m_5\right)-f\left(m_{53}\right)=153;$$

$$g{\prime }_{GN}\left(m_5{m}_{52}\right)={\alpha }_k-f\left(m_5\right)-f\left(m_{52}\right)=144;$$

$$g{\prime }_{GN}\left(m_5{m}_{51}\right)={\alpha }_k-f\left(m_5\right)-f\left(m_{51}\right)=105.$$

Define

$$g{\prime }_{GN}\left(m_6{m}_{67}\right)={\alpha }_k-f\left(m_6\right)-f\left(m_{67}\right)=106;$$

$$g{\prime }_{GN}\left(m_6{m}_{66}\right)={\alpha }_k-f\left(m_6\right)-f\left(m_{66}\right)=100;$$

$$g{\prime }_{GN}\left(m_6{m}_{65}\right)={\alpha }_k-f\left(m_6\right)-f\left(m_{65}\right)=102;$$

$$g{\prime }_{GN}\left(m_6{m}_{64}\right)={\alpha }_k-f\left(m_6\right)-f\left(m_{64}\right)=103;$$

$$g{\prime }_{GN}\left(m_6{m}_{63}\right)={\alpha }_k-f\left(m_6\right)-f\left(m_{63}\right)=104;$$

$$g{\prime }_{GN}\left(m_6{m}_{62}\right)={\alpha }_k-f\left(m_6\right)-f\left(m_{62}\right)=105;$$

$$g{\prime }_{GN}\left(m_6{m}_{61}\right)={\alpha }_k-f\left(m_6\right)-f\left(m_{61}\right)=106.$$

Define

$$g{\prime }_{GN}\left(m_7{m}_{77}\right)={\alpha }_k-f\left(m_7\right)-f\left(m_{77}\right)=104;$$

$$g{\prime }_{GN}\left(m_7{m}_{76}\right)={\alpha }_k-f\left(m_7\right)-f\left(m_{76}\right)=105;$$

$$g{\prime }_{GN}\left(m_7{m}_{75}\right)={\alpha }_k-f\left(m_7\right)-f\left(m_{75}\right)=106;$$

$$g{\prime }_{GN}\left(m_7{m}_{74}\right)={\alpha }_k-f\left(m_7\right)-f\left(m_{74}\right)=106;$$

$$g{\prime }_{GN}\left(m_7{m}_{73}\right)={\alpha }_k-f\left(m_7\right)-f\left(m_{73}\right)=101;$$

$$g{\prime }_{GN}\left(m_7{m}_{72}\right)={\alpha }_k-f\left(m_7\right)-f\left(m_{72}\right)=102;$$

$$g{\prime }_{GN}\left(m_7{m}_{71}\right)={\alpha }_k-f\left(m_7\right)-f\left(m_{71}\right)=103.$$

$$g{\prime }_{GN}\left(m_{1i^{*}}{m}_{2k}\right)={\alpha }_k-f\left(m_{1i^{*}}\right)-f\left(m_{2k}\right),1\le i^{*}\le t,1\le k\le j_2{}^{*};$$

$$g{\prime }_{GN}\left(m_{2i^{*}}{m}_{3k}\right)={\alpha }_k-f\left(m_{2i^{*}}\right)-f\left(m_{3k}\right),1\le i^{*}\le t,1\le k\le j_3{}^{*};$$

$$g{\prime }_{GN}\left(m_{3i^{*}}{m}_{4k}\right)={\alpha }_k-f\left(m_{3i^{*}}\right)-f\left(m_{4k}\right),1\le i^{*}\le t,1\le k\le j_4{}^{*};$$

$$g{\prime }_{GN}\left(m_{4i^{*}}{m}_{5k}\right)={\alpha }_k-f\left(m_{4i^{*}}\right)-f\left(m_{5k}\right),1\le i^{*}\le t,1\le k\le j_5{}^{*};$$

$$g{\prime }_{GN}\left(m_{5i}{m}_{6k}\right)={\alpha }_k-f\left(m_{5i}\right)-f\left(m_{6k}\right),1\le i^{*}\le t,1\le k\le j_6{}^{*};$$

$$g{\prime }_{GN}\left(m_{6i^{*}}{m}_{7k}\right)={\alpha }_k-f\left(m_{6i^{*}}\right)-f\left(m_{7k}\right),1\le i^{*}\le t,1\le k\le j_7{}^{*}.$$

The ELG network for L_SN ≡ a_sn (mod t), where a_sn = 0 and t = 7. Say H′_GN-(7) is shown in Figure 5.

7.4.3. DECRYPTING L_SN, 12,935

Step 1: Find the E_eff DS,  $S{\prime }_{GN}=\left\{m_1,m_2,m_3,m_4,m_5,m_6,m_7\right\}$ such that $N_{GN}\left[m_1\right]\cap N_{GN}\left[m_2\right]\cap N_{GN}\left[m_3\right]\cap N_{GN}\left[m_4\right]\cap N_{GN}\left[m_5\right]\cap N_{GN}\left[m_6\right]\cap N_{GN}\left[m_7\right]=\phi$

Step 2:

$$L_0=a_0+t{{\displaystyle \sum }}_{n=1}^{j_1{}^{*}}g(m_1{m}_{1n}) \mathrm{where} a_{i^{*}}\equiv i^{*}\left(mod 7\right) = 7(125 + 188 + 164 + 244) = 5047$$

$$L_1=a_1+t{{\displaystyle \sum }}_{n=1}^{j_2{}^{*}}g{\prime }_{GN}(m_2{m}_{2n})=1+7\left(195+213+103+102+109\right)=5055$$

$$L_2=a_2+t{{\displaystyle \sum }}_{n=1}^{j_3{}^{*}}g{\prime }_{GN}(m_3{m}_{3n})=2+7\left(176+104+135+102+100+106\right)=5063$$

$$L_3=a_3+t{\displaystyle \sum _{n=1}^{j_4{}^{\ast }}g{\prime }_{GN}(m_4{m}_{4n}})= 3+7(105+104+103+102+160+150)=5071$$

$$L_4=a_4+t{{\displaystyle \sum }}_{n=1}^{j_5{}^{*}}g{\prime }_{GN}(m_5{m}_{5n})=4+7\left(105+144+153+148+175\right)=5079$$

$$L_5=a_5+t{\displaystyle \sum _{n=1}^{j_6{}^{\ast }}g{\prime }_{GN}(m_6{m}_{6n}}) = 5+7(106+105+104+103+102+100+106)=5087$$

$$L_6=a_6+t{{\displaystyle \sum }}_{n=1}^{j_7{}^{*}}g{\prime }_{GN}(m_7{m}_{7n})=6+7\left(103+102+101+106+106+105+104\right)=5095.$$

Step 3:  $L={\sum }_{n=0}^{t-1}{L}_n$ = 5047 + 5055 + 5063 + 5071 + 5079 + 5087 + 5095 = 35,497.

8. Adversary Model

In the realms of cybersecurity, cryptography and security analysis, an adversary model—often termed a threat model—is a conceptual framework designed to characterize and delineate potential attackers or threats that a system, protocol or application might face. This model assists in identifying and understanding the myriad strategies an adversary might employ to compromise a system’s security [51,52,53].

Capabilities: This aspect pertains to the abilities of an attacker in terms of resources, knowledge and access. The spectrum of capabilities can span from rudimentary attacks by novices, often called “script kiddies”, to intricate assaults orchestrated by well-funded and adept hackers. Our cryptosystem, grounded in a network construction based on modulo t, total labeling and efficient domination, hinges on knowledge-based resources. If an intruder is privy to this information, they can evolve into proficient attackers of this system.

Goal: This dimension focuses on the objectives of the attacker. Potential aims might encompass data theft, service disruption, user impersonation or other malicious endeavors. The primary objective of adversaries targeting this cryptosystem is to decipher the concealed information.

Knowledge: This refers to the attacker’s understanding of the system, protocol or technology they aim to exploit. Such knowledge encompasses awareness of potential weaknesses, entry points and vulnerabilities. In the context of our cryptosystem, knowledge is anchored in two pivotal parameters: efficient domination and total labeling. If the constructed network exhibits minimal connectivity, attackers can more readily pinpoint the nodes associated with efficient domination.

Constraints: These represent the limitations or challenges an attacker might encounter. A quintessential constraint might be the attacker’s finite processing power or a narrow window of opportunity to strike. Within our cryptosystem, certain constraints are inherent, such as the necessity to select an appropriate secret number aligned with modulo t, partitioning this secret number and utilizing the partitions to assign weights to the network’s edges.

Resources: This facet delves into the arsenal at the attacker’s disposal, which could encompass financial resources, computational prowess, network infrastructure and access to specialized tools or software. In the context of our cryptosystem, the network’s construction hinges on the analysis of a secret number. An astute attacker might deduce that the concealed information is encapsulated as a numerical value.

9. Conclusions

We have presented a combinatorial approach to ascertain the secret number as manifested in the efficiently constructed graph network. The principles of total magic labeling and efficient domination are pivotal in crafting such an efficient graph network. The key to this system lies in identifying the most efficient and dominant set, termed  $E_{eff}DS$. By assigning repeated values of  $m_{ij}$ and considering the maximum number of edges present in the constructed  $E_{eff}DS$, the network’s complexity is heightened, making it more challenging to decode.