Abstract
A class of controlled objects is considered, the dynamics of which are determined by a vector system of ordinary differential equations with a partially known right-hand side. It is presumed that the state variables and their velocities can be measured. Designing a robust tracking controller under some constraints to admissible state variables is the research goal. This construction, which extends the results for the average subgradient technique (ASG), and is an update of the subgradient descent technique (SDM) and integral sliding mode (ISM) approach, is realized by using the Legendre–Fenchel transform. A two-link robot manipulator with three revolute joints, powered by individual PMDC motors, is presented as an illustrative example of the suggested approach implementation.
Keywords:
robust control; trajectory tracking; convex constrained optimization; subgradient descent method; sliding mode; robot manipulator MSC:
93B12; 93B51; 93B52; 93D09; 93D21
1. Introduction
1.1. Brief Survey
Constrained optimization is the process of optimizing an objective function with respect to some variables, subject to constraints on those variables. The objective function is either a cost function or energy function to be minimized, or a reward function or utility function to be maximized. Constraints can be either hard constraints, which set conditions on the variables that must be satisfied, or soft constraints, which have some variable values that are penalized in the objective function if and depending on the extent to which the conditions on the variables are not satisfied (see, for example, [1,2,3,4,5,6]).
All control strategies in most publications, treated as Static Optimization Methods (SOM), in continuous time may be represented in the following form
where is a convex (not obligatory strongly convex) mapping, is the admissible convex set of arguments, and the process is generated by the simple ordinary differential equation (ODE)
with any initial conditions . The relation (1) is referred to hereafter as a static plant. All known procedures of SOM differ only in the designing of the control action (or an optimization algorithm) as a function of the current state (Markov’s strategy) or more profound available history, namely, .
Here we consider a more general, and hence, more complex situation when the process is generated by the dynamic plant
where the vector function f in the right-hand side is supposed to be unknown but belongs to some class of nonlinearities.
This problem is more closed to the, so-called, Extremum Seeking Problem [7,8,9,10] and includes the first-order derivatives only. Thus, in [11], several optimization schemes are considered and it is shown that under appropriate conditions, these schemes achieve the extremum point from an arbitrarily large domain of initial conditions if the parameters in the controller are appropriately adjusted. This approach was applied in [12] for two levels of plant’s economic optimization. Many advanced process control systems use some form of model predictive control approach [13,14]. Article [15] describes a new algorithm for finding an extremum using stochastic online gradient estimation. Article [16] considers the optimization problem with constraints in dynamic linear time-invariant (LTI) systems characterized by the dimension of the control vector being smaller than the dimension of the system state vector. Convergence in finite time to a neighborhood of order of the optimal equilibrium point is proven. Ref. [17] presents variable structure convex programming control for a class of linear uncertain accessible state systems.
It is also crucial to discuss the relationship between the problem under consideration and the Model Predictive Control (MPC) approach, commonly referred to as moving or receding horizon control; see the two known surveys [18,19] as well as some new recent papers on Robust MPC (RMPC) [20,21,22,23]. MPC is a group of model-based control theories that anticipate system behavior using linear or nonlinear process models. The quality of the open-loop predictions, which in turn depends on the correctness of the process models, determines how well the MPC control performance operates. The estimated trajectory could not match the behavior of the plant in real life. The performance of the control system may be sluggish or unstable due to the mismatch between the plant and the model, sometimes referred to as model uncertainty. Robust predictive controllers are those that explicitly take the process and model uncertainty into account while establishing the best control strategies. Similar to H-infinity controllers, the core principle behind these controllers is to minimize the worst possible disruption to the behavior of the process. This idea is very different from the one suggested in this paper:
- –
- The prediction process cannot be accomplished precisely since the right-hand side of the ODE, representing the object model, is considered to be unknown (only dimensions of states and control are available);
- –
- Because the control action should be implemented in real-time online utilizing feedback (but not open-loop control), it is difficult to test-repeat the appropriate produced trajectories for various potential uncertainties.
In this paper, we consider a class of controlled plants with dynamics governed by a vector system of the second-order ordinary differential equations (ODE) with an unknown right-hand side. All mechanical Lagrange models belong to this class. The state variables and their velocities are assumed to be measurable. We design a controller minimizing a loss function subjected to a set of constraints to the state of the controlled plant. The designed control action is admitted to be a function of the current subgradients of loss function and constraints only, which are also supposed to be measurable online. The control is designed based on the SDM (subgradient descent method) version [24,25] of the integral sliding mode (ISM) concept [26,27,28] aimed at minimizing “on average” a given convex (not obligatory strongly convex) cost function of the current state under a set of given constraints. An optimization type algorithm is developed and analyzed using ideas from the SDM technique [1]. We prove the reachability of the “desired regime” (nonstationary analogue of sliding surface) [27] from the beginning of the process and obtain an explicit upper bound for the cost function decrement; that is, the convergence is proven and the rate of convergence is estimated as . This paper generalizes the approach, suggested in [29] for unconstrained dynamic optimization, to the constraint optimization problem realized by an uncertain second-order dynamic plant.
1.2. Main Contributions
- The robust tracking problem is reformulated as a constrained optimization realized by a dynamic plant with an unknown (but bounded) right-hand side. When we refer to “robust tracking”, we imply two distinct characteristics that are connected to imperfect a priori knowledge. While the exact control plant models and tracking trajectories are unavailable, a robust controller should nevertheless be able to successfully operate. It is just necessary to measure states and corresponding velocities online.
- The cost as well as the constraints are admitted to be convex but not obligatory strictly or strongly convex.
- The mirror descent method (MDM) and ASG version of sliding mode control are suggested and realized.
- The convergence of the obtained trajectories of the controlled uncertain plant to the corresponding admissible zone close to the minimal point is realized.
2. Uncertain Plant Description and Admitted Dynamic Zone
2.1. Dynamic Model
The second-order dynamic model (2) can be represented in the following extended format
Here the extended state variables are the current coordinates and their velocities at time Function is piecewise continuous in all arguments and admits to being unknown but is bounded as
with final positive constants , , and . Hereafter the symbol means the Euclidean norm.
2.2. Reference Trajectory, Tracking Error Dynamics, and Admissible Zone
The aim of the controller (which will be exactly formulated below) is to realize the tracking of the state for the given reference trajectory . Define the tracking error as
where is the continuously differentiable trajectory to be tracked satisfying
In view of that, the error tracking dynamics can be represented as follows
Let us require that the dynamics of should be realized after time within a bounded admissible zone
This paper’s primary objective is to build a control that minimizes the tracking error . The minimization of the assumed convex loss function can be used to represent this. For example, the class of convex loss functions under consideration includes the following functions:
2.3. Basic Assumptions
- A1
- The current states of the plant (3) are supposed to be measurable (available) online for all .
- A2
- The function , satisfying (4), is piecewise continuous in all arguments and admits to being unknown.
- A3
- The current states of the reference trajectory are also supposed to be available online for any .
- A4
- Here we assume that the subgradient (Recall that a vector , satisfying the inequality + for all is called the subgradient of the function at the point and is denoted by , which is the set of all subgradients of F at the point x. If is differentiable at a point x, then . In the minimal point , we have .) of the loss function is available online for a current time , and the set of minimizers of on the set includes the origin ; that is,
- A5
- The admissible set is nonempty convex compact, i.e., .
3. Desired Dynamics
3.1. Mirror Descent Method in Continuous Time
Let us apply the mirror descent approach using the Legendre–Fenchel transformation [30] as follows. For any define
so that (see, for instance, [31,32])
Define the dynamics for the vector function as
3.2. Why the Dynamics Are Desired
The following theorem explains why the dynamics may be considered as desired.
Theorem 1.
Under Assumptions A1–A5 on the trajectories , generated by (11), for all the following property holds
where
Proof.
Defining , , we have from (11)
Due to the convexity property for , we have
and in view of the relation
it follows
or equivalently,
After integration, we obtain
which implies
Using (9), we obtain
and
Since by (9) and (10)
and defining
we obtain
Therefore, we obtain
□
Example 1.
Assume that
To calculate according to (13), it is sufficient to note that the solution of the problem
is
4. Robust Controller Design
4.1. Auxiliary Sliding Variable and Its Dynamics
4.2. Robust Control Structure
Since
and taking
we obtain
which implies
This means that for all where
Finally, the robust control is
where
Remark 2.
If we wish to obtain , we need to complete the identity
Since , we may conclude that parameters and initial conditions should be consistent in the sense that
Remark 3.
For example, with Euclidean r-ball in being the admissible set , from (9) and (10) one has
From (18) it follows that
and
Notice that -function (10) is nondifferential in the points of r-sphere of the ball, and it is continuously differential in all other points of . The formulas in (20) and (23) are presented as their continuous versions on the ball, including the r-sphere.
4.3. Main Result
We are ready to formulate the main result.
Theorem 2.
5. Discussion
6. Numerical Example
A two-link robot manipulator with three revolute joints powered by individual PMDC motors is presented below as an illustrative example of the suggested approach.
6.1. Model Description
A dynamic model of a Lagrangian mechanical system with n degrees of freedom in standard form driven by n independent Permanent Magnet Direct Current (PMDC) motors [33] is defined by the following system of differential equations:
where are the state and velocity vectors, is a vector of external torques, is the armature current vector, is the matrix of electromotive force constants (possibly taking into account engine gear ratios), is the matrix of constants of direct electromotive forces, is a positive definite inertia matrix, that is =≥ and, therefore, invertible for all , J = is the rotor inertia matrix, is the matrix of the Lagrangian system corresponding to the armature inertia matrix in the original coordinates, is the matrix corresponding to the generalized nonpotential forces , which can describe friction, hysteresis, Coriolis, damping, centripetal effects, etc., is a vector corresponding to the generalized potential forces, is the matrix of reverse electromotive force constants, and are armature inductance and resistant positive matrices, respectively, is the disturbance (or uncertainty) vector, and is the armature voltage vector, which is treated below as a control designed to achieve the desired behavior. In fact, the third equation in (25) describes the dynamics of the actuator implementing the applied control action . Equation (25) assumes fully allocated control.
We assume that , and are available online. From (25) it follows that
(—any fixed time), and selecting (neglecting the Joule effect, related to the dependence of the winding motor resistance)
with
the relation (26) becomes
Substituting (29) into (25) gives
Note that in the standard matrix format (3) with new state vectors and velocity vectors , the Lagrange dynamics under consideration (30) have the following form:
Thus, in this representation, the dimension of control vector u is n and the extended state dimension is .
6.2. Intended Moving Point
The considered mechanical construction is depicted in Figure 1.
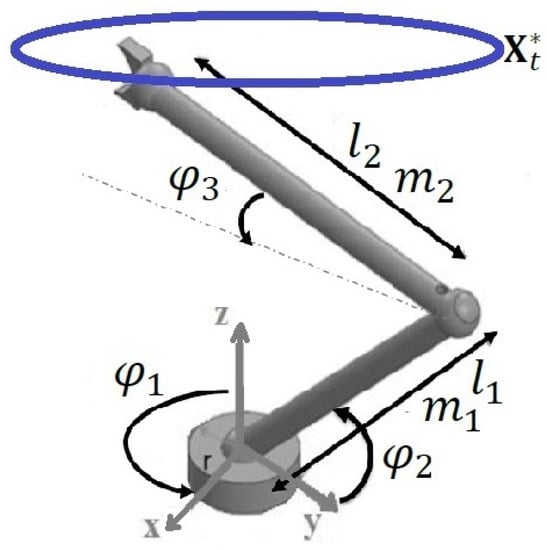
Figure 1.
Robot with two links.
The challenge is to move the robot’s cueing point such that it follows the intended moving point , maintaining a tiny space between them. Here, we suppose that the point accomplishes travel along a certain ellipse at a constant module speed v:
The corresponding cost function F (8) to be minimized is the function of the tracking error = and is selected as
6.3. Relation between Cartesian and Angular Coordinates
The relation between vectors and q
is as follows:
To implement the simulation, the following form of immeasurable nonpotential forces (friction, hysteresis, Coriolis, damping, centripetal effects, and others) was modeled as
6.4. Applied Robust Controller Structure
6.5. Parameters of Simulation
The following are the computer simulation parameters:
is generated by uniformly distributed random numbers at an interval [−0.8, 0.8], and
| Parameter | Numerical Value | Description |
| 1.1 | environmental (air) resistance | |
| g | 9.81 m/s | Gravitational acceleration |
| 1 kg | Mass | |
| 0.35 m, 0.67 m | Length |
6.6. Results of Numerical Simulations
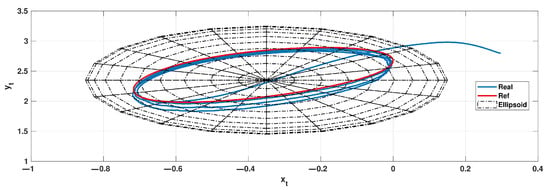
Figure 2.
Tracking ellipse.
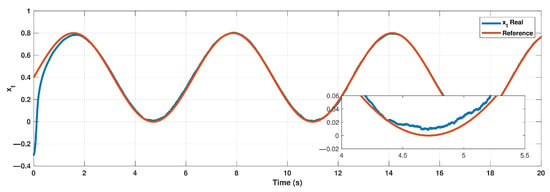
Figure 3.
tracking of .
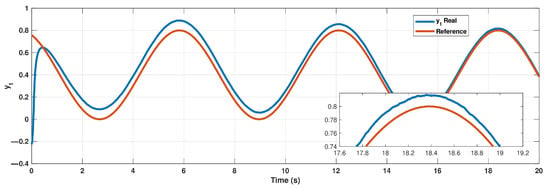
Figure 4.
Tracking of with .
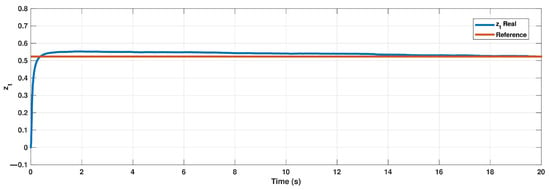
Figure 5.
Tracking of with .
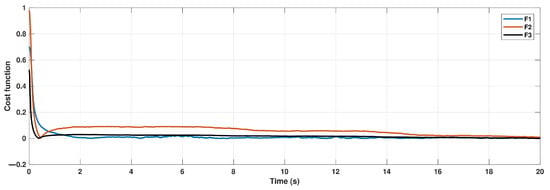
Figure 6.
Cost function components.
As one can see, the suggested method demonstrates a successful workability in the presence of essential model uncertainties and external perturbations.
7. Conclusions
- -
- The constrained optimization problem is addressed in this study using a second-order differential controlled plant with an unknown (but bounded) right side of the model.
- -
- The desired dynamics in the tracking error variables is designed based on the mirror descent method.
- -
- The continuous time convergence to the set of minimizing points is established, and the associated rate of convergence is analytically evaluated.
- -
- The robust controller, containing both the continuous (compensating) and the discontinuous , is proposed using the ASG version of the integral sliding mode approach.
- -
- The suggested controller, under the special relations of it parameters with the initial conditions, is proved to provide the desired regime from the beginning of the control process.
- -
- This method may have several applications in the development of robust control in mechanical systems, including soft robotics and moving dynamic plants.
Author Contributions
Conceptualization, A.N. and A.P.; methodology, H.A.; formal analysis, A.N. and A.P.; data curation: H.A.; resources: H.A.; software: H.A.; validation: A.N. and A.P.; visualization: A.N., H.A. and A.P.; writing—original draft preparation, A.N. and A.P.; writing—review and editing, A.N. and A.P.; supervision, A.P.; project administration, A.P.; funding acquisition, A.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ASG | Average subgradient |
| SDM | Subgradient descent Method |
| ISM | Integral sliding mode |
| SOM | Static Optimization Methods |
| ODE | Ordinary differential equation |
References
- Bertsekas, D.P. Constrained Optimization and Lagrange Multiplier Methods; Academic Press: New York, NY, USA, 1982; ISBN 0-12-093480-9. [Google Scholar]
- Dechter, R. Constraint Processing; Morgan Kaufmann: Burlington, MA, USA, 2003; ISBN 1-55860-890-7. [Google Scholar]
- Leader, J.J. Numerical Analysis and Scientific Computation; Addison Wesley: Boston, MA, USA, 2003; ISBN 0-201-73499-0. [Google Scholar]
- Posser, M.; Posser, M.J. Basic Mathematics for Economists; Routledge: New York, NY, USA, 1993; ISBN 0-415-08424-5. [Google Scholar]
- Rossi, F.; van Beek, P.; Walsh, T. Chapter 1—Introduction. In Foundations of Artificial Intelligence: Handbook of Constraint Programming; Rossi, F., van Beek, P., Walsh, T., Eds.; Elsevier: Amsterdam, The Netherlands, 2006; Volume 2, pp. 3–12. [Google Scholar] [CrossRef]
- Sun, W.; Yua, Y.-X. Optimization Theory and Methods: Nonlinear Programming; Springer: New York, NY, USA, 2010; ISBN 978-1441937650. [Google Scholar]
- Rastrigin, L.A. Systems of Extremal Control; Nauka: Moscow, Russia, 1974. (In Russian) [Google Scholar]
- Krstic, M.; Wang, H.H. Stability of extremum seeking feedback for general nonlinear dynamic systems. Automatica 2000, 36, 595–601. [Google Scholar] [CrossRef]
- Ariyur, K.B.; Krstic, M. Real-Time Optimization by Extremum-Seeking Control; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Tan, Y.; Moase, W.H.; Manzie, C.; Nešić, D.; Mareels, I.M.Y. Extremum seeking from 1922 to 2010. In Proceedings of the 29th Chinese Control Conference, Beijing, China, 29–31 July 2010; pp. 14–26. [Google Scholar]
- Tan, Y.; Nešić, D.; Mareels, I. On non-local stability properties of extremum seeking control. Automatica 2006, 42, 889–903. [Google Scholar] [CrossRef]
- Rawlings, J.B.; Amrit, R. Optimizing process economic performance using model predictive control. In Nonlinear Model Predictive Control; Magni, L., Raimondo, D.M., Allgöwer, F., Eds.; Lecture Notes in Control and Information Sciences; Springer: Berlin/Heidelberg, Germany, 2009; Volume 384, pp. 119–138. [Google Scholar]
- Dehaan, D.; Guay, M. Extremum-seeking control of state-constrained nonlinear systems. Automatica 2005, 41, 1567–1574. [Google Scholar] [CrossRef]
- Chunlei, Z.; Ordóñez, R. Robust and adaptive design of numerical optimization-based extremum seeking control. Automatica 2009, 45, 634–646. [Google Scholar]
- Solis, C.U.; Clempner, J.B.; Poznyak, A.S. Extremum seeking by a dynamic plant using mixed integral sliding mode controller with synchronous detection gradient estimation. Int. J. Robust Nonlinear Control 2018, 29, 702–714. [Google Scholar] [CrossRef]
- Ferrara, A.; Utkin, V.I. Sliding Mode Optimization in Dynamic LTI Systems. J. Optim. Theory Appl. 2002, 115, 727–740. [Google Scholar] [CrossRef]
- Ferrara, A. A variable structure convex programming based control approach for a class of uncertain linear systems. Syst. Control Lett. 2005, 54, 529–538. [Google Scholar] [CrossRef]
- Bemporad, A.; Morari, M. Robust model predictive control: A survey. In Robustness in Identification and Control; Garulli, A., Tesi, A., Eds.; Lecture Notes in Control and Information Sciences; Springer: London, UK, 1999; Volume 245, pp. 207–226. [Google Scholar] [CrossRef]
- Jalali, A.A.; Nadimi, V. A Survey on Robust Model Predictive Control from 1999–2006. In Proceedings of the 2006 International Conference on Computational Inteligence for Modelling Control and Automation and International Conference on Intelligent Agents Web Technologies and International Commerce (CIMCA’06), Sydney, NSW, Australia, 28 November–1 December 2006; p. 207. [Google Scholar] [CrossRef]
- Li, H.; Wang, S.; Shi, H.; Su, C.; Li, P. Two-Dimensional Iterative Learning Robust Asynchronous Switching Predictive Control for Multiphase Batch Processes with Time-Varying Delays. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 6488–6502. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, W.; Zhang, Q.; Shi, H.; Zhang, R.; Gao, F. Terminal constrained robust hybrid iterative learning model predictive control for complex time-delayed batch processes. Nonlinear Anal. Hybrid Syst. 2023, 47, 101276. [Google Scholar] [CrossRef]
- Liu, X.; Ma, L.; Kong, X.; Lee, K.Y. An efficient iterative learning predictive functional control for nonlinear batch processes. IEEE Trans. Cybern. 2020, 52, 4147–4160. [Google Scholar] [CrossRef] [PubMed]
- Shi, H.; Li, P.; Cao, J.; Su, C.; Yu, J. Robust fuzzy predictive control for discrete-time systems with interval time-varying delays and unknown disturbances. IEEE Trans. Fuzzy Syst. 2019, 28, 1504–1516. [Google Scholar] [CrossRef]
- Simpson-Porco, J.W. Input/output analysis of primal-dual gradient algorithms. In Proceedings of the 54th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 27–30 September 2016; pp. 219–224. [Google Scholar]
- Nazin, A.V. Algorithms of Inertial Mirror Descent in Convex Problems of Stochastic Optimization. Autom. Remote Control 2018, 79, 78–88. [Google Scholar] [CrossRef]
- Utkin, V. Sliding Modes in Control and Optimization; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Fridman, L.; Poznyak, A.; Bejarano, F.J. Robust Output LQ Optimal Control via Integral Sliding Modes; Birkhäuser: Basel, Switzerland; Springer Science and Business Media: New York, NY, USA, 2014. [Google Scholar]
- Utkin, V.; Poznyak, A.; Orlov, Y.V.; Polyakov, A. Conclusions. In Road Map for Sliding Mode Control Design; SpringerBriefs in Mathematics; Springer International Publishing: Cham, Switzerland, 2020; pp. 125–127. [Google Scholar]
- Poznyak, A.S.; Nazin, A.V.; Alazki, H. Integral Sliding Mode Convex Optimization in Uncertain Lagrangian Systems Driven by PMDC Motors: Averaged Subgradient Approach. IEEE Trans. Autom. Control 2021, 66, 4267–4273. [Google Scholar] [CrossRef]
- Rockafellar, R.T. Convex Analysis; Princeton University Press: Princeton, NJ, USA, 1970. [Google Scholar]
- Ben-Tal, A.; Nemirovski, A. The Conjugate Barrier Mirror Descent Method for Non-Smooth Convex Optimization; Minerva Optimization Center, Technion Institute of Technology: Haifa, Israel, 1999. [Google Scholar]
- Juditsky, A.B.; Nazin, A.V.; Tsybakov, A.B.; Vayatis, N. Recursive aggregation of estimators by the mirror descent algorithm with averaging. Probl. Inf. Transm. 2005, 41, 368–384. [Google Scholar] [CrossRef]
- Patel, D.K. Mathematical modeling of open loop PMDC motor using MATLAB/Simulink. Int. J. Eng. Develop. Res 2015, 3, 495–500. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).