High-Quality Reversible Data Hiding Based on Multi-Embedding for Binary Images

Abstract

Unlike histogram-based reversible data hiding (RDH), the general distortion-based framework considers pixel-by-pixel distortions, which is a new research direction in RDH. The advantage of the general distortion-based RDH method is that it can enhance the visual quality of the marked image by embedding data into visually insensitive regions (e.g., edges and textures). In this paper, following this direction, a high-capacity RDH approach based on multi-embedding is proposed. The cover image is decoupled to select the embedding sequence that can better utilize texture pixels and reduce the size of the reconstruction information, and a multi-embedding strategy is proposed to embed the secret data along with the reconstruction information by matrix embedding. The experimental results demonstrate that the proposed method provides a superior visual quality and higher embedding capacity than some state-of-the-art RDH works for binary images. With an embedding capacity of 1000 bits, the proposed method achieves an average PSNR of 49.45 dB and an average SSIM of 0.9705 on the test images. This marks an improvement of 1.1 dB in PSNR and 0.0242 in SSIM compared to the latest state-of-the-art RDH method.

1. Introduction

Data hiding can be classified as steganography [1], digital watermarking [2,3] and reversible data hiding (RDH) [4,5]. For both steganography and digital watermarking, permanent distortions are introduced to the original carrier. However, unlike steganography and digital watermarking, RDH enables reversibility and can losslessly recover the original carrier. Due to the lossless recovery property, RDH can be used as authentication protection for active forensics, or for covert communication and integrity authentication for medical and military images [6,7].

For grayscale and color images, many RDH methods have been developed in recent years [8,9,10,11,12,13,14]. Early RDH methods aimed to release redundant space by losslessly compressing the cover image features. The performance of such approaches depends on the selected compression algorithm and features, resulting in a low embedding capacity [15]. Subsequently, the difference expansion (DE) algorithm was proposed in [16]. Using DE, the embedding units are constructed by chunking the cover image and the secret data are embedded into each unit by a specifically designed integer transform. However, RDH based on an integer transform cannot effectively control the embedding distortion [17]. Presently, RDH research primarily focuses on histogram-based methods, exploiting the statistical properties of the cover image. The histogram of a given cover image is first generated, and then different histogram modification rules are designed. The histogram-based approach successfully achieves capacity increase and distortion control by fully utilizing the image redundancy. However, for histogram-based methods, the same distortion is introduced for each pixel in the same bin and cannot integrate adaptive embedding with the Human Visual System (HVS) [18,19,20].

In addition, binary images lack access to histograms and have limited space for reversible embedding, which has not received much attention in RDH [21,22,23,24,25]. In general, black pixels are usually the foreground of a binary image, while most white pixels are the background. Therefore, a significant visual impact will be introduced if the black and the white pixels are swapped. By considering the probabilities of different pattern sequences, Ho et al. proposed the pattern substitution (PS) method for binary images [21]. As an improvement of [21], based on the optimal transfer probability matrix, Zhang et al. proposed a new RDH method [23]. Recently, Xiao et al. proposed a general distortion-based RDH method for binary images [25]. When using general distortion, each pixel is assigned a distortion value that represents the visual impact of flipping the pixel, and secret data are embedded into the pixels of visually insensitive regions. In this way, the visual quality of the marked image is improved. However, in [25], to ensure reversibility, only half of the cover pixels are used for data embedding, while the other half are unmodified. As a result, numerous cover pixels suitable for data embedding are not utilized. Therefore, intuitively, the visual quality of the marked image can be further improved by involving more pixels for data embedding.

In this paper, a high-capacity RDH method is proposed for binary images based on multi-embedding, which improves upon the method of [25]. The proposed method can better utilize texture cover pixels to ameliorate the marked image visual quality. Specifically, the cover image is decoupled to derive several disjoint parts for pixel selection, and a multi-embedding strategy is proposed to embed the secret data along with the reconstruction information by matrix embedding. In this way, unlike [25], almost all texture cover pixels can be exploited for data embedding. Moreover, by multi-embedding, more neighboring pixels can be utilized for better prediction so that the size of the reconstruction information is reduced. Compared with some state-of-the-art works [21,23,25], it is demonstrated that the proposed method can provide better visual quality and higher embedding capacity for binary images.

The remainder of this paper is organized as follows. A brief overview of traditional and general distortion-based RDH frameworks is presented in Section 2. The proposed embedding and extraction processes are described in Section 3. The superiority of the proposed method is verified by experiments in Section 4. Finally, the conclusion is given in Section 5.

2. Preliminary

2.1. Traditional RDH Framework

Without loss of generality, let $X=(x_1,\dots ,x_n)$ be the cover sequence with n elements, and the corresponding marked sequence is denoted as $Y=(y_1,\dots ,y_n)$. The cover sequence may consist of pixels or prediction-errors. In [26], X is assumed to be an i.i.d. sequence, and the upper bound on the payload for a given distortion $\Delta$ is given as

$${\rho }_{\mathrm{rev}}(\Delta )=maximize\left\{H\left(Y\right)\right\}-H\left(X\right)$$

(1)

where H denotes the entropy function. Thus, ${\rho }_{\mathrm{rev}}$ represents the maximum capacity of reversible embedding (the number of bits that can be embedded) under a given distortion constraint. The previous histogram-based RDH method is designed by the transfer probability matrix $P_{Y\mid X}$, by which the distortion constraint for maximum entropy is

$$\sum _{i=1}^n{P}_X\left(x_i\right)P_{Y\mid X}(y_i\mid x_i)D(x_i,y_i)\le \Delta$$

(2)

where $P_X$ is the distribution of X and D is a distortion measure usually defined as the squared distortion. In this situation, the distortion of the histogram-based RDH is only related to the histogram of X. Most subsequent histogram-based methods follow this direction, and the embedding process includes two steps: histogram generation and histogram modification [8,9,10,11,12,13,14].

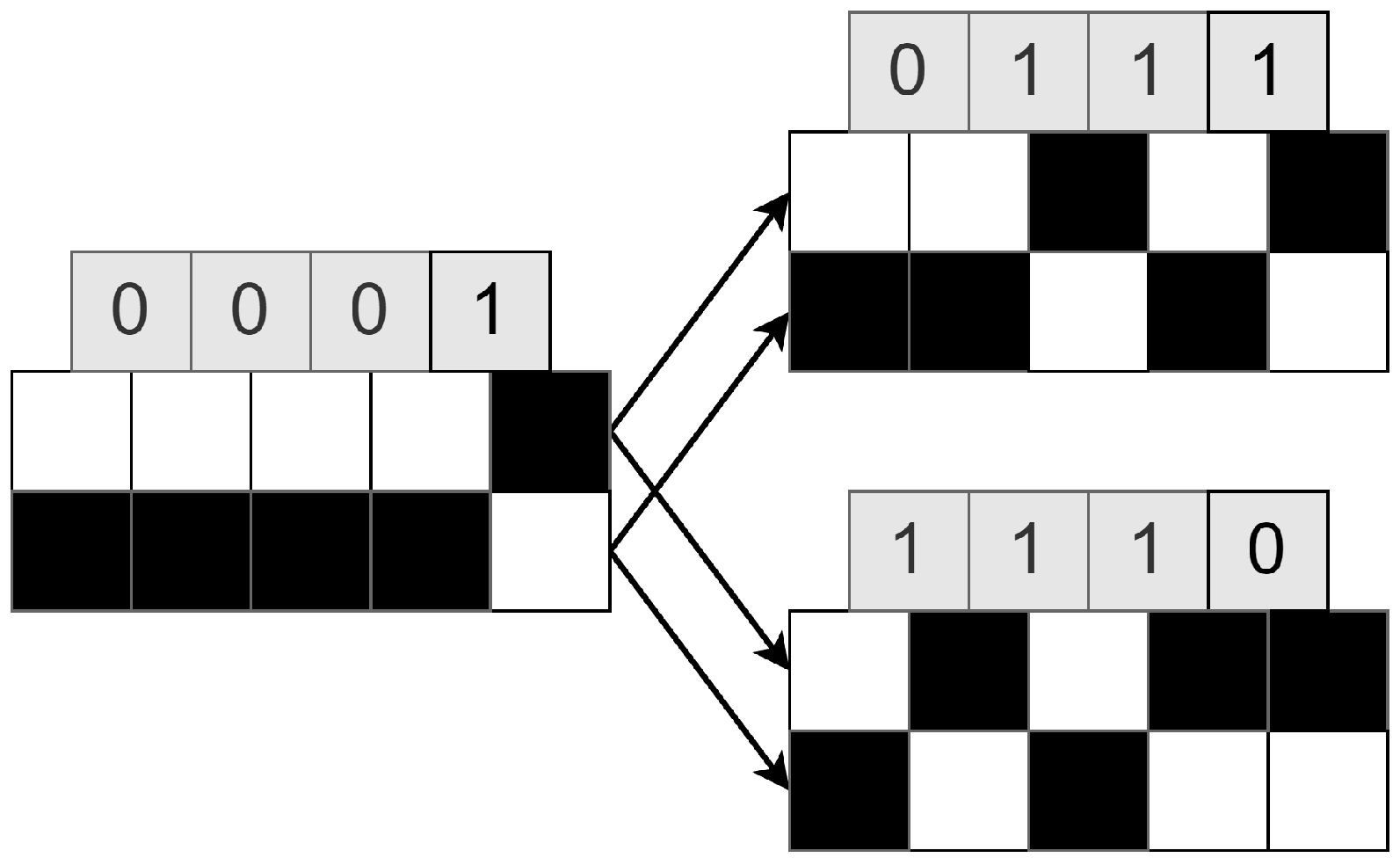
2.2. Pattern Substitution RDH Method for Binary Images

Following the traditional RDH framework, a method called PS for binary images was proposed in [21] by estimating the frequency of pattern occurrences. In this method, by establishing connections between patterns, secret data can be embedded into binary images through the substitution of patterns. During the extraction stage, the patterns are reversed to their initial states by the transfer table to reconstruct the cover image.

For data embedding, the difference image denoted D of the cover image X is first computed as

$$D(i,j)=\left\{\begin{array}{cc}X(i,j),\hfill & \mathrm{if}i=1\mathrm{and}j=1\hfill \\ X(i,j)\oplus X(i-1,j),\hfill & \mathrm{if}i\ne 1\mathrm{and}j=1\hfill \\ X(i,j)\oplus X(i,j-1),\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(3)

where ⊕ denotes the XOR logic operation, and i and j are the coordinates of the cover image. The difference image can identify the edges in binary images, and modifying the difference image may alter the cover edge pixels, which makes it hard for humans to recognize. Specifically, the difference image D is first divided into non-overlapping blocks, each containing four consecutive pixels. Four pixels correspond to sixteen patterns. The pixel with $D(i,j)=1$ appears only at the edges of the color exchange in the cover image X, so the probability of a pattern with a large number of “1” is low. To reduce the embedding distortion, the patterns in D are separated into odd and even groups depending on the number of “1”. It is not permitted to substitute patterns between groups. That is to say, if a pattern has an odd number of “1”, the adjusted number of “1” must also be odd. Likewise, if a pattern has an even number of “1”, the adjusted “1” must also be even. Take the pattern (0,0,0,1) in the odd group as an example (see Figure 1). The pattern has a “1”, so the number of “1” can only remain the same or change to 3. Replacing pattern (0,0,0,1) with (0,1,1,1) modifies only one pixel of X. In this situation, there are two cases in X, i.e., change (0,0,0,0,1) to (0,0,1,0,1) or change (1,1,1,1,0) to (1,1,0,1,0). However, replacing (0,0,0,1) with (1,1,1,0) will modify three pixels of X.

Based on the above procedure, the PS method [21] and its improvement [23] optimize the modified minimum target pattern within the same group for each pattern in the group. The two patterns are then paired for data embedding. If the embedded bit is 0, the pattern remains unchanged. Conversely, if the embedded bit is 1, the pattern transforms into the target pattern. To achieve a high embedding capability, the modified pattern should have a high occurrence, while the target pattern should have a low occurrence. The embedding process is scanned in a raster order to ensure the reversibility.

2.3. General Distortion-Based RDH Framework

Using general distortion, each pixel is assigned a specific distortion value, meaning the visual impact for flipping a pixel [25] and the visual quality of the marked image is improved by embedding data into visually insensitive regions. The general distortion is defined as, for each $1\le i\le n$,

$$D(x_i,y_i)={\rho }_i{(y_i-x_i)}^2={\rho }_i{z}_i^2$$

(4)

where ${\rho }_i>0$ is a predefined distortion value and $Z=Y-X=(z_1,\dots ,z_n)$. With the general distortion, reversible embedding cannot be realized by traditional histogram-based methods unless ${\rho }_i$ is a constant. Here, RDH is concerned with visual distortion rather than the usual mean square distortion. The general distortion problem can be solved by matrix embedding. Specifically, in [25], the authors proposed to consider the following optimization problem:

$$\left\{\begin{array}{cc}\underset{Z}{minimize}\hfill & \sum _{i=1}^n{\rho }_i{z}_i^2\hfill \\ \mathrm{subject}\mathrm{to}\hfill & \mathbb{H}Y=M^{*}\hfill \end{array}\right.$$

(5)

where $\mathbb{H}$ is a given matrix shared by the sender and receiver and $M^{*}$ consists of the secret data M and the reconstruction information R. Moreover, as $Z=Y-X$, the constraint can be rewritten as

$$\mathbb{H}Z=M^{*}-\mathbb{H}X.$$

(6)

For a binary image, $z_i^2=z_i$, since $z_i\in \{0,1\}$. In this way, a reversible embedding framework for binary images is proposed in [25], as shown in Figure 2, and it contains the following two steps.

Cover selection. First, the cover image is evenly divided into two parts (represented by two colors in Figure 2), where half of the pixels form the candidate embedding group U and the others form the prediction group V. Then, the local complexity is defined as the sum of the absolute difference of any two surrounding pixels in the prediction group and the pixels in U are sorted by the local complexity in ascending order. The cover pixels $X\subset U$ are composed of the pixels with smaller local complexity, while the remaining pixels in $U-X$ are included in the prediction group V.

Reconstruction information generation. For each cover pixel $x_i$, the surrounding pixels in the prediction group are selected to obtain the prediction value denoted ${\widehat{x}}_i$. Then, the prediction-error is calculated as $e_i=x_i\oplus {\widehat{x}}_i$, where ⊕ denotes the XOR logic operation. Then, the prediction-error sequence is losslessly compressed into reconstruction information, which is then combined with the secret data M into the final to-be-embedded data $M^{*}$. Here, the lossless compression is achieved through run-length encoding (RLE). In the steganography area, there are well-established distortion costs to preserve the statistical undetectability of the cover image. Various distortions have been proposed to better utilize complex image regions. Leveraging prior knowledge, the proposed method adopts a simple yet effective cost function known as High-pass, Low-pass and Low-pass (HILL) [27] as the visual distortion measure to validate the general distortion model for visual improvement. In this way, the marked sequence $Y=\mathrm{Emb}(X,M^{*})$ is derived by the Syndrome–Trellis Codes (STC) [28].

On the extraction side, the marked sequence Y is obtained in the same way as the cover selection. Then, the secret data and the reconstruction information can be extracted by $M^{*}=\mathbb{H}Y$ and separated by RLE. Finally, the cover image can be recovered by the unmodified pixels with the decompressed reconstruction information.

Note that, for the method by Xiao et al. [25], to ensure reversibility, only half of the cover pixels are utilized for data embedding, while the other half of the cover pixels are unmodified. As a result, numerous cover pixels suitable for data embedding are not utilized. Although this method has achieved state-of-the-art visual quality, the performance can still be improved.

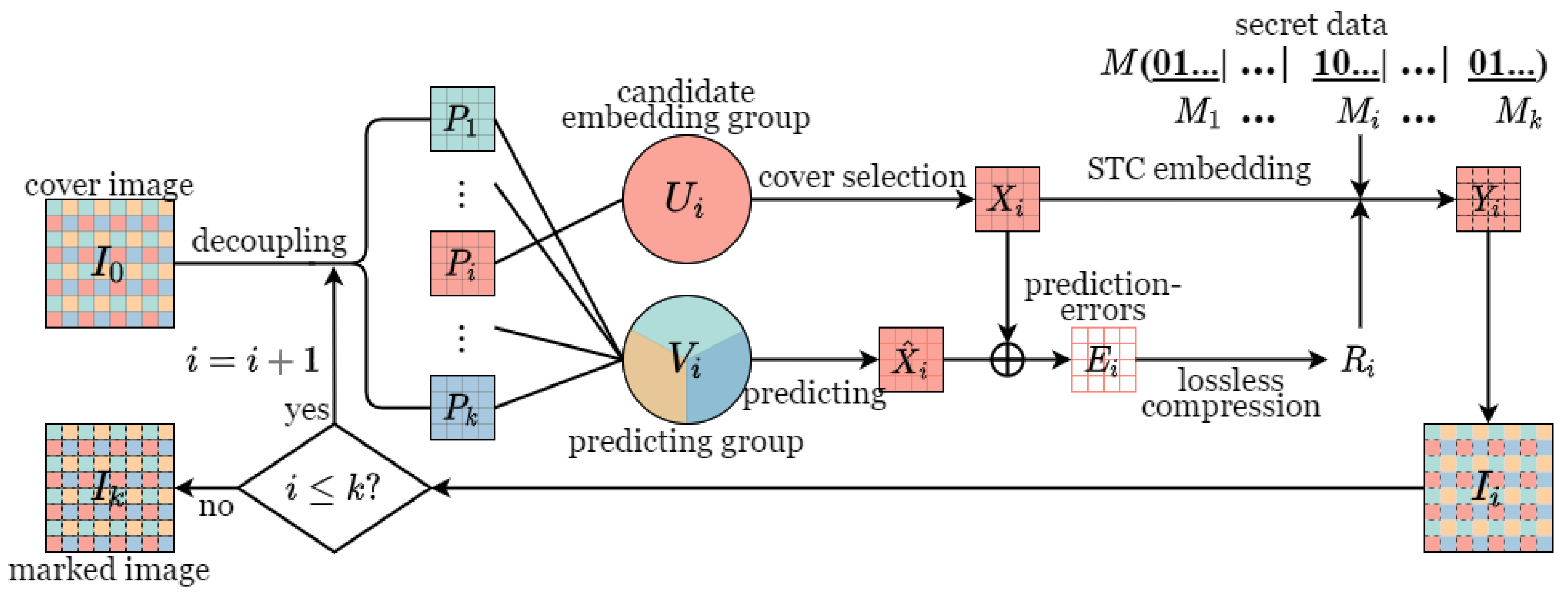
3. Proposed Method

In this paper, a new RDH method based on multi-embedding is proposed to ameliorate the visual quality of binary marked images. The cover image is decoupled to derive several disjointed parts for pixel selection. The secret data and the reconstruction information are iteratively embedded into each part.

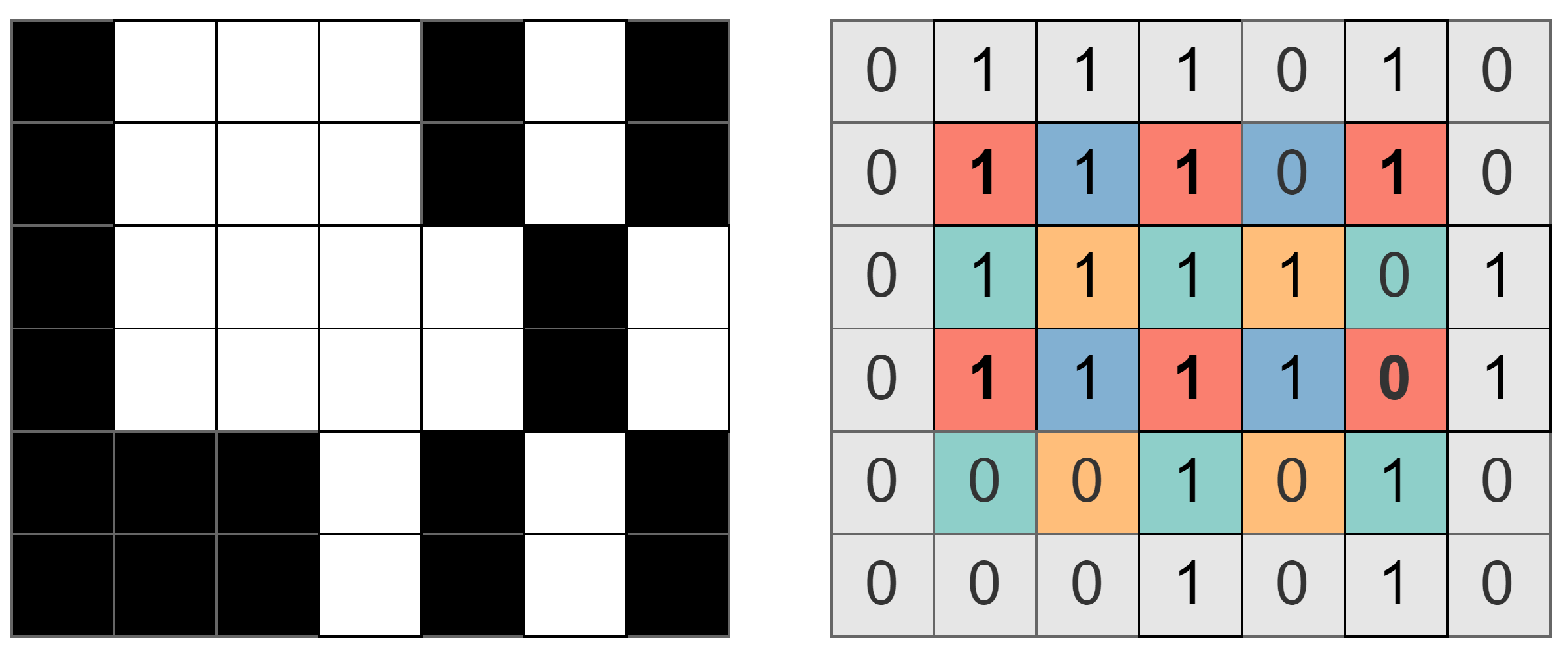
3.1. Cover Selection

To ensure reversibility, some pixels are preselected for data embedding, while unmodified pixels are required to record these pixels using prediction. Specifically, the cover image is divided into k parts and each part is iterated as a candidate embedding group, while the remaining $k-1$ parts are in the prediction group. In this way, all texture cover pixels are explored for data embedding and there are enough surrounding pixels in the prediction group.

Taking $k=4$ as an example, as shown in Figure 3, the cover image is first divided into four parts as $P_1$, $P_2$, $P_3$ and $P_4$, to evenly embed the secret data. Suppose the candidate embedding group $U=\{u_1,\dots ,u_{n/4}\}=P_1$ embeds the first part of the secret data, where $n/4$ is supposed to be an integer. Then, the prediction group is

$$V=P_2\cup P_3\cup P_4=\bigcup _{i=1}^{n/4}{V}_i$$

(7)

where $V_i=\{v_i^1,\dots ,v_i^8\}$ contains the surrounding eight unmodified pixels for predicting $u_i$. For cover selection, the local complexity $L_i$ of each $u_i$ is defined as the expectation of the absolute difference of any two surrounding pixels in $V_i$, and the selected cover sequence is

$$X=\{u_i:L_i\le T\}$$

(8)

where T is the local complexity threshold. For better prediction, T is set to 1/4 to include the pixels for which at most one of the eight surrounding pixels differs in value. Then, the prediction value ${\widehat{x}}_i$ of $x_i$ is calculated by voting using the pixels in $V_i$. As a result, for each cover pixel, the remaining pixels in its $3\times 3$ sized neighborhood are all utilized for prediction, which allows for a more accurate prediction. Finally, the prediction-error is calculated by $e_i=x_i\oplus {\widehat{x}}_i$, and the prediction-error sequence is losslessly compressed into the reconstruction information. The cover selection for the other three parts is similar to the first part and is omitted here.

An example to illustrate the cover selection strategy is presented in Figure 4. As shown, the cover image with a size of $7\times 6$ is divided into four layers. A layer consists of 6 candidate embedded pixels $U=(u_1,\dots ,u_6)=(1,1,1,1,1,0)$ shown in red. The remaining 8 pixels in the $3\times 3$ sized neighborhood of each candidate embedded pixels are denoted as $V_i$, for each $i\in \{1,\dots ,6\}$. As an illustration, the neighborhood pixels for the first pixel are three white pixels and five black pixels, making the color proportion 3:5. Moreover, the ratio set of the two colors in the six groups of predicted pixels is {3:5, 2:6, 3:5, 3:5, 2:6, 3:5}. Thus, the local complexity $L_i$ of each candidate embedded pixel can be calculated by $V_i$. When $T=1/4$, $X=(u_2,u_5)$ is selected for inclusion in the vector sequence. The corresponding predicted values $\widehat{X}=(1,1)$ are determined by voting for elements in $V_2$ and $V_5$. Thus, in this example, the prediction-error in the first layer is $(0,0)$. Lossless compression does not involve any additional reconstruction information.

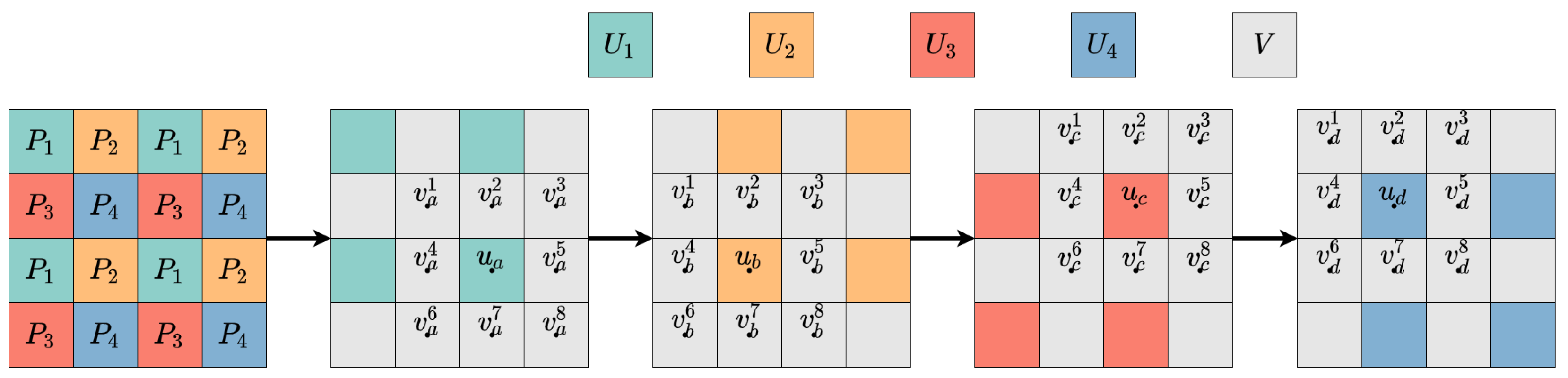
3.2. Multi-Embedding Process

For each part of the pixels, after cover selection, one part of the secret data is embedded into the selected pixels. The cover selection and embedding processes are repeated k times to embed all the secret data. The multi-embedding process is shown in Figure 5, and the specific embedding steps are described as follows.

1.

Divide the cover image $I_0$ into k parts and the secret data M into k segments.

2.

Take one part as the candidate embedding group $U_1$ and the remaining parts as the prediction group V.

3.

Calculate the local complexity of pixels in $U_1$ and select the cover sequence $X_1$ by Equation (8).

4.

Predict the pixels in $X_1$ by V and derive the prediction-error sequence $E_1$.

5.

Losslessly compress $E_1$ into reconstruction information $R_1$ and combine $R_1$ with $M_1$ to derive $M_1^{*}$.

6.

Embed $M_1^{*}$ into $X_1$ with STC and update the cover image to derive $I_1$.

7.

Repeat the above steps until all secret data segments are embedded to derive the marked image $I_k$.

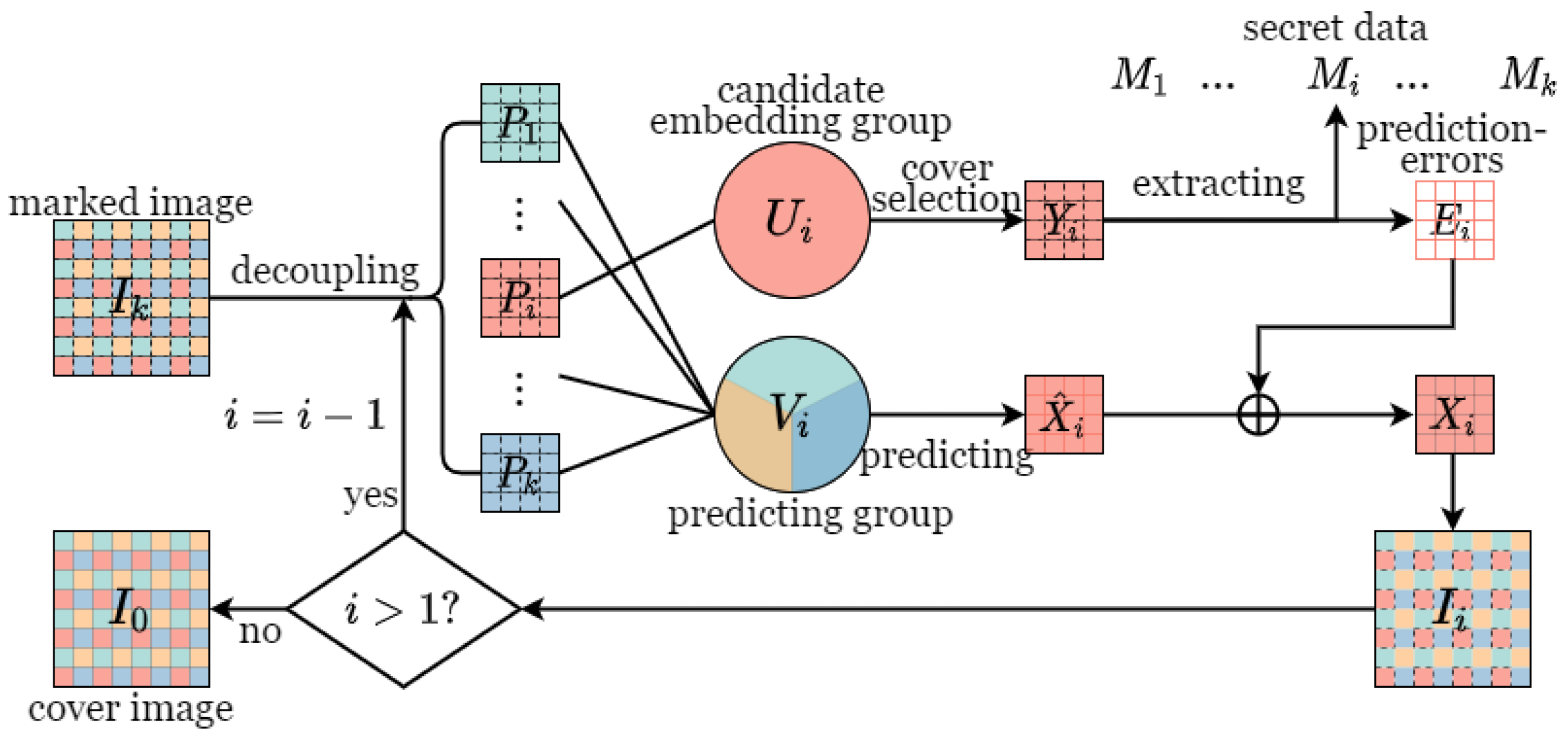
3.3. Mutil-Extraction Process

Data extraction is just the inverse process of data embedding, which requires extracting the secret data M and recovering the original cover image $I_0$. The multi-extraction process is shown in Figure 6, and the specific extraction steps are described as follows.

1.

Divide the received marked image $I_k$ into k parts in the same way as data embedding.

2.

Arrange the candidate embedding group $U_k$ and the prediction group V in inverse order.

3.

Calculate the local complexity of pixels in $U_k$ and derive the marked sequence $Y_k$ by Equation (8).

4.

Extract $M_k^{*}=\mathbb{H}{Y}_k$ and then separate the secret data $M_k$ and the reconstruction information $R_k$.

5.

Decompress $R_k$ to derive $E_k$ and recover the last marked image $I_{k-1}$ by the predicting group V.

6.

Repeat the above steps until all data segments are extracted and the cover image $I_0$ is recovered.

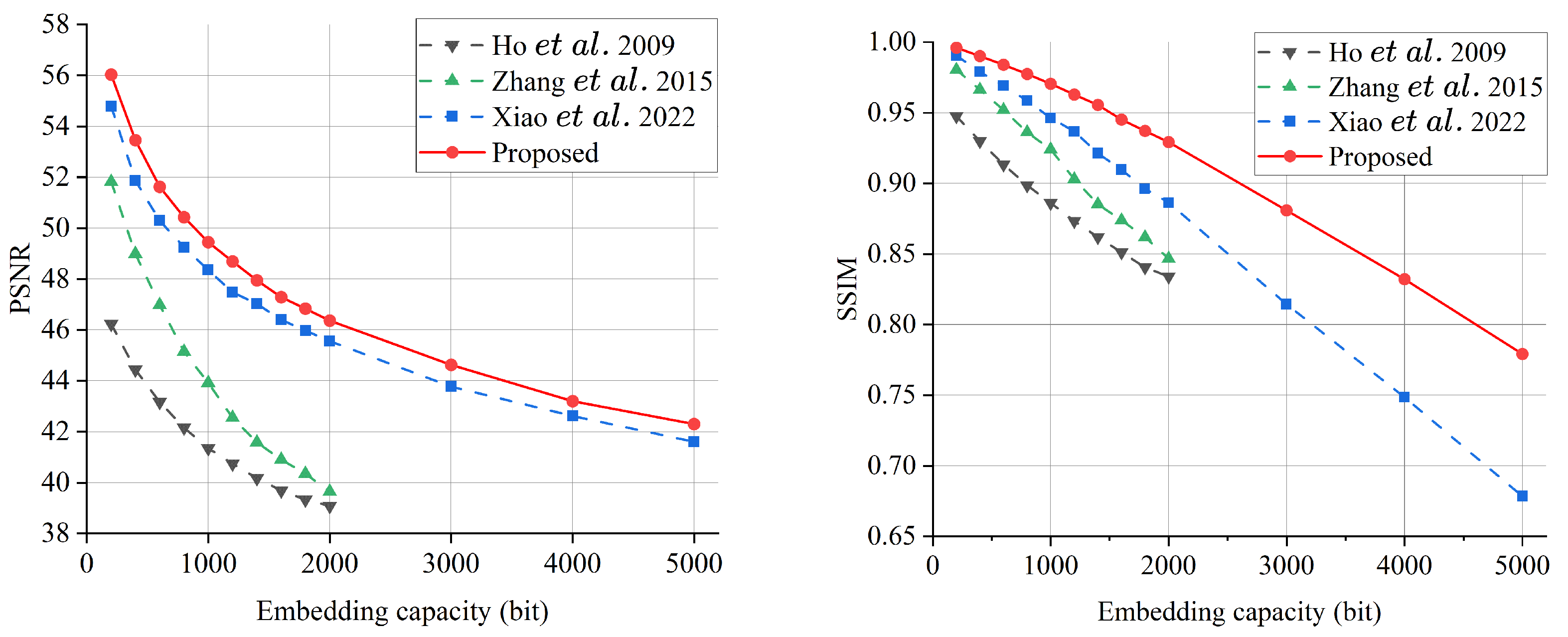
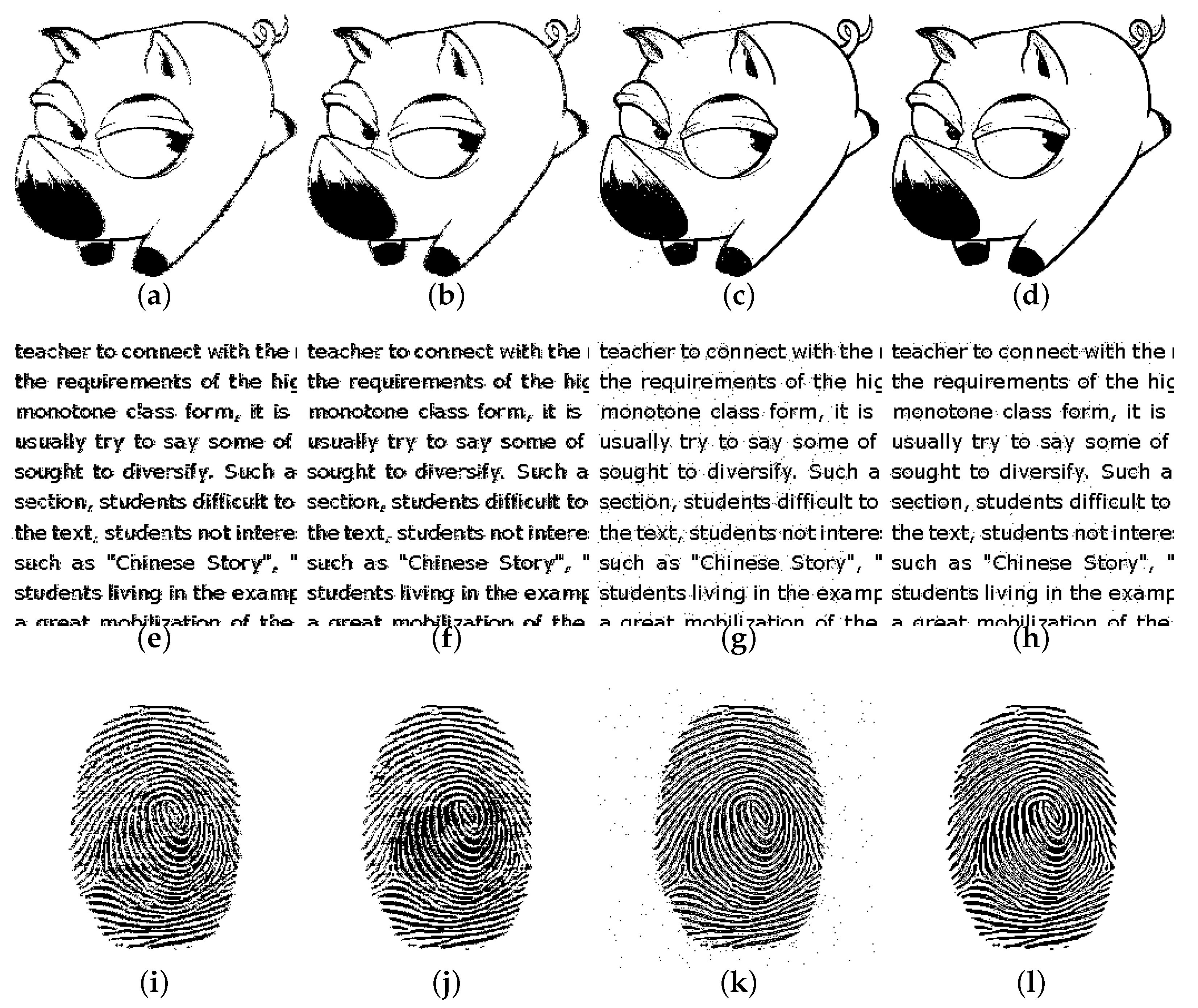
4. Experimental Results

The experiments involve conducting embedding and comparison analyses on diverse categories of binary images, each sized 256 × 256. The image categories comprised cartoons, documents and fingerprints, as depicted in Figure 7. These images also serve as test samples in other RDH works [22,25]. The typical HILL cost [27] is adopted as the visual distortion for matrix embedding with STC. Three state-of-the-art works [21,23,25] are selected for comparison. In [21,23], reversible embedding is achieved by PS, where the optimal pattern tables are derived by calculating the probability of various patterns in [21] and by estimating the optimal probability transfer matrix in [23]. In [25], the first general distortion-based RDH method for binary images is proposed, where half of the cover pixels are used for reversible embedding and the other half are unmodified to ensure reversibility.

The marked images generated by the four methods are depicted in Figure 8. Compared to [21,23,25], the proposed method exhibited minimal perceptible modifications. The marked images maintain better clarity and edges. Specifically, for the cartoon image “Pig”, the edges of the marked images in Figure 8a,b generated by [21,23] are blurred to varying degrees and similar effects are observed in other examples. Marked images using the proposed method have fewer blurred edges, maintaining the original appearance of the cartoon image “Pig” better than those generated by [21,23]. The noise points in Figure 8c are relatively random and the image in Figure 8d is primarily modified in the pig’s tail. For document images, the proposed method resulted in marked images with improved readability compared to [21,23]. For instance, the image in Figure 8h has better readability than the image in Figure 8g. For the fingerprint images with high embedding capacity, obvious noise appears in the smooth region in Figure 8k due to the insufficient embedding capacity. The proposed method achieved a higher embedding capacity, resulting in less noise in the smooth regions of fingerprint images compared to [25]. In addition, since data embedding is achieved by PS, the embedding capacities are limited in [21,23]. For example, for the “Boy” image, the maximum embedding capacities for [21,23] are 2706 and 2507 bits, respectively. Furthermore, the proposed method achieved a maximum embedding capacity exceeding 5000 bits for the “Boy” image, showcasing a significant improvement compared to that achieved by [21,23].

Moreover, a comparison between [25] and the proposed method is made, focusing on visual quality in Figure 9, where the boy’s leg is enlarged for better comparison. It can be observed that the proposed method modifies fewer smoothing pixels than [25]. Within tolerable visual distortion, the proposed method demonstrates a higher embedding capacity than [25] due to its multi-embedding strategy. In summary, compared with [21,23,25], the proposed method achieves the best visual effect for various test images, as well as the highest embedding capacity.

The obtained Peak Signal-to-Noise Ratio (PSNR) and Structural SIMilarity (SSIM) of the marked images are presented in Figure 10, where the results represent average values for all test images. The PSNR and SSIM of [21,23] decrease rapidly as the embedding capacity increases. The proposed method exhibited superior performance, maintaining higher PSNR even at high embedding capacities and showcasing less distortion. The proposed method demonstrated significant performance improvements in SSIM, indicating better preservation of structural similarity even at high embedding capacities. Compared with [25], the proposed method achieves better embedding performance regardless of the embedding capacity. Additionally, it is noteworthy that the obtained PSNR remains above 42 dB even at an embedding capacity of 5000 bits. In summary, the proposed method results in less distortion, superior visual quality and a higher embedding capacity than all the compared RDH methods.

The results highlight several significant findings. First and foremost, the proposed method consistently outperforms [21,23,25] in terms of both visual quality and embedding capacity. The perceptibility of modifications in the marked images is significantly reduced in the proposed method compared to [21,23], as evidenced by the decreased blurring of edges in cartoon images and the improved readability in document images. Moreover, the embedding capacity of the proposed method far exceeded that of [21,23], demonstrating the effectiveness of the iterative embedding strategy. Regarding [25], while it showcased a competitive approach, the proposed method consistently demonstrated superior visual quality and embedding capacity, making it the most effective approach among the compared RDH methods. Overall, the proposed method not only achieves superior visual effects for various test images but also provides the highest embedding capacity.

5. Conclusions

In this paper, a novel RDH method is proposed to improve the visual quality of binary-marked images. By using the proposed multi-embedding strategy, the texture pixels are better utilized for cover selection and reversible embedding. The experimental results show that the marked images generated by the proposed method have excellent visual quality, and the proposed method outperforms some state-of-the-art works [21,23,25] in both visual quality and embedding capacity. The reversible embedding performance can be improved by exploring different local complexity measures and using larger local neighborhoods for prediction in the future. Additionally, it is vital to integrate advanced visual quality metrics that precisely gauge human vision. Moreover, extending the proposed approach to grayscale images is also a valuable future direction.