Vibrations of Nonlocal Polymer-GPL Plates at Nanoscale: Application of a Quasi-3D Plate Model
Abstract
:1. Introduction
2. Problem Statement
3. Displacements and Strains
4. Local Constitutive Relations
5. Nonlocal Model
6. Governing Equations of Motion
7. Analytical Solution
8. Results and Discussion
8.1. Comparison Studies
8.2. Parametric Studies
9. Conclusions
- with an acceptable accuracy, a ten-layer nanocomposite-laminated nanoplate model can be treated as an FGM plate with continuous variation of material properties.
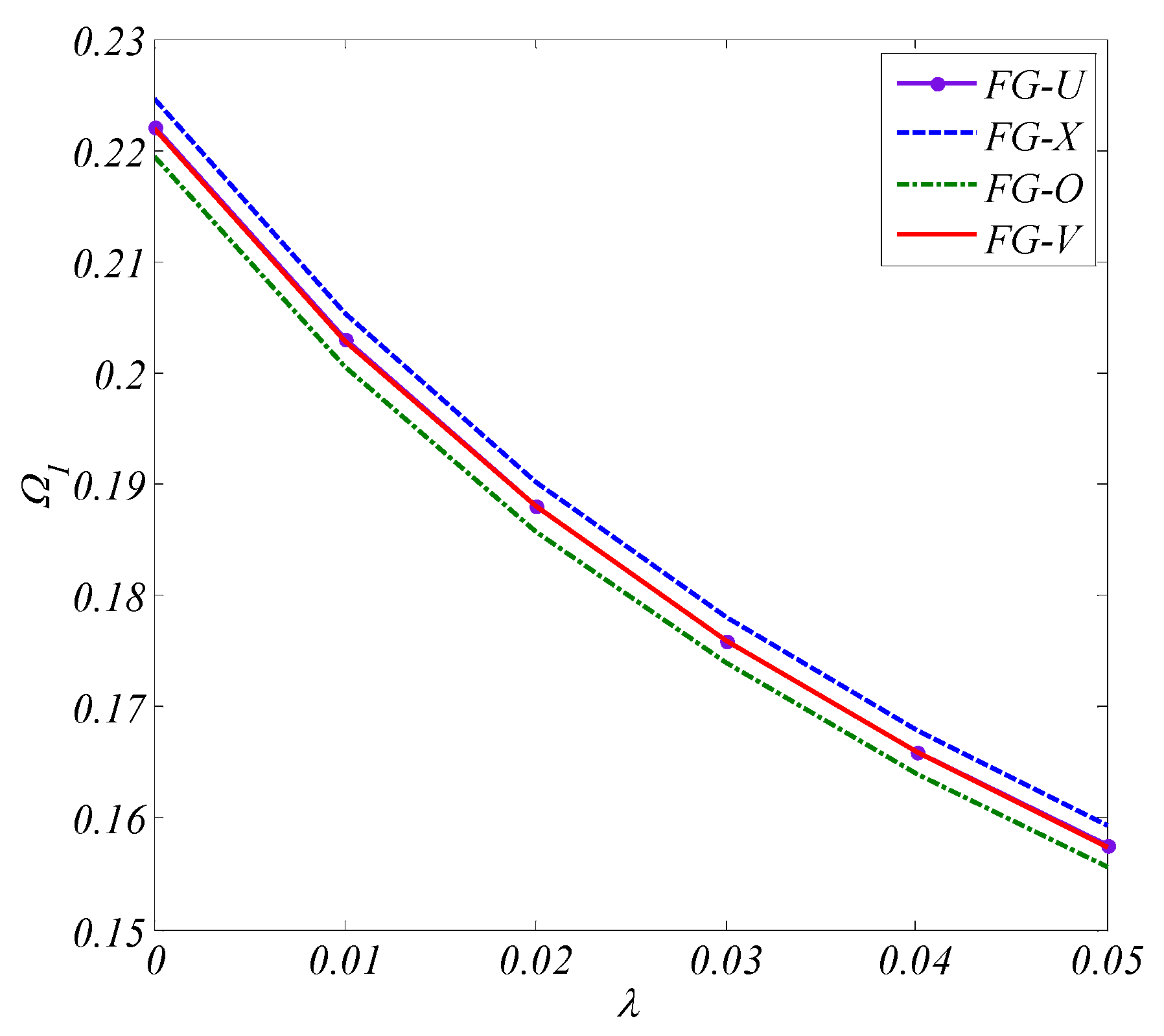
- By considering the nonlocal elasticity, the frequencies are reduced.
- It was clearly revealed that frequencies are highly affected by non-local parameter changes and this effect is more significant for higher frequencies.
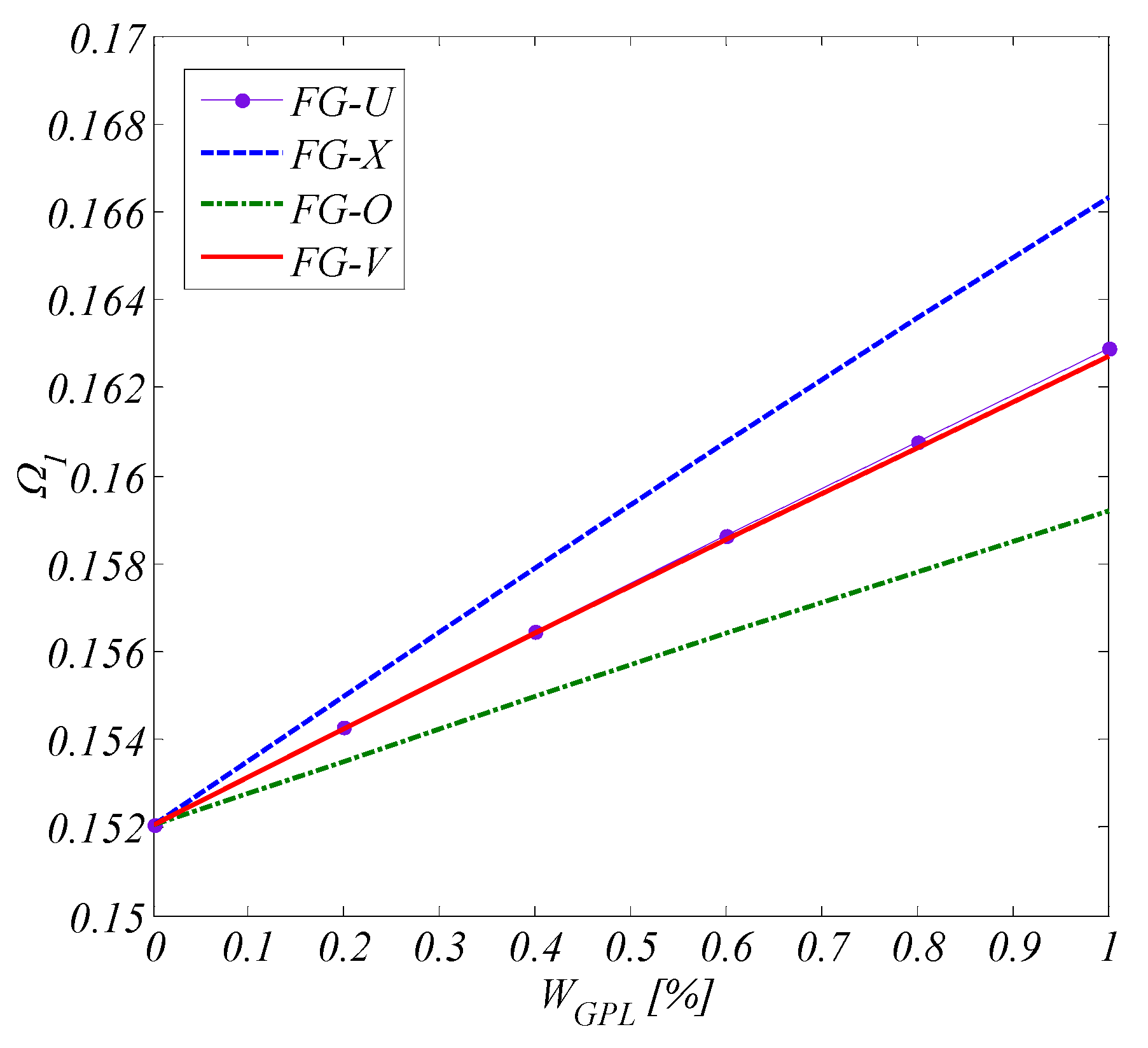
- With the introduction of GPLs in the matrix of the composite nanoplate, frequencies are enhanced.
- FG-X and FG-O patterns have maximum and minimum frequencies of the plate.
- The introduced quasi-3D plate model may serve as an excellent theory for estimation of mechanical response of arbitrary thick plates made of GPLRCs at nano and macro scales.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rafiee, M.A.; Rafiee, J.; Wang, Z.; Song, H.; Yu, Z.; Koratkar, N. Enhanced Mechanical Properties of Nanocomposites at Low Graphene Content. ACS Nano 2009, 3, 3884–3890. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Zhao, Z.; Yang, Z.; Ke, L.L.; Kitipornchai, S.; Yang, J. Functionally graded graphene reinforced composite structures: A review. Eng. Struct. 2020, 210, 110339. [Google Scholar] [CrossRef]
- Song, M.; Kitipornchai, S.; Yang, J. Free and forced vibrations of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos. Struct. 2017, 159, 579–588. [Google Scholar] [CrossRef]
- Guo, H.; Cao, S.; Yang, T.; Chen, Y. Vibration of laminated composite quadrilateral plates reinforced with graphene nanoplatelets using the element-free IMLS-Ritz method. Int. J. Mech. Sci. 2018, 142–143, 610–621. [Google Scholar] [CrossRef]
- Zhao, Z.; Feng, C.; Wang, Y.; Yang, J. Bending and vibration analysis of functionally graded trapezoidal nanocomposite plates reinforced with graphene nanoplatelets (GPLs). Compos. Struct. 2017, 180, 799–808. [Google Scholar] [CrossRef]
- Guo, H.; Cao, S.; Yang, T.; Chen, Y. Geometrically nonlinear analysis of laminated composite quadrilateral plates reinforced with graphene nanoplatelets using the element-free IMLS-Ritz method. Compos. B Eng. 2018, 154, 216–224. [Google Scholar] [CrossRef]
- Gholami, R.; Ansari, R. Nonlinear stability and vibration of pre/post-buckled multilayer FG-GPLRPC rectangular plates. Appl. Math. Model. 2019, 65, 627–660. [Google Scholar] [CrossRef]
- Wu, H.; Yang, J.; Kitipornchai, S. Parametric instability of thermo-mechanically loaded functionally graded graphene reinforced nanocomposite plates. Int. J. Mech. Sci. 2018, 135, 431–440. [Google Scholar] [CrossRef]
- Muni Rami Reddy, R.; Karunasena, W.; Lokuge, W. Free vibration of functionally graded-GPL reinforced composite plates with different boundary conditions. Aerosp. Sci. Technol. 2018, 78, 147–156. [Google Scholar] [CrossRef]
- Gao, K.; Gao, W.; Chen, D.; Yang, J. Nonlinear free vibration of functionally graded graphene platelets reinforced porous nanocomposite plates resting on elastic foundation. Compos. Struct. 2018, 204, 831–846. [Google Scholar] [CrossRef]
- Yang, J.; Chen, D.; Kitipornchai, S. Buckling and free vibration analyses of functionally graded graphene reinforced porous nanocomposite plates based on Chebyshev-Ritz method. Compos. Struct. 2018, 193, 281–294. [Google Scholar] [CrossRef]
- Lin, H.G.; Cao, D.Q.; Xu, Y.Q. Vibration, buckling, aeroelastic analysis of functionally graded multilayer graphene-platelets-reinforced composite plates embedded in piezoelectric layers. Int. J. Appl. Mech. 2018, 10, 1850023. [Google Scholar] [CrossRef]
- Gholami, R.; Ansari, R. On the nonlinear vibrations of polymer nanocomposite rectangular plates reinforced by graphene nanoplatelets: A unified higher-order shear deformable model. Iran. J. Sci. Technol. Trans. Mech. Eng. 2019, 43, 603–620. [Google Scholar] [CrossRef]
- Torabi, J.; Ansari, R. Numerical phase-field vibration analysis of cracked functionally graded GPL-RC plates. Mech. Based Des. Struct. 2022, 50, 3491–3510. [Google Scholar] [CrossRef]
- Pashmforoush, F. Statistical analysis on free vibration behavior of functionally graded nanocomposite plates reinforced by graphene platelets. Compos. Struct. 2019, 213, 14–24. [Google Scholar] [CrossRef]
- Ansari, R.; Hassani, R.; Gholami, R.; Rouhi, H. Free vibration analysis of postbuckled arbitrary-shaped FG-GPL-reinforced porous nanocomposite plates. Thin Wall. Struct. 2021, 163, 107701. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Wang, Y.X.; Pan, H.G.; Gao, X.S.; Cai, Y. Analytical solution for vibration characteristics of rotating graphene nanoplatelet-reinforced plates under rubimpact and thermal shock. Adv. Compos. Mater. 2020, 29, 1–15. [Google Scholar]
- Thai, C.H.; Phung-Van, P. A meshfree approach using naturally stabilized nodal integration for multilayer FG GPLRC complicated plate structures. Eng. Anal. Bound. Elem. 2020, 117, 346–358. [Google Scholar] [CrossRef]
- Jafari, P.; Kiani, Y. Free vibration of functionally graded graphene platelet reinforced plates: A quasi 3D shear and normal deformable plate model. Compos. Struct. 2021, 275, 114409. [Google Scholar] [CrossRef]
- Shi, X.; Suo, R.; Xia, L.; Yu, X.; Babaie, M. Static and free vibration analyses of functionally graded porous skew plates reinforced by graphene platelet based on three-dimensional elasticity theory. Waves Random Complex Media 2022. [Google Scholar] [CrossRef]
- Kiani, Y.; Żur, K.K. Free vibrations of graphene platelet reinforced composite skew plates resting on point supports. Thin Wall. Struct. 2022, 176, 109363. [Google Scholar] [CrossRef]
- Abbaspour, F.; Arvin, H.; Shahriari-Kahkeshim, M. Active control of vibrations of piezoelectric rectangular nanocomposite micro plates reinforced with graphene platelet in thermal ambient considering the structural damping. Int. J. Comp. Methods Eng. Sci. Mech. 2022, 23, 243–262. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Thai, C.H.; Nguyen-Xuan, H.; Nguyen-Thanh, N.; Le, T.H.; Nguyen-Thoi, T.; Rabczuk, T. Static, free vibration, and buckling analysis of laminated composite Reissner–Mindlin plates using NURBS-based isogeometric approach. Int. J. Numer. Methods Eng. 2012, 91, 571–603. [Google Scholar] [CrossRef]
- Thai, C.H.; Ferreira, A.J.M.; Bordas, S.P.A.; Rabczuk, T.; Nguyen-Xuan, H. Isogeometric analysis of laminated composite and sandwich plates using a new inverse trigonometric shear deformation theory. Eur. J. Mech. A 2014, 43, 89–108. [Google Scholar] [CrossRef]
- Thai, C.H.; Kulasegaram, S.; Tran, L.V.; Nguyen-Xuan, H. Generalized shear deformation theory for functionally graded isotropic and sandwich plates based on isogeometric approach. Compos. Struct. 2014, 141, 94–112. [Google Scholar] [CrossRef]
- Lu, P.; Zhang, P.Q.; Lee, H.P.; Wang, C.M.; Reddy, J.N. Non-local elastic plate theories. Proc. R. Soc. A 2007, 463, 3225–3240. [Google Scholar] [CrossRef]
- Duan, W.H.; Wang, C.M. Exact solutions for axisymmetric bending of micro/nanoscale circular plates based on nonlocal plate theory. Nanotechnology 2007, 18, 385704. [Google Scholar] [CrossRef]
- Aksencer, T.; Aydogdu, M. Levy type solution method for vibration and buckling of nanoplates using nonlocal elasticity theory. Phys. E Low Dimens. Syst. Nanostruct. 2011, 43, 954–959. [Google Scholar] [CrossRef]
- Pradhan, S.C.; Murmu, T. Small scale effect on the buckling of single-layered graphene sheets under biaxial compression via nonlocal continuum mechanics. Comput. Mater. Sci. 2009, 47, 268–274. [Google Scholar] [CrossRef]
- Pradhan, S.C.; Phadikar, J.K. Small scale effect on vibration of embedded multilayered graphene sheets based on nonlocal continuum models. Phys. Lett. A 2009, 373, 1062–1069. [Google Scholar] [CrossRef]
- Xu, X.; Karami, B.; Janghorban, M. On the dynamics of nanoshells. Int. J. Eng. Sci. 2021, 158, 103431. [Google Scholar] [CrossRef]
- Karami, B.; Janghorban, M.; Tounsi, A. Variational approach for wave dispersion in anisotropic doubly-curved nanoshells based on a new nonlocal strain gradient higher order shell theory. Thin Wall. Struct. 2018, 129, 251–264. [Google Scholar] [CrossRef]
- Karami, B.; Shahsavari, D. On the forced resonant vibration analysis of functionally graded polymer composite doubly-curved nanoshells reinforced with graphene-nanoplatelets. Comput. Methods Appl. Mech. Eng. 2020, 359, 112767. [Google Scholar] [CrossRef]
- Pradhan, S.C.; Phadikar, J.K. Nonlocal elasticity theory for vibration of nanoplates. J. Sound Vib. 2009, 325, 206–223. [Google Scholar] [CrossRef]
- Ansari, R.; Arash, B.; Rouhi, H. Vibration characteristics of embedded multilayered graphene sheets with different boundary conditions via nonlocal elasticity. Compos. Struct. 2011, 93, 2419–2429. [Google Scholar] [CrossRef]
- Ansari, R.; Sahmani, S.; Arash, B. Nonlocal plate model for free vibrations of single-layered graphene sheets. Phys. Let. A 2010, 375, 53–62. [Google Scholar] [CrossRef]
- Panyatong, M.; Chinnaboon, B.; Chucheepsakul, S. Free vibration analysis of FG nanoplates embedded in elastic medium based on second-order shear deformation plate theory and nonlocal elasticity. Compos. Struct. 2016, 153, 428–441. [Google Scholar] [CrossRef]
- Baratim, M.R.; Shahverdim, H. Nonlinear vibration of nonlocal four-variable graded plates with porosities implementing homotopy perturbation and Hamiltonian methods. Acta Mech. 2018, 229, 343–362. [Google Scholar] [CrossRef]
- Aghababaei, R.; Reddy, J.N. Nonlocal third-order shear deformation plate theory with application to bending and vibration of plates. J. Sound Vib. 2009, 326, 277–289. [Google Scholar] [CrossRef]
- Daneshmehr, A.; Rajabpoor, A.; Hadi, A. Size dependent free vibration analysis of nanoplates made of functionally graded materials based on nonlocal elasticity theory with high order theories. Int. J. Eng. Sci. 2015, 95, 23–35. [Google Scholar] [CrossRef]
- Natarajan, S.; Chakraborty, S.; Thangavel, M.; Bordas, S.; Rabczuk, T. Sizedependent free flexural vibration behavior of functionally graded nanoplates. Comput. Mater. Sci. 2012, 65, 74–80. [Google Scholar] [CrossRef]
- Cutolo, A.; Mallardo, V.; Fraldi, M. Third-order nonlocal elasticity in buckling and vibration of functionally graded nanoplates on Winkler-Pasternak media. Ann. Solid Struct. Mech. 2020, 12, 141–154. [Google Scholar] [CrossRef]
- Phung Van, P.; Lieu, X.Q.; Ferreira, A.J.M.; Thai, C.H. A refined nonlocal isogeometric model for multilayer functionally graded graphene platelet-reinforced composite nanoplates. Compos. Struct. 2021, 164, 107862. [Google Scholar] [CrossRef]
- Xie, J.; Li, J.; Zhen, L.; Zhang, C.; Mohammadi, R. A novel nonlocal higher-order theory for the accurate vibration analysis of 2D FG nanoplates. Proc. Inst. Mech. Eng. Part C 2022, 236, 2161–2171. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Shojaee, M. Free vibration of nanoplates based on a nonlocal two-variable refined plate theory. Compos. Struct. 2013, 95, 443–452. [Google Scholar] [CrossRef]
- Sobhy, M.; Radwan, A.F. A New Quasi 3D Nonlocal Plate Theory for Vibration and Buckling of FGM Nanoplates. Int. J. Appl. Mech. 2017, 9, 1750008. [Google Scholar] [CrossRef]
- Kiani, Y.; Mirzaei, M. Isogeometric thermal postbuckling of FG-GPLRC laminated plates. Steel Comp. Struct. 2019, 32, 821–832. [Google Scholar]
- Kiani, Y. NURBS-based thermal buckling analysis of graphene platelet reinforced composite laminated skew plates. J. Therm. Stress. 2020, 43, 90–108. [Google Scholar] [CrossRef]
- Shaoping, B.; Zhang, E.; Babaei, M.; Tornabene, F.; Dimitri, R. The Influence of GPL Reinforcements on the Post-Buckling Behavior of FG Porous Rings Subjected to an External Pressure. Mathematics 2023, 11, 2421. [Google Scholar]
- Ebrahimi, F.; Ezzati, H. A Machine-Learning-Based Model for Buckling Analysis of Thermally Affected Covalently Functionalized Graphene/Epoxy Nanocomposite Beams. Mathematics 2023, 11, 1496. [Google Scholar] [CrossRef]
- Melaibari, A.; Daikh, A.A.; Basha, M.; Abdalla, A.W.; Othman, R.; Almitani, K.H.; Hamed, M.A.; Abdelrahman, A.; Elthaher, M.A. Free Vibration of FG-CNTRCs Nano-Plates/Shells with Temperature-Dependent Properties. Mathematics 2022, 10, 583. [Google Scholar] [CrossRef]
- Melaibari, A.; Daikh, A.A.; Basha, M.; Wagih, A.; Othman, R.; Almitani, K.H.; Hamed, M.A.; Abdelrahman, A.; Elthaher, M.A. A Dynamic Analysis of Randomly Oriented Functionally Graded Carbon Nanotubes/Fiber-Reinforced Composite Laminated Shells with Different Geometries. Mathematics 2022, 10, 408. [Google Scholar] [CrossRef]
- Avey, M.; Fantuzzi, N.; Sofiyev, A. Mathematical Modeling and Analytical Solution of Thermoelastic Stability Problem of Functionally Graded Nanocomposite Cylinders within Different Theories. Mathematics 2022, 10, 1081. [Google Scholar] [CrossRef]
- Animasaun, I.L.; Oke, A.S.; Al-Mdallal, Q.M.; Zidan, A.M. Exploration of water conveying carbon nanotubes, graphene, and copper nanoparticles on impermeable stagnant and moveable walls experiencing variable temperature: Thermal analysis. J. Therm. Anal. Calorim. 2023, 148, 4513–4522. [Google Scholar] [CrossRef]

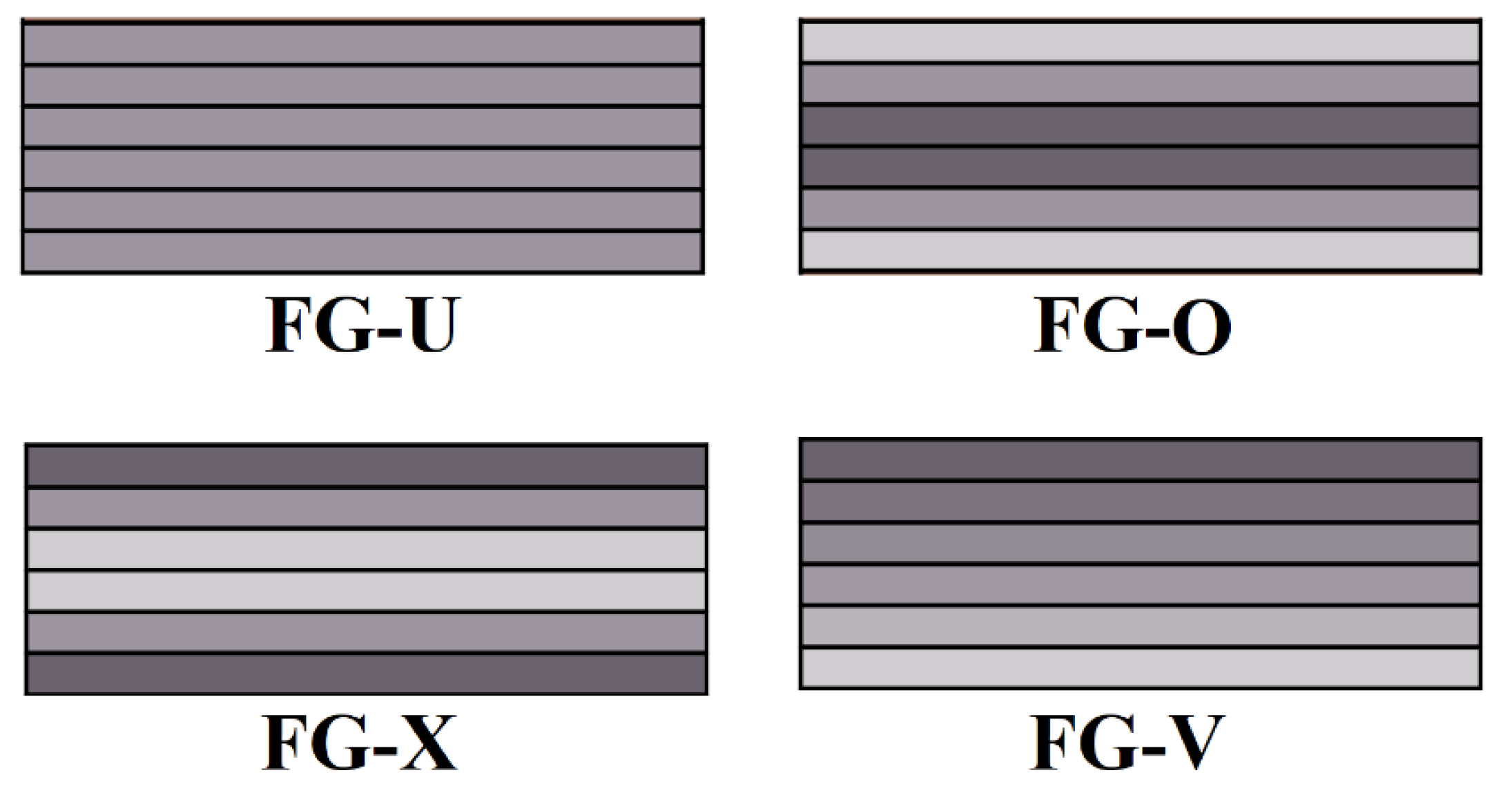
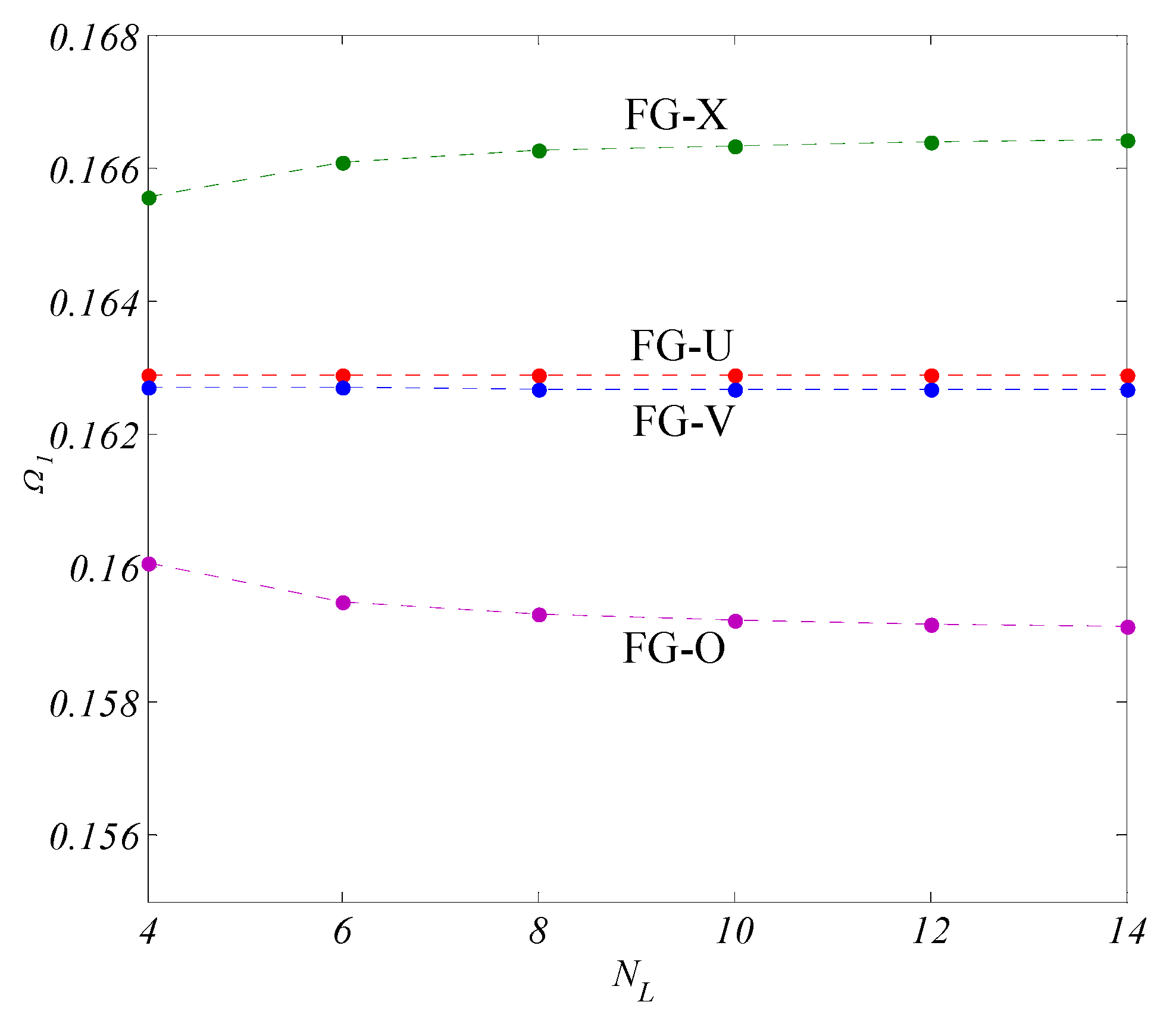
| Property Name | Epoxy | GPLs |
|---|---|---|
| Modulus of elasticity (E) [GPa] | 3 | 1010 |
| Density () [kg/m3] | 1200 | 1062.5 |
| Poisson’s ratio (ν) | 0.34 | 0.186 |
| Two-Variable Model | Four-Variable 2D Model | Four-Variable 3D Model | Present | ||
|---|---|---|---|---|---|
| 10 | 0 | 0.093029 | 0.093031 | 0.093228 | 0.093151 |
| 0.01 | 0.085016 | 0.085017 | 0.085197 | 0.085127 | |
| 0.02 | 0.078771 | 0.078772 | 0.078939 | 0.078874 | |
| 0.03 | 0.073726 | 0.073728 | 0.073884 | 0.073823 | |
| 20 | 0 | 0.023864 | 0.023864 | 0.023895 | 0.023872 |
| 0.01 | 0.021808 | 0.021808 | 0.021837 | 0.021816 | |
| 0.02 | 0.020206 | 0.020206 | 0.020233 | 0.020213 | |
| 0.03 | 0.018912 | 0.018912 | 0.018937 | 0.018919 |
| a/h | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Present | [44] | Present | [44] | Present | [44] | Present | [44] | ||
| 5 | Pure | 0.2143 | 0.2132 | 0.1959 | 0.1948 | 0.1698 | 0.1690 | 0.1520 | 0.1513 |
| UD | 0.2296 | 0.2285 | 0.2099 | 0.2088 | 0.1820 | 0.1811 | 0.1629 | 0.1621 | |
| FG-X | 0.2345 | 0.2326 | 0.2143 | 0.2126 | 0.1858 | 0.1843 | 0.1663 | 0.1650 | |
| FG-O | 0.2244 | 0.2241 | 0.2051 | 0.2048 | 0.1779 | 0.1776 | 0.1592 | 0.1590 | |
| FG-V | 0.2293 | 0.2281 | 0.2096 | 0.2085 | 0.1817 | 0.1808 | 0.1627 | 0.1618 | |
| 10 | Pure | 0.0585 | 0.0584 | 0.0535 | 0.0534 | 0.0464 | 0.0463 | 0.0415 | 0.0415 |
| UD | 0.0627 | 0.0626 | 0.0573 | 0.0572 | 0.0497 | 0.0496 | 0.0445 | 0.0444 | |
| FG-X | 0.0644 | 0.0641 | 0.0589 | 0.0585 | 0.0511 | 0.0508 | 0.0457 | 0.0454 | |
| FG-O | 0.0609 | 0.0611 | 0.0557 | 0.0559 | 0.0483 | 0.0484 | 0.0432 | 0.0434 | |
| FG-V | 0.0626 | 0.0625 | 0.0572 | 0.0571 | 0.0496 | 0.0495 | 0.0444 | 0.0443 | |
| 50 | Pure | 0.0024 | 0.0024 | 0.0022 | 0.0022 | 0.0019 | 0.0019 | 0.0017 | 0.0017 |
| UD | 0.0026 | 0.0026 | 0.0024 | 0.0024 | 0.0021 | 0.0021 | 0.0018 | 0.0019 | |
| FG-X | 0.0027 | 0.0027 | 0.0024 | 0.0024 | 0.0021 | 0.0021 | 0.0019 | 0.0019 | |
| FG-O | 0.0025 | 0.0025 | 0.0023 | 0.0023 | 0.0020 | 0.0020 | 0.0018 | 0.0018 | |
| FG-V | 0.0026 | 0.0026 | 0.0024 | 0.0024 | 0.0021 | 0.0021 | 0.0018 | 0.0019 | |
| Distribution Pattern | ||||||
|---|---|---|---|---|---|---|
| FG-U | 4 | 0.16290(1,1) | 0.26997(2,1) | 0.32713(2,2) | 0.35315(3,1) | 0.38218(3,2) |
| 6 | 0.16290(1,1) | 0.26997(2,1) | 0.32713(2,2) | 0.35315(1,3) | 0.38218(2,3) | |
| 8 | 0.16290(1,1) | 0.26997(2,1) | 0.32713(2,2) | 0.35315(1,3) | 0.38218(2,3) | |
| 10 | 0.16290(1,1) | 0.26997(1,2) | 0.32713(2,2) | 0.35315(3,1) | 0.38218(2,3) | |
| 12 | 0.16290(1,1) | 0.26997(2,1) | 0.32713(2,2) | 0.35315(3,1) | 0.38218(3,2) | |
| 14 | 0.16290(1,1) | 0.26997(1,2) | 0.32713(2,2) | 0.35315(3,1) | 0.38218(3,2) | |
| FG-X | 4 | 0.16557(1,1) | 0.27267(2,1) | 0.32912(2,2) | 0.35462(1,3) | 0.38291(3,2) |
| 6 | 0.16608(1,1) | 0.27323(2,1) | 0.32960(2,2) | 0.35503(1,3) | 0.38323(2,3) | |
| 8 | 0.16626(1,1) | 0.27343(2,1) | 0.32977(2,2) | 0.35518(1,3) | 0.38336(3,2) | |
| 10 | 0.16634(1,1) | 0.27353(2,1) | 0.32986(2,2) | 0.35526(1,3) | 0.38342(2,3) | |
| 12 | 0.16639(1,1) | 0.27358(1,2) | 0.32990(2,2) | 0.35530(3,1) | 0.38345(2,3) | |
| 14 | 0.16642(1,1) | 0.27361(2,1) | 0.32993(2,2) | 0.35533(1,3) | 0.38347(3,2) | |
| FG-O | 4 | 0.16008(1,1) | 0.26690(2,1) | 0.32464(2,2) | 0.35112(1,3) | 0.38083(3,2) |
| 6 | 0.15950(1,1) | 0.26619(1,2) | 0.32397(2,2) | 0.35049(1,3) | 0.38027(2,3) | |
| 8 | 0.15930(1,1) | 0.26593(2,1) | 0.32371(2,2) | 0.35025(3,1) | 0.38005(3,2) | |
| 10 | 0.15921(1,1) | 0.26581(2,1) | 0.32360(2,2) | 0.35014(3,1) | 0.37995(3,2) | |
| 12 | 0.15915(1,1) | 0.26575(2,1) | 0.32353(2,2) | 0.35008(1,3) | 0.37989(3,2) | |
| 14 | 0.15912(1,1) | 0.26571(1,2) | 0.32349(2,2) | 0.35004(3,1) | 0.37985(3,2) | |
| FG-V | 4 | 0.16271(1,1) | 0.26970(2,1) | 0.32685(2,2) | 0.35287(3,1) | 0.38190(3,2) |
| 6 | 0.16270(1,1) | 0.26968(1,2) | 0.32682(2,2) | 0.35284(1,3) | 0.38188(3,2) | |
| 8 | 0.16269(1,1) | 0.26967(2,1) | 0.32681(2,2) | 0.35283(3,1) | 0.38187(2,3) | |
| 10 | 0.16269(1,1) | 0.26967(2,1) | 0.32681(2,2) | 0.35282(1,3) | 0.38186(3,2) | |
| 12 | 0.16269(1,1) | 0.26966(2,1) | 0.32681(2,2) | 0.35282(3,1) | 0.38186(3,2) | |
| 14 | 0.16269(1,1) | 0.26966(1,2) | 0.32680(2,2) | 0.35282(1,3) | 0.38186(3,2) |
| Distribution Pattern | ||||||
|---|---|---|---|---|---|---|
| FG-U | 0 | 0.22207(1,1) | 0.48611(1,2) | 0.56274(1,1) | 0.7036(2,2) | 0.83186(3,1) |
| 0.01 | 0.20294(1,1) | 0.39777(2,1) | 0.51427(1,1) | 0.52596(2,2) | 0.59014(3,1) | |
| 0.02 | 0.18803(1,1) | 0.34486(2,1) | 0.43812(2,2) | 0.47649(1,1) | 0.48237(3,1) | |
| 0.03 | 0.17599(1,1) | 0.30865(1,2) | 0.38335(2,2) | 0.41798(3,1) | 0.41798(1,3) | |
| 0.04 | 0.16600(1,1) | 0.28188(1,2) | 0.34504(2,2) | 0.37397(3,1) | 0.37397(1,3) | |
| 0.05 | 0.15754(1,1) | 0.26106(1,2) | 0.31631(2,2) | 0.34146(3,1) | 0.34146(1,3) | |
| FG-X | 0 | 0.22459(1,1) | 0.48963(2,1) | 0.56278(1,1) | 0.70691(2,2) | 0.83474(3,1) |
| 0.01 | 0.20524(1,1) | 0.40066(1,2) | 0.51430(1,1) | 0.52844(2,2) | 0.59218(1,3) | |
| 0.02 | 0.19017(1,1) | 0.34736(2,1) | 0.44018(2,2) | 0.47652(1,1) | 0.48405(3,1) | |
| 0.03 | 0.17799(1,1) | 0.31089(2,1) | 0.38515(2,2) | 0.41943(1,3) | 0.41943(3,1) | |
| 0.04 | 0.16789(1,1) | 0.28393(1,2) | 0.34667(2,2) | 0.37527(1,3) | 0.37527(3,1) | |
| 0.05 | 0.15933(1,1) | 0.26295(1,2) | 0.31780(2,2) | 0.34265(3,1) | 0.34265(1,3) | |
| FG-O | 0 | 0.21944(1,1) | 0.48228(2,1) | 0.56278(1,1) | 0.69979(2,2) | 0.82837(3,1) |
| 0.01 | 0.20054(1,1) | 0.39464(2,1) | 0.51430(1,1) | 0.52311(2,2) | 0.58766(3,1) | |
| 0.02 | 0.18581(1,1) | 0.34214(2,1) | 0.43574(2,2) | 0.47652(1,1) | 0.48035(1,3) | |
| 0.03 | 0.17391(1,1) | 0.30622(2,1) | 0.38127(2,2) | 0.41622(3,1) | 0.41622(1,3) | |
| 0.04 | 0.16404(1,1) | 0.27966(2,1) | 0.34317(2,2) | 0.37240(3,1) | 0.37240(1,3) | |
| 0.05 | 0.15568(1,1) | 0.25900(1,2) | 0.31460(2,2) | 0.34003(3,1) | 0.34003(1,3) | |
| FG-V | 0 | 0.22198(1,1) | 0.48596(1,2) | 0.56274(1,1) | 0.70340(2,2) | 0.83164(3,1) |
| 0.01 | 0.20286(1,1) | 0.39765(1,2) | 0.51427(1,1) | 0.52581(2,2) | 0.58998(3,1) | |
| 0.02 | 0.18796(1,1) | 0.34475(1,2) | 0.43799(2,2) | 0.47649(1,1) | 0.48225(1,3) | |
| 0.03 | 0.17592(1,1) | 0.30856(1,2) | 0.38324(2,2) | 0.41787(3,1) | 0.41787(1,3) | |
| 0.04 | 0.16594(1,1) | 0.28179(2,1) | 0.34494(2,2) | 0.37388(1,3) | 0.37388(3,1) | |
| 0.05 | 0.15748(1,1) | 0.26097(2,1) | 0.31622(2,2) | 0.34137(1,3) | 0.34137(3,1) |
| Distribution Pattern | ||||||
|---|---|---|---|---|---|---|
| FG-U | 0.0 | 0.15204(1,1) | 0.25192(1,2) | 0.30523(2,2) | 0.32949(3,1) | 0.35656(2,3) |
| 0.2 | 0.15426(1,1) | 0.25560(1,2) | 0.30970(2,2) | 0.33432(1,3) | 0.36178(2,3) | |
| 0.4 | 0.15645(1,1) | 0.25925(2,1) | 0.31412(2,2) | 0.33909(1,3) | 0.36695(2,3) | |
| 0.6 | 0.15862(1,1) | 0.26286(1,2) | 0.31850(2,2) | 0.34382(3,1) | 0.37208(2,3) | |
| 0.8 | 0.16077(1,1) | 0.26643(2,1) | 0.32283(2,2) | 0.34851(1,3) | 0.37715(2,3) | |
| 1.0 | 0.16290(1,1) | 0.26997(1,2) | 0.32713(2,2) | 0.35315(3,1) | 0.38218(3,2) | |
| FG-X | 0.0 | 0.15204(1,1) | 0.25192(1,2) | 0.30523(2,2) | 0.32949(3,1) | 0.35656(2,3) |
| 0.2 | 0.15499(1,1) | 0.25639(2,1) | 0.31033(2,2) | 0.33483(1,3) | 0.36212(2,3) | |
| 0.4 | 0.15789(1,1) | 0.26078(1,2) | 0.31533(2,2) | 0.34006(1,3) | 0.36758(2,3) | |
| 0.6 | 0.16075(1,1) | 0.26510(1,2) | 0.32025(2,2) | 0.34521(3,1) | 0.37294(3,2) | |
| 0.8 | 0.16357(1,1) | 0.26934(1,2) | 0.32509(2,2) | 0.35027(1,3) | 0.37822(3,2) | |
| 1.0 | 0.16634(1,1) | 0.27353(2,1) | 0.32986(2,2) | 0.35526(1,3) | 0.38342(3,2) | |
| FG-O | 0.0 | 0.15204(1,1) | 0.25192(1,2) | 0.30523(2,2) | 0.32949(3,1) | 0.35656(2,3) |
| 0.2 | 0.15351(1,1) | 0.25479(1,2) | 0.30903(2,2) | 0.33376(3,1) | 0.36140(3,2) | |
| 0.4 | 0.15496(1,1) | 0.25761(1,2) | 0.31276(2,2) | 0.33796(1,3) | 0.36615(3,2) | |
| 0.6 | 0.15639(1,1) | 0.26038(2,1) | 0.31643(2,2) | 0.34208(3,1) | 0.37083(3,2) | |
| 0.8 | 0.15780(1,1) | 0.26311(2,1) | 0.32004(2,2) | 0.34614(1,3) | 0.37542(3,2) | |
| 1.0 | 0.15921(1,1) | 0.26581(2,1) | 0.32360(2,2) | 0.35014(3,1) | 0.37995(2,3) | |
| FG-V | 0.0 | 0.15204(1,1) | 0.25192(1,2) | 0.30523(2,2) | 0.32949(3,1) | 0.35656(2,3) |
| 0.2 | 0.15424(1,1) | 0.25559(2,1) | 0.30968(2,2) | 0.33430(3,1) | 0.36177(2,3) | |
| 0.4 | 0.15641(1,1) | 0.25919(1,2) | 0.31406(2,2) | 0.33903(3,1) | 0.36690(3,2) | |
| 0.6 | 0.15854(1,1) | 0.26274(1,2) | 0.31837(2,2) | 0.34370(3,1) | 0.37195(3,2) | |
| 0.8 | 0.16063(1,1) | 0.26623(2,1) | 0.32262(2,2) | 0.34829(3,1) | 0.37694(3,2) | |
| 1.0 | 0.16269(1,1) | 0.26967(2,1) | 0.32681(2,2) | 0.35282(1,3) | 0.38186(2,3) |
| Distribution Pattern | ||||||
|---|---|---|---|---|---|---|
| FG-U | 2 | 0.731410(1,1) | 1.051700(1,1) | 1.052500(2,1) | 1.193100(2,2) | 1.289900(2,1) |
| 5 | 0.166000(1,1) | 0.281880(1,2) | 0.345040(2,2) | 0.373970(3,1) | 0.406340(3,2) | |
| 10 | 0.045327(1,1) | 0.083897(1,2) | 0.108900(2,2) | 0.121660(1,3) | 0.137130(2,3) | |
| 50 | 0.001874(1,1) | 0.003627(1,2) | 0.004897(2,2) | 0.005604(1,3) | 0.006530(2,3) | |
| FG-X | 2 | 0.733050(1,1) | 1.050200(2,1) | 1.051700(1,1) | 1.188800(2,2) | 1.290000(2,1) |
| 5 | 0.167890(1,1) | 0.283930(1,2) | 0.346670(2,2) | 0.375270(1,3) | 0.407170(3,2) | |
| 10 | 0.045996(1,1) | 0.084978(2,1) | 0.110140(2,2) | 0.122930(1,3) | 0.138420(2,3) | |
| 50 | 0.001905(1,1) | 0.003686(2,1) | 0.004976(2,2) | 0.005693(3,1) | 0.006634(3,2) | |
| FG-O | 2 | 0.729240(1,1) | 1.051700(1,1) | 1.054100(1,2) | 1.196700(2,2) | 1.290000(2,1) |
| 5 | 0.164040(1,1) | 0.279660(2,1) | 0.343170(2,2) | 0.372400(3,1) | 0.405220(3,2) | |
| 10 | 0.044647(1,1) | 0.082784(2,1) | 0.107610(2,2) | 0.120320(1,3) | 0.135770(3,2) | |
| 50 | 0.001844(1,1) | 0.003568(2,1) | 0.004818(2,2) | 0.005514(1,3) | 0.006425(3,2) | |
| FG-V | 2 | 0.731240(1,1) | 1.051300(1,1) | 1.052300(1,2) | 1.193000(2,2) | 1.288700(1,2) |
| 5 | 0.165940(1,1) | 0.281790(2,1) | 0.344940(2,2) | 0.373880(1,3) | 0.406250(2,3) | |
| 10 | 0.045308(1,1) | 0.083864(1,2) | 0.108860(2,2) | 0.121610(3,1) | 0.137090(2,3) | |
| 50 | 0.001874(1,1) | 0.003626(2,1) | 0.004895(2,2) | 0.005602(1,3) | 0.006527(3,2) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, Y.; Kiani, Y. Vibrations of Nonlocal Polymer-GPL Plates at Nanoscale: Application of a Quasi-3D Plate Model. Mathematics 2023, 11, 4109. https://doi.org/10.3390/math11194109
Zou Y, Kiani Y. Vibrations of Nonlocal Polymer-GPL Plates at Nanoscale: Application of a Quasi-3D Plate Model. Mathematics. 2023; 11(19):4109. https://doi.org/10.3390/math11194109
Chicago/Turabian StyleZou, Yunhe, and Yaser Kiani. 2023. "Vibrations of Nonlocal Polymer-GPL Plates at Nanoscale: Application of a Quasi-3D Plate Model" Mathematics 11, no. 19: 4109. https://doi.org/10.3390/math11194109
APA StyleZou, Y., & Kiani, Y. (2023). Vibrations of Nonlocal Polymer-GPL Plates at Nanoscale: Application of a Quasi-3D Plate Model. Mathematics, 11(19), 4109. https://doi.org/10.3390/math11194109







