The Influence of GPL Reinforcements on the Post-Buckling Behavior of FG Porous Rings Subjected to an External Pressure
Abstract
1. Introduction
2. Theoretical Formulation
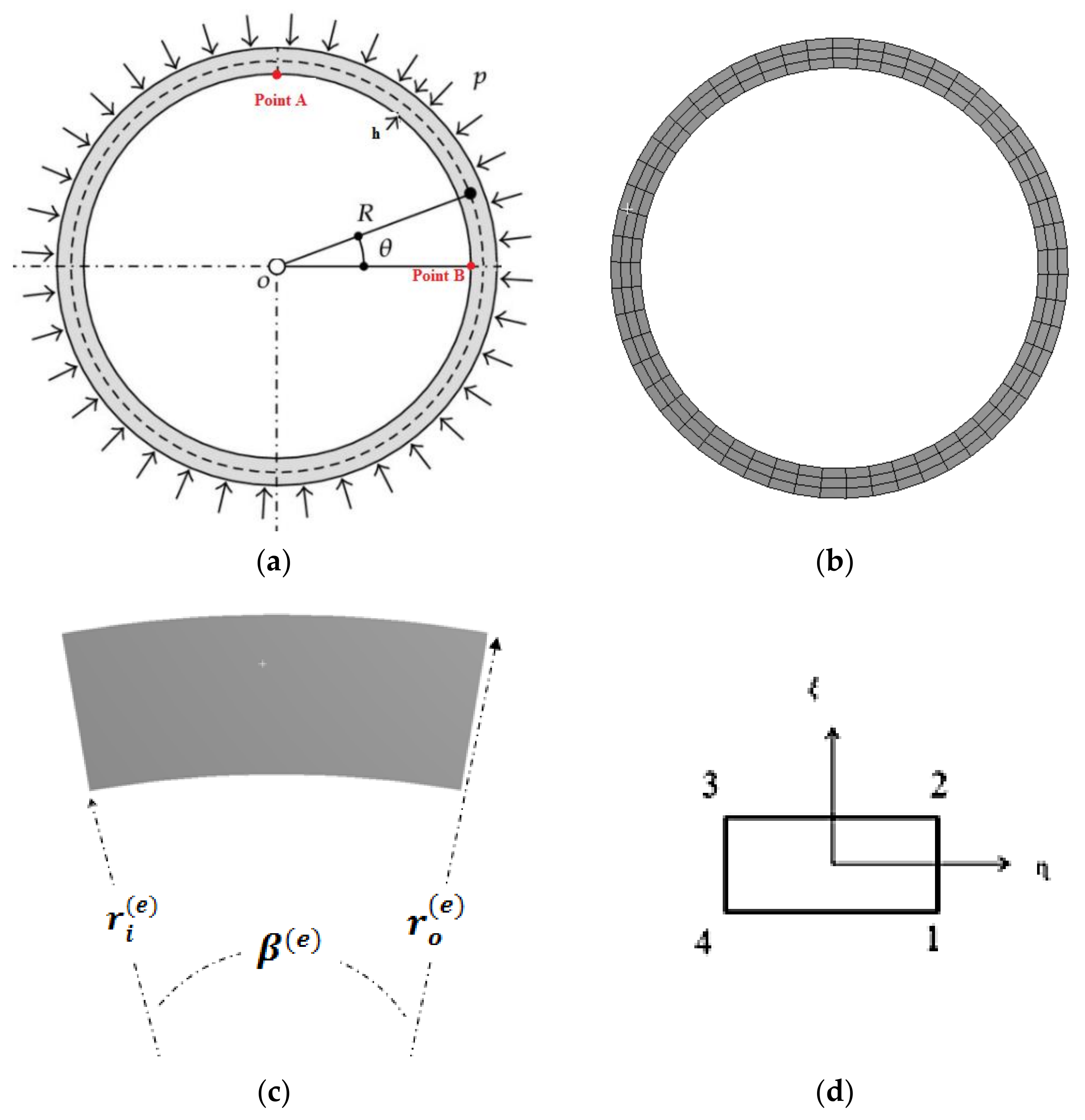
2.1. Description of the Geometry
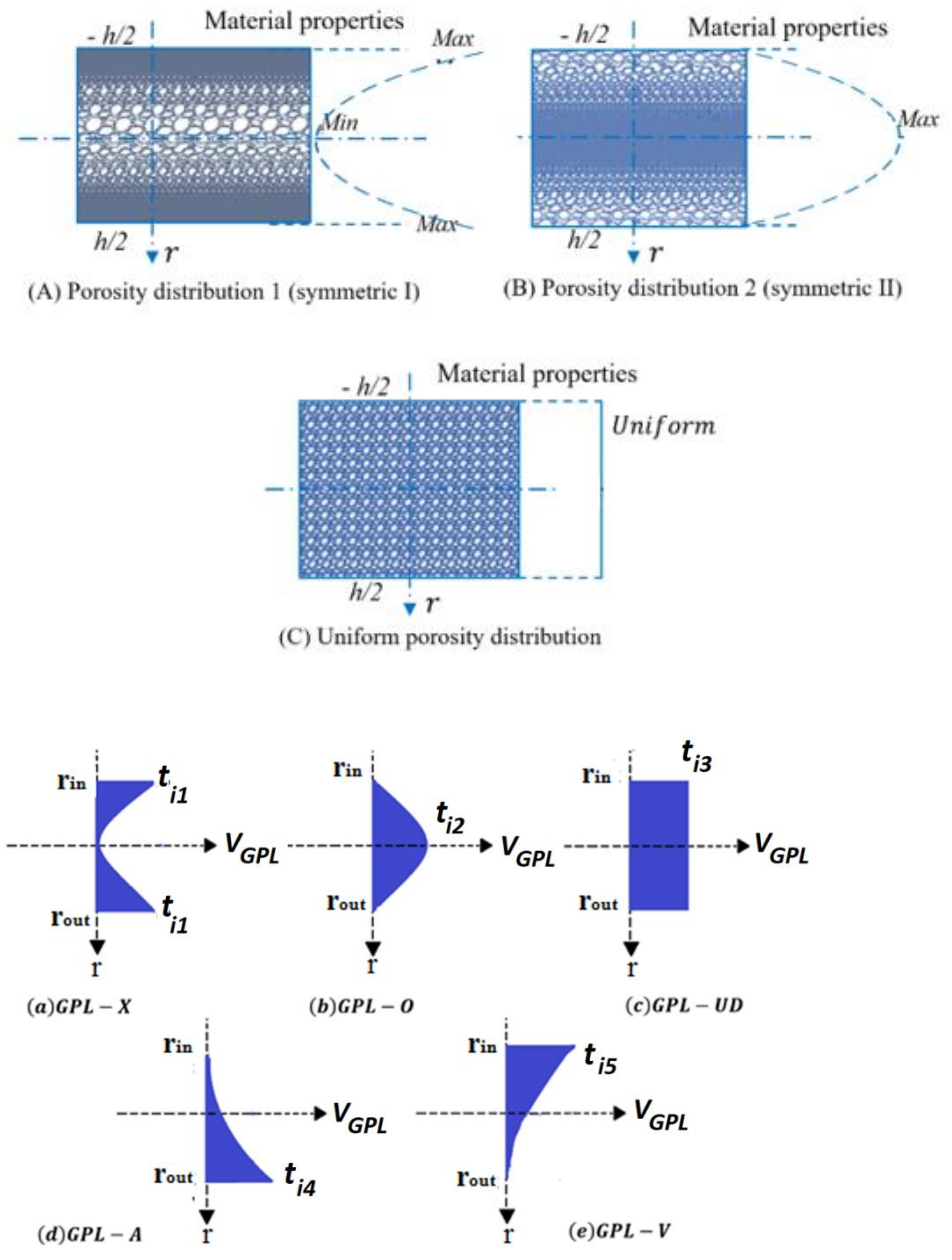
2.2. Obtaining the Effective Mechanical Properties of the Ring
2.3. Stress–Strain Relation
3. Finite Element Modelling
4. Numerical Results and Discussion
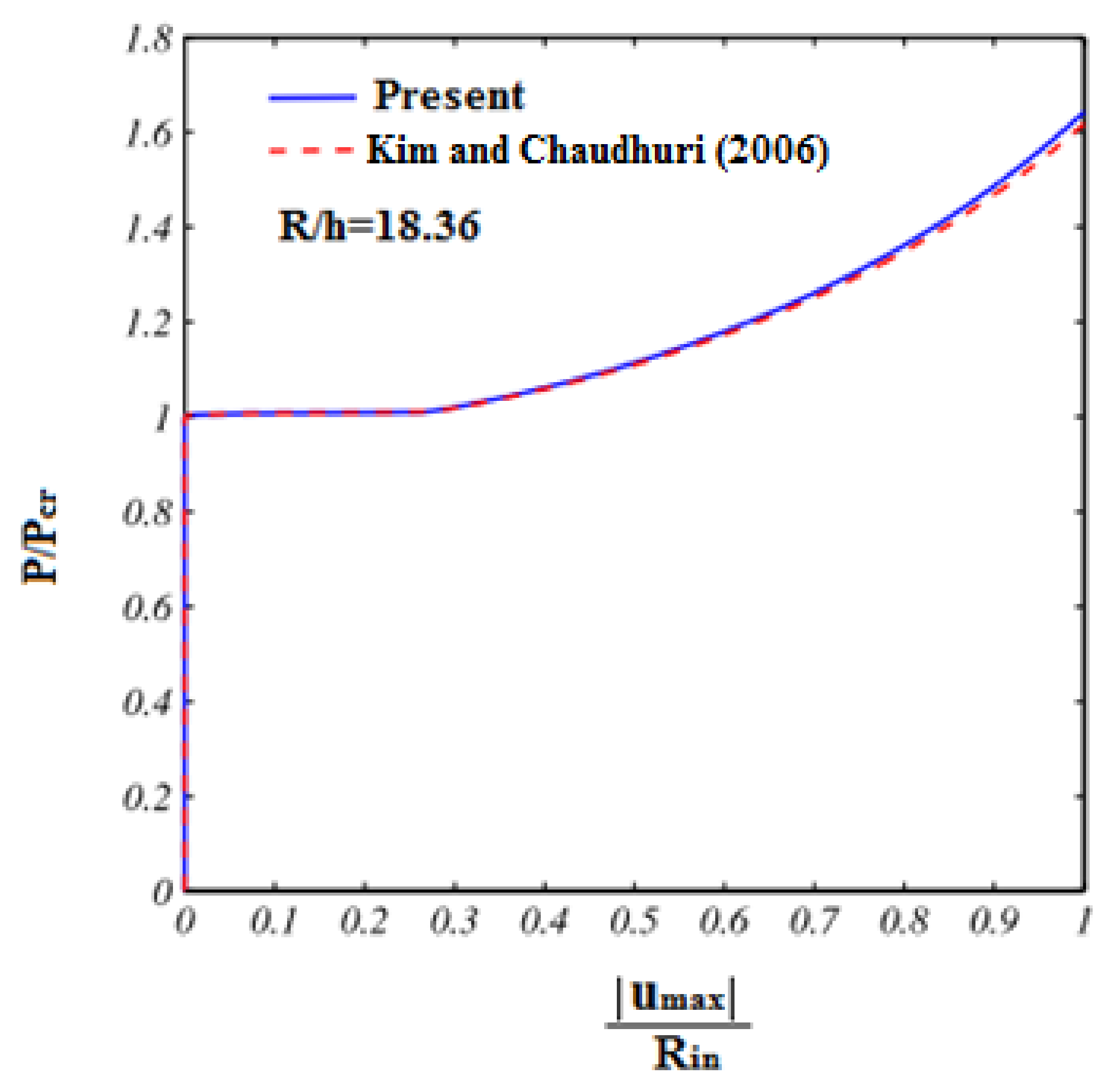
4.1. Validation of the Present Study
4.2. Post-Buckling Behavior of FG-GPL Porous Ring
4.2.1. The Effect of GPLs Distributions and Weight Fractions
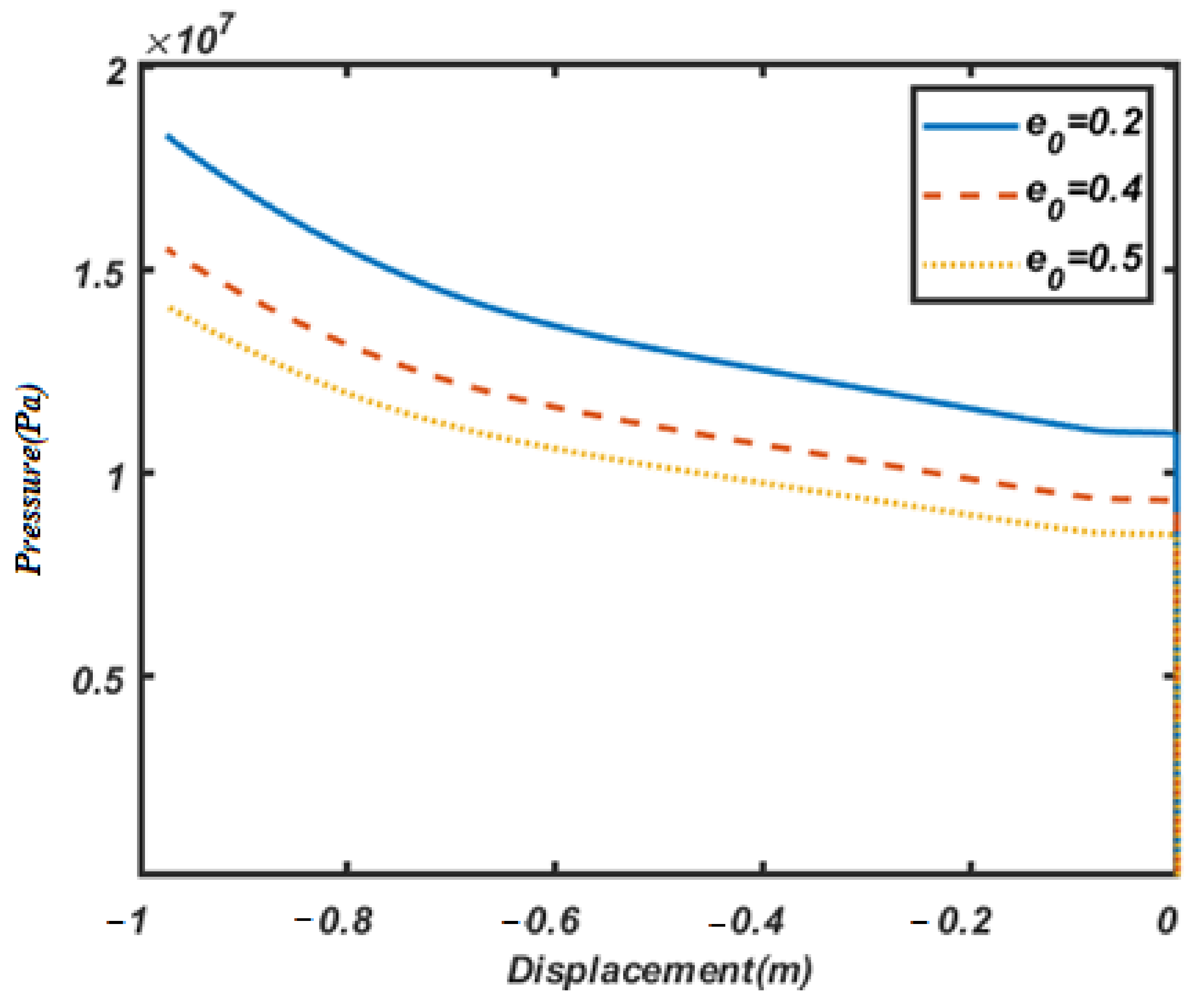
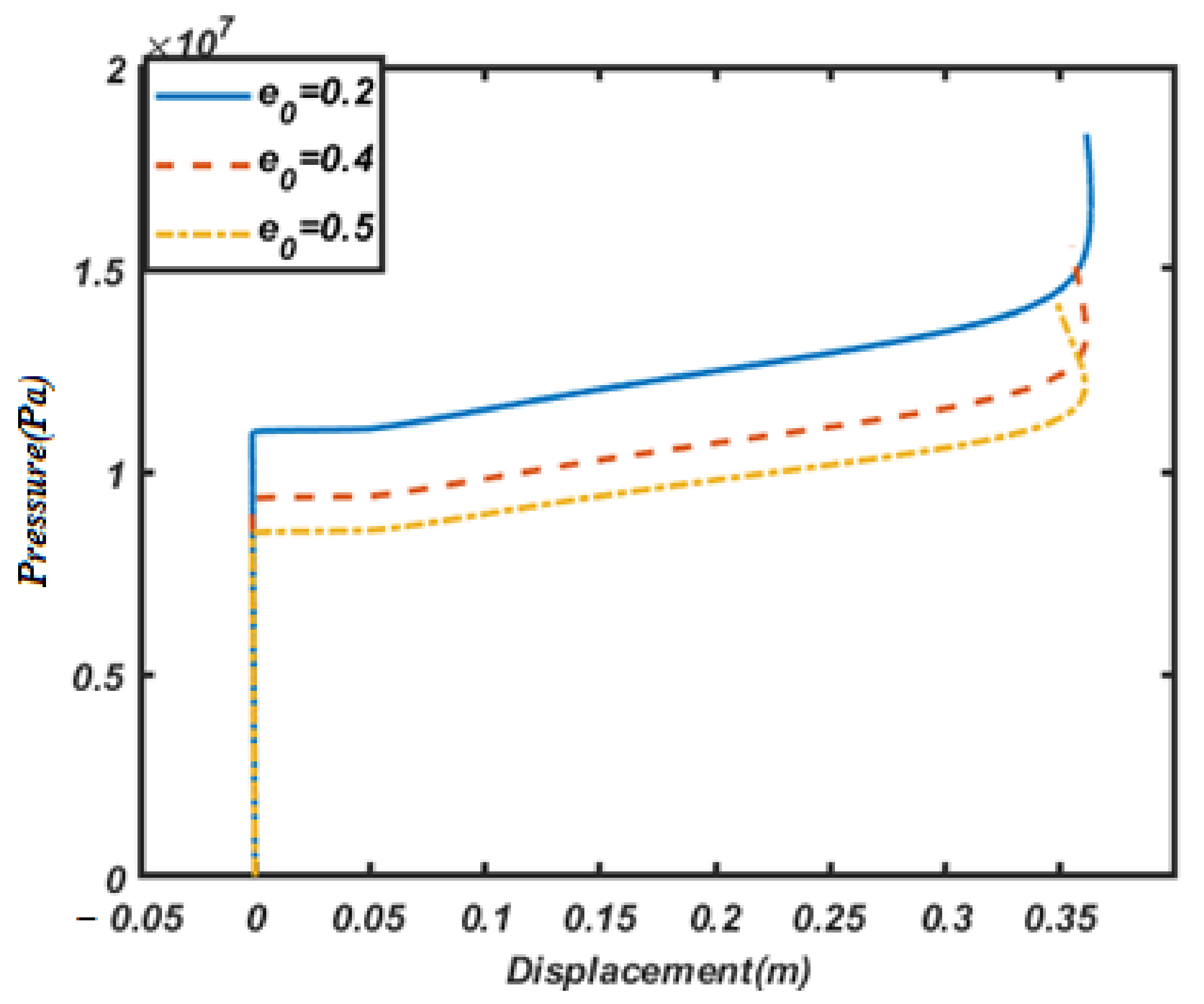
4.2.2. The Effect of Porosity Distribution and Coefficient of Porosity
5. Conclusions
- The maximum and minimum buckling loads and post-buckling strength of the ring belong to GPLX and GPL-O distributions. Besides, for GPL-V and GPL-O, the buckling load values and post-buckling paths are approximately the same;
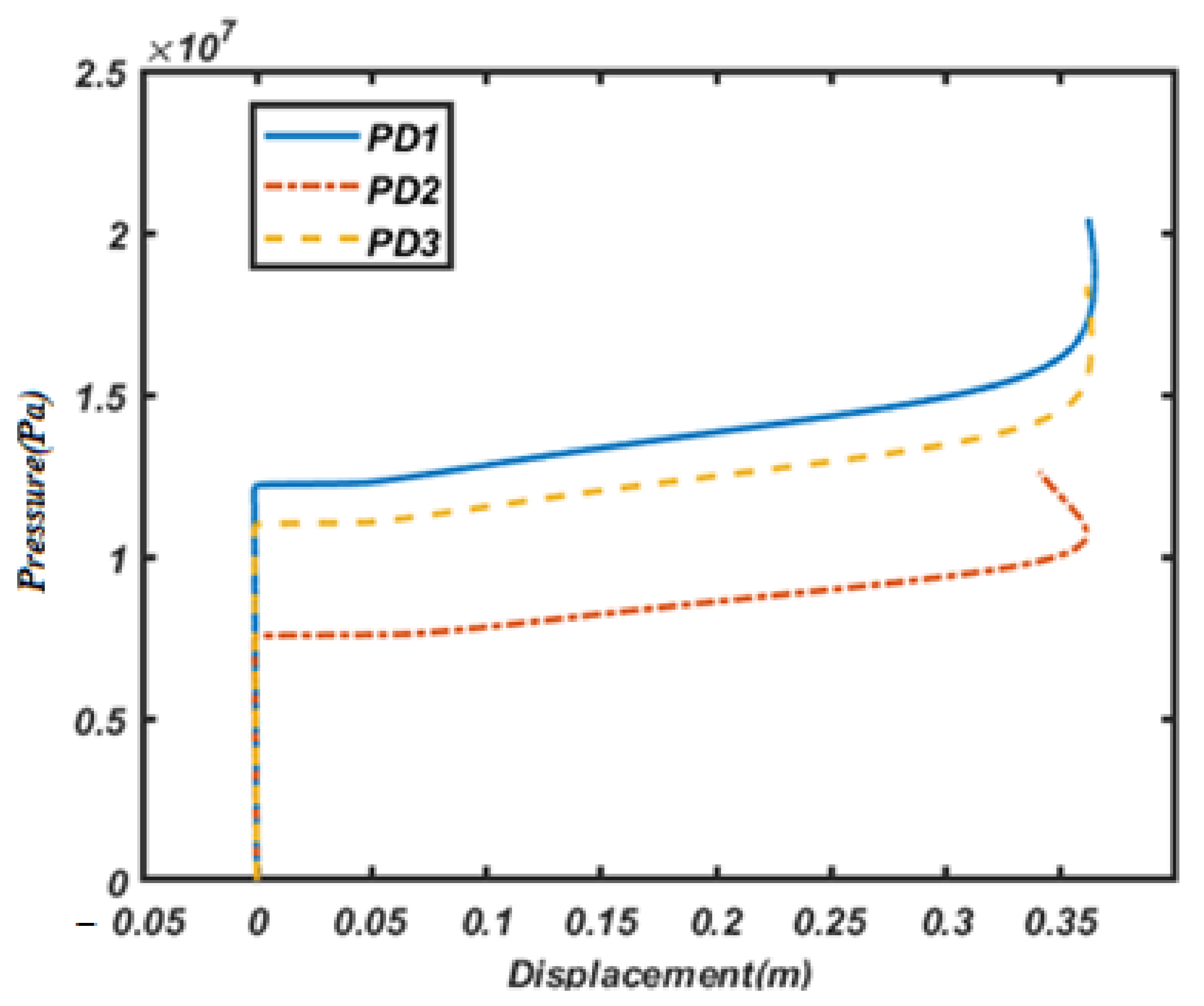
- The maximum and minimum buckling loads and post-buckling strength of the ring belong to PD1 and PD2, respectively;
- The impact of porosity distribution on the buckling load and post-buckling path is more pronounced than the effect of weight fractions of nanofillers;
- By increasing the weight fraction of nanofiller about 1%, the buckling value and post-buckling strength considerably increase (by approximately 80%);
- By increasing the porosity coefficient from 0.2 to 0.5, the buckling load and post-buckling strength decreases (by approximately 28%);
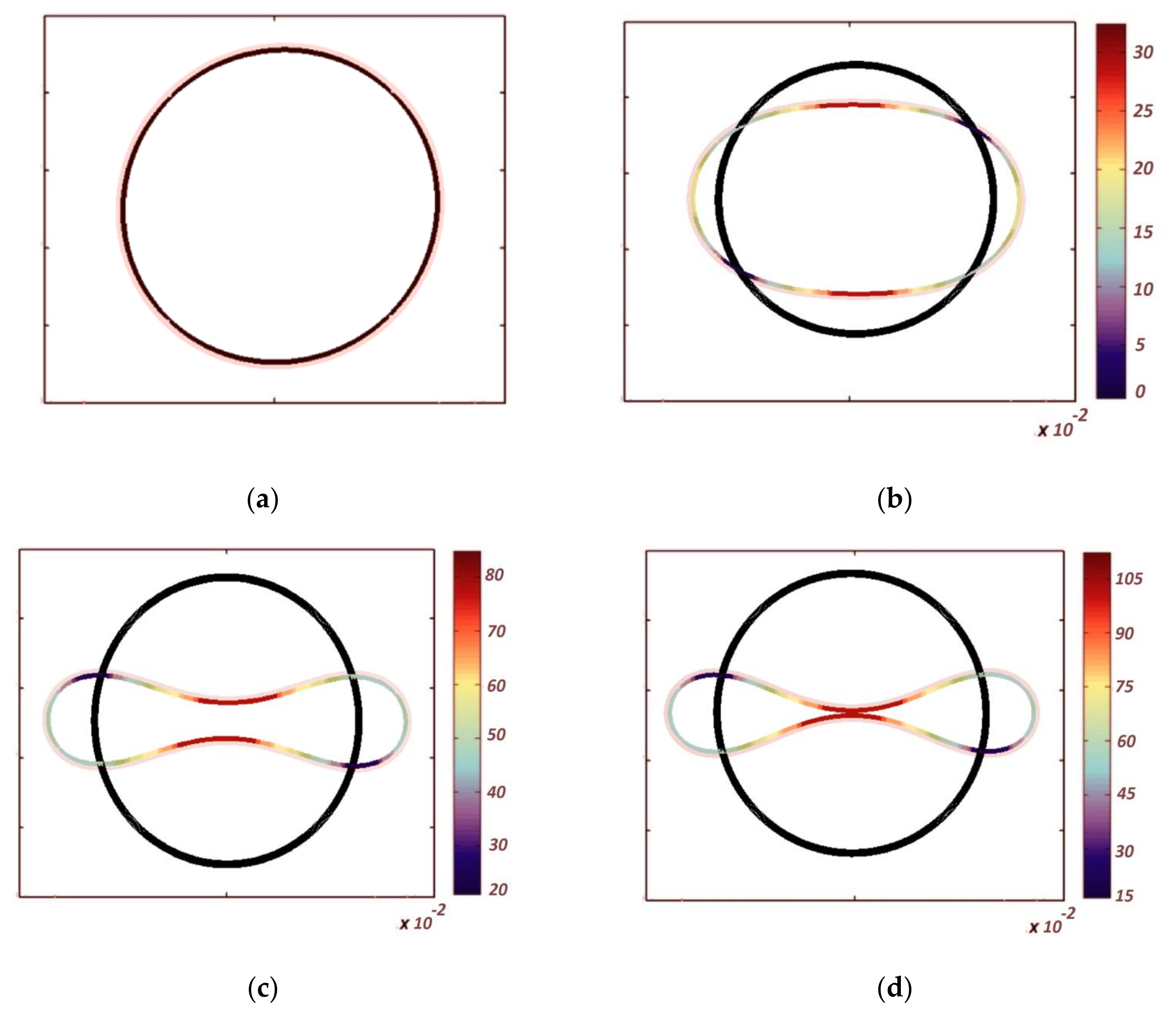
- The behavior of the post-buckling path of the ring may vary from one point to another.
Author Contributions
Funding
Conflicts of Interest
References
- Wah, T. Buckling of thin circular rings under uniform pressure. Int. J. Solids Struct. 1967, 3, 967–974. [Google Scholar] [CrossRef]
- Hazel, A.L.; Mullin, T. On the buckling of elastic rings by external confinement. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2017, 375, 20160227. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Azzuni, E.; Guzey, S. A perturbation approach on buckling and postbuckling of circular rings under nonuniform loads. Int. J. Mech. Sci. 2018, 137, 86–95. [Google Scholar] [CrossRef]
- Seide, P.; Weingarten, V.I. Buckling of circular rings and long cylinders enclosing an elastic material under uniform external pressure. ARS J. 1962, 32, 680–687. [Google Scholar] [CrossRef]
- Azzuni, E.; Guzey, S. Behavior of thin elastic circular rings with large deformations under nonuniform loads. J. Press. Vessel. Technol. 2019, 141, 011201. [Google Scholar] [CrossRef]
- Kerdegarbakhsh, M.; Kiani, Y.; Esfahani, S.E.; Eslami, M.R. Postbuckling of FGM rings. Int. J. Mech. Sci. 2014, 85, 187–195. [Google Scholar] [CrossRef]
- Lagrange, R.; Jiménez, F.L.; Terwagne, D.; Brojan, M.; Reis, P. From wrinkling to global buckling of a ring on a curved substrate. J. Mech. Phys. Solids 2016, 89, 77–95. [Google Scholar] [CrossRef][Green Version]
- Thurston, G.A. Application of Newton’s Method to the Postbuckling of Rings under Pressure Loadings; NASA: Washington, DC, USA, 1989. [Google Scholar]
- Sills, L.B.; Budiansky, B. Postbuckling ring analysis. J. App. Mech T ASME 1978, 45, 208–210. [Google Scholar] [CrossRef]
- Asemi, K.; Kiani, Y. Postbuckling up to collapse of polar orthotropic linearly elastic rings subjected to external pressure. Int. J. Struct. Stab. Dyn. 2016, 16, 1450091. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, Z.; Huang, H.; Zhang, H.; Zheng, H.; Kuai, H. Stability of submarine bi-material pipeline-liner system with novel polyhedral composites subjected to thermal and mechanical loading fields. Mar. Struct. 2023, 90, 103424. [Google Scholar] [CrossRef]
- Smith, B.H.; Szyniszewski, S.; Hajjar, J.F.; Schafer, B.W.; Arwade, S.R. Steel foam for structures: A review of applications, manufacturing and material properties. J. Constr. Steel Res. 2012, 71, 1–10. [Google Scholar] [CrossRef][Green Version]
- Lefebvre, L.P.; Banhart, J.; Dunand, D.C. Porous metals and metallic foams: Current status and recent developments. Adv. Eng. Mater. 2008, 10, 775–787. [Google Scholar] [CrossRef][Green Version]
- Babaei, M.; Asemi, K. Stress analysis of functionally graded saturated porous rotating thick truncated cone. Mech. Based Des. Struct. Mach. 2022, 50, 1537–1564. [Google Scholar] [CrossRef]
- Babaei, M.; Kiarasi, F.; Asemi, K.; Dimitri, R.; Tornabene, F. Transient thermal stresses in FG porous rotating truncated cones reinforced by graphene platelets. Appl. Sci. 2022, 12, 3932. [Google Scholar] [CrossRef]
- Kiarasi, F.; Babaei, M.; Asemi, K.; Dimitri, R.; Tornabene, F. Three-dimensional buckling analysis of functionally graded saturated porous rectangular plates under combined loading conditions. Appl. Sci. 2021, 11, 10434. [Google Scholar] [CrossRef]
- Mousavi, S.B.; Amir, S.; Jafari, A.; Arshid, E. Analytical solution for analyzing initial curvature effect on vibrational behavior of PM beams integrated with FGP layers based on trigonometric theories. Adv. Nano Res. 2021, 10, 235–251. [Google Scholar]
- Bouhadra, A.; Menasria, A.; Rachedi, M.A. Boundary conditions effect for buckling analysis of porous functionally graded nanobeam. Adv. Nano Res. 2021, 10, 313–325. [Google Scholar]
- Keleshteri, M.M.; Jelovica, J. Nonlinear vibration analysis of bidirectional porous beams. Eng. Comput. 2022, 38, 5033–5049. [Google Scholar] [CrossRef]
- Beg, M.S.; Khalid, H.M.; Yasin, M.Y.; Hadji, L. Exact third-order static and free vibration analyses of functionally graded porous curved beam. Steel Compos. Struct. Int. J. 2021, 39, 1–20. [Google Scholar]
- Akbaş, Ş.D. Dynamic analysis of axially functionally graded porous beams under a moving load. Steel Compos. Struct. Int. J. 2021, 39, 811–821. [Google Scholar]
- Huang, W.; Tahouneh, V. Frequency study of porous FGPM beam on two-parameter elastic foundations via Timoshenko theory. Steel Compos. Struct. Int. J. 2021, 40, 139–156. [Google Scholar]
- Madenci, E.; Özkılıç, Y.O. Free vibration analysis of open-cell FG porous beams: Analytical, numerical and ANN approaches. Steel Compos. Struct. Int. J. 2021, 40, 157–173. [Google Scholar]
- Rahmani, M.; Mohammadi, Y. Vibration of two types of porous FG sandwich conical shell with different boundary conditions. Struct. Eng. Mech. 2021, 79, 401–413. [Google Scholar]
- Xu, X.; Zhang, C.; Musharavati, F.; Sebaey, T.A.; Khan, A. Wave propagation analysis of porous functionally graded curved beams in the thermal environment. Struct. Eng. Mech. 2021, 79, 665–675. [Google Scholar]
- Farrokh, M.; Taheripur, M. Optimization of porosity distribution of FGP beams considering buckling strength. Struct. Eng. Mech. 2021, 79, 711–722. [Google Scholar]
- Yüksel, Y.Z.; Akbaş, D. Hygrothermal stress analysis of laminated composite porous plates. Struct. Eng. Mech. 2021, 80, 1–13. [Google Scholar]
- Chen, S.X.; Sahmani, S.; Safaei, B. Size-dependent nonlinear bending behavior of porous FGM quasi-3D microplates with a central cutout based on nonlocal strain gradient isogeometric finite element modelling. Eng. Comput. 2021, 37, 1657–1678. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Farazmandnia, N.; Kokaba, M.R.; Mahesh, V. Vibration analysis of porous magneto-electro-elastically actuated carbon nanotube-reinforced composite sandwich plate based on a refined plate theory. Eng. Comput. 2021, 37, 921–936. [Google Scholar] [CrossRef]
- Xia, X.C.; Chen, X.W.; Zhang, Z.; Chen, X.; Zhao, W.M.; Liao, B.; Hur, B. Effects of porosity and pore size on the compressive properties of closed-cell Mg alloy foam. J. Magnes. Alloy. 2013, 1, 330–335. [Google Scholar] [CrossRef][Green Version]
- Jena, S.K.; Chakraverty, S.; Malikan, M. Application of shifted Chebyshev polynomial-based Rayleigh–Ritz method and Navier’s technique for vibration analysis of a functionally graded porous beam embedded in Kerr foundation. Eng. Comput. 2021, 37, 3569–3589. [Google Scholar] [CrossRef]
- Rafiee, M.A.; Rafiee, J.; Wang, Z.; Song, H.; Yu, Z.Z.; Koratkar, N. Enhanced mechanical properties of nanocomposites at low graphene content. ACS Nano 2009, 3, 3884–3890. [Google Scholar] [CrossRef] [PubMed]
- Mittal, G.; Dhand, V.; Rhee, K.Y.; Park, S.J.; Lee, W.R. A review on carbon nanotubes and graphene as fillers in reinforced polymer nanocomposites. J. Ind. Eng. Chem. 2015, 21, 11–25. [Google Scholar] [CrossRef]
- Liew, K.M.; Lei, Z.X.; Zhang, L.W. Mechanical analysis of functionally graded carbon nanotube reinforced composites: A review. Compos. Struct. 2015, 120, 90–97. [Google Scholar] [CrossRef]
- Tornabene, F.; Bacciocchi, M.; Fantuzzi, N.; Reddy, J.N. Multiscale approach for three-phase CNT/polymer/fiber laminated nanocomposite structures. Polym. Compos. 2019, 40, E102–E126. [Google Scholar] [CrossRef]
- Jena, S.K.; Chakraverty, S.; Malikan, M.; Tornabene, F. Effects of surface energy and surface residual stresses on vibro-thermal analysis of chiral, zigzag, and armchair types of SWCNTs using refined beam theory. Mech. Based Des. Struct. Mach. 2022, 50, 1565–1579. [Google Scholar] [CrossRef]
- Zhou, J.; Yao, Z.; Chen, Y.; Wei, D.; Xu, T. Fabrication and mechanical properties of phenolic foam reinforced with graphene oxide. Polym. Compos. 2014, 35, 581–586. [Google Scholar] [CrossRef]
- Dong, Y.H.; Li, Y.H.; Chen, D.; Yang, J. Vibration characteristics of functionally graded graphene reinforced porous nanocomposite cylindrical shells with spinning motion. Compos. Part B Eng. 2018, 145, 1–13. [Google Scholar] [CrossRef]
- Shahgholian-Ghahfarokhi, D.; Rahimi, G.; Khodadadi, A.; Salehipour, H.; Afrand, M. Buckling analyses of FG porous nanocomposite cylindrical shells with graphene platelet reinforcement subjected to uniform external lateral pressure. Mech. Based Des. Struct. Mach. 2019, 49, 1059–1079. [Google Scholar] [CrossRef]
- Shahgholian-Ghahfarokhi, D.; Safarpour, M.; Rahimi, A. Torsional buckling analyses of functionally graded porous nanocomposite cylindrical shells reinforced with graphene platelets (GPLs). Mech. Based Des. Struct. Mach. 2021, 49, 81–102. [Google Scholar] [CrossRef]
- Dong, Y.H.; He, L.W.; Wang, L.; Li, Y.H.; Yang, J. Buckling of spinning functionally graded graphene reinforced porous nanocomposite cylindrical shells: An analytical study. Aerosp. Sci. Technol. 2018, 82, 466–478. [Google Scholar] [CrossRef]
- Chen, D.; Yang, J.; Kitipornchai, S. Nonlinear vibration and postbuckling of functionally graded graphene reinforced porous nanocomposite beams. Compos. Sci. Technol. 2017, 142, 235–245. [Google Scholar] [CrossRef][Green Version]
- Kitipornchai, S.; Chen, D.; Yang, J. Free vibration and elastic buckling of functionally graded porous beams reinforced by graphene platelets. Mater. Des. 2017, 116, 656–665. [Google Scholar] [CrossRef]
- Yang, J.; Chen, D.; Kitipornchai, S. Buckling and free vibration analyses of functionally graded graphene reinforced porous nanocomposite plates based on Chebyshev-Ritz method. Compos. Struct. 2018, 193, 281–294. [Google Scholar] [CrossRef]
- Zhou, Z.; Ni, Y.; Tong, Z.; Zhu, S.; Sun, J.; Xu, X. Accurate nonlinear buckling analysis of functionally graded porous graphene platelet reinforced composite cylindrical shells. Int. J. Mech. Sci. 2019, 151, 537–550. [Google Scholar] [CrossRef]
- Ansari, R.; Hassani, R.; Gholami, R.; Rouhi, H. Buckling and Postbuckling of Plates Made of FG-GPL-Reinforced Porous Nanocomposite with Various Shapes and Boundary Conditions. Int. J. Struct. Stab. Dyn. 2021, 21, 2150063. [Google Scholar] [CrossRef]
- Yaghoobi, H.; Taheri, F. Analytical solution and statistical analysis of buckling capacity of sandwich plates with uniform and non-uniform porous core reinforced with graphene nanoplatelets. Compos. Struct. 2020, 252, 112700. [Google Scholar] [CrossRef]
- Tao, C.; Dai, T. Isogeometric analysis for postbuckling of sandwich cylindrical shell panels with graphene platelet reinforced functionally graded porous core. Compos. Struct. 2021, 260, 113258. [Google Scholar] [CrossRef]
- Nguyen, Q.H.; Nguyen, L.B.; Nguyen, H.B.; Nguyen-Xuan, H. A three-variable high order shear deformation theory for isogeometric free vibration, buckling and instability analysis of FG porous plates reinforced by graphene platelets. Compos. Struct. 2020, 245, 112321. [Google Scholar] [CrossRef]
- Priyanka, R.; Twinkle, C.M.; Pitchaimani, J. Stability and dynamic behavior of porous FGM beam: Influence of graded porosity, graphene platelets, and axially varying loads. Eng. Comput. 2021, 38 (Suppl. S5), 4347–4366. [Google Scholar] [CrossRef]
- Barati, M.R.; Zenkour, A.M. Analysis of postbuckling of graded porous GPL-reinforced beams with geometrical imperfection. Mech. Adv. Mater. Struct. 2019, 26, 503–511. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Q.; Shen, H.; Xiao, X.; Kuai, H.; Zheng, J. Buckling performance of the encased functionally graded porous composite liner with polyhedral shapes reinforced by graphene platelets under external pressure. Thin Walled Struct. 2023, 183, 110370. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, Q.; Zheng, J.; Li, Z. Analytical model for the nonlinear buckling responses of the confined polyhedral FGP-GPLs lining subjected to crown point loading. Eng. Struct. 2023, 282, 115780. [Google Scholar] [CrossRef]
- Xiao, X.; Bu, G.; Ou, Z.; Li, Z. Nonlinear in-plane instability of the confined FGP arches with nanocomposites reinforcement under radially-directed uniform pressure. Eng. Struct. 2022, 252, 113670. [Google Scholar] [CrossRef]
- Anirudh, B.; Ganapathi, M.; Anant, C.; Polit, O. A comprehensive analysis of porous graphene-reinforced curved beams by finite element approach using higher-order structural theory: Bending, vibration and buckling. Compos. Struct. 2019, 222, 110899. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, J. Nonlinear stability of the encased functionally graded porous cylinders reinforced by graphene nanofillers subjected to pressure loading under thermal effect. Compos. Struct. 2020, 233, 111584. [Google Scholar] [CrossRef]
- Bahaadini, R.; Saidi, A.R.; Arabjamaloei, Z.; Ghanbari-Nejad-Parizi, A. Vibration analysis of functionally graded graphene reinforced porous nanocomposite shells. Int. J. Appl. Mech. 2019, 11, 1950068. [Google Scholar] [CrossRef]
- Kiarasi, F.; Babaei, M.; Sarvi, P.; Asemi, K.; Hosseini, M.; Omidi Bidgoli, M. A review on functionally graded porous structures reinforced by graphene platelets. J. Comput. Appl. Mech. 2021, 52, 731–750. [Google Scholar]
- Arshid, E.; Amir, S.; Loghman, A. Thermal buckling analysis of FG graphene nanoplatelets reinforced porous nanocomposite MCST-based annular/circular microplates. Aerosp. Sci. Technol. 2021, 111, 106561. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Mohammadi, K.; Barouti, M.M.; Habibi, M. Wave propagation analysis of a spinning porous graphene nanoplatelet-reinforced nanoshell. Waves Random Complex Media 2021, 31, 1655–1681. [Google Scholar] [CrossRef]
- Arshid, E.; Amir, S.; Loghman, A. Static and dynamic analyses of FG-GNPs reinforced porous nanocomposite annular micro-plates based on MSGT. Int. J. Mech. Sci. 2020, 180, 105656. [Google Scholar] [CrossRef]
- Affdl, J.H.; Kardos, J.L. The Halpin-Tsai equations: A review. Polym. Eng. Sci. 1976, 16, 344–352. [Google Scholar] [CrossRef]
- Adab, N.; Arefi, M.; Amabili, M. A comprehensive vibration analysis of rotating truncated sandwich conical microshells including porous core and GPL-reinforced face-sheets. Compos. Struct. 2022, 279, 114761. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Ezzati, H. A Machine-Learning-Based Model for Buckling Analysis of Thermally Affected Covalently Functionalized Graphene/Epoxy Nanocomposite Beams. Mathematics 2023, 11, 1496. [Google Scholar] [CrossRef]
- Liu, G.R. A step-by-step method of rule-of-mixture of fiber-and particle-reinforced composite materials. Compos. Struct. 1997, 40, 313–322. [Google Scholar] [CrossRef]
- Guo, H.; Yang, T.; Żur, K.K.; Reddy, J.N.; Ferreira, A.J.M. Effect of thermal environment on nonlinear flutter of laminated composite plates reinforced with graphene nanoplatelets. In Modeling and Computation in Vibration Problems, Volume 1: Numerical and Semi-analytical Methods; IOP Publishing: Bristol, UK, 2021. [Google Scholar]
- Babaei, H. Thermomechanical analysis of snap-buckling phenomenon in long FG-CNTRC cylindrical panels resting on nonlinear elastic foundation. Compos. Struct. 2022, 286, 115199. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite Element Procedures; Klaus-Jurgen Bathe: Cambridge, MA, USA, 2006. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Kim, D.; Chaudhuri, R.A. Postbuckling of moderately thick imperfect rings under external pressure. J. Eng. Mech. 2006, 132, 1273–1276. [Google Scholar] [CrossRef]





| 0.1 | 0.1738 | 0.9361 |
| 0.2 | 0.3442 | 0.8716 |
| 0.3 | 0.5103 | 0.8064 |
| 0.4 | 0.6708 | 0.7404 |
| 0.5 | 0.8231 | 0.6733 |
| 0.6 | 0.9612 | 0.6047 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bi, S.; Zhang, E.; Babaei, M.; Tornabene, F.; Dimitri, R. The Influence of GPL Reinforcements on the Post-Buckling Behavior of FG Porous Rings Subjected to an External Pressure. Mathematics 2023, 11, 2421. https://doi.org/10.3390/math11112421
Bi S, Zhang E, Babaei M, Tornabene F, Dimitri R. The Influence of GPL Reinforcements on the Post-Buckling Behavior of FG Porous Rings Subjected to an External Pressure. Mathematics. 2023; 11(11):2421. https://doi.org/10.3390/math11112421
Chicago/Turabian StyleBi, Shaoping, Enming Zhang, Masoud Babaei, Francesco Tornabene, and Rossana Dimitri. 2023. "The Influence of GPL Reinforcements on the Post-Buckling Behavior of FG Porous Rings Subjected to an External Pressure" Mathematics 11, no. 11: 2421. https://doi.org/10.3390/math11112421
APA StyleBi, S., Zhang, E., Babaei, M., Tornabene, F., & Dimitri, R. (2023). The Influence of GPL Reinforcements on the Post-Buckling Behavior of FG Porous Rings Subjected to an External Pressure. Mathematics, 11(11), 2421. https://doi.org/10.3390/math11112421








