Modeling of Viral Infection with Inflammation
Abstract
:1. Introduction
1.1. Inflammation in Viral Infections
1.2. Mathematical Modeling of Viral Infections
2. Analysis of the Model
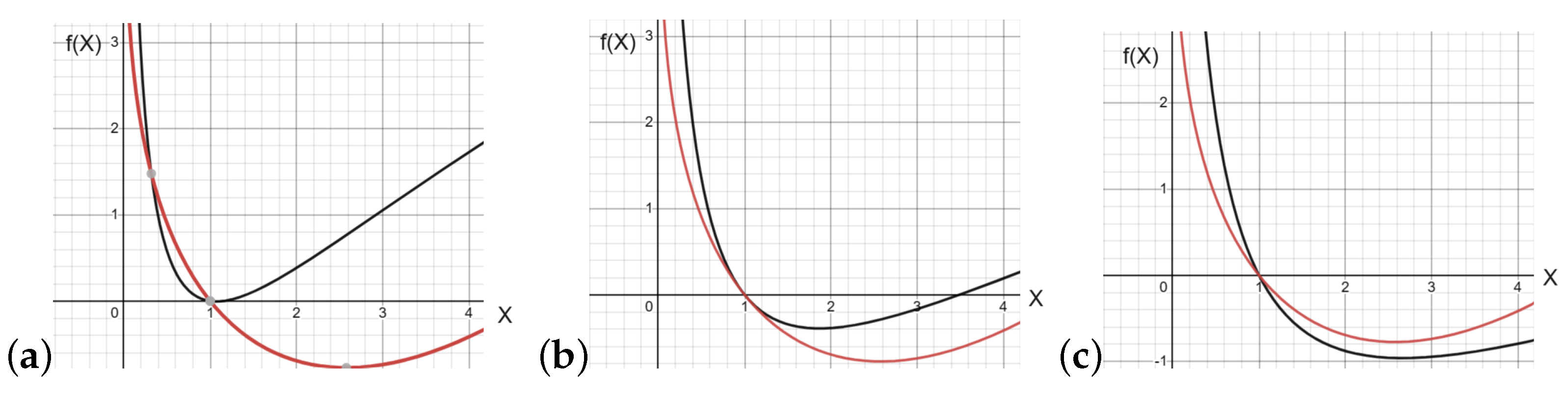
2.1. Stationary Points
2.2. Wave Propagation
- Without degradation of inflammatory cytokines.
- With degradation of inflammatory cytokines.
2.3. Wave Speed
- Simplification.
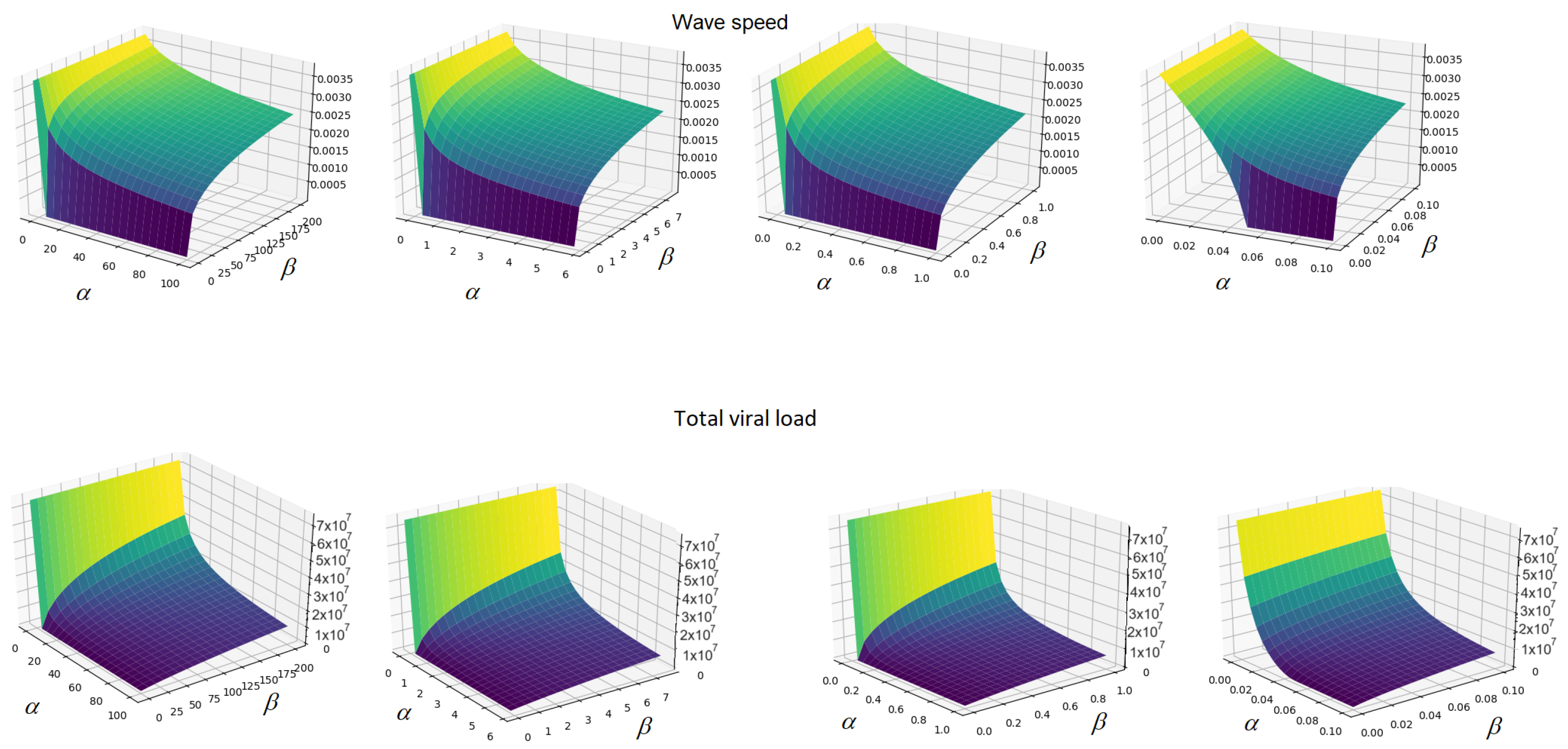
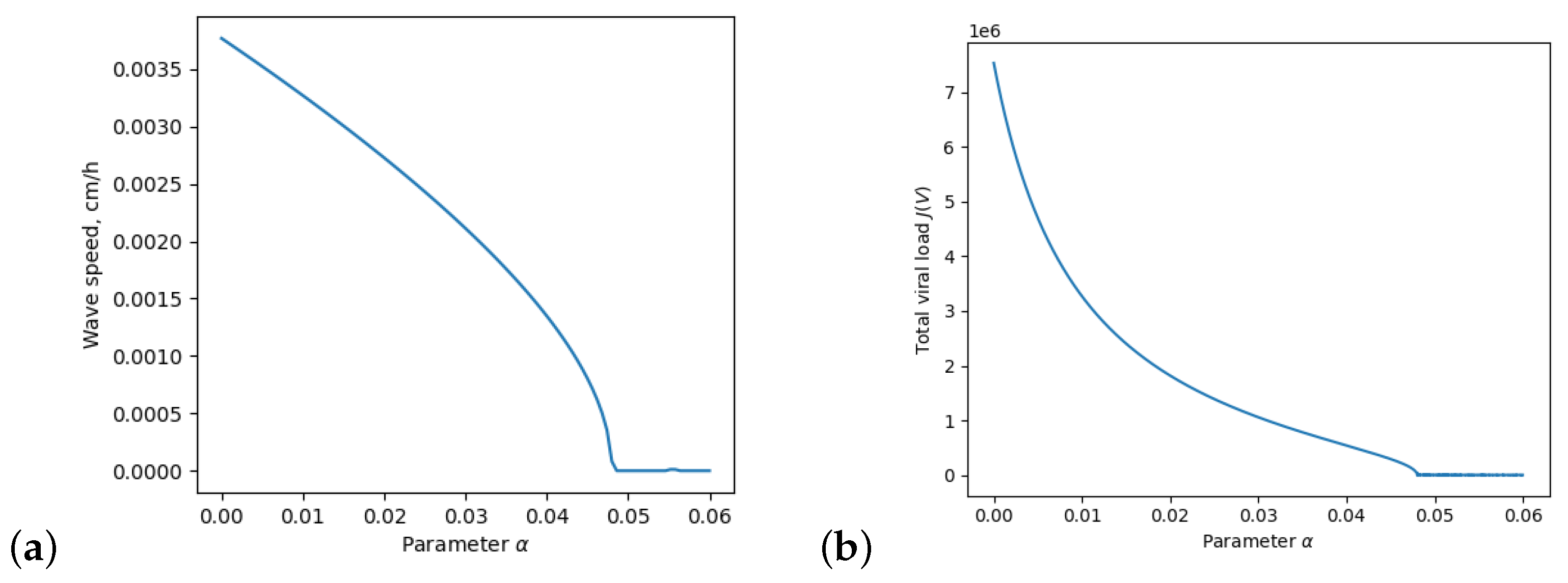
3. Dependence on the Inflammation Parameters
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Values of Parameters
Appendix B. Spatial Discretization
Appendix C. Derivation of Equation (23)
References
- Nguyen, L.N.; Kanneganti, T.-D. PANoposis in Viral Infection: The Missing Puzzle Piece in the Cell Death Field. J. Mol. Biol. 2021, 434, 167249. [Google Scholar] [CrossRef]
- Medzhitov, R. Recognition of microorganisms and activation of the immune response. Nature 2007, 449, 819–826. [Google Scholar] [CrossRef]
- Medzhitov, R.; Janeway, C.A. Innate immunity: Impact on the adaptive immune response. Curr. Opin. Immunol. 1997, 9, 4–9. [Google Scholar] [CrossRef] [PubMed]
- Carty, M.; Guy, C.; Bowie, A.G. Detection of viral infections by innate immunity. Biochem. Pharmacol. 2020, 183, 114316. [Google Scholar] [CrossRef] [PubMed]
- Place, D.E.; Lee, S.; Kanneganti, T.D. PANoptosis in microbial infection. Curr. Opin. Microbiol. 2021, 59, 42–49. [Google Scholar] [CrossRef]
- Fajgenbaum, D.C.; June, C.H. Cytokine Storm. N. Engl. J. Med. 2020, 383, 2255–2273. [Google Scholar] [CrossRef] [PubMed]
- Karki, R.K. The ‘cytokine storm’: Molecular mechanisms and therapeutic prospects. Trends Immunol. 2021, 42, 681–705. [Google Scholar] [CrossRef] [PubMed]
- Leon, C.; Tokarev, A.; Bouchnita, A.; Volpert, V. Modelling of the Innate and Adaptive Immune Response to SARS Viral Infection, Cytokine Storm and Vaccination. Vaccines 2023, 11, 127. [Google Scholar] [CrossRef]
- Funk, G.A.; Jansen, V.A.A.; Bonhoeffer, S.; Killingback, T. Spatial models of virus-immune dynamics. J. Theor. Biol. 2005, 233, 221–236. [Google Scholar] [CrossRef]
- Labadie, M.; Marciniak-Czochra, A. A Reaction-Diffusion Model for Viral Infection and Immune Response. Preprint, 2011, fhal-00546034v2. Available online: http://hal.archives-ouvertes.fr (accessed on 1 August 2023).
- Rodriguez-Brenes, I.A.; Hofacre, A.; Fan, H.; Wodarz, D. Complex Dynamics of Virus Spread from Low Infection Multiplicities: Implications for the Spread of Oncolytic Viruses. PLoS Comput. Biol. 2017, 13, e1005241. [Google Scholar] [CrossRef] [PubMed]
- Graziano, F.M.; Kettoola, S.Y.; Munshower, J.M.; Stapleton, J.T.; Towfic, G.J. Effect of spatial distribution of T-Cells and HIV load on HIV progression. Bioinformatics 2008, 24, 855–860. [Google Scholar] [CrossRef] [PubMed]
- Grebennikov, D.; Karsonova, A.; Loguinova, M.; Casella, V.; Meyerhans, A.; Bocharov, G. Predicting the Kinetic Coordination of Immune Response Dynamics in SARS-CoV-2 Infection: Implications for Disease Pathogenesis. Mathematics 2022, 10, 3154. [Google Scholar] [CrossRef]
- Chhetri, B.; Bhagat, V.M.; Vamsi, D.K.K.; Ananth, V.S.; Prakash, B.D.; Mandale, R.; Muthusamy, S.; Sanjeevi, C.B. Within-host mathematical modeling on crucial inflammatory mediators and drug interventions in COVID-19 identifies combination therapy to be most effective and optimal. Alex. Eng. J. 2021, 60, 2491–2512. [Google Scholar] [CrossRef]
- Fadai, N.T.; Sachak-Patwa, R.; Byrne, H.M.; Maini, P.K.; Bafadhel, M.; Nicolau, D.V. Infection, inflammation and intervention: Mechanistic modelling of epithelial cells in COVID-19. J. R. Soc. Interface 2021, 18, 175. [Google Scholar] [CrossRef]
- Vodovotz, Y.; Clermont, G.; Chow, C.; An, G. Mathematical models of the acute inflammatory response. Curr. Opin. Crit. Care 2004, 10, 383–390. [Google Scholar] [CrossRef]
- Minucci, S.B.; Heise, R.L.; Reynolds, A.M. Review of Mathematical Modeling of the Inflammatory Response in Lung Infections and Injuries. Front. Appl. Math. Stat. 2020, 6, 36. [Google Scholar] [CrossRef]
- Ait Mahiout, L.; Bessonov, N.; Kazmierczak, B.; Sadaka, G.; Volpert, V. Infection spreading in cell culture as a reaction-diffusion wave. ESAIM Math. Model. Numer. Anal. 2022, 56, 791–814. [Google Scholar] [CrossRef]
- Ait Mahiout, L.; Mozokhina, A.; Tokarev, A.; Volpert, V. Virus Replication And Competition In A Cell Culture: Application to the SARS-CoV-2 Variants. Appl. Math. Lett. 2022, 133, 108217. [Google Scholar] [CrossRef]
- Tokarev, A.; Mozokhina, A.; Volpert, V. Competition of SARS-CoV-2 Variants in Cell Culture and Tissue: Wins the Fastest Viral Autowave. Vaccines 2022, 10, 995. [Google Scholar] [CrossRef]
- Ait Mahiout, L.; Mozokhina, A.; Tokarev, A.; Volpert, V. The Influence of Immune Response on Spreading of Viral Infection. Lobachevskii J. Math. 2022, 43, 2699–2713. [Google Scholar] [CrossRef]
- Bessonov, N.; Bocharov, G.; Mozokhina, A.; Volpert, V. Viral Infection Spreading in Cell Culture with Intracellular Regulation. Mathematics 2023, 11, 1526. [Google Scholar] [CrossRef]
- Bessonov, N.; Volpert, V. Airway obstruction in respiratory viral infections due to impaired mucociliary clearance. Int. J. Numer. Methods Biomed. Eng. 2023, e3707. [Google Scholar] [CrossRef] [PubMed]
- Volpert, A.; Volpert, V.; Volpert, V. Traveling Wave Solutions of Parabolic Systems; American Mathematical Society: Providence, RI, USA, 1994. [Google Scholar]
- Hecht, F.; Auliac, S.; Pironneau, O.; Morice, J.; Le Hyaric, A.; Ohtsuka, K. Freefem++ (Manual). 2007. Available online: www.freefem.org (accessed on 10 September 2023).
- Nathanson, N.; Gonzalez-Scarano, F. Chapter 7 Patterns of Infection. In Viral Pathogenesis, 3rd ed.; Academic Press: Boston, MA, USA, 2016; p. 81. [Google Scholar] [CrossRef]
- Reis, R.F.; Pigozzo, A.; Bonin, C.R.B.; Quintela, B.M.; Pompei, L.T.; Vieira, A.C.; de Lima e Silva, L.; Xavier, M.P.; dos Santos, R.W.; Lobosco, M. A Validated Mathematical Model of the Cytokine Release Syndrome in Severe COVID-19. Front. Mol. Biosci. 2021, 8, 639423. [Google Scholar] [CrossRef] [PubMed]
- Friedman, A.; Turner, J.; Szomolay, B. A model on the influence of age on immunity to infection with Mycobacterium tuberculosis. Exp. Gerontol. 2008, 43, 275–285. [Google Scholar] [CrossRef]
- Abi Younes, G.; El Khatib, N. Mathematical modeling of inflammatory processes of atherosclerosis. Math. Model. Nat. Phenom. 2022, 17, 5. [Google Scholar] [CrossRef]
- El Hajj, W.; El Khatib, N.; Volpert, V. Inflammation propagation modeled as a reaction–diffusion wave. Math. Biosci. 2023, 365, 109074. [Google Scholar] [CrossRef]
- de Klaver, M.; Manning, L.; Palmer, L.; Rich, G. Isoflurane pretreatment inhibits cytokine-induced cell death in cultured rat smooth muscle cells and human endothelial cells. Anesthesiology 2002, 97, 24–32. [Google Scholar] [CrossRef]
- Altan- Bonnet, G.; Mukherjee, R. Cytokine- mediated communication: A quantitative appraisal of immune complexity. Nat. Rev. Immunol. 2019, 19, 205–217. [Google Scholar] [CrossRef]
- Höfer, T.; Krichevsky, O.; Altan-Bonnet, G. Competition for IL-2 between regulatory and effectorT cells to chisel immune responses. Front. Immunol. 2012, 3, 268. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mozokhina, A.; Ait Mahiout, L.; Volpert, V. Modeling of Viral Infection with Inflammation. Mathematics 2023, 11, 4095. https://doi.org/10.3390/math11194095
Mozokhina A, Ait Mahiout L, Volpert V. Modeling of Viral Infection with Inflammation. Mathematics. 2023; 11(19):4095. https://doi.org/10.3390/math11194095
Chicago/Turabian StyleMozokhina, Anastasia, Latifa Ait Mahiout, and Vitaly Volpert. 2023. "Modeling of Viral Infection with Inflammation" Mathematics 11, no. 19: 4095. https://doi.org/10.3390/math11194095
APA StyleMozokhina, A., Ait Mahiout, L., & Volpert, V. (2023). Modeling of Viral Infection with Inflammation. Mathematics, 11(19), 4095. https://doi.org/10.3390/math11194095







